Comparison of Searching Behaviour of Three Evolutionary Algorithms Applied to Water Distribution System Design Optimization
Abstract
1. Introduction
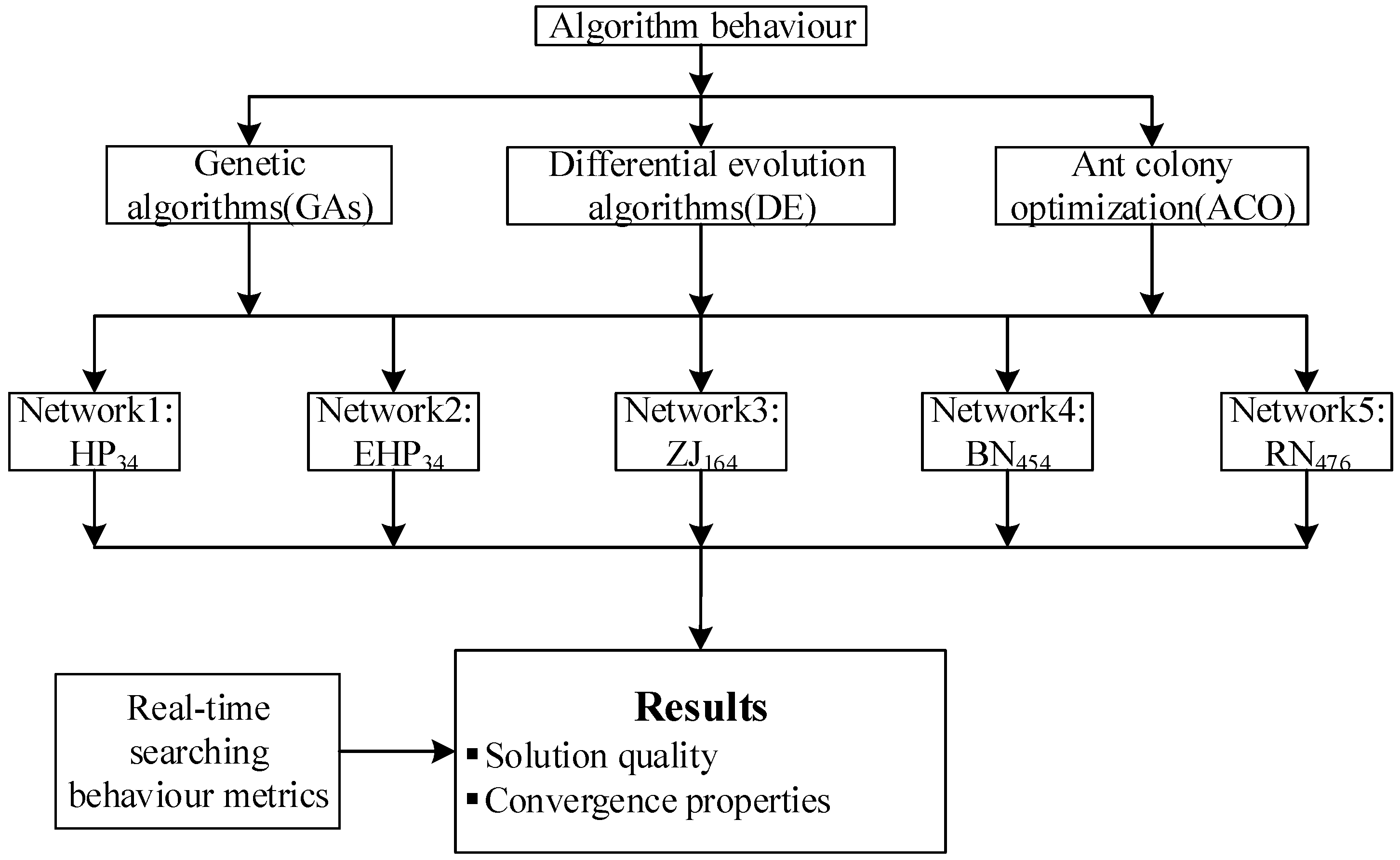
2. Methodology
2.1. Evolutionary Algorithms and Their Parameterization
2.2. Case Studies
3. Searching Measure Metrics
3.1. Search Quality Measure Metrics
3.2. Convergence Measure Metrics
4. Case Study Results and Discussion
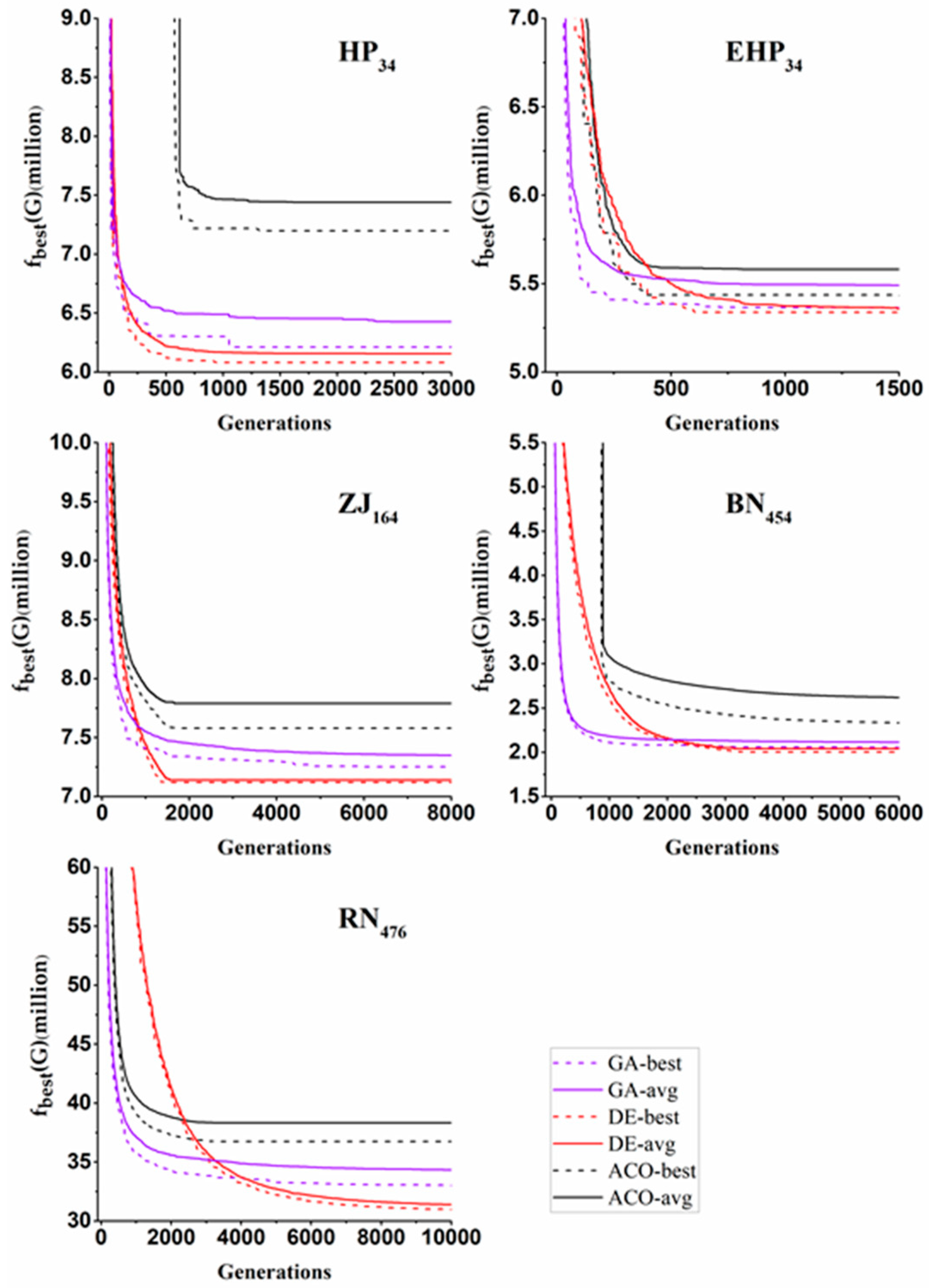
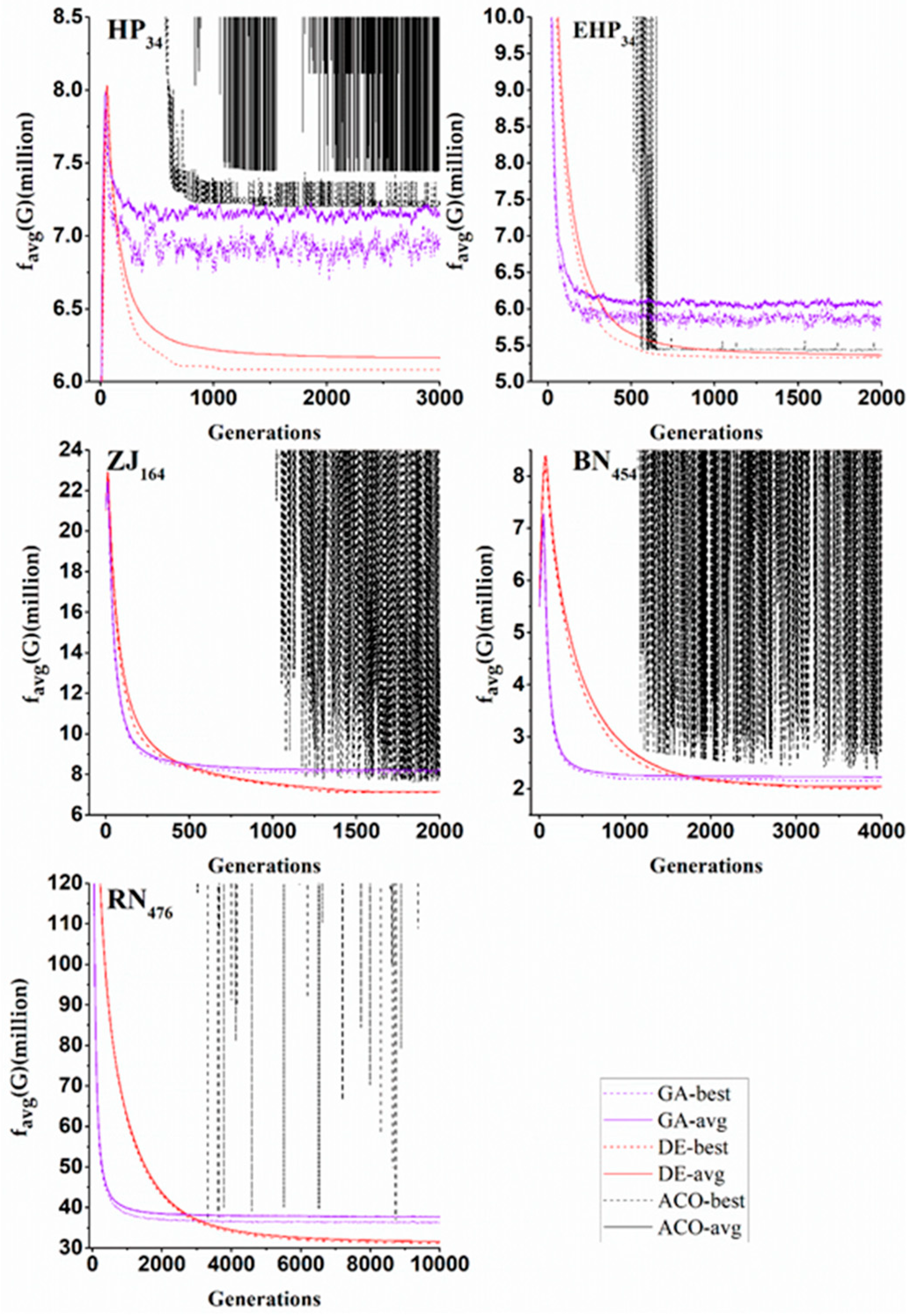
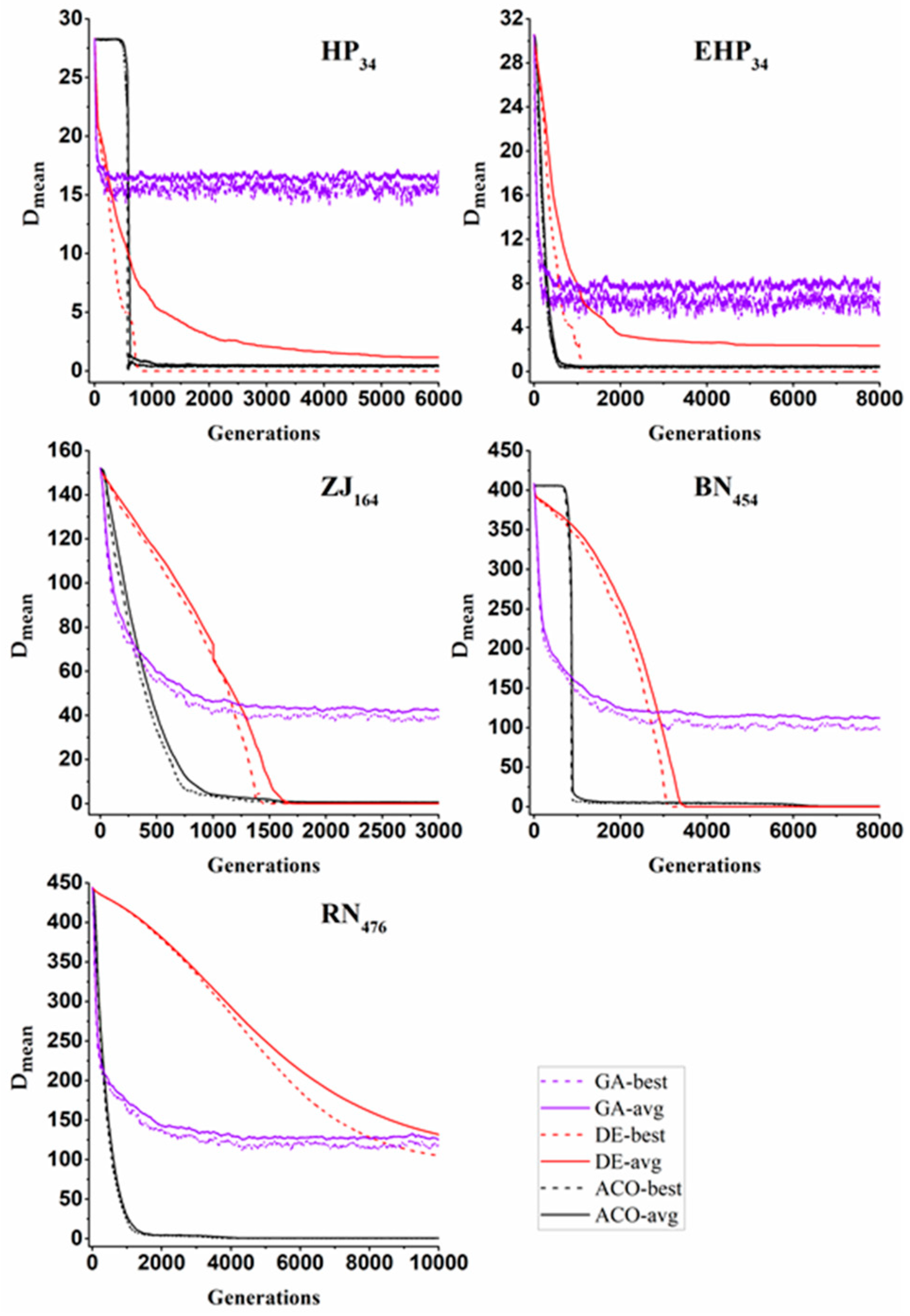
4.1. Search Quality Results
4.2. Convergence Measure Results
4.3. Solution Comparisons
5. Conclusions
- The three EAs have exhibited significantly different searching behaviours in both the solution space and decision space. Such differences can be related to their underlying model structures and the searching mechanisms. This demonstrates that the proposed run-time metrics are effective in revealing the searching properties of the EAs.
- From the obtained real-time metric results, it can be concluded that the DE has an overall best ability to locate feasible solutions as well as high quality solutions for the WDS design problems. The ACO performed overall the worst in identifying the optimal solutions as observed in this study. This provides a guideline for the selection of the algorithms for WDS design optimization.
- If the computational budget is rather limited, the GA can identify better solutions than the DE as shown in this study. This suggests that the GA is promising for the case when the optimization solution needs to be identified in a short time such as real-time WDS operation and management.
Author Contributions
Funding
Conflicts of Interest
References
- Maier, H.R.; Kapelan, Z.; Kasprzyk, J.; Kollat, J.; Matott, L.S.; Cunha, M.C.; Dandy, G.C.; Gibbs, M.S.; Keedwell, E.; Marchi, A.; et al. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions. Environ. Model. Softw. 2014, 62, 271–299. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savic, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; Karamouz, M.; Minsker, B.; Ostfeld, A.; Singh, A.; et al. State of the art for genetic algorithms and beyond in water resources planning and management. J. Water Resour. Plan. Manag. 2010, 136, 412–432. [Google Scholar] [CrossRef]
- El-Ghandour, H.A.; Elbeltagi, E. Comparison of five evolutionary algorithms for optimization of water distribution networks. J. Comput. Civ. Eng. 2018, 32, 04017066. [Google Scholar] [CrossRef]
- Monsef, H.; Naghashzadegan, M.; Jamali, A.; Farmani, R. Comparison of evolutionary multi objective optimization algorithms in optimum design of water distribution network. Ain Shams Eng. J. 2019, 10, 103–111. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Ballesteros-Pérez, P. Efficiency of evolutionary algorithms in water network pipe sizing. Water Resour. Manag. 2015, 29, 4817–4831. [Google Scholar] [CrossRef]
- Guercio, R.; Xu, Z. Linearized optimization model for reliability-based design of water systems. J. Hydraul. Eng. 1997, 123, 1020–1026. [Google Scholar] [CrossRef]
- Sonak, V.V.; Bhave, P.R. Global optimum tree solution for single-source looped water distribution networks subjected to a single loading pattern. Water Resour. Res. 1993, 29, 2437–2443. [Google Scholar] [CrossRef]
- Fujiwara, O.; Khang, D.B. A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour. Res. 1990, 26, 539–549. [Google Scholar] [CrossRef]
- Lansey, K.E.; Mays, L.W. Optimization model for water distribution system design. J. Hydraul. Eng. 1989, 115, 1401–1418. [Google Scholar] [CrossRef]
- Maier, H.R.; Kapelan, Z.; Kasprzyk, J.; Matott, L.S. Thematic issue on evolutionary algorithms in water resources. Environ. Model. Softw. 2015, 69, 222–225. [Google Scholar] [CrossRef][Green Version]
- Ji, C.; Jiang, Z.; Sun, P.; Zhang, Y.; Wang, L. Research and application of multidimensional dynamic programming in cascade reservoirs based on multilayer nested structure. J. Water Resour. Plan. Manag. 2015, 141, 04014090. [Google Scholar] [CrossRef]
- Zheng, F. Comparing the real-time searching behavior of four differential-evolution variants applied to water-distribution-network design optimization. J. Water Resour. Plan. Manag. 2015, 141. [Google Scholar] [CrossRef]
- Bi, W.; Maier, H.R.; Dandy, G.C. Impact of starting position and searching mechanism on the evolutionary algorithm convergence rate. J. Water Resour. Plan. Manag. 2016, 142, 04016026. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Zheng, F.; Zecchin, A.C.; Simpson, A.R.; Lambert, M.F. Noncrossover dither creeping mutation-based genetic algorithm for pipe network optimization. J. Water Resour. Plan. Manag. 2014, 140, 553–557. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C. A decomposition and multistage optimization approach applied to the optimization of water distribution systems with multiple supply sources. Water Resour. Res. 2013, 49, 380–399. [Google Scholar] [CrossRef]
- Reca, J.; Martínez, J. Genetic algorithms for the design of looped irrigation water distribution networks. Water Resour. Res. 2006, 42, W05416. [Google Scholar] [CrossRef]
- Mambretti, S. Optimization of the pumping station of the milano water supply network with genetic algorithms. In Energy and Sustainability III; WIT Press: Southampton, UK, 2011; pp. 185–194. [Google Scholar]
- Li, M.; Liu, S.; Zhang, L.; Wang, H.; Meng, F.; Bai, L. Non-dominated sorting genetic algorithms-iibased on multi-objective optimization model in the water distribution system. Procedia Eng. 2012, 37, 309–313. [Google Scholar] [CrossRef]
- Suribabu, C.R. Differential evolution algorithm for optimal design of water distribution networks. J. Hydroinform. 2010, 12, 66–82. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A. An efficient decomposition and dual-stage multi-objective optimization method for water distribution systems with multiple supply sources. Environ. Model. Softw. 2014, 55, 143–155. [Google Scholar] [CrossRef]
- Maier, H.R.; Simpson, A.R.; Zecchin, A.C.; Foong, W.K.; Phang, K.Y.; Seah, H.Y.; Tan, C.L. Ant colony optimization for design of water distribution systems. J. Water Resour. Plan. Manag. 2003, 129, 200–209. [Google Scholar] [CrossRef]
- Szemis, J.M.; Maier, H.R.; Dandy, G.C. A framework for using ant colony optimization to schedule environmental flow management alternatives for rivers, wetlands, and floodplains. Water Resour. Res. 2012, 48, W08502. [Google Scholar] [CrossRef]
- Szemis, J.M.; Maier, H.R.; Dandy, G.C. An adaptive ant colony optimization framework for scheduling environmental flow management alternatives under varied environmental water availability conditions. Water Resour. Res. 2014, 50, 7606–7625. [Google Scholar] [CrossRef]
- Nguyen, D.C.H.; Maier, H.R.; Dandy, G.C.; Ascough, J.C. Framework for computationally efficient optimal crop and water allocation using ant colony optimization. Environ. Model. Softw. 2016, 76, 37–53. [Google Scholar] [CrossRef]
- Nguyen, D.C.H.; Ascough, J.C.; Maier, H.R.; Dandy, G.C.; Andales, A.A. Optimization of irrigation scheduling using ant colony algorithms and an advanced cropping system model. Environ. Model. Softw. 2017, 97, 32–45. [Google Scholar] [CrossRef]
- Foong, W.K.; Maier, H.R.; Simpson, A.R. Power plant maintenance scheduling using ant colony optimization: An improved formulation. Eng. Optim. 2008, 40, 309–329. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R.; Nixon, J.B. Parametric study for an ant algorithm applied to water distribution system optimization. IEEE Trans. Evol. Comput. 2005, 9, 175–191. [Google Scholar] [CrossRef]
- Zecchin, A.C.; Simpson, A.R.; Maier, H.R.; Marchi, A.; Nixon, J.B. Improved understanding of the searching behavior of ant colony optimization algorithms applied to the water distribution design problem. Water Resour. Res. 2012, 48, W09505. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.C.; Newman, J.P.; Maier, H.R.; Dandy, G.C. An adaptive convergence-trajectory controlled ant colony optimization algorithm with application to water distribution system design problems. IEEE Trans. Evol. Comput. 2017, 21, 773–791. [Google Scholar] [CrossRef]
- Yazdi, J.; Choi, Y.H.; Kim, J.H. Non-dominated sorting harmony search differential evolution (ns-hs-de): A hybrid algorithm for multi-objective design of water distribution networks. Water 2017, 9, 587. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.C.; Maier, H.R.; Simpson, A.R. Comparison of the searching behavior of nsga-ii, samode, and borg moeas applied to water distribution system design problems. J. Water Resour. Plan. Manag. 2016, 142, 04016017. [Google Scholar] [CrossRef]
- Simpson, A.R.; Dandy, G.C.; Murphy, L.J. Genetic algorithms compared to other techniques for pipe optimization. J. Water Resour. Plan. Manag. 1994, 120, 423–443. [Google Scholar] [CrossRef]
- Bi, W.; Dandy, G.C.; Maier, H.R. Improved genetic algorithm optimization of water distribution system design by incorporating domain knowledge. Environ. Model. Softw. 2015, 69, 370–381. [Google Scholar] [CrossRef]
- Zheng, F.; Zecchin, A.C.; Simpson, A.R. Investigating the run-time searching behavior of the differential evolution algorithm applied to water distribution system optimization. Environ. Model. Softw. 2015, 69, 292–307. [Google Scholar] [CrossRef]
- Zheng, F.; Simpson, A.R.; Zecchin, A.C. A combined nlp-differential evolution algorithm approach for the optimization of looped water distribution systems. Water Resour. Res. 2011, 47, W08531. [Google Scholar] [CrossRef]
- Marchi, A.; Dandy, G.; Wilkins, A.; Rohrlach, H. Methodology for comparing evolutionary algorithms for optimization of water distribution systems. J. Water Resour. Plan. Manag. 2014, 140, 22–31. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (cma-es). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Beyer, H.G. Self-adaptive genetic algorithms with simulated binary crossover. Evol. Comput. 2001, 9, 197–221. [Google Scholar] [CrossRef]


| The Algorithm Name | Parameters of Each Algorithm | Parameter Values for Five Different Case Studies | ||||
|---|---|---|---|---|---|---|
| Hanoi (HP) | Extend Hanoi (EHP) | ZJ | Balerma (BN) | Rural Network (RN) | ||
| ACO | 100 | 100 | 500 | 500 | 500 | |
| 1 | 1 | 1 | 1 | 1 | ||
| 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | ||
| 5 | 5 | 5 | 5 | 5 | ||
| DE | 100 | 100 | 500 | 1000 | 1000 | |
| 0.5 | 0.5 | 0.3 | 0.3 | 0.3 | ||
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | ||
| GA | 100 | 100 | 500 | 1000 | 1000 | |
| 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | ||
| 0.02 | 0.02 | 0.06 | 0.02 | 0.02 | ||
| Case Study | No. of Decision Variables | No. of Diameter Options | Size of Total Search Space | Pressure Head Constraint | Reference |
|---|---|---|---|---|---|
| Hanoi (HP) | 34 | 6 | [8] | ||
| Extend Hanoi (EHP) | 34 | 10 | [34] | ||
| ZJ | 164 | 14 | [36] | ||
| Balerma (BN) | 454 | 10 | [17] | ||
| Rural network (RN) | 476 | 15 | [37] |
| Case Studies | Current Best Known Solution | GA | DE | ACO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best Solution | Worst Solution | Average Cost | Best Solution | Worst Solution | Average Cost | Best Solution | Worst Solution | Average Cost | ||
| Hanoi (HP) ($M) | 6.081 [17] | 6.174 (1.5%) | 6.560 | 6.395 | 6.081 (0%) | 6.329 | 6.155 | 7.198 (18.4%) | 7.761 | 7.440 |
| Extend Hanoi (EHP) ($M) | 5.346 [34] | 5.357 (0.2%) | 5.616 | 5.460 | 5.338 (−0.2%) | 5.364 | 5.341 | 5.432 (1.6%) | 5.718 | 5.582 |
| ZJ ($M) | 7.082 [36] | 7.248 (2.3%) | 7.509 | 7.345 | 7.125 (0.6%) | 7.176 | 7.140 | 7.579 (7.0%) | 8.0362 | 7.787 |
| Balerma (BN) (€M) | 1.923 [36] | 2.045 (6.3%) | 2.152 | 2.103 | 2.002 (4.1%) | 2.075 | 2.040 | 2.332 (21.3%) | 2.846 | 2.618 |
| Rural Network (RN) ($M) | 31.220 [37] | 33.010 (5.7%) | 35.821 | 34.332 | 30.989 (−0.7%) | 31.776 | 31.396 | 36.737 (17.7%) | 39.963 | 38.332 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, W.; Xu, Y.; Wang, H. Comparison of Searching Behaviour of Three Evolutionary Algorithms Applied to Water Distribution System Design Optimization. Water 2020, 12, 695. https://doi.org/10.3390/w12030695
Bi W, Xu Y, Wang H. Comparison of Searching Behaviour of Three Evolutionary Algorithms Applied to Water Distribution System Design Optimization. Water. 2020; 12(3):695. https://doi.org/10.3390/w12030695
Chicago/Turabian StyleBi, Weiwei, Yihui Xu, and Hongyu Wang. 2020. "Comparison of Searching Behaviour of Three Evolutionary Algorithms Applied to Water Distribution System Design Optimization" Water 12, no. 3: 695. https://doi.org/10.3390/w12030695
APA StyleBi, W., Xu, Y., & Wang, H. (2020). Comparison of Searching Behaviour of Three Evolutionary Algorithms Applied to Water Distribution System Design Optimization. Water, 12(3), 695. https://doi.org/10.3390/w12030695




