Abstract
Agricultural intensification has stimulated the economy in the Guayas River basin in Ecuador, but also affected several ecosystems. The increased use of pesticides poses a serious threat to the freshwater ecosystem, which urgently calls for an improved knowledge about the impact of pesticide practices in this study area. Several studies have shown that models can be appropriate tools to simulate pesticide dynamics in order to obtain this knowledge. This study tested the suitability of the Soil and Water Assessment Tool (SWAT) to simulate the dynamics of two different pesticides in the data scarce Guayas River basin. First, we set up, calibrated and validated the model using the streamflow data. Subsequently, we set up the model for the simulation of the selected pesticides (i.e., pendimethalin and fenpropimorph). While the hydrology was represented soundly by the model considering the data scare conditions, the simulation of the pesticides should be taken with care due to uncertainties behind essential drivers, e.g., application rates. Among the insights obtained from the pesticide simulations are the identification of critical zones for prioritisation, the dominant areas of pesticide sources and the impact of the different land uses. SWAT has been evaluated to be a suitable tool to investigate the impact of pesticide use under data scarcity in the Guayas River basin. The strengths of SWAT are its semi-distributed structure, availability of extensive online documentation, internal pesticide databases and user support while the limitations are high data requirements, time-intensive model development and challenging streamflow calibration. The results can also be helpful to design future water quality monitoring strategies. However, for future studies, we highly recommend extended monitoring of pesticide concentrations and sediment loads. Moreover, to substantially improve the model performance, the availability of better input data is needed such as higher resolution soil maps, more accurate pesticide application rate and actual land management programs. Provided that key suggestions for further improvement are considered, the model is valuable for applications in river ecosystem management of the Guayas River basin.
1. Introduction
Agricultural intensification in South America is leading to severe pollution of the river ecosystems by pesticides [1,2,3]. An example of this is the Guayas River basin in Ecuador wherein key ecosystems are at risk due to an increased application of pesticides. The current intensification of the human activities within the basin (agriculture, fishery, hydropower and industry) is a severe threat to the aquatic ecosystem and causes the impairment of many important ecosystem services, including habitat provision (affecting biodiversity), water provision and the safety of potable water [4,5,6]. Moreover, the changes in tillage practices negatively affected pesticide adsorption and have caused an increasing degradation of soils. Reported effects of pesticides in surface water are the reduction of activity and reproduction and biomass of aquatic organisms [7]. The use of pesticides in developing countries is especially of concern because of weak legislation, the use of highly hazardous pesticides and the lack of adequate information [8,9]. The reduction of the current anthropogenic pressure on freshwater resources requires the development and application of effective tools that provide insight into pollutant transport, even under data-poor conditions. Computer models, simulating the system’s hydrology, sediment transport and ultimately pesticide dynamics can be of use in this situation.
There is a wide variety of models simulating surface water pesticide concentrations, ranging from simple, data-driven tools to complex watershed models [10,11]. These models differ in scale, model complexity, input data requirements and spatial and temporal output detail [12]. Studying the effect of pesticide application on water quality at the watershed scale requires a long-term hydrological watershed model that includes a land use and management module and provides sufficient spatial detail [13]. The flows simulated by the hydrological model can be used to estimate pesticide transport and dilution processes, at a temporal resolution that captures the dynamic character of pesticide concentrations. Such a model allows an extensive analysis of a given system, enabling to pinpoint major polluting sources, priority areas, main transfer pathways and data gaps. Moreover, it allows an assessment of water quality parameters (e.g., distributed pollutant fluxes) and provides valuable insights for monitoring campaigns [14]. It also allows comparing different scenarios (e.g., best management practices and land use) and supports cost–benefit analyses [11,15]. Hence, these models are valuable tools to get an understanding of system functioning and to support decision making. Especially in developing countries, the application of these models can be beneficial to provide insights into the spatial and temporal impact of pesticide application on ecosystems. However, data scarcity in many developing countries hinders the simulation of pesticide dynamics. Therefore, the aim of this study was to investigate whether these watershed models have the potential to provide valuable insights into the pesticide dynamics under data scarcity.
To answer this question, a benchmarking study of potentially useful non-point source pollution watershed models was carried out (see Section 2 and Section A.1, Tables SA1 and SA2 in Supplementary A). As a result, the Soil and Water Assessment Tool (SWAT) was considered as potentially suitable for a simulation of the pesticide dynamics in the Guayas River case study. The SWAT literature database [16] shows that 79 papers dealing with pesticide simulations were published between 1998 and 2018. In this study, the model was applied to simulate pesticide fate in the Guayas River basin, the largest watershed and main agricultural region in Ecuador. We investigated: (1) the main data gaps of the basin; (2) the ability of SWAT to reflect the hydrologic processes in the basin; and (3) opportunities and limitations of the model to simulate pesticide dynamics under data scarcity.
2. Materials and Methods
2.1. Study Area
Due to its size, high agricultural productivity and economic contributions, the Guayas River basin is the most important watershed of the coastal region in Ecuador. It has a drainage area of approximately 34,000 km2 and a population of 4.8 million inhabitants [17,18]. The basin is located in the central, western part of the country (Figure 1a) and is characterised by a wide variation in elevation, ranging 0–6310 m a.s.l. wherein 46% of the basin’s surface is lower than 200 m a.s.l. [19]. The basin has a humid tropical climate with a rainy season from December to May with an average annual precipitation of 1849 mm. The mean precipitation during the rainy season is 1130 mm [19] and the mean temperature varies between 22 and 27 °C [20]. The two main tributaries of the basin are the Daule and Babahoyo Rivers, forming the Guayas River at their confluence. The average discharge at the outlet of the basin is 974 m3 [21]. The soil types of the basin consist of 23% loam, 20% clay loam, 15.3% sandy loam and 41.6% other types (e.g., heavy clay, sand and sandy loam). In the northern part of the basin, a dam is constructed at the Daule River (Figure 1b, Point 1). This dam, named Daule Peripa, is built for hydropower generation, irrigation, drinking water and river control purposes [17].
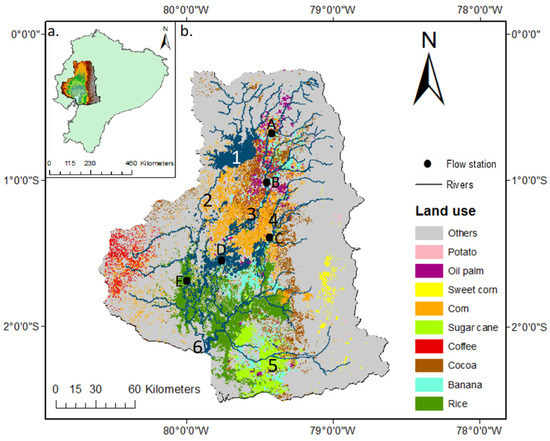
Figure 1.
Location of the Guayas River basin in Ecuador (a). Land use, river network and streamflow stations (b). Numbers indicate the Daule Peripa Dam (1) and the main rivers, being Daule (2), Vinces (3), Babahoyo (4), Chimbo (5) and Guayas (6). Letters indicate the streamflow stations, being Baba dam (A), Quevedo en Quevedo (B), Zapotal en Lechugal (C), Vinces en Vinces (D) and Daule en La Capilla (E).
Being the most productive agricultural region in Ecuador (providing 70% of the national crop production), the watershed is indispensable for the country’s economy [19]. The most produced crops in Ecuador (sugar cane, banana, palm oil, cacao, rice and corn) are cultivated on the numerous arable lands and plantations of the basin (Figure 1b). Maize represents 11.50% of total land use cover of the basin, followed closely by rice (9.34%), cacao (9.19%), cane (3.45%) and banana (3.02%). As this intensification in agricultural production is promoted by the Ecuadorian government, ecosystem management should be included in the economic growth assessment. Therefore, it is urgent to improve the knowledge about these pressures and find proper management tools to mitigate their negative ecological impacts.
The agricultural intensification in the basin leads to the application of numerous pesticides. In particular, banana and rice plantations were identified as the major sources of pesticide pollution in water [1] while almost no pesticides are applied to cacao and palm. Only two pesticides were selected to simulate their dynamics. This selection was first based on prior estimated importance (risk of polluting the surface water). This risk was estimated in consultation with local river managers and farmers. Moreover, the analysis results of a sampling campaign (cf. Section B.1. in Supplementary B) gave an indication of which pesticides are both frequently applied throughout the basin and have the characteristics (e.g., solubility and decay rate) to persist in the water phase. The second criterion for the pesticide selection was the availability of application data. These data were scarce (see Section B.1–B.4 in Supplementary B) but there were sufficient available application data for two (pendimethalin and fenpropimorph) of the six abundant pesticides.
2.2. Tools to Simulate Pesticide Dynamics
In the presented research, a benchmarking study was conducted to select an appropriate model to simulate the pesticide dynamics in the Guayas River basin. The tools that were reviewed are Annualized Agricultural Non-Point Source (AnnAGNPS) [22], Hydrological Simulation Program—FORTRAN (HSPF) [23], MIKE SHE [24] and SWAT (Soil and Water Assessment Tool) (see details in Section A.1. in Supplementary A). A useful feature of AnnAGNPS is the ability to identify the contribution of land or reach components to the output loadings (source accounting) [25]. However, its limitation is the routing of the loads to the watershed outlet before simulating the next day. Furthermore, no groundwater flow is simulated and the precipitation is considered to be homogeneously distributed throughout the study area. In addition, the documentation of the tool is limited [15,25]. Although AnnAGNPS has a reservoir compound, management options are not available. HSPF simulates interaction between the spatial units by routing the output of one unit to the next one downstream, where it is subject to the processes of that unit, instead of routing it immediately into a reach segment [10]. HSPF allows the implementation of impervious land zones, making it an attractive tool to model the influence of urbanisation [26]. The major disadvantage of the tool is its complexity, being highly demanding with respect to expertise, available data (e.g., hourly precipitation inputs) and calibration efforts [11,27]. In addition, reservoirs are treated the same as channel reaches and no reservoir management options are available [28,29]. MIKE SHE uses a distributed structure by dividing the watersheds into rectangular or square grids, each consisting of several horizontal layers [24]. This structure, combined with detailed process descriptions and multi-dimensional flow equations, makes the developed model computationally and data intensive. The advantages of MIKE SHE are the broad range of agricultural practices and water control structures that can be simulated [30] and the possibility of flexible reservoir management implementations by means of user-defined functions in the MIKE 11 module [31] while the disadvantages are its complexity and the occurrence of numerical instabilities [26]. Although holding several disadvantages such as the requirement of numerous parameters, no spatial linkage between the subunits and the routing of only one pesticide per simulation, SWAT was assessed to be the better option. The reasons for this selection are its flexibility, the opportunity for further development (open source, both the software and the source code), the semi-distributed approach, the scale of application, its continuous development by the USDA-ARS and its worldwide user and developer community (see Section A.1. in Supplementary A) [32,33].
2.3. Soil and Water Assessment Tool
SWAT represents the watershed by spatially explicit subbasins, further subdivided into lumped, non-interacting Hydrologic Response Units (HRUs). HRUs are the unique combinations of land use, soil and slope within a subbasin. Simulations consist of two main parts: a land phase and a routing phase. During the land phase, the daily loadings of water and pollutants are calculated for each subbasin. In the second phase, which is the routing phase, these loadings are routed via the main channel network to the outlet of the basin. With respect to pesticide fate, first, the amount available for transport is calculated considering a certain application efficiency, wash-off and degradation. Subsequently, pesticides are transported to the channels via surface runoff and lateral flow to the stream channels. Surface runoff or overland flow is generally considered to be the most important transport route [34,35,36,37]. During runoff events, pesticides are transported both in solution and attached to sediment particles. The detachment and entrainment of particles, also called soil erosion, is caused by the combined effect of rainfall impact and runoff flow. Where the fraction of pesticides transported in the dissolved phase mostly dominates, the transfer via erosion is non-negligible for pesticides with a high adsorption capacity [15,38]. Additionally, rapid pesticide transfer via drains can cause temporary peak concentrations in small streams [39,40]. During the routing phase, solid–liquid partitioning, settling and degradation processes are simulated. Next to the water concentration, the fraction adsorbed to the sediment is important as well. Sediments can be an important sink of contamination, thereby slowing down degradation rates and forming a secondary source [41]. Groundwater pollution is less common but can persist longer [42,43]. In this study, pesticide transport via groundwater was not implemented. The implementation technique of important processes is indicated in Table SA1 and extensive theoretical documentation is provided by Neitsch et al. [44]. For this study, the ArcGIS interface of SWAT was used [45]. This GIS interface facilitates the pre-processing of input data, the determination and calibration of model parameters and the visualisation and analysis of model outputs [46].
The number of SWAT applications is extensive (Table SA2), as is their diversity [32]. Pesticide-related studies include the simulation of pesticide transport and fate [35,47,48,49,50], comparison of best management practices [51,52,53], land use change analysis [42] and climate change research [54]. These studies illustrate that SWAT is a useful and versatile tool for pesticide simulations for large-scale watersheds. However, a challenge that was encountered by multiple studies is to obtain reliable data on pesticide practices. Fohrer et al. [50] stressed the importance of having detailed data on application timing but underlined the difficulty to obtain these data. To cope with this, the authors recommended varying the date of application throughout the basin. Alternatively, pesticide application rate (AR) and timing can be considered as calibration parameters [47,48]. A second challenge is to obtain pesticide concentration data [42,51]. These challenges explain why, at the moment, the applications are almost completely concentrated in developed countries. Only seven pesticide applications in developing countries were found, simulating pesticide fate in small watersheds [47,48,55,56,57,58,59].
2.4. Model Inputs and Setup
Table 1 provides an overview of the used model input data. The digital elevation model (DEM) (see Figure SC1) was used to define the stream network and delineate the subbasins of the watershed. To improve this process, the river network was “burned” into the DEM, as recommended by Luo et al. [60]. Important during this step is the choice of the threshold drainage area. This is the minimum drainage area required to form the “origin” of a stream and it determines the degree of detail of the delineation [61]. In addition, it affects the spatial resolution of the input data. A threshold of 3% (102,000 ha) of the total watershed area was chosen, following the suggestions of Jha et al. [62]. In total, 29 subbasins were delineated with an average area of 1092 km2. With respect to the subdivision of the subbasins, only two slope classes were used in order to avoid the generation of a too large number of HRUs. The limit between the two classes was arbitrarily set at 10%. The HRU thresholds were chosen to be 5% for land use and 20% for soil and slope, as suggested in the SWAT tutorial.

Table 1.
Model input data sources for the Guayas River basin. Gaps refer to missing data in the time series, whereas clustered refers to measurements obtained from stations that are heterogeneously distributed throughout the basin. Details can be found in Section C.1. of Supplementary C.
A satellite image-based classification of land cover, developed by MAGAP [63], was used to differentiate land use in the SWAT model setup. Agricultural land (69%) was the most important land use next to native forests (15.3%), urban (2.9%) and shrub vegetation (2.7%). Based on the land cover data, agricultural land was further differentiated into nine classes of cultivated crops, wherein the most important crops are maize, rice and sugar cane. Parameterisation of land use and cultivated crops was taken from the SWAT crop database (see Figure SC2). As information on pesticide application practices within the basin is scarce, these data were compiled via farmer consultation and interviews, agricultural guidelines and by using a national database of registered products (see Tables SB1–SB3 and Section B.1. in Supplementary B). Due to data scarcity and the consultation of only a limited number of farmers, the resulting application schedules simplify the reality and thus include a certain degree of uncertainty. Information on the soil type was extracted from the Harmonized World Soil Database (HWSD) map (Table 1 and Figure SC3) as the associated database contains many soil parameters required by SWAT. The methods to obtain the remaining parameters are presented in Table SC1. Studies that used similar methods are presented by Nielsen et al. [64] and Stehr et al. [65]. To consider the effects of the Daule Peripa dam on the hydrology, properties of the dam and reservoir were used as input data such as maximal and normal surface area and volume and minimum and maximum water level (Table SC2). The remaining reservoir parameters, such as equilibrium sediment concentration and the hydraulic conductivity of the bottom, were set to default values (i.e., values suggested by the tool). As operational input, daily outflow measurements of the Instituto Nacional de Meteorología e Hidrología (national meteorological and hydrological institute) (INAMHI) were used. Besides the dam, many natural lakes are present in the basin. For the Abras de Mantequilla wetland, which is located in the central part of the basin, topographical data were available from a local survey [66]. The lakes were implemented in SWAT as ponds, being conceptual water bodies that aggregate the lakes per subbasin [44]. The lake area was obtained from the river basin map and the volume was estimated using a volume-area ratio of 2 m, which is in agreement with the data from the Abras de Mantequilla survey. Several other lakes are present in the river basin. Unfortunately, no information about the dimensions of these lakes is available. Since these lakes are rather small, it was assumed that the influence on the hydrologic cycle is rather limited, considering the size of the catchment.
Besides information on pesticide application, precipitation data are a key input for a reliable simulation of the water balance and of pesticide dynamics. As such, an accurate description of rainfall patterns is required. For this study, two types of precipitation data are available for the basin: in-situ measurement and reanalysis data. The in-situ measurements are expected to provide accurate and precise daily values but measurement periods, number and spatial coverage of the stations are limited. Especially in the mountainous region of the basin, stations are scarce. Reanalysis products, on the other hand, are large datasets based on analysis and interpolation of the station, forecast and/or satellite data [73]. These products were preferred for use in this study due to their larger spatial coverage, the use of one method for the whole period and the absence of data gaps. However, their performance is location dependent; thus, it is important to compare them with the ground station data before use [74]. To do so, the measurements of 14 ground stations with data gaps smaller than 20% during the period of 1990–2015 were compared with four reanalysis products: CFSR, CHIRPS, ERA-Interim and WFDEI. The reanalysis product was selected based on resolution and period by using four statistics (for formulation, see Section D.1. in Suplementary D), calculated on a monthly basis. The results of this comparison show that the WFDEI dataset corresponds the best with the ground station precipitation data (Table SD1). Consequently, the WFDEI dataset was selected as input for the SWAT model. To further improve its agreement with the station data, the WFDEI values were multiplied by 1.32. This correction factor was obtained as an average of the 12 × 14 monthly, station-specific correction factors:
where is the correction factor for station X for month j (-), is the registered monthly average of the total daily precipitation for month j of year i at station X (mmday−1), is the WFDEI monthly average of the total daily precipitation for month j of year i in cell X (the cell where station X is located) (mmday−1) and is the total number of years for which both the station and the reanalysis dataset contain a precipitation value for month j (-). Alternatively, a spatially and/or temporally variable CF could have been applied, as was done by Monteiro et al. [73]. However, as no trend was observed for the CF as a function of elevation, location or month, it was decided to apply one constant CF.
With respect to the air temperature, station data were used because of a poor agreement between the WFDEI data and the stations’ measurements. The station data indicate that the temperature is rather constant throughout the basin (for regions of the same elevation) but strongly dependent on the elevation. Therefore, five equally represented elevation bands for each subbasin were defined. The temperature lapse rate was calculated by linear regression between the yearly average temperature registered at a station and its elevation. The monthly statistics of the remaining weather variables, i.e., relative humidity, solar radiation and wind speed, were calculated by station data and using the weather generator function to generate the daily values since the measured time series contained numerous gaps.
2.5. Model Calibration
For the calibration of SWAT for the Guayas River basin, streamflow data for 17 gauges were provided by INAMHI. Only five of the gauges had a percentage of data gaps smaller than 20% for the period from 1990 to 2015. These gauges, which are rather well-distributed throughout the basin (Figure 1), were used to calibrate the streamflow. An important limitation is the lack of a streamflow gauge at the outlet of the basin. As no sediment or pesticide concentration time series were available (i.e., a data scarce area), the calibration is limited to streamflow. However, pesticide concentration data in river water from a sampling campaign in 2016 (Section B.1. in Supplementary B) can provide at least minimal support for the model simulations. Manual streamflow calibration was performed on a monthly basis for the period 1993–2000, which is longer than the recommended minimum of five years. In addition, it includes dry, e.g., 1996, and wet years, e.g., 1997–1998 associated with an El Niño event [75]. A warm-up period of three years (1990–1992) was used to estimate initial conditions for soil water and groundwater storage. We decided to calibrate manually as this allows obtaining a better understanding of the dynamics and the effect of parameter values on the simulated streamflow. Nash–Sutcliffe efficiency (NSE) (Equation (2)), frequently used and recommended by several authors, was selected as objective function [76,77]:
where NSE is the Nash-Sutcliffe efficiency (-), is the observed streamflow (m3), is the simulated streamflow (m3), is the average value of the observed streamflow (m3) and is the total number of observations (-). To avoid systematic over- or underestimation, the percent bias (PBIAS) (Equation (3)) was used as a second criterion during manual calibration and parameters that maximise NSE while minimising PBIAS were sought for.
First, a preliminary selection of 11 parameters relevant to streamflow processes was composed based on a number of pilot runs and on the literature [15,44,78,79,80,81] (see Supplementary E). For each of these parameters the initial value, being a default value or value based on the pilot runs, was changed by 50% to assess the effect on the streamflow simulations. Subsequently, the seven most influential parameters were selected. This selection consists of four groundwater parameters, one parameter influencing actual evapotranspiration, one governing streamflow routing and the last parameter influencing runoff (see Table SE1). A multi-site approach was used to improve the reliability of the large-scale model [49]. Hence, the delineated subbasins were divided into three drainage areas of the three main rivers (Daule, Vince and Babayoho Rivers, Figure 1). The drainage area of the Chimbo River, where no station is located, was joined to the adjacent drainage area of the Babahoyo River. Within each of these regions, the same parameter values for the different subbasins were used and the flow stations located the most downstream were selected for calibration.
To evaluate the calibrated model, NSE and PBIAS (Equations (2) and (3)) were calculated on both a daily and a monthly basis for the calibration (1993–2000) and validation (2001–2009) period for each of the five selected stations (Figure 1). These daily and monthly NSE and PBIAS values were compared with the values for watershed-scale models recommended by Moriasi et al. [82]. As such, model performance was classified as “very good”, “good” and “satisfactory” when daily or monthly NSE values exceeded 0.80, 0.70 and 0.50, respectively. With respect to daily and monthly PBIAS, the model was rated as “very good”, “good” and “satisfactory” for values smaller than or equal to 5%, 10%, and 15%, respectively. When the model performance was appointed a different rating based on the two statistics, the most conservative rating was used. In addition, the simulated discharge at the outlet of the basin was compared with the reported average value.
2.6. Pesticide Simulation
The aim of the pesticide simulations was to investigate the related system dynamics and model functioning. As no calibration of the pesticide loads could be carried out, the analysis of the results focuses on simulated trends instead of predicted concentrations. As such, values should be interpreted as relative values, rather than absolute. Pesticide applications were implemented according to the schedules presented in Table SB2, considering the spatial variation for corn (one or two cultivation cycles) and rice (the application rate (AR) in Los Rios is twice the amount of the one in Guayas). Pesticide properties influencing the land use phase of the pesticide simulations were taken from the SWAT database or online databases. Default parameters values were used for the routing of the pesticides (Table SC3). The model was run using monthly time steps, as the hydrological model performance was rated as unsatisfactory on a daily basis. As agricultural activities are roughly defined on a monthly basis, the monthly time steps are considered as an acceptable resolution. The year 2009 was used for the simulations, assuming that this year represents normal conditions with respect to pesticide transport and fate, as the average daily precipitation during this year (4 mm) is the median value of the yearly averages of the nine validation years. Four simulations were carried out: pendimethalin application practices at cornfields (Simulation 1), at corn and rice fields (Simulation 2) and at corn, rice and sugar cane fields (Simulation 3) and fenpropimorph application practices at banana and cornfields (Simulation 4). Then, the temporal and spatial variations of the results were analysed. The pesticide output of a subbasin, given in total load of dissolved pesticides transported with the streamflow, was recalculated to concentration using the simulated streamflow (Equation (4)).
where C the average pesticide concentration at the outlet of a subbasin for a given month () or (), M the total simulated dissolved pesticide load at that subbasin’s outlet during that month (, Q the average monthly streamflow at the subbasin’s outlet during the month () and S the number of seconds in that month ().
3. Results
3.1. Hydrology
The performance statistics for the model calibration and validation of streamflow are presented in Table 2 and Table 3 respectively. The model performance on a monthly basis is assessed as very good during the calibration period for “Daule en La Capilla” and “Quevedo en Quevedo”. The performance is classified as satisfactory for “Baba dam” and “Vinces en Vinces” and unsatisfactory for “Zapotal en Lechugal” for the calibration period. The validation is rated as very good for “Vinces en Vinces” and “Zapotal en Lechugal”, as good for “Daule en La Capilla” and as unsatisfactory for “Baba dam” and “Quevedo en Quevedo”. It has to be noted that the difference in average registered streamflow during the calibration and validation period (Table 2 and Table 3) is explained by the occurrence of an El Niño event during the calibration period.

Table 2.
Evaluation statistics with model performance assessment according to Moriasi et al. [82] and average registered streamflows (Qav, whole period; dry, dry season; rainy, rainy season) for the calibration period (1993–2000). The stations for which manual calibration was done are indicated in grey. NSE, Nash–Sutcliffe efficiency (Equation (2)); PBIAS, percent bias (Equation (3)); VG, very good; G, good; S, satisfactory; US, unsatisfactory.

Table 3.
Evaluation statistics with model performance assessment according to Moriasi et al. [82] and average registered streamflows (Qav, whole period; dry, dry season; rainy, rainy season) for the validation period (2001–2009). The stations for which manual calibration was done are indicated in grey. NSE, Nash–Sutcliffe efficiency (Equation (2)); PBIAS, percent bias (Equation (3)); VG, very good; G, good; S, satisfactory; US, unsatisfactory.
The comparison between the observed and simulated monthly average streamflow is exemplified for two stations for the calibration in Figure 2. The visual comparison suggests that the simulated streamflow at the “Daule en La Capilla” station follows the observed trends quite well. This agrees with the ratings based on the monthly statistics (very good) (Table 2). However, an underestimation of the streamflow during low flow periods can be observed. This is also the case at other stations, especially at the “Baba dam” station. Despite this underestimation, PBIAS values for the “Daule en La Capilla” station are negative, which can be explained by the overestimation of the peak flow in 1998 (Figure 2a). During other years, the peak flow volume agrees well with the observations (in 1995 and 1996) or is underestimated (e.g., in 1993). The overestimation of the peak flow during the 1998 El Niño event and the underestimation of peak flows during the other calibration years are observed at all other stations. A last remark with respect to the monthly time series for the calibration period is that the slope of the recession curve is sometimes not steep enough (e.g., in 1998). Simulated flows at the “Zapotal en Lechugal” station fit the observations less well (Figure 2b), as was also pointed out by a poor PBIAS value (Table 2). This is especially because of the large underestimation of the peak flows, resulting in a highly positive PBIAS. Moreover, a slight underestimation during the low flow periods can be observed. The average simulated discharge at the outlet amounts to 1353, 770 and 1045 m3·s−1 for the calibration, validation and whole simulation periods, respectively. Especially the simulated average for the whole simulation period is close to the reported value of 974 m3·s−1. This gives an indication that the order of magnitude of the simulated flow at the tributary of the Guayas where no station is located (i.e., the Chimbo River) is realistic.
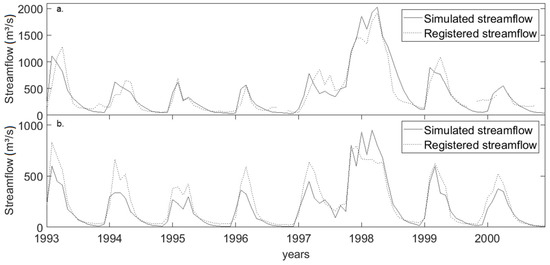
Figure 2.
Monthly time series for the “Daule en la Capilla” (a) and “Zapotal en Lechugal” (b) stations during the calibration period (1993–2000).
3.2. Pesticide
A general observation related to the pesticide simulations is the relationship between the simulated runoff for a certain subbasin and its pesticide output. This relationship is the most pronounced for subbasin outlets located directly downstream of the main cultivation area. For example at the “Vinces en Vinces” station that is located downstream of the main corn cultivation region, the pendimethalin outputs are clearly related to the simulated runoff values (Figure 3a,c). The absence of a pendimethalin peak in May can be explained by the long time interval after the application occurred. In December, moreover, no pesticide transport occurs because the precipitation does not exceed the 2.54 mm·day−1 threshold for wash-off of the pesticides from the crops to the soil. The relationship between runoff and pesticide load becomes less clear when the distance to the pesticide source increases. Pesticide concentration trends differ from the simulated pesticide load due to dilution or increased concentration effects. These effects explain the decline in concentration in February and the small concentration peak in May, respectively (Figure 3b,d). As such, a decrease in streamflow can cause a large concentration peak even when the simulated pesticide load is rather low, as observed for the fenpropimorph simulations. A second aspect that is a characteristic of the simulation results is the seasonal variation. Pesticide outputs are maximal during the rainy season (mostly in February or March) and low (Daule River) or zero (Babahoyo and Chimbo Rivers) during the dry season. Pesticide peaks start earlier in the eastern part of the basin, where orographic effects cause higher and earlier rainfalls.
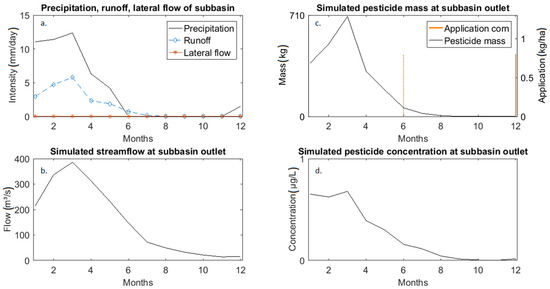
Figure 3.
Monthly average precipitation, runoff and lateral flow normalised by the subbasin area (a); monthly average streamflow (b); total dissolved pendimethalin load transported with streamflow and indication of application rate, where dotted line indicates that the application occurs only at a fraction of the HRUs (c); and calculated monthly average pendimethalin concentrations (d) at the “Vinces en Vinces” station for pendimethalin application at corn farms.
Pesticide application practices were simulated for each land use type to identify their respective impact. For instance, the cultivation of corn, first, causes a widespread presence of pesticides in the rivers. Pendimethalin application affects all the three main rivers (Daule, Vinces and Babahoyo) with the highest concentrations occurring immediately downstream of the main corn cultivation region. Further downstream, the simulated concentrations gradually decrease because of dilution, degradation and diffusion processes. The maximal pendimethalin concentration was simulated at the “Vinces en Vinces” station. The cultivation of rice, on the contrary, has a negligible contribution to the simulated pendimethalin input into the rivers. This is because the simulated application to rice fields happens at a low rate and only during the dry season. In addition, rice is cultivated in flat areas and, consequently, all HRUs where rice is grown have a slope class lower than 10% (Table SB4), which implies low runoff rates. Nevertheless, a high pendimethalin concentration was measured at the Babahoyo River in the middle of the rice cultivation region, which might indicate that the simulations underestimate the contribution of the pesticide application at rice farms. Pesticide practices at sugar cane farms, thirdly, have major but localised contributions to the pesticide input into the rivers. These are explained by the high AR and application frequency and the large fraction of HRUs with a slope above 10% (Table SB4). There is no influence of the sugar cane practices on the simulated pesticide concentration in the Daule and Vinces Rivers, due to the absence of sugar cane fields in the drainage area of these rivers (Figure 1). With respect to the fenpropimorph application, the contribution of corn farms practices to the river pesticide concentrations is negligible. This is because fenpropimorph is (according to the available data) only applied during the dry season on corn fields. As such, the simulated concentrations in the Daule River are zero. This does not agree with the many observations in the upstream region of the Daule River during the sampling campaign (cf. [1]), which might indicate that the available data about the timing of fenpropimorph application at corn fields (only during the dry season when pesticide transport is negligible) are not correct. Another plausible explanation is that fenpropimorph is also applied to crops other than banana and corn, which is suggested by the two highest measured concentrations, both sampled in the vicinity of cocoa farms. The application on banana plantations has a larger contribution. Simulated fenpropimorph concentrations are highest upstream of the Vinces River and downstream of the Babahoyo River, associated with the location of the banana plantations. The simulated fenpropimorph concentrations are lower compared to pendimethalin concentrations, which also holds true for the measured concentrations (see Supplementary B). This can be explained by the small area of the banana fields (Figure 1).
4. Discussion
4.1. Pesticide Dynamics in the Guayas River Basin
Based on the results of analysing the pesticide simulations, the following implications for the Guayas River basin can be formulated. First, the drainage area of the Vinces river was identified as a critical zone that should be prioritised in future research and management. For the “Vinces en Vinces” station, high concentrations were simulated, which is caused by its location downstream of the main corn cultivation area. It was observed that the pesticide application at banana farms, located more upstream, affects the same catchment. Unfortunately, during the sampling campaign of 2016 (Section B.1. in Supplementary B) only five samples were taken for this river, being insufficient to confirm the catchment as a risk area. Therefore, it is recommended for future campaigns to increase the sampling density along the Vinces River, especially in the vicinity of banana and corn fields. It is important to note that these conclusions are based on the simulation of the pesticide pendimethalin and fenpropimorph. Deknock et al. [1] analysed all pesticide detections observed in the Guayas River basin and concluded that soluble concentrations of pesticides mainly increased from the upstream to downstream the catchment. Contrary to our study, Deknock et al. [1] were not able to consider seasonality, which potentially affects the identification of priority zones. As such, future samples should be taken in other months [83], as model simulations indicate pesticide concentrations can be higher in months other than those considered in the study of Deknock et al. [1]. This second fact, being the seasonal variation of the pesticide concentrations, is, in general, a valuable insight that can optimise future sampling campaigns. With respect to river management, it could be used as an argument to impose limitations on pesticide use during the rainy season. Third, the importance of runoff as a transport route was confirmed by the simulations. Thus, a suggestion for river management is the implementation of runoff control measurements, especially at fields with a high slope (e.g., sugar cane farms). Fourth, the simulations gave an insight into the dominant areas of pesticide sources and the impact of the different land uses. However, samples should be taken at the downstream region of the Babahoyo River to verify the low simulated contribution of pesticide application at rice farms. Additionally, as reported by Arias-Hidalgo et al. [66], the use of toxic pesticides within the basin should be prohibited.
4.2. Mechanistic Modelling of Pesticide Dynamics under Data Scarcity
This case study demonstrated that SWAT is able to sufficiently represent the hydrological conditions of a complex and large watershed with limited data availability. An insight into pesticide transport and fate could also be obtained. Unfortunately, the accuracy and precision of these pesticide simulations could not be estimated as calibration or validation data were not available at the simulated locations. As such, we suspect the accuracy and precision of the pesticide simulations are low. Nonetheless, the simulations show gaps in knowledge and can be used to steer future sampling campaigns.
It can be concluded that the streamflow component of the model performs well on a monthly basis based on: (1) the satisfactory or better performance ratings for most of the stations (Table 2 and Table 3); (2) the good ratings for the station with the largest discharge (“Daule en La Capilla”); and (3) the fact that none of the statistics is close to the thresholds that define unacceptable model performance (NSE < 0 and PBIAS > 30%). The lack of data at the watershed outlet, however, impedes to estimate the model performance at locations more downstream than the streamflow stations. A main reason for the good performance is probably the good monthly performance of the WFDEI dataset. It should be noted, however, that the use of this dataset provides a plausible reason for the overestimated streamflow during the 1998 El Niño event at all stations. Indeed, the average daily corrected WFDEI precipitation during this year (12.6 mm) is twice as much compared to the stations (5.9 mm). This is due to the fact that the application of the correction factor (i.e., 1.32) to the WFDEI precipitation values might lead to an overestimation of the rainfall with respect to the station measurements. As the measured precipitation is only representative for one point (the location of the rain gauge), the measured value is expected to be higher than the precipitation values averaged over a whole grid (i.e., the WFDEI precipitation); therefore, a correction factor was used to the WFDEI precipitation values. The high positive percent bias (PBIAS) values that were obtained at some stations indicate an underestimation of the streamflow simulations. This suggests some shortcomings of the model, e.g., inadequate simulation of the groundwater processes. However, measurement errors might also contribute to the high PBIAS. The increasing trend of the streamflow registered at the “Quevedo en Quevedo” station, for example, might indicate some data inaccuracies (e.g., outdated Q,h-relationships). In addition, a better balance between the NSE and PBIAS values during calibration might reduce the high PBIAS values.
The calibration of the hydrological model, lastly, is challenged by the presence of a complex stream network, the limited availability of (spatially distributed) information and the absence of an outlet station. When using SWAT, the aim is to include spatial variability into the model as was done during model setup, e.g., with respect to land use and management. During the calibration, however, achieving this aim is limited by the low density of the streamflow stations network. Since it is not possible to calibrate each of the 29 subbasins separately, the subbasins need to be grouped into larger regions that are calibrated together. A question here is how to handle large areas without streamflow stations (e.g., Chimbo River). As it is useful to have an indication of the model performance at locations not used for calibration, specifically in the availability of large areas without stations, the number of stations used for calibration in this study was intentionally limited, in contrast to the approach of Neitsch et al. [84]. If data from all stations would have been used for calibration, good statistics for these stations could give a misleading idea of the model performance at other locations without stations. Therefore, the multi-site approach is considered to be a more powerful validation strategy than the split sample in time methodology [85]. Nevertheless, it should be noted that good validation statistics do not necessarily guarantee good model performance in regions where no station is located. To further improve the model performance, the effect of different calibration approaches should be investigated. For instance, the subdivision of the subbasins into different calibration regions and the number of stations used for calibration could be considered. The use of more streamflow stations can refine the spatial variability of the model, ideally in combination with the collection of more data and the refinement of the delineated network, e.g., via a smaller threshold drainage area. Meanwhile, the arguments for not using all the stations during calibration remain valid. The calibration could focus on a smaller time step, in order to improve the performance at a smaller time scale.
The question remains if a data intensive hydrological model is an optimal way to investigate pesticide pollution in data-poor regions. The development of such complex models is ambitious and involves a number of assumptions. Especially when data availability is low, the models are a strong simplification of reality. It can be argued that there is no point in simulating spatial variable and dynamic outputs while data limitations impede verifying the accuracy of these simulations. The use of alternative tools, e.g., simple screening tools that assume steady-state conditions, might be more appropriate in developing countries. Nevertheless, these simpler tools impede capturing the real pesticide dynamics or gaining an understanding of the underlying processes. As it is crucial, especially in developing countries where effective management decisions are urgent, to improve this understanding, the use of more complex hydrological tools seems legitimate. In addition, hydrological tools enable developing a well-performing hydrological model, in contrast to simpler tools. However, to unlock the full potential of the hydrological tools, monitoring efforts are indispensable. As such, a good balancing of monitoring and hydrological modelling efforts arises as an important contribution to the establishment of integrated management and thus the protection of valuable freshwater ecosystems.
4.3. Case-Specific Strengths and Limitations to SWAT
The application of SWAT for the Guayas River basin made it possible to identify case-specific strengths and shortcomings of the tool. A first strength is its semi-distributed structure. This balance among model complexity, spatial variation, data requirements and computational efficiency was experienced as very useful for this case study. On the one hand, it enables differentiating between different land use and slope classes, which are required to implement the application practices, and observing the effect of slope on pesticide dynamics. On the other hand, the model was experienced as computationally efficient, opposed to distributed models (e.g., AnnAGNPS and MIKE SHE, based on the benchmarking study, cf. Table SA1). Moreover, these tools would require more data, which was already a limitation for SWAT. Compared to a lumped model that is limited to the generation of outputs at the outlet of a watershed, the semi-distributed model allows investigating the pesticide dynamics within a watershed and identifying problematic areas. The second strength of SWAT that was experienced during the case study is the availability of extensive online documentations, internal databases (e.g., pesticide properties) [48] and user support. In addition, many new tools and the model itself are constantly being developed [86]; however, only the ArcGIS interface tool was tested during this study. This interface was found to be convenient for manipulating the input data layers. A third strength is the possibility to implement reservoirs into the model. To end, SWAT has a broad range of potential applications, being, however, constrained by case-specific limitations. The main limitation that is often encountered during SWAT applications, certainly in developing countries, is the high data requirement of the tool [87]. First, the development of a physically-based, semi-distributed model imposes high data requirements with respect to data quantity, variety, accuracy and precision [13]. In addition, SWAT is developed primarily with regard to application in the United States, implying that climate and soil databases need to be extended or adapted if used elsewhere [46]. Especially the objective to simulate pesticide dynamics is highly data demanding, e.g., necessitating a detailed application data. The second disadvantage of mechanistic models in general, and SWAT more specifically, is the time-intensive model development and challenging streamflow calibration. The model development was found to be inflexible with respect to the delineation of the watershed and the river network, which could not be adjusted apart from choosing another threshold drainage area. This limitation is in contrast with the flexibility towards the number of subbasins mentioned above. Because of the difficult code and a high number of parameters, expertise is required to run the tool and calibrate the model [88]. Despite the importance of these limitations, especially the first one, SWAT enabled to obtain insights into the system functioning.
4.4. Recommendations for Pesticide Monitoring and Model Developments
This case study demonstrated that the developed model can provide useful insights into the system functioning. A key boundary condition for use of the model is that it is further refined and under continuous critical review and revision. At this stage of model development, the availability of sufficient qualitative data is identified as the main bottleneck for further improvements. In this section, specific suggestions for further data collection and model improvements are explored, together with alternative uses. To structure the discussion, an adapted version of the model building steps of Jakeman et al. [89] is used (Figure 4).
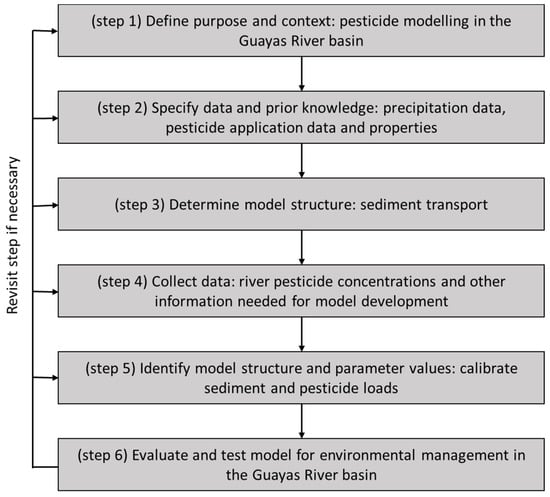
Figure 4.
Revisited model building steps to further refine the Guayas River basin SWAT model (adapted from Jakeman et al. [89]). For concrete suggestions for each step, the reader is referred to the main text in Section 4.4.
This study applied SWAT to determine its potential in providing valuable insights into pesticide dynamics under data-poor circumstances. One could question whether the goal of developing or setting up a pesticide model is justified (Step 1). The data required to calibrate such a model are tedious to collect, without the limited possibility for automatisation. As such, SWAT can also be employed for an alternative use in water resource management, e.g., modelling of nutrients to steer wastewater management or refined hydrological modelling for irrigation management. SWAT can also serve these purposes if the model is evaluated in this context. Consequently, it is important to indicate that these alternative uses are available, before further tuning modelling efforts.
The quality of the input data must be improved (Step 2). For instance, the availability of better data (e.g., precipitation) can enhance streamflow simulations and model calibration. Considering the importance of precipitation data for hydrological modelling and the limitations of both the station and the WFDEI datasets, it would be interesting to compare the current model performance with the one obtained using the stations’ data. The accuracy of the WFDEI dataset might be too low to obtain good performance on a daily basis. Besides, the precipitation data could potentially be improved by including elevation bands and accounting for orographic effects, using the methodology outlined by Strauch et al. [90]. Second, the available HWSD soil map is possibly outdated and has a coarse spatial resolution (Figure SC3). In addition, measurements were not available for some of the required soil parameters (Table SC1). As most of the hydrologic process during the land phase, e.g., evaporation and runoff, are influenced by soil parameters, an improvement in soil data is expected to increase the model performance [91]. Moreover, the collection of qualitative pesticide input data is required if a deeper mechanistic insight is needed. In essence, one is required to know when and where specific pesticides are applied. This encloses the collection of the type of applied pesticide (active ingredient), the application timing, application rate (AR) (i.e., kilogram of active ingredient per hectare) and application type (by hand or airplane). This step is as important as it is difficult to take. The gathering of pesticide application data is a challenging task because strict application schemes do often not exist, pesticide application being driven by a variety of factors [48]. In addition, farmers do not always keep track of the amounts they apply or do not want to share that information (personal communication). The collected information used in this study is associated with a high uncertainty because only one interview per land use was conducted, impeding to obtain spatially distributed information. For sugar cane, the spatial variation can be assumed to be limited as the cultivation area is concentrated in two regions and the farmer that was interviewed possesses one-third of the total sugarcane cultivation area within the basin. Besides, the interviews were conducted at big farms, so no information was gathered about the practices at small farms. The approximated AR suffices, however, to learn how the system functions. Furthermore, the accuracy of the application timing is less important due to the monthly time step and to the coarse model setup. This model setup makes that the subbasins have large times of concentration, smoothening the pesticide transfer from the field to the outlet of the basin out over multiple days. Nevertheless, to simulate pesticide dynamics at a smaller time step, more reliable information on pesticide application practices for the different land uses should be gathered. As such, it is suggested to standardise the survey and expand it to other areas in the Guayas River basin. Information on organic carbon adsorption rates can determine whether the sediment layer of the river should be targeted and modelled (Step 3). More ideally, the sediment layer is considered by default, and monitoring schemes for measuring sediment loads are implemented. Not only would it greatly benefit insight in cumulated pesticide loads in the ecosystem, but it would also serve as a proxy for problematic areas with respect to erosion and sub-optimal soil management.
Based on the input data and pesticide properties, specific areas should be targeted and additional river water and sediment samples, as well as land management (e.g., crops, planting dates, tillage practices and harvesting dates) that can be used for model development, should be collected (Step 4). Continuous monitoring (with passive samplers) during and shortly after pesticide application at hotspots is advised, as cumulative loads can be used to calibrate the model running at a resolution of one month. Following the number of adaptations in Steps 2 and 4, the model should be recalibrated and re-evaluated (Steps 5 and 6). Subsequent the recalibration of the model with better input data and when the model performance is evaluated as sufficient, management recommendations can be formulated and formalised in order to decrease the impact of pesticide use on the river ecosystem. Revisiting and evaluating the defined steps is key to further advance in system knowledge of the Guayas River basin.
5. Conclusions
In this case study, several strengths of SWAT were identified, being its semi-distributed structure, the availability of extensive online documentation and user support, the constant development of the tool and the possibility of implementing reservoirs into the model. Limitations are high data requirements, the time-intensive model development and challenging streamflow calibration. Despite being constraint by data limitations, the application of SWAT improved the understanding of its functioning and of the system dynamics in the Guayas River basin. However, to substantially improve model performance, the availability of better input data such as higher resolution soil maps, more accurate pesticide application rates and actual land management programs would be needed. The insights gained from this case study can be used to optimise future sampling campaigns and designate zones that require in-depth research and priority management. Currently, the use of the developed model has a number of limitations. Notwithstanding, this research has provided a solid basis for further development and outlined a number of priorities in this development. Having in mind its limitations, the model can be used for the Guayas River basin to analyse the system’s functioning, design future hypothesis and steer future sampling efforts.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/12/3/696/s1, Figure SC1: Digital elevation model and river network of the basin, Figure SC2: Illustration of the land use reclassification, Figure SC3: Soil types within the Guayas River basin, Table SA1: Comparison of four tools to develop hydrological watershed models extended for pesticide modelling, Table SA2: Total number and relative importance per continent of Web of Science studies using AnnAGNPS, HSPF, MIKE SHE or SWAT for hydrological modelling and pesticide fate modeling, Table SB1: Application data for pendimethalin, Table SB2: Application data for fenpropimorph, Table SB3: Concentrations of active ingredient (AI) in commercial pesticide products, Table SB4: Pesticide application timing, application rates (AR), cultivation area and slope classes for the different crops for which pesticide application was implemented, Table SC1: Methods to obtain the required soil parameter for SWAT, Table SC2: Available data for the Daule Peripa Dam, Table SC3: Pesticide properties for fenpropimorph (F) and pendimathalin (P) as implemented in the model, Table SD1: Statistics for the monthly average of daily precipitation for 14 ground stations and four reanalysis products, Table SE1: Parameters selected for streamflow calibration based on pilot runs and literature.
Author Contributions
Conceptualisation, P.L.M.G., S.G. and N.C.; data curation, N.C., M.A.E.F. and I.N.; formal analysis, N.C.; funding acquisition, P.L.M.G. and L.D.-G.; investigation, N.C., S.G. and I.N.; methodology, N.C., S.G., M.V. and F.W.; project administration, P.G.; resources: I.N., P.L.M.G., M.V. and F.W.; supervision: S.G., I.N. and P.L.M.G.; validation, M.V. and F.W.; visualisation, N.C. and, S.G.; writing—original draft, N.C. and S.G.; and writing—review and editing, S.G.; M.A.E.F., I.N., M.A.-H., M.V., F.W. and P.L.M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was performed in the context of the VLIR Biodiversity Ecuador network and was co-funded by the VLIR-UOS Global Minds. N.C. was funded by the international mobility fund of VLIR-UOS. M.A.E.F. was funded by the Special Research Fund of Ghent University.
Acknowledgments
We thank Javier Osorio, Niels De Troyer, David Matamoros, Gonzalo Villa Cox, Christophe Fatras, Patricia Urdiales and Ruben Jerves Cobo for the technical support and facilitating the acquisition of data.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Deknock, A.; De Troyer, N.; Houbraken, M.; Dominguez-Granda, L.; Nolivos, I.; Van Echelpoel, W.; Forio, M.A.E.; Spanoghe, P.; Goethals, P. Distribution of agricultural pesticides in the freshwater environment of the Guayas river basin (Ecuador). Sci. Total Environ. 2019, 646, 996–1008. [Google Scholar] [CrossRef]
- Matamoros, D.E.; van Griensven, A.; van Biesen, L.; Vanrolleghem, P.A. Development of a geographical information system for pesticide assessment on an Ecuadorian watershed. Water Sci. Technol. 2005, 52, 259–265. [Google Scholar] [CrossRef] [PubMed]
- FAO. Agronoticias: Agriculture News from Latin America and the Caribbean. Available online: http://www.fao.org/in-action/agronoticias/detail/en/c/1141953/ (accessed on 10 January 2017).
- Damanik-Ambarita, M.N.; Everaert, G.; Forio, M.A.E.; Nguyen, T.H.T.; Lock, K.; Musonge, P.L.S.; Suhareva, N.; Dominguez-Granda, L.; Bennetsen, E.; Boets, P.; et al. Generalized linear models to identify key hydromorphological and chemical variables determining the occurrence of macroinvertebrates in the Guayas river basin (Ecuador). Water 2016, 8, 297. [Google Scholar] [CrossRef]
- Forio, M.A.E.; Mouton, A.; Lock, K.; Boets, P.; Tien, N.T.H.; Ambarita, M.N.D.; Musonge, P.L.S.; Dominguez-Granda, L.; Goethals, P.L.M. Fuzzy modelling to identify key drivers of ecological water quality to support decision and policy making. Environ. Sci. Policy 2017, 67, 58–68. [Google Scholar] [CrossRef]
- Forio, M.A.E.; Landuyt, D.; Bennetsen, E.; Lock, K.; Nguyen, T.H.T.; Ambarita, M.N.D.; Musonge, P.L.S.; Boets, P.; Everaert, G.; Dominguez-Granda, L.; et al. Bayesian belief network models to analyse and predict ecological water quality in rivers. Ecol. Model. 2015, 312, 222–238. [Google Scholar] [CrossRef]
- Shuman-Goodier, M.E.; Propper, C.R. A meta-analysis synthesizing the effects of pesticides on swim speed and activity of aquatic vertebrates. Sci. Total Environ. 2016, 565, 758–766. [Google Scholar] [CrossRef]
- De Gerónimo, E.; Aparicio, V.C.; Bárbaro, S.; Portocarrero, R.; Jaime, S.; Costa, J.L. Presence of pesticides in surface water from four sub-basins in Argentina. Chemosphere 2014, 107, 423–431. [Google Scholar] [CrossRef]
- Grung, M.; Lin, Y.; Zhang, H.; Steen, A.O.; Huang, J.; Zhang, G.; Larssen, T. Pesticide levels and environmental risk in aquatic environments in China—A review. Environ. Int. 2015, 81, 87–97. [Google Scholar] [CrossRef]
- Mottes, C.; Lesueur-Jannoyer, M.; Le Bail, M.; Malézieux, E. Pesticide transfer models in crop and watershed systems: A review. Agron. Sustain. Dev. 2014, 34, 229–250. [Google Scholar] [CrossRef]
- Quilbé, R.; Rousseau, A.N.; Lafrance, P.; Leclerc, J.; Amrani, M. Selecting a pesticide fate model at the watershed scale using a multi-criteria analysis. Water Qual. Res. J. 2006, 41, 283–295. [Google Scholar] [CrossRef]
- Tuo, Y.; Chiogna, G.; Disse, M. A multi-criteria model selection protocol for practical applications to nutrient transport at the catchment scale. Water 2015, 7, 2851–2880. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part i: Model development1. J. Am. Water Resour. Assoc. 2007, 34, 73–89. [Google Scholar] [CrossRef]
- Bende-Michl, U.; Volk, M.; Harmel, D.; Newham, L.; Dalgaard, T. Monitoring strategies and scale-appropriate hydrologic and biogeochemical modelling for natural resource management: Conclusions and recommendations from a session held at the IEMSS 2008. Environ. Model. Softw. 2011, 26, 538–542. [Google Scholar] [CrossRef]
- Holvoet, K. Monitoring and Modelling the Dynamic Fate and Behaviour of Pesticides in River Systems at Catchment Scale. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2006. [Google Scholar]
- Swat Journal Article Literature Database. Available online: https://www.card.iastate.edu/swat_articles/ (accessed on 21 June 2019).
- Arriaga, L. The Daule-peripa dam project, urban development of Guayaquil and their impact on shrimp mariculture. In A Sustainable Shrimp Mariculture Industry for Ecuador; Olsen, S., Arriaga, L., Eds.; Coastal Resources Center, University of Rhode Island: Narragansett, RI, USA, 1989; pp. 148–152. [Google Scholar]
- Castro, B.A. Sedimentation Processes at the Confluence of the Daule and Babahoyo Rivers, Guayaquil, Ecuador. El Palmar Island; University of Birmingham: Birmingham, UK, 2009. [Google Scholar]
- Frappart, F.; Bourrel, L.; Brodu, N.; Riofrío Salazar, X.; Baup, F.; Darrozes, J.; Pombosa, R. Monitoring of the spatio-temporal dynamics of the floods in the guayas watershed (Ecuadorian pacific coast) using global monitoring envisat asar images and rainfall data. Water 2017, 9, 12. [Google Scholar] [CrossRef]
- Madonado, M.E.S. Remote Sensing Based Hydrologic Modeling in the Babahoyo River Sub-Basin for Water Balance Assessment; University of Twente: Enschede, The Netherlands, 2011. [Google Scholar]
- Damanik-Ambarita, M.N.; Lock, K.; Boets, P.; Everaert, G.; Nguyen, T.H.T.; Forio, M.A.E.; Musonge, P.L.S.; Suhareva, N.; Bennetsen, E.; Landuyt, D.; et al. Ecological water quality analysis of the Guayas river basin (Ecuador) based on macroinvertebrates indices. Limnologica 2016, 57, 27–59. [Google Scholar] [CrossRef]
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. ANGPS, Agricultural Non-Point-Source Pollution Model: A Watershed Analysis Tool. Research Report; U.S. Department of Agriculture, Agricultural Research Service: Albany, CA, USA, 1987.
- Crawford, N.H.; Linsley, R.K. Digital Simulation in Hydrology: Stanford Watershed Model IV; Stanford University: Standford, CA, USA, 1966. [Google Scholar]
- Abu El-Nasr, A.; Arnold, J.G.; Feyen, J.; Berlamont, J. Modelling the hydrology of a catchment using a distributed and a semi-distributed model. Hydrol. Process. 2005, 19, 573–587. [Google Scholar] [CrossRef]
- Bingner, R.L.; Theurer, F.D.; Yuan, Y. Annagnps Technical Processes; Documentation Version 5.5; U.S. Department of Agriculture, Natural Resource Conservation Service and Agricultural Research Service: Washington, DC, USA, 2018.
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases. Trans. ASAE 2003, 46, 1553–1566. [Google Scholar] [CrossRef]
- Kalin, L.; Hantush, M.M. Evaluation of Sediment Transport Models and Comparative Application of Two Watershed Models; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2003.
- Borah, D.K.; Yagow, G.; Saleh, A.; Barnes, P.L.; Rosenthal, W.; Krug, E.C.; Hauck, L.M. Sediment and nutrient modeling for TMDL development and implementation. Trans. ASAE 2006, 49, 967–986. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.V.; Arnold, J.G.; Demissie, M. Hydrological modeling of the Iroquois river watershed using HSPF and SWAT. J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating three hydrological distributed watershed models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef]
- Saxton, K.; Willey, P. The spaw model for agricultural field and pond hydrologic simulation. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2010; pp. 400–435. [Google Scholar]
- Krysanova, V.; White, M. Advances in water resources assessment with SWAT—An overview. Hydrol. Sci. J. 2015, 60, 771–783. [Google Scholar] [CrossRef]
- Volk, M.; Bosch, D.; Nangia, V.; Narasimhan, B. Swat: Agricultural water and nonpoint source pollution management at a watershed scale. Agric. Water Manag. 2016, 175, 1–3. [Google Scholar] [CrossRef]
- Bach, M.; Huber, A.; Frede, H.G. Input pathways and river load of pesticides in Germany--a national scale modeling assessment. Water Sci. Technol. 2001, 43, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Boithias, L.; Sauvage, S.; Taghavi, L.; Merlina, G.; Probst, J.L.; Perez, J.M. Occurrence of metolachlor and trifluralin losses in the save river agricultural catchment during floods. J. Hazard. Mater 2011, 196, 210–219. [Google Scholar] [CrossRef] [PubMed]
- Huber, A.; Bach, M.; Frede, H.G. Modeling pesticide losses with surface runoff in Germany. Sci. Total Environ. 1998, 223, 177–191. [Google Scholar] [CrossRef]
- Neumann, M.; Schulz, R.; Schäfer, K.; Müller, W.; Mannheller, W.; Liess, M. The significance of entry routes as point and non-point sources of pesticides in small streams. Water Res. 2002, 36, 835–842. [Google Scholar] [CrossRef]
- Tang, X.; Zhu, B.; Katou, H. A review of rapid transport of pesticides from sloping farmland to surface waters: Processes and mitigation strategies. J. Environ. Sci. 2012, 24, 351–361. [Google Scholar] [CrossRef]
- Brown, C.D.; Dubus, I.G.; Fogg, P.; Spirlet, M.; Gustin, C. Exposure to sulfosulfuron in agricultural drainage ditches: Field monitoring and scenario-based modelling. Pest Manag. Sci. 2004, 60, 765–776. [Google Scholar] [CrossRef]
- Leu, C.; Singer, H.; Stamm, C.; Muller, S.R.; Schwarzenbach, R.P. Variability of herbicide losses from 13 fields to surface water within a small catchment after a controlled herbicide application. Environ. Sci. Technol. 2004, 38, 3835–3841. [Google Scholar] [CrossRef]
- Radović, T.T.; Grujić, S.D.; Kovačević, S.R.; Laušević, M.D.; Dimkić, M.A. Sorption of selected pharmaceuticals and pesticides on different river sediments. Environ. Sci. Pollut. Res. 2016, 23, 25232–25244. [Google Scholar] [CrossRef]
- Love, B.J.; Einheuser, M.D.; Nejadhashemi, A.P. Effects on aquatic and human health due to large scale bioenergy crop expansion. Sci. Total Environ. 2011, 409, 3215–3229. [Google Scholar] [CrossRef] [PubMed]
- Vonberg, D.; Vanderborght, J.; Cremer, N.; Putz, T.; Herbst, M.; Vereecken, H. 20 years of long-term atrazine monitoring in a shallow aquifer in western Germany. Water Res. 2014, 50, 294–306. [Google Scholar] [CrossRef] [PubMed]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute, USDA Agricultural Research Service: College Station, TX, USA, 2011.
- Soil & Water Assessment Tool Software. Available online: https://swat.tamu.edu/software/ (accessed on 10 September 2016).
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J.G. Arcswat Interface for Swat2012. User’s Guide; Texas Water Resources Institute, USDA Agricultural Research Service: College Station, TX, USA, 2013.
- Bannwarth, M.A.; Grovermann, C.; Schreinemachers, P.; Ingwersen, J.; Lamers, M.; Berger, T.; Streck, T. Non-hazardous pesticide concentrations in surface waters: An integrated approach simulating application thresholds and resulting farm income effects. J. Environ. Manag. 2016, 165, 298–312. [Google Scholar] [CrossRef] [PubMed]
- Bannwarth, M.A.; Sangchan, W.; Hugenschmidt, C.; Lamers, M.; Ingwersen, J.; Ziegler, A.D.; Streck, T. Pesticide transport simulation in a tropical catchment by SWAT. Environ. Pollut. 2014, 191, 70–79. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Zhang, M. Watershed modelling of hydrology and water quality in the Sacramento river watershed, California. Hydrol. Process. 2012, 27, 236–250. [Google Scholar] [CrossRef]
- Fohrer, N.; Dietrich, A.; Kolychalow, O.; Ulrich, U. Assessment of the environmental fate of the herbicides flufenacet and metazachlor with the SWAT model. J. Environ. Qual. 2014, 43, 75–85. [Google Scholar] [CrossRef]
- Lescot, J.-M.; Bordenave, P.; Petit, K.; Leccia, O. A spatially-distributed cost-effectiveness analysis framework for controlling water pollution. Environ. Model. Softw. 2013, 41, 107–122. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M. Modeling effectiveness of agricultural bmps to reduce sediment load and organophosphate pesticides in surface runoff. Sci. Total Environ. 2011, 409, 1949–1958. [Google Scholar] [CrossRef]
- Singh, G.; Saraswat, D.; Sharpley, A. A sensitivity analysis of impacts of conservation practices on water quality in L’anguille river watershed, Arkansas. Water 2018, 10, 443. [Google Scholar] [CrossRef]
- Ahmadi, M.; Records, R.; Arabi, M. Impact of climate change on diffuse pollutant fluxes at the watershed scale. Hydrol. Process. 2013, 28, 1962–1972. [Google Scholar] [CrossRef]
- Matamoros, D. Predicting River Concentrations of Pesticides from Banana Plantations under Data-Poor Conditions. Ph.D. Thesis, Ghent University, Gent, Belgium, 2004; p. 206. [Google Scholar]
- Vasco, A.N.; Netto, A.d.O.A.; Britto, F.B.; da Silva, M.G. SWAT model for in potential contamination a tributary of the Rio São Francisco, Brazil. Sci. Plena 2017, 13, 10. [Google Scholar] [CrossRef][Green Version]
- Ligaray, M.; Kim, M.; Baek, S.; Ra, J.S.; Chun, A.J.; Park, Y.; Boithias, L.; Ribolzi, O.; Chon, K.; Cho, H.K. Modeling the fate and transport of malathion in the Pagsanjan-lumban basin, Philippines. Water 2017, 9, 451. [Google Scholar] [CrossRef]
- Bautista-ÁValos, D.; Cruz-CÁRdenas, G.; Moncayo-Estrada, R.; Silva GarcÍA, J.T.; Estrada-Godoy, F. Aplicación del modelo swat para evaluar la contaminación por fuentes difusas en la subcuenca del lago de chapala, México. Rev. Int. Contam. Ambient. 2014, 30, 263–274. [Google Scholar]
- Kimwaga, R.J.; Mashauri, D.A.; Bukirwa, F.; Banadda, N.; Wali, U.G.; Nhapi, I. Development of best management practices for controlling the non-point sources of pollution around lake Victoria using SWAT model: A case of simiyu catchment Tanzania. Open Environ. Eng. J. 2012, 5, 77–83. [Google Scholar] [CrossRef]
- Luo, Y.; Su, B.; Yuan, J.; Li, H.; Zhang, Q. GIS techniques for watershed delineation of SWAT model in plain polders. Procedia Environ. Sci. 2011, 10, 2050–2057. [Google Scholar] [CrossRef]
- Omran, A.; Dietrich, S.; Abouelmagd, A.; Michael, M. New ArcGIS tools developed for stream network extraction and basin delineations using python and java script. Comput. Geosci. 2016, 94, 140–149. [Google Scholar] [CrossRef]
- Jha, M.; Gassman, P.W.; Secchi, S.; Gu, R.; Arnold, J. Effect of watershed subdivision on SWAT flow, sediment, and nutrient predictions1. J. Am. Water Resour. Assoc 2007, 40, 811–825. [Google Scholar] [CrossRef]
- MAGAP. Mapas Provinciales. Available online: http://geoportal.agricultura.gob.ec/mapas-provinciales (accessed on 9 September 2016).
- Nielsen, A.; Trolle, D.; Me, W.; Luo, L.; Han, B.-P.; Liu, Z.; Olesen, J.E.; Jeppesen, E. Assessing ways to combat eutrophication in a Chinese drinking water reservoir using SWAT. Mar. Freshw. Res. 2013, 64, 475–492. [Google Scholar] [CrossRef]
- Stehr, A.; Debels, P.; Romero, F.; Alcayaga, H. Hydrological modelling with swat under conditions of limited data availability: Evaluation of results from a Chilean case study. Hydrol. Sci. J. 2008, 53, 588–601. [Google Scholar] [CrossRef]
- Arias-Hidalgo, M.; Villa-Cox, G.; Griensven, A.V.; Solórzano, G.; Villa-Cox, R.; Mynett, A.E.; Debels, P. A decision framework for wetland management in a river basin context: The “abras de mantequilla” case study in the Guayas river basin, Ecuador. Environ. Sci. Policy 2013, 34, 103–114. [Google Scholar] [CrossRef]
- Shuttle Radar Topography Mission. Available online: https://www2.jpl.nasa.gov/srtm/ (accessed on 9 September 2016).
- Fischer, G.; Nachtergaele, F.; Prieler, S.; van Velthuizen, H.T.; Verelst, L.; Wiberg, D. Global Agro-Ecological Zones Assessment for Agriculture (Gaez 2008); IIASA, FAO: Rome, Italy, 2008. [Google Scholar]
- Instituto Geografico Militar. Visor Geografico. Available online: http://www.geoportaligm.gob.ec/portal/ (accessed on 10 September 2016).
- Warnaars, T.; de Jong, F. Watch Water and Global Change. Available online: http://www.eu-watch.org/data_availability (accessed on 11 September 2016).
- Secretaria del Agua. Available online: https://www.agua.gob.ec (accessed on 10 September 2019).
- Instituto Nacional de Meteorología e Hidrología. Red de Estaciones Meteorologicas e Hidrologicas. Available online: http://www.serviciometeorologico.gob.ec/ (accessed on 10 September 2019).
- Monteiro, J.A.F.; Strauch, M.; Srinivasan, R.; Abbaspour, K.; Gücker, B. Accuracy of grid precipitation data for brazil: Application in river discharge modelling of the Tocantins catchment. Hydrol. Process. 2015, 30, 1419–1430. [Google Scholar] [CrossRef]
- Essou, G.R.C.; Sabarly, F.; Lucas-Picher, P.; Brissette, F.; Poulin, A. Can precipitation and temperature from meteorological reanalyses be used for hydrological modeling? J. Hydrometeorol. 2016, 17, 1929–1950. [Google Scholar] [CrossRef]
- Yew Gan, T.; Dlamini, E.M.; Biftu, G.F. Effects of model complexity and structure, data quality, and objective functions on hydrologic modeling. J. Hydrol. 1997, 192, 81–103. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for europe: Calibration and uncertainty of a high-resolution large-scale swat model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large rwer basin with point and nonpoint sources. J. Am. Water Resour. Assoc. 2007, 37, 1169–1188. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, L.; Liao, Q.; Liu, R.; Hong, Q. Impact of spatial rainfall variability on hydrology and nonpoint source pollution modeling. J. Hydrol. 2012, 472–473, 205–215. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Bosch, D.D. Problems and potential of autocalibrating a hydrologic model. Trans. ASABE 2005, 48, 1025–1040. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Goethals, P.L.M.; Forio, M.A.E. Advances in ecological water system modeling: Integration and leanification as a basis for application in environmental management. Water 2018, 10, 1216. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool User’s Manual Version 2000; Technical Report; Texas Water Resources Institute: College Station, TX, USA, 2002. [Google Scholar]
- Refsgaard, J.C. Parameterisation, calibration and validation of distributed hydrological models. J. Hydrol. 1997, 198, 69–97. [Google Scholar] [CrossRef]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M.; Volk, M.; Srinivasan, R. Introduction to SWAT+, a completely restructured version of the soil and water assessment tool. J. Am. Water Resour. Assoc. 2016, 53, 115–130. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The soil and water assessment tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Letcher, R.A.; Norton, J.P. Ten iterative steps in development and evaluation of environmental models. Environ. Model. Softw. 2006, 21, 602–614. [Google Scholar] [CrossRef]
- Strauch, M.; Kumar, R.; Eisner, S.; Mulligan, M.; Reinhardt, J.; Santini, W.; Vetter, T.; Friesen, J. Adjustment of global precipitation data for enhanced hydrologic modeling of tropical andean watersheds. Clim. Chang. 2017, 141, 547–560. [Google Scholar] [CrossRef]
- Wahren, F.T.; Julich, S.; Nunes, J.P.; Gonzalez-Pelayo, O.; Hawtree, D.; Feger, K.H.; Keizer, J.J. Combining digital soil mapping and hydrological modeling in a data scarce watershed in north-central Portugal. Geoderma 2016, 264, 350–362. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).