Abstract
In some arid regions, groundwater is the only source of water for human needs, so understanding groundwater potential is essential to ensure its sustainable use. In this study, three machine learning models (Genetic Algorithm for Rule-Set Production (GARP), Quick Unbiased Efficient Statistical Tree (QUEST), and Random Forest (RF)) were applied and verified for spatial prediction of groundwater in a mountain bedrock aquifer in Piranshahr Watershed, Iran. A spring location dataset consisting of 141 springs was prepared by field surveys, and from this three different sample datasets (S1–S3) were randomly generated (70% for training and 30% for validation). A total of 10 groundwater conditioning factors were prepared for modeling, namely slope percent, relative slope position (RSP), plan curvature, altitude, drainage density, slope aspect, topographic wetness index (TWI), terrain ruggedness index (TRI), land use, and lithology. The area under the receiver operating characteristic curve (AUC) and true skill statistic (TSS) were used to evaluate the accuracy of models. The results indicated that all models had excellent goodness-of-fit and predictive performance, but that RF (AUCmean = 0.995, TSSmean = 0.89) and GARP (AUCmean = 0.957, TSSmean = 0.82) outperformed QUEST (AUCmean = 0.949, TSSmean = 0.74). In robustness analysis, RF was slightly more sensitive than GARP and QUEST, making it necessary to consider several random partitioning options for preparing training and validation groups. The outcomes of this study can be useful in sustainable management of groundwater resources in the study region.
1. Introduction
Groundwater is the most vital natural resource in many arid and semi-arid regions, where it is often the only source of water for human needs. Groundwater resources are related to some important social issues such as environment, resources, and population. Population growth leads to increasing demand for water in the domestic, industrial, and agricultural sectors. In both rural and urban areas in arid and semi-arid regions, almost 90% of all water used primarily derives from groundwater [1]. As the demand for groundwater increases around the world, groundwater potential mapping is becoming an essential tool in enabling successful groundwater management schemes, determination, and safety [2].
The methods used for groundwater potential mapping can be grouped into two main categories: knowledge-driven techniques based on the conceptual component and data-driven techniques based on the empirical component of groundwater evaluations. The knowledge-driven techniques, e.g., analytical hierarchy process (AHP), are based on expert experience [3,4] and are thus affected by the knowledge and subjectivity of experts, while they are also generally site-specific. The data-driven techniques involve probabilistic, statistical, and data mining approaches, and the quality and quantity of data are the major characteristics affecting the predictive accuracy. In the literature, various types of probabilistic and statistical techniques utilizing bivariate and multivariate methods have been employed for preparing groundwater potential zone maps such as frequency ratio [5,6], the weight-of-evidence method [7], Dempster-Shafer theory [8,9], logistic regression [10,11], evidential belief function [12,13], certainty factor [14,15], statistical index [9], and index of entropy [16]. In recent years, machine learning techniques (MLTs) have been applied for mapping of groundwater potential. Various MLTs, such as aquifer sustainability factor [17], classification and regression tree [18], random forest [19,20,21], boosted regression tree [22], maximum entropy [19], artificial neural network model [23], and generalized additive model [2], have been found to be helpful for modeling groundwater potential. In previous studies, MLTs have provided better accuracy in many situations due to their ability to handle, in a robust manner, data characterized by a non-linear format, representing different scales, and deriving from different sources [24,25,26]. Recently, Chen et al. [27] devised methodology for preparing groundwater potential maps that involves kernel logistic regression, random forest, and alternating decision tree models. The results of their research indicated that the artificial intelligence technique can be considered an accurate and valid approach for groundwater potential mapping. Bui et al. [28] proposed a hybrid computational intelligence technique, “AB-ADTree”, which is a combination of alternating decision tree classifier and AdaBoost ensemble, for groundwater potential mapping and compared it with other models, including single ADTree, support vector machine, stochastic gradient descent, logistic model tree, logistic regression, and random forest (RF). The results revealed that the hybrid AB-ADTree was a robust and powerful model for groundwater potential mapping in the study area, and significantly improved the predictive capability of the ADTree-based classifier [28]. Davoudi Moghaddam et al. [29] evaluated the effect of sample size on the accuracy of various individual and hybrid techniques, including adaptive neuro-fuzzy inference system, ANFIS-imperial competitive algorithm, alternating decision tree, and RF, to model groundwater potential for a number of springs ranging from 177 to 714. The outcomes of their study provide valuable reference and practical guidelines for choosing machine learning models when a complete spring inventory in a watershed is unavailable.
The aim of the present study was to delineate potential zones for groundwater springs by employing Genetic Algorithm for Rule-Set Production (GARP), Quick Unbiased Efficient Statistical Tree (QUEST), and Random Forest (RF), three state-of-the-art machine-learning models. The GARP modeling technique uses a training and testing process to analyze the relationships between environmental variables and spatial data. A benefit of the GARP model compared with other models is that it allows various outputs to be run to reach an optimum result [30]. On the other hand, the QUEST model has many benefits over other algorithms, as it is a fast, efficient, and impartial statistical tree, it employs an unbiased or linear variable selection model, and it applies imputation instead of substitute splits to handle missing values [31]. The RF model, a modern nonparametric method, has proven to be one of the best learning techniques in recent years. The RF model can be applied for a large dataset and can make precise classifications [32].
All three models can be used for accurate identification of complex relationships between variables in a dataset [33]. They were used here to analyze the relationship between groundwater occurrence and hydrogeological and geological parameters that act as conditioning factors for groundwater occurrence. The novelty of this research and its contribution to the literature is that it describes, for the first time, application of the GARP and QUEST models in groundwater research in a mountain bedrock aquifer (north-western Iran). The results can be useful in future natural resources planning and management. Specific objectives of the study were to: (i) spatially predict groundwater potential by applying the GARP, QUEST, and RF models; (ii) assess the importance of selected geo-environmental spring-affecting factors in modeling; (iii) compare the predictive performance of these techniques by means of cutoff-dependent and cutoff-independent indices, and (iv) conduct robustness analysis.
2. Materials and Methods
2.1. Description of the Study Area
The study area was Piranshahr Watershed (36°39′–36°56′ N; 44°49′–45°11′ E) in Western Azerbaijan province, Iran, which is characterized by mountainous morphology and occupies an area of approximately 42,617 ha (Figure 1). The topographical elevation of the watershed varies between 1433 and 3563 m above mean sea level. Mean annual precipitation is 650 mm and most falls in the form of snow in winter. According to the Emberger classification, Piranshahr Watershed is characterized by a cold semi-arid climate. Rangeland is the major land use in the watershed, occupying 68.5% of total area. The lithology of the watershed varies, with 45% falling within the Precambrian units and Late Cretaceous units, including amphibolite and diabase, respectively (Table 1) [34]. Evaluation of groundwater is vital within this area, because groundwater supplies drinking water and irrigation requirements, and many people living in the area depend on irrigated and dryland farming for their livelihood.
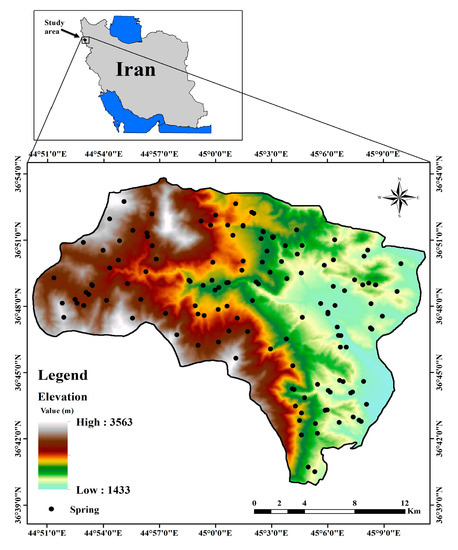
Figure 1.
Map of the study area in north-western Iran, showing the 141 spring locations used in the present study.

Table 1.
Lithology of the study area.
2.2. Methodology
In this study, we used groundwater springs as good indications of groundwater availability for groundwater potential mapping. This is because in the study area, as in most other mountainous environments, few hydrogeological and hydrological data (i.e., groundwater levels, well yields, and stream discharge) are available due to a lack of piezometric wells in these high-elevation settings [35]. The methodology used in this research comprised several steps. First, the datasets were prepared for modeling. GARP, QUEST, and RF algorithms were then applied for mapping of groundwater potential. Next, the relative importance of conditioning factors was determined. Then, the area under the ROC curve (AUC), and true skill statistic (TSS) were applied for validation of algorithms in the novel application tested in this study. Finally, robustness analysis was applied to compare the capabilities of the three machine learning models (Figure 2).
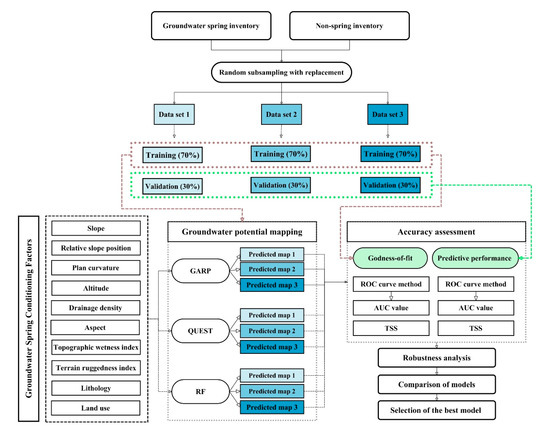
Figure 2.
Methodological flowchart of the study. GARP, Genetic Algorithm for Rule-Set Production; QUEST, Quick Unbiased Efficient Statistical Tree; RF, Random Forest; ROC, receiver operating characteristics; AUC, area under the receiver operating characteristic curve; TSS, true skill statistic.
2.2.1. Springs Dataset
The occurrence locations of springs depict groundwater potential across the study area. Hence, a total of 141 spring occurrence locations in Piranshahr Watershed were determined by field surveys and using handheld GPS. For this modeling, the spring inventory locations were randomly divided into two groups, of 70% (99 spring locations) and 30% (42 spring locations), for training and validation steps, respectively. To clarify, the validation group was determined through randomization, and was not applied in model building. It is generally suggested in spatial modeling to apply approximately equal proportions of spring-present (1) and spring-absent (0) pixels [10]. Keeping this in mind, the 141 spring-present pixels and 141 randomly generated spring-absent pixels were applied in the modeling. Note that to investigate the robustness of the models, three training and three validation datasets (S1–S3) were created by performing random selection of the dependent variable (spring occurrence locations) in a GIS environment (Figure 3) [36,37]. The training datasets included 99 spring occurrence locations, while the validation datasets consisted of 42 spring occurrence locations.
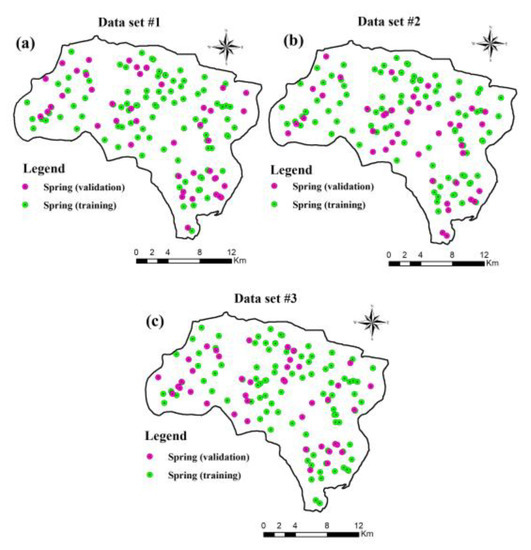
Figure 3.
Sites included in the three sample datasets (S1–S3) used for modeling in the study area, (a) Data set 1; (b) Data set 2; (c) Data set 3.
2.2.2. Geo-Environmental Factors
Drawing on a comprehensive literature review, the most representative groundwater conditioning factors were chosen to model groundwater potential. Regarding data availability, 10 groundwater effective factors were chosen for this investigation, comprising slope percent, relative slope position (RSP), plan curvature, altitude, drainage density, slope aspect, topographic wetness index (TWI), terrain ruggedness index (TRI), land use, and lithology.
To evaluate the multicollinearity of groundwater conditioning factors and to avoid bias, we applied the variance inflation factor (VIF) and tolerance (TOL) indices, which are customarily used to estimate multicollinearity of predictive variables in geospatial modeling [38]. According to the literature [38], VIF > 10 or tolerance < 0.1 indicates critical multicollinearity, which itself recommends that the factor has such a strong correlation to others that it should be eliminated from modeling [38].
Then, a vector-type spatial database was extracted by converting groundwater conditioning factors using ArcGIS. A digital elevation model (DEM) with 20 × 20 m grid size was prepared using survey base points, with elevation contours displaying the elevation values extracted from 1:50,000-scale topographic maps. The DEM was used as input to extract thematic maps of slope percent, RSP, plan curvature, altitude, slope aspect, TWI, and TRI (Figure 4a–h).
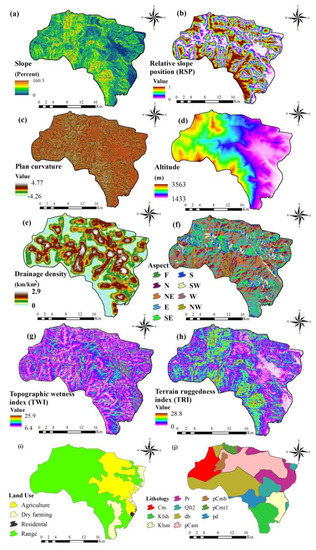
Figure 4.
Maps showing the 10 groundwater conditioning factors considered in groundwater mapping in Piranshahr Watershed, Iran. (a) Slope, (b) relative slope position (RSP), (c) plan curvature, (d) altitude, (e) drainage density, (f) aspect, (g) topographic wetness index (TWI), (h) terrain ruggedness index (TRI), (i) land use, and (j) lithology.
Slope factor has a very significant role in groundwater potential mapping, and therefore a slope percent map of the study area was prepared [29] (Figure 4a). RSP can be applied to identify topographic characteristics such as valleys, ridge tops, flat surfaces, mid-slopes, foot-slopes, and upper slopes, with the value for RSP ranging from 0 (flat surface and valleys) to 1 (upper-slopes and ridge tops) [39]. In this study, a RSP map was prepared using SAGA-GIS (Figure 4b). Regarding plan curvature, positive curvature indicates convex forms, zero curvature represents flat surfaces and negative curvature represents concave forms. A plan curvature map of the study area was prepared using SAGA-GIS (Figure 4c). Elevation has important effects on climate conditions in any area, because of differences in vegetation and soil [40]. Accordingly, an altitude map of the study area was prepared (Figure 4d). Drainage density is calculated as the ratio of the sum of drainage lengths in a grid cell and the area of the corresponding cell, and displays the potential water flow throughout the study area [6]. Here, the drainage density map was calculated considering a 20 × 20 m grid cell (Figure 4e). Slope aspect in the study area was classified into nine groups, including flat land and eight directions (Figure 4f).
Topography plays an essential role in the spatial variation of hydrological characteristics such as soil moisture and groundwater flow, and hence secondary topographic indices can be applied to describe spatial soil moisture patterns [41]. Topographic wetness index (TWI) is a subordinate topographic factor within the runoff model, defined as [41]:
where ß is the cumulative upslope area draining through a point (per unit contour length) and tan is the slope angle at the point. The tendency of water to accumulate at any point in a catchment (in terms of ß) and the tendency of gravitational forces to move that water downslope (illustrated in terms of tan as an approximate hydraulic gradient) are reflected by the index. Water infiltration mainly depends on material characteristics such as permeability, soil strength, and pore water pressure. Consequently, TWI was considered as a contributing factor in this study (Figure 4g).
Terrain ruggedness index (TRI) is the mean difference between a central pixel and its surrounding cells and was used here to quantify landscape heterogeneities (Figure 4h). It is defined as [42]:
where zc is the elevation of a central cell and zi is the elevation of one of the eight neighboring cells (i = 1, 2, 3, …, 8).
TRI = (∑(zc − zi)2)2
Using Landsat images and the maximum likelihood and supervised classification algorithms, a land use map of the study area with spatial resolution 20 × 20 m was generated. Four main land use categories were identified: agriculture, dryland farming, residential, and rangeland (Figure 4i). One of the most significant factors in predicting groundwater potential zones is lithology. Using the 1:100,000-scale geological map, a lithology map of the study area was obtained and classified into 10 categories (Figure 4j, Table 1).
All 10 conditioning factors were converted to a raster grid with 20 × 20 m cells for application of the GARP, QUEST, and RF models.
2.2.3. Description of Models
Genetic Algorithm for Rule-Set Production (GARP)
The GARP model is inspired by algorithms of genetic evolution and is a technique that was particularly developed in the context of ecological niche modeling [30]. GARP develops predictive techniques consisting of a set of conditional rules in the form of ‘if-then’ statements that explain the ecological ‘niches’ of the species [43]. Niches are recognized by searching iteratively for non-random correlations between known locations of species and a variety of environmental factors. The GARP technique consists of a set of mathematical rules based on environmental conditions. Given a particular environmental condition, if all rules are satisfied, the technique predicts presence of the species. Different types of rules are possible, including atomic, logistic regression, negated bioclimatic envelope, and bioclimatic envelope. All sets of rules are an individual of a population in the representative context of a genetic algorithm [44]. GARP creates an initial population, which is assessed in each iteration to examine if the problem has converged to a solution. Genetic operators (join, cross-over, and mutation) are used in the start of each new iteration on the best individuals from previous steps, generating a new population of solutions. GARP is therefore a non-deterministic technique that generates boolean responses (present/absent) for each various environment condition.
The GARP model was applied here, as DesktopGarp [45], to predict groundwater potential in the study area, as a presence-only modeling tool to analyze the relationship between the groundwater potential dataset and geo-environmental factors through an iterative process, applying conditional rules for modeling that enhanced the stability of model output [46]. DesktopGarp is an integrated, user-friendly software and is able to import GIS layers of groundwater conditioning variables directly, with presence-only occurrence data [47]. This feature makes application of this model easier, since absence or non-occurrence data are not always available, especially in data-scarce areas such as Iran and Middle Eastern countries. However, with GARP, which is claimed to be robust with its default settings, there is a need to be careful with some model parameters, such as the size of quad-rates for the background environmental variable layers and the extent of the study area [47]. The only data needed as input for DesktopGarp in the present application were the spring occurrence locations and the environmental datasets formed of groups of environmental factors. Performing multiple runs to achieve various outputs of the GARP model and applying the best-subset method are vital in choosing the best output with optimum parameters. The set of techniques that obtains harmony between omission (sensitivity) and commission (specificity) error thresholds is defined by the user [46,48]. The output of GARP in this case was a collection of grids of the study area, which was applied in a GIS environment to identify areas with groundwater potential [46].
Quick Unbiased Efficient Statistical Tree (QUEST)
The QUEST model is a binary split-decision tree model for data mining and classification that yields subsets of data that are as homogeneous as possible with respect to the response variable [48,49]. QUEST is an efficient, quick, unbiased, and statistical tree-structured classification algorithm that produces a growing binary-split decision tree [50]. In addition, it employs a sequential tree growing technique, which uses a linear discriminate analysis method in splitting of tree nodes. This has many benefits over recursive tree construction techniques such as classification and regression tree (CART) [51]. Furthermore, it is unbiased in selecting splitting rules and does not use an exhaustive variable search routine [52]. By using an unbiased variable selection method in modeling, QUEST has negligible bias [53]. As a result, it can easily cope with categorical and continuous factors [50,54,55]. In other words, the process of tree growing in QUEST consists of choosing a split predictor, choosing a split point for the selected predictor, and stopping. In this technique, only univariate splits are considered. The following steps are involved in a choosing split predictor: First, for each continuous predictor X, carry out an ANOVA F-test that tests if all the various classes of the dependent variable Y have the same mean of X, and compute the p value in accord with the F statistics. For each categorical predictor, carry out Pearson’s X2-test of Y and the independence of X, and compute the p value in accordance with the X2 statistics. Then, find the predictor with the smallest p value and denote it X∗. If this smallest p value is less than α/M, where α ∈ (0, 1) is a user-specified level of significance and 𝑀 is the total number of predictor variables, predictor X∗ is chosen as the split predictor for the node. If not, for each continuous predictor X, compute Levene’s F statistic in accordance with the absolute deviation of X from its class mean to test if the variances of X for various classes of Y are the same, and compute the p value for the test. Then, find the predictor with the smallest p value and denote it X∗∗. Finally, if this smallest p value is less than α/(M + M1), where M1 is the number of continuous predictors, X∗∗ is chosen as the split predictor for the node. Otherwise, this node is not split [56].
Random Forest (RF)
The RF model is an ensemble classifier that consists of many decision trees, applying the random forest algorithm of Breiman for classification and regression [57]. When classifying a new object from an input vector, RF runs the input vector down each of the trees in the forest. Each tree gives a classification (which is usually called the tree ‘votes’ for that class). The forest chooses the classification with the most votes (from all the trees in the forest). The RF model is not sensitive to the problem of multicollinearity; it manages correlated variables well. With large databases, it runs efficiently and it can process thousands of input variables without variable deletion. It prepares estimates of variables that are important in the classification, it is robust with unbalanced datasets and missing data, and it offers an experimental technique for detecting variable interactions [57]. RF requires the modeler to choose two parameters: the number of variables and the number of trees. Furthermore, RF provides two importance ranking indices, “mean decrease Gini” and “mean decrease accuracy” (also termed percent increase in mean square error (MSE)) [58]. The higher the MSE percentage, the greater the importance of the independent variable considered [59]. These indices can be applied to reveal the sensitivity of the model to input variables and to help decrease uncertainty. In this study, this model was used by applying the ‘randomForest’ package in R. and the default of 500 trees (parameter “ntree”) was used as error rate stabilized at 100–150 trees [26]. A random one-third of predictor variables was used to carry out data partitioning at each node (parameter “mtry”). Two-thirds of the overall dataset were randomly chosen and utilized to create the RF model, and the other one-third retained for testing the model.
2.2.4. Accuracy Assessment of Models
The outputs of models (maps) are not reliable without validation [60,61]. In this study, the accuracy and suitability of the models was assessed using both cutoff-dependent and cutoff-independent methods. One of the most widely used metrics of performance is receiver operating characteristics (ROC) curve, which has been used in many hydrological and geo-environmental studies such as susceptibility and potential modeling of flood inundation, landslide, gully erosion, and groundwater [62,63]. The area under the ROC curve (AUC-ROC), a cutoff-independent metric, was constructed in this study using groundwater potential maps and the spring locations allocated to the training dataset [64,65]. Its value ranges from 0 to 1, with higher values indicating better model performance [66,67]. To plot and calculate the area under the ROC curve, the validation dataset was applied.
Among cutoff-dependent criteria, the true skill statistic (TSS) was selected in this study. TSS can be computed as [68]:
where TPR describes true positive rate and FPR depicts false positive rate. TPR and FPR can be computed by applying the following equations [69]:
where TP = true positives, TN = true negatives, FP = false positives (Error Type I), and FN = false negatives (Error Type II). TP and TN are the numbers of pixels that are correctly grouped, while FP and FN are the numbers of pixels that are erroneously grouped. The value of TSS ranges from −1 to +1, where −1 indicates that predictive performance is not better than that of a random model, 0 indicates an indiscriminate model, and +1 indicates a perfect model [68].
TSS = TPR − FPR
The robustness of a model can be investigated by assessing the change in model efficiency when small changes in input data are made [37,70]. In this study, three datasets were applied for both training and validation steps. The three models were run using the training datasets, and then verified using the validation datasets. “The robustness of the predictive model can be defined as the constancy of the model’s prediction accuracy when the training and validation data sets are changed” [71]. The robustness of the models was computed by differentiating the maximum and minimum accuracy values regarding each evaluation criterion [36]:
where RTSS, and RAUC are the robustness of a model in terms of TSS and AUC, respectively, TSSmax and AUCmax are the maximum values of accuracy among the three datasets, and TSSmin and AUCmin are the minimum values of accuracy among the three datasets. These analyses were carried out in both training and validation steps.
RTSS = TSSmax − TSSmin
RAUC = AUCmax − AUCmin
3. Results
3.1. Multicollinearity Analysis of Predictive Factors
The outputs of multicollinearity analysis revealed that the highest VIF value was 3.547 and the lowest TOL value was 0.238, which shows that there was no multicollinearity among the predictive factors (Table 2). Hence, all the predictive factors were applied in modeling.

Table 2.
Multicollinearity of predictive factors based on the variance inflation factor (VIF) and tolerance (TOL) indices.
3.2. Application of the Models for Groundwater Potential Mapping
Figure 5, Figure 6 and Figure 7 show groundwater potential maps produced by the GARP, QUEST, and RF models, respectively, for the three different training datasets (a–c).
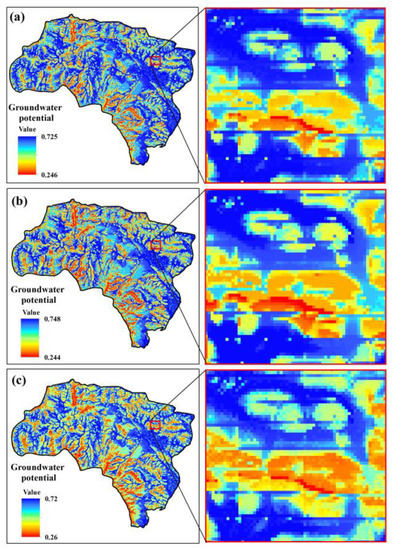
Figure 5.
Groundwater potential maps produced by GARP and three sample datasets (a–c).
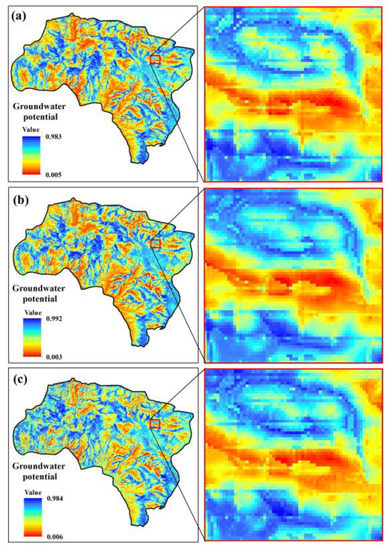
Figure 6.
Groundwater potential maps produced by QUEST and three sample datasets (a–c).
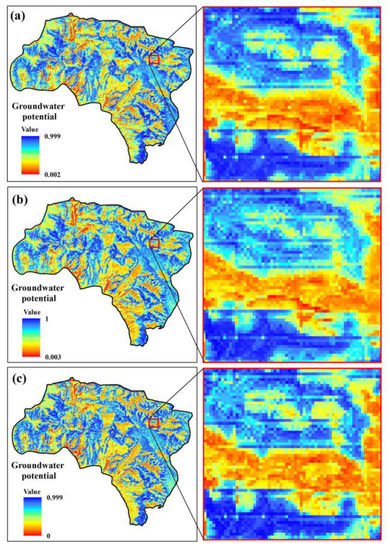
Figure 7.
Groundwater potential maps produced by RF and three sample datasets (a–c).
The groundwater potential maps created by sample dataset 3 (because of higher accuracy in validation step) and the GARP (Figure 5c), QUEST (Figure 6c), and RF (Figure 7c) models were then imported into ArcGIS 10.3 software and, using the quantile classification scheme [19,71], categorized into five different classes (very low, low, moderate, high, and very high potential) (Figure 8).
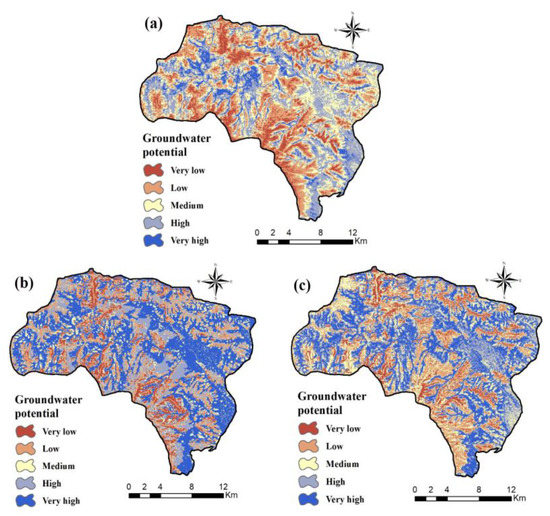
Figure 8.
Groundwater potential maps produced by sampling dataset 3 and (a) GARP, (b) QUEST, and (c) RF.
Table 3 shows the watershed area (%) occupied by these five groundwater potential classes determined according to the different models and sampling dataset 3 (Figure 8).

Table 3.
Watershed area occupied by five groundwater potential classes according to the GARP, QUEST, and RF models.
3.3. Accuracy of the Groundwater Potential Maps
The results of goodness-of-fit are shown in Table 4 and Figures S1 to S9. For GARP, performance values ranged from 0.81 to 0.86 (mean = 0.82) based on TSS, and from 0.952 to 0.965 (mean = 0.957) based on AUC-ROC. For RF, TSS and AUC-ROC values were 0.86-0.94 (mean = 0.89), and 0.99–1 (mean = 0.995), respectively. Accuracy assessment of QUEST results indicated that TSS varied between 0.69 and 0.79 (mean = 0.74), and AUC-ROC ranged between 0.943 and 0.957 (mean = 0.949). Hence, all three models showed good-excellent performance. In fact, the TSS and AUC-ROC criteria demonstrated substantial agreement between the trained models and reality. However, as the training datasets were applied to generate the models, they could not be used to evaluate their prediction capability. In other words, the goodness-of-fit step only showed how well the models fit the training dataset, and could not be interpreted as indicating the prediction ability of the model [38]. The validation analysis showed how well the models predicted groundwater potential in the study area.

Table 4.
Goodness-of-fit of the machine learning models based on different performance evaluation metrics.
In the validation step, the results of the three models were verified by applying validation datasets and the two evaluation criteria (Table 5) (Figures S1–S9). For GARP, TSS varied between 0.74 and 0.81 (mean = 0.78), and AUC-ROC between 0.892 and 0.925 (mean = 0.910). For RF, the TSS value ranged from 0.79 to 0.91 (mean = 0.83), and the AUC-ROC value from 0.893 to 0.946 (mean = 0.925). For the QUEST model, TSS and AUC-ROC values ranged between 0.62 and 0.70 (mean = 0.67) and 0.881 and 0.899 (mean = 0.890), respectively. Thus, the RF model exhibited the highest predictive performance according to both evaluation criteria (TSS = 0.83, AUC-ROC = 0.925), followed by GARP (TSS = 0.78, AUC-ROC = 0.910), and QUEST (TSS = 0.67, AUC-ROC = 0.890). In other words, the validation of the results indicated strong agreement between the distribution of the existing springs (validation dataset) and the predictive maps of the RF model. Based on the accuracy classification, RF and GARP indicated excellent predictive skill (AUC-ROC > 0.9), while the QUEST model exhibited good accuracy (AUC-ROC = 0.8–0.9).

Table 5.
Predictive performance of the machine learning models based on different performance evaluation metrics.
3.4. Robustness Analysis
Model robustness results according to the two different evaluation criteria are presented in Figure 9. There were only slight variations in these results following changes in the training and validation samples. Therefore, it can be concluded that all three models were stable and robust in both the training and validation steps. However, as can be seen in Figure 9a, the stability of GARP (RTSS = 0.070) was slightly better than that of QUEST (RTSS = 0.080) and RF (RTSS = 0.120). As shown in Figure 9b, QUEST (RAUC ≥ 0.018) displayed high stability and robustness, while GARP (RAUC = 0.033) and RF (RAUC = 0.053) showed slight asymmetry in their results. In terms of both RTSS and RAUC, RF showed lower stability than the other models.
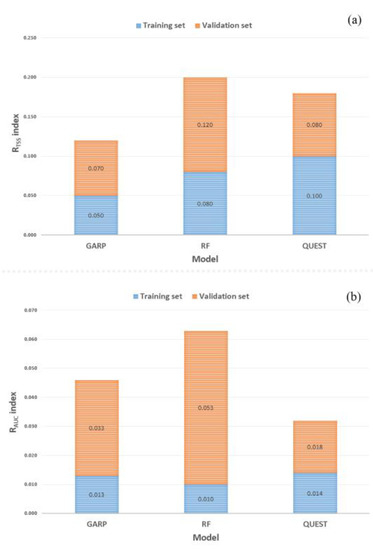
Figure 9.
Robustness of the three models in the training and validation steps, based on two evaluation criteria: (a) true skill statistic (TSS) and (b) area under the receiver operating characteristic curve (AUC).
3.5. Importance Analysis of Predictive Factors
The variable importance assessment in this study was conducted using the RF model. As one of its main benefits, RF can estimate the importance of predictor variables applied in the modeling process using the index percentage increase in mean square error (PIMSE) [59,71]. Table 6 shows the importance of predictor variables in predicting groundwater potential. As can be seen, RSP, lithology, and TWI were the three most important variables for spatially predicting groundwater potential, with PIMSE equal to 82.6%, 69.2%, and 55.1%, respectively.

Table 6.
Results of variable importance analysis of groundwater conditioning factors using the Random Forest (RF) model.
4. Discussion
Machine learning techniques have been gaining popularity in the field of spatial modeling, especially groundwater potential modeling. Machine learning models show particular promise when dealing with the challenge of groundwater potential mapping in mountainous and large regions, which may not have sufficient hydrogeological and geotechnical data to run numerical and/or physically-based models [72]. Thus new models must be developed and their capability and applicability evaluated, to find the most accurate and robust model with the best possible results from the least amount of input data. However, there are various sources of uncertainty in spatial modeling of groundwater potential, including those related to input variables, sampling strategy, and the modeling process [73]. According to Garosi et al. [74], random classification of datasets for training and validation steps can be a significant cause of uncertainty in groundwater potential modeling using groundwater spring occurrence locations. From the validation findings in this study and based on cutoff-dependent and cutoff–independent evaluation criteria, it is obvious that all three models tested showed good to excellent performance in predicting groundwater potential. Importantly, the results demonstrated that the RF model had the highest TSS and AUC values for all training and validation datasets, even when based on various evaluation criteria, but this model exhibited slightly lower robustness (but acceptable) compared with the other models. The values of AUC for the validation dataset showed that GARP and QUEST achieved excellent and good performance, respectively.
An interesting finding was that, while RF was identified as the best model in terms of accuracy, it had slightly lower robustness for groundwater potential modeling using spring occurrence locations. This is partly consistent with findings by Rahmati et al. [20] and Naghibi et al. [75], who concluded that RF is a powerful predictive model that can run accurately with large databases and can process thousands of input variables without variable deletion. Similarly, Davoudi Moghaddam et al. [29] found that RF prepares estimates of the variables that are vital for classification, is robust with unbalanced datasets and missing data, and offers an experimental technique for detecting variable interactions [57]. In an earlier study in the Bojnourd Watershed, Iran, RF also demonstrated excellent performance in groundwater potential modeling [20] and similar findings have been made in some other areas [75,76]. However, as illustrated by the results in the present study, RF was slightly sensitive to random changes in the input data, although its robustness was still within the acceptable range. Thus while the RF model was found to generate more accurate predictions in the present case, it is important to recognize the main sources of variations that influence its robustness.
Furthermore, from Figure 5 and Table 3 it is clear that GARP indicated different repartition of groundwater potential areas than the QUEST and RF models. This can be related to the fact that GARP is a presence-only approach that is appropriate for most cases in which true absence data are lacking. Theoretically, it fits models from background and presence data, whereas other presence-only models either generate pseudo-absence data by sampling points outside the boundary of presence data, or strictly use presence-only modeling [77,78]. GARP projects the realized niche into a geographical space without giving weight to observed absence data, which could cause a poorer fit to the current observed distribution than presence-absence approaches such as RF and QUEST, which are tree-based models [79]. Therefore, the reason why the outputs of QUEST and RF are more similar is because they belong to the same (tree-based) model group. Such models provide a transparent tree-like structure with easily interpreted rules [38]. In addition, they use a type of statistical analysis with no statistical distribution assumption and they can handle data from various scales. Furthermore, they permit identification of homogeneous groups with various potential levels, and facilitate construction of rules for prediction of complex relationships [80]. Overall, according to the groundwater potential maps obtained (Figure 8), central and eastern parts of Piranshahr Watershed have the highest potential for groundwater and should be the subject of further investigation and exploitation.
In addition, credible knowledge of the relationships between predictor variables (e.g., geo-environmental factors, etc.) and the respective target variable (i.e., groundwater potential) can help decision-makers achieve sustainable groundwater management, but these associations are still somewhat complicated and poorly documented [29]. The results of variable importance analysis using the RF model indicated higher importance of RSP, lithology, TWI, altitude, and drainage density, which shows the significant impact of DEM-derived factors on groundwater potential modeling (Table 3). Application of RSP is novel in the field of groundwater potential mapping and proved here to be a significant conditioning factor in the modeling process. Higher contributions of the RSP and lithology factors have also been reported in a previous study on groundwater resources [71]. Overall, DEM-derived factors were found to be very important in the present study. This could be related to the impact of topography on flow speed on slopes, and subsequently on permeability and erosion ratio. Therefore, these factors should be prepared with higher accuracy and finer spatial resolution. Focusing on DEM-derived factors might increase the performance of the models. Different groundwater conditioning factors are reported to be important in groundwater potential modeling, but so far there are no comprehensive and universal guidelines on choosing independent variables among geo-environmental factors. For example, Rahmati et al. [8] mention altitude, drainage density, and lithology as the most significant factors, while Naghibi et al. [2] list NDVI, altitude, and slope angle as the most significant conditioning factors. This lack of agreement on the importance of conditioning factors could be associated with variations in climate, geological, and topographical characteristics between study areas. Importance analysis of conditioning factors is useful for multi-source groundwater studies and solves the problem of high data dimensionality, by eliminating redundant predictor variables [71]. This can help decision-makers allocate resources to accurate determination of variables that significantly affect the accuracy of groundwater potential mapping.
5. Conclusions
This study evaluated the capability of two machine learning techniques, GARP and QUEST, for predicting groundwater potential for the first time, and also compared their capability and robustness with that of RF, a state-of-the-art model. The importance of groundwater conditioning factors was also evaluated. The following main conclusions were reached:
- All three machine learning models showed good-excellent accuracy (AUC > 0.7) in prediction of groundwater potential, although there were some differences between the models in terms of predictive performance and robustness. Thus even when conducting model comparisons using clear criteria, such as prediction performance and robustness, understanding limitations and strengths remains somewhat difficult in model selection and identifying the best model. Here, RF showed the best performance based on two cutoff-dependent and cutoff–independent evaluation criteria, but exhibited slight sensitivity (lack of robustness) to changes in the training/validation data. In terms of pure prediction performance, GARP and QUEST showed slightly lower accuracy than RF. Therefore, RF provides the most accurate groundwater potential mapping, with acceptable robustness.
- Variable importance analysis demonstrated that RSP was the most important groundwater conditioning factor, followed by lithology factor, while slope, aspect, and plan curvature were the least important factors for modeling. These findings could be of practical help for water resources managers in handling the existing uncertain situation and understanding various aspects that affect groundwater potential.
- In future research, other metrics could be included in model comparisons, such as time spent in model generation and prediction calculation. A focus on DEM-derived factors and on obtaining high accuracy data could enhance the performance of the models. In order to raise the accuracy and reduce the uncertainties in models, hybrid modeling can be recommended, as it reduces some problems in classification models such as over-fitting.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/12/3/679/s1. Figure S1: ROC curves of the training and validation steps for the RF model using dataset S1, Figure S2: ROC curves of the training and validation steps for the RF model using dataset S2, Figure S3: ROC curves of the training and validation steps for the RF model using dataset S3, Figure S4: ROC curves of the training and validation steps for the GARP model using dataset S1, Figure S5: ROC curves of the training and validation steps for the GARP model using dataset S2, Figure S6: ROC curves of the training and validation steps for the GARP model using dataset S3, Figure S7: ROC curves of the training and validation steps for the QUEST model using dataset S1, Figure S8: ROC curves of the training and validation steps for the QUEST model using dataset S2, Figure S9: ROC curves of the training and validation steps for the QUEST model using dataset S3.
Author Contributions
Conceptualization, D.D.M. and O.R.; methodology, D.D.M., O.R., A.H.; software, D.D.M. and O.R.; validation D.D.M. and O.R.; investigation, D.D.M., O.R., and A.H.; data curation, D.D.M.; writing—original draft preparation, D.D.M., O.R., A.H., and Z.K.; writing—review and editing, D.D.M., O.R., A.H., and Z.K.; visualization, D.D.M. All authors have read and agree the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank the Iranian Department of Water Resources Management (IDWRM) and Department of Geological Survey of Iran (GSI) for providing necessary data and maps.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Magesh, N.S.; Chandrasekar, N.; Soundranayagam, J.P. Delineation of groundwater potential zones in Theni district, Tamil Nadu, using remote sensing, GIS and MIF techniques. Geosci. Front. 2012, 3, 189–196. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Davoudi Moghaddam, D.; Kalantar, B.; Pradhan, B.; Kisi, O. A comparative assessment of GIS-based data mining models and a novel ensemble model in groundwater well potential mapping. J. Hydrol. 2017, 548, 471–483. [Google Scholar] [CrossRef]
- Rahmati, O.; Nazari Samani, A.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2014, 8, 7059–7071. [Google Scholar] [CrossRef]
- Yin, H.; Shi, Y.; Niu, H.; Xie, D.; Wei, J.; Lefticariu, L.; Xu, S. A GIS-based model of potential groundwater yield zonation for a sandstone aquifer in the Juye Coalfield, Shangdong, China. J. Hydrol. 2017, 557, 434–447. [Google Scholar] [CrossRef]
- Oh, H.J.; Kim, Y.S.; Choi, J.K.; Park, E.; Lee, S. GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J. Hydrol. 2011, 399, 158–172. [Google Scholar] [CrossRef]
- Davoodi Moghaddam, D.; Rezaei, M.; Pourghasemi, H.R.; Pourtaghie, Z.S.; Pradhan, B. Groundwater spring potential mapping using bivariate statistical model and GIS in the Taleghan watershed, Iran. Arab. J. Geosci. 2015, 8, 913–929. [Google Scholar] [CrossRef]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of evidence and artificial neural networks for potential groundwater spring mapping: An application to the Mt. Modino area (Northern Apennines, Italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Rahmati, O.; Melesse, A.M. Application of Dempster–Shafer theory, spatial analysis and remote sensing for groundwater potentiality and nitrate pollution analysis in the semi-arid region of Khuzestan, Iran. Sci. Total Environ. 2016, 568, 1110–1123. [Google Scholar] [CrossRef] [PubMed]
- Haghizadeh, A.; Davoodi Moghaddam, D.; Pourghasemi, H.R. GIS-based bivariate statistical techniques for groundwater potential analysis (an example of Iran). J. Earth Syst. Sci. 2017, 126, 109. [Google Scholar] [CrossRef]
- Ozdemir, A. Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J. Hydrol. 2011, 405, 123–136. [Google Scholar] [CrossRef]
- Chen, W.; Li, H.; Hou, E.; Wang, S.; Wang, G.; Panahi, M.; Li, T.; Peng, T.; Guo, C.; Niu, C. GIS-based groundwater potential analysis using novel ensemble weights-of-evidence with logistic regression and functional tree models. Sci. Total Environ. 2018, 634, 853–867. [Google Scholar] [CrossRef] [PubMed]
- Kordestani, M.D.; Naghibi, S.A.; Hashemi, H.; Ahmadi, K.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using a novel data-mining ensemble model. Hydrogeol. J. 2019, 27, 211–224. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Beheshtirad, M. Assessment of a data-driven evidential belief function model and GIS for groundwater potential mapping in the Koohrang Watershed, Iran. Geocarto Int. 2014, 30, 662–685. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; SamaniNeisani, N.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Hou, E.; Wang, J.; Chen, W. A comparative study on groundwater spring potential analysis based on statistical index, index of entropy and certainty factors models. Geocarto Int. 2018, 33, 754–769. [Google Scholar] [CrossRef]
- Al-Abadi, A.M.; Shahid, S. A comparison between index of entropy and catastrophe theory methods for mapping groundwater potential in an arid region. Environ. Monit. Assess. 2015, 187, 1–21. [Google Scholar] [CrossRef]
- Smith, A.J.; Walker, G.; Turner, J. Aquifer Sustainability Factor: A review of previous estimates. In Proceedings of the Groundwater 2010: The challenge of sustainable management, Canberra, Australia, 31 October–4 November 2010. [Google Scholar]
- Naghibi, A.; Pourghasemi, H.R. A comparative assessment between three machine learning models and their performance comparison by bivariate and multivariate statistical methods for groundwater potential mapping in Iran. Water Resour. Manag. 2015, 29, 5217–5236. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping, a case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Rahmati, O.; Davoudi Moghaddam, D.; Moosavi, V.; Kalantari, Z.; Samadi, M.; Lee, S.; Tien Bui, D. An Automated Python Language-Based Tool for Creating Absence Samples in Groundwater Potential Mapping. Remote Sens. 2019, 11, 1375. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Behzadfar, M. GIS-based multivariate adaptive regression spline and random forest models for groundwater potential mapping in Iran. Environ. Earth Sci. 2016, 75, 665. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Wang, X.; Bin Ahmad, B. Evaluating the usage of tree-based ensemble methods in groundwater spring potential mapping. J. Hydrol. 2020, 583, 124602. [Google Scholar] [CrossRef]
- Lee, S.; Hong, S.M.; Jung, H.S. GIS-based groundwater potential mapping using artificial neural network and support vector machine models: The case of Boryeong city in Korea. Geocarto Int. 2018, 33, 847–861. [Google Scholar] [CrossRef]
- Pham, B.T.; Son, L.H.; Hoang, T.A.; Nguyen, D.M.; Tien Bui, D. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.D.; Pham, B.; Bui, Q.T.; Tran, C.T.; Panahi, M.; Ahmad, B.B.; et al. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Tien Bui, D.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater Spring Potential Mapping Using Artificial Intelligence Approach Based on Kernel Logistic Regression, Random Forest, and Alternating Decision Tree Models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Chapi, K.; Shahabi, H.; Pradhan, B.; Pham, B.T.; Singh, V.P.; Chen, W.; Khosravi, K.; Bin Ahmad, B.; et al. A Hybrid Computational Intelligence Approach to Groundwater Spring Potential Mapping. Water 2019, 11, 2013. [Google Scholar] [CrossRef]
- Davoudi Moghaddam, D.; Rahmati, O.; Panahi, M.; Tiefenbacher, J.; Darabi, H.; Haghizadeh, A.; Torabi Haghighi, O.; Asadi Nalivan, O.; Tien Bui, D. The effect of sample size on different machine learning models for groundwater potential mapping in mountain bedrock aquifers. Catena 2020, 187, 104421. [Google Scholar] [CrossRef]
- Stockwell, D. The GARP modelling system: Problems and solutions to automated spatial prediction. Int. J. Geogr. Inf. Sci. Int. 1999, 13, 143–158. [Google Scholar] [CrossRef]
- Sut, N.; Simsek, O. Comparison of regression tree data mining methods for prediction of mortality in head injury. Expert Syst. Appl. 2011, 38, 15534–15539. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley-Interscience: New York, NY, USA, 2000. [Google Scholar]
- Davoudi Moghaddam, D.; Pourghasemi, H.R.; Rahmati, O. Assessment of the Contribution of Geo-environmental Factors to Flood Inundation in a Semi-arid Region of SW Iran: Comparison of Different Advanced Modeling Approaches. In Natural Hazards GIS-Based Spatial Modeling Using Data Mining Techniques, Advances in Natural and Technological Hazards Research; Pourghasemi, H., Rossi, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 48, pp. 59–78. [Google Scholar]
- Geology Survey of Iran (GSI). Available online: https://gsi.ir/en (accessed on 5 October 1997).
- Voeckler, H.; Allen, D.M. Estimating regional-scale fractured bedrock hydraulic conductivity using discrete fracture network (DFN) modeling. Hydrogeol. J. 2012, 20, 1081–1100. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of GIS-based logistic regression: A case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef]
- Angileri, S.E.; Conoscenti, C.; Hochschild, V.; Märker, M.; Rotigliano, E.; Agnesi, V. Water erosion susceptibility mapping by applying stochastic gradient Treeboost to the Imera Meridionale River Basin (Sicily, Italy). Geomorphology 2016, 262, 61–76. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Choubin, B.; Rahmati, O.; Soleimani, F.; Alilou, H.; Moradi, E.; Alamdari, N. Regional Groundwater Potential Analysis Using Classification and Regression Trees. In Spatial Modeling in GIS and R for Earth and Environmental Sciences, 1st ed.; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 485–498. [Google Scholar]
- Aniya, M. Landslide-susceptibility mapping in the Amahata river basin, Japan. Ann. Assoc. Am. Geogr. 1985, 75, 102–114. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modeling: A review of hydrological, geomorphological and biological applications. Hydro. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Schlögl, M.; Matulla, C. Potential future exposure of European land transport infrastructure to rainfall-induced landslides throughout the 21st century. Nat. Hazards Earth Syst. Sci. 2018, 18, 1121–1132. [Google Scholar] [CrossRef]
- Peterson, A.T.; Ball, L.G.; Cohoon, K.P. Predicting distributions of Mexican birds using ecological niche modelling methods. Ibis 2002, 144, 27–32. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Sanchez-Flores, E. GARP modeling of natural and human factors affecting the potential distribution of the invasives Schismus arabicus and Brassica tournefortii in ‘El Pinacate y Gran Desierto de Altar’ Biosphere Reserve. Ecolog. Model. 2007, 204, 457–474. [Google Scholar] [CrossRef]
- Boeckmann, M.; Joyner, T.A. Old health risks in new places? An ecological niche model for I. ricinus tick distribution in Europe under a changing climate. Health Place 2014, 30, 70–77. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y. Applying various algorithms for species distribution modelling. Integr. Zool. 2013, 8, 124–135. [Google Scholar] [CrossRef] [PubMed]
- Rattray, A.; Ierodiaconou, D.; Laurenson, L.; Burq, S.; Reston, M. Hydro-acoustic remote sensing of benthic biological communities on the shallow South East Australian continental shelf. Estuar. Coast. Shelf Sci. 2009, 84, 237–245. [Google Scholar] [CrossRef]
- Ture, M.; Tokatli, F.; Kurt, I. Using Kaplan–Meier analysis together with decision tree methods (C&RT, CHAID, QUEST, C4. 5 and ID3) in determining recurrence-free survival of breast cancer patients. Expert Syst. Appl. 2009, 36, 2017–2026. [Google Scholar]
- Lee, S.; Park, I. Application of decision tree model for the ground subsidence hazard mapping near abandoned underground coal mines. J. Environ. Manag. 2013, 127, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Ierodiaconou, D.; Monk, J.; Rattray, A.; Laurenson, L.; Versace, V.L. Comparison of automated classification techniques for predicting benthic biological communities using hydroacoustics and video observations. Cont. Shelf Res. 2011, 31, 28–38. [Google Scholar] [CrossRef]
- Zabihi, M.; Pourghasemi, H.R.; Motevalli, A.; Zakeri, M.A. Gully erosion modeling using GIS-Based data mining techniques in northern Iran: A comparison between boosted regression tree and multivariate adaptive regression spline. In Natural Hazards GIS-Based Spatial Modeling Using Data Mining Techniques, Advances in Natural and Technological Hazards Research; Pourghasemi, H., Rossi, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 48, pp. 1–26. [Google Scholar]
- Ture, M.; Kurt, I.; Kurum, A.T.; Ozdamar, K. Comparing classification techniques for predicting essential hypertension. Expert Syst. Appl. 2005, 29, 583–588. [Google Scholar] [CrossRef]
- Chou, J.S. Comparison of multilabel classification models to forecast project dispute resolutions. Expert Syst. Appl. 2012, 39, 10202–10211. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.W. Application of decision-tree model to groundwater productivity-potential mapping. Sustainability 2015, 7, 13416–13432. [Google Scholar] [CrossRef]
- Loh, W.Y.; Shih, Y.S. Split selection methods for classification trees. Stat. Sin. 1997, 7, 815–840. [Google Scholar]
- Breiman, L. Statistical modelling: The two cultures. Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Youssefi, S.; Sadhasivam, N.; Pourghasemi, H.R.; Ghaffari Nazarlou, H.; Golkar, F.; Tavangar, S.; Santosh, M. Groundwater spring potential assessment using new ensemble data mining techniques. Measurement 2020, 107652. [Google Scholar] [CrossRef]
- Hollister, J.W.; Milstead, W.B.; Kreakie, B.J. Modeling lake trophic state: A random forest approach. Ecosphere 2016, 7, 1–14. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Bui, D.T. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Khosravi, K.; Nohani, E.; Maroufinia, E.; Pourghasemi, H.R. A GIS-based flood susceptibility assessment and its mapping in Iran: A comparison between frequency ratio and weights-ofevidence bivariate statistical models with multi-criteria decisionmaking technique. Nat. Hazards 2016, 83, 947–987. [Google Scholar] [CrossRef]
- Gaprindashvili, G.; Guo, J.; Daorueang, P.; Xin, T.; Rahimy, P. A new statistic approach towards landslide hazard risk assessment. Int. J. Geosci. 2014, 5, 38–49. [Google Scholar] [CrossRef][Green Version]
- Pham, B.T.; Khosravi, K.; Prakash, I. Application and comparison of decision tree-based machine learning methods in landside susceptibility assessment at Pauri Garhwal Area, Uttarakhand, India. Environ. Process. 2017, 4, 711–730. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. Catena 2012, 96, 28–40. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Tien Bui, D.; Hoang, N.D. GIS-based spatial prediction of tropical forest fire danger using a new hybrid machine learning method. Ecol. Inform. 2018, 48, 104–116. [Google Scholar] [CrossRef]
- Ngoc-Thach, N.; Ngo, D.B.T.; Xuan-Canh, P.; Hong-Thi, N.; Thi, B.H.; NhatDuc, H.; Dieu, T.B. Spatial pattern assessment of tropical forest fire danger at Thuan Chau area (Vietnam) using GIS-based advanced machine learning algorithms: A comparative study. Ecol. Inform. 2018, 46, 74–85. [Google Scholar] [CrossRef]
- Allouche, O.; Tsoar, A.; Kadmon, R. Assessing the accuracy of species distribution models: Prevalence, kappa and the true skill statistic (TSS). J. Appl. Ecol. 2006, 43, 1223–1232. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Dayal, K.S.; Deo, R.C.; Mohammadi, F.; Davoudi Moghaddam, D.; Naghibi, S.A.; Bui, D.T. Machine learning approaches for spatial modeling of agricultural droughts in the south-east region of Queensland Australia. Stoten 2020, 699, 134230. [Google Scholar] [CrossRef] [PubMed]
- Conoscenti, C.; Ciaccio, M.; Caraballo-Arias, N.A.; Gómez-Gutiérrez, Á.; Rotigliano, E.; Agnesi, V. Assessment of susceptibility to earth-flow landslide using logistic regression and multivariate adaptive regression splines: A case of the Belice River basin (western Sicily, Italy). Geomorphology 2015, 242, 49–64. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei Sardooi, E.; Nazari Samani, A.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Nampak, H.; Pradhan, B.; Manap, M.A. Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J. Hydrol. 2014, 513, 283–300. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; van der Sluijs, J.P.; Højberg, A.L.; Vanrolleghem, P.A. Uncertainty in the environmental modelling process-A framework and guidance. Environ. Model. Softw. 2007, 22, 1543–1556. [Google Scholar] [CrossRef]
- Garosi, Y.; Sheklabadi, M.; Pourghasemi, H.R.; Besalatpour, A.A.; Conoscenti, C.; Van Oost, K. Comparison of differences in resolution and sources of controlling factors for gully erosion susceptibility mapping. Geoderma 2018, 330, 65–78. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef]
- Ye, Y.; Wu, Q.; Huang, J.Z.; Ng, M.K.; Li, X. Stratified sampling for feature subspace selection in random forests for high dimensional data. Pattern Recogn. 2013, 46, 769–787. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modelling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Li, W.K.; Guo, Q.H.; Elkan, C. Can we model the probability of presence of species without absence data? Ecography 2011, 34, 1096–1105. [Google Scholar] [CrossRef]
- Pearson, R.G.; Thuiller, W.; Araujo, M.B. Model-based uncertainty in species range prediction. J. Biogeogr. 2006, 33, 1704–1711. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Spatial prediction of flood susceptible areas using rule based decision tree (DT) and a novel ensemble bivariate and multivariate statistical models in GIS. J. Hydrol. 2013, 504, 69–79. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).