CFD–DEM Simulations of Seepage-Induced Erosion
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.1.1. Governing Equations for the Fluid System
2.1.2. Governing Equations for the Particle System
2.2. Fluid-Particle Interaction Force
2.3. Coupling Procedures of CFD–DEM
3. Validation of Developed Software
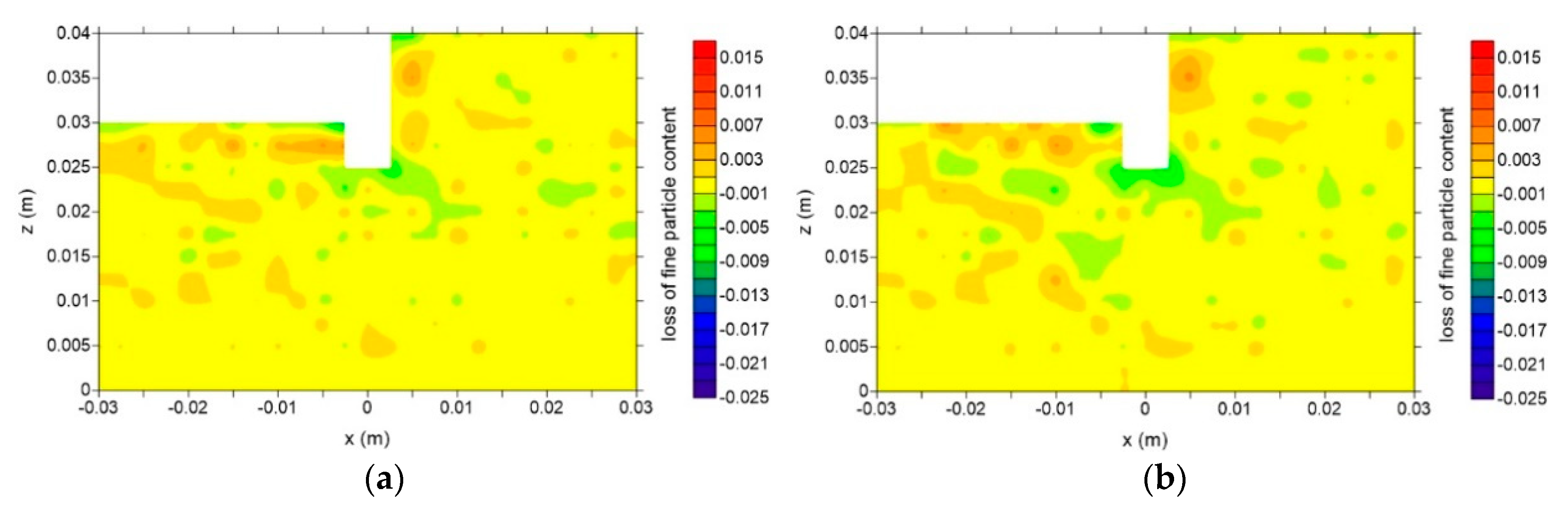
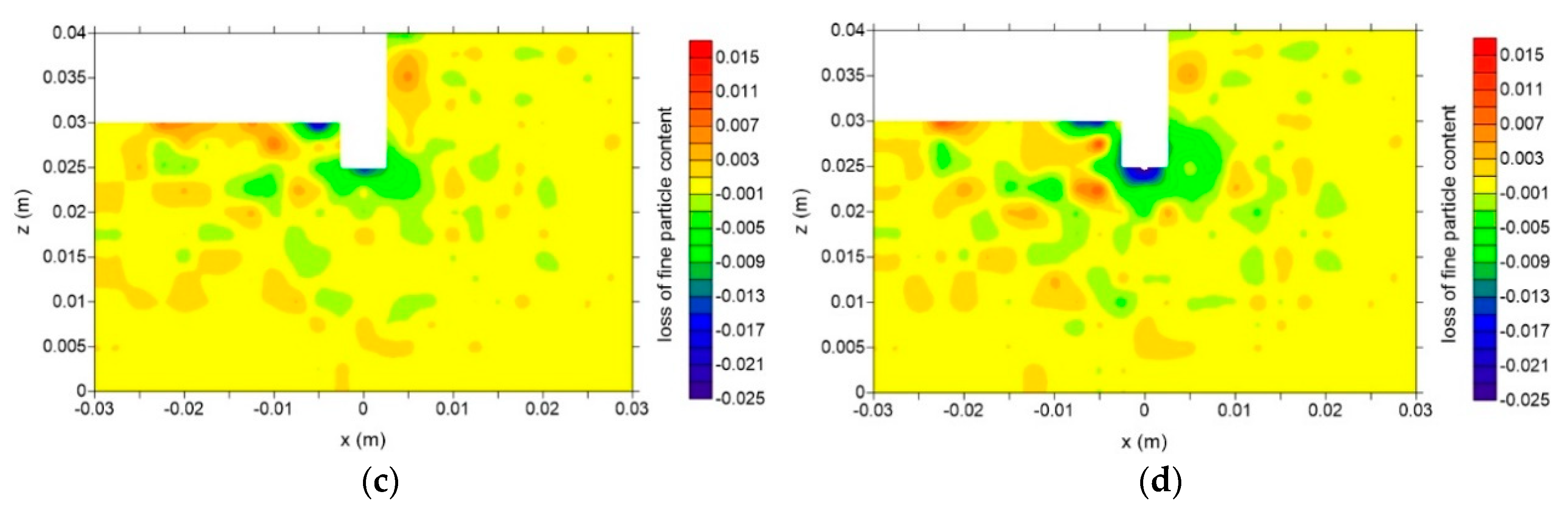
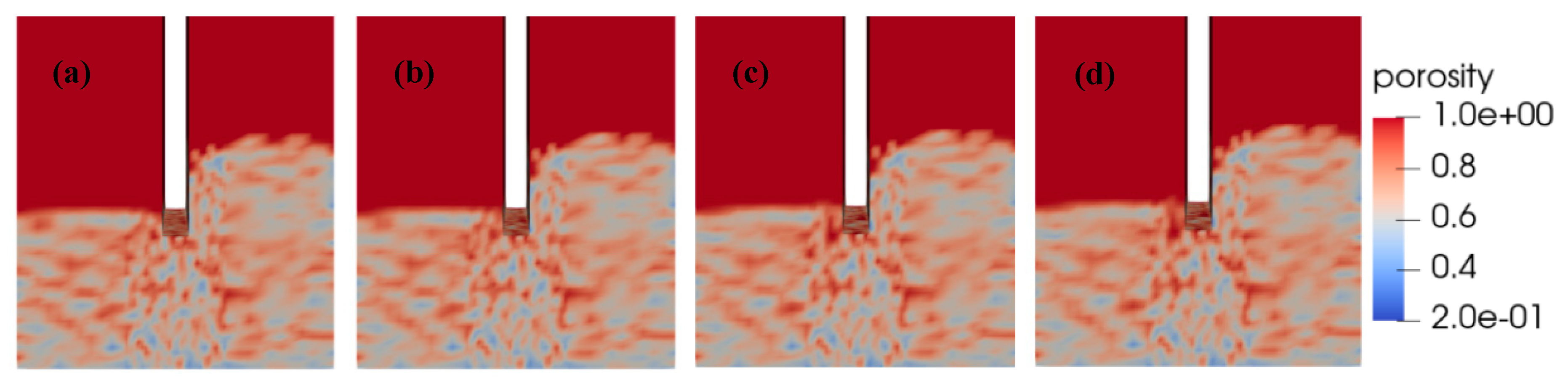
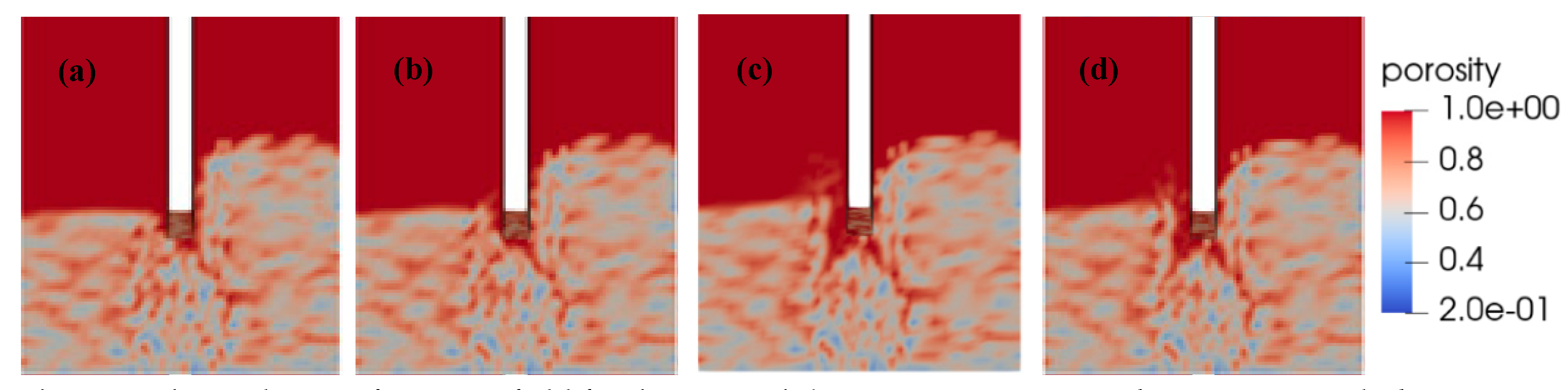
4. Observations of Seepage Failure
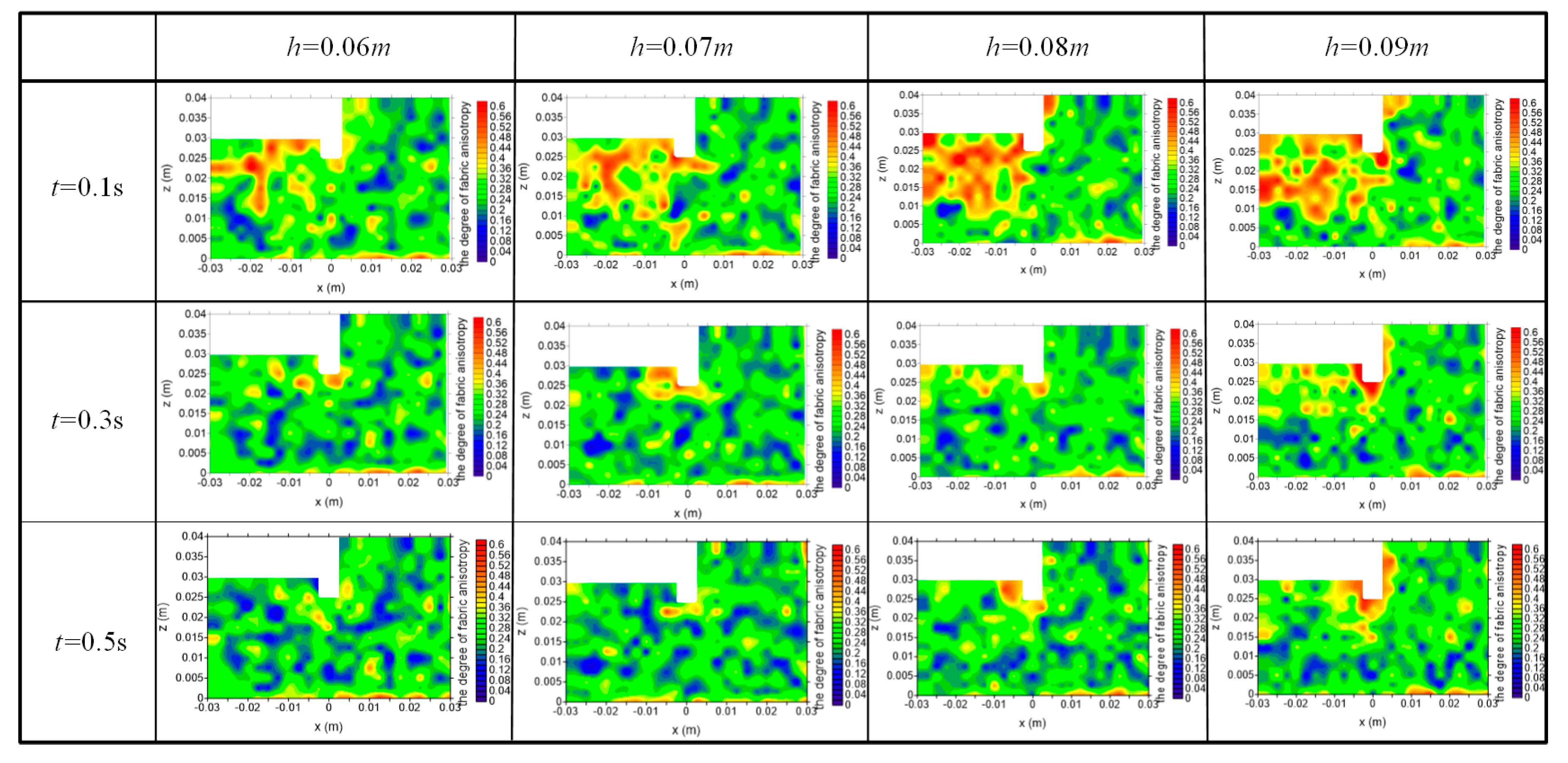
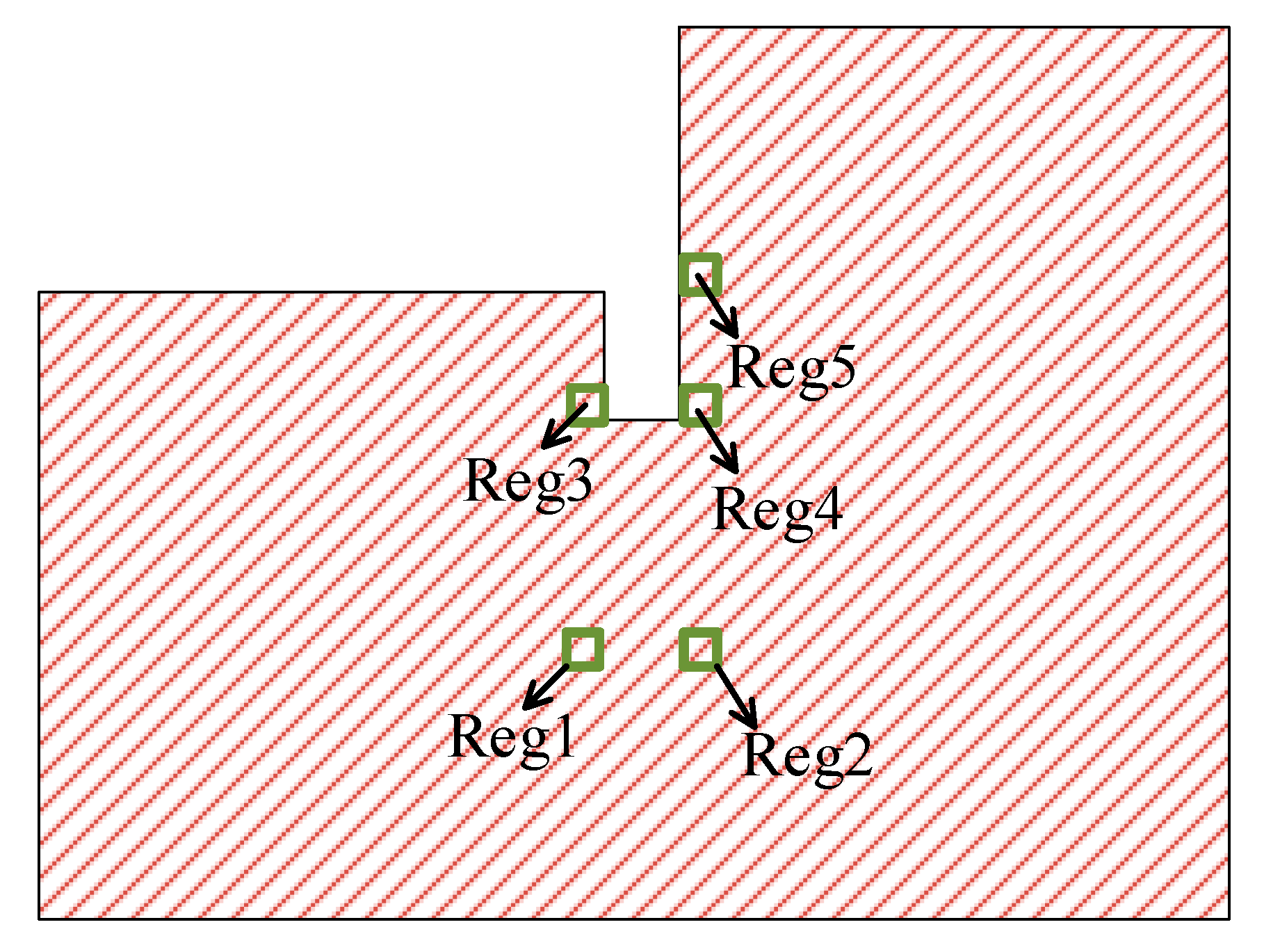
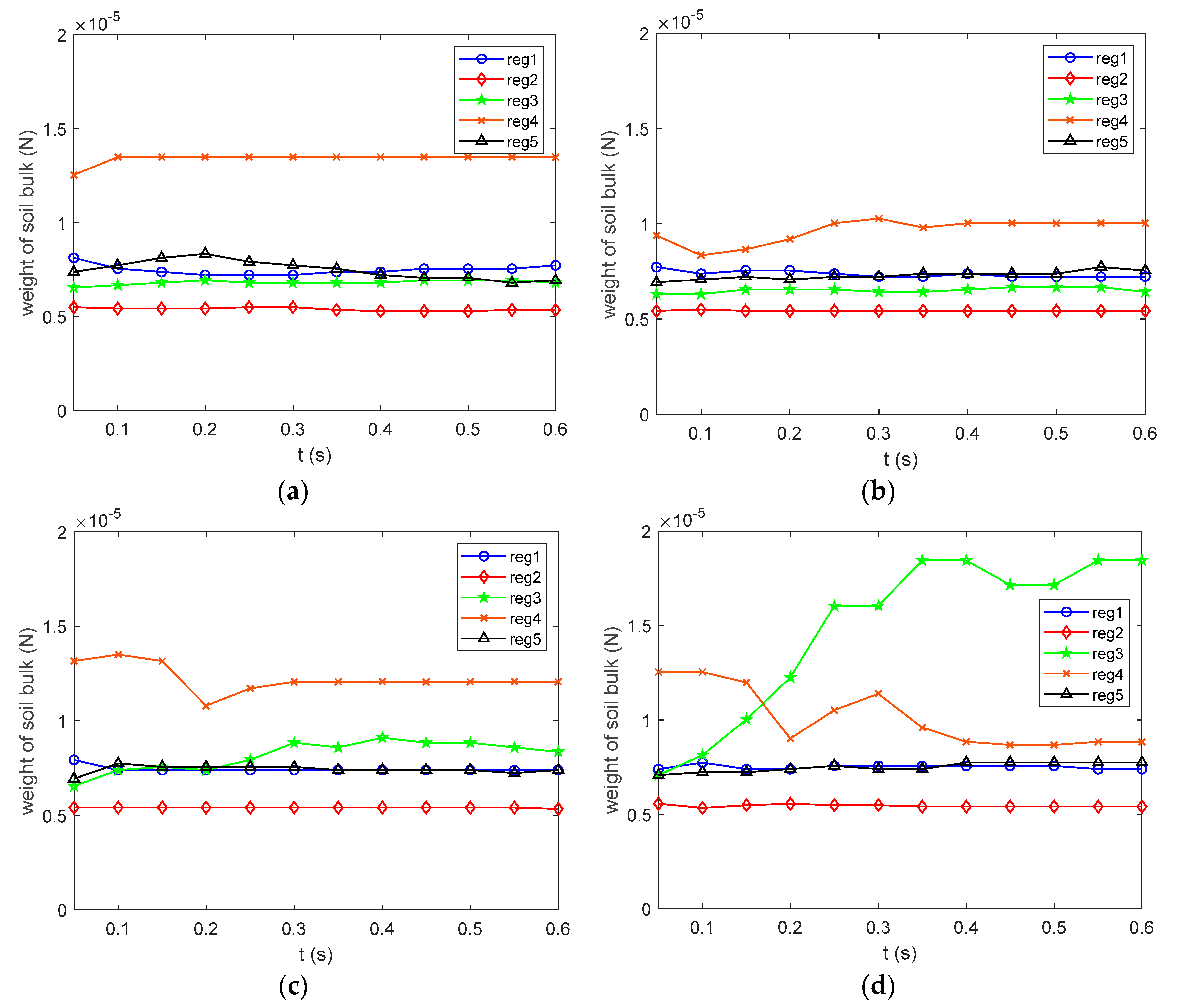
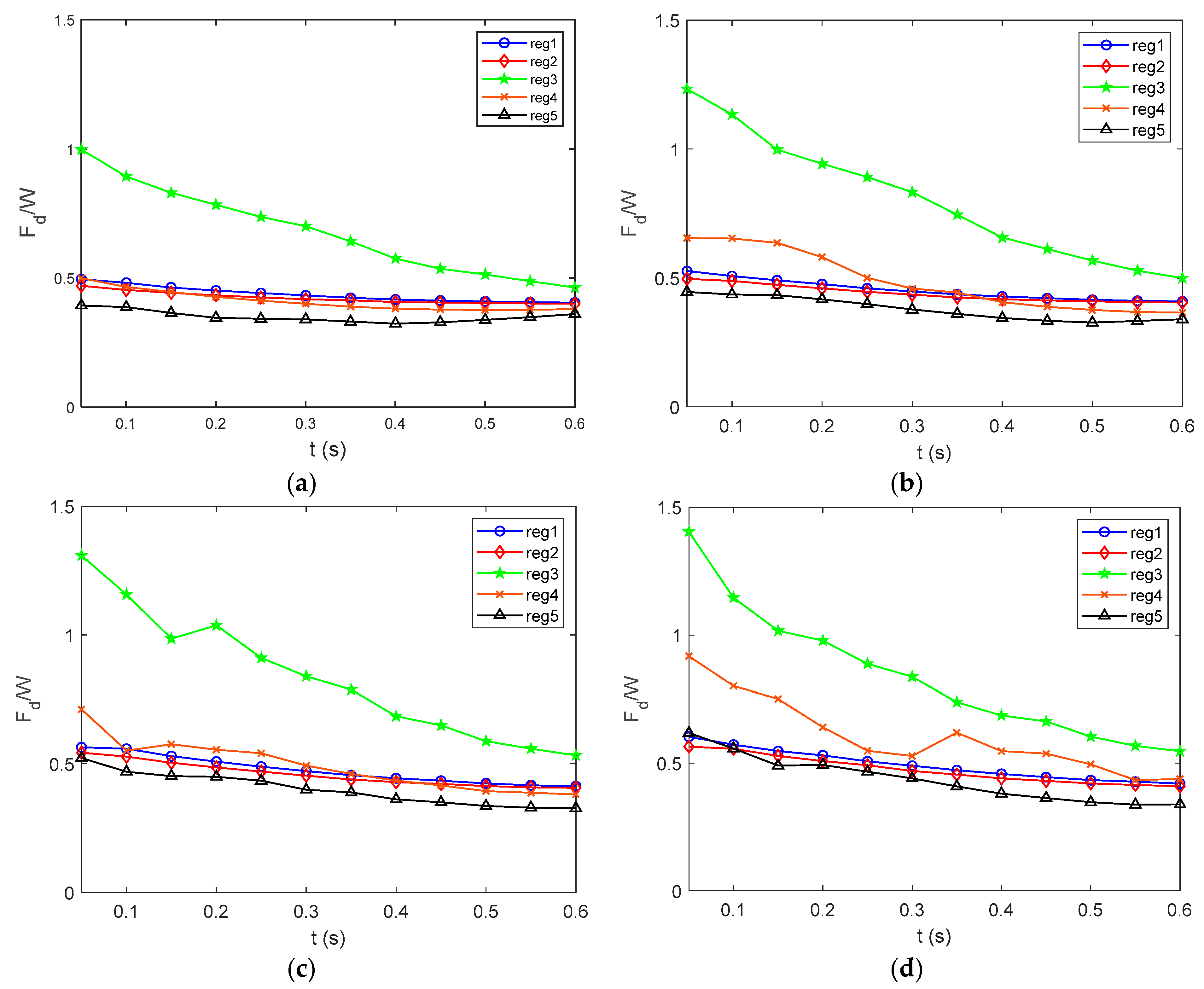
5. Micro-Scale Mechanisms of Seepage Failure and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sterpi, D. Effects of the erosion and transport of fine particles due to seepage flow. Int. J. Geomech. 2003, 3, 111–122. [Google Scholar] [CrossRef]
- Richards, K.S.; Reddy, K.R. Critical appraisal of piping phenomena in earth dams. Bull. Eng. Geol. Environ. 2007, 66, 381–402. [Google Scholar] [CrossRef]
- Arulanandan, K.; Perry, E.B. Erosion in relation to filter design criteria in earth dams. J. Geotech. Eng. 1983, 109. [Google Scholar] [CrossRef]
- Shaikh, A.; Ruff, J.F.; Abt, S.R. Erosion rate of compacted Na-Montmorillonite soils. J. Geotech. Eng. 1988, 114. [Google Scholar] [CrossRef]
- Sharif, Y.A.; Elkholy, M.; Hanif Chaudhry, M.; Imran, J. Experimental Study on the Piping Erosion Process in Earthen Embankments. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Moore, W.L.; Masch, F.D. Experiments on the scour resistance of cohesive sediments. J. Geophys. Res. 1962, 67, 1437–1446. [Google Scholar] [CrossRef]
- Chapuis, R.P. Quantitative measurement of the scour resistance of natural solid clays. Can. Geotech. J. 1986, 23, 132–141. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Gatien, T. An improved rotating cylinder technique for quantitative measurements of the scour resistance of clays. Can. Geotech. J. 1986, 23, 83–87. [Google Scholar] [CrossRef]
- Chang, D.S.; Zhang, L.M. Critical Hydraulic Gradients of Internal Erosion under Complex Stress States. J. Geotech. Geoenviron. Eng. 2013, 139, 1454–1467. [Google Scholar] [CrossRef]
- Reddi, L.N.; Lee, I.; Bonala, M. Comparison of internal and surface erosion using flow pump tests on a sand-kaolinite mixture. Geotech. Test. J. 2000, 23, 116–122. [Google Scholar]
- Wan, C.F.; Fell, R. Investigation of rate of erosion of soils in embankment dam. J. Geotech. Geoenviron. Eng. 2004, 130, 373–380. [Google Scholar] [CrossRef]
- Hanson, G.J. Development of a jet index to characterize erosion resistance of soils in earthen spillways. Trans. ASAE 1991, 34, 2015–2020. [Google Scholar] [CrossRef]
- Tomlinson, S.S.; Vaid, Y.P. Seepage forces and confining pressure effects on piping erosion. Can. Geotech. J. 2000, 37, 1–13. [Google Scholar] [CrossRef]
- Bendahmane, F.; Marot, D.; Rosquoët, F.; Alexis, A. Characterization of internal erosion in sand kaolin soils. Revue Européenne de Génie Civil 2011, 10, 505–520. [Google Scholar] [CrossRef]
- Sato, M.; Kuwano, R. Laboratory testing for evaluation of the influence of a small degree of internal erosion on deformation and stiffness. Soils Found. 2018, 58, 547–562. [Google Scholar] [CrossRef]
- Xie, Q.; Liu, J.; Han, B.; Li, H.; Li, Y.; Li, X. Critical Hydraulic Gradient of Internal Erosion at the Soil–Structure Interface. Processes 2018, 6, 92. [Google Scholar] [CrossRef]
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Tanaka, T.; Verruijt, A. Seepage Failure of Sand behind Sheet Piles. The Mechanism and Practical Approach to Analyze. Soils Found. 1999, 39, 27–35. [Google Scholar] [CrossRef]
- Moffat, R.; Fannin, R.J.; Garner, S.J. Spatial and temporal progression of internal erosion in cohesionless soil. Can. Geotech. J. 2011, 48, 399–412. [Google Scholar] [CrossRef]
- Luo, Y.; Nie, M.; Xiao, M. Flume-scale experiments on suffusion at bottom of cutoff wall in sandy gravel alluvium. Can. Geotech. J. 2017, 54, 1716–1727. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.; Sheng, J.; Luo, Y. Laboratory investigation of stress state and grain composition affecting internal erosion in soils containing a suspended cut-off wall. KSCE J. Civ. Eng. 2015, 20, 1283–1293. [Google Scholar] [CrossRef]
- Fleshman, M.S.; Rice, J.D. Laboratory Modeling of the Mechanisms of Piping Erosion Initiation. J. Geotech. Geoenviron. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Kawano, K.; O’Sullivan, C.; Shire, T. Using DEM to assess the influence of stress and fabric inhomogeneity and anisotropy on susceptibility to suffusion. In Proceedings of the ICSE 2016 (8th International Conference on Scour and Erosion), Oxford, UK, 12–15 September 2016. [Google Scholar]
- Shire, T.; O’Sullivan, C.; Hanley, K.J.; Fannin, R.J. Fabric and Effective Stress Distribution in Internally Unstable Soils. J. Geotech. Geoenviron. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Yerro, A.; Rohe, A.; Soga, K. Modelling Internal Erosion with the Material Point Method. Procedia Eng. 2017, 175, 365–372. [Google Scholar] [CrossRef]
- Chen, S.Y.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Zhou, Y.; Shi, Z.; Zhang, Q.; Jang, B.; Wu, C. Damming process and characteristics of landslide-debris avalanches. Soil Dyn. Earthq. Eng. 2019, 121, 252–261. [Google Scholar] [CrossRef]
- El Shamy, U.; Denissen, C. Microscale characterization of energy dissipation mechanisms in liquefiable granular soils. Comput. Geotech. 2010, 37, 846–857. [Google Scholar] [CrossRef]
- Schmeeckle, M.W. The role of velocity, pressure, and bed stress fluctuations in bed load transport over bed forms: Numerical simulation downstream of a backward-facing step. Earth Surf. Dyn. 2015, 3, 105–112. [Google Scholar] [CrossRef]
- Cui, X.; Li, J.; Chan, A.; Chapman, D. Coupled DEM–LBM simulation of internal fluidisation induced by a leaking pipe. Powder Technol. 2014, 254, 299–306. [Google Scholar] [CrossRef]
- Kawano, K.; Shire, T.; O’Sullivan, C.; Nezamabadi, S.; Luding, S.; Delenne, J.Y. Coupled DEM-CFD Analysis of the Initiation of Internal Instability in a Gap-Graded Granular Embankment Filter. EPJ Web Conf. 2017, 140, 10005. [Google Scholar] [CrossRef]
- Tao, H.; Tao, J. Quantitative analysis of piping erosion micro-mechanisms with coupled CFD and DEM method. Acta Geotech. 2017, 12, 573–592. [Google Scholar] [CrossRef]
- LIGGGHTS. LIGGGHTS (R)-Public Documentation, Version 3.X. Available online: http://www.cfdem.com (accessed on 18 February 2015).
- OpenFOAM. OpenFOAM—The Open Source CFD Toolbox. The OpenFOAM Foundation. 2015. Available online: http://www.openfoam.org (accessed on 22 May 2015).
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, Imperial College, London, UK, 1996. [Google Scholar]
- Cundall, P.A.; Strack, O. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Goniva, C.; Blais, B.; Radl, S.; Kloss, C. Open source CFD-DEM modelling for particle-based processes. In Proceedings of the Eleventh International Conference on CFD in the Minerals and Process Industries, CSIRO, Melbourne, Australia, 7–9 December 2015. [Google Scholar]
- Kloss, C.; Goniva, C.; Aichinger, G.; Pirker, S. Comprehensive DEM-DPM-CFD simulations-Model synthesis, experimental alidation and scalability. In Proceedings of the Seventh International Conference on CFD in the Minerals and Process Industries, CSIRO, Melbourne, Australia, 9–11 December 2009. [Google Scholar]
- Sande, P.C.; Ray, S. Mesh size effect on CFD simulation of gas-fluidized Geldart A particles. Powder Technol. 2014, 264, 43–53. [Google Scholar] [CrossRef]
- Benmebarek, N.; Benmebarek, S.; Kastner, R. Numerical studies of seepage failure of sand within a cofferdam. Comput. Geotech. 2005, 32, 264–273. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering; John Wiley & Sons: New York, NY, USA, 1948. [Google Scholar]
- Oda, M.; Nakayama, H. Yield function for soil with anisotropic fabric. J. Eng. Mech. 1989, 115, 89–104. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Rothenburg, L. Observations on stress-force-fabric relationships in idealized granular materials. Mech. Mater. 1990, 9, 65–80. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.-S. On the stress-force-fabric relationship for granular materials. Int. J. Solids Struct. 2013, 50, 1285–1302. [Google Scholar] [CrossRef]


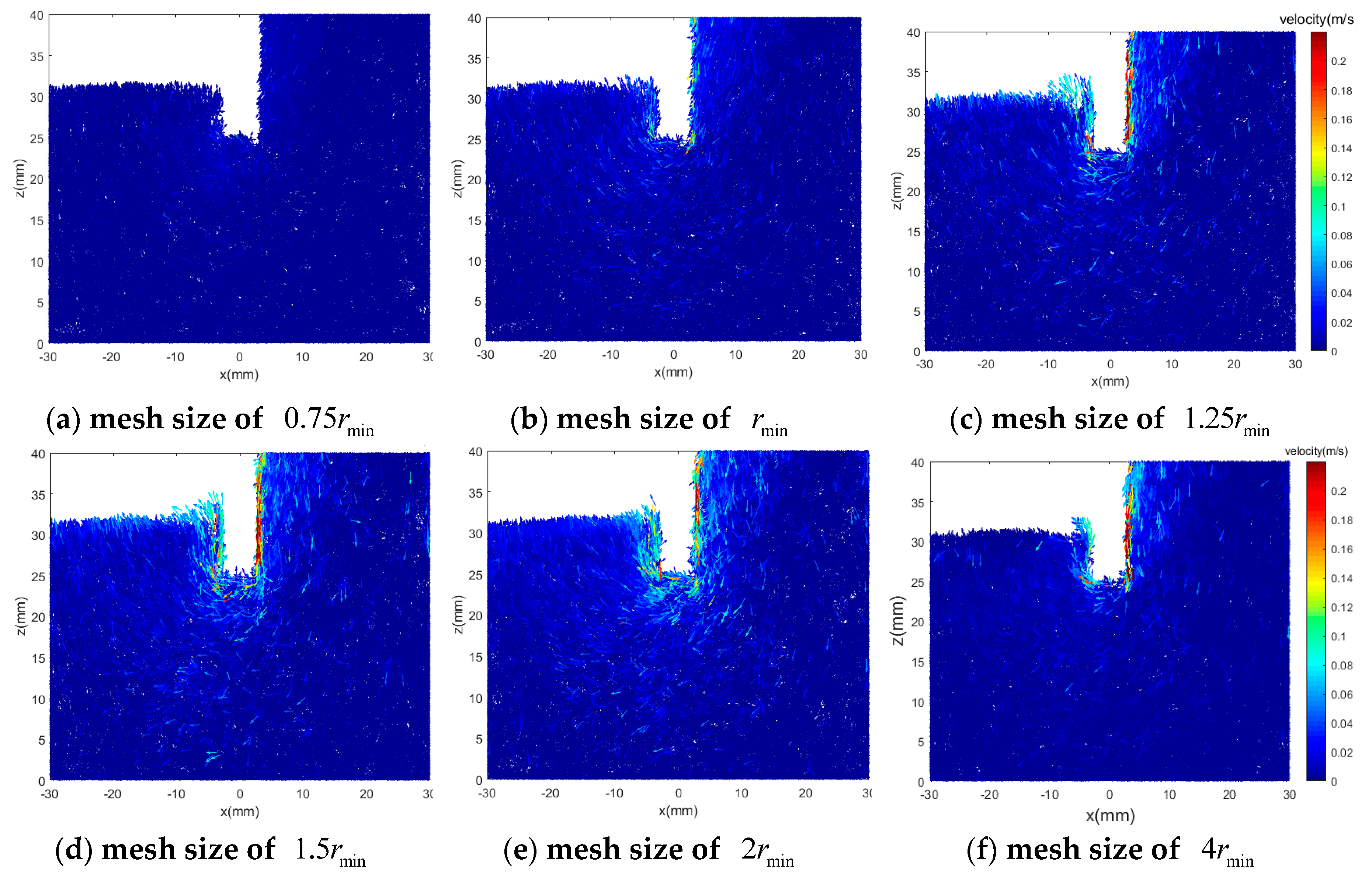
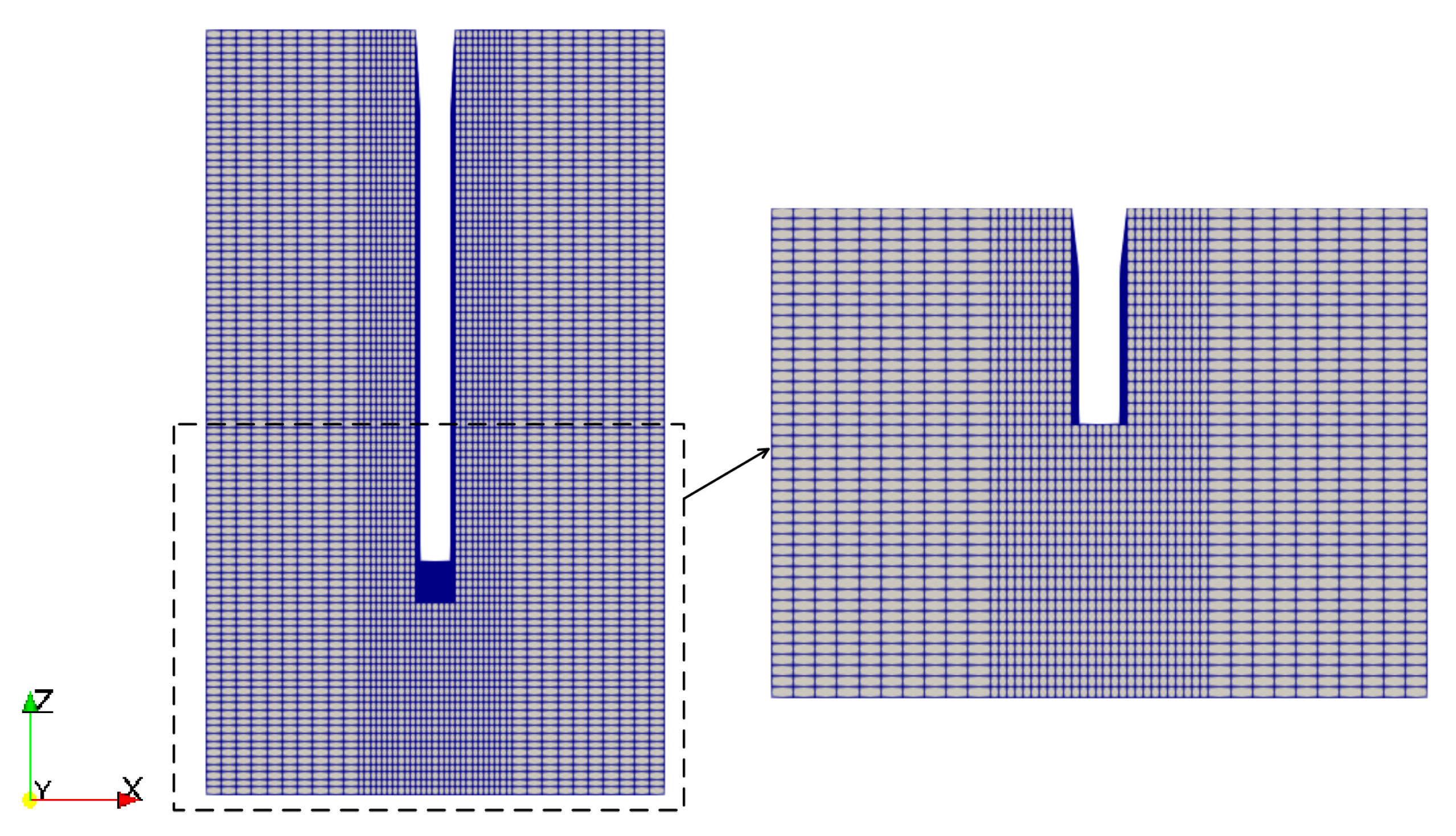
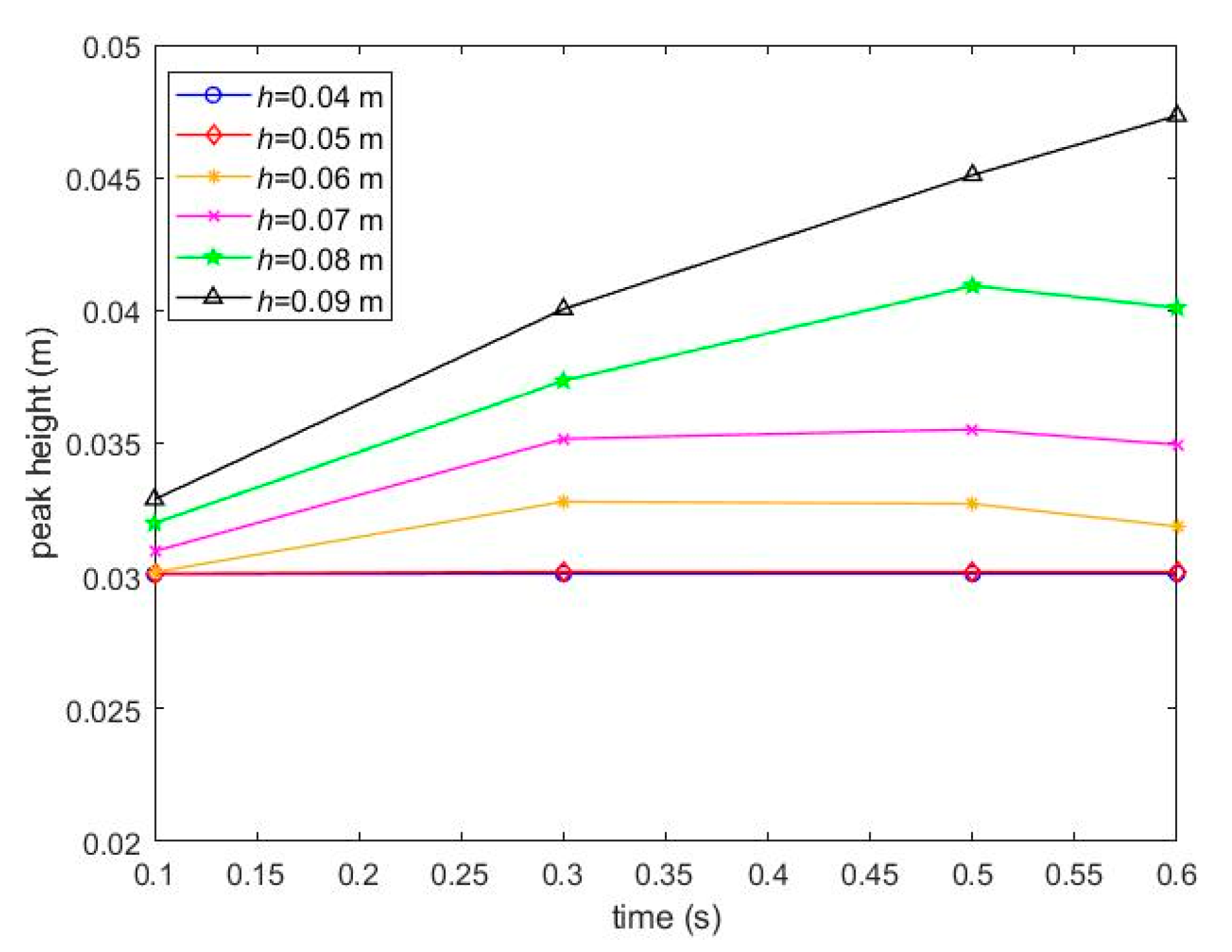
| Young’s Modulus | Density of Particles | Radii of Particles | Friction Coefficient | Poission’s Ratio | Restitution Coefficient |
|---|---|---|---|---|---|
| 5 MPa | 2500 kg/m3 | 0.85 | 0.45 | 0.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Q.; Wang, J.-P. CFD–DEM Simulations of Seepage-Induced Erosion. Water 2020, 12, 678. https://doi.org/10.3390/w12030678
Xiao Q, Wang J-P. CFD–DEM Simulations of Seepage-Induced Erosion. Water. 2020; 12(3):678. https://doi.org/10.3390/w12030678
Chicago/Turabian StyleXiao, Qiong, and Ji-Peng Wang. 2020. "CFD–DEM Simulations of Seepage-Induced Erosion" Water 12, no. 3: 678. https://doi.org/10.3390/w12030678
APA StyleXiao, Q., & Wang, J.-P. (2020). CFD–DEM Simulations of Seepage-Induced Erosion. Water, 12(3), 678. https://doi.org/10.3390/w12030678





