Abstract
Jet flows often have an important role in the water environment. The aim of this research is to study the dilution of jets due to complex velocity fields induced by internal solitary waves in stratified water. Direct numerical simulations are used to study vertical jet flows during the propagation and breaking of internal solitary waves (ISWs) with elevation type on a slope. Energy analysis shows that the internal interface is able to absorb kinetic energy from the jet and that for Re < 10,000 with Ri > 3.7, the ISWs can stay stable during the propagation within the presence of jet flows. The vortices jointly induced by the jets and the ISWs are observed at the bottom behind the ISW’s crest. The transport of the jet’s emitted scalar by the ISWs can be divided into two parts; some is transported by the moving interface and the rest by the bottom vortices. The ultimate transport length scales of two types are defined, and it is found that when the center of the jet inlet approaches the slope, the extension of the bottom vortices into the slope will lead to strong mixing. That causes increasing scalar concentration over the slope of the scalar that originated from the jet.
1. Introduction
Jet flows are a common physical phenomenon in nature, such as thermals in the atmosphere [1]. Deposition of polluted water to the river and sea environment can be modeled as jet flow. It is of interest to study the developments of jet flows because they usually contain large amounts of contamination and have an important role in the water environment. On the other hand, many researchers have shown that internal solitary waves (ISWs) widely exist in the sea, while usually shallowing and breaking at coastal areas. As a result, the ISWs often bring sediment and contamination from the deep sea to shallow waters and coastal regions. Both the jet flows and the ISWs are commonly found in the coastal area, such as in the South China Sea [2]. So, it is of strong interest to clarify how jets develop along with ISWs that propagate from the deep water to the shallow water.
Previous studies have developed various theories on the trajectories of the jets while having background flows using, for example, the modified integral models [3]. Because most of the theories are restricted to laminar flows, numerical simulations and laboratory experiments are still needed to study the fluctuated jet trajectories in turbulent flows [4]. Stanley used the direct numerical simulations (DNS) approach to study evolution and dilution of the turbulent jet starting from the mixing region near the free surface up to the self-similar region, albeit the simulation was limited to a moderate Reynolds number due to the computational cost of DNS [5]. Nevertheless, the DNS predicted the jet mixing well. Jet research also looked at uses of jets in the vicinity of gravity waves. Chen carried out experiments in a wave tank in order to study the dilutions of jets in the case of random surface waves and claimed that the waves can accelerate the dilution of jets [6]. Furthermore, the jet impinging on the interface in stratified water has also been widely studied. Andreani found in his numerical study that stratified gas would break up by a vertical jet with high Reynolds numbers [7]. However, in the stratified water, the internal interface is more stable than that in gas. Despite Kelvin–Helmholtz instability occurring on the interface, the stratified water does not break up by the vertical jet according to Chandana’s theoretical results [8]. It was found by Mahalov that there was usually an eddy mixing at the interface, and it was one of the most important processes that resulted in a decay of energy during the jet’s impingement [9]. Bondur explored the mechanism of the turbulent jet’s convection in a stratified medium with the help of the field observation data from the Mamala Bay. In his study, the jet can remain stable at the interface, and the mass carried by the jet is transported with the moving of the interface [10]. Although many researchers have focused on jets in stratified water, little attention was given on jets interacting with ISWs until now.
The ISWs, which are commonly seen in the stratified sea, are recognized as a dominant cause of sediment resuspension at the bottom of the seabed, especially when ISWs are breaking on a slope [11]. Michallet found from his experimental results that a large amount of energy was released when the ISWs broke on a slope [12]. It was observed by Klymak that the breaking ISWs with elevation type in the Oregon shelf had enough energy to transport the sediment into the slope [13]. Actually, the breaking types of ISWs can be summarized as collapsing, plunging, surging and fission according to Aghsaee, Boegman and Cheng’s study [14,15,16]. They all claimed that whatever the breaking type was, there was a tremendous energy being released, leading to a mixture of water and sediment resuspension due to the break down process.
Furthermore, it has been found by Druzhinin that a turbulent jet in stratified water can generate internal waves [17]. It means that two basic problems can be classified for the study of jets interacting with ISWs. One is the influence of the ISWs on the jet in terms of the trajectory of the jet and its dilution. Another one is the influence of the jet on the ISWs in terms of the stabilities of the interface and the ISWs. Consequently, this paper is intended to study (1) the jet’s influence on the ISWs when the ISWs propagate and (2) the transport of scalar carried by the jet when the ISWs are shallow and break on a slope. Both aims will be achieved using direct numerical simulations (DNS). The next section is a brief introduction to the numerical models of the DNS. Verifications of the numerical models are followed. Then, DNS results are discussed for jet’s impinging on an interface in stratified water and when the ISWs propagate and break on slopes. The last section is the conclusions of this study.
2. Numerical Models
2.1. Momentum Equations and Continuity Equation
The motion of three dimensional (3D) unsteady incompressible flow governed by Navier–Stokes equations in rectangular coordinates can be described as follows:
where ρ is the fluid density; t is time; i, j (i,j = 1, 2, 3) is three dimensions in Cartesian coordinates; xi is the spatial coordinate; u is the fluid velocity; p is the pressure; ν is the kinematic viscosity, and f is the body force.
2.2. Scalar Transport Equation
In this study, the ISW is produced in a two-layer water system and is induced by the density variation due to salinity. The following equation governing the convective-diffusive effect is used as the governing equation for the scalar C:
where C is a volume concentration of scalar ranging from zero to one; S is a source or sink term; and k is the molecular diffusivity coefficient. Both the flow density of the stratified water and the scalar concentration carried by the jet are described by the convective-diffusive equation. The relationship of flow density and the volume concentration can be established by the equation: ρ = Cρlow + (1 − C)ρup, where ρlow and ρup are the designed fluid density in the two-layer system, respectively. The other scalar concentration carried by the jet, also prescribed by Equation (3), has no influence on the flow density when the concentration is relatively small [18]. This means that it has no influence on the flow development that is governed by Equations (1) and (2).
2.3. Numerical Methods
In this study, our in-house CgLES code is used where the LES model is turned off. The projection method is utilized to solve the Navier–Stokes equations, taking the divergence of the momentum equation (Equation (2)) to fulfill the continuity equation and solving the pressure Poisson equation [19]. The explicit Adams–Bashforth scheme is employed to obtain a second-order accuracy in time when solving the momentum equation. The Finite Volume Method is used in discretizing the convection term in Equation (3). In addition, the Total Variation Diminishing method and Superbee function as the flux limiter are employed to avoid numerical fluctuation. The central difference is employed in the diffusion term. The Runge–Kutta scheme in time is employed to discretize the convection–diffusion equation (Equation (3)), maintaining second-order accuracy in space and time. The Immersed Boundary Method (IBM) is employed to deal with the solid–fluid interactions. The verifications of the numerical schemes and the IBM have been carried out by our researches [20,21], which are not repeated here. Instead, a verification specific to this study is described next.
3. Model Verifications
In this section, a numerical water tank is used to verify the implementation of the code to the problems in the questions. A schematic diagram of the numerical tank can be seen in Figure 1. It is a cuboid tank with a length of 8.0 m, width of 0.5 m and height of 0.5 m. The inlet of the jet is located on the domain bottom set x0 = 2.0 m and z0 = 0.25 m as corresponding to the coordinate systems in Figure 1. The diameter of the round jet d0 is 10.0 mm. The dimensionless length scale of the nozzle is 0.2 when normalized with the water’s depth. The jet velocity Vjet is 0.58 m/s in this case, and the background free stream velocity remains constant at 0.055 m/s during the simulation. The scalar concentration carried by the jet is small, and its effects on the flow density can be neglected according to Xu’s laboratory experiments [18]. The computational domain is discretized using a rectangular grid of 8192 × 128 × 256 points corresponding to the x × y × z directions, respectively, which makes sure that there are about 50 grid points in the jet inlet. The bottom and side walls are set as non-slip, and the rigid-lid assumption is used at the free surface. The inflow boundary condition is implemented on the left face of the computational domain, and an advection outflow condition is employed on the right face.
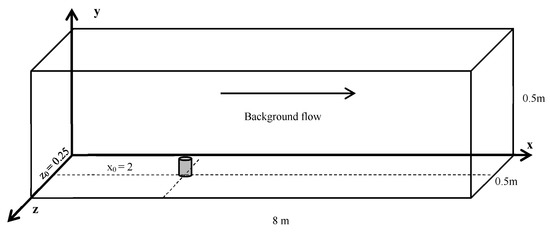
Figure 1.
Schematic diagrams of the computational domain in the verification case.
It has been shown that the azimuthal forcing method is effective in large eddy simulations of a buoyant jet [22]. In this method, the fluctuating component of the vertical velocity at grid point (I, k) of the jet inlet boundary takes the following form [23]:
where A is the amplitude of fluctuation (set to 0.2); the mean jet velocity V(r) is a function of the distance r from the center of jet inlet (set to Vjet); N is the number of the jet modes (set to 6 in this case); the f is the frequency determined by the Strouhal number (0.3 in this case); θ is the phase angle; all these parameters are set with reference to Xu and Chen’s study [18,24].
The numerical results are extracted and compared with the laboratory experiments carried by Xu [18]. In order to correspond with the laboratory experiments, a translation of coordinates in the x direction is applied by employing X = (x − x0), which means that the center of the jet inlet is at X = 0 after the translation. The results of the mean streamwise velocity <U> and the mean vertical velocity <V> are shown, respectively, in Figure 2a,b. Velocities U0, V0 are nondimensionalized by the jet mean inlet velocity Vjet, and the horizontal axis is the vertical length scale Y0 nondimensionalized by the diameter of the round diameter inlet D.
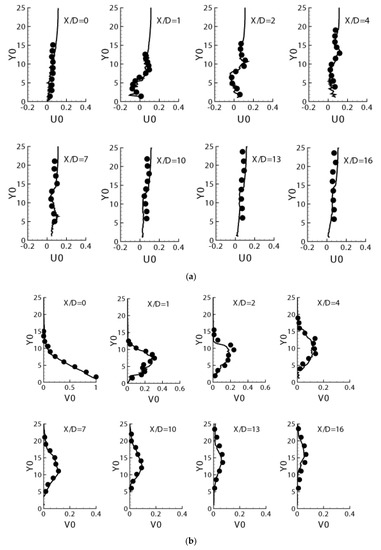
Figure 2.
(a) The distribution of normalized streamwise mean velocities along different vertical lines in the xy-plane of z = 0.25 m. (Dots are the experiment results, U0 = <U>/Vjet and Y0 = y/D). (b) The distribution of normalized vertical mean velocities along different vertical lines in the xy-plane of z = 0.25 m. (Dots are the experiment results, V0 = <V>/Vjet and Y0 = y/D).
As depicted in Figure 2a, the numerical results of the mean streamwise velocities U show excellent agreement with the experiments at X/D = 0, namely the jet’s center line. The agreement is still very good at X/D = 1 and X/D = 2. The small differences can be related to the differences in the nozzle’s geometry between the simulation and the experiment. In the experiment, the exit of jet inflow is actually 10 mm above the bottom, and this will cause differences near the jet nozzle’s lip. At X/D = 10, 13 and 16, the influence of the jet becomes weak, and the profile of the mean streamwise velocity is determined by the distribution of the inflow velocity. An excellent to very good agreement seen in Figure 2a is repeated in Figure 2b. The numerical mean vertical velocities profiles show excellent agreement with the experiment at X/D = 0. At X/D = 1, 2 and 4, despite a little difference, the agreement is still very good, as seen by the vertical velocity profile and its peak. When X/D is larger than 7, the vertical velocity profiles become shallow both in the numerical and experimental results but once again show excellent agreement between the two results. The position of the maximum velocity moves upward with the increasing of X/D. Overall, one can conclude, the numerical results agree with the experiment very well in terms of both magnitudes and distributions of the mean velocity.
4. Numerical Results
In order to accommodate a large number of simulations for different parameters of jets’ interaction with ISWs breaking on a slope, we pursued essentially 2D simulations in this study. Although 2D simulations are somewhat limited in terms of not capturing the flow development in the spanwise direction, the main features of the problems are essentially 2D, as already discussed by Forgia [25] and Aghsaee [11]
The size of the computational domain is 20 × 1 × 1 m, with the corresponding grid number points of 8192 × 256 × 32. A streamwise-vertical cross-section view of the domain is shown in Figure 3. The ratio of the depth of the lower layer to the upper layer is 1:3. The relative density difference across the interface is 0.03. The slope toe fixed on the bottom at x = 15 m, and there is a shelf set at the end of the slope with a height of 0.75 m. It is a level that the ISWs cannot climb in the cases considered here. The boundary conditions are set the same as those in the verification case except some changes in the inflow and outflow conditions. Velocities that satisfy the theory of the ISWs corresponding to the MCC theory are prescribed in the left boundary, and the outflow boundary is only set above the shelf [26].
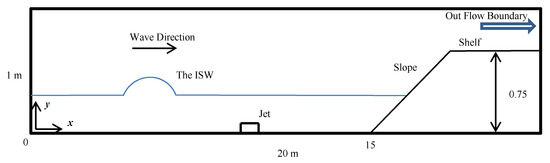
Figure 3.
The frontal view of the computational domain.
The three families of numerical cases to be studied are detailed in Table 1. In Table 1, the amplitude of the ISWs a0 and the position of the jet x0 vary as listed. In addition, the Richardson and Reynolds numbers are based on the jet or plume characteristics (width and vertical velocity) before impingement on the ISW and the initial density difference across the interface. They can be calculated by the following equations:
where the width of the jet D in the following cases is 0.05 m, and g’ is the buoyancy acceleration due to the density difference across the interface. And the dimensionless length scale of the nozzle is 0.0025 normalized with the width of the water tank.

Table 1.
The parameters of different cases.
The family of Case P is focused on studying the process of jet impingement on the interface without any ISWs, while varying the Richardson and Reynolds numbers. The family of Case I is designed for studying the mutual effects of the ISWs and jets with the variation of amplitudes of the ISWs, while again varying the Reynolds numbers and the Richardson numbers. The processes of jet dilution and transport when the ISWs shallow and break on the slope in variation with the position of the jet are simulated in the family of Case S, containing five cases with a specific slope 0.5, where the ISWs break thoroughly. One should note, the verifications of implementation of the CgLES code to the simulations of the ISWs can be seen in our researches [27].
The ISW with an amplitude of 0.15m in the designed tank will induce a horizontal friction velocity at the bottom boundary, of which the value is estimated to be 0.0007m/s. The dimensionless grid scales corresponding to the shear velocity and the kinematic viscosity are 1.7 and 2.3, respectively, in two directions (Δx+, Δy+). Furthermore, the maximum of Re is 104 in these cases, which is noted as the low Reynold number cases. Camussi’s study showed that in the high Reynold number cases (where the Re is larger than 105), there are many intermittent coherent structures in the near field, while it is not a significant phenomenon in the low Reynold number cases [28]. Actually, this paper is mainly focused on the effects between jets and ISWs, so the grid is fine enough to capture the jets with low Reynold numbers under the condition that turbulence of jets is not significant in our cases.
Furthermore, an independence study based on the case of I4 (Re = 10,000, a0 = 0.15 m) is carried out to ensure reliability of the numerical simulated results with the specific grid sizes. The parameters of different cases are listed in Table 2.

Table 2.
The parameters of grids in different cases.
Vertical velocity along the jet trajectory below the pycnocline without the influence of the ISWs and the decay of amplitude of the ISWs in the downstream area are extracted in Table 3.

Table 3.
Decay of vertical velocity and the amplitude of the internal solitary waves (ISWs) (%).
It can be seen from Table 3 that the decay amplitude of the wave remains constant at 1.98% in the three cases, which means that all the three grids sizes are available to simulate the ISWs. While in terms of simulating the jet with Re = 10,000, the results show that the decay of vertical velocity in the T2 case agrees with that in T3 well. Consequently, the moderate mesh is fine enough to simulate the cases listed in Table 1.
4.1. Jets Impinging on an Interface
As noted, jets impinging on a stratified interface have been commonly found in nature. In our study, the family of Case P is intended to simulate this phenomenon. The dimensionless time scale T is employed to describe the development of impingements, defined as T = tVjet/h2 (where the h2 is the depth of the lower layer). The contours of the fluid density are plotted in Figure 4.
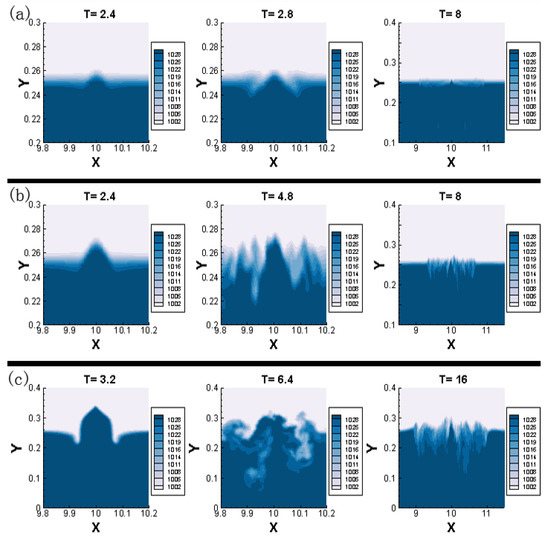
Figure 4.
Instantaneous density contours of the mid-plane of the computational domain during the jet impinging on the internal interface in three cases. (a) P1 (Re = 2500, Ri = 5.89); (b) P2 (Re = 5000, Ri = 1.47); (c) P3 (Re = 10,000, Ri = 0.37) (Unit of axes: meter).
Figure 4 shows the process of the jet impinging on the interface. A bolus can be found at the beginning of the impingement. The size of the bolus, namely the entrainment height, grows with the Reynolds number. In the case of P1, the interface is disturbed by the bolus, leading to fluctuations at the interface. These fluctuations spread over the interface, and the effect is dumped at T = 8. Meanwhile, in the cases of P2 and P3, the bolus breaks during the process, which results in a large mixing at the interface. Such processes of jet impingements with that high Re were also found by Cotel’s and Zhang’s experimental studies [29,30]. Considering the kinetic energy of the whole domain continuously increases with time due to the jet, the normalized change in the kinetic energy between the two time steps is calculated by the following formula:
where the ΔKE is the change in the kinetic energy between the two time steps; KEjet is the kinetic energy contributed by the jet at a t time. Consequently, the ΔKE0 means the change in kinetic energy between the two time steps normalized by the contribution from the jet. Figure 5 plots ΔKE0 variation with the dimensionless time scale T0.
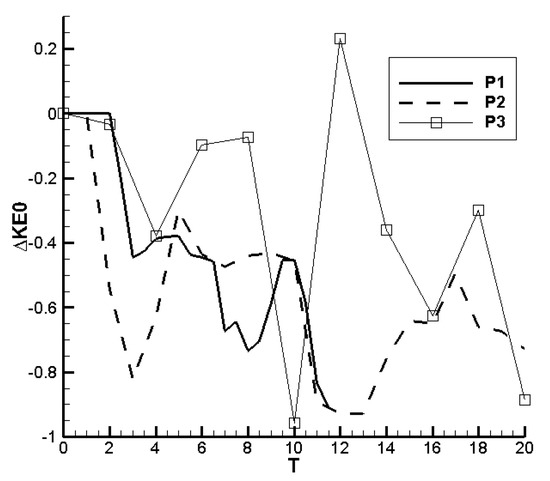
Figure 5.
Dimensionless change in the kinetic energy varies with time for Cases P1, P2, P3.
As shown in Figure 5, the kinetic energy experiences a decrease during the generation of the bolus at the beginning of the jet impingement in these cases, which means that the jet kinetic energy transforms into potential energy of the interface. At around T = 3, ΔKE0 reaches the minimum, and the interface absorbs about 45%, 40% and 80% energy from the jet flow for Cases P1, P2 and P3, respectively. In Cases P2 and P3, with the bolus breaking, the kinetic energy grows sharply, while in Case P1, there is only a little increase of kinetic energy after T = 3 because the bolus does not break in this case. In Cases P1 and P2, the interface absorbed a large amount of kinetic energy, with the development of the impinging jet. Meanwhile, in Case P3, the kinetic energy fluctuation results from a strong mixing at the interface. Due to the strong mixing, the energy transformation between the potential and kinetic energy frequently occurs during the impingement of the jet on the internal interface.
The family of Case P implies that the interface plays an important role in absorbing kinetic energy contained in the jet flow, and these cases can also be seen as a preliminary work for the following study. It can be concluded from the numerical results above and the literature review that the stratified interface can exist under the conditions of low jet velocity and strong differences of density, when corresponding to Re < 10,000, Ri > 3.7, respectively [31].
4.2. The Effects on the ISWs by the Jet
The cases of the jets impinging on an ISW during propagation are simulated, namely family of Case I. According to the numerical results, the influences of the jet on the ISW during its propagation can be summarized as follows: (1) Affecting the mixture of the two layers at the frontal wave crest and (2) Causing disturbances behind the wave crest. The influence of the jet depends on the Ri and Re numbers. In Figure 6, two typical cases are plotted to show the influence of the jet on the ISWs. Considering the propagation of ISW, it is hard to establish a standard time scale to characterize the development of jets [32], so the dimensional time t is used because it determines the wave crests in different cases. It should also be noted that the beginning ISWs’ crest is at x = 5 m.
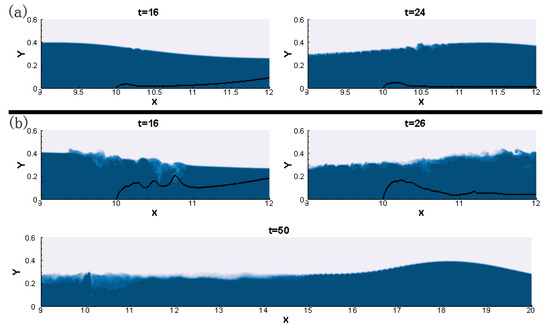
Figure 6.
Instantaneous density contour plots illustrating the jet effect on the ISW in two cases. (a) I1 (Re = 2500, Ri = 5.89, a = 0.15 m); (b) I4 (Re = 10,000, Ri = 0.37, a = 0.15 m); (Unit of axes is meter; Unit of time is second).
As shown in Figure 6, the background colored dark is the lower layer with the larger density. In addition, the black trajectory is the jet trajectory, which is defined as the streamline emanating from the center of the jet [33]. In the case of low Re and large Ri (Case I1), there is a small bolus at the frontal wave crest, and it decays with the propagation of the ISW. Despite having a small disturbance from the jet in Case I1, instabilities still occur behind the wave crest. While in the case of large Re and small Ri (Case I4), both the mixtures ahead and behind the wave crest at the interface are large. Furthermore, the results showed that the ISWs with small amplitude in Cases I5–I7 (where a = 0.10 m), were more easily affected by the jet in terms of the mixture at the interface and the K-H instabilities vortical structures behind the wave crest. However, it can be found in the snapshot of t = 50 s when the ISW has propagated far away from the nozzle without any dispersion that the jet fails to break the ISW. Similar results can be seen in all case families I where Re < 10,000 and Ri > 0.37, which means that the jet in those cases cannot break the ISW as thoroughly as the complex geometry does, regardless of the variation in the amplitudes of the ISWs [14]. As for the jet trajectory, it bends because of the high local velocity at the crest of the ISWs, which is similar to the cases with background currents.
From the numerical simulations, it was found that there were always some regions with local high vorticity at the bottom of the bed. Figure 7 shows the vortex areas in different cases, where (a) and (b) with amplitudes of the ISWs of 0.15 m and (c) and (d) of 0.1 m.
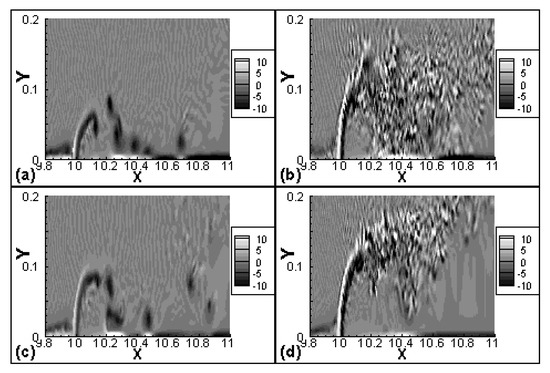
Figure 7.
Instantaneous vorticity contour plots in four cases. (a) I2 (Re = 5000, a = 0.15 m); (b) I4 (Re = 10,000, a = 0.15 m); (c) I6 (Re = 5000, a = 0.10 m); (d) I7 (Re = 10,000, a = 0.10 m); (Unit of axes is meter).
The areas of local high vorticity and the jet are usually well separated, as seen in Figure 7. The results of case I2 and case I6, in which the Reynolds number is 5000, show that the bottom vortices are induced by the drop of vorticity from the jet. In Figure 7a,c, the negative vorticity at the bottom is developed from the negative vorticity or the bending jet, while the positive vorticity at the bottom responds to the dropping vortices above them. On the other hand, in Cases I4 and I7, both the negative and positive vorticity at the bottom is induced by the vortices frequently dropping from the jet. The local vortices at the bottom in this study are different from the vortices obtained in Lamb’s study [34] in terms of the magnitudes and position. The vortices shedding in this study are stronger than those induced by the ISWs, and they lead to a locally increasing bed stress contributing to the possibilities of sediment motion [35]. Furthermore, in this study, the counterclockwise and clockwise vortices move in the opposite direction, while the boundary between the two versions lie around x = 10.4 m, which seems to be independent of the velocities of the jet and the amplitudes of the ISWs.
4.3. The Dilution and Transport of Jet by an ISW Encountering a Slope
In the family of Case S, the slope is fixed at 0.5m, and the amplitude of the ISW is 0.15m. So, according to Helfrich’s study [36], the slope is steep enough to obstruct the propagation of the ISWs, making sure that the ISWs will completely break on the slope. The length ls is defined as the distance from the center of the jet’s nozzle to the toe of the slope, namely ls = 15 – x0.
The results of Case S1 are shown in Figure 8, in which the jet is far enough from the slope that there is nearly no scalar concentration found on the slope during the whole process, in order to show the transport of the jet during the propagation of the ISWs. In order to differentiate the ISWs from the scalar, the upper layer is colored red, and the plots of relative concentration C carried by the jet are in the grey style.
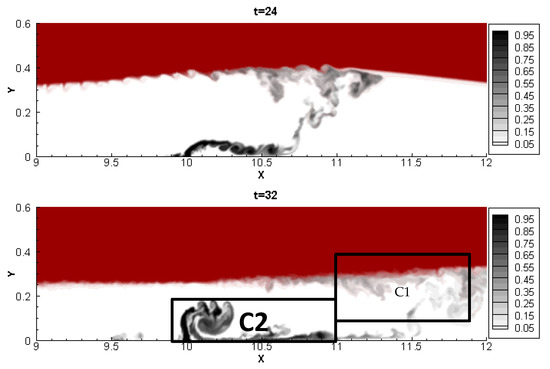
Figure 8.
Instantaneous scalar transport of the jet during the propagation of the ISWs in Case S1 (ls = 5 m). (Unit of axes is meter; Unit of time is second).
As shown in Figure 8, at t = 24 s, the ISW propagates near the jet and the jet trajectory bends due to the velocities induced by the ISW. The scalar concentration carried by the jet starts to split into two parts. One part of the concentration (C1) is transported with the moving of the interface and it dilutes gradually with the propagation of the ISWs and another part of the concentration (C2) is transported by the vortices induced at the bottom floor, as seen in the second panel at t = 32 s.
The averaged relative scalar concentrations of the two parts vary with the direction of the wave propagation. They are calculated and plotted in Figure 9. It is found that the scalar of C1, which is transported with the interface, decreases more slowly than C2, and the head of the C1 scalar can reach x1 = 13 m. On the other hand, the C2 scalar, which is transported by the bottom shedding vortices, contains more concentration than C1, and it decays at x2 = 11.7 m.
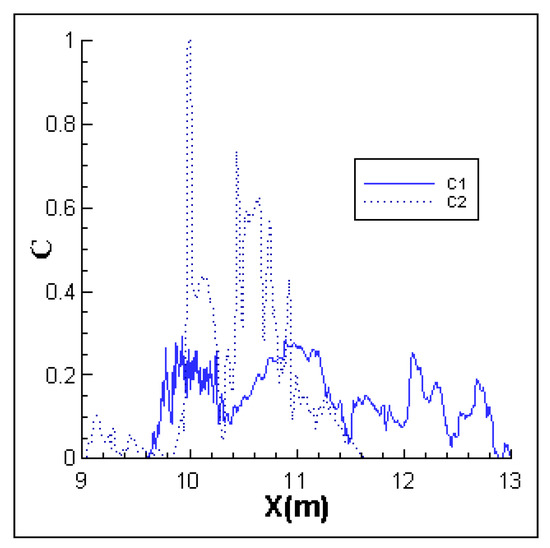
Figure 9.
The dilution of concentration of two parts in Case S1.
As a result, two length scales l1 and l2 are defined as corresponding to x1 and x2; that is l1 = x1 − x0, l2 = x2 − x0. In the case with specific Re numbers, Ri numbers and the amplitudes of the ISWs, the l1 and the l2 are 3.0 m and 1.7 m, respectively. The length l1 can be seen as the farthest distance where the jet can transport with the ISW and the l2 is the farthest distance where the bottom vortices induced by the ISW and the jet are able to transport from the jet.
The integral of the concentration M above the slope can be defined as follows;
where A is the area over the slope, and C is the scalar originated from the jet. In Cases S2–S5, the integral M variation from time is calculated and nondimensionalized by its maximum in Case S2, as seen in Figure 10. The processes of ISWs running up and breaking are plotted in Figure 11a.
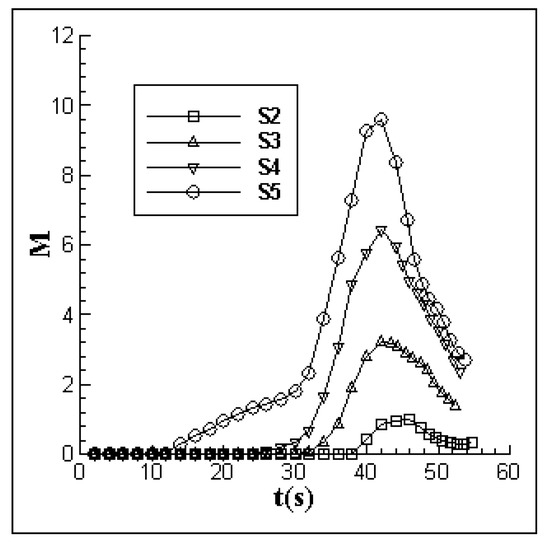
Figure 10.
The integral concentration M on the slope.
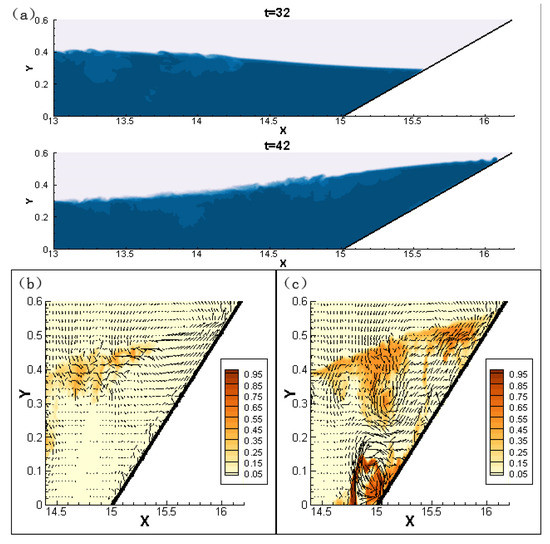
Figure 11.
Results of the ISWs running up. (a) the instantaneous density contour in Case S2; Scalar concentration contours and velocity vectors (b) in Case S2 (ls = 3.8 m) and (c) in Case S5 (ls = 0.2 m) at t =42 s. (Unit of axes is meter; Unit of time is second).
As shown in Figure 10; Figure 11a, the integrals reach their maximum in all cases at the same time with t = 42 s. It is just the time when the ISW runs up to the ultimate height on the slope, and after that, the ISW tends to slide down, bringing the scalar concentration on the slope back to the deep water. The process of ISW’s running up will also cause the scalar motion at the bottom of the slope [37].
In Case S5 (ls = 0.2 m), the peak value of M is 9.7 times as much as that in the Case S2. The results show that at t = 42 s, the M increases with the jet’s nozzle approaching the slope. In Cases S3–S5, the M has a sharp increase at t = 32 s when the ISWs begin to run up (seen in Figure 11a). At the end of the ISWs process, it leaves a considerable scalar concentration on the slope, and the concentration within the interface accounts for most of it. On the basis of this analysis, Cases S2–S5 can be divided into two groups in terms of the ls. The first group is Case S2, where ls is larger than l2 but is smaller than l1. When ls is less than l2, this is the second group.
The integrals of scalar concentration remain higher in the second group than in the first group. It results from the increased C1 scalar transported on the slope due to the center of jets approaching the slope, and also the influences of vortices. The result shows that the vortices at the bottom induced jointly by the ISW and the jet lead to a strong mixing of water on the slope during the process of breaking (seen in Figure 11b). While in Case S2, the scalar concentration on the slope is only contributed by the C1 because ls is too large for C2 to be transported, and the same holds for the vortices. As a result, there is little scalar concentration left on the slope at the end.
5. Conclusions
In this paper, direct numerical simulations (DNS) were carried out to study jets with cases of propagation and breaking of the internal solitary waves (ISWs) with elevation type on a slope. The processes of jet impinging on the interface, the mutual influences of the jets and the ISWs and the transport of jets when the ISWs run up the slope were studied, and the following conclusions are drawn from the numerical results.
- (1)
- When the horizontal length scale of the interface is far larger than the jet nozzle, the stratified interface can exist under the conditions of low jet velocity with strong differences of density, corresponding to Re < 10,000, Ri > 3.7. This is because most of the kinetic energy from the jet flows will be absorbed by the interface and transfers to potential energy of the interface.
- (2)
- There are vortices at the bottom behind the crest and at a distance from the center of the jet inlet. This observation implies that the vortices result from the joint effects of the curved jets and the flow velocities induced by the ISWs. When the ISWs propagate, the scalar concentrations carried by jet are transported in two ways: moved by the interface or moved by the bottom vortices.
- (3)
- Two transport lengths of the two ways were related to the scalar transport by the interface and by the bottom vorticity. In the period of the ISWs running up and down, the integrals of scalar concentration over the slope reach the maximum at the end of the ISWs running up the slope. That concentration integral also grows as the jet approaches the slope.
- (4)
- It can be concluded that when the distance from the center of the jet to the slope toe ls is smaller than the l2, there are vortices induced jointly by the jet and the ISW on the slope, leading to a strong mixing of water. As a result, more scalar concentration is left on the slope.
Author Contributions
Supervision, L.W.; Writing—original draft, J.X.; Writing—review & editing, E.J.A. All authors have read and agreed to the published version of the manuscript.
Funding
National Key R&D Program of China: 2017YFC0405605; National Natural Science Foundation of China: 51879086, 51609068; the 111 Project: B17015; the Special Fund of State Key Laboratory of China (20185044412).
Acknowledgments
This research utilized Queen Mary’s Apocrita HPC facility, supported by QMUL Research-IT. The work was also supported by National Key R&D Program of China (2017YFC0405605), the National Natural Science Foundation of China (51879086, 51609068), the 111 Project (B17015), the Special Fund of State Key Laboratory of China (20185044412).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bond, D.; Johari, H. Effects of initial geometry on the development of thermals. Exp. Fluids 2005, 39, 591–601. [Google Scholar] [CrossRef]
- Xie, J.; He, Y.; Chen, Z. Simulations of Internal Solitary Wave Interactions with Mesoscale Eddies in the Northeastern South China Sea. J. Phys. Oceanogr. 2015, 45. [Google Scholar] [CrossRef]
- Nikiforakis, I.K.; Stamou, A.I.; Christodoulou, G.C. A modified integral model for negatively buoyant jets in a stationary ambient. Environ. Fluid Mech. 2014, 15, 1–19. [Google Scholar] [CrossRef]
- Christodoulou, G.C.; Papakonstantis, I.G. Simplified estimates of trajectory of inclined negatively buoyant jets. Environ. Hydraul. 2010, 1, 165–170. [Google Scholar]
- Stanley, S.A.; Sarkar, S.; Mellado, J.P. A study of the flow-field evolution and mixing in a planar turbulent jet using direct numerical simulation. J. Fluid Mech. 2002, 450, 377–407. [Google Scholar] [CrossRef]
- Chen, Y.P.; Li, C.W.; Zhang, C.K. Numerical modeling of a round jet discharged into random waves. Ocean Eng. 2008, 35, 77–89. [Google Scholar] [CrossRef]
- Andreani, M.; Kapulla, R.; Zboray, R. Gas stratification break-up by a vertical jet: Simulations using the GOTHIC code. Nucl. Eng. Des. 2012, 249, 71–81. [Google Scholar] [CrossRef]
- Somayajic, R.; Swatersg, E. Kelvin-Helmholtz instability of a bottom-intensified jet in a stratified-fluid. Environ. Fluid Mech. 2014, 14, 743–769. [Google Scholar]
- Mahalov, A.; Nicolaenko, B.; Tse, K.L.; Joseph, B. Eddy mixing in jet- stream turbulence under stronger stratification. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Bondur, V.G.; Zhurbas, V.M.; Grebenuk, Y.V. Modeling and experimental research of turbulent jet propagation in the stratified environment of coastal water areas. Oceanology 2009, 49, 595. [Google Scholar] [CrossRef]
- Aghsaee, P.; Boegman, L.; Diamessis, P.J.; Lamb, K.G. Boundary-layer-separation-driven vortex shedding beneath internal solitary waves of depression. J. Fluid Mech. 2012, 690, 321–344. [Google Scholar] [CrossRef]
- Michallet, H.; Ivey, G.N. Experiments on mixing due to internal solitary waves breaking on uniform slopes. J. Geophys. Res. Ocean. 1999, 104, 13467–13477. [Google Scholar] [CrossRef]
- Klymak, J.M.; Moum, J.N. Internal solitary waves of elevation advancing on a shoaling shelf. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Aghsaee, P.; Boegman, L.; Lamb, K.G. Breaking of shoaling internal solitary waves. J. Fluid Mech. 2010, 659, 289–317. [Google Scholar] [CrossRef]
- Cheng, M.H.; Hsu, J.R.C.; Chen, C.Y. Laboratory experiments on waveform inversion of an internal solitary wave over a slope-shelf. Environ. Fluid Mech. 2011, 11, 353–384. [Google Scholar] [CrossRef]
- Likens, G.E.; Boegman, L. Currents in Stratified Water Bodies 2: Internal Waves. Encycl. Inland Waters 2009, 539–558. [Google Scholar] [CrossRef]
- Druzhinin, O.A. Generation of internal waves by a turbulent jet in a stratified fluid. Fluid Dyn. 2009, 44, 213–223. [Google Scholar] [CrossRef]
- Xu, Z.S.; Chen, Y.P.; Zhang, C.K. Study on three-dimensional movement and dilution of a vertical round jet under the wave-current effect. Adv. Water Sci. 2017, 2, 265–275. (In Chinese) [Google Scholar]
- Singh, K.M.; Avital, E.J.; Williams, J.J.R.; Ji, C.; Bai, X.; Munjiza, A. On parallel pre-conditioners for pressure Poisson equation in LES of Complex Geometry Flows. Int. J. Numer. Methods Fluids 2016. [Google Scholar] [CrossRef]
- Thomas, T.G.; Williams, J.J.R. Turbulent simulation of open channel flow at low Reynolds number. Int. J. Heat Mass Transf. 1995, 38, 259–266. [Google Scholar] [CrossRef]
- Ji, C.; Munjiza, A.; Williams, J.J.R. A novel iterative direct-forcing immersed boundary method and its finite volume applications. J. Comput. Phys. 2012, 231, 1797–1821. [Google Scholar] [CrossRef]
- Ghiti, N. Large Eddy Simulation of Three Dimensional Impinging Jets. CMES Comput. Modeling Eng. Sci. 2014, 99, 195–208. [Google Scholar]
- Zhou, X.; Luo, K.H.; Williams, J.J.R. Large-eddy simulation of a turbulent forced plume. Eur. J. Mech. B Fluids 2001, 20, 233–254. [Google Scholar] [CrossRef]
- Chen, Y. Three-Dimensional Modelling of Vertical Jets in Random Waves; The Hong Kong Polytechnic University: Hong Kong, China, 2006. [Google Scholar]
- Forgia, G.L.; Adduce, C.; Falcini, F. Laboratory investigation on internal solitary waves interacting with a uniform slope. Adv. Water Resour. 2017. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, L.L.; Avital, E.J.; Tang, H.W.; Willams, J.J.R. Numerical Simulation of Shoaling Broad-Crested Internal Solitary Waves. J. Hydraul. Eng. 2017, 143, 04017006. [Google Scholar] [CrossRef]
- Xu, J.; Wang, L.L.; Tang, H.W.; Hai, Z.; Williams, J.J.R. Scalar Transport by Propagation of an Internal Solitary Wave over a Slope-Shelf. J. Hydrodyn. 2018, 31, 317–325. [Google Scholar] [CrossRef]
- Camussi, R.; Guj, G. Experimental analysis of intermittent coherent structures in the near field of a high Re turbulent jet flow. Phys. Fluids 1999, 11, 423. [Google Scholar] [CrossRef]
- Cotel, A.J.; Gjestvang, J.A.; Ramkhelawan, N.N.; Breidenthal, R.E. Laboratory experiments of a jet impinging on a stratified interface. Exp. Fluids 1997, 23, 155–160. [Google Scholar] [CrossRef]
- Zhang, Q.; Cotel, A. Entrainment due to a thermal impinging on a stratified interface with and without buoyancy reversal. J. Geophys. Res. Atmos. 2000, 105, 15457–15467. [Google Scholar] [CrossRef]
- Cotel, A.J.; Kudo, Y. Impingement of buoyancy-driven flows at a stratified interface. Exp. Fluids 2008, 45, 131–139. [Google Scholar] [CrossRef]
- Meftah, M.B.; De Serio, F.; Malcangio, D.; Mossa, D.; Petrillo, A.F. Experimental study of a vertical jet in a vegetated crossflow. J. Environ. Manag. 2015, 164, 19–31. [Google Scholar] [CrossRef] [PubMed]
- New, T.H.; Lim, T.T.; Luo, S.C. Effects of jet velocity profiles on a round jet in cross-flow. Exp. Fluids 2006, 40, 859–875. [Google Scholar] [CrossRef]
- Lamb, K.G. A numerical investigation of solitary internal waves with trapped cores formed via shoaling. J. Fluid Mech. 2002, 451, 109–144. [Google Scholar] [CrossRef]
- Boegman, L.; Ivey, G.N. Flow separation and resuspension beneath shoaling nonlinear internal waves. J. Geophys. Res. Ocean. 2009, 114. [Google Scholar] [CrossRef]
- Helfrich, K.R. Internal solitary wave breaking and run-up on a uniform slope. J. Fluid Mech. 1992, 243, 133–154. [Google Scholar] [CrossRef]
- Rivera, G.; Diamessis, P.; Jenkins, J. Wave-Induced Pressure under an Internal Solitary Wave and Its Impact at the Bed. In Proceedings of the Meeting of the Aps Division of Fluid Dynamics, Boston, MA, USA, 22–24 November 2015. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).