Obviously, pipes are not bulbs. A bulb is the classical example of a non-repairable element. It works until it fails and then, it must be replaced for a new bulb. Conversely, a pipe can be considered as a repairable element, because it can be repaired after the first failure, and again every time, after a new failure happens. From the pipe installation moment, its service life keeps increasing, no matter the repairs undertaken, until it is finally replaced. Such replacement will probably have a direct relationship to the number of repairs occurred, although this does not necessarily have to be always the case. In maintenance engineering, the analysis of the service life of non-repairable elements, like bulbs, can be posed in simpler terms than that for repairable elements, like mechanical machines or electronic devices [
32,
33]. The complexity of the current statistical models for pipe failure analysis [
3,
10,
17,
34] confirm this fact. However, a pipe is essentially different from a complex machine—though being repairable as a whole, a pipe could be considered as a non-repairable element if only the length of the pipe intervened in the reparation (or partial replacement) is focused on. Through an assumable simplification, that short length of the pipe has reached the end of its service life. This way, by taking advantage of dividing, virtually, each pipe into short segments, which could be individually analyzed, the basics of statistical analysis of non-repairable elements may be applied to pipe networks. These are the fundamentals of the BPLA model.
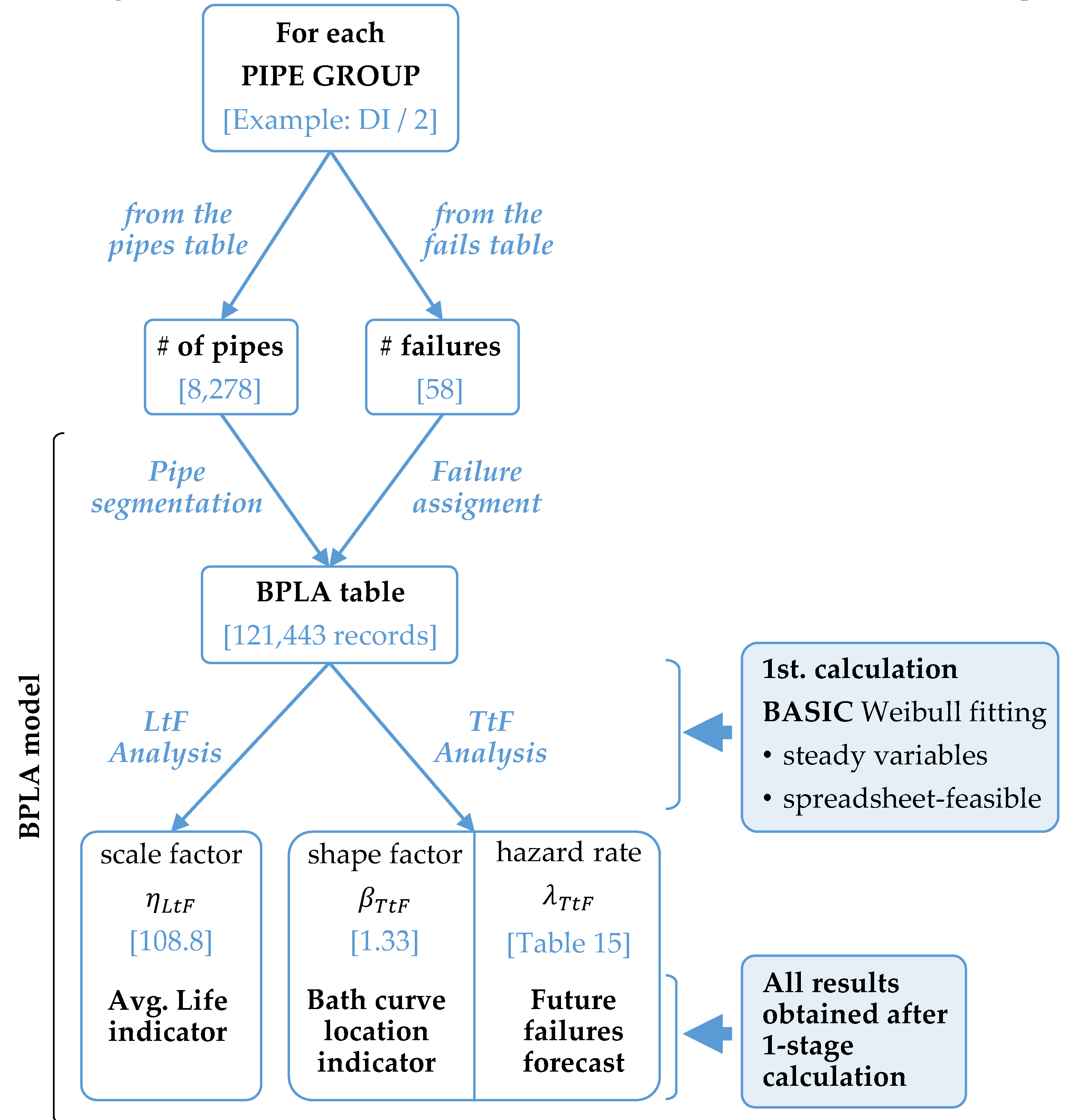
2.1. Development and Application of the BPLA
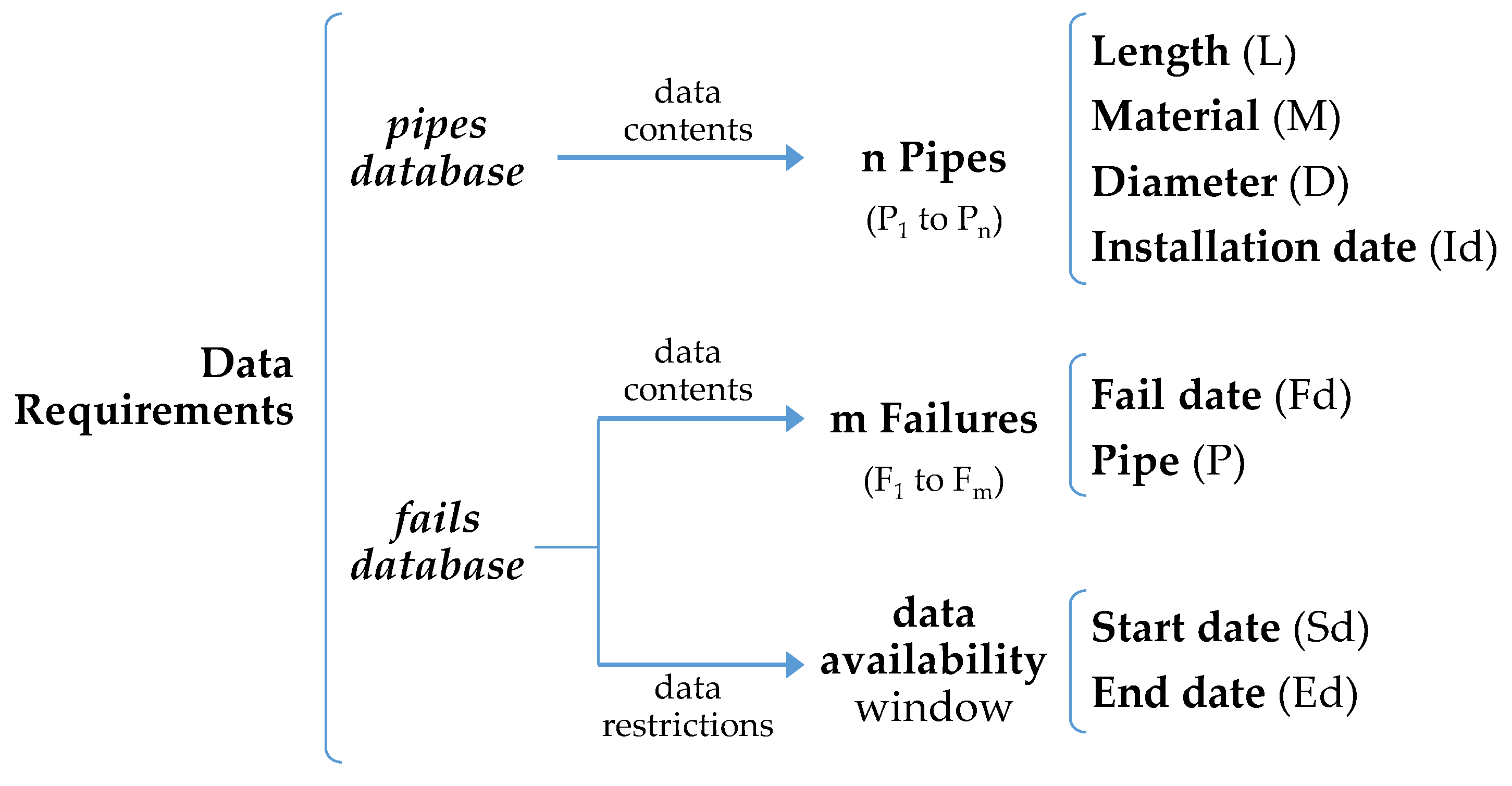
Data requirements and organization: The information needed for the BPLA comes from two different sections of the infrastructure database: pipes and failure records (
Figure 2). For the pipes, the only needed characteristics are the length, diameter, material, and installation date, although other kind of information might be also welcome; for example, the DMA, which might help later to select the groups of pipes.
This information may be organized in the so-called pipes table as shown in
Table 1—n being the total number of pipes, the pipes table will be compounded by n rows. For clarity purposes, four pipes (1, i, j and n) will be used in this paper to follow the development of the model.
As to the failures information, the basic data needed are the date and pipe for each failure occurrence. Additionally, the position, in a temporal order, of all the failures occurred in the same pipe must be also considered. That information may be structured in the fails table (
Table 2), where m is the total number of failures.
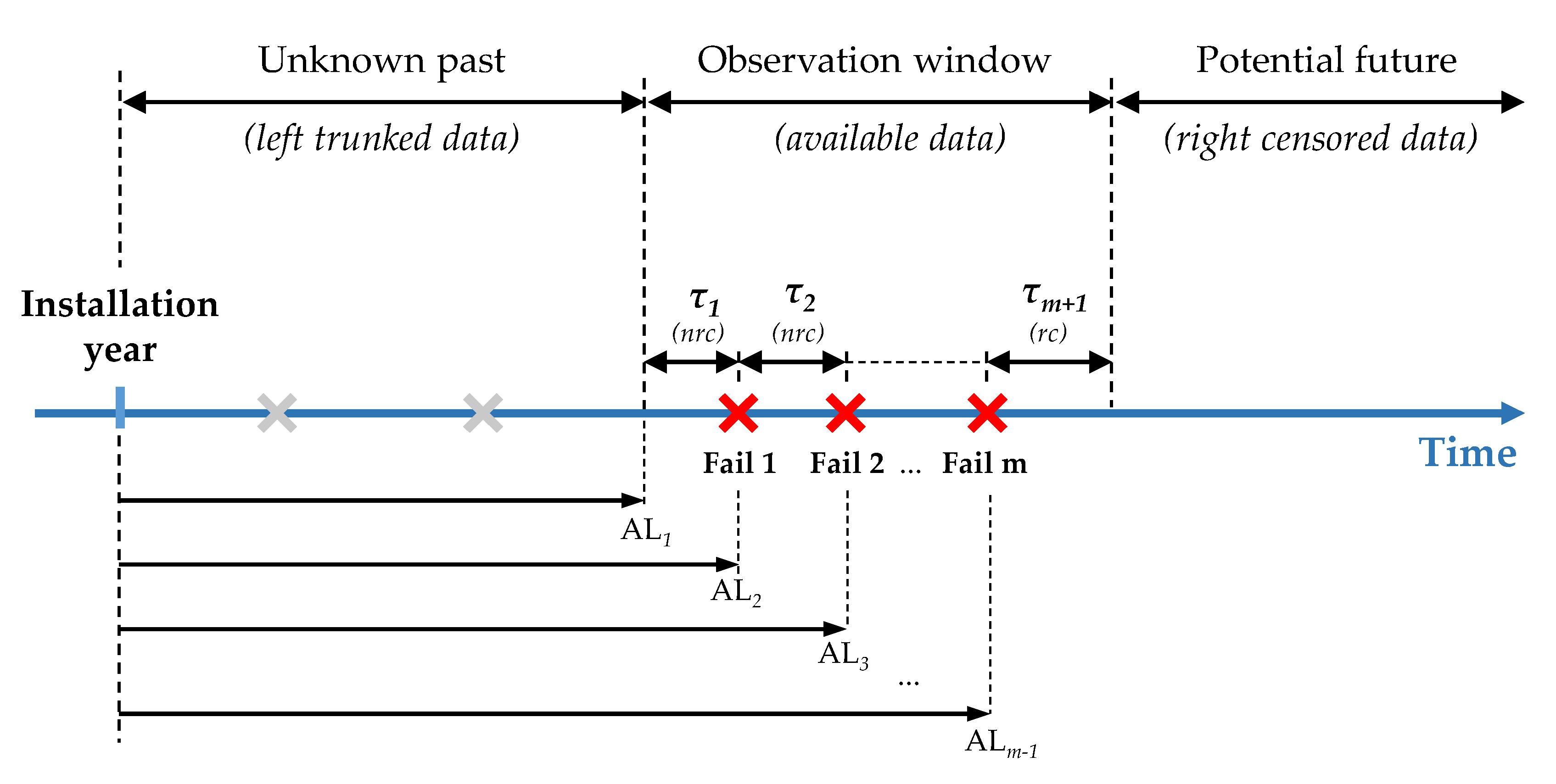
In many cases, the way the failure information was recorded in the past by many water utilities was not as accurate as required by this kind of analysis. This means that it is not unusual to find large gaps of accurate information from the time the pipes were installed. Because of this inequity on the available failure data, it is essential to find the widest possible window of failure data, in which all the network pipes are included. These start date and end date (Sd and Ed) of the availability window, which are not data information but data restrictions instead, will be key for the time variables of the model.
Once that window is identified, all the failures within are the ones to be displayed in the fails table. Unavoidably, the knowledge of failure data is (left) trunked for dates before the window’s start—failures might have occurred or not, but it is an unknown past. Furthermore, the failure data is (right) censored for dates after the window’s end—pipes are in operation in that moment, but they might fail later, which is the potential future [
35].
The common renovation and maintenance operations in the network affect these two tables in two different ways. Repairs are considered as works that do not affect significantly the length of a pipe. In consequence, the pipe characteristics remain the same after a repair. This kind of intervention should be recorded as a failure occurrence and it will enlarge the fails table. Conversely, renovations are partial or total physical replacements of a pipe. After a renovation, there is a change in one or more components of the pipe database. In accordance, those changes will be reflected on the pipes table.
Pipe groups definition: The BPLA model works on the assumption that the groups of pipes to analyze are homogenous enough. Therefore, the first task consists of distributing all the network pipes into different groups according to their characteristics. As the case study will show, initial criteria rely on material, diameter ranges, or age ranges.
The most important condition is that each group of pipes must have at least 30 registered failures. This is imposed by the statistical fitting method that will be used later (maximum likelihood estimation) [
36].
Data management: Once the pipe groups have been formed, the initial pipes table and fails table, must be divided into as many pipe and fail tables as there are pipe groups—one pipes table and one fails table containing the information of (only) the pipes that are gathered in each pipe group. Calculations will be individually applied to each group.
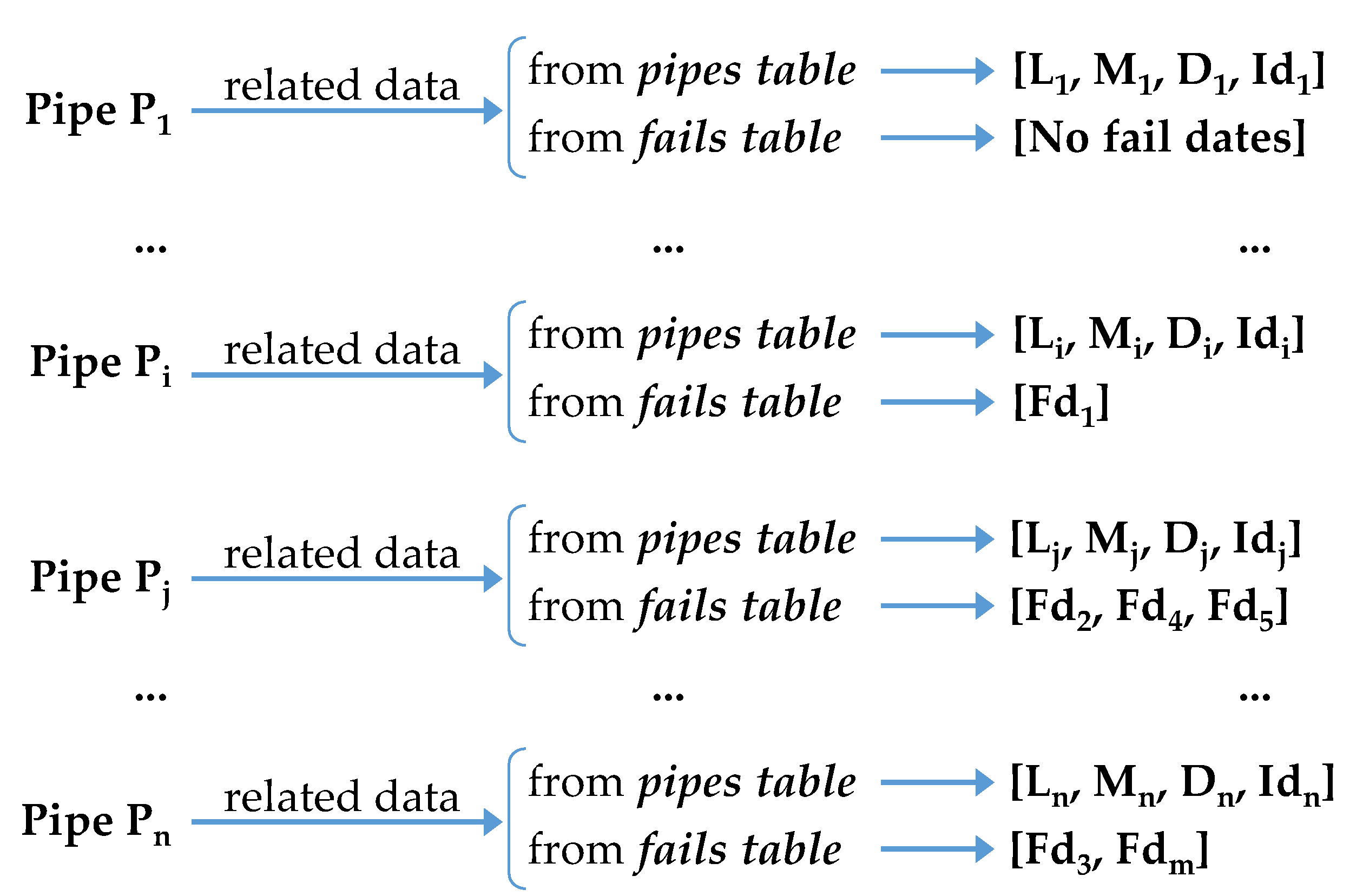
For the case of the four pipes taken as examples,
Figure 3 shows the pipe data (distribution and origin) and
Figure 4 shows the way the failure information is considered in the model.
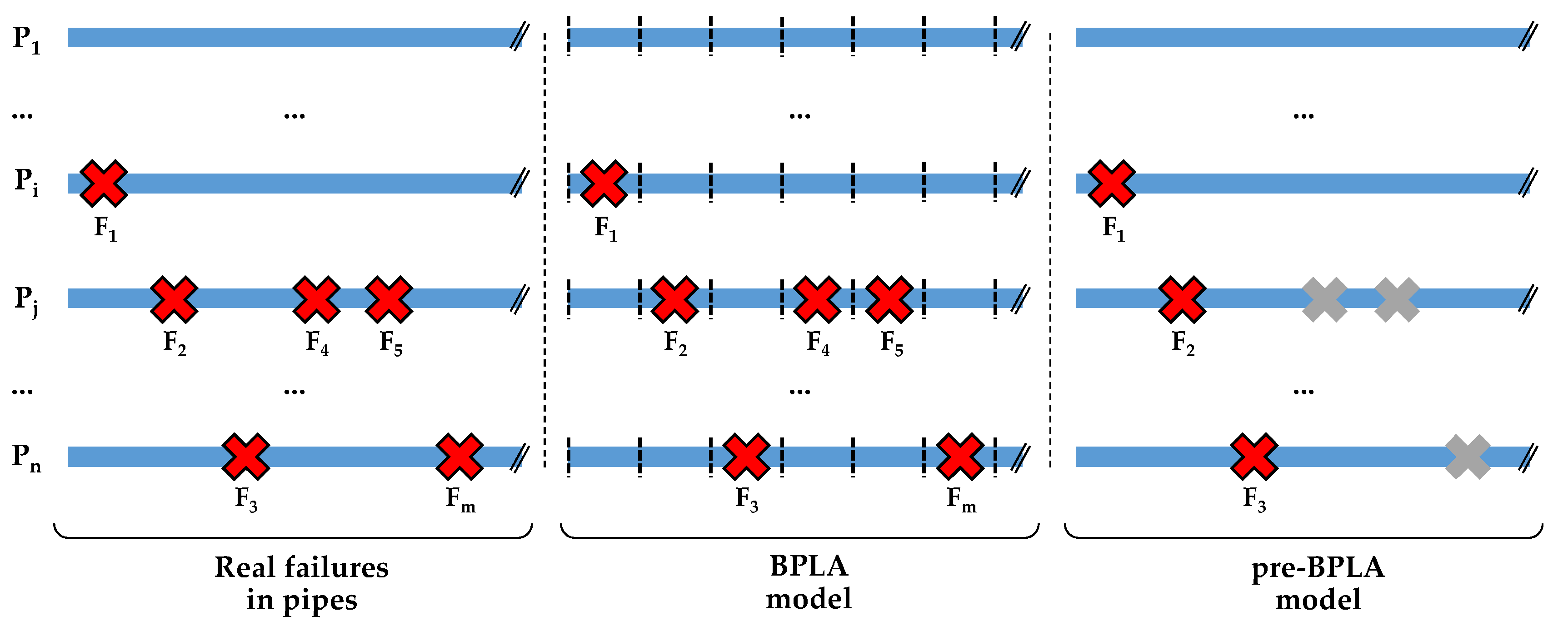
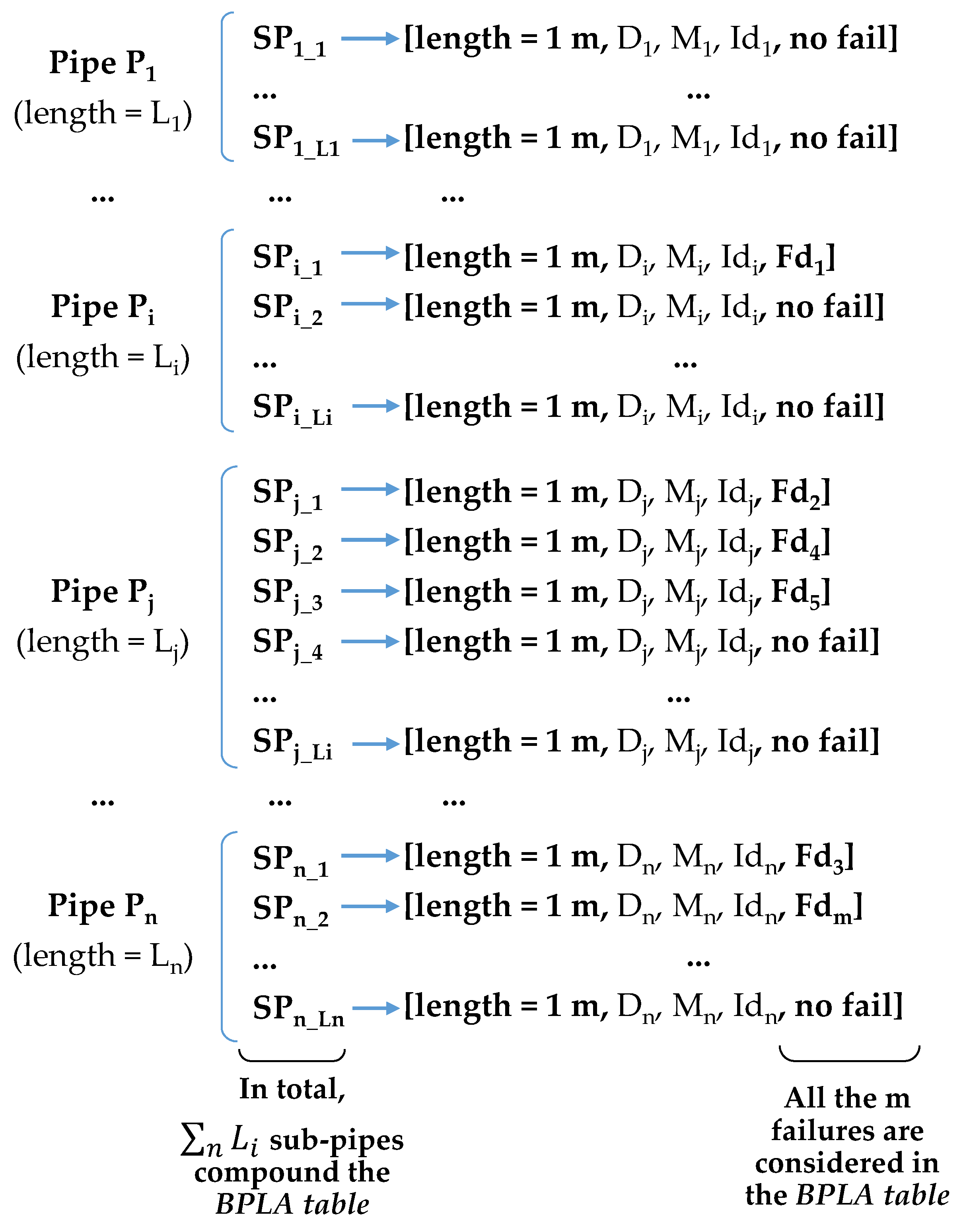
Regardless the total length of each one, pipe had no failures during the time window, pipe had only 1 failure, and pipes and had 3 and 2 failures, respectively. For the BPLA model, each pipe, of length L, is divided into L sub-pipes of 1 meter-length, and each one of the failures recorded in the original pipe is assigned to one of the resulting sub-pipes. This way, all the failures are considered in the model, all the lengths of each original pipe are properly kept in the model, and each sup-pipe can be considered as a non-repairable element. One part of each pipe (the sub-pipes with assigned failures) is contributing to the failure function, but not the rest of it.
Figure 5 shows the generation of sub-pipes and the way pipe properties are transferred to them. The number of failures are distributed to the same number of sub-pipes, the rest remaining with no fails assigned. The outcome of this process is the BPLA table (
Table 3). Each row in this table corresponds to each sub-pipe, so that it is compounded by as many rows as the network length in meters—for this purpose, the actual length of each pipe should be rounded to the nearest whole number. As all the dates are transferred, the last two columns of the BPLA table can be calculated:
(life till failure) is the time elapsed between the installation date (Id) and the fail date (Fd) in case the sub-pipe has one failure assigned, or between the installation date (Id) and the end date (Ed) of the availability window in case the sub-pipe has not a failure assigned. Later analysis of will provide the estimation for the average service life of the pipe group.
(time till failure) is the time elapsed between the start date (Sd) of the availability window and the fail date (Fd) in case the sub-pipe has one failure assigned, or between the start date (Sd) and the end date (Ed) of the availability window in case the sub-pipe has not a failure assigned. Analysis of will provide the location on the bath curve and the hazard rate for future failures forecasting.
Finally,
Figure 4 also shows the pre-BPLA approach [
37], which could be understood as a simplified version of the BPLA. Pre-BPLA only takes into account the first failure occurred in each pipe, and discard the rest. In fact, this procedure is a straight application of the techniques of maintenance engineering to network pipes. It is simpler and faster than the BPLA, and therefore, more feasible for novel utilities. At the same time, the simplifications assumed biased the results in a greater extent. Results provided by the pre-PBLA model will secondarily be obtained and shown in the case study. However, because of the limited data it works with, the pre-BPLA should be kept apart in favor of the BPLA.
Statistical analysis: The BPLA table now contains all the relevant information for all the sub-pipes, of each pipe group, ready for the statistical analysis. Following a univariate parametric model, such analysis consists in finding the distribution that best fits the failure information contained in the BPLA table. The Weibull distribution is the first recommended candidate because of its characteristics and flexibility, and the one considered in this paper, though there are other possible options. Several techniques may be employed to perform the fitting—maximum likelihood estimation method, method of moment, least-squares regression method, graphical methods, etc. [
38,
39]. The outcome of the adjustment are the two specific parameters of the Weibull distribution—shape (
) and scale (
)—thus assuming that the location parameter (
) has no influence in this type of analysis. In consequence,
being the failure time for each sub-pipe, Equations (1) to (4) [
40] show the failure behavior in each pipe group:
Equation (1) is the failure probability (probability density function), Equation (2) is the failure function (cumulative distribution function), Equation (3) is the survival function (complementary cumulative distribution function) and Equation (4) is the failure rate (hazard function).
Each failure time should be accounted since the pipe installation moment (LtF) or since the time window onset (TtF). Then, as advanced above, the statistical analysis will be performed independently on each of them. In consequence, the results finally obtained will be two sets of Equations (1) to (4), one per each time variable considered.
Once each analysis is completed, and before coming to any first conclusion, the goodness of fit must be checked. There are several techniques available—chi-squared, Kolmogorov–Smirnov, etc. [
38,
39,
40,
41]. In case they do not validate the Weibull fitting, other distributions could be tested; for example, normal, log-normal, or gamma.
Interpretation of results: Two Weibull parameters are obtained after each fitting: shape and scale for LtF (denoted as and ) and, also, shape and scale for TtF (denoted as and ). Their meanings are quite direct because of the characteristics of the Weibull distribution itself.
The scale factor, , is generally called characteristic life. It is not the mean life of the distribution, but the life that is reached by the 63.2% of the units. Therefore, for the LtF distribution, the provides a quick assessment of the age at which each meter of pipe will likely have its first failure.
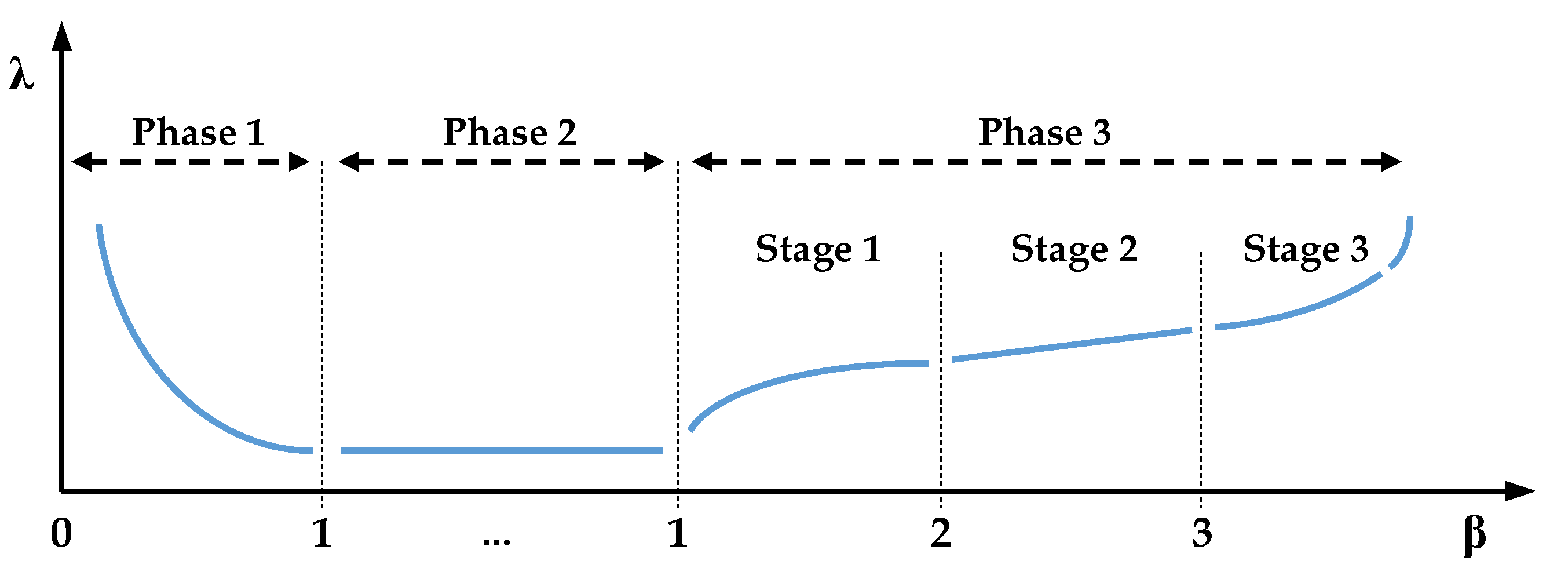
In maintenance engineering, the shape factor,
, is closely related to the failure rate,
, (
Figure 6) and, in consequence, to the bath curve [
32]. Taking advantage of the variable TtF, for which all the sub-pipes have been analyzed from the same time onset, the shape parameter
and the failure rate
(Equation (4)) are now known. According to
Figure 6, the value of the
will show the location of the pipe group onto the bath curve. This way, the kind of failures that are currently occurring on the pipe group can be categorized as early, useful or wearout life, and utility managers may set future planning according to this. Secondly, based on the value of
, a prediction of the number of future expected failures can be made for the pipe group. It is assumed that this calculation should be limited to the short-term. It will be valid as long as the location on the bath curve does not change from one stage to the next one. In case it happens, that would be unveiled by a new value of
, that, in turn, should be the one considered for a new calculation.
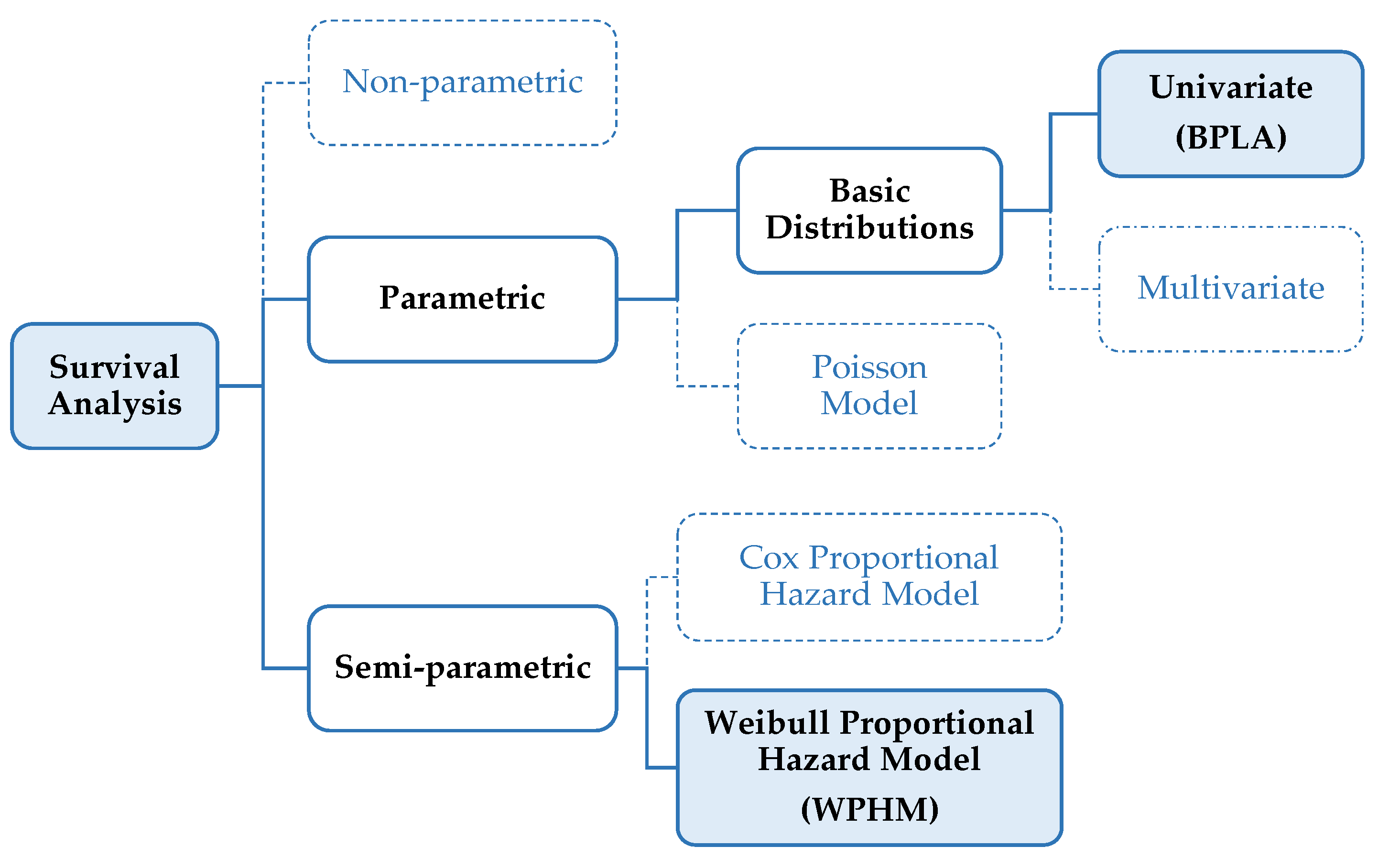
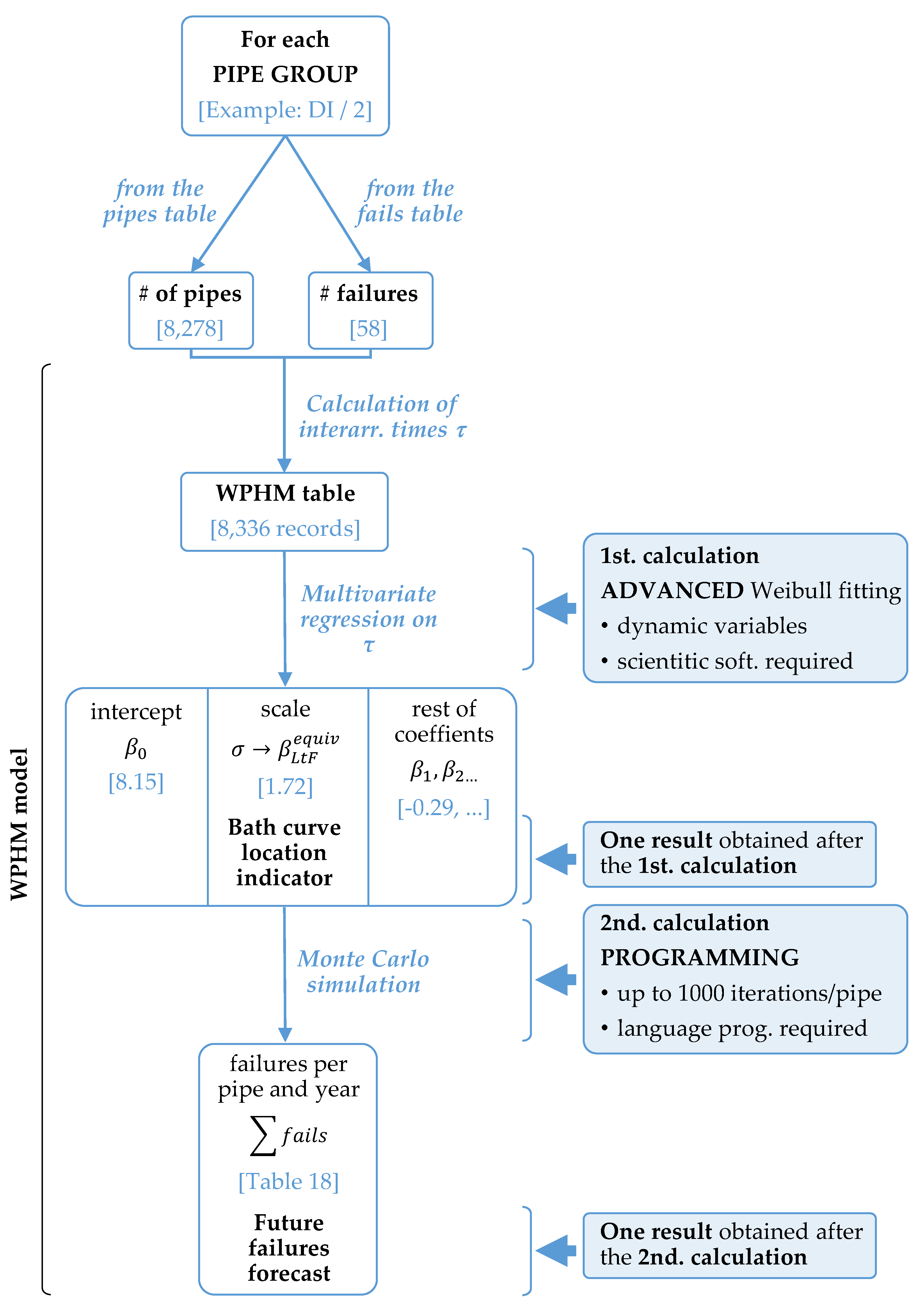
2.2. Quick Summary of the WPHM
The WPHM is a well-known semi-parametric model (
Figure 1) that is taken as a reference in this work for comparison purposes. Only some main features are summarized below. Full information on the WPHM is available in the literature [
3,
10,
15,
16,
17,
18,
19].
One main different is that the WPHM does not require the network pipes to be categorized in homogeneous groups. Instead, all the pipes may be kept in the same table because the particular features of each one are taken by the model as explicative covariates; after the calculation, its influence will be assessed through particular coefficients.
The second difference is the, more complex, way the failure data is organized, combined with the pipe data and, processed. As shown in
Figure 7, the WPHM focuses on the so-called interarrival time (
). This is, for each failure in each pipe, the time elapsed since the immediately preceding failure occurred. For the case of the first recorded failure, it is the time since the onset of the time window. After the last recorded failure, one additional interarrival time is considered—the time between the last failure and the end of the time window. This last interarrival time is treated as censored (it ends at the end of the time window, not at a new failure) while the others are treated as uncensored (they end at the next failure) [
32]. If all the failures in all the pipes are processed in this way, the final table obtained, here called WPHM table, will have the structure shown in
Table 4 (consistent with
Table 1 and
Table 2). Each row contains the information of each interarrival time and, additionally, the additional information (covariates) of the pipe in which that failure occurred.
The population formed by all the interarrival times, organized in the vector
, may be described by a Weibull distribution and that vector may be related to the vector of the covariates
as shown by Equation (5) [
15]:
where
is the vector that contains the covariates coefficients,
is the vector of the random errors and
is a regression parameter.
Each coefficient
, shows the influence of each covariate,
, on the failure occurrences
. Yet, the more relevant parameters are
and
, which are called respectively intercept and scale. This notation is purposely kept the same as the one usually found in the literature [
15,
16], and therefore, it should be remarked that while both coefficients are not the same as those already defined for the BPLA, they are closely related to them. The reason for this is that the Weibull distribution lays on the core of both methodologies. In particular the relation between the coefficients employed by both models is [
42]:
The number of the future expected failures can also be predicted through the WPHM. However, it entails a more complex calculation. It is performed through Equation (8) [
15] and a Monte Carlo simulation process. In summary, for each pipe, random values (up to 1000) of
(survival) are produced and the corresponding interarrival time,
, for each value is obtained. With each iteration, the
coefficients influence each new
. Eventually, the end of the simulation period is reached and the calculations are performed again for the following pipe of the network.
Finally, the results obtained for each pipe are added up to get the final single figure—the total failures. Equation (9) shows the total failures during the first year of the simulation for each pipe group,
, where
is the current year,
is that first year,
is the order number of each pipe within the group,
is the number of failures of pipe
and
is the total number of pipes in the group. By extending the simulation time one more year and detracting the failures occurred up to the year before, the increment of total failures for each successive year can be easily obtained through Equations (9) and (10) [
16].