Experimental Study of Local Scour around Caissons under Unidirectional and Tidal Currents
Abstract
1. Introduction
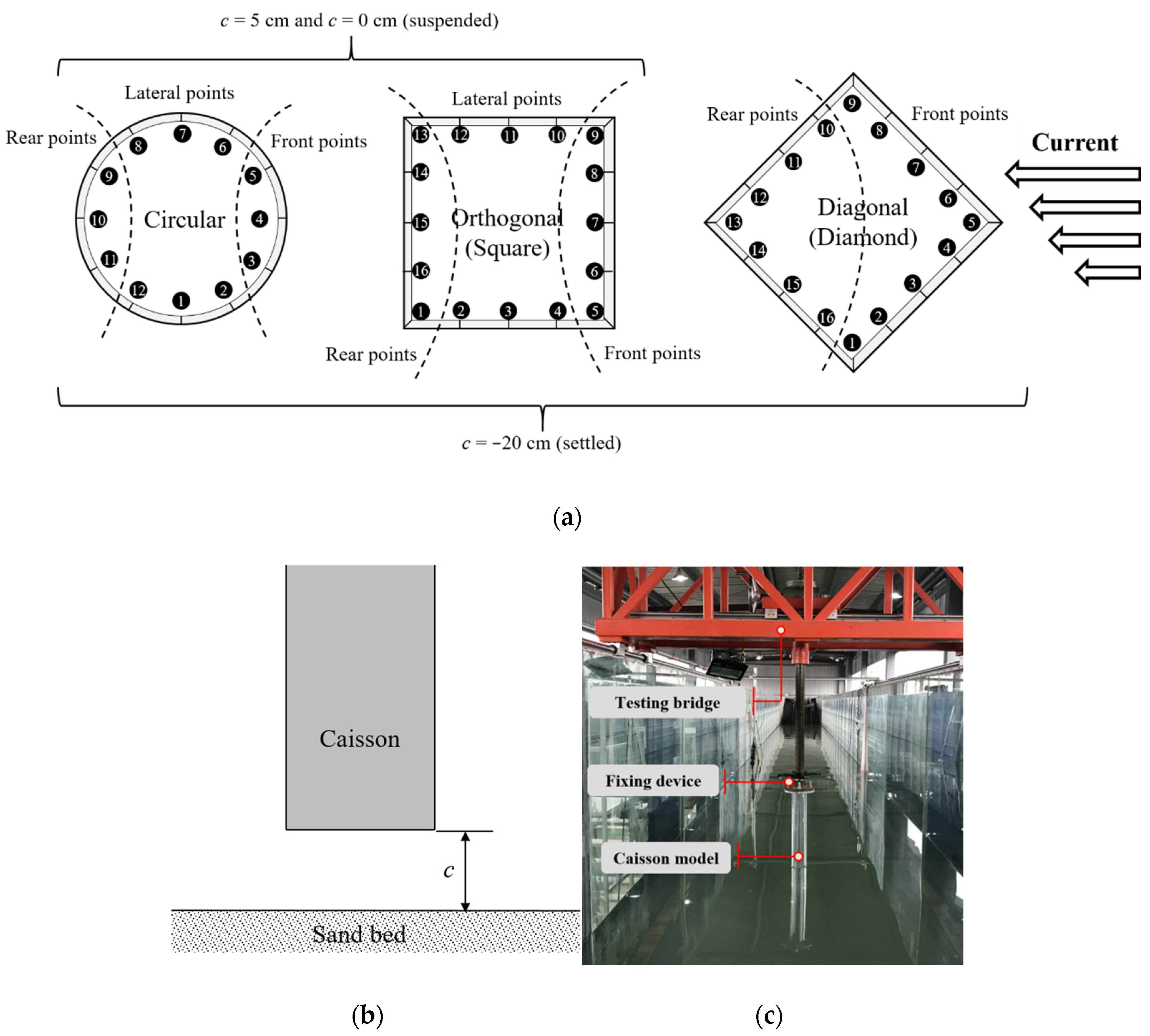
2. Materials and Methods
2.1. Testing Facilities
2.2. Calculation of Test Parameters
2.3. Testing Currents and Cases
3. Results
3.1. Local Scour around Caissons Settled into the Sediment
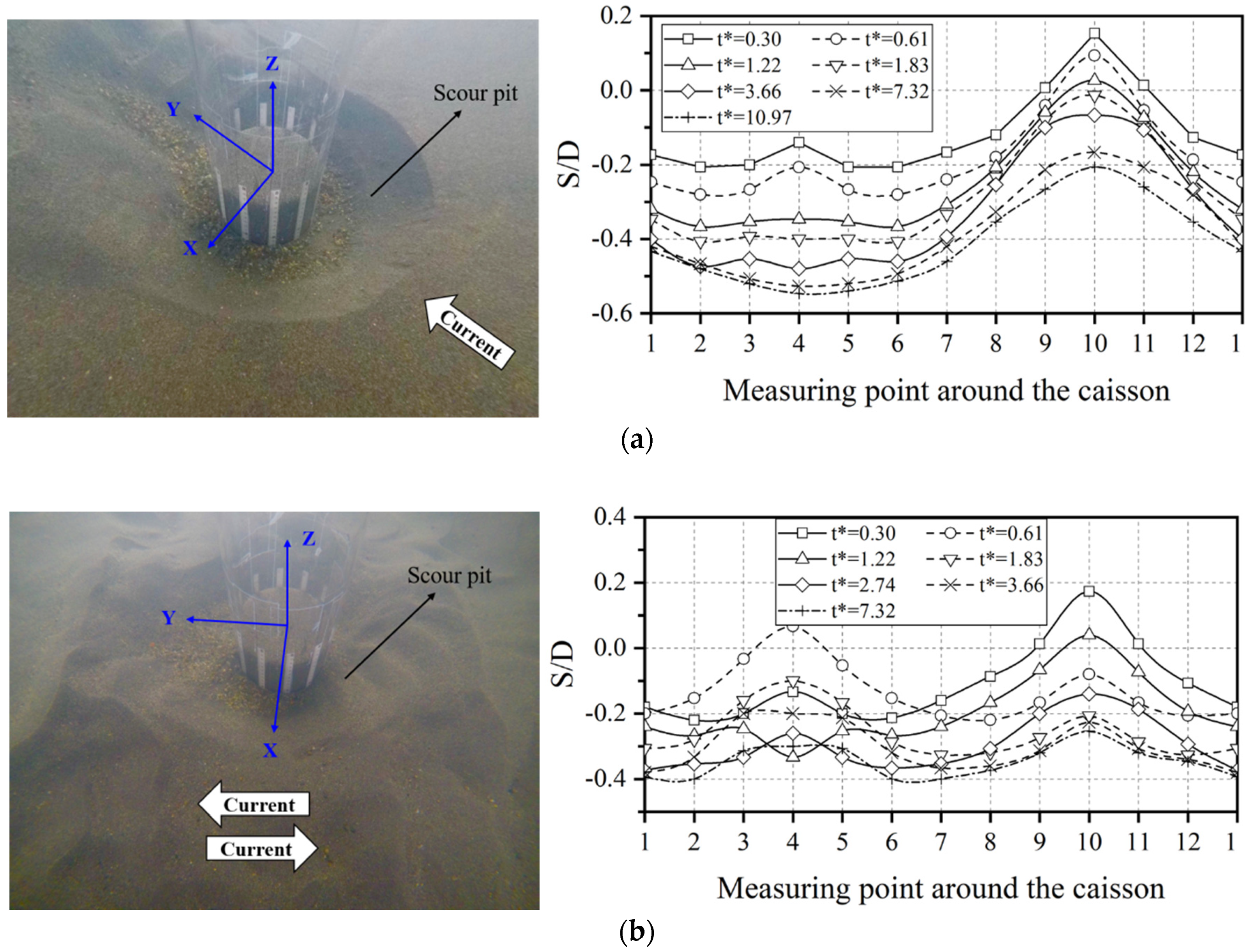
3.1.1. Circular Caisson
3.1.2. Square Caisson
3.1.3. Diamond Caisson
3.1.4. Analysis and Comparison of the Maximum Scour Depths
3.2. Local Scour under Caissons Suspended in Water
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ti, Z.; Zhang, M.; Li, Y.; Wei, K. Numerical study on the stochastic response of a long-span sea-crossing bridge subjected to extreme nonlinear wave loads. Eng. Struct. 2019, 196, 109287. [Google Scholar] [CrossRef]
- Zhang, M.; Yu, J.; Zhang, J.; Wu, L.; Li, Y. Study on the wind-field characteristics over a bridge site due to the shielding effects of mountains in a deep gorge via numerical simulation. Adv. Struct. Eng. 2019, 22, 3055–3065. [Google Scholar]
- Wei, K.; Liu, Q.; Qin, S. Nonlinear assessment of offshore steel trestle subjected to wave and current loads. Ships Offshore Struct. 2019, 1–13. [Google Scholar] [CrossRef]
- Liang, F.; Wang, C.; Yu, X. Performance of Existing Methods for Estimation and Mitigation of Local Scour around Bridges: Case Studies. J. Perform. Constr. Facil. 2019, 33, 04019060. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Sites; The University of Auckland: Auckland, New Zealand, 1975. [Google Scholar]
- Blanco, G.; Ye, A.; Wang, X.; Goicolea, J.M. Parametric Pushover Analysis on Elevated RC Pile-Cap Foundations for Bridges in Cohesionless Soils. J. Bridge Eng. 2019, 24, 04018104. [Google Scholar] [CrossRef]
- Wang, X.; Ye, A.; Shang, Y.; Zhou, L. Shake-table investigation of scoured RC pile-group-supported bridges in liquefiable and nonliquefiable soils. Earthq. Eng. Struct. Dyn. 2019, 48, 1217–1237. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, K.; Qin, S. An efficient numerical model for hydrodynamic added mass of immersed column with arbitrary cross—Section. Ocean Eng. 2019, 187, 106192. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. The Mechanics of Scour in the Marine Environment; World Scientific: Singapore, 2002. [Google Scholar]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publications: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Arneson, L.A.; Zevenbergen, L.W.; Lagasse, P.F.; Clopper, P.E. Evaluating Scour at Bridges, 5th ed.; Hydraulic Engineering Circular No. 18 (HEC-18); Federal Highway Administration: Washington, DC, USA, 2012. [Google Scholar]
- Ataie-Ashtiani, B.; Beheshti, A.A. Experimental Investigation of Clear-Water Local Scour at Pile Groups. J. Hydraul. Eng. 2006, 132, 1100–1104. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutment Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Penna, N.; Coscarella, F.; Gaudio, R. Turbulent Flow Field around Horizontal Cylinders with Scour Hole. Water 2020, 12, 143. [Google Scholar] [CrossRef]
- Oliveto, G.; Comuniello, V.; Bulbule, T. Time-dependent local scour downstream of positive-step stilling basins. J. Hydraul. Res. 2011, 49, 105–112. [Google Scholar] [CrossRef]
- Breusers, H.N.C.; Nicollet, G.; Shen, H.W. Local scour around cylindrical piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Wang, S.; Wei, K.; Shen, Z.; Xiang, Q. Experimental Investigation of Local Scour Protection for Cylindrical Bridge Piers Using Anti-Scour Collars. Water 2019, 11, 1515. [Google Scholar] [CrossRef]
- Schendel, A.; Welzel, M.; Hildebrandt, A.; Schlurmann, T.; Hsu, T.-W. Role and Impact of Hydrograph Shape on Tidal Current-Induced Scour in Physical-Modelling Environments. Water 2019, 11, 2636. [Google Scholar] [CrossRef]
- McGovern, D.J.; Ilic, S.; Folkard, A.M.; McLelland, S.J.; Murphy, B.J. Time Development of Scour around a Cylinder in Simulated Tidal Currents. J. Hydraul. Eng. 2014, 140, 04014014. [Google Scholar] [CrossRef]
- Wang, J. Research on Local Scour at Bridge Pier under Tidal Action. Matec Web Conf. 2015, 25, 01013. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.-S.; Gao, P.; Zheng, J.-H.; Wu, X.-G.; Peng, Y.-X.; Zhang, T.-T. Current-Induced Seabed Scour Around a Pile-Supported Horizontal-Axis Tidal Stream Turbine. J. Mar. Sci. Technol. 2015, 23, 929–936. [Google Scholar]
- Schendel, A.; Hildebrandt, A.; Goseberg, N.; Schlurmann, T. Processes and evolution of scour around a monopile induced by tidal currents. Coast. Eng. 2018, 139, 65–84. [Google Scholar] [CrossRef]
- Ma, L.; Wang, L.; Guo, Z.; Jiang, H.; Gao, Y. Time development of scour around pile groups in tidal currents. Ocean Eng. 2018, 163, 400–418. [Google Scholar] [CrossRef]
- Xiang, Q.; Li, Y.; Wei, K.; Wang, S.; Yao, C. Review of Bridge Foundation Scour. J. Southwest Jiaotong Univ. 2019, 54, 235–248. [Google Scholar]
- Veerappadevaru, G.; Gangadharaiah, T.; Jagadeesh, T.R. Vortex scouring process around bridge pier with a caisson. J. Hydraul. Res. 2011, 49, 378–383. [Google Scholar] [CrossRef]
- Veerappadevaru, G.; Gangadharaiah, T.; Jagadeesh, T.R. Temporal variation of vortex scour process around caisson piers. J. Hydraul. Res. 2012, 50, 200–207. [Google Scholar] [CrossRef]
- Zhao, M.; Zhu, X.; Cheng, L.; Teng, B. Experimental study of local scour around subsea caissons in steady currents. Coast. Eng. 2012, 60, 30–40. [Google Scholar] [CrossRef]
- Liang, F.; Wang, C.; Huang, M.; Li, J. Scale Effect on Local Scour Configurations around Caisson Foundation and Dynamic Evolution. China J. Highw. Transp. 2016, 29, 59–67. [Google Scholar]
- Oliveto, G.; Marino, M.C. Temporal scour evolution at non-uniform bridge piers. Proc. Inst. Civ. Eng.-Water Manag. 2017, 170, 254–261. [Google Scholar] [CrossRef]
- Burkow, M.; Griebel, M. A full three dimensional numerical simulation of the sediment transport and the scouring at a rectangular obstacle. Comput. Fluids 2016, 125, 1–10. [Google Scholar] [CrossRef]
- Gao, Z.R.; Huang, J.W.; Zhao, X.D. Research on Local Scour during Settling of Steel Caissons for Large-scale Bridges. Ocean Eng. 2006, 24, 31–35. [Google Scholar]
- Sun, M.X. Study on Local Scour Characteristics of Caisson under the Action of Wave and Flow; Southewest Jiaotong University: Chengdu, China, 2018. [Google Scholar]
- Soulsby, R.L.; Whitehouse, R.J.S. Threshold of sediment motion in coastal environments. In Pacific Coasts and Ports ’97: Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Christchurch, New Zealand, 7–11 September 1997; University of Canterbury: Christchurch, New Zealand; pp. 145–150.
- Soulsby, R.L. Dynamics of Marine Sands; Tomas Telford Ltd.: New York, NY, USA, 1998. [Google Scholar]
- Babaeyan-Koopaei, K.; Ervine, D.A.; Carling, P.A.; Cao, Z. Velocity and Turbulence Measurements for Two Overbank Flow Events in River Severn. J. Hydraul. Eng. 2002, 128, 891–900. [Google Scholar] [CrossRef]
- Marta, K.; Zbigniew, P. Bed Shear Stress Influence on Local Scour Geometry Properties in Various Flume Development Conditions. Water 2019, 11, 2346. [Google Scholar]
- Biron, P.M.; Robson, C.; Lapointe, M.F.; Gaskin, S.J. Comparing different methods of bed shear stress estimates in simple and complex flow fields. Earth Surf. Process. Landf. 2004, 29, 1403–1415. [Google Scholar] [CrossRef]
- Sumer, B.M.; Christiansen, N.; Fredsøe, J. Time scale of scour around a vertical pile. In Proceedings of the 2nd International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 14–19 June 1992; Volume 3, pp. 308–315. [Google Scholar]
- Vasquez, J.A.; Walsh, B.W. CFD Simulation of Local Scour in Complex Piers under Tidal Flow. In Proceedings of the 33th IAHR Congress: Water Engineering for a Sustainable Environment, Vancouver, BC, Canada, 9–14 August 2009; Volume 604, pp. 913–920. [Google Scholar]
- Wang, C.; Yu, X.; Liang, F. A review of bridge scour: Mechanism, estimation, monitoring and countermeasures. Nat. Hazards 2017, 87, 1881–1906. [Google Scholar] [CrossRef]












| Case | Shape of Caissons | Horizontal Dimension in the Cross-Flow Direction D (m) | Type of Current | Clearance c (cm) | Velocity (m/s) | Water Depth (m) |
| 1 | Circular | 0.15 | Unidirectional | −20 | 0.35 | 0.4 |
| 2 | Square | 0.15 | ||||
| 3 | Diamond | 0.212 | ||||
| 4 | Circular | 0.15 | Tidal | |||
| 5 | Square | 0.15 | ||||
| 6 | Diamond | 0.212 | ||||
| 7 | Circular | 0.15 | Unidirectional | 5 | ||
| 8 | 0 | |||||
| 9 | Tidal | 5 | ||||
| 10 | 0 | |||||
| 11 | Square | Unidirectional | 5 | |||
| 12 | 0 | |||||
| 13 | Tidal | 5 | ||||
| 14 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Q.; Wei, K.; Qiu, F.; Yao, C.; Li, Y. Experimental Study of Local Scour around Caissons under Unidirectional and Tidal Currents. Water 2020, 12, 640. https://doi.org/10.3390/w12030640
Xiang Q, Wei K, Qiu F, Yao C, Li Y. Experimental Study of Local Scour around Caissons under Unidirectional and Tidal Currents. Water. 2020; 12(3):640. https://doi.org/10.3390/w12030640
Chicago/Turabian StyleXiang, Qiqi, Kai Wei, Fang Qiu, Changrong Yao, and Yadong Li. 2020. "Experimental Study of Local Scour around Caissons under Unidirectional and Tidal Currents" Water 12, no. 3: 640. https://doi.org/10.3390/w12030640
APA StyleXiang, Q., Wei, K., Qiu, F., Yao, C., & Li, Y. (2020). Experimental Study of Local Scour around Caissons under Unidirectional and Tidal Currents. Water, 12(3), 640. https://doi.org/10.3390/w12030640






