Abstract
Groundwater level in coastal aquifers is usually affected by tidal waves and rainfall recharge. Therefore, the objective of this study is to present a mathematical model to account for the effects of tidal waves and rainfall recharge simultaneously. The model is based on the Dupuit–Forchheimer assumptions and is separated into a tidal waves component and rainfall recharge component. A new more general analytical solution for the recharge component is acquired by the generalized integral transform technique. The beach slope, the inclination of an impermeable base of an aquifer, and any randomly distributed rainfall recharge are taken into account in the model. A new finding is that the highest fluctuation in groundwater levels might occur when the range of rainfall recharge is larger than the decay length.
1. Introduction
The estimation of groundwater levels is usually simulated by numerical models in addition to field observations of wells. Only a small portion of previous research exploring groundwater problems employs analytical approaches, especially about the effect of tidal waves on groundwater levels. In the early stages, Parlange et al. [1] applied the theory proposed by Dagan [2] to analytically investigate tidal waves’ effect on the groundwater level fluctuations in spatial and temporal variations. Their results agree very well with that obtained by numerical models but are only restricted to vertical beach slopes. Then, Nielsen et al. [3] investigated the variation of the beach slopes of coastal aquifers and derived analytical solutions for groundwater tables inside horizontal aquifers. The results of wave numbers were compared with observations from a Hele–Shaw cell. However, in their study, the shoreline, i.e., the free water surface at the interface between the aquifer and ocean water, is considered to be fixed. This is not true for real physical phenomena. The discrepancy of their solution increases while the beach slope decreases. Later, Li et al. [4] proposed a moving boundary method to modify the shortcomings of the fixed boundary concept for an inclined beach.
On the other hand, Zissis et al. [5] and Bansal and Das [6] linearized the Boussinesq equation with constant hydraulic conductivity to discuss the effect of increasing stream flow and water depth on groundwater levels. Their results show that the linear solution almost coincides with the nonlinear one under the same conditions without considering rainfall events. While the heavy rainfall and mild slopes are taken into account, the discrepancy becomes apparent. Polubarinova-Kochina [7] proposed the linearized Boussinesq equation to study the effect of permeable ground on unconfined inclined aquifer. Asadi-Aghbolaghi et al. [8] investigated the temporal fluctuations of groundwater for leaky aquifers with inclined bottoms and found the tidal waves also affect the groundwater fluctuation. Sun [9] derived a two-dimensional analytical solution of groundwater response to tidal loading in an estuary by taking the depth-average of the governing equations and comparing their results with the numerical modeling.
Currently, Teo [10] applied perturbation methods to solve the nonlinear equation and improved the results of Nielsen et al. [3] for the groundwater fluctuations in a coastal aquifer. He concluded that the water table increases while the beach slope decreases. Hsieh et al. [11] studied the similar problem with consideration of both beach slopes and inclined impervious bottoms of coastal aquifers under distinct spatially linearly distributed rainfall events. To satisfy Dupuit–Forchheimer assumptions, their results are acceptable for a limited mild inclined angle of the sloping bottom of unconfined aquifers by employing the remarks of Chapman [12].
The present study aims to analytically derive the groundwater response to any temporally varied recharge as well as tidal waves by an integral-transform technique. Although a similar study has been proposed by Hsieh et al. [11], their analytical approach can only deal with uniform rainfall recharge and linearly distributed rainfall recharge. Comparatively, any various recharge rates and tidal waves as well as the beach slope and inclination of the base of a coastal aquifer can be simulated by the presented model. Furthermore, in the previous work of Hsieh et al. [11], the authors divided the whole domain into two sub-domains and solved two governing equations of groundwater levels separately, whereas the present study only uses one governing equation of groundwater levels to model the groundwater flow in the entire domain.
2. Mathematical Formulation
The schematic of the present study is depicted in Figure 1. In the figure, the beach slope of the coastal aquifer is β and the slope of the impermeable bottom base is θ. hz is the average water depth [L], h is the water depth induced by waves and rainfall [L], xr is the cover range of rainfall recharge [L], and r is the recharge rate [L/T].
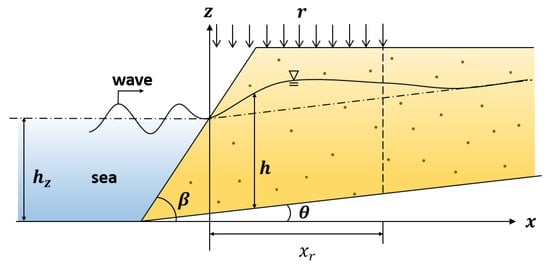
Figure 1.
Schematic of study problem. Replot from Figure 1 of Hsieh et al. [11].
Because the response of groundwater levels to the effect of tidal waves and recharge rates is very complex, and the water level is mainly affected by specific yield and hydraulic conductivity of the aquifer, we assumed that the soil texture is homogeneous and isotropic, and soil particle is incompressible and unmovable for a coastal unconfined aquifer. Further, some researchers report that the tidal water table fluctuations in a coastal aquifer are driven by tides or the tide-induced water table height in coastal aquifers, with sloping beaches on a moving boundary that varies with the beach slope and slowly generates a damped water table fluctuation in the aquifer. Therefore, the groundwater level in an unconfined aquifer could be affected by the tide oscillations. Both fresh water and saline water will not mix with each other. In this study, the water existing in the land side (X > 0) is only fresh water, so there is no density difference needed to be considered. The condition is such that the water table heights at the boundary of the ocean and coast are equal to the specified tidal variation (Li et al. [4], Teo et al. [10]).
2.1. Governing Equation and Boundary Conditions
In general, the Boussinesq equation is usually employed to elucidate groundwater flow in an unconfined aquifer, so the governing equation, by referring to Chapman [12], can be represented as
where S is the specific yield; K is the hydraulic conductivity; r is the recharge rate; x is the progressive direction of tide waves; and t is time.
The nonlinear governing equation, Equation (1), is difficult to be solved analytically, so a linearization technique provided by Brutsaert [13] and Zissis et al. [5] was employed to subsequently obtain the following linearized equation:
in which ε is a calibration parameter, and ε ϵ [0,1]. Then, the fluctuation of groundwater levels Δh is denoted by
Substituting Equation (3) into Equation (2) yields
The seaward boundary is inclined at an angle β to the horizontal (x) axis and exposed to tides. Therefore, by referring to Hsieh et al. [11], it can be expressed by
where a is the amplitude of the tidal waves and ω is the wave frequency. x0 is the horizontal range induced by tides with the following expression:
Substituting Equation (3) into Equation (5) yields
Because the effects of tidal waves and rainfall recharge rates at the sufficiently far area of the inland vanish, there is no change of the water depth, i.e.;
2.2. Non-Dimensionalization
Adopting the decay length presented by Chapman [12] and Nielsen [14] along the x direction, the following dimensionless variables are introduced:
It should be noted that the cover range of rainfall recharge xr might be equal to, larger than, or less than the decay length , i.e. xr = , xr > , or xr < . These three scenarios will be discussed in the Results and Discussion section.
Considering the beach slope and referring to Li et al. [4] and Hsieh et al. [11], Equations (7) and (6) subsequently become
and if we set X1 = X − X0(T) for the moving boundary, the governing equation, Equation (4), subsequently becomes
where U(X) is the unit step function.
Then, the boundary conditions, Equations (7) and (8), become
where
Note that in the work of Hsieh et al. [11], the domain of the aquifer is first divided into two subdomains, and then the solutions to two governing equations are separately acquired by the continuity conditions at the interface between the two subdomains. However, in this study, there is no necessity to do so, and Equation (12) models the groundwater levels in the whole domain.
To solve the above boundary value problem, the solution is separated into two parts HW and Hr, i.e., one solution for tidal waves effect and the other for rainfall recharge effect, and then both solutions are incorporated by the linear superposition principle.
2.3. Solution for Tidal Waves Effect
Considering the solution for tidal waves effect only, and setting η(T) = α − τAδcotβsinT, the boundary value problem, Equations (12) to (14), becomes
The solution for HW can be easily obtained by separating the solutions into a transient solution and a steady state solution (see Hsieh et al., [11]), and finally we can obtain
with , and . This solution, with consideration of the moving boundary, is more general than that presented in Hsieh et al. [11] and includes the solution of Parlange et al. [1] when .
2.4. Solution for Rainfall Recharge Effect
Considering the solution for rainfall recharge effect without tidal waves, the boundary value problem, Equations (12) to (14), becomes
To solve Equations (20) to (23), the generalized integral transformation method was employed by the following procedures:
The following relationship is set to eliminate the first-order derivative in Equation (20):
Equation (24) is substituted into Equations (20) to (23), resulting in
Referring to Özisik [15], the following solution by the generalized integral transforms method can be obtained:
Therefore, the dimensionless fluctuation of groundwater levels can be obtained by incorporating Equations (19) and (29) into the dependent variable H’ in Equation (12).
Referring to Kazezyılmaz-Alhan [16], while considering any dimensionless randomly distributed rainfall recharge rates, R can be represented by
and if the duration of the rainfall recharge is given, Equation (29) becomes
Then, the dimensionless groundwater level is acquired as follows:
3. Results and Discussion
Since the work of Hsieh et al. [11] has been verified, the present solutions were compared with theirs. As such, the parameters in Hsieh et al. [11], θ = 0°, β = 90°, S = 0.005, K = 0.1 cm/s, hz = 200 cm, a = 65 cm, ω = 4π were first employed, and the effects of tidal waves and uniform rainfall recharge are illustrated in Figure 2. From the figure, the present solutions agree very well with the ones of previous research, and thus, the present results are satisfactory, which validates the present analytical solutions.
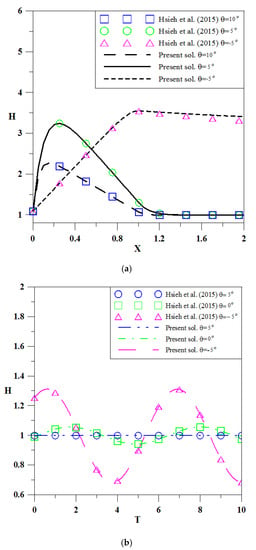
Figure 2.
Verification of the present solutions with previous results for groundwater levels under (a) rainfall recharge effect; td = 5 h, r = 15 mm/h. and (b) tidal waves effect; X = 1.
Next, the extensive application of various rainfall recharge effects on groundwater levels is discussed. The mid-peak and double-peak distributed rainfall recharge rates are inputted into the present solution, Equation (31), and the groundwater levels are shown in Figure 3. For example, the rates for the mid-peak case are 10, 15, 20, 25, 30, 25, 20, 15, 10, 5 mm/h, and the rates for the double peak case are 5, 10, 15, 10, 5, 5, 5, 15, 10, 0 mm/h with a total duration td = 10 h. It should be noted that the total accumulative rainfall recharge is different, and the former is larger than the latter. The peak value of groundwater levels in Figure 3a occurs at the location (X,T) = (0.7, 3.15), whereas the first peak in Figure 3b occurs at (X,T) = (0.7, 2.1) and the second one at (X,T) = (0.75, 4.7). Although the two peak recharge rates of the double peak case are the same, the maximum water level occurs at the second peak rather than the first one because of the piling-up effect for the double peak case. Moreover, Figure 3 successfully demonstrates that the present solution can simulate the spatiotemporal variation of groundwater levels in a sloping unconfined aquifer under any randomly distributed rainfall recharge, and this was not done in the work of Hsieh et al. [11].
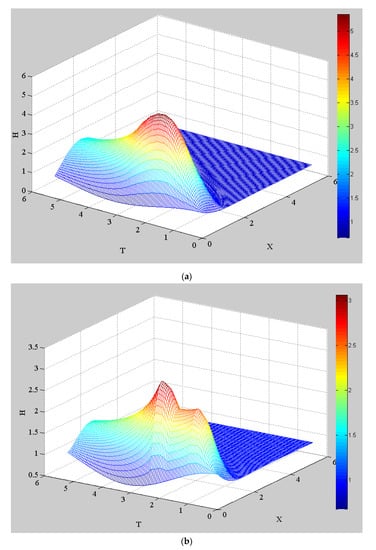
Figure 3.
Variation of groundwater levels under different rainfall recharge effects (T > Td); (a) mid-peak rainfall recharge; (b) double peak rainfall recharge rate.
Consequently, the tidal waves’ effect on groundwater levels is investigated. The effect of the beach slope on groundwater levels is shown in Figure 4. In the figure, θ = 0°, β = 30°, 60°, 90° and δ = 0.3386, S = 0.07, K =0.0038 cm/s for silt inside a coastal aquifer are selected, and the result indicates that the water level fluctuates more apparently for a smaller slope. This means more wave energy id transmitted into the aquifer for small slopes. This finding agrees with the results of Hsieh et al. [11]
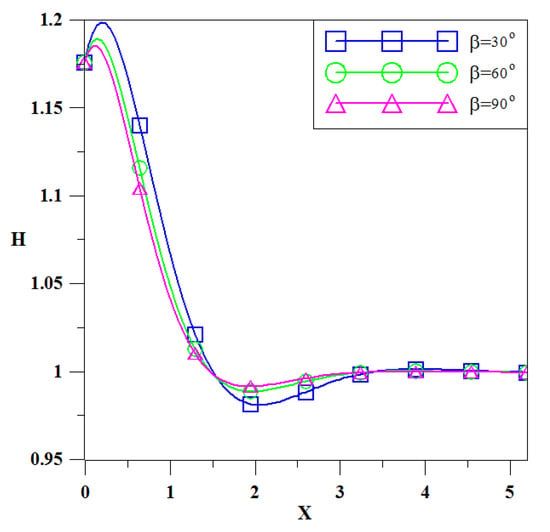
Figure 4.
Variation of groundwater levels under the beach slope effect (T = 1).
Further, although Hsieh et al. [11] has explained the effect of the relationship between the range of rainfall recharge (xr) and the decay length () on groundwater levels, and considered the representative scenario, xr = , of groundwater level fluctuations under the common effect of tidal waves and rainfall recharge, this study investigated the effect again for xr > , xr = and xr < , as shown in Figure 5; Figure 6 for different materials (fine sand and sandy clay) of the coastal aquifer, in which θ = 0° and β = 90°, r = 25 mm/h. From Figure 5, the simulated peaks of the cases of xr > and xr = are very close to each other, which complies with the discussion in Hsieh et al. [11]. After some more distinct cases of different materials for the aquifer were tested, the same findings were obtained for most cases as were obtained in Hsieh et al. [11]. However, Figure 6 shows the exception that larger fluctuations of groundwater levels might occur for the case of xr > , which indicates the dependence of the alluvial deposits on the texture of the stratum.
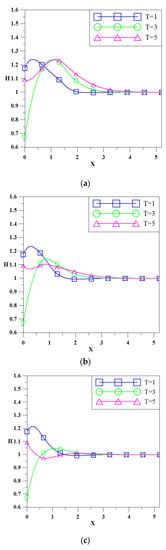
Figure 5.
Variation of groundwater levels for different ranges of rainfall recharge (fine sand, S = 0.21, K = 0.0023 cm/s); (a) xr > ; (b) xr = ; (c) xr < .
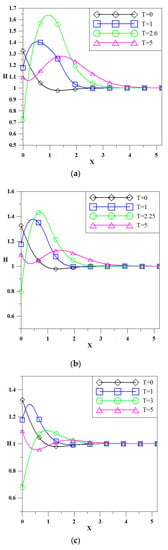
Figure 6.
Variation of groundwater levels for different ranges of rainfall recharge (sandy clay, S = 0.07, K = 0.000217 cm/s); (a) xr > ; (b) xr = ; (c) xr < .
Moreover, to apply the present solution to realistic groundwater problems, an illustration was made, as shown in Figure 7. The aquifer consists of younger alluvial soils in Chiayi County, Taiwan. The rainfall recharge and the field data of the groundwater levels was collected from Liuxi station and Pingxi station of Chiayi County from 2018/07/06 to 2018/10/13, respectively. Referring to Chinchmalatpure et al. [17], the hydraulic conductivity K = 120 cm/day, and the specific yield S = 0.1 were employed. Figure 7 shows that the present solution captures the general pattern of fluctuation, but the solution seems to have a faster response and decay of h. The discrepancy was conjectured to arise from the variability of property of soils. In fact, the hydraulic conductivity in an aquifer is anisotropic and heterogeneous. However, typical values of these two parameters are generally employed for the analytical solutions. Although a discrepancy between the present solution and field data exists, the result could be acceptable. Furthermore, the present analytical solution could be helpful for the verification of a new developed numerical model.
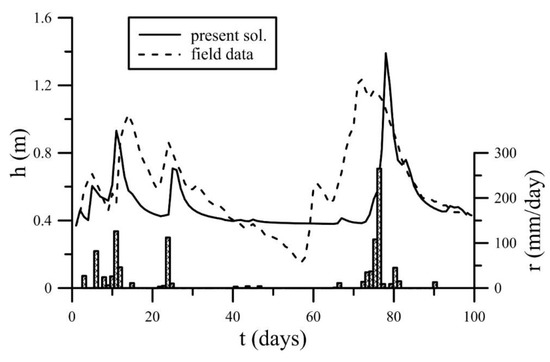
Figure 7.
Application of the present solution under randomly temporally distributed rainfall recharge and comparison of groundwater levels between the present solution and field data.
4. Conclusions
The present study contributes to developing one general governing equation, Equation (12), to dominate the whole study domain under any randomly temporally varied rainfall recharge, as well as tidal waves, as opposed to using two governing equations that consider uniform and linearly distributed rainfall recharge, as is the case in previous research, such as that by Hsieh et al. [11]. The present solutions which consider the moving boundary are more general than the previous solutions of Parlange et al. [1] and Hsieh et al. [11].
Moreover, two more new findings are obtained. One is that the largest fluctuation of groundwater levels depends on the material of the coastal aquifer, and it might occur when the range of rainfall recharge is larger than the decay length, even if it is not commonly seen. The other is that the maximum water level of the double peak case with the same peak recharge occurs at the second peak rather than the first one because of the piling-up effect.
Author Contributions
Conceptualization, P.-C.H.; Data curation, M.-C.W.; Formal analysis, J.-L.H.; Funding acquisition, P.-C.H.; Investigation, P.-C.H. and J.-L.H.; Methodology, P.-C.H. and J.-L.H.; Software, J.-L.H. and M.-C.W.; Supervision, P.-C.H.; Validation, J.-L.H. and M.-C.W.; Writing—original draft, P.-C.H.; Writing—eview and editing, P.-C.H. All authors have read and agreed to the published version of the manuscript.
Funding
Ministry of Science and Technology, Taiwan: MOST 103-2313-B-005 -007 -MY3.
Acknowledgments
This study was financially supported by the Ministry of Science and Technology of Taiwan under Grant No.: MOST 103-2313-B-005 -007 -MY3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Parlange, J.Y.; Stagnitti, F.; Starr, J.L.; Braddock, R.D. Free-surface flow in porous media and periodic solution of the shallow-flow approximation. J. Hydrol. 1984, 70, 251–263. [Google Scholar] [CrossRef]
- Dagan, G. Second order theory of shallow free surface flow in porous media. Q. J. Mech. Appl. Math. 1967, 20, 517–526. [Google Scholar] [CrossRef]
- Nielsen, P.; Aseervatham, R.; Fenton, J.D.; Perrochet, O. Groundwater waves in aquifers of intermediate depths. Adv. Water Resour. 1997, 20, 37–43. [Google Scholar] [CrossRef]
- Li, L.; Barry, D.A.; Stagnitti, F.; Parlange, J.Y.; Jeng, D.S. Beach water table fluctuations due to spring-neap tides: Moving boundary effects. Adv. Water Resour. 2000, 23, 817–824. [Google Scholar] [CrossRef]
- Zissis, T.S.; Teloglou, I.S.; Terzidis, G.A. Response of a sloping aquifer to constant replenishment and to stream varying water level. J. Hydrol. 2001, 243, 180–191. [Google Scholar] [CrossRef]
- Bansal, R.K.; Das, S.K. Response of an unconfined sloping aquifer to constant recharge and seepage from the stream of varying water level. Water Resour. Manag. 2011, 25, 893–911. [Google Scholar] [CrossRef]
- Polubarinova-Kochina, P.Y. Theory of Ground Water Movement; Princeton University: New Jersey, NJ, USA, 1962; pp. 404–430. [Google Scholar]
- Asadi-Aghbolaghi, M.; Chuang, M.H.; Yeh, H.D. Groundwater response to tidal fluctuation in a sloping leaky aquifer system. Appl. Math. Model. 2012, 36, 4750–4759. [Google Scholar] [CrossRef]
- Sun, H. A two-dimensional analytical solution of groundwater response to tidal loading in an estuary. Water Resour. Res. 1997, 33, 1429–1435. [Google Scholar] [CrossRef]
- Teo, H.T.; Jeng, D.S.; Seymour, B.R.; Barry, D.A.; Li, L. A new analytical solution for water table fluctuations in coastal aquifers with sloping beaches. Adv. Water Res. 2003, 26, 1239–1247. [Google Scholar] [CrossRef]
- Hsieh, P.C.; Hsu, H.T.; Liao, C.B.; Chiueh, P.T. Groundwater response to tidal fluctuation and rainfall in a coastal aquifer. J. Hydrol. 2015, 521, 132–140. [Google Scholar] [CrossRef]
- Chapman, T.G. Modeling groundwater flow over sloping beds. Water Resour. Res. 1980, 16, 1114–1118. [Google Scholar] [CrossRef]
- Brutsaert, W. The unit response of groundwater outflow from a hillslope. Water Resour. Res. 1994, 30, 2759–2763. [Google Scholar] [CrossRef]
- Nielsen, P. Tidal dynamics of the water table in beaches. Water Resour. Res. 1990, 26, 2127–2134. [Google Scholar] [CrossRef]
- Özisik, M.N. Boundary Value Problems of Heat Conduction; Dover Publications, INC: New York, NY, USA, 1968. [Google Scholar]
- Kazezyılmaz-Alhan, C.M. An improved solution for diffusion waves to overland flow. Appl. Math. Model. 2012, 36, 1465–4172. [Google Scholar] [CrossRef]
- Chinchmalatpure, A.R.; Bardhan, G.; Nayak, A.K.; Rao, G.G.; Chaudhari, S.K.; Sharma, D.K. Effect of Sodium Adsorption Ratio with Different Electrolyte Concentrations on Saturated Hydraulic Conductivity of Selected Salt Affected Soils of Gujarat. J. Indian Soc. Sci. 2014, 62, 1–8. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).