Abstract
Wear due to sediment particles in fluid flows, also termed ‘hydroabrasion’ or simply ‘abrasion’, is an omnipresent issue at hydraulic structures as well as in bedrock rivers. However, interactions between flow field, particle motion, channel topography, material properties and abrasion have rarely been investigated on a prototype scale, leaving many open questions as to their quantitative interrelations. Therefore, we investigated hydroabrasion in a multi-year field study at two Swiss Sediment Bypass Tunnels (SBTs). Abrasion depths of various invert materials, hydraulics and sediment transport conditions were determined and used to compute the abrasion coefficients kv of different abrasion models for high-strength concrete and granite. The results reveal that these models are useful to estimate spatially averaged abrasion rates. The kv‑value is about one order of magnitude higher for granite than for high-strength concrete, hence, using material-specific abrasion coefficients enhances the prediction accuracy. Three-dimensional flow structures, i.e., secondary currents occurring both, in the straight and curved sections of the tunnels cause incision channels, while also longitudinally undulating abrasion patterns were observed. Furthermore, hydroabrasion concentrated along joints and protruding edges. The maximum abrasion depths were roughly twice the mean abrasion depths, irrespective of hydraulics, sediment transport conditions and invert material.
1. Introduction
Reservoir sedimentation is a phenomenon of increasing evidence both, in Alpine regions and worldwide. This negatively affects the multifold purposes of reservoirs, e.g., water supply, irrigation, hydropower and flood protection. As the worldwide reservoir sedimentation volume meanwhile exceeds the increase of reservoir capacity, the net storage capacity has been decreasing since about the turn of the millenium [1,2,3,4,5]. The situation becomes even worse accounting for the population growth and increasing per capita consumption resulting in an inevitable water shortage in the near future [3,4,5,6,7]. Therefore, sustainable long-term sediment management strategies are required to maintain and provide sufficient reservoir storage capacity.
Sediment bypass tunnels (SBTs) are an effective countermeasure against reservoir sedimentation for small- to medium-sized reservoirs with high water availability, as e.g., typical in geologically young and therefore, erosive mountains, such as the Alps, Andes and Himalayas [8,9]. Sediment-laden flows are diverted through SBTs around reservoir dams, so that the sediment transport is restored to pre-dam status. Thus, SBTs contribute to a sustainable use of reservoirs, while enhancing the eco-morphology and aquatic habitat quality of the downstream river reaches [8,10,11,12,13,14,15,16]. However, the prevailing hydraulics and sediment transport conditions in the SBTs, i.e., high-speed sediment-laden flows, can cause severe invert hydroabrasion, which provokes high maintenance cost and, in the worst case, endangering the tunnel stability [17].
Hydroabrasion is a common phenomenon occurring not only in SBTs and at other hydraulic structures, e.g., weirs, flushing channels, bottom outlets and diversion tunnels, but also in high-gradient bedrock rivers. Hence, it plays an import role in river incision and landscape evolution. Hydroabrasion is defined as continuous material loss from a fixed, submerged surface caused by the contacts of solid particles transported in the flow [18,19]. Depending on the hydraulic conditions and sediment properties, such as size and shape, sediment particles can be transported in sliding, rolling, saltation, or suspension mode causing grinding, rolling, or saltation impact stresses on the surface, respectively. Among these, impacts of saltating bedload particles govern not only material loss at SBTs and hydraulic structures, but also long-term bedrock incision and landscape evolution by driving hydroabrasion and macroabrasion–a process of fracturing bedrock into pluckable sizes mediated by particle impacts [19,20,21,22,23].
Prediction of hydroabrasion is crucial for design service life analysis of invert materials used in hydraulic structures as well as for landscape evolution studies with potential applications in steep bedrock channels and channel knickpoint evolutions of exposed bedrock, such as waterfalls [19,24,25,26,27]. Bedrock river incision is mostly modelled with a stream power equation [24,28,29,30]. These equations relate incision rate to hydraulics, i.e., stream power or bed shear stress without accounting for sediment transport and are found to be adequate for describing overall long-term developments [19]. However, they are not suitable for studies with particular interest in the transient local behavior, i.e., on small spatial or temporal scales, because of lumping potentially complex physical interactions between flow field, particle motion, bed material properties and hydroabrasion [19,31,32]. In contrast to the stream power models, mechanistic abrasion models account for the physical process of saltating bedload particle impacts and relate the incision rate to the kinetic energy transferred to the bed by the impinging particles. The “saltation abrasion model” (SAM) developed by [21] is a mechanistic abrasion model often used for bedrock incision analysis. Its basic form reads:
where Ar = vertical abrasion rate, YM = Young’s modulus of the abraded material, kv = dimensionless resistance coefficient, also termed abrasion coefficient, fst = splitting tensile strength of the abraded material, Wim = mean vertical particle impact velocity, LP = particle hop length, qs = specific gravimetric bedload transport rate and qs* = specific gravimetric bedload transport capacity. The term fst2/YM is related to the fracture energy required to detach a unit volume from the base material, while kv accounts for the efficiency of energy transfer from impinging particles to the invert material. The second term of Equation (1) is the flux of kinetic impact energy per unit area and time. The last term in parentheses accounts for the cover effect considering transient alluvial deposits hindering bedload particle impacts and, hence, bedrock incision. The application of particle motion equations, developed from a wide range of data from literature (including fixed and movable beds, and subcritical as well as supercritical flow conditions), has led to the following form of the SAM [21]:
with g = gravitational acceleration, s = ρs/ρ = 2.65 = ratio of solid to water density, T* = (θ/θc − 1) = excess transport stage, θ = U*2/((s − 1)gd) = Shields parameter, θc = critical Shields parameter, U* = (g·Rh·Se)1/2 = friction velocity, Vs = particle settling velocity, d = particle diameter, Rh = hydraulic radius and Se = energy slope. The excess transport stage accounts for the threshold of particle motion, whereas the last term relates to the mode shift from saltation to suspension.
The SAM was successfully tested on laboratory and field data [19,31,33,34,35,36]. However, the determination of the abrasion coefficient kv is yet a challenging issue of ongoing research. The kv-values were determined for various materials by using a self-developed abrasion mill set-up resulting in the widely accepted value of kv = 106 for rock, despite large variations of kv = 1 × 106–9 × 106 [21,37]. Variations in kv values are expected since [21] treated YM as a constant, i.e., YM = 50 GPa, which is a rough simplification regarding the large range of YM for rocks and concretes. Moreover, the properties of the impinging sediment, e.g., size, angularity and hardness, and of the abraded material, e.g., Young’s modulus, splitting tensile strength, density, porosity and crystal and clast size, which significantly affect hydroabrasion, are only partly accounted for in the SAM [19,38,39,40,41,42,43,44].
Although the SAM was established based on a wide data set, data for high-speed flows over planar beds with relatively low roughness, like those found at hydraulic structures and in high-gradient bedrock rivers, are sparse, in particular regarding information on particle impact. Particle motion and hydroabrasion under these particular conditions were investigated by [23] based on direct particle impact measurements with a high-speed camera [23,44,45]. Incorporation of newly developed equations for particle motion into the basic form of the SAM (Equation (1)) resulted in the “Saltation Abrasion Model adapted by Auel” (SAMA), which holds for sub- to highly supercritical flows over fixed planar beds [44,46]:
In [44], the abrasion coefficient kv was determined for a range of materials based on laboratory, field and literature data [21,23,26,32,47]. The authors reported that kv increases with the invert material’s splitting tensile strength and tends to stabilize at kv ≈ 105 for hard materials, such as rock and concrete with fst > 1 MPa.
Despite an increasing number of investigations in the recent past, there is still a considerable uncertainty regarding the determination of kv. More field data not subjected to potential laboratory scale and model effects are needed to advance knowledge on the governing processes of hydroabrasion and to validate kv-values [44]. To this end, we investigated hydroabrasion at two Swiss SBTs by testing various concretes and granite under field conditions for a period of 4 and 19 years [48,49]. The hydraulics and sediment transport conditions and hence the hydroabrasion processes in SBTs and high-gradient bedrock rivers are similar. Consequently, the findings of the present investigation also apply to bedrock incision and landscape evolution processes, although the incision rates are generally several orders of magnitude smaller due to considerable lower erosive potential [42].
Herein, we introduce the test sites at the Pfaffensprung and Runcahez SBTs and present the field data used for the evaluation and validation of both saltation abrasion models, i.e., SAM and SAMA. Furthermore, the abrasion patterns and their temporal evolution are discussed with respect to three-dimensional flow structures and sediment transport conditions.
2. Field Sites and Data Acquisition
Field investigations were conducted at the Pfaffensprung and Runcahez SBTs in Switzerland. Table 1 and Table 2 list the key data of these test sites, including information on respective reservoirs and rivers. The abrasion depths of various invert materials were quantified and analyzed with respect to the hydraulics and sediment transport conditions. The monitoring period was four years for Pfaffensprung SBT and 19 years for Runcahez SBT. The Runcahez data set is, to the authors’ knowledge, the first systematic long-term field investigation on hydroabrasion for different invert materials and hence is of prime importance to evaluate the material behavior and hydroabrasion patterns in a process-relevant time-scale.

Table 1.
Data of case study sediment bypass tunnels (SBTs) and respective reservoirs and rivers [48,50].

Table 2.
Properties of tested invert materials (mean value ± standard deviation) in the SBTs Pfaffensprung, Runcahez and Val d’Ambra (data from [18,48]).
In addition to the two case study SBTs, hydroabrasion data of the Swiss Val d’Ambra SBT provided by its operator were included in the data analysis (Table 1, Table 2 and Table 3). The monitoring period at this SBT is 47 years. The data set only includes the operator’s experience and concrete volumes used for the refurbishment of the tunnel invert. Since no direct abrasion measurement was conducted at this site, the available data set includes more uncertainty and does not provide information on the spatial and temporal evolution of hydroabrasion.

Table 3.
SBT operation conditions and abrasion depths in the Val d’Ambra SBT between 1967 and 2014 [48].
2.1. Pfaffensprung
The Pfaffensprung reservoir is located on the Reuss River in Wassen, Canton Uri, in the Swiss Alps. The reservoir built in 1922, was equipped with an SBT from the beginning to reduce reservoir sedimentation [52,53]. Figure 1 shows the layout of the Pfaffensprung SBT. Four test fields were implemented on the invert of the Pfaffensprung SBT within the scope of refurbishment works performed during the low flow winter seasons 2011/2012 and 2012/2013: two 10 m long test fields at the end of the straight section close to the outlet (location 1 in Figure 1) and two 20 m long test fields in the curvature section (location 2 in Figure 1). Test location 1 still exists, whereas the invert at test location 2 was removed after two years of operation during an extensive refurbishment of the tunnel invert. The observation periods considered for test location 1 and 2 are four and two years, respectively. Both test locations contained a 0.3 m thick pavement of 1 × 1 m2 Urner Granite blocks placed in a staggered order without joints (accuracy ± 2 mm) and a 0.3 m thick high-strength concrete section. Although the concrete mixtures are identical (except for steel fibers included in C1, but not in C2 due to their negative effect on the processability) their properties differ due to varying site conditions during construction (Table 2). The quarry provided the compressive strength fc, splitting tensile strength fst and elastic Young’s modulus YM for granite (Table 2). The compressive strength and density of the high-strength concretes were determined using 28 days old cube (150 mm × 150 mm × 150 mm) and drill core (100 mm × 100 mm) samples. The bending tensile strength fbt was determined by testing beam samples (120 mm × 120 mm × 360 mm). The compressive strength and the cylindrical compressive strength fc,cyl are related [54], as follows:
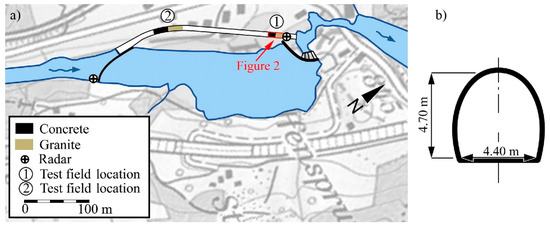
Figure 1.
(a) Overview and (b) cross section of the Pfaffensprung SBT (position 46°42′49.8″ N 8°36′36.7″ E) with test field locations 1 and 2 and radar instrumentation for discharge monitoring, position of Figure 2 highlighted red.
The splitting tensile strength is calculated based on the bending tensile strength [55]:
The Young’s modulus was computed according to [56]:
with k1 = 1.005 for river gravel aggregate, k2 = 0.95 for silica fume addition, ρ* = reference concrete density = 2.4 to/m3 and f* = reference concrete compressive strength = 60 MPa holding for concretes with fc,cyl = 40–160 MPa.
The operator of the facility (Hydropower plant Amsteg of the Swiss Federal Railways SBB) provided discharge data of the Reuss River and the Pfaffensprung SBT. The discharges were continuously monitored at a 15 min time interval by radar instruments installed both, in the SBT and in the river at the reservoir head (Figure 1). However, due to considerable gaps in the continuous time series, daily averaged discharge data were used in this study. Despite a certain information loss, this is an acceptable approach, since the SBT is in operation for several months per year.
The invert material surfaces of the test fields were mapped by using a terrestrial laser scanner (TLS), as shown in Figure 2. The abrasion depths are defined as the vertical distance between two TLS recordings. Each TLS recording consists of a three-dimensional-point cloud of roughly 108 measurement points, being the limit for data analysis. The first (reference) surface scan was performed after installation of the test fields. The subsequent scans followed every winter during the low flow season. The scan resolution in horizontal and vertical direction was 0.036°. The measurement errors stem from possible shifts of the target bolts, the target-based registration of the TLS scans and the errors of the laser beam. The error of each measurement point is ±3.3 mm and is smaller for abrasion depth calculation over large spatial scales due to averaging.

Figure 2.
Measurement installation in Pfaffensprung SBT at test field location 1 during scanning in March 2014, (1) terrestrial laser scanner (TLS), (2) temporary mounted targets and (3) ground water drainage, view in flow direction from high-strength concrete (C1) over granite pavement (G1) to SBT outlet.
2.2. Runcahez
The Runcahez reservoir was built in 1962 at the Rein da Sumvitg River [18,48]. It was equipped with an SBT from the beginning to reduce reservoir sedimentation. The layout of the SBT is shown in Figure 3 and general information is given in Table 1.
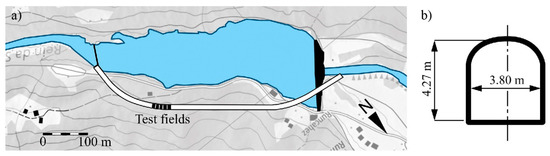
Figure 3.
(a) Overview and (b) cross section of the Runcahez SBT (position 46°40′45.0″ N 8°58′05.7″ E; adapted from [18]).
The SBT is used for bypassing sediment-laden discharges during flood peaks lasting a few hours resulting in a mean annual operation duration of only some hours [18,48]. Although the design discharge of the SBT is Qd = 110 m3/s under free-surface flow conditions, it can still bypass a maximum discharge of Qmax = 190 m3/s under pressurized inflow conditions [57].
Five 10 m long and 3.8 m wide test fields were implemented downstream of the inlet bend in 1995 (Figure 3). The compressive strength fc of the tested invert materials was determined from cube samples (120 mm × 120 mm × 120 mm) and the bending tensile strengths fbt and elastic Young’s modulus YM from beam samples (120 mm × 120 mm × 360 mm) [18]. The splitting tensile strength was derived from the bending tensile strength according to Equation (5). Table 2 summarizes the material properties. Note that the roller compacted concrete (RCC) suffered massive abrasion along the tunnel walls due to improper compaction and required a replacement after 1999.
No discharge measurement data, neither from the Rein da Sumvitg River at Runcahez nor from the SBT, are available from 1999 to 2014. Therefore, the 15-min. hydrograph of the neighboring national gauging station (Encardens, Federal Office of the Environment (FOEN)-Station Number 2430) was scaled to derive discharge data of the Rein da Sumvitg River at Runcahez. The scaling factor of 4.4 was obtained from least square fitting of flood discharge data in the Rein da Sumvitg at Runcahez, provided by [18] and at Encardens, provided by the FOEN, between 1996 and 1999 [48]. The SBT was assumed to be in operation at inflow discharges of Q ≥ 45 m3/s lasting for more than 2.5 h, since no measurement data of the operation are available [48].
The hydroabrasion depths of the test fields were geodetically surveyed using a leveling device. The initial measurement was performed after implementation of the test fields by using an analogue leveling device [18]. Afterwards, annual surveys were conducted until 1999. The resolution and accuracy of the measurements are 0.5 m × 0.2 m and ±2 mm, respectively. The subsequent survey was undertaken in the scope of the present study in fall 2014 using a digital leveling device. The resolution and measurement accuracy were 0.5 m × 0.4 m and ±2 mm, respectively. The abrasion depths were determined by directly comparing point measurements of the different recordings. The abrasion depths within the first four years were small, i.e., close to the measurements error, did not penetrate the core material and were partly affected by a systematic error resulting in implausible mean abrasion depths am. Therefore, the 19 years data set (considering only the initial measurement in 1996 and the one after 19 years in 2014) was considered as the most significant and representative one and hence, was used herein to compute the abrasion coefficient kv. For the RCC test field, only the four years data of the properly compacted zone were used (only considering the initial measurement in 1996 and the one after four years in 1999).
3. Methods
This chapter first presents the methods and procedures applied to quantify the hydraulics and sediment transport parameters in the SBTs and corresponding rivers. The determination of spatial abrasion maps, mean and maximum abrasion depths is explained in a second step and finally the abrasion model calibration procedure is presented.
3.1. Hydraulics
The flow velocities and depths in the rivers and SBTs were determined based on the hydrograph data. The mean flow velocities in the rivers were calculated based on the Manning-Strickler flow equation:
Assuming uniform flow in the river, the slope of the energy line equals the bed slope, i.e., Se = S and the hydraulic radius Rh follows from the continuity equation. The river bed roughness kSt follows from the 90-percentile particle diameter of the river bed material d90 [58]:
The flow in the SBTs gradually varies, as the SBTs are too short to attain uniform flow. The flow is accelerated to supercritical conditions at the inlet slightly decelerates along the SBT, but remains supercritical until the outlet. Therefore, the flow velocities and depths in the SBTs were determined based on backwater calculations using the Darcy-Weisbach Equation:
The friction coefficient λ for turbulent flows, as existing in SBTs and in most civil and river engineering applications, is a function of the bed roughness ks and the Reynolds number R = 4URh/ν, with ν = kinematic viscosity [59]:
The bed roughness height in the SBTs is ks = 0.003 m, was obtained from back-water calculations for design discharge and respective flow depths and corresponds to typical values for rough concrete [60].
3.2. Bedload Transport and Particle Motion
Bedload transport in the SBT depends on the initiation of bedload transport in the river, the extent of bedload transport in the river and the SBT operating regime. Bedload transport is assumed to be initiated as soon as the Shields number exceeds a critical value, i.e., θ > θc [61]. Numerous studies have been conducted on the initiation of bedload transport resulting in a variety of critical Shields number due to different test conditions and definitions of initiation of particle motion [62]. In the present study, θc = 0.047 for movable beds in rivers according to [63] and θc = 0.005 for SBTs exhibiting planar beds of low relative roughness with ks << d according to [45] were selected. At both case study sites, the rivers exhibit an armor layer, protecting the substrate due to its higher resistance against erosion [48]. This was accounted for by adapting θc based on the mean grain size of both, the armor layer dm,a ≈ 0.30 m and the substrate dm,s = dm [64]:
The extent of bedload transport depends on both, the sediment supply and the sediment transport capacity. The following three equations for the specific gravimetric bedload transport capacity qs* in the river are applied herein. The first one is a simplification of an implicit probability function for bedload transport [65] and was published by Parker [66]:
The second and third equations are empirical. The well established formula of Smart and Jäggi [67] is based on a wide data set for slopes of S = 0.0004–0.2. including experimental as well as literature data of [63] and reads:
with θc, depending on the bed slope and the angle of repose φ of the sediment particles:
According to [67], the effect of the term (d90/d30)0.2 in Equation (13) is weak, so that it can be replaced by 1.05. The last applied equation published by Cheng [68] is based on literature data for S = 0.0013–0.19 [63,69,70] and follows for θ ≥ θc:
Bedload transport is furthermore affected by site-specific conditions. Large immobile boulders cause significant additional turbulences and hence energy dissipation resulting in an overestimation of bedload transport capacity in steep channels with S ≥ 0.02–0.03 [71,72]. This phenomenon was accounted by either using a reduced slope S′ as proposed by [72], or a slope-corrected Shields parameter θS according to [73]:
with h = flow depth and fr = 1 = macro roughness factor for moderate roughness. To avoid bedload transport overestimation due to energy dissipation in the rivers, a reduced slope correction S′ (Equation (16)) was used in Equation (13) instead of Se and a slope corrected Shields parameter θS (Equation (17)) instead of θ was used in Equations (12) and (15).
The bedload transport capacity in the Reuss River was computed by applying Equations (12), (13) and (15) with the corrections described above to the daily discharge data and arithmetically averaging the resulting values. Finally, the effective specific gravimetric bedload transport qs in the Reuss was computed using the relation qs/qs* = 0.80 according to [74]. This approach was validated based on a former comprehensive study of the bedload transport in the Reuss River including a numerical investigation as well as extensive field surveys [74,75,76].
The bedload transport capacity of the Rein da Sumvitg River was determined by applying Equation (13) to the 15-min discharge data, while accounting for the energy dissipation by using Equation (16). The effective bedload transport is smaller than the bedload transport capacity due to limited sediment supply and follows qs/qs* = 0.45 according to [18]. The result was validated by means of literature data [18] and morphologic field surveys including gravel excavation volumes [48].
The effective bedload transport width of a river exhibiting several flow paths at low and medium discharges does not correspond to the actual channel width [77]. To account for that, the bedload effective channel width b′ instead of the channel width b was used to compute gravimetric bedload transport capacities at both sites. For gravel bed rivers, [77] proposed:
with Q = discharge.
The estimation of the bedload transport capacity for SBTs differs from that for alluvial beds due to the low relative roughness of ks/d << 0.1 and non-movable planar bed conditions [67]. For SBTs with slopes of S = 0.01–0.04, [23] proposed the following empirical formula for the gravimetric bedload transport capacity:
The rolling probability PR and particle hop length LP are given with [45]:
whereas the probability of motion in suspension Psu can be defined as [78]:
The bedload transport capacity in the SBT was computed by applying Equation (19) to the hydrograph of the SBT, while the effective bedload transport rates in the SBT depend on the sediment supplied by the river and the SBT operation.
In general, SBTs are designed to bypass all the incoming sediments and to avoid sediment aggradation and clogging of the SBT. Therefore, the bedload transport capacity of the SBTs is considerably higher than that of the feeding river.
3.3. Hydroabrasion
In a first step, the spatially averaged abrasion depths am (obtained from discrete surface measurements by either a TLS or geodetic levelling) were computed. In a second step, mean abrasion rates Ar were calculated by dividing spatially averaged abrasion depths am with the corresponding SBT operation durations T. Furthermore, the 95%-percentile abrasion depths, herein denoted as maximum abrasion depths amax, were determined. This parameter is assumed to be decisive for design service life analysis and economical investigations of hydraulic structures.
3.4. Model Calibration
Re-writing the Saltation Abrasion Model (SAM) (Equation (2)) and the Saltation Abrasion Model adapted by Auel (SAMA) (Equation (3)) leads to:
with Vs = particle settling velocity according to [79]:
The abrasion coefficient kv was calibrated based on the present field data for the (i) SAM assuming a constant Young’s modulus YM = 50 GPa, (ii) SAM using the effective Young’s moduli (SAM*) and (iii) SAMA also accounting for the effective Young’s moduli.
The model input parameters, i.e., mean hydraulic parameters, gravimetric sediment transport rates and capacities and spatially averaged abrasion depths for the Pfaffensprung and the Runcahez SBTs are described hereafter. Thereby, the cumulative bedload mass BL was obtained by integrating the volumetric bedload transport in the SBTs over time and multiplying with the specific sediment density of 2.65 to/m3. The specific gravimetric bedload transport in the SBTs follows from the cumulative bedload mass, the operation duration and the SBT widths with qs = BL/(b·T). The sediment transport capacity and particle settling velocity in the SBTs follow from Equations (19) and (25) using the averaged hydraulic parameters listed in Table 3, Table 4 and Table 5 for the corresponding period. The invert material properties used for the determination of the abrasion coefficients are given in Table 2.

Table 4.
Mean annual SBT operation conditions, bedload transport masses and abrasion depths in the Pfaffensprung SBT for the years 2012 to 2015.

Table 5.
Mean SBT operation conditions, bedload transport masses and abrasion depths in the Runcahez SBT for 1996–1999 and 2000–2014 and the overall average.
4. Results
4.1. Pfaffensprung
The annual SBT operation durations and discharges both, in the Reuss River and in the Pfaffensprung SBT are listed in Table 4, whereby only SBT operations above the threshold for initiation of bedload transport were considered. The over-annually averaged bypassed discharge is SBT = 32.1 m3/s, the corresponding mean flow depth, flow velocity and Shields parameter in the SBT were = 0.75 m, = 9.79 m/s and = 0.040, respectively.
The adapted critical Shields parameter for the Reuss River exhibiting an armor layer is θc′ = 0.049 (Equation (11)), which is in agreement with literature data [63,80,81]. The corresponding critical discharge for initiation of bedload transport amounts to Qc = 38 m3/s. The discharge in the river never exceeded the design discharge capacity of the SBT during the observation period from 2012 to 2015, so that the entire bedload mass supplied by the river was assumed to be bypassed (Table 4). Thereby, the transport capacity in the SBT was always considerably larger compared to that of the river so that no depositions in the SBT are expected to have taken place. This is in line with the operator’s experiences confirming no significant accumulations in the reservoir as well as in the SBT. The rolling and suspension probability of the mean particle size dm are PR = 0.30 (Equation (20)) and Psu = 0.00 (Equation (22)), respectively. The saltation probability follows with Psal = 1 − PR − Psu = 0.70 indicating that saltation was the dominating, rolling the minor transport mode. The corresponding particle hop length amounts to Lp = 2.70 m (Equation (21)).
Close-up pictures of the concrete test fields C1 and C2 show that the cement top layer was washed away, the coarse aggregates were abraded and a few break-offs of invert fragments and aggregates occurred (Figure 4a,b). The granite shows a different abrasion pattern, with concentrated material losses along the longitudinal joints and the upstream edges of the blocks (Figure 4c,d). The abrasion depths at the upstream edges of the plates, oriented perpendicular to the flow are significantly higher compared to the block itself, while the abrasion rates decrease with increasing distance to the joints in flow direction. Abrasion depths along the joints oriented parallel to the flow direction are also significantly higher compared to the block itself and grow in depth, width and extent with the flow direction affecting the downstream granite blocks.

Figure 4.
Close-up view of the abraded surface of the Pfaffensprung SBT: (a) high-strength concrete test field C1 after four operational years, (b) high-strength concrete test field C2 after two operational years, (c) granite test field G1 after four operational years showing abrasion concentration at upstream edges and (d) granite test field G1 after four operational years showing abrasion concentration along joints with downstream abrasion shadows.
The high-resolution abrasion maps of the concrete test fields C1 and C2 are shown in Figure 5 and Figure 6, respectively, those of the granite test fields G1 and G2 in Figure 7 and Figure 8, respectively. All abrasion maps show survey-device-specific patterns not related to material loss. Regular radial patterns are attributed to the repeating self-adjustment of the laser scanner. Circular patterns are caused by beam deflection at the device casing and appear around each laser scan position. The magnitude of the resulting scatter amounts to < ±3 mm. Apart from these artifacts, the mean detection uncertainty is < ±3.3 mm. The relative error is significant for small abrasion depths in the range of some millimeters, but decreases with increasing abrasion depths. The abrasion depths of the granite test fields were mostly in the range of the detection uncertainty resulting in unrealistic negative abrasion depths of some millimeters as shown by the blue colored areas in Figure 7 and Figure 8. These unrealistic negative abrasion values were not considered when determining the spatially averaged abrasion depths (mean abrasion depths in Table 4), which were later used for hydroabrasion analysis.
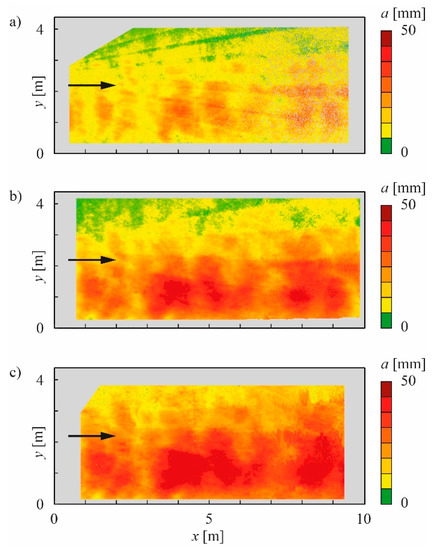
Figure 5.
High-resolution abrasion maps of the 10 m long high-strength concrete test field C1 installed at test location 1 in Pfaffensprung SBT after (a) one, (b) two and (c) four operational years (the grey colored areas could not be scanned due to ground water drainage installation).
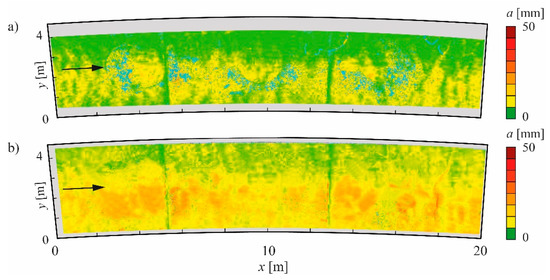
Figure 6.
High-resolution abrasion maps of the 20 m long high-strength concrete test field C2 installed at test location 2 in Pfaffensprung SBT after (a) one and (b) two operational years (the grey colored areas could not be scanned due to ground water drainage installation).
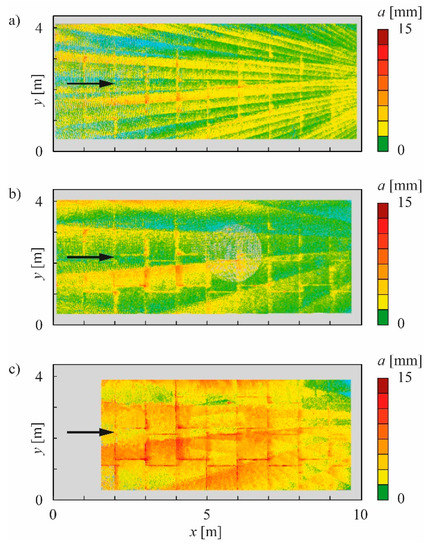
Figure 7.
High-resolution abrasion maps of the 10 m long granite test field G1 installed at test location 1 in Pfaffensprung SBT after (a) one, (b) two and (c) four operational years (blue colored points mark theoretically negative abrasion depths corresponding to detection uncertainty; grey colored areas could not be scanned due to ground water drainage installation).
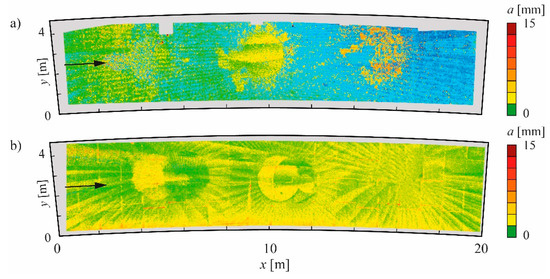
Figure 8.
High-resolution abrasion maps of the 20 m long granite test filed G2 installed at test location 2 in Pfaffensprung SBT after (a) one and (b) two operational years (blue colored points mark theoretically negative abrasion depths corresponding to detection uncertainty; grey areas could not be scanned due to ground water drainage installation).
Both high-strength concrete test fields C1 and C2 show abrasion lines perpendicular to the flow direction, associated to working joints (at x ≈ 4.7 m in Figure 5; at x ≈ 5.5 m and at x = 13 m in Figure 6). Despite this, the abrasion is dominated by a characteristic longitudinally undulating pattern with a wavelength of λw = 1.25 ± 0.6 m. Furthermore, a significant abrasion concentration on the orographic right side is visible and clearly shown by the super-elevated longitudinally averaged cross-sectional abrasion profiles in Figure 9. The abrasion depths of both high-strength concretes C1 and C2 were considerably higher after the first year compared to subsequent years. However, the shape of the abrasion profiles observed after the first year of operation were conserved during the following years with a slight trend of amplification.
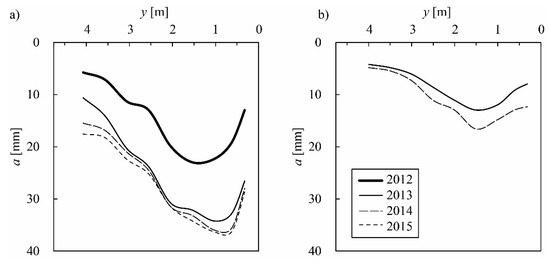
Figure 9.
Super-elevated longitudinally averaged cross-sectional abrasion profiles of high-strength concrete test fields (a) C1 at test location 1 and (b) C2 at test location 2 installed at Pfaffensprung SBT for the years 2012 to 2015; view in flow direction.
The granite test fields G1 and G2 partly indicate implausible negative abrasion depths (colored in blue) because of small abrasion depths close to the detection uncertainty. Overall, they confirm the visual surveys revealing abrasion concentrations along the joints.
The mean and maximum cumulative abrasion depths of the high-strength concrete and granite test fields are shown as a function of the cumulative bedload mass in Figure 10. The abrasion depths linearly increase with increasing bedload mass confirming the theory expressed by the mechanistic abrasion models. The ratio between maximum and mean abrasion depths defined by the gradients of the fits amounts to 43.8/25.0 = 1.8 for high-strength concrete and to 8.2/3.9 = 2.1 for granite. Overall, the results from the Pfaffensprung SBT show that the abrasion depths and hence abrasion rates of the granite pavement were on average approx. six times lower compared to those of high-strength concrete for identical hydraulics and sediment transport conditions.
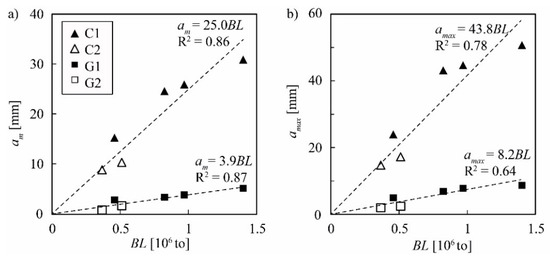
Figure 10.
(a) Mean and (b) maximum cumulative abrasion depths as a function of cumulative bedload mass at Pfaffensprung SBT for high-strength concrete test fields C1 and C2 and granite test fields G1 and G2 for the years 2012 to 2015.
Although abrasion on the tunnel walls was not monitored in this study, visual surveys indicated considerably smaller abrasion at the walls compared to those of the tunnel invert. Furthermore, abrasion at the walls mainly occurred close to the invert and decreased with increasing vertical distance from the invert. The tunnel walls only required small repair works since the commissioning in 1922, which is in contrast to the tunnel invert with several refurbishments in the same period.
4.2. Runcahez
Mean SBT operation duration and hydraulic conditions for the years 1996 to 2000 and 2001 to 2014 are listed in Table 5. Overall, the SBT was in operation for = 1.5 d per year bypassing a discharge of SBT = 56 m3/s. The corresponding mean flow depth, flow velocity and Shields parameter were = 2.0 m, = 7.4 m/s and = 0.036, respectively.
The Rein da Sumvitg River exhibits an armor layer. The adapted critical Shields parameter for initiation of bedload transport (Equation (11)) is θc′ = 0.058, which is in agreement with literature data [63,80,81]. The corresponding critical discharge for the initiation of motion is Qc = 33 m3/s.
The design discharge of the SBT was never exceeded during the observation period, so that the entire discharge including bedload was assumed to be bypassed without any depositions in the reservoir. The gravimetric bedload transport capacity of the SBT for the mean discharge amounts to Qs* = 0.50 to/s and is thus significantly larger than the corresponding bedload transport capacity of the Rein da Sumvitg River of Qs* = 0.08 to/s. As a result, no depositions in the SBT occurred. This was confirmed by the operator’s experiences revealing no depositions in the SBT. Table 5 lists the bypassed bedload masses for the years 1996–1999 and 2000–2014.
The rolling and suspension probabilities of the mean particle size in the SBT were PR = 0.33 (Equation (20)) and Psu = 0.00 (Equation (22)), respectively. This results in a saltation probability of Psal = 1 − PR − Psu = 0.67 indicating that particles were mainly transported in saltation. The computed particle hop length of the mean particle size amounts to Lp = 2.3 m (Equation (21)).
The individual test fields in the Runcahez SBT show similar abrasion patterns, except for the RCC exhibiting high material losses close to the tunnel walls due to improper compaction. As a representative for the other concretes, Figure 11a,b show the interpolated abrasion map of the silica fume concrete (SC) after four and 19 operational years, respectively. The abrasion map in Figure 11 shows a longitudinally undulating abrasion pattern with a wavelength λw = 2.5 ± 0.5 m and with two incision channels along the tunnel walls. The temporal evolution of these channels is seen in the longitudinally averaged cross-sectional profiles of the SC test field (Figure 12). The incision channels developed close to the tunnel walls and grew both, in depth and width over time. Furthermore, the abrasion profile is asymmetric. The abrasion depths on the orographic left side are higher than on the right side.
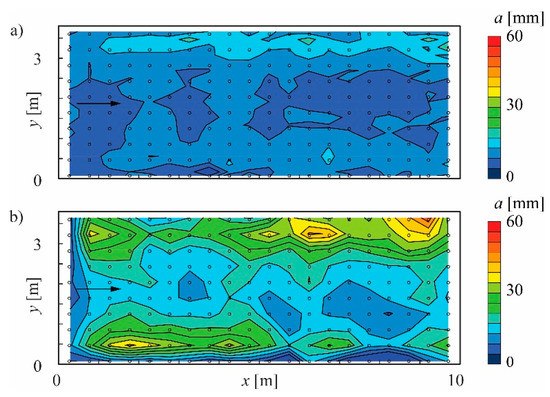
Figure 11.
Abrasion depths of the silica fume concrete (SC) test field in Runcahez SBT in (a) 1999 after four years of operation and (b) 2014 after 19 years of operation (circles represent measurement points).
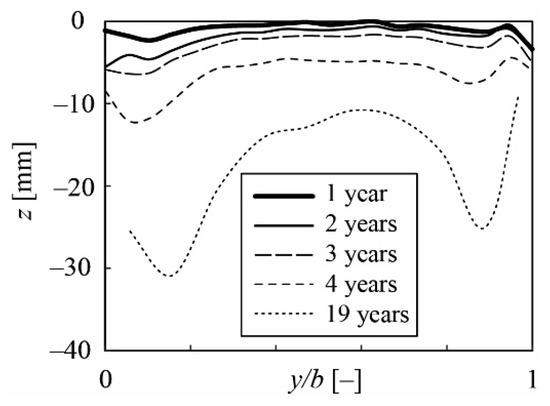
Figure 12.
Super-elevated, longitudinally averaged cross-sectional abrasion profiles of the silica fume concrete test field (SC) in Runcahez SBT.
The mean abrasion depths of all test fields given in Table 5 are plotted as a function of the cumulative bedload mass in Figure 13. The ratio between the maximum and mean abrasion depth depends on the material and ranges between amax/am = 1.6 and 2.2 at the end of the observation period.
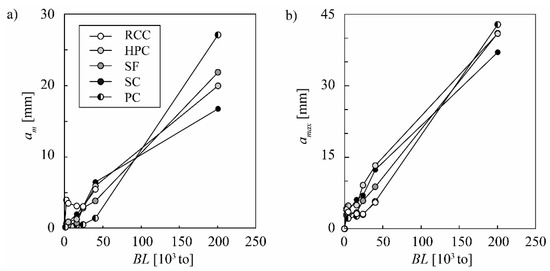
Figure 13.
(a) Mean and (b) maximum cumulative abrasion depths as a function of cumulative bedload mass of invert material test fields in Runcahez SBT.
The abrasion on the tunnel walls was not monitored in this study. However, several refurbishments were required at the invert, but none at the walls since the commissioning of the tunnel in 1962. Furthermore, visual surveys revealed that abrasion at the tunnel walls mainly occurred close to the invert and decreased with increasing vertical distance from the invert.
4.3. Abrasion Model Calibration
The computed kv-values based on the field data are plotted as a function of the corresponding material splitting tensile strengths in Figure 14. Irrespective of the model, the resulting data scatter is comparable, whereas the results of the SAMA are generally one order of magnitude smaller compared to those of the SAM and SAM*. Furthermore, a strong material dependency is evident. The kv-values determined for different types of concrete are similar, except for the polymer concrete (PC) and fluctuate around kv = 1.3 × 106 for the SAM, kv = 8.8 × 105 for the SAM* and kv = 1.9 × 105 for the SAMA, respectively. The kv-values of granite are kv = 1.4 × 107 for the SAM, kv = 1.6 × 107 for the SAM* and kv = 2.4 × 106 for the SAMA, hence being roughly one order of magnitude higher than those of the concretes.
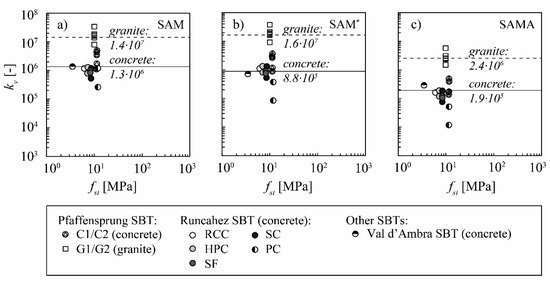
Figure 14.
Abrasion coefficient kv as a function of splitting tensile strength of various SBT invert materials for (a) SAM, (b) SAM* and (c) SAMA.
5. Discussion
5.1. Abrasion Pattern
It was shown that the bedload transport in the SBTs is mainly in saltation mode. Hence, impingement of saltating particles on the invert governs hydroabrasion in these tunnels. The mechanistic saltation abrasion models accounting for this mechanism are therefore applicable. The smoothly abraded surfaces indicate that the bed-parallel component of the kinetic energy trajectory of the impacting particles is dominant. This is in line with physical scale model test results, revealing that the particle impact angle in supercritical flows ranges from 2° to 8° for fixed planar beds [44].
The fact that no refurbishments of the tunnel walls were required, while several refurbishments of the inverts were performed in the Pfaffensprung and Runcahez SBTs, indicate that the abrasion rates on the walls were orders of magnitudes smaller compared to those of the tunnel inverts. This implies that the particle saltation trajectories exhibit a negligible component normal to the tunnel walls in agreement with [82].
The abrasion monitoring of the invert material test fields in the Pfaffensprung SBT revealed material-dependent abrasion characteristics (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). The concrete test fields show irregularities at the construction joints. Although such joints are supposed to represent spots of structural weakness where hydroabrasion initiates, the abrasion rates were not significantly higher compared to the rest of the test field. This suggests a proper implementation and high material quality. The irregularities of the abrasion patterns are rather caused by smoothing small initial surface irregularities that originated from implementation in the first year of operation, while no further amplification was observed in the subsequent years. The joints of the granite pavement also constitute spots of weakness and can be regarded as the equivalent of the concrete construction joints. While the joints perpendicular to the flow show similar characteristics as the working joints, i.e., smoothing out initial geometric irregularities at the upstream edges of the blocks, the joints oriented parallel to the flow direction exhibit a different behavior revealing a strong self-intensifying process, i.e., growing grooves (Figure 4d and Figure 7c). The concrete test fields in the Runcahez as well as the Pfaffensprung SBT exhibit a longitudinally undulating abrasion pattern (Figure 5, Figure 6 and Figure 11) similar to that observed in physical scale model tests [23]. This abrasion pattern is presumably triggered by saltating sediment particles. Bed irregularities prompt sediment particles to saltate and, hence, initiate abrasion further downstream due to particle impingement and in return cause bed irregularities initiating abrasion further downstream. This results in the formation of a regularly undulating abrasion pattern. In the Runcahez SBT, the abrasion wavelength of λw = 2.5 ± 0.5 m roughly scales with the mean computed particle hop length of LP = 2.28 m, whereas in the Pfaffensprung SBT λw = 1.25 ± 0.6 m is approximately half the computed particle hop length of LP = 2.70 m. The discharge at which the mean particle hop length is LP = 1.25 m amounts to Q ≈ 12 m3/s, which was frequently exceeded in the SBT, i.e., for 30 to 90 days per year between 2012 and 2015. A relation between particle motion and abrasion pattern is thus plausible. On the one hand, the observed variations of the abrasion wavelength could stem from the considerably fluctuating hydraulics and sediment transport conditions in the Pfaffensprung SBT (flow depths varying from a few centimeters to some meters and size of particles in motion varying between submillimeter to meter range), causing significant variations in particle hop length. On the other hand, these variations could result from a superposition of different abrasion patterns reducing the observed abrasion wavelength. In order to clarify possible relationships between bedload particle transport mode and abrasion pattern, further systematic investigations are needed. A comparable undulating abrasion pattern was not observed for the granite pavement in the Pfaffensprung SBT, which might be attributed to the fact that abrasion concentrations along the joints are orders of magnitude higher compared to those of the large-area invert and hence make the latter unrecognizable.
The abrasion pattern further depends on the local flow field and the presence of three-dimensional flow structures. Regarding SBTs, the secondary currents of Prandtl’s first and second type are of particular interest [83]. The first type occurs in channel bends, where a spiral flow, induced by centripetal forces, causes a concentration of sediment transport at the inner side of the bend [84]. The second type exists in straight narrow open channel flows due to non-homogeneity and anisotropy of turbulence [85]. As a result, bed shear stresses close to the walls are 20–50% higher compared to the spanwise averaged values for aspect ratios between 2 and 4 [23,86].
The ratio between maximum and mean abrasion depths determined from the field data was amax/am = 1.6–2.2. This agrees with literature data on mortar abrasion obtained from physical scale model tests of [23]. The detected asymmetric abrasion profiles in the Pfaffensprung and Runcahez SBTs (Figure 9 and Figure 12) are in line with field surveys in other SBTs revealing the formation of an incision channel along the inner side of a bend and further downstream of the bend [48,87,88]. These incisions are attributed to Prandtl’s first type of secondary currents [85]. Such currents cause high bed shear stresses and hence bedload transport concentration at the inner side of the bend leading to an incision channel. This channel, in return, stabilizes the spiral flow and promotes bedload transport concentrations in this topographic depression due to gravity [89], resulting in a self-intensifying process. The effect of Prandtl’s first type of secondary currents is still visible downstream of a bend in the Pfaffensprung SBT, but gradually re-distributes across the tunnel width downstream of the bend.
Overall, many observed abrasion characteristics, e.g., abrasion concentrations along irregularities, the formation of incision channels and undulating abrasion patterns, indicate that hydroabrasion is a self-intensifying process triggered by surface irregularities and structural weaknesses, as already hypothesized by [18,23]. This results in material-specific abrasion patterns and implies that abrasion rates vary considerably in space, provoking unevenly distributed material loss of the invert.
To the authors’ knowledge, the present study encompasses the first systematic long-term field investigation on hydroabrasion. Despite this, the time-scale of this study is still relatively small compared to that of hydroabrasion processes in nature and at hydraulic structures, the latter with a typical design service life time of several decades. However, the results can be regarded as representative, since the mean abrasion depths of the concrete test fields are large enough to (i) capture the effect of increasing structural weakening due to particle impingement, (ii) encompass the effect of surface roughness changes and (iii) observe abrasion behavior of the core material and not only of the topmost cement layer. The composition and, hence, abrasion behavior of the topmost cement layer differs from the core material due to the effect of the aggregates [90,91,92,93]. The results obtained from the high-strength concretes at the Pfaffensprung SBT might be attributed to this depth-dependent abrasion resistance. The abrasion depths observed in the first years were considerably larger than those of the following years (Figure 9), despite similar impact conditions, which indicates a strengthening effect of the aggregates.
5.2. Abrasion Model Calibration
The abrasion coefficient kv varies significantly for the different abrasion models, as shown in Figure 14, due to different particle trajectories and particle impact equations implied in those models. The kv-values of the SAMA are generally one order of magnitude smaller than those of the SAM [44]. There is a considerable data scatter in the abrasion coefficient kv. Accounting for the effective Young’s modulus in the SAM* did not reduce this data scatter. Instead, other uncertainties and errors dominate the model accuracy, such as (i) the determination of representative hydraulic conditions; (ii) the abrasion measurement errors (±3.3 mm and ±2.0 mm for TLS and geodetic leveling, respectively); (iii) spatial variations of the invert material bending tensile strength (on average = ±10%) and the uncertainty of Equation (5) (±6% according to [51]), both used for computing splitting tensile strength; (iv) the uncertainty of Equation (6) applied for computing invert material Young’s modulus (±5 GPa according to [56]); (v) the uncertainty of representative sediment particle size (assumed to ±20%); and (vi) the estimation error of sediment transport rates (assumed to ±50%). Following error propagation, these uncertainties result in a relative error for kv of σr ≈ 87% for the SAM and SAM* and σr ≈ 91% for the SAMA on average. Despite this, the present values are in good agreement with literature data for high-strength concrete as well as for granite. For concrete, both kv = 106 proposed by [21,37] for the SAM and kv = 1.9 × 105 proposed by [44] for the SAMA were confirmed herein with kv = 1.3 × 106 and kv = 1.9 × 105, respectively. Furthermore, kv = 1.4 × 107 for granite is in line with kv ≈ 107 proposed by [21,37] for hard rocks such as granite, quartzite and marble. Therefore, the obtained values listed in Table 6 are realistic and can be used in a first step for long-term abrasion prediction of brittle materials.

Table 6.
Recommended abrasion coefficients.
The data scatter, error margins and observed trends for both models are comparable (Figure 14). Therefore, the calibration of the SAMA is exemplarily discussed in the following. The kv-values from the present prototype data and from literature data [21,23,32,36,39,44,47,94] are plotted in Figure 15 for the SAMA as a function of splitting tensile strength. A general trend of increasing kv with increasing fst, in agreement with [44], is evident indicating that abrasion rates decrease with increasing splitting tensile strength. However, the stabilization of kv ≈ 105 for hard materials at fst > 1 MPa as revealed by [44] is not identified. The data from [36,94] considerably deviate from the general trend. The computed kv-values of the foams tested by [36] are significantly lower compared to the other materials because of the considerably lower Young’s moduli of YM = 3.9–330 MPa and densities ρc = 87–960 kg/m3. Note that the latter is not included in the mechanistic abrasion models, although presumed to also affect hydroabrasion [36,40,41,42]. The field study of [94] was conducted in a weir stilling basin, presumably retaining sediments in a recirculating flow field. As a result, the same sediments repeatedly impacted the invert [95], resulting in a bias of kv towards lower values. Omitting the kv-values of [36,94] due to different properties of invert materials and the non-representative test set-up, respectively, significantly reduces the data scatter. Furthermore, Figure 15 displays a certain material-dependency. The highest kv-values were obtained for rock, followed by concrete and mortar/soft rock. The values for concrete (denoted by circular symbols) are roughly one order of magnitude smaller than those for hard rocks, such as granite, quartzite and marble. This implies that the abrasion resistance of concrete is roughly one order of magnitude lower compared to that of hard rocks. The value for the polymer concrete (PC) is significantly lower (Figure 14) likely due to the polymer matrix, which increases the material ductility. As a result, the mechanistic saltation abrasion model developed for brittle materials is not suitable for predicting the abrasion behavior of such relatively ductile concretes. Therefore, the PC was not considered herein for model calibration.
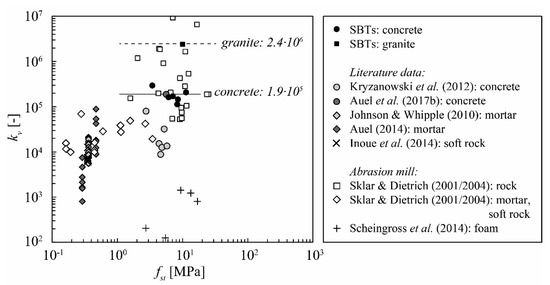
Figure 15.
Abrasion coefficient kv as a function of splitting tensile strength fst for the saltation abrasion model modified by [44] (SAMA).
The abrasion coefficients obtained from the prototype data are, in contrast to laboratory results, not subjected to potential model and scale effects. Despite this, the kv-values derived from laboratory and prototype data are in a similar range. This is a promising result indicating that there are no major scale effects and the mechanistic saltation abrasion models are applicable to both, laboratory and prototype scale.
The data scatter of the obtained kv-values originates not only from measurement errors and input parameter uncertainties, but also from model uncertainties. Hydroabrasion depends on the abrasiveness of the sediment (e.g., hardness and shape [96,97,98,99,100]) on the loading side and on various invert material parameters (e.g., density, porosity, crystal and clast size [36,40,41,42], or the characteristic length introduced by [101]) on the material resistance side. These parameters are either inadequately or not at all accounted for in the models discussed herein, which also contributes to the significant data scatter. Furthermore, the simplification of T*0.78 ≈ T*0.8 of [44] (in Equation (3)) presumes that the excess transport stage T* has no effect on abrasion, as already stated by [22,32,47]. A reason for this might be the fact that increasing flow velocity results on the one hand in higher particle impact velocities and increased specific energy transfer, but on the other hand, in lower impact angle and longer particle hop length, which in return reduce the specific energy transfer [44]. This might apply for small excess transport stages. However, the negligence of the excess transport stage in the SAMA might be questioned in particular for high excess transport stages. In SBTs, the excess transport stage can reach T* ≈ 100, so that the term T*0.78/T*0.8 becomes 100−0.02 ≈ 0.9. This value and also its effect on the abrasion rate is probably non-negligible. Measurement of the bedload transport through the SBTs, e.g., by using a Swiss plate geophone system, is strongly recommended to reduce the unavoidable uncertainty of bedload transport estimation [14,34,48]. Furthermore, additional comprehensive laboratory studies, as performed by [102] and field studies, as presented herein, are needed to further enhance the model prediction accuracy and to clarify the effects of (i) excess transport stage; (ii) invert material properties other than Young’s modulus and splitting tensile strength; and (iii) sediment properties on the abrasion rate.
6. Conclusions and Outlook
This paper reports the setup, methods and results of a field investigation on hydroabrasion in two Swiss SBTs and its modelling for fixed planar beds subjected to supercritical flows with high bedload transport rates. Based on the obtained field data, a well-known mechanistic saltation abrasion model and its recently modified version were calibrated for high-strength concretes and granite used as invert materials in the studied SBTs. The present findings apply not only to SBTs, but also for high-gradient non-alluvial plane bedrock rivers as well as concrete and rock lined hydraulic structures, e.g., weir facilities, flushing channels, bottom outlets and diversion and sediment sluicing tunnels, due to the similarity of flow structures, particle motion characteristics and channel bed properties.
The main findings are: (I) the channel geometry and the flow field considerably affect the abrasion pattern. Horizontal channel bends cause secondary currents of Prandtl’s first type resulting in bed shear stress and bedload transport concentrations at the inner side of the bend and, as a result, lead to the formation of an incision channel. (II) The 95-percentile abrasion depths amount to about 1.6 to 2.2 times the spatially averaged abrasion depths for high-strength concrete and granite. (III) The abrasion coefficient kv is material-dependent and roughly an order of magnitude higher for granite than for high-strength concrete. (IV) The abrasion resistance of granite with fc = 240–280 MPa is roughly six times higher than that of high-strength concrete with fc = 75–110 MPa despite little variations in splitting tensile strength and elastic Young’s modulus.
Regarding engineering applications, the findings of this study imply that the mechanistic saltation abrasion models are useful for realistic predictions of mean abrasion rates. However, instead of a constant kv-value proposed by [21,37], the application of material-specific kv-values listed in Table 6 are recommended to enhance the prediction accuracy of the models. The saltation abrasion models are one-dimensional models not able to reproduce the three-dimensional processes of hydroabrasion. To account for that, the local abrasion concentrations can be accounted for with amax/am ≈ 2 as a preliminary estimate, while their locations can be derived from the local flow field.
Overall, this paper sheds light on hydroabrasion processes in high-speed open-channel flows and contributes to a better understanding of hydroabrasion at hydraulic structures and of bedrock incision due to bedload transport. The findings help to enhance the accuracy of mechanistic abrasion models for a range of applications, but also indicate a considerable potential for model enhancement.
To enhance the model accuracy the challenges of (i) reduction of the uncertainty of model input parameters; (ii) determination of the interactions and effects of hydraulics, sediment transport conditions and hydroabrasion; (iii) analysis of the effects of sediment particle and invert material properties on hydroabrasion; and (iv) finally advancing the saltation abrasion model should be tackled in further research projects both, in laboratory and field. Thereby, for an accurate determination of bedload transport and hydroabrasion depths in the field, the use of a Swiss plate geophone system and a high resolution 3D laser scanner, respectively, are recommended [14,34,48].
Author Contributions
Conceptualization, M.M.-H., I.A., C.A. and R.M.B.; Data curation, M.M.-H.; Formal analysis, M.M.-H.; Funding acquisition, M.M.-H., I.A., C.A. and R.M.B.; Investigation, M.M.-H.; Methodology, M.M.-H., I.A., C.A. and R.M.B.; Supervision, I.A.; Visualization, M.M.-H.; Writing—original draft, M.M.-H.; Writing—review & editing, I.A., C.A. and R.M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Swiss Federal Office of Energy SFOE, grant number SI/500731 and SI/501114, swisselectric research, the association of the Swiss cement industry cemsuisse and the Lombardi Ingegneria Foundation.
Acknowledgments
The authors gratefully acknowledge the support of the Swiss Federal Railways SBB, Axpo Hydro Surselva AG and Officine Idroelettriche della Maggia SA (OFIMA) as operators of Paffensprung, Runcahez and Val d’Ambra SBTs, respectively. The project is embedded in the framework of the Swiss Competence Centre of Energy Research—Supply of Electricity (SCCER–SoE) supported by Innosuisse—Swiss Innovation Agency.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Boes, R.M.; Hagmann, M. Sedimentation countermeasures—Examples from Switzerland. In Proceedings of the First International Workshop on Sediment Bypass Tunnels, ETH Zurich, Switzerland, 27–29 April 2015; Boes, R., Ed.; pp. 193–210. [Google Scholar]
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation. JHR 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Annandale, G. Quenching the Thirst—Sustainable Water Supply and Climate Change; CreateSpace Independent Publication Platform: Charleston, SC, USA, 2013. [Google Scholar]
- White, R. Evacuation of Sediments from Reservoirs; Thomas Telfors Limited: London, UK, 2001. [Google Scholar]
- Kundzewicz, Z.W.; Mata, L.J.; Arnell, N.W.; Döll, P.; Jimenez, B.; Miller, K.; Oki, T.; Şen, Z.; Shiklomanov, I. The implications of projected climate change for freshwater resources and their management. HSJ 2008, 53, 3–10. [Google Scholar] [CrossRef]
- Wisser, D.; Frolkin, S.; Hagen, S.; Bierkens, M.F. Beyond peak reservoir storage? A global estimate of declining water storage capacity in large reservoirs. Water Resour. Res. 2013, 49, 5732–5739. [Google Scholar] [CrossRef]
- Annandale, G. Sustainable water supply, climate change and reservoir sedimentation management: Technical and economic viability. In Proceedings of the Riverflow 2014, Lausanne, Switzerland, 3–5 September 2014; Schleiss, A., De Cesare, G., Franca, M.J., Pfister, M., Eds.; pp. 3–10. [Google Scholar]
- Boes, R.M.; Auel, C.; Hagmann, M.; Albayrak, I. Sediment bypass tunnels to mitigate reservoir sedimentation and restore sediment continuity. In Proceedings of the Riverflow 2014, Lausanne, Switzerland, 3–5 September 2014; Schleiss, A.J., De Cesare, G., Franca, M.J., Pfister, M., Eds.; pp. 221–228. [Google Scholar]
- Boes, R.M.; Müller-Hagmann, M.; Albayrak, I. Design, operation and morphological effects of bypass tunnels as a sediment routing technique. In Proceedings of the 3rd Intnernational Workshop on Sediment Bypass Tunnels, Taipei, Taiwan, 9–12 April 2019; Chang, T.-J., Ed.; pp. 40–50. [Google Scholar]
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earth’s Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Kantoush, S.A.; Sumi, T. River Morphology and Sediment Management Strategies for Sustainable Reservoir in Japan and European Alps; Annuals of Disaster Prevention Research Institute 53B, Kyoto University: Kyoto, Japan, 2010. [Google Scholar]
- Auel, C.; Boes, R.M. Sediment bypass tunnel design—Review and outlook. In Proceedings of the ICOLD Symposium “Dams under changing challenges”, 79th Annual Meeting, Lucerne, Switzerland, 1 June 2011; pp. 403–412. [Google Scholar]
- Sumi, T.; Kantoush, S.A. Comprehensive sediment management strategies in Japan: Sediment bypass tunnels. In Proceedings of the 34th IHAR World Congress, Brisbane, Australia, 26 June–1 July 2011; pp. 1803–1810. [Google Scholar]
- Hagmann, M.; Albayrak, I.; Boes, R.M.; Auel, C.; Sumi, T. Reviewing research and experience on sediment bypass tunnels. Int. J. Hydropower Dams 2016, 23, 54–58. [Google Scholar]
- Boes, R.M.; Müller-Hagmann, M.; Albrayrak, I.; Müller, B.; Caspescha, L.; Flepp, A.; Jacobs, F.; Auel, C. Sediment bypass tunnels: Swiss experiences with bypass efficiency and abrasion-resistant invert materials. In Proceedings of the 86th ICOLD Annual Meeting, Vienna, Austria, 1–7 July 2019; pp. 625–638. [Google Scholar]
- Auel, C.; Kobayashi, S.; Takemon, Y.; Sumi, T. Effects of sediment bypass tunnels on grain size distribution and benthic habitats in regulated rivers. JRBM 2017, 15, 433–444. [Google Scholar] [CrossRef]
- Vischer, D.; Hager, W.H.; Casanova, C.; Joos, B.; Lier, P.; Martini, O. Bypass tunnels to prevent reservoir sedimentation. In Proceedings of the 19th ICOLD Congress, Florence, Italy, 26–30 May 1997; pp. 605–624. [Google Scholar]
- Jacobs, F.; Winkeler, W.; Hinkeler, F.; Volkart, P. Betonabrasion im Wasserbau (‘Concrete Abrasion at Hydraulic Structures’); VAW-Mitteilung 168; Minor, H.-E., Ed.; ETH Zurich: Zurich, Switzerland, 2001. [Google Scholar]
- Beer, A.R.; Turowski, J.M. Bedload transport controls bedrock erosion under sediment-starved conditions. Earth Surf. Dyn. 2015, 3, 291–309. [Google Scholar] [CrossRef]
- Whipple, K.X.; Hancock, G.S.; Anderson, R.S. River incision into bedrock: Mechanics and relative efficacy of plucking, abrasion, and cavitation. GSA Bull. 2000, 112, 490–503. [Google Scholar] [CrossRef]
- Sklar, L.S.; Dietrich, W.E. A mechanistic model for river incision into bedrock by saltating bed load. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Chatanantavet, P.; Parker, G. Physically based modeling of bedrock incision by abrasion, plucking, and macroabrasion. JGR Earth Surf. 2009, 114. [Google Scholar] [CrossRef]
- Auel, C. Flow Characteristics, Particle Motion and Invert Abrasion in Sediment Bypass Tunnels. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2014. [Google Scholar] [CrossRef]
- Lague, D. The stream power river incision model: Evidence, theory and beyond. ESPL 2014, 39, 38–61. [Google Scholar] [CrossRef]
- Beer, A.; Turowski, J.M.; Kirchner, J.W. Spatial patterns of erosion in a bedrock gorge. JGR Earth Surf. 2017, 122, 191–214. [Google Scholar] [CrossRef]
- Auel, C.; Boes, R.M.; Sumi, T. Abrasion prediction at Asahi sediment bypass tunnel based on Ishibashi’s formula. JAWER 2018, 6, 125–138. [Google Scholar] [CrossRef]
- Auel, C.; Thene, J.R.; Carroll, J.; Holmes, C.; Boes, R.M. Rehabilitation of the Mud Mountain bypass tunnel invert. In Proceedings of the 26th ICOLD Congress, Vienna, Austria, 1–7 July 2018. [Google Scholar]
- Howard, A.D.; Kerby, G. Channel changes in badlands. Geol. Soc. Am. Bull. 1983, 94, 739–752. [Google Scholar] [CrossRef]
- Seidl, M.A.; Dietrich, W.E.; Kirchner, J.W. Longitudinal profile development into bedrock: An analysis of Hawaiian channels. J. Geol. 1994, 102, 457–474. [Google Scholar] [CrossRef]
- Attal, M.; Cowie, P.; Whittaker, A.; Hobley, D.; Tucker, G.; Roberts, G.P. Testing fluvial erosion models using the transient response of bedrock rivers to tectonic forcing in the Apennines, Italy. JGR Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Sklar, L.S.; Dietrich, W.E. The role of sediment in controlling steady-state bedrock channel slope: Implications of the saltation–abrasion incision model. Geomorphology 2006, 82, 58–83. [Google Scholar] [CrossRef]
- Johnson, J.P.L.; Whipple, K.X. Evaluating the controls of shear stress, sediment supply, alluvial cover, and channel morphology on experimental bedrock incision rate. JGR Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Lamb, M.P.; Dietrich, W.E.; Sklar, L.S. A model for fluvial bedrock incision by impacting suspended and bed load sediment. JGR Earth Surf. 2008, 113. [Google Scholar] [CrossRef]
- Turowski, J.M.; Böckli, M.; Rickenmann, D.; Beer, A.R. Field measurements of the energy delivered to the channel bed by moving bed load and links to bedrock erosion. JGR Earth Surf. 2013, 118, 2438–2450. [Google Scholar] [CrossRef]
- Johnson, J.P. A surface roughness model for predicting alluvial cover and bed load transport rate in bedrock channels. JGR Earth Surf. 2014, 119, 2147–2173. [Google Scholar] [CrossRef]
- Scheingross, J.S.; Brun, F.; Lo, D.Y.; Omerdin, K.; Lamb, M.P. Experimental evidence for fluvial bedrock incision by suspended and bedload sediment. Geology 2014, 42, 523–526. [Google Scholar] [CrossRef]
- Sklar, L.S.; Dietrich, W.E. Correction to “A mechanistic model for river incision into bedrock by saltating bed load”. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Whipple, K.X.; Tucker, G.E. Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs. JGR Solid Earth 1999, 104, 17661–17674. [Google Scholar] [CrossRef]
- Sklar, L.S.; Dietrich, W.E. Sediment and rock strength controls on river incision into bedrock. Geology 2001, 29, 1087–1090. [Google Scholar] [CrossRef]
- Beyeler, J.D.; Sklar, L.S. Bedrock resistance to fluvial erosion: The importance of rock tensile strength, crystal grain size and porosity in scaling from the laboratory to the field. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 13–17 December 2010. Abstract EP41D-0740. [Google Scholar]
- Momber, A.W. Effects of target material properties on solid particle erosion of geomaterials at different impingement velocities. Wear 2014, 319, 69–83. [Google Scholar] [CrossRef]
- Lamb, M.P.; Finnegan, N.J.; Scheingross, J.S.; Sklar, L.S. New insights into the mechanics of fluvial bedrock erosion through flume experiments and theory. Geomorphology 2015, 244, 33–55. [Google Scholar] [CrossRef]
- Small, E.E.; Blom, T.; Hancock, G.S.; Hynek, B.M.; Wobus, C.W. Variability of rock erodibility in bedrock-floored stream channels based on abrasion mill experiments. JGR Earth Surf. 2015, 120, 1455–1469. [Google Scholar] [CrossRef]
- Auel, C.; Albayrak, I.; Sumi, T.; Boes, R.M. Sediment transport in high-speed flows over a fixed bed: 2. Particle impacts and abrasion prediction. ESPL 2017, 42, 1384–1396. [Google Scholar] [CrossRef]
- Auel, C.; Albayrak, I.; Sumi, T.; Boes, R.M. Sediment transport in high-speed flows over a fixed bed: 1. Particle dynamics. ESPL 2017, 42, 1365–1383. [Google Scholar] [CrossRef]
- Auel, C. Sediment bypassing—A sustainable and eco-friendly strategy against reservoir sedimentation. In Proceedings of the 26th ICOLD Congress, Vienna, Austria, 1–7 July 2018. [Google Scholar]
- Inoue, T.; Izumi, N.; Shimizu, Y.; Parker, G. Interaction among alluvial cover, bed roughness, and incision rate in purely bedrock and alluvial-bedrock channel. JGR Earth Surf. 2014, 119, 2123–2146. [Google Scholar] [CrossRef]
- Müller-Hagmann, M. Hydroabrasion in High-Speed Sediment-Laden Flows in Sediment Bypass Tunnels. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2017. [Google Scholar] [CrossRef]
- Müller-Hagmann, M.; Albayrak, I.; Boes, R.M. Field calibration of abrasion prediction models for concrete and granite invert linings. In Proceedings of the 2nd International Workshop on Sediment Bypass Tunnels, Kyoto, Japan, 8–12 May 2017. [Google Scholar]
- Müller, B.; Walker, M. The Pfaffensprung sediment bypass tunnel: 95 years of experience. In Proceedings of the First International Workshop on Sediment Bypass Tunnels, VAW, Zurich, Switzerland, 27–29 April 2015; pp. 247–258. [Google Scholar]
- Arioglu, N.; Girini, Z.C.; Arigolue, E. Evaluation of ratio between splitting tensile strength and compressive strength for concretes up to 120 MPa and its application in strength criterion. ACI Mater. J. 2006, 103, 18–24. [Google Scholar]
- Studer, H. Das Kraftwerk Amsteg der Schweizerischen Bundesbahnen (‘Power plant Amsteg of the Swiss Federal Railways’). Sonderdruck der Schweizerischen Bauzeitung 1925–1926, 86–87, 1–29. [Google Scholar]
- SBZ. Rekonstruktion des Umleittunnels am Pfaffensprung des Kraftwerks Amsteg der SBB (‘Reconstruction of the bypass tunnel Pfaffensprung of the power plant Amsteg of the SBB’). Schweiz. Bauzeitg. 1943, 121, 41–42. (In German) [Google Scholar]
- SIA. Betonbau (‘Concrete Structures’); Schweizerischer Ingenieur und Architektenverein: Zurich, Switzerland, 2003; Volume 262. (In German) [Google Scholar]
- Bamforth, P.; Chisholm, D.; Gibbs, J.; Harrison, T. Properties of Concrete for Use in Eurocode 2; The Concrete Center Report CCIP-029; CCIP: Camberley, UK, 2008. [Google Scholar]
- Noguchi, T.; Tomosawa, F.; Nemati, K.M.; Chiaia, B.M.; Fantilli, A.P. A practical equation for elastic modulus of concrete. ACI Structur. J. 2009, 106, 690–696. [Google Scholar]
- Axpo. Fragebogen Sedimentumleitstollen Runcahez (‘Questionnaire about Runcahez Sediment bypass Tunnel’); Laboratory of Hydraulics, Hydrology and Glaciology (VAW), ETH Zurich: Zurich, Switzerland, 2011; unpublished. (In German) [Google Scholar]
- Strickler, A. Beiträge zur Frage der Geschwindigkeitsformel und der Rauhigkeitszahlen für Ströme, Kanäle und geschlossene Leitungen (‘Contirbution to the Velocity Equation and the Roughness Number of Streams, Channels and PIPES’); Eidgenössisches Amt für Wasserwirtschaft: Bern, Switzerland, 1923; Volume 16. (In German) [Google Scholar]
- Colebrook, C.F. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J. ICE 1939, 12, 133–156. [Google Scholar] [CrossRef]
- Wallisch, S. Hydraulische Methoden zur Erfassung von Rauheiten-Äquivalente Sandrauheiten und Strickler-Beiwerte fester und beweglicher Strömungsberandungen (‘Hydraulic methods to capture equivalent sandroughness heights and Strickler values of fixed and movable beds’); DVWK: Hennef, Germany, 1990; Volume 92. [Google Scholar]
- Shields, A. Anwendung der Ähnlichkeits-Mechanik und der Turbulenzforschung auf die Geschiebebewegung (‘Application of Similarity Principles and Turbulence Research to Bed-Load Movement’); Mitteilungen der Preussische Versuchsanstalt für Wasserbau und Schiffbau 26, Berlin; California Institute of Technology: Pasadena, CA, USA, 1936; pp. 524–526. (In German) [Google Scholar]
- Chatanantavet, P.; Whipple, K.X.; Adams, M.A.; Lamb, M.P. Experimental study on coarse grain saltation dynamics in bedrock channels. JGR Earth Surf. 2013, 118, 1161–1176. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bedload transport. In Proceedings of the 2nd Meeting of International Association of Science, Engineering and Technology, Series A, Stockholm, Sweden, 6–9 June 1948; pp. 39–64. [Google Scholar]
- Günter, A. Die Kritische Mittlere Sohlenschubspannung bei Geschiebemischungen unter Berücksichtigung der Deckschichtbildung und der Turbulenzbedingten Sohlenschubspannungsschwankungen (‘Critical Mean Bed Shear Stress of Grain Size Mixtures in Respect of Armor Layer Building und Turbulence Induced Fluctuations of Bed Shear Stresses’); VAW-Mitteilungen 3; Vischer, D., Ed.; VAW, ETH Zurich: Zurich, Switzerland, 1971. (In German) [Google Scholar]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; United States Department of Agriculture: Washington, DC, USA, 1950.
- Parker, G. Hydraulic geometry of active gravel rivers. ASCE J. Hydraul. Div. 1979, 105, 1185–1201. [Google Scholar]
- Smart, G.M.; Jäggi, M.N.R. Sedimenttransport in Steilen Gerinnen (‘Sediment transport in steep channels’); VAW-Mitteilung 64; Vischer, D., Ed.; VAW, ETH Zürich: Zurich, Switzerland, 1983. (In German) [Google Scholar]
- Cheng, N. Exponential formula for bedload transport. JHE 2002, 128, 942–946. [Google Scholar] [CrossRef]
- Gilbert, G.K. The Transportation of Debris by Running Water; USGS Professional Paper; U.S. Geological Survey: Washington, DC, USA, 1914.
- Wilson, K.C. Bed-load transport at high shear stress. ASCE J. Hydraul. Div. 1966, 92, 49–59. [Google Scholar]
- Smart, G.M. Sediment transport formula for steep channels. JHE 1984, 110, 267–276. [Google Scholar] [CrossRef]
- Rickenmann, D. Geschiebetransport bei steilen Gefällen (‘Bedload transport in steep slopes’). In Proceedings of the 75 Jahre VAW, ETH Zurich, Zurich, Switzerland, 7 October 2005; Minor, H.-E., Ed.; pp. 107–119. (In German). [Google Scholar]
- Cheng, N.; Chen, X. Slope correction for calculation of bedload sediment transport rates in steep channels. JHE 2014, 140, 04014018. [Google Scholar] [CrossRef]
- VAW. Flussmorphologie des Mittellaufes zwischen Göschenen und Amsteg (‘River Morphology of the Middle Reaches between Göschenen and Amsteg’); Report No. 4014/3967; VAW, ETH Zurich: Zurich, Switzerland, 1992; unpublished. (In German) [Google Scholar]
- Bezzola, G.; Hunzinger, R.; Jäggi, M. Flussmorphologie und Geschiebehaushalt während des Ereignisses vom 24./25. August 1987 im Reusstal (‘River Morphology and Bed Load Transport during the Flood Event of August 24 and 25 1987 in the Reuss Valley’); Bundesamt für Wasserwirtschaft Mitteilung Nr. 4, Mitteilung Nr. 14 der Landeshydrologie und –geologie; Bern, Switzerland, 1991; (In German). Available online: https://www.bafu.admin.ch/dam/bafu/de/dokumente/naturgefahren/uw-umwelt-wissen/ursachenanalyse_derhochwasser1987.pdf.download.pdf/ursachenanalyse_derhochwasser1987.pdf (accessed on 23 November 2015).
- Bezzola, G.R. The effect of sediment transport during the 1987-flood in the Reuss River. In Proceedings of the Grain Sorting Seminar, Ascona, Switzerland, 21–26 October 1991; pp. 331–343. [Google Scholar]
- Marti, C. Morphologie von verzweigten Gerinnen: Ansätze zur Abfluss-, Geschiebetransport-und Kolktiefenberechnung (‘Morphology of Branched Streams: Approaches for Discharge, Bedload and Scour Calculations’); VAW-Mitteilungen 199; Minor, H.-E., Ed.; VAW, ETH Zurich: Zurich, Switzerland, 2006. (In German) [Google Scholar]
- Bose, S.K.; Dey, S. Sediment entrainment probability and threshold of sediment suspension: Exponential-based approach. JHE 2013, 139, 1099–1106. [Google Scholar] [CrossRef]
- Ferguson, R.I.; Church, M. A simple universal equation for grain settling velocity. JSR 2004, 74, 933–937. [Google Scholar] [CrossRef]
- Fernandez Luque, R.; Van Beek, R. Erosion and transport of bed-load sediment. JHR 1976, 14, 127–144. [Google Scholar] [CrossRef]
- Prancevic, J.P.; Lamb, M.P. Particle friction angles in steep mountain channels. JGR Earth Surf. 2015, 120, 242–259. [Google Scholar] [CrossRef]
- Huda, S.A.; Small, E.E. Modeling the effects of bed topography on fluvial bedrock erosion by saltating bed load. JGR Earth Surf. 2014, 119, 1222–1239. [Google Scholar] [CrossRef]
- Prandtl, L. Führer durch die Strömungslehre (‘Guide through Fluid Mechanics’); Vieweg und Sohn: Braunschweig, Germany, 1949. (In German) [Google Scholar]
- Müller-Hagmann, M.; Albayrak, I.; Boes, R.M. Field calibration of bedload monitoring system in a sediment bypass tunnel: Swiss plate geophone. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017; pp. 995–1004. [Google Scholar]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; A. A. Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Auel, C.; Albayrak, I.; Boes, R.M. Turbulence characteristics in supercritical open channel flows: Effects of Froude number and aspect ratio. JHE 2014, 140, 04014004. [Google Scholar] [CrossRef]
- Nakajima, H.; Otsubo, Y.; Omoto, Y. Abrasion and corrective measurement of a sediment bypass system at Asahi Dam. In Proceedings of the First International Workshop on Sediment Bypass Tunnels, Zurich, Switzerland, 27–29 April 2015; Boes, R.M., Ed.; [Google Scholar]
- Müller-Hagmann, M.; Auel, C.; Albayrak, I.; Boes, R.M. Bedload transport and hydro-abrasive erosion at steep bedrock rivers and hydraulic structures. In Proceedings of the Riverflow 2018, Lyon-Villeurbanne, France, 5–8 September 2018. [Google Scholar]
- Johnson, J.P.; Whipple, K.X. Feedbacks between erosion and sediment transport in experimental bedrock channels. ESPL 2007, 32, 1048–1062. [Google Scholar] [CrossRef]
- Kunterding, R. Beanspruchung der Oberfläche von Stahlbetonsilos durch Schüttgüter (2018Surface Stress of Concrete Silos due to Bulk Solids’). Ph.D. Thesis, Institut für Massivbau und Baustofftechnologie, Karlsruhe, Germany, 1991. (In German). [Google Scholar]
- Haroske, G. Beitrag zum Hydroabrasionsverschleiss von Betonoberflächen (‘Contribution to Hydroabrasive Wear at Concrete Surfaces’). Ph.D. Thesis, University Rostock, Rostock, Germany, 1998. (In German). [Google Scholar]
- Horszczaruk, E. Abrasion resistance of high-strength concrete in hydraulic structures. Wear 2005, 259, 62–69. [Google Scholar] [CrossRef]
- Vogel, M. Schädigungsmodell für die Hydroabrasionsbeanspruchung zur probabilistischen Lebensdauerprognose von Betonoberflächen im Wasserbau (Hydroabrasion Harming Model for Probabilistic Service Life Prediction of Hydraulic Structures). Ph.D. Thesis, Technical University Karlsruhe, Karlsruhe, Germany, 2011. (In German). [Google Scholar]
- Kryžanowski, A.; Mikoš, M.; Šušteršič, J.; Ukrainczyk, V.; Planinc, I. Testing of concrete abrasion resistance in hydraulic structures on the Lower Sava River. SV-JME 2012, 58, 245–254. [Google Scholar] [CrossRef]
- Spörel, F.; Helbig, U.; Westendrap, A.; Stamm, J. Hydroabrasionsbeanspruchung von Verkehrswasserbauwerken (‘Hydroabrasive Impact at Water Traffic Structures’). Bautechnik 2015, 92, 538–548. [Google Scholar] [CrossRef]
- Bovet, T. Contribution à l’étude du phénomène d’erosion par frottement dans le domaine des turbines hydrauliques (‘Contribution to the Study of the Phenomenon of Friction Erosion at Hydraulic Turbines’). Bulletin Technique de la Suisse Romande 1958, 84, 37–49. (In French) [Google Scholar]
- Wellinger, K.; Uetz, H. Gleitverschleiß, Spülverschleiß, Stahlverschleiß unter der Wirkung von körnigen Stoffen (‘Sliding, Flushing and Jetting Wear under the Impact of Granular Materials’); VDI-Verlag: Düsseldorf, Germany, 1955. [Google Scholar]
- Uetz, H. Abrasion und Erosion (‘Abrasion and Erosion’); Verlag Carl Hanser: München, Germany, 1986. (In German) [Google Scholar]
- Bajracharya, T.; Acharya, B.; Joshi, C.; Saini, R.; Dahlhaug, O. Sand erosion of Pelton turbine nozzles and buckets: A case study of Chilime hydropower plant. Wear 2008, 264, 177–184. [Google Scholar] [CrossRef]
- Winkler, K.; Dekumbis, R.; Wedmark, A. Finding a way to estimate the amount of abrasion. In Proceedings of the Hydro 2010, Lisbon, Spain, 27–29 September 2010. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Demiral, D.; Albayrak, I.; Boes, R.M. Particle saltation trajectories in supercritical open channel flows over a smooth fixed bed. In Proceedings of the 3rd Intnernational Workshop on Sediment Bypass Tunnels, Taipei, Taiwan, 9–12 April 2019; pp. 146–153. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).