Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves
Abstract
1. Introduction
2. Materials and Methods
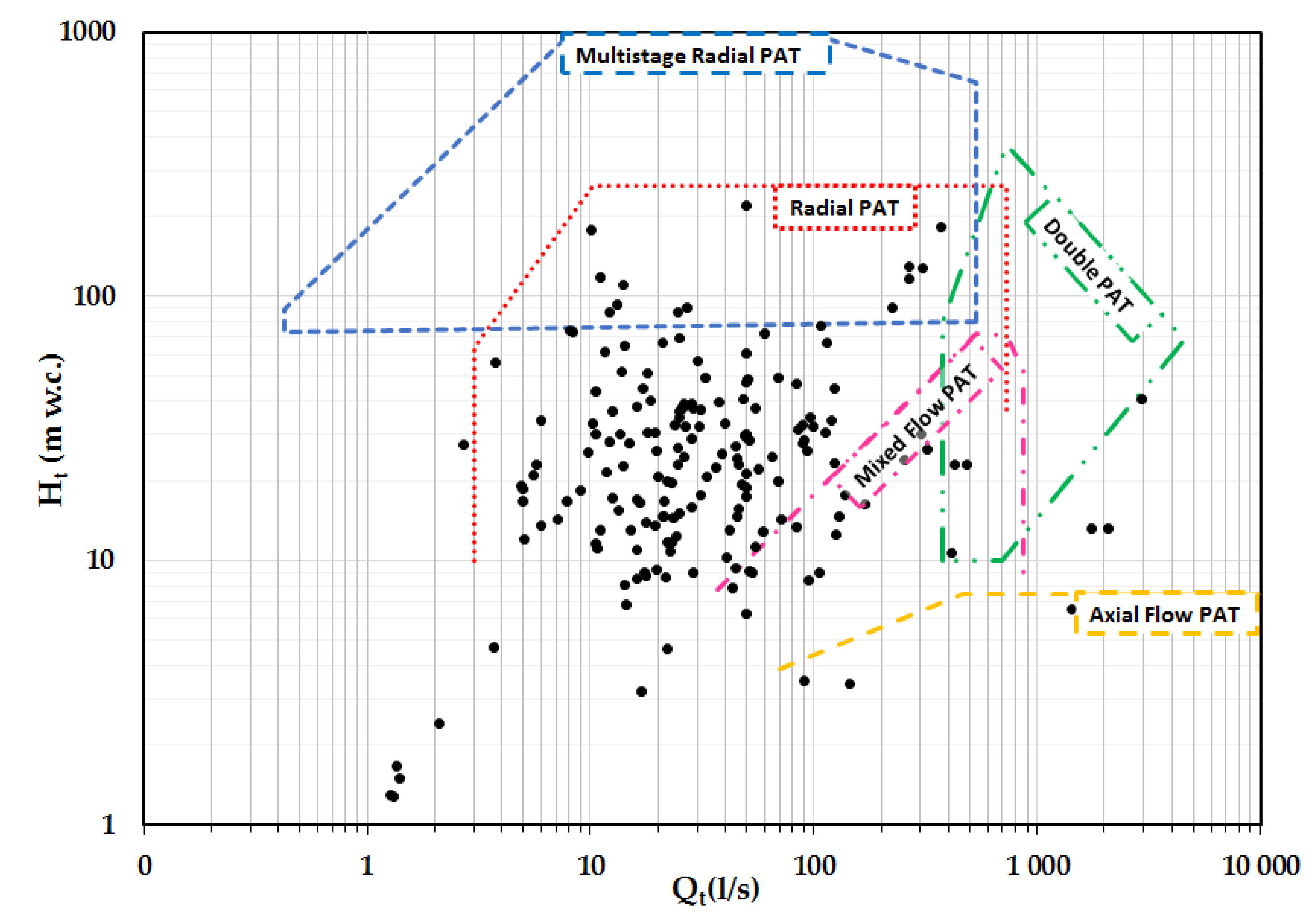
2.1. Definition of the Characteristic Numbers of PATs
- (i)
- Choosing a pump according to pump catalogues through the operation point ( as a turbine in the network. Therefore, the use of empirical expressions to predict the BEP location of a PAT with respect to its known BEP as a pump () is necessary.
- (ii)
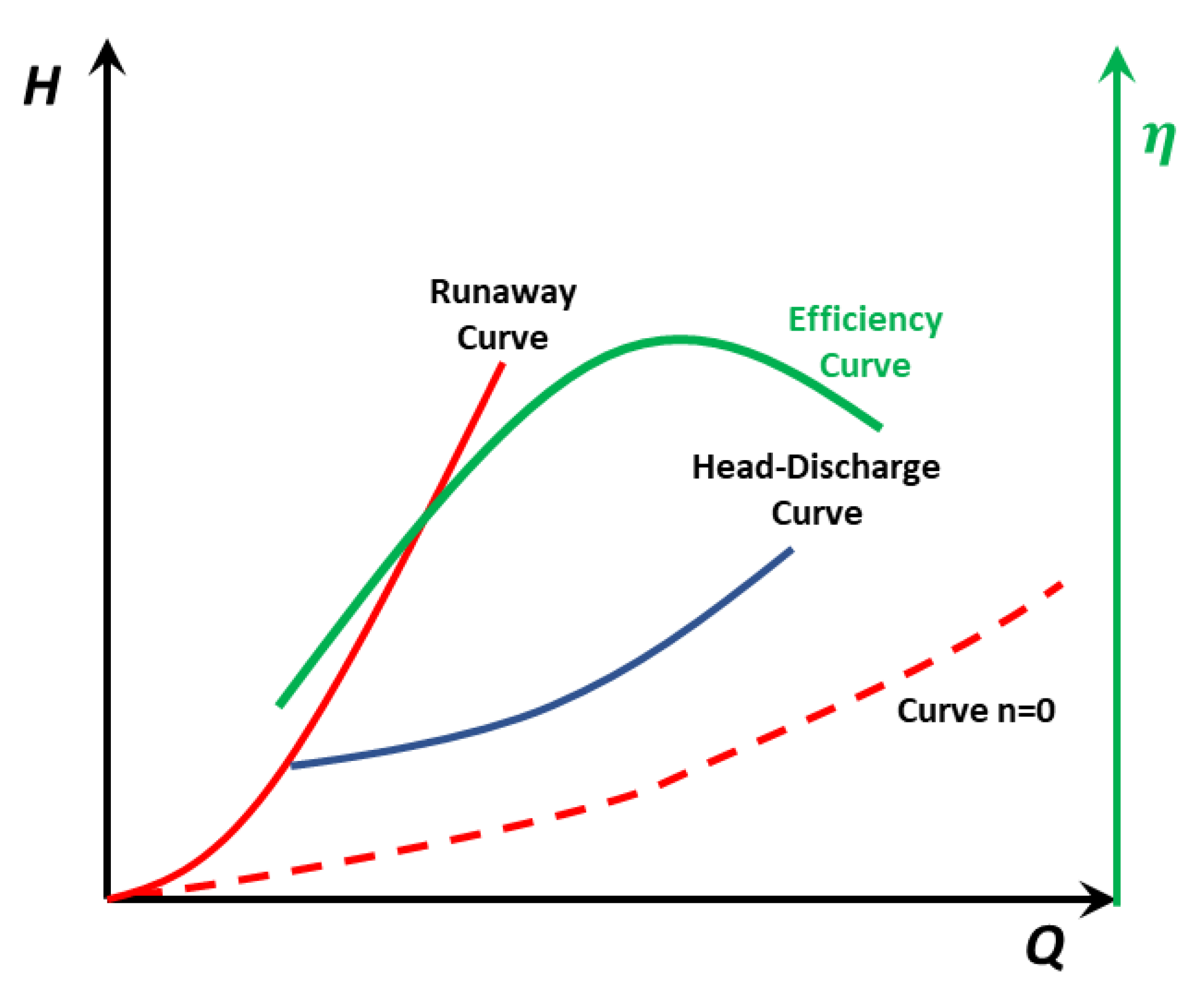
- Defining empirical expressions which enable to define the head-discharge curve and efficiency curve, as well as the runaway curve, as a function of the discharge.
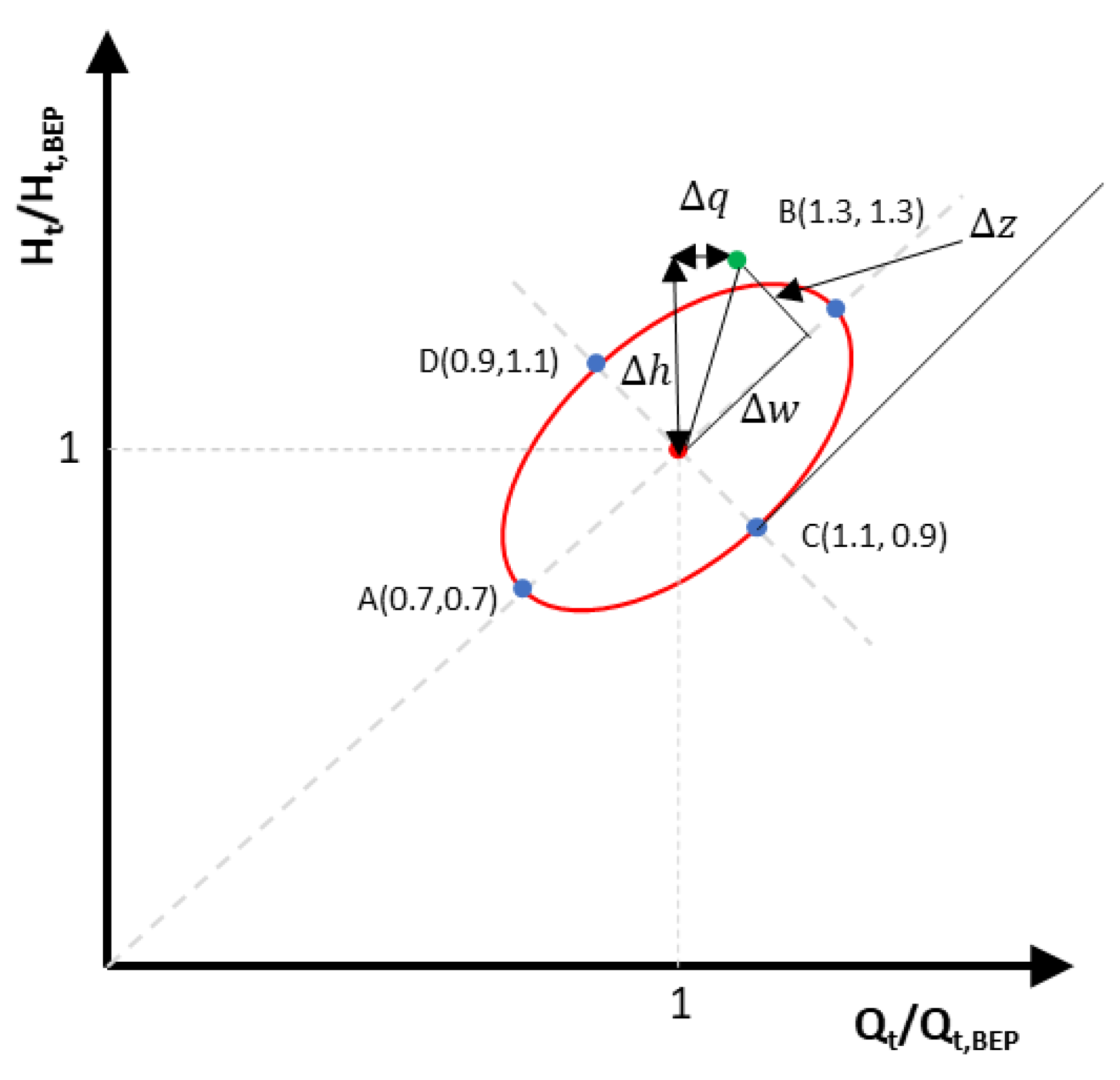
2.2. Coefficient Proposal to Estimate the Operation Point of PAT Using Pump Manufacture
- Determination of the RMSE. This error index is a standard way to measure the error of a model in predicting quantitative data. If the RMSE is zero, this value indicates a perfect fit. Formally, it is defined as follows:where are the estimated values, the experimental values and x the number of observations.
- Determination of the MAD. This index measures the average magnitude of the errors in a set of predictions without considering their direction. It is the average over the test sample of the absolute differences between prediction and actual observation where all individual differences have equal weight. If the MAD is zero, this value indicates a perfect fit. Formally, it is defined as follows:
- Determination of the MRD. This index considers the weight of the error to the variable value. If the MRD is zero, this value indicates a perfect fit. Formally, it is defined as follows:
- Determination of the bias (BIAS). In this case, the index measures the tendency of the prediction in the variable (Q, H or efficiency), determining if the predicted values are smaller or larger than the experimental values. If the BIAS value is negative, it indicates that the method overestimates the variable, while, if the BIAS value is positive, it indicates that the variable is underestimated. This index is defined by the equation [34]:
2.3. Estimation of the Head-Discharge and Efficiency Curves Considering
2.4. Materials
3. Results
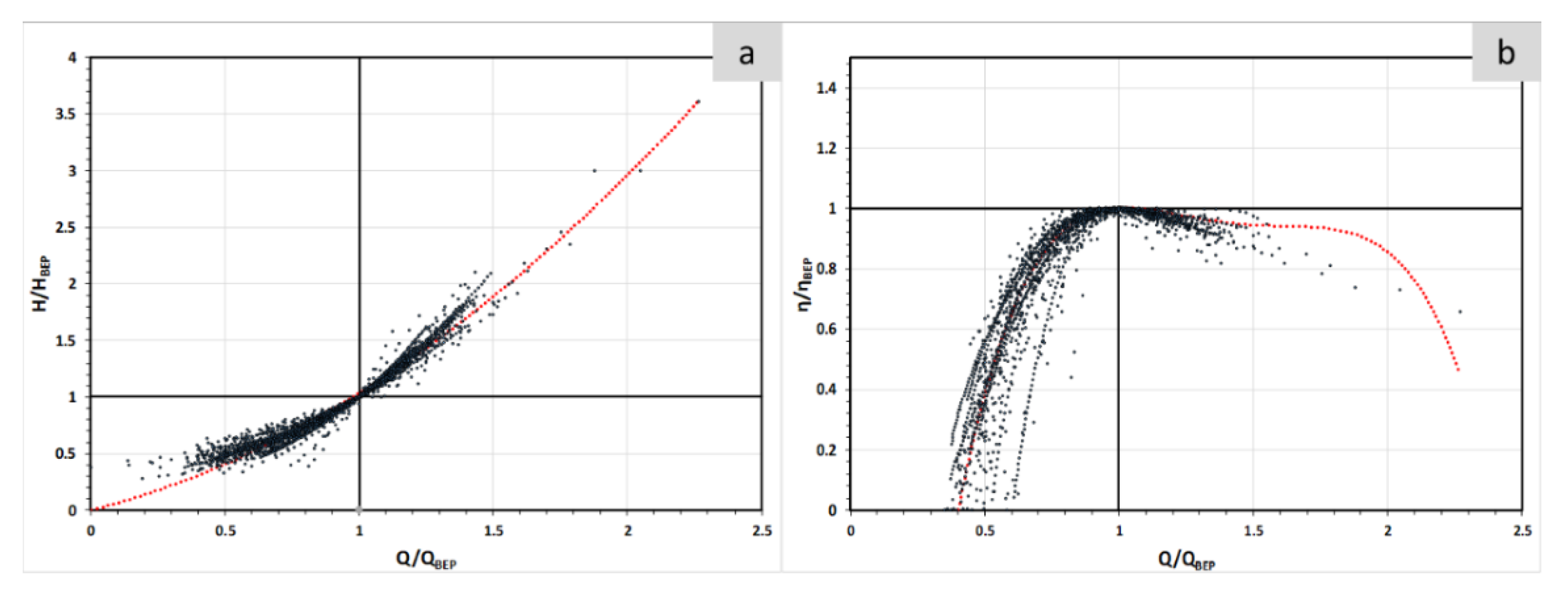
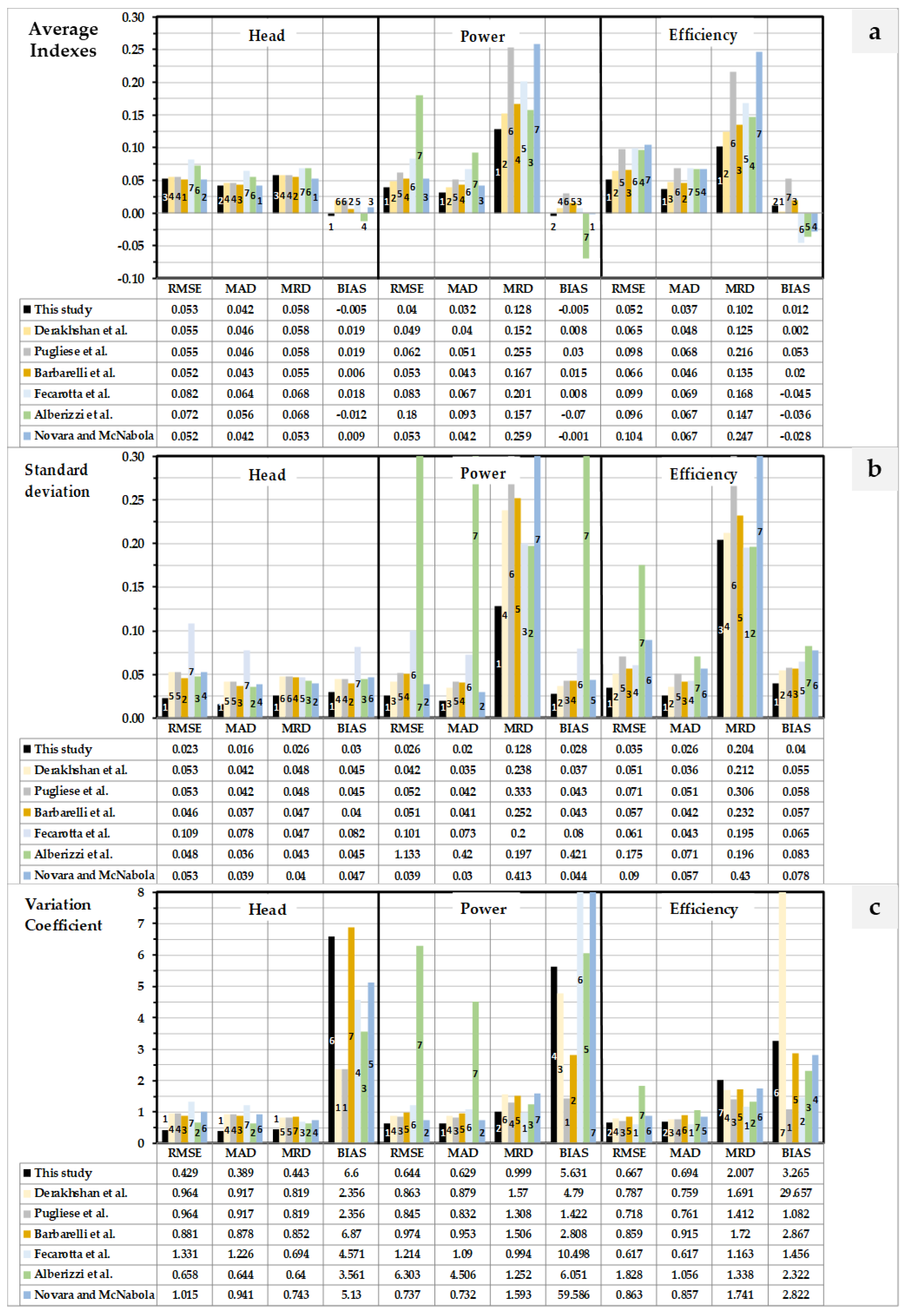
3.1. Comparison between the Proposed and Others Methods to Predict the Flow and Head in Pump Mode. First Approach to Predict Runaway Curve
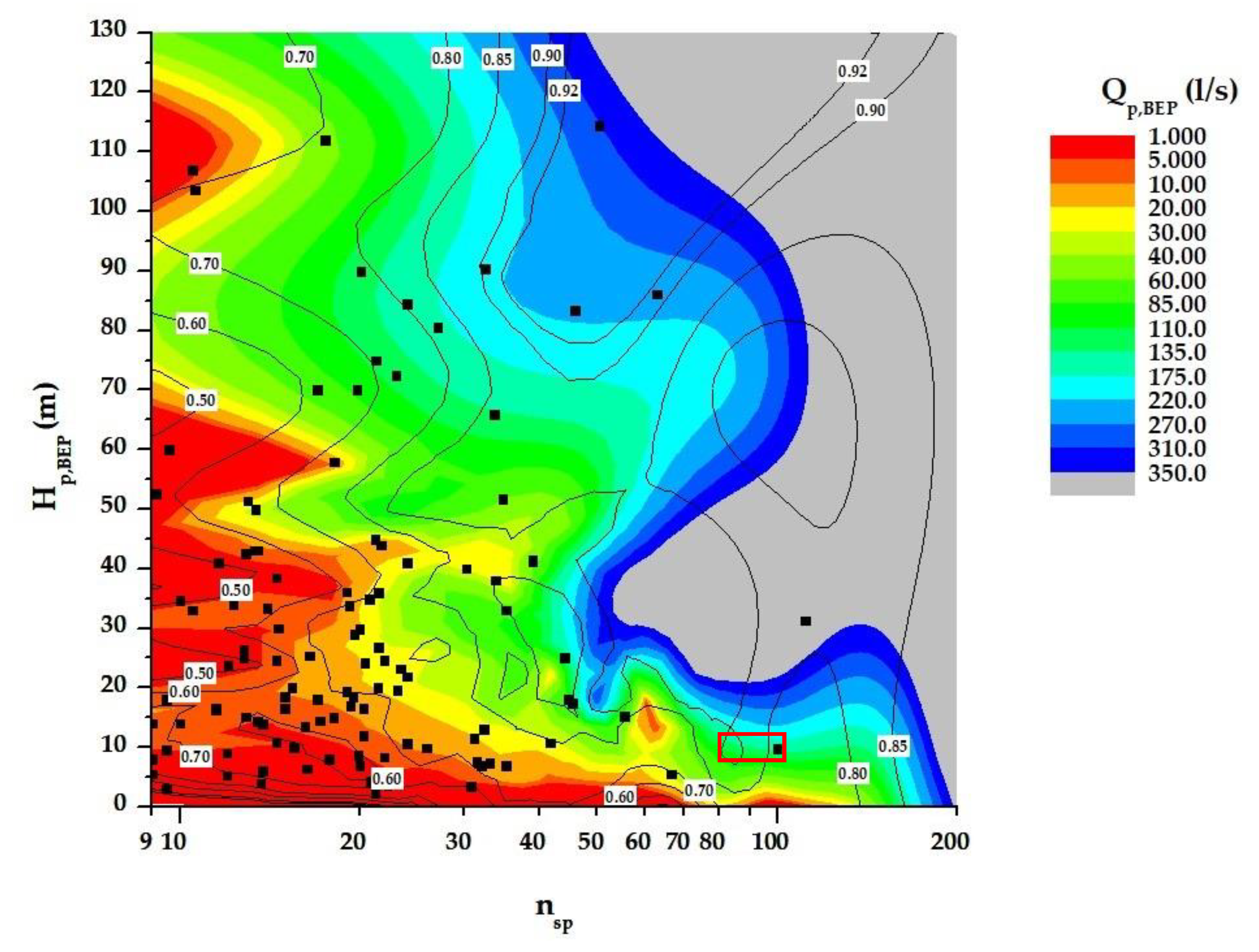
3.2. Estimation of the Operation and Effciency Curve
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| D | Impeller diameter (m) |
| g | Gravity constant (9.81 m2/s) |
| Head in the best efficiency point in pump mode (m w.c.) | |
| Head in the best efficiency point in turbine mode (m w.c.) | |
| Head in turbine mode (m w.c.) | |
| Specific rotational speed (m, kw) | |
| Specific rotational speed in pump mode (m, kw) | |
| Specific rotational speed in turbine mode (m, kw) | |
| Rotational speed in rpm using in specific speed. The units are rps when it is used to determine the dimensionless numbers (, and ). | |
| Shaft power in the best efficiency point in turbine mode (w) | |
| Shaft power in turbine mode (w) | |
| Discharge in the best efficiency point in pump mode (m3/s) | |
| Discharge in the best efficiency point in turbine mode (m3/s) | |
| Discharge in turbine mode (m3/s) | |
| Greek symbols | |
| Discharge coefficient (dimensionless) | |
| Head coefficient (dimensionless) | |
| Efficiency coefficient (dimensionless) | |
| Water density (kg/ m3) | |
| Head number (dimensionless) | |
| Head number in turbine mode (dimensionless) | |
| Best efficiency in pump mode (dimensionless) | |
| Best efficiency in turbine mode (dimensionless) | |
| Efficiency in turbine mode (dimensionless) | |
| Power number (dimensionless) | |
| Discharge number (dimensionless) | |
| Discharge number referred to turbine mode (dimensionless) | |
References
- Coelho, B.; Andrade-Campos, A. Efficiency achievement in water supply systems—A review. Renew. Sustain. Energy Rev. 2014, 30, 59–84. [Google Scholar] [CrossRef]
- Ramos, H.; Borgå, Å. Pumps as turbines: An unconventional solution to energy production. Urban Water 1999, 1, 261–263. [Google Scholar] [CrossRef]
- Goonetilleke, A.; Vithanage, M. Water Resources Management: Innovation and Challenges in a Changing World. Water 2017, 9, 281. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Del Giudice, G.; Ramos, H. Energy Recovery in Water Systems by PATs: A Comparisons among the Different Installation Schemes. Procedia Eng. 2014, 70, 275–284. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy Recovery in Existing Water Networks: Towards Greater Sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Capurso, T.; Balacco, G.; Binetti, M.; Torresi, M.; Camporeale, S.M. Pump as Turbine for Throttling Energy Recovery in Water Distribution Networks; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2191, p. 020142. [Google Scholar]
- Muhammetoglu, A.; Nursen, C.; Karadirek, I.E.; Muhammetoglu, H. Evaluation of performance and environmental benefits of a full-scale pump as turbine system in Antalya water distribution network. Water Sci. Technol. Water Supply 2018, 18, 130–141. [Google Scholar] [CrossRef]
- Stefanizzi, M.; Capurso, T.; Balacco, G.; Torresi, M.; Binetti, M.; Piccinni, A.F.; Camporeale, S.M. Preliminary assessment of a pump used as turbine in a water distribution network for the recovery of throttling energy. In Proceedings of the 13th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, European Turbomachinery Society, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Optimization Strategy for Improving the Energy Efficiency of Irrigation Systems by Micro Hydropower: Practical Application. Water 2017, 9, 799. [Google Scholar] [CrossRef]
- Novara, D.; McNabola, A. The Development of a Decision Support Software for the Design of Micro-Hydropower Schemes Utilizing a Pump as Turbine. Proceedings 2018, 2, 678. [Google Scholar] [CrossRef]
- Novara, D.; McNabola, A. A model for the extrapolation of the characteristic curves of Pumps as Turbines from a datum Best Efficiency Point. Energy Convers. Manag. 2018, 174, 1–7. [Google Scholar] [CrossRef]
- Fecarotta, O.; Carravetta, A.; Ramos, H.M.; Martino, R. An improved affinity model to enhance variable operating strategy for pumps used as turbines. J. Hydraul. Res. 2016, 54, 332–341. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. Modified Affinity Laws in Hydraulic Machines towards the Best Efficiency Line. Water Resour Manag. 2018, 32, 829–844. [Google Scholar] [CrossRef]
- Williams, A.A. The Turbine Performance of Centrifugal Pumps: A Comparison of Prediction Methods. Proc. Inst. Mech. Eng. Part A J. Power Energy 1994, 208, 59–66. [Google Scholar] [CrossRef]
- Mataix, C. Turbomáquinas Hidráulicas; Universidad Pontificia Comillas: Madrid, Spain, 2009. [Google Scholar]
- Ulanicki, B.; Kahler, J.; Coulbeck, B. Modeling the Efficiency and Power Characteristics of a Pump Group. J. Water Resour. Plan. Manag. 2008, 134, 88–93. [Google Scholar] [CrossRef]
- Capurso, T.; Stefanizzi, M.; Pascazio, G.; Ranaldo, S.; Camporeale, S.M.; Fortunato, B.; Torresi, M. Slip Factor Correction in 1-D Performance Prediction Model for PaTs. Water 2019, 11, 565. [Google Scholar] [CrossRef]
- Stepanoff, A.J. Centrifugal and Axial Flow Pumps. Theory, Design, and Application; Krieger Publishing Company: Malabar, FL, USA, 1957. [Google Scholar]
- McClaskey, B.M.; Lundquist, J.A. Hydraulic power recovery turbine. In Mechanical Engineering; AMER Soc Mechanical Eng 345 E 47TH ST; ASME: New York, NY, USA, 1977; Volume 10017, p. 106. [Google Scholar]
- Alatorre-Frenk, C. Cost Minimisation in Micro-Hydro Systems Using Pumps-as-Turbines. 1994. Available online: http://wrap.warwick.ac.uk/36099/ (accessed on 20 December 2019).
- Sharma, K. Small Hydroelectric Project-Use of Centrifugal Pumps as Turbines; Kirloskar Electric Co.: Bangalore, India, 1985. [Google Scholar]
- Krivchenko, G.I. Recomendaciones Para la Utilización de Bombas Como Turbinas (en ruso); Muraviob, O.A., Natarius, E.M., Eds.; Infoenergo: Saint Petersburg, Russia, 1990. [Google Scholar]
- Yang, S.-S.; Derakhshan, S.; Kong, F.-Y. Theoretical, numerical and experimental prediction of pump as turbine performance. Renew. Energy 2012, 48, 507–513. [Google Scholar] [CrossRef]
- Hancock, J.W. Centrifugal pump or water turbine. Pipe Line News 1963, 6, 25–27. [Google Scholar]
- Schmiedl, E. Serien-Kreiselpumpen im Turbinenbetrieb; Pumpentagung: Karlsruhe, Germany, 1988. [Google Scholar]
- Mijailov, L.P.; Feldman, B.N. Pequeña Hidroenergía (en ruso); Energoatomizdat: Moscú, Russia, 1989. [Google Scholar]
- Audisio, O. Bombas Utilizadas Como Turbinas; Universidad nacional del Comahue: Buenos Aires, Argentina, 2009. [Google Scholar]
- Carvalho, N. Bombas de Fluxo Operando Como Turbina. Por Que Usá-Las? Seção de Artigos Técnicos. PCH Notícias & SPH News. 2012. Available online: http://www.proceedings.scielo.br/scielo.php?script=sci_arttext&pid=MSC0000000022002000100033&lng=en&nrm=iso (accessed on 31 December 2019).
- Nautiyal, H.; Kumar, A. Reverse running pumps analytical, experimental and computational study: A review. Renew. Sustain. Energy Rev. 2010, 14, 2059–2067. [Google Scholar] [CrossRef]
- Barbarelli, S.; Amelio, M.; Florio, G. Experimental activity at test rig validating correlations to select pumps running as turbines in microhydro plants. Energy Convers. Manag. 2017, 149, 781–797. [Google Scholar] [CrossRef]
- Grover, K.M. Conversion of Pumps to Turbines; GSA Inter Corp.: Katonah, NY, USA, 1980. [Google Scholar]
- Lewinsky-Kesslitz, H.-P. Pumpen als turbinen fur kleinkraftwerke. Wasserwirtschaft 1987, 77, 531–537. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Rossi, M.; Renzi, M. A general methodology for performance prediction of pumps-as-turbines using Artificial Neural Networks. Renew. Energy 2018, 128, 265–274. [Google Scholar] [CrossRef]
- Rossi, M.; Nigro, A.; Renzi, M. Experimental and numerical assessment of a methodology for performance prediction of Pumps-as-Turbines (PaTs) operating in off-design conditions. Appl. Energy 2019, 248, 555–566. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Experimental study of characteristic curves of centrifugal pumps working as turbines in different specific speeds. Exp. Therm. Fluid Sci. 2008, 32, 800–807. [Google Scholar] [CrossRef]
- Flórez, R.; Abella Jiménez, J. Máquinas Hidráulicas Reversibles Aplicadas a Micro Centrales Hidroeléctricas. IEEE Lat. Am. Trans. 2008, 6, 170–175. [Google Scholar]
- Alberizzi, J.; Renzi, M.; Righetti, M.; Pisaturo, G.; Rossi, M. Speed and Pressure Controls of Pumps-as-Turbines Installed in Branch of Water-Distribution Network Subjected to Highly Variable Flow Rates. Energies 2019, 12, 4738. [Google Scholar] [CrossRef]
- Gülich, J.F. Centrifugal Pumps; Springer: Berlin, Germany, 2008; Volume 2. [Google Scholar]

| Autor | |||
|---|---|---|---|
| Stepanoff [19] | 1 | ||
| Mc. Claskey [20] | 1 | ||
| Alatorre-Frenk [21] | |||
| Sharma-Williams [22] | 1 | ||
| MICI [23] | 0.9–1.0 | 1.56–1.78 | 0.75–0.80 |
| Yang et al. [24] | - | ||
| Hancock [25] | - | ||
| Schmiedl [26] | - | ||
| Mijailov [27] | 0.078 3.292 | 0.078 3.112 | 0.0014 0.96 |
| Audisio [28] | 1.21 | 1.21 | 0.95 |
| Carvalho [29] | 5·10−5 | 2·10−5 | - |
| Nautiyal [30] | 30.303[( 0.212)/ln()]3.424 | 41.667[(0.212)/ln()]5.042 | - |
| Barbarelli [31] | |||
| Grover [32] | 2.379 − 0.0264 | 2.693 − 0.0229 | - |
| Hergt [33] | - |
| Author | Variable | Expression | Range (Experimental Data) | Reference |
|---|---|---|---|---|
| Derakhshan and Nourbakhsh | <60 (4) | [37] | ||
| + | <60 (4) | [37] | ||
| Plugiese et al. | They use Derakhshan’s equation. | <60 (4) | [38] | |
| + | <45 (2) | [38] | ||
| Barbarelli et al. | <55 (12) | [31] | ||
| + 1.185 | <55 (12) | [31] | ||
| Fecarotta et al. | 120–165 (4) | [13] | ||
| 1.85 | 120–165 (4) | [13] | ||
| Alberizzi et al. | 3 (1) | [39] | ||
| −1.9778 | 3 (1) | [39] | ||
| Novara and McNabola | <100 (113) | [12] | ||
| <100 (113) | [12] |
| Coefficient | Empirical Equation | R2 | Experimental Data |
|---|---|---|---|
| 99.34 | 163 | ||
| 98.85 | 150 | ||
| 97.59 | 150 | ||
| 99.34 | 163 | ||
| 97.15 | 157 | ||
| 96.39 | 153 | ||
| 96.39 | 11 | ||
| 90.92 | 11 |
| Method | Flow (Q) | Head (H) | Efficiency | Q,H | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAD | MRD | BIAS | RMSE | MAD | MRD | BIAS | RMSE | MAD | MRD | BIAS | % data C<1 | |
| This study | 0.181 (1) | 0.135 (1) | 0.091 (1) | −0.037 (2) | 0.294 (2) | 0.211 (2) | 0.129 (2) | −0.02 (3) | 0.078 (1) | 0.059 (1) | 0.068 (1) | −0.004 (1) | 79.20 (1) |
| Yang | 0.192 (2) | 0.138 (2) | 0.092 (2) | −0.036 (1) | 0.288 (1) | 0.209 (1) | 0.129 (1) | −0.011 (2) | − | − | − | − | 78.81 (2) |
| Mc Claskey | 0.205 (3) | 0.16 (3) | 0.107 (3) | −0.073 (3) | 0.466 (7) | 0.381 (7) | 0.206 (7) | −0.343 (8) | 0.114 (4) | 0.088 (4) | 0.106 (4) | 0.08 (4) | 62.42 (5) |
| Sharma-Williams | 0.238 (4) | 0.195 (5) | 0.128 (5) | −0.163 (5) | 0.379 (5) | 0.303 (6) | 0.169 (5) | −0.245 (7) | 0.114 (4) | 0.088 (4) | 0.106 (4) | 0.08 (4) | 71.83 (4) |
| Audisio | 0.252 (5) | 0.192 (4) | 0.122 (4) | −0.148 (4) | 0.359 (4) | 0.257 (4) | 0.145 (4) | −0.117 (4) | 0.192 (7) | 0.161 (7) | 0.162 (7) | −0.16 (7) | 74.49 (3) |
| Alatorre-Frenk | 0.321 (6) | 0.259 (6) | 0.185 (6) | 0.184 (7) | 0.321 (3) | 0.223 (3) | 0.135 (3) | −0.009 (1) | 0.089 (2) | 0.064 (2) | 0.075 (2) | 0.039 (3) | 60.93 (6) |
| Stepanoff | 0.339 (7) | 0.29 (7) | 0.187 (7) | −0.285 (8) | 0.466 (7) | 0.381 (7) | 0.206 (7) | −0.343 (8) | 0.114 (4) | 0.09 (4) | 0.106 (4) | 0.08 (4) | 46.98 (8) |
| Carvalo | 0.6 (8) | 0.558 (9) | 0.371 (9) | −0.558 (10) | 0.875 (9) | 0.62 (9) | 0.352 (9) | −0.195 (6) | − | − | − | − | 9.27 (11) |
| Barbarelli | 0.878 (9) | 0.312 (8) | 0.244 (8) | 0.177 (6) | 10.717 (12) | 2.087 (12) | 1.668 (12) | −1.798 (12) | − | − | − | − | 60.27 (7) |
| Nautiyal | 1.304 (10) | 0.784 (10) | 0.504 (10) | −0.332 (9) | 1.858 (10) | 1.166 (10) | 0.655 (10) | −0.505 (10) | − | − | − | − | 21.85 (9) |
| Schimiedl | 2.504 (11) | 1.783 (12) | 1.153 (12) | 1.783 (12) | 0.395 (6) | 0.282 (5) | 0.173 (6) | 0.194 (5) | − | − | − | − | 3.35 (12) |
| Mijailov | 2.523 (12) | 1.362 (11) | 1.038 (11) | −1.143 (11) | 2.725 (11) | 1.64 (11) | 1.087 (11) | −1.588 (11) | 0.091 (3) | 0.068 (3) | 0.076 (3) | −0.02 (2) | 13.91 (10) |
| Method | Flow (Q) | Head (H) | Efficiency | Q,H | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAD | MRD | BIAS | RMSE | MAD | MRD | BIAS | RMSE | MAD | MRD | BIAS | % C<1 | |
| This study | 0.291 (1) | 0.206 (1) | 0.144 (1) | 0.068 (1) | 0.357 (1) | 0.264 (1) | 0.165 (1) | −0.006 (1) | 0.072 (1) | 0.054 (1) | 0.063 (1) | −0.003 (1) | 69.54 (1) |
| Hergt | 1.602 (2) | 0.462 (2) | 0.272 (2) | −0.433 (2) | 1.157 (3) | 0.835 (3) | 0.419 (3) | −0.82 (3) | - | - | - | 31.79 (2) | |
| Grover | 1.915 (3) | 1.173 (3) | 0.882 (3) | −1.125 (3) | 0.624 (2) | 0.487 (2) | 0.331 (2) | 0.225 (2) | - | - | - | - | 7.28 (3) |
| Curve | RMSE | MAD | MRD | BIAS |
|---|---|---|---|---|
| Runaway | 0.139 | 0.0946 | 0.0529 | −0.0135 |
| Zero-speed | 0.1289 | 0.0855 | 0.1036 | −0.0183 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves. Water 2020, 12, 468. https://doi.org/10.3390/w12020468
Pérez-Sánchez M, Sánchez-Romero FJ, Ramos HM, López-Jiménez PA. Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves. Water. 2020; 12(2):468. https://doi.org/10.3390/w12020468
Chicago/Turabian StylePérez-Sánchez, Modesto, Francisco Javier Sánchez-Romero, Helena M. Ramos, and P. Amparo López-Jiménez. 2020. "Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves" Water 12, no. 2: 468. https://doi.org/10.3390/w12020468
APA StylePérez-Sánchez, M., Sánchez-Romero, F. J., Ramos, H. M., & López-Jiménez, P. A. (2020). Improved Planning of Energy Recovery in Water Systems Using a New Analytic Approach to PAT Performance Curves. Water, 12(2), 468. https://doi.org/10.3390/w12020468








