1. Introduction
Control of seepage is crucial for the safety of earth-fill dams and levees. One of the failure mechanisms in hydraulic structures is internal erosion, which is initiated by detaching and transferring the soil particles due to seepage forces [
1,
2]. Internal erosion is the cause of half of all dam failures [
3] and more than one-third of all levee accidents [
4]. Overall about 1 in 80 embankment dams have failed or experienced an accident by seepage and internal erosion [
5]. The other seepage induced failure due to the increase in pore pressures is drop in effective stress and shear strength and consequent loss of stability [
6]. In order to decrease the negative effect of seepage on the overall stability, impervious central core and drainage systems are constructed inside earth-fill dams. A seepage monitoring system should be installed to check whether seepage is in the limit defined by the designed project and that dams and levees are safe enough. It would be beneficial to use measurements that give results continuously in time and space. One of the seepage monitoring techniques, which can provide continuous measurement both in time and space, is the thermometric method using optical fiber Distributed Temperature Sensor (DTS). The thermometric method is defined as continuous or time periodically repeating measurements of the temperature in the ground to trace the groundwater flow.
Kappelmeyer [
7] firstly employed the thermometric method by embedding the thermometers into the shallow soil layer and studied the temperature regime during the seepage process. The method has been developed and used in the field by installing the thermometers in existing boreholes and vertical standpipes [
8,
9]. Using the thermometers for seepage monitoring guarantees the temperature measurement in short time intervals; however, the monitoring system was still subjected to some shortages because it measures the temperature only in vertical profiles and not over a wide area.
With the development in optical fiber technology and the invention of the optical fiber distributed temperature sensor (DTS) in the 1980s [
10], a new window was opened for the seepage monitoring by the temperature measurements [
11]. Optical fiber DTS made it possible to expand the area of investigation and the temperature measurement [
3] with high sensitivity, low cost, and small influences on the mechanical properties of the soil [
12]. The optical fiber cable can be embedded in the soil at the downstream face of the existing embankments and earthen dams, where the signs for increased seepage and erosion is mostly observed. Additionally, the cable can be installed into the vertical standpipes to monitor the presence of the seepage in deeper parts of the dam body. For the new embankments, the cables can be embedded into the structure’s body during the construction phase.
The thermometric method by DTS can be applied by measuring the natural temperature of the embankment body, which is called the passive method. However, sometimes it is advisable to identify seepage characteristics by imposing the heat into the embankment and monitoring its dissipation, called active method [
3]. In this study, the passive approach was used.
Johansson and Sjodahl [
13] used passive temperature monitoring by the optical fiber DTS for seepage observation. Considering the seasonal variation of the temperature in air and reservoir water, the seasonal thermal response was observed in the dam body. The results of a long-term monitoring present that the constant temperature in a dam indicates small seepage, while large seasonal temperature variation indicates significant seepage. During the winter, the water in the seepage zone warms up the relatively cooler body of the embankment, while in the summer the seepage water cools down the dam body [
14].
The other method for leakage detection using the optical fiber DTS was developed by Perzlmaier et al. [
15]. The method is based on the active temperature measurement, inserting heat into the dam along the optical fiber cable and monitoring the heat dissipation. This can be implemented by introducing heat into a metal wire within the optical fiber coating [
16] or a separate wire along the optical fiber cable. The active method was used to estimate the seepage velocity [
15,
17] and the degree of saturation [
15] in the vicinity of the optical fiber cable. The accuracy of the method depends on the heating power [
17] that is introduced into the embankment, thus, for long cables, a high power source is required.
Yosef et al. [
18] performed a coupled hydro-thermal modeling and analyzed one year temperature measurements in an embankment. They presented the ability of hydro-thermal coupled analysis to trace the anomalies of the heat sources, variation in the permeability, and the existence of anomalies such as a sinkhole in dam. Using DTS temperature monitoring, techniques were developed to distinguish the temperature variation due to seepage from other reasons such as seasonal temperature variation of soil, existing structure in the dam, precipitations, and soil heterogeneity [
15,
19,
20].
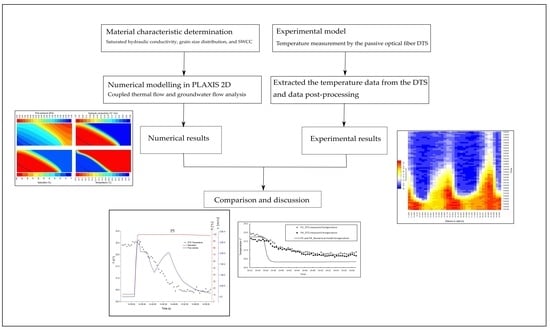
This work focuses on the monitoring of the seepage process in a laboratory scaled model by a passive DTS system. Most of the studies on this topic were performed by laboratory or field experiments. In this work, we combined a laboratory experiment with the numerical study for both thermal and groundwater flow. The study consists of the determination of material properties, a set-up of an experimental model of seepage while the optical fiber cable is embedded in the sand model and the numerical modeling of the seepage and heat flow in a geotechnical engineering software for two-dimensional finite element analysis (PLAXIS 2D). The experimental results from the physical model were compared with the numerical results obtained from the thermal and groundwater flow analysis. No optimization of material parameters was made, all the calculations were performed by using material parameters obtained from the laboratory tests and the related reference literature.
For the low temperature difference between the entered water and the soil, the active method was developed [
15]. However, in this study, we showed the ability of the passive optical fiber DTS to monitor the seepage at the low temperature difference between the unsaturated sand and water in a laboratory scaled sand model.
2. Materials and Method
This study consists of the determination of material properties by the respective laboratory tests, an experimental model of seepage while the optical fiber cable is embedded in the sand model and the numerical modeling of the seepage and thermal flow in the PLAXIS 2D software.
2.1. Seepage and Heat Flow
The heat is transferred in soils by three mechanisms: conduction, convection, and radiation. In the thermometric analysis of seepage, the influence of the radiation process can be neglected because it affects only the surface layers of the soil due to its short day-night cycles duration [
8]. A simplified equation based on energy conservation presents the heat transfer mechanism in the porous media which is shown in Equation (1) [
21]. The second and third terms represent the heat transfer due to convection and conduction, respectively:
where
is the bulk density of soil,
is temperature,
is the specific heat of the soil,
is time,
presents the water density (1000 kg/m
3),
is the specific heat of water (4181 J/kg/°C),
is the specific discharge or Darcy velocity, and
is the soil thermal conductivity.
Both
and
are dependent on the saturation (
and porosity (
for a given mineral composition [
21,
22].
Specific discharge is calculated using the continuity equation for mass conservation of water in porous media:
Considering constant
, the equation for the volumetric water content
, and Darcy’s law
, Equation (2) leads to:
where
is the hydraulic conductivity and depends on the saturation and porosity, and
is the piezometric head.
Oftentimes, the Soil Water Characteristic Curve (SWCC) is used to describe the saturation - negative pore pressure (i.e., suction) relationship. We described the SWCC by the van Genuchten model [
23] that relates the saturation
to the pressure head
:
where:
where
is the saturation of the sand at the saturated condition usually equals to 1,
is the residual saturation and
,
, and
are empirical fitting parameters for the van Genuchten model.
is related inversely to the air entry value (suction at which the soil begins to de-saturate).
is the slope of SWCC once the air entry value has been exceeded [
24] and
is related to the curvature of the SWCC model in the high suction range.
is usually fixed to
in order to have an analytical solution for hydraulic conductivity. The hydraulic conductivity of material at the unsaturated condition
() can be calculated using SWCC as seen from Equation (6) [
23]:
where
is hydraulic conductivity of saturated soil,
is the fitting parameter (mostly 0.5).
The thermal conductivity of the soil (
and the heat capacity (
) as a function of soil saturation and porosity were estimated as [
25]:
where
,
, and
are the thermal conductivities of the particles, water (0.6 W/m/°C), and air (0.026 W/m/°C at normal laboratory conditions; 101.3 kPa, 20 °C) [
26], respectively,
is the particle density, and
is the heat capacity of particles.
The heat flow boundaries are described by the Dirichlet and Neumann boundary condition types. In the Dirichlet type, a known temperature
is prescribed on the boundary domain
and time
t [
25,
27]:
The Neumann type boundary condition for the heat transfer can be described by Equation (10):
where
is the heat flux across the boundary
and
is the prescribed Neumann heat flux.
2.2. Soil
Silica dominated sand was used in this study. The material was purchased in 2019 from TERMIT d.d., a mining company that produces silica sand from the mines located in Moravče, Slovenia. We determined the saturated hydraulic conductivity, SWCC, dry and saturated densities, porosity, and the grain size distribution of the sand in the laboratory tests. The vendor provided the chemical composition of the sand [
28]. The heat capacity and thermal conductivity of the sand particles were estimated from the literature based on the chemical composition of the material (
1.36 W/m/°C [
29],
= 730 J/kg/°C [
30]).
The chemical composition of the material, dry density
, particle density
, porosity
, and coefficient of uniformity
Cu are presented in
Table 1.
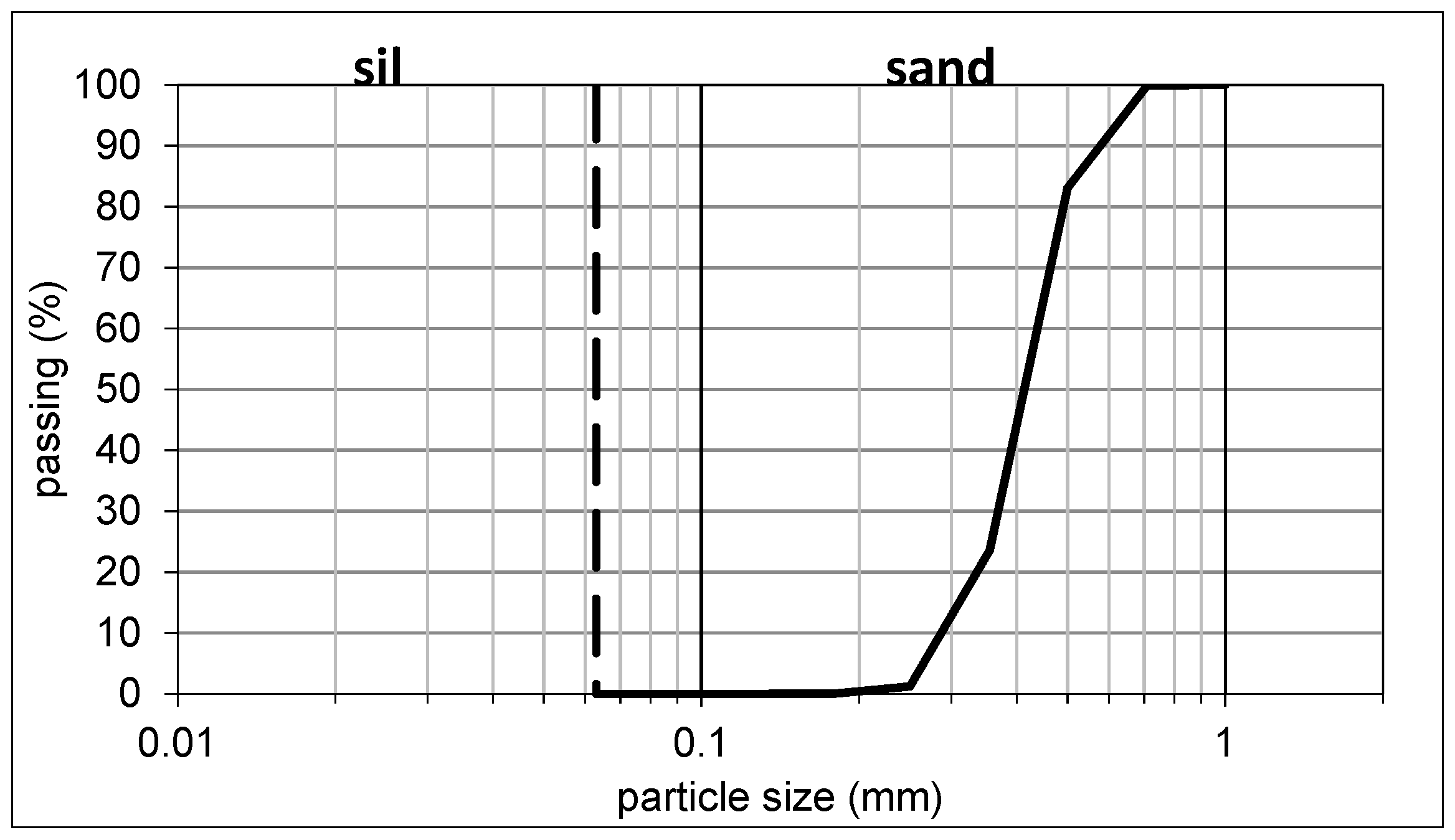
We determined the grain size distribution of the sand by the sieve analysis test, which is given in
Figure 1.
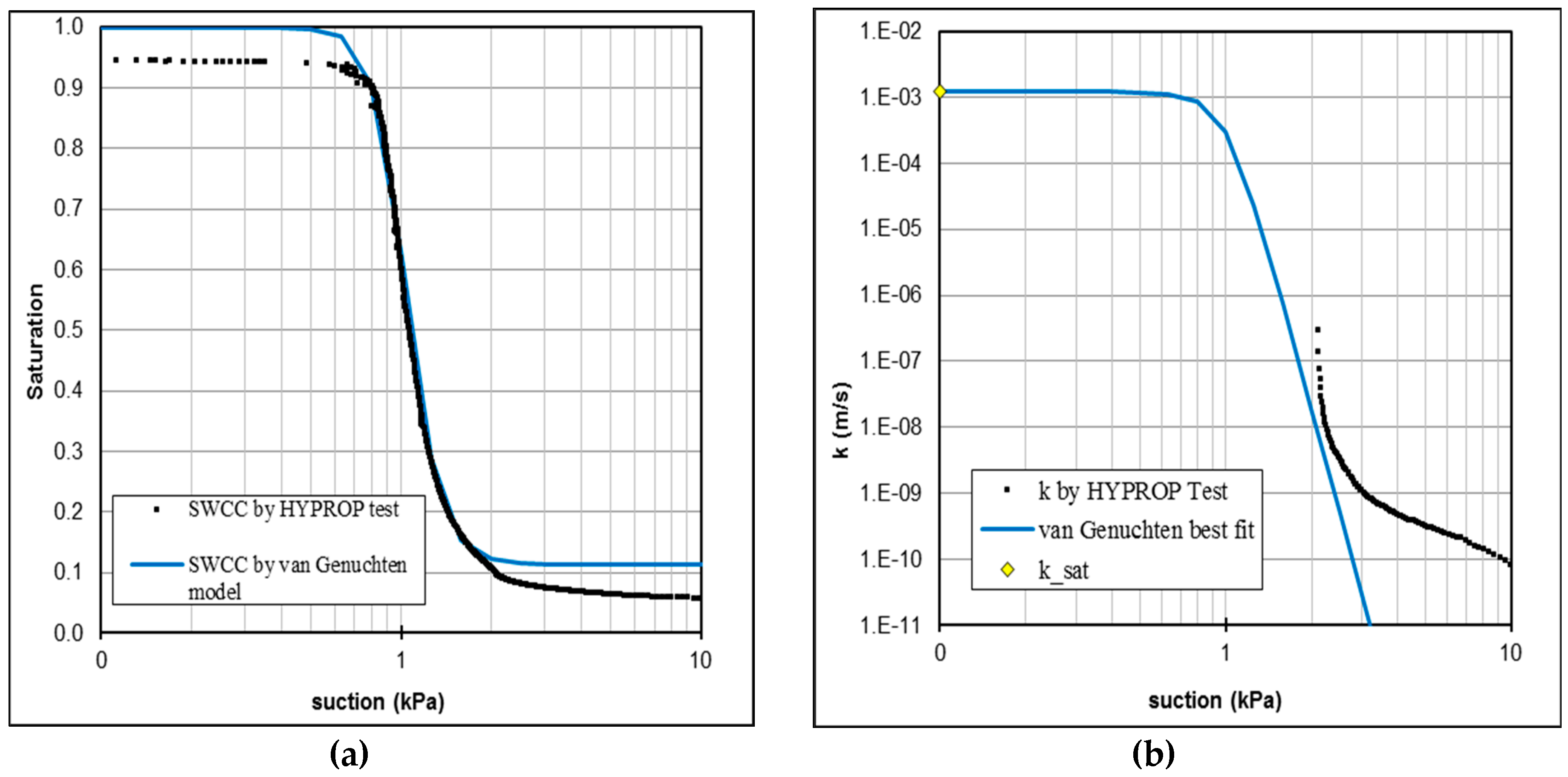
SWCC was developed using the HYPROP evaporation method device (Meter group) [
31,
32] on a compacted sample. The sample was compacted to the same dry density as in the experimental model. With the HYPROP device, a continuous SWCC is obtained by simultaneously and continuously measuring suction with two high capacity tensiometers installed at different heights of the soil sample and weight change during drying. The typical range of the HYPROP device is from 0 to slightly above 100 kPa. When the suction difference between upper and lower tensiometer is greater than hydrostatic, the hydraulic conductivity as a function of saturation,
could be measured for the unsaturated state. In the case of sand without fine particles (<0.063 mm), the volume change during the test is negligible and from the change in the mass of water the saturation could be calculated.
The saturated hydraulic conductivity, , was measured in constant head rigid wall permeameter using local total head measurements without saturation control (class 2 measurements). A permeameter with a diameter of 113 mm and a height of 405 mm was used. The sand was compacted to the same dry density as in the experimental sand model.
2.3. Experimental Model
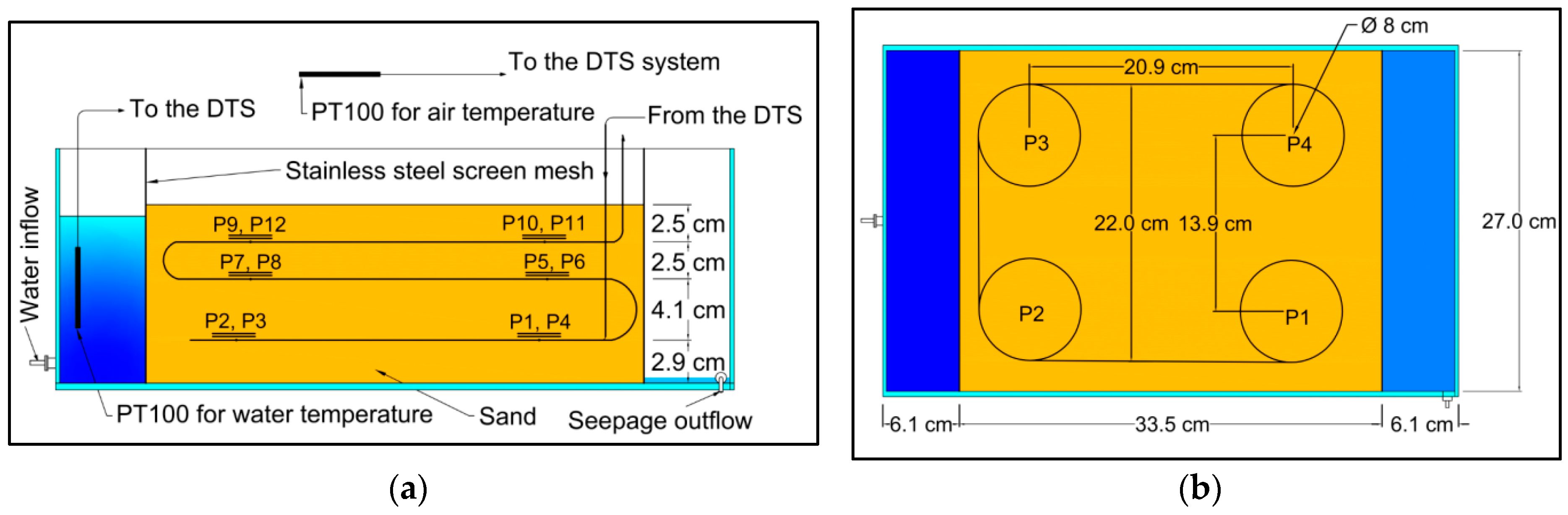
The physical model consisted of a rectangular box filled with sandy soil supported by wire mesh on the upstream and downstream faces and plexiglass at the sidewalls, with upstream and downstream tanks attached to it (
Figure 2). Soil fill was 33.5 cm × 27 cm × 12 cm (length, width, height). The optical fiber cable was installed during soil placement. Homogeneous sand fill was assumed. It was anticipated that installed optical cables did not significantly influence the water and heat flow. Additionally, two thermometers were used to measure air and water temperature. The water level in the upper tank was controlled only by manual adjusting the position of a ball valve.
A passive optical fiber DTS system (SILIXA-XT-DTS) with 50/125 μm multi-mode optical fiber was used for the experiment. Optical fiber DTS employs the Optical Time Domain Reflectometry (OTDR) technique and uses characteristics of the Raman Spectroscopy of the light for temperature measurement. In this technique, DTS launches short pulses of light into the fiber optic cable and detects the Raman backscatter photons (Stokes and anti-Stokes) at regular time intervals by the fast photonic detector system [
33,
34]. The distance from the measurement point is determined by the runtime of the light, knowing its propagation velocity. The Raman scattering will be generated due to the transfer of energy between the launched laser photons and molecules of the material in optical fiber cable. The temperature in the vicinity of cable changes the energy state of molecules in the cable and influences the characteristics of Raman scattered photons. The Stokes intensity is irrelevant to the temperature, while the anti-Stokes intensity is highly dependent on the temperature. DTS measures the intensity of detected Raman scattered photons and use their ratio to obtain the temperature [
35].
We performed the DTS measurement based on the duplexed single-ended configuration [
36]. The distance between each temperature successive measurement (sampling interval) was selected as 10 inches (25.4 cm; the minimum allowable sampling interval for our system) to provide as many measuring points as possible in the model. The sampling time interval was 30 s. These intervals were appropriate to provide accurate and reliable measurements in our experiment. DTS temperature measurement is not fully independent for the adjacent sampling interval [
37] and the abrupt change in temperature may be missed by the system. The distance between points reporting 10 to 90%, respectively, the true temperature changes at a step shift in temperature along the cable is called spatial resolution [
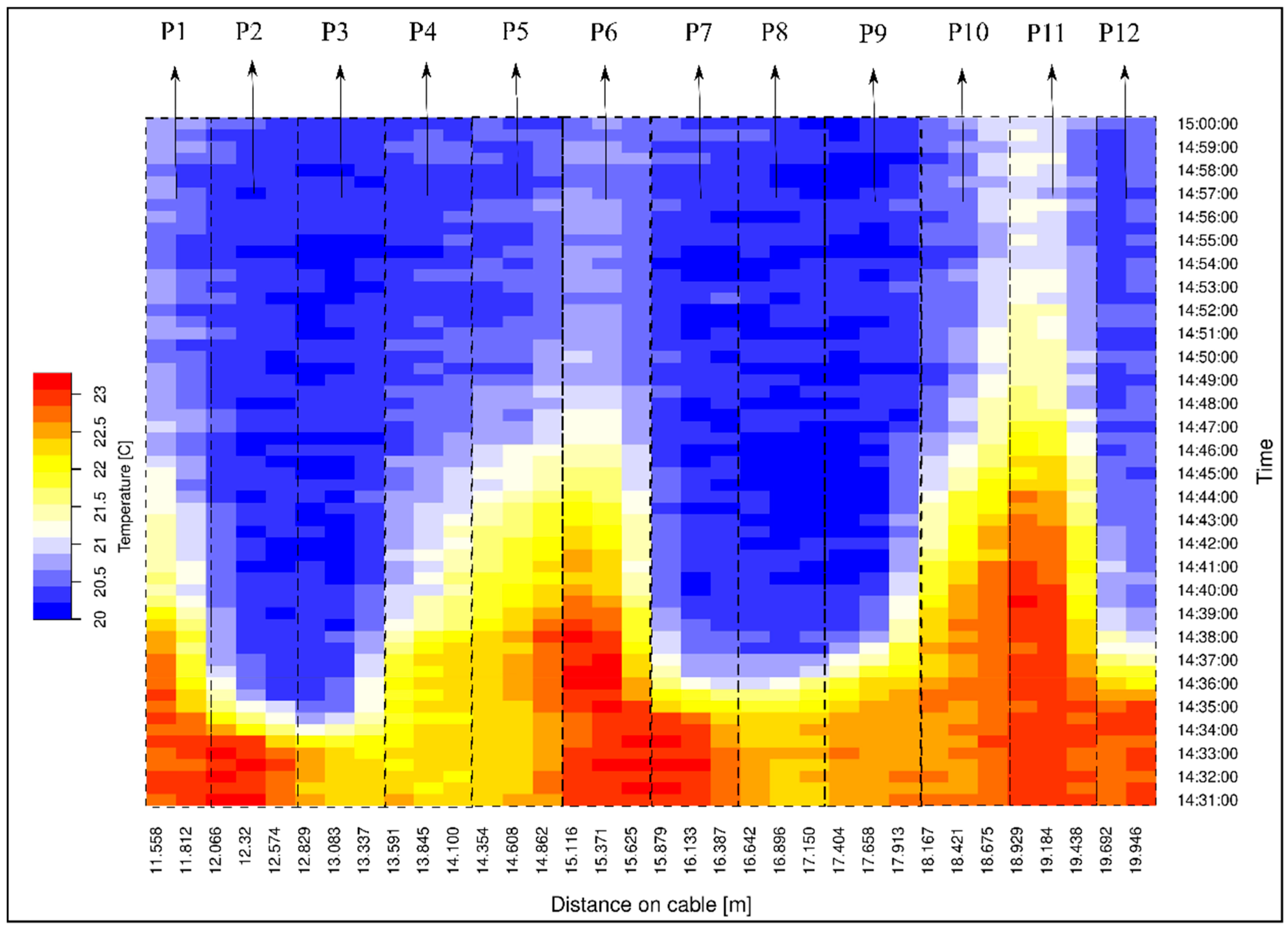
38], which in our case was around 64 cm. In order to measure point temperature accurately, the length of the cable surrounds each measuring point (sensory ring) was increased to more than 50 cm by using two loops with the diameter of circa 8 cm. The loops were placed horizontally in the soil so the water flow was along the optical fiber cable. We made 12 measuring points by the cable loops as shown in
Figure 2.
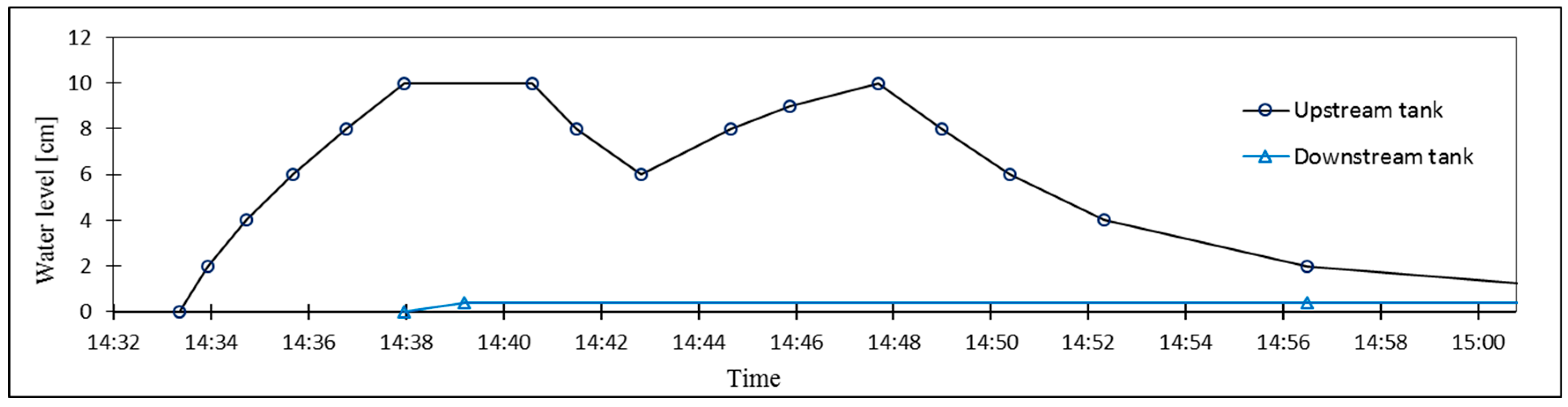
After the placement of the dry sand, the model was left in the laboratory for more than 48 h in order to equilibrate its temperature with the ambient temperature in the room (approximately 23 °C). Then, the measurement started to obtain the initial temperature of dry unsaturated sand. Filling of the upstream tank and seepage experiment started by opening the valve of the tap water. A PT100 thermometer was replaced in the upstream tank to measure the water temperature. The water temperature during the test was 19.6 ± 0.1 °C. The water level in the upstream tank was measured manually by measuring tape at given time intervals. After the maximum desired level at the upstream tank was reached the valve was closed. It was found that the volume of the upper tank was too small to maintain a nearly constant water level. As the water level dropped more than expected, due to the flow of water into the sand, the valve was temporarily opened again and after reaching the maximum desired level, the valve was closed (see Figure 6). At the downstream tank, the outflow gauge was opened for the free outflow from the tank. The water depth at the downstream tank corresponding to the steady-state flow was about 4 mm.
The DTS system is equipped with two PT100 thermometers. One of the thermometers was installed in the upstream tank to continuously measure the water temperature and the other one was used to measure the air temperature adjacent to the experimental model. The temperature measurement in our model was based on the internal calibration of the DTS system. A constant differential loss of light power equals to 0.255 dB/km was assigned for the system, as this was advised by the system guideline [
39]. In the adjacent of the experimental model, a PT100 thermometer was placed to measure the ambient temperature. In this location, we placed 10 m of the cable as a reference section for the system to calibrate its measurements. SILIXA XT-DTS is calibrating its measurements using one or two reference sections where the PT100 thermometers are placed. In addition to that, the system calibrates the measurement using 200 m of the cable reference coil and a highly precise internal thermometer that existed inside the system. We calibrated the system and validated the DTS measurements by the internal calibration before the experiment, using two reference water baths containing hot and cold water with the constant temperatures.
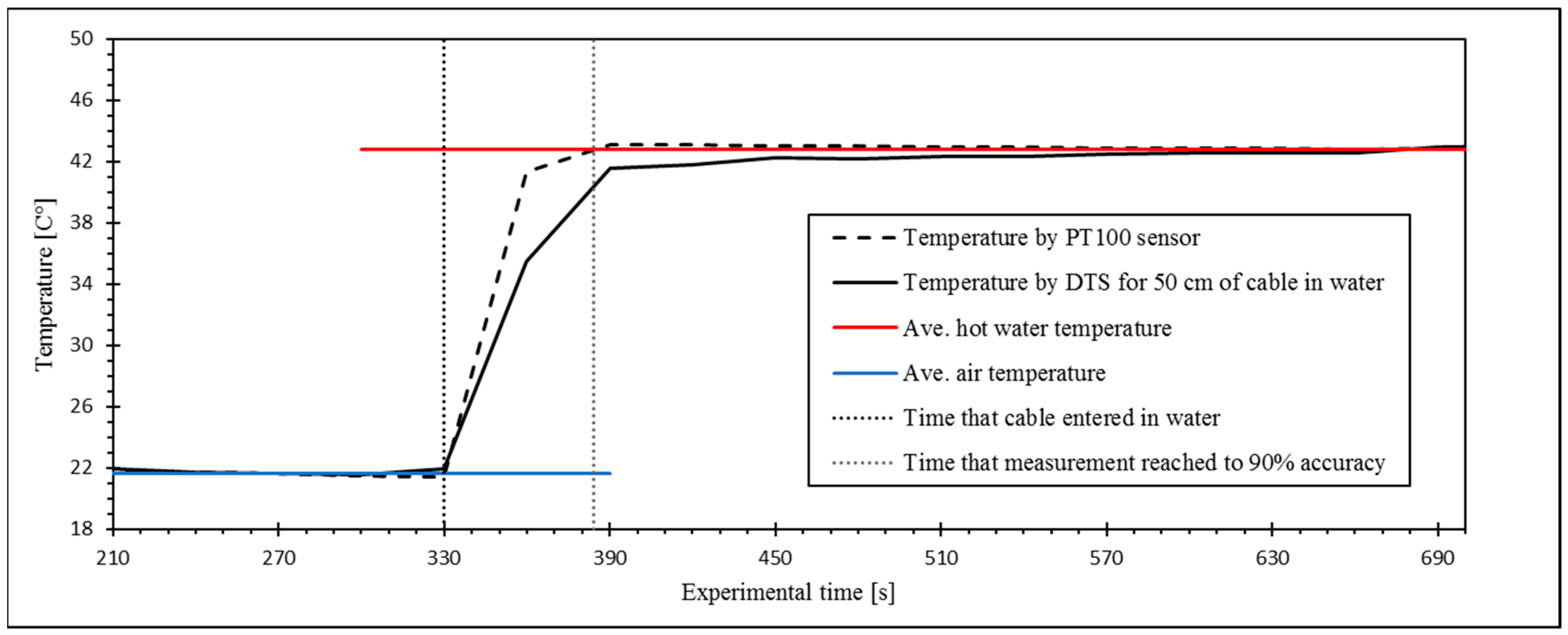
To describe the effect of the DTS system response time on the measurement of the step change in temperature, we conducted a separate experiment by embedding 50 cm of the cable together with a PT100 thermometer into an isolated hot water bath with a constant temperature of 43.8 °C. The result for the time response of the DTS system to reach 90% of the temperature change is shown in
Figure 3.
2.4. Numerical Modeling
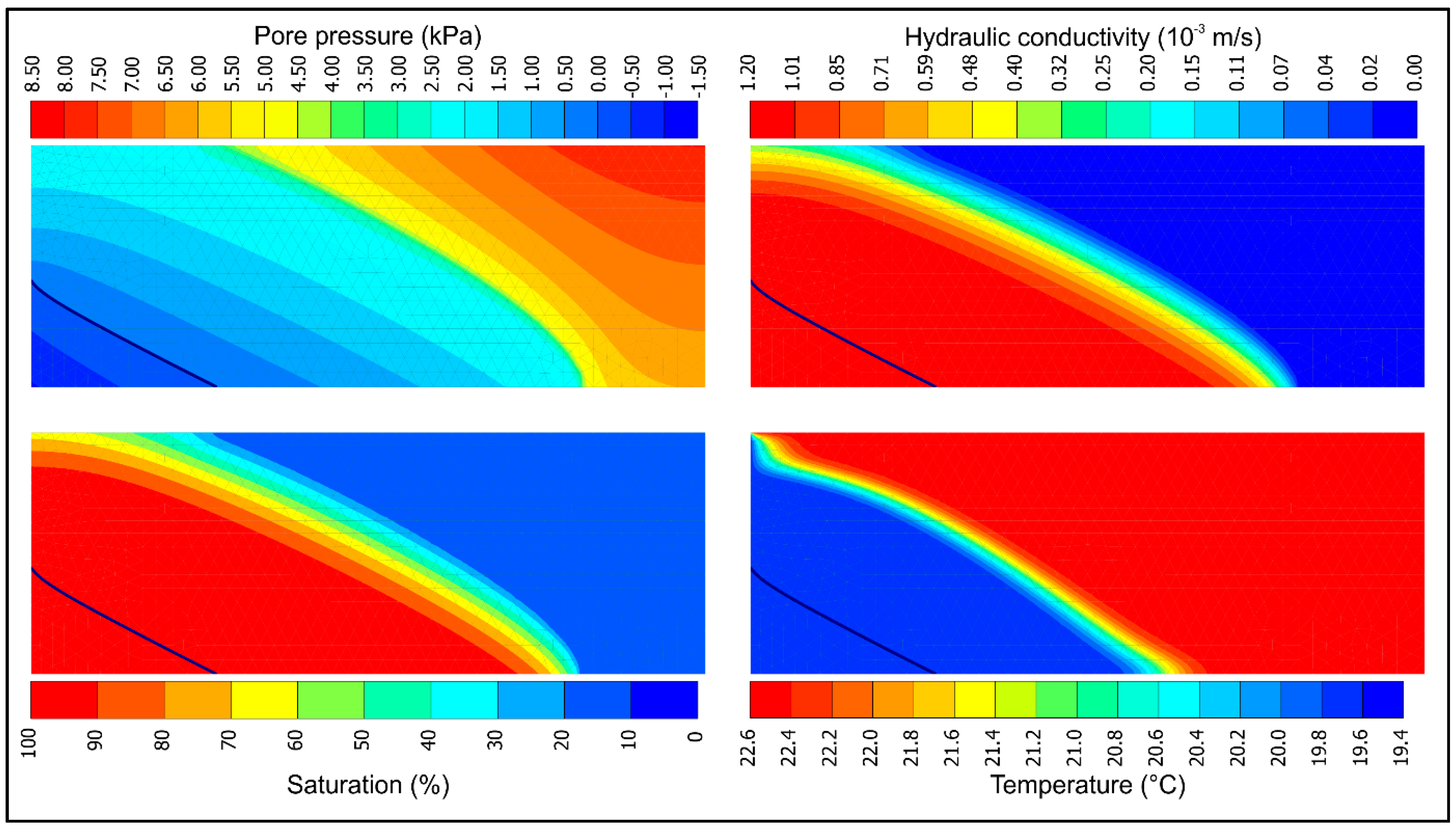
The numerical modeling of the seepage was performed in the geotechnical program PLAXIS 2D. PLAXIS 2D provides a continuous time-dependent analysis of groundwater and thermal flow in unsaturated media considering both conduction and convection in transient state. The soil is considered as homogeneous media and is not divided into different phases (local thermal equilibrium). The heat transfer due to vapor flow was neglected and heat transfer into the core of sand particles is not considered. Equations given in
Section 2.1 are used by the PLAXIS for thermal and seepage analysis. The van Genucthen model (with parameters in
Table 2) was used to describe the behavior of the sand at the unsaturated condition.
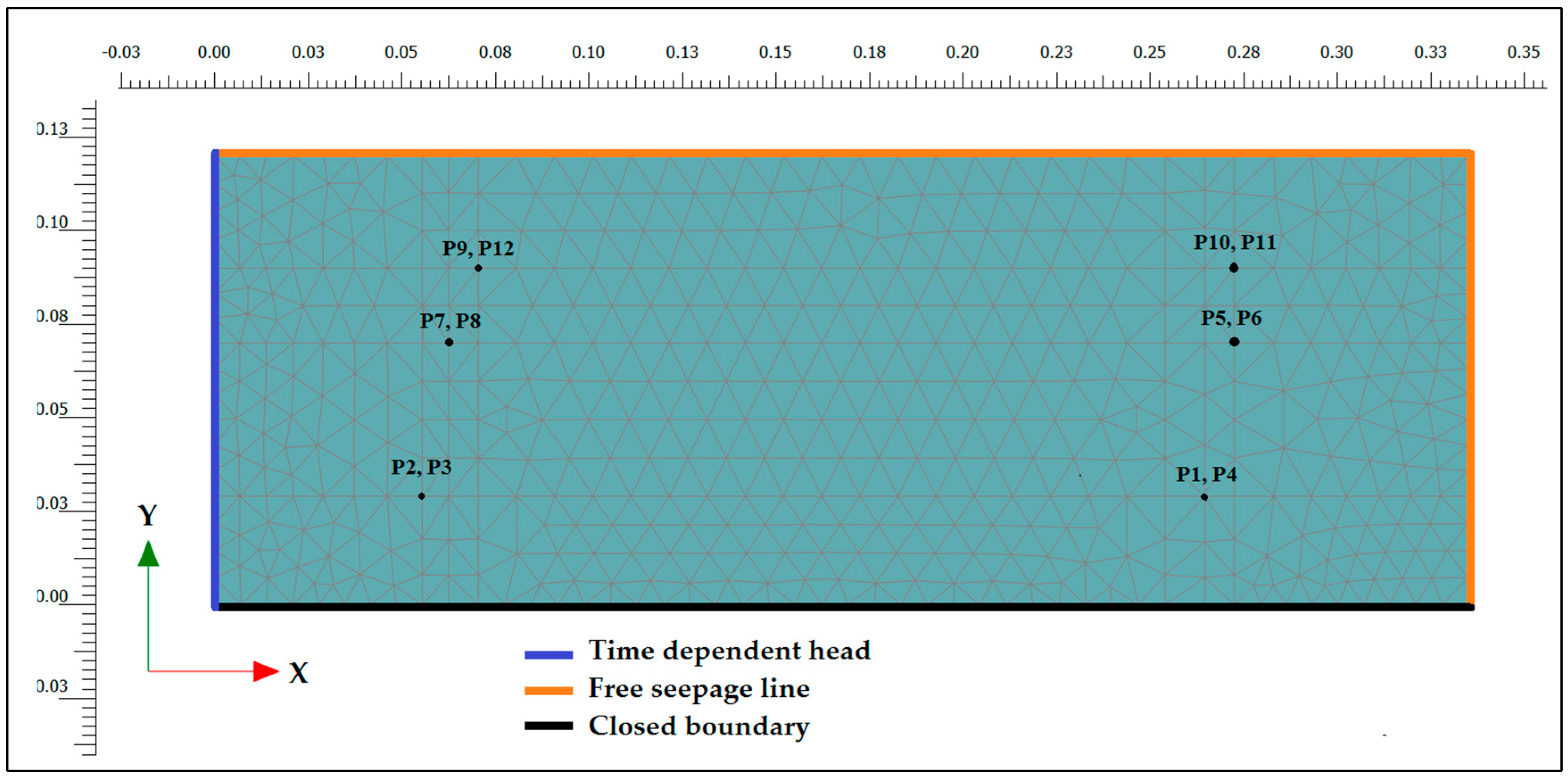
The numerical model was designed based on the material properties, the geometry of the experimental model, and the thermal and hydraulic boundary conditions of the experimental model. A coupled thermo-hydro analysis was performed using a two-dimensional (2D) numerical model consists of 913 15-nodes finite elements (
Figure 4). Initially, the soil temperature was the same as measured before the seepage started and the sand was at residual saturation. The boundary conditions of the model with respect to the flow are presented in
Figure 4. On the left, a time-dependent water head boundary has been assigned based on the experimental measurements (Figure 6). The top and right boundaries are seepage boundaries, which are closed boundaries until fully saturated when they start to allow outflow of water at pore pressure of 0 kPa (atmospheric pressure).
The boundary conditions in terms of temperature were defined as follows: at the upstream face, the Dirichlet boundary condition (see Equation (9)) was governed by the water temperature in the upstream tank, right and upper boundary had constant temperature equal to initial soil temperature, and at the bottom zero thermal flow was considered (see Neumann boundary condition, Equation (10)).
The first 30 min of the experimental model was simulated by the numerical model. The results of the calculations were saved every 30 s. The thermal conductivity, heat capacity, and hydraulic conductivity in each node were calculated continuously due to the change in saturation using Equations (4)–(8) based on the calculated pressure head by the PLAXIS 2D program.
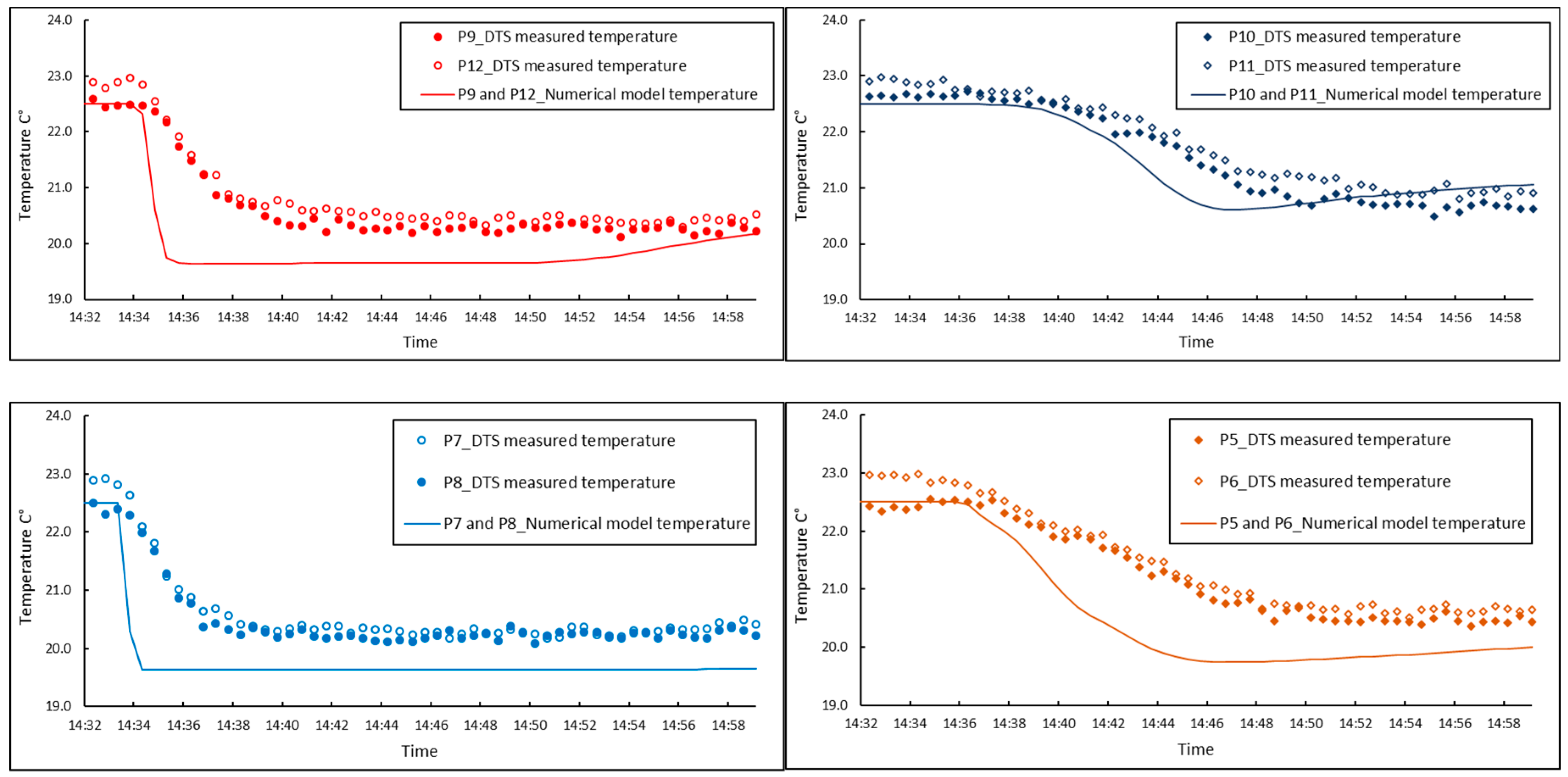
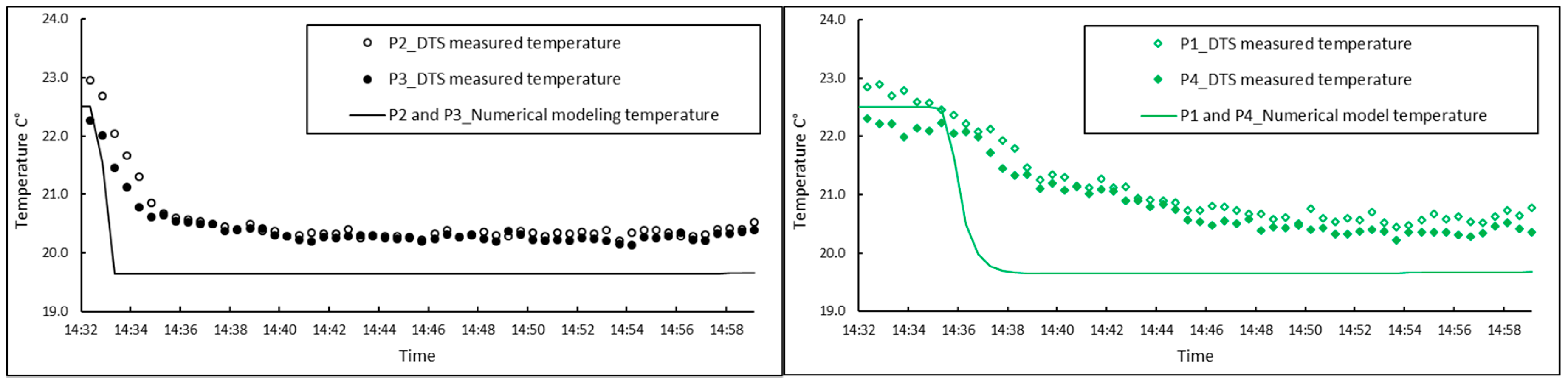
4. Discussion and Comparison
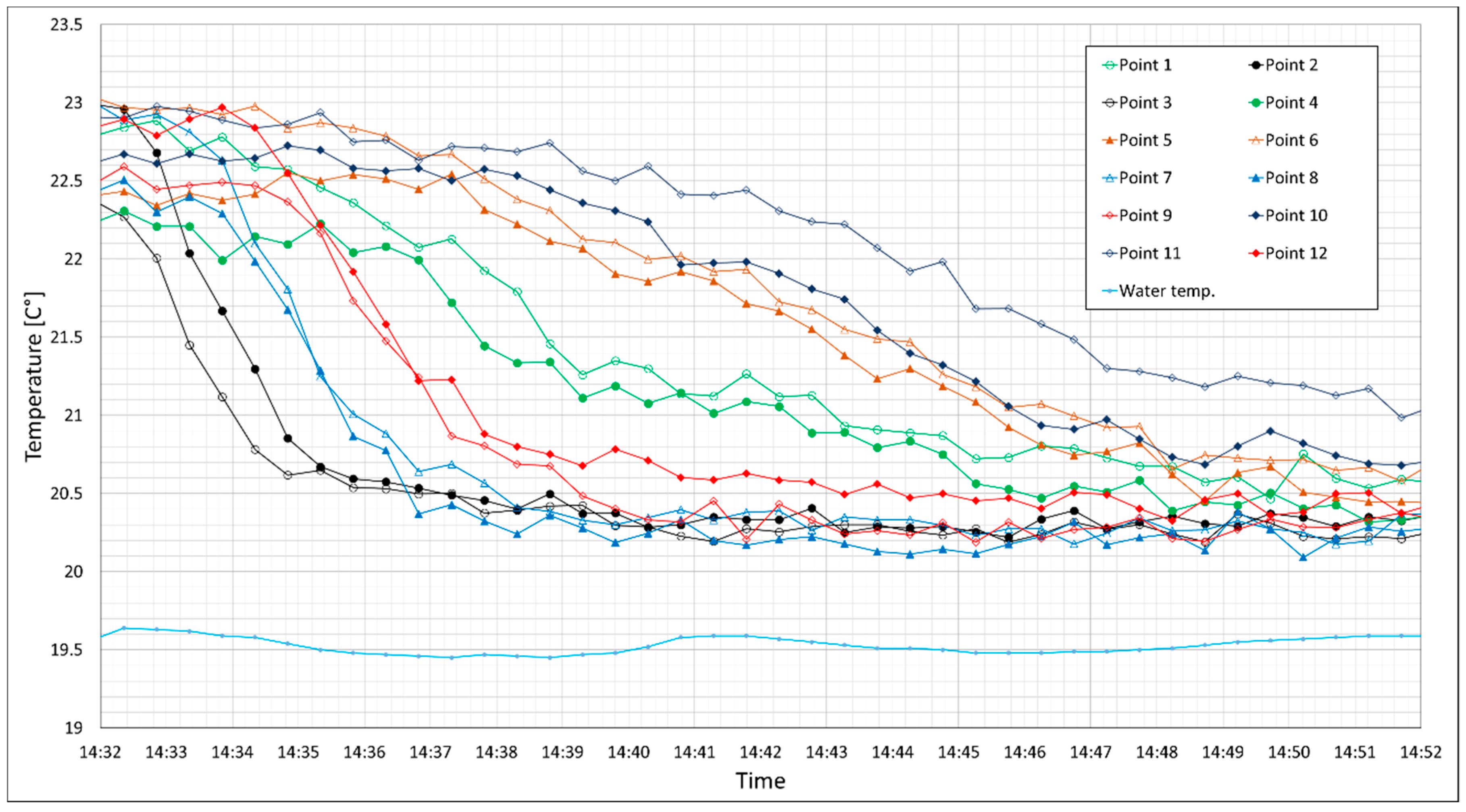
The temperature variations for 12 measuring points were compared to the results from numerical modeling (
Figure 10).
A short time gap can be observed between the temperature drop in the numerically modeled and measured temperatures. This is mostly due to the response time of the DTS system (about 60 s, see
Figure 3) to fast changes of temperature. This shows that the response time has a significant role in the heat measurement by the DTS system in a small-scale experimental model with fast seepage. However, for the long-term temperature monitoring in real size structures, this effect can be negligible. The response time of the DTS system also attributed to the gradual change in the measured temperature in the sand model. The temperature gradient is higher for the points that are in the upstream zone. This phenomenon will be described by looking at the results from the seepage flow velocity in
Figure 11. The temperature gap between the DTS measurements and numerical results (
Figure 10) can be partially described by the accuracy of the DTS measurement. The accuracy of point-mode measurements also depends on the size of the sensory ring (inner diameter of the ring) and the length of optical fiber in the sensory ring [
40]. Studies show that the ideal size and length of the sensory ring also depend on the type and external diameter of the optical fiber [
40,
41]. The inner diameter of the sensory ring should be kept in a range to measure specifically the one-year point and to avoid the adverse effects of optical fiber bending. A ring with a smaller diameter than the critical value can cause step losses in the optical fiber, which must be corrected with further manual calibration techniques [
42,
43].
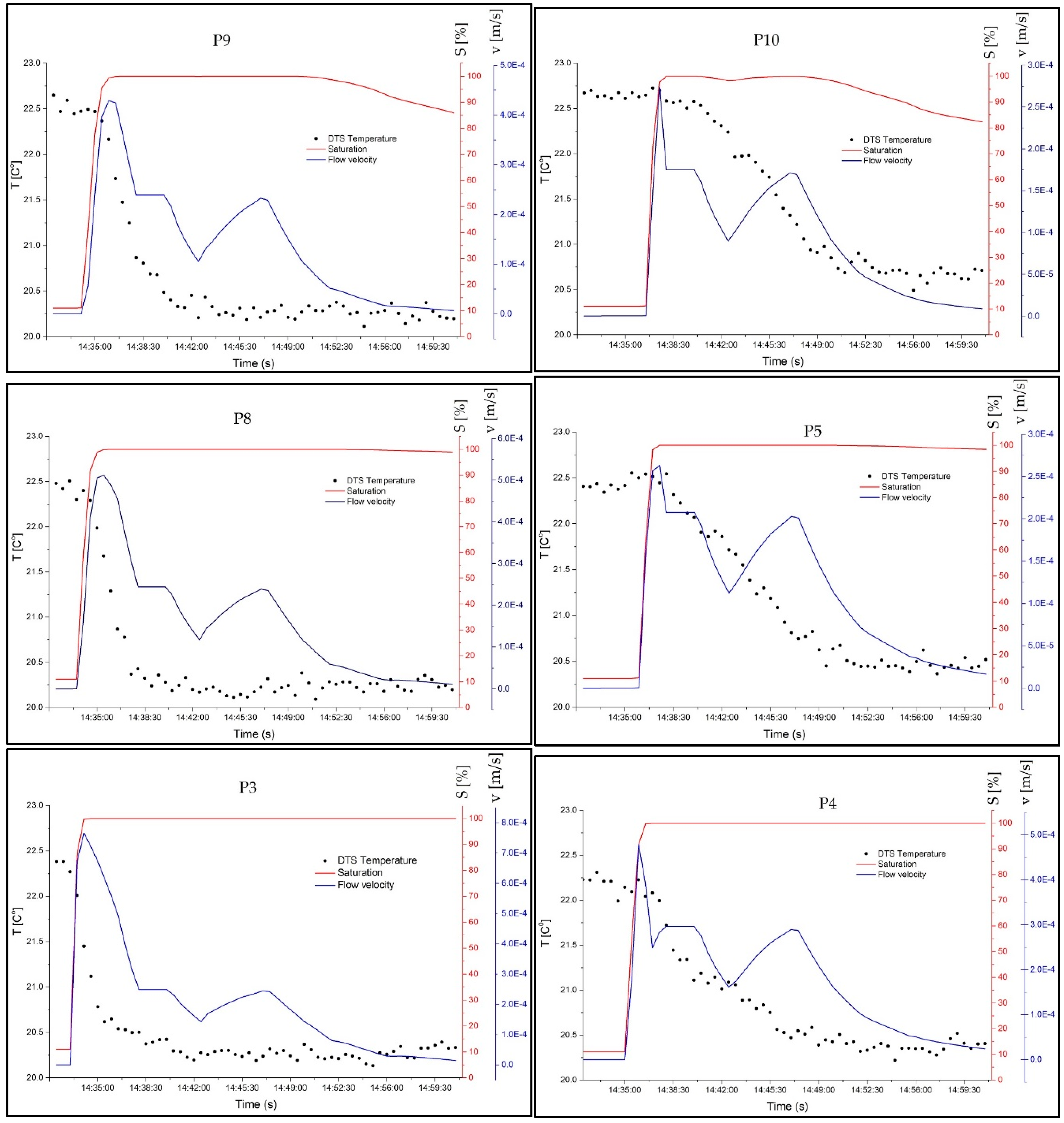
The other factor that was studied is the relationship between the degree of saturation and seepage flow velocity with the measured temperature by DTS.
Figure 11 presents the numerical results for the degree of saturation, the flow velocity, and the measured temperature variation during the experiment. The results demonstrated in
Figure 11 present the ability of temperature monitoring for detecting the seepage presence. With increasing the water content in the sand, the temperature is decreasing. The results show that saturation can be monitored in the early phases by temperature measurement. The temperature reduction is started by increasing the degree of saturation in the sand. The average seepage velocity may be estimated using the time gap between the start of temperature drop in various zones of the sand model. It is evident from the results in
Figure 11 that this time gap approximately represents the time between the seepage propagation in the selected measured points of the model.
The amount of heat transfer by the advection process directly depends on the average velocity of seepage, as can be seen in Equation (1). The results in
Figure 11 show the strong dependency of temperature variation on the magnitude of the flow velocity. For the points which are located at the upstream boundary, the seepage flow velocity is increased dramatically high. Due to this effect, the temperature values in these points are decreasing with a high gradient. On the other hand, for the points at the downstream side, the flow velocity is increased less and causes a gradual temperature variation. Higher flow velocity increases the gradient of temperature reduction graph in the sand and a low flow velocity causes a gradual temperature decreasing in the model.
The temperature changes occur by the increase in the degree of saturation. This is due to changes in the thermal conductivity of the porous media. However, when the seepage flow propagates into the sand, the temperature variation is due to the convection process, which is directly proportional to the flow velocity. In this case, the temperature is decreasing faster.
In this experiment, the water seepage observed to flow out of the sand model at 14:39:00. For Point 10, which is located at the upper layer of downstream, there is not any clear temperature reduction at this time. It means that seepage detection by visual observation was faster than the temperature monitoring in Point 10 for this experimental model. For real scale structures, it is economic to perform a seepage analysis and install the optical fiber based on the magnitude of leakage risk. This will decrease the monitoring system cost and increase the ability of the system for early seepage detection.