Solving Transient Groundwater Inverse Problems Using Space–Time Collocation Trefftz Method
Abstract
:1. Introduction
2. The Methodology
2.1. The Governing Equation
2.2. The Space–Time Collocation Trefftz Method
2.2.1. Space–Time Trefftz Functions
2.2.2. The Space–Time Collocation Scheme
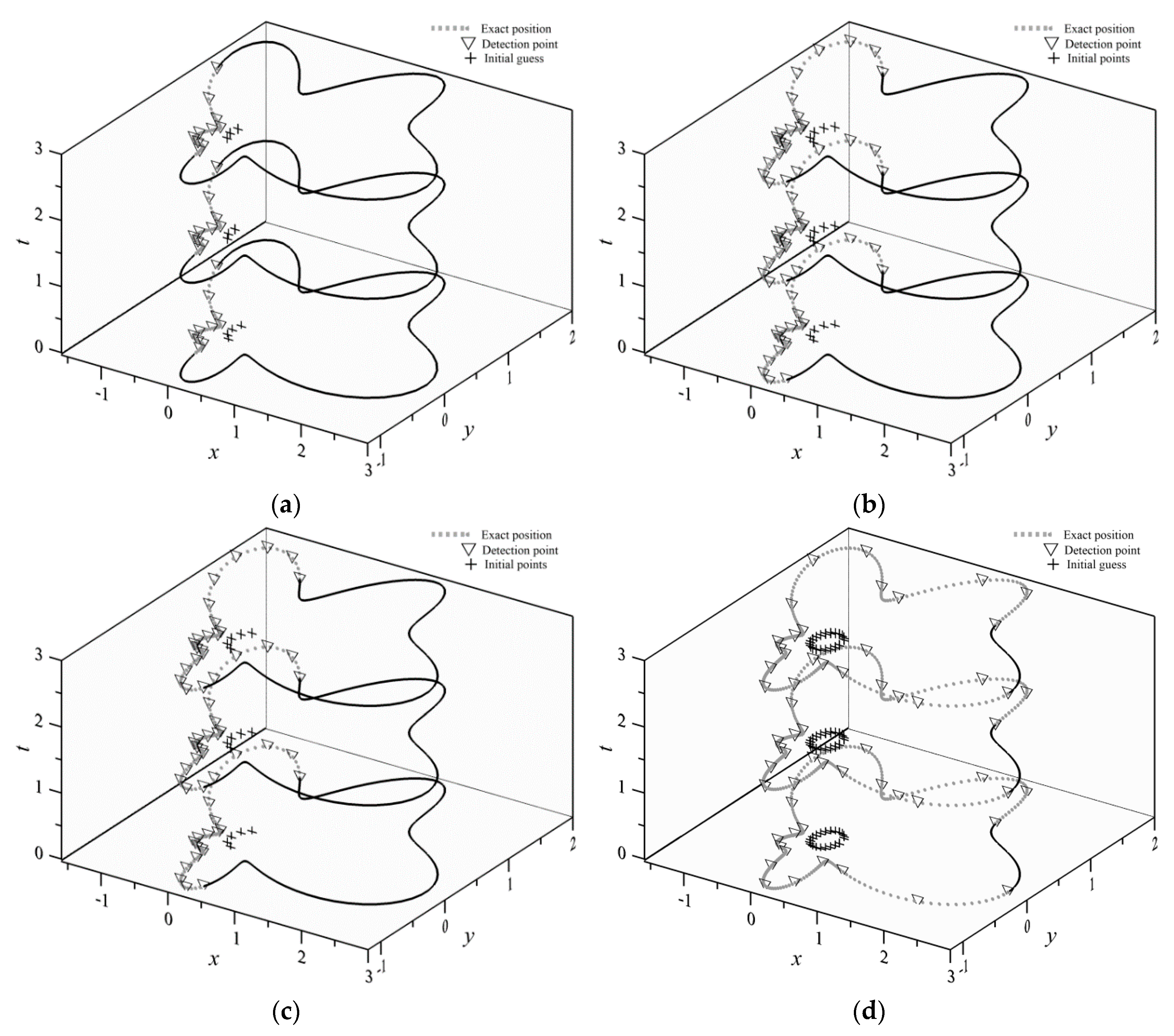
2.2.3. The Iterative Scheme for Modeling Boundary Detection Problem
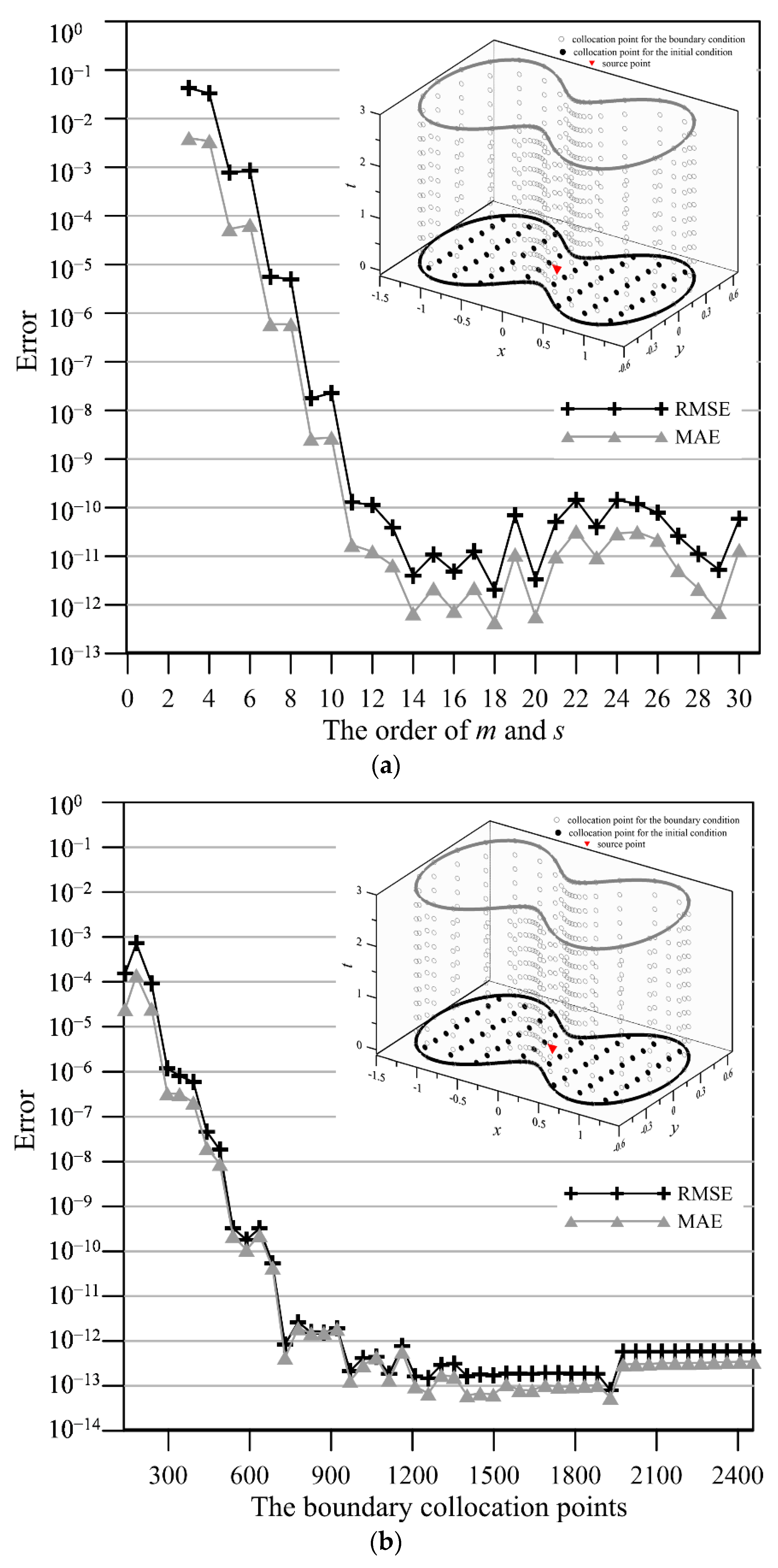
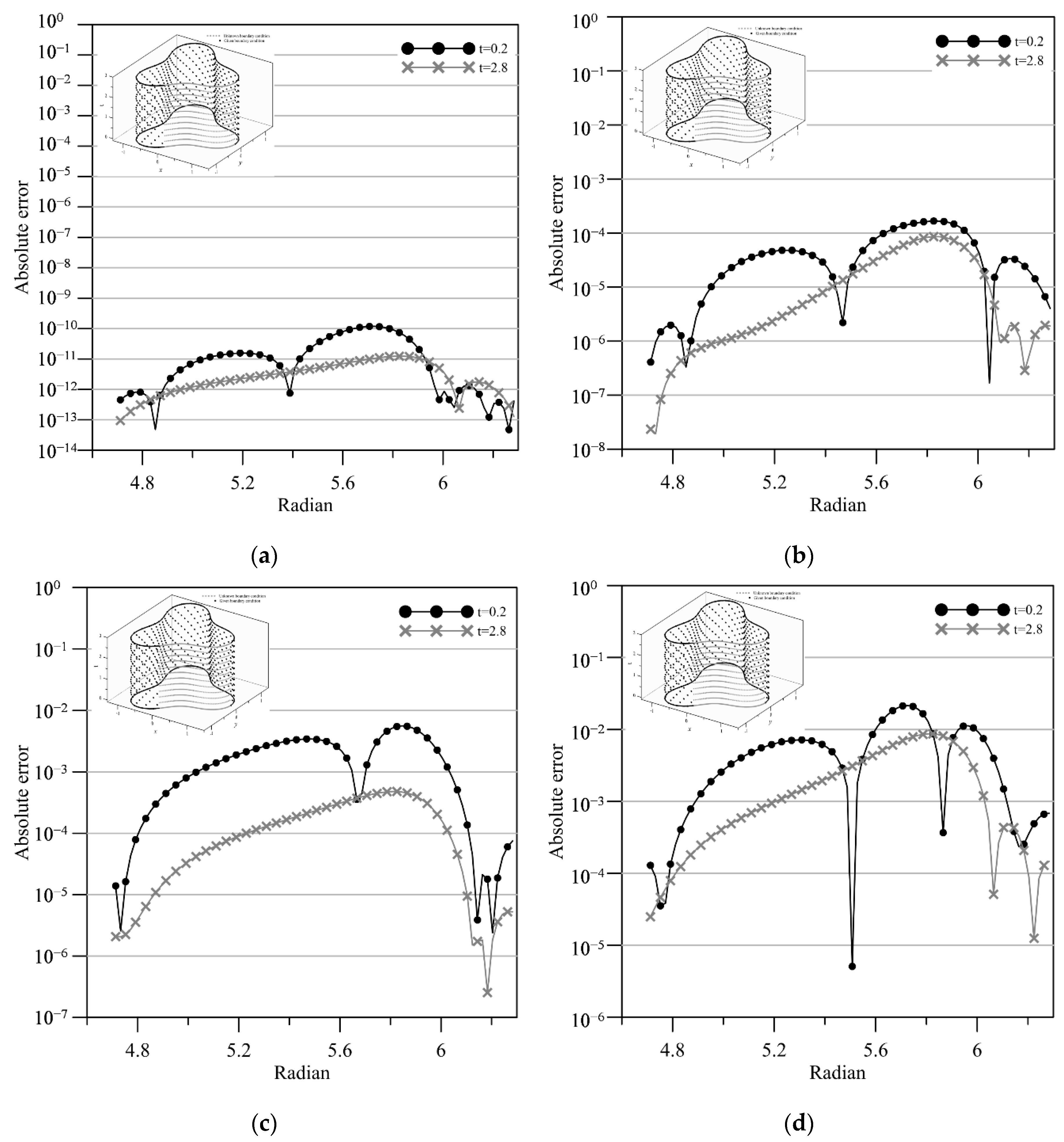
3. Accuracy and Convergence Analysis
4. Numerical Examples
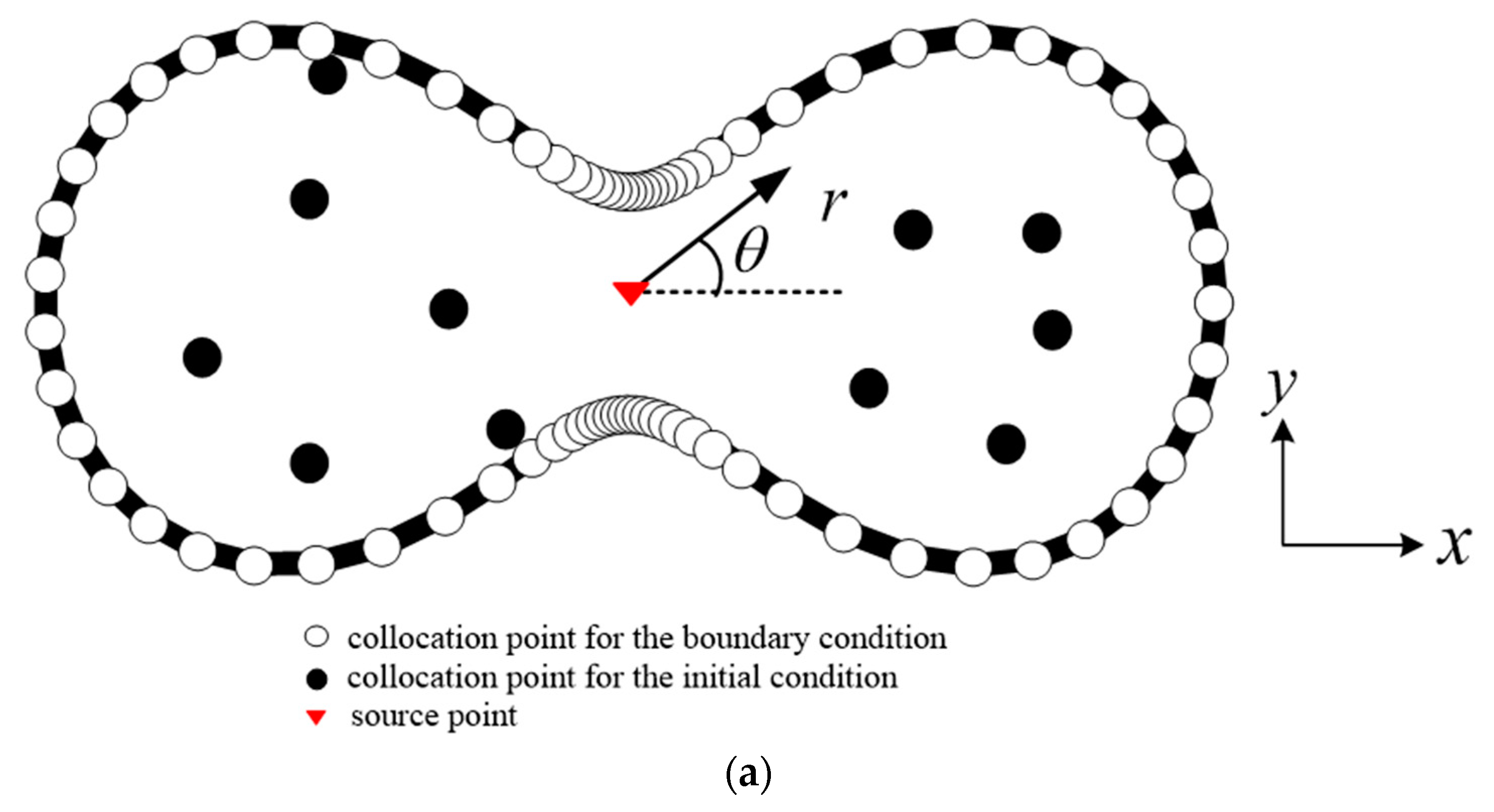
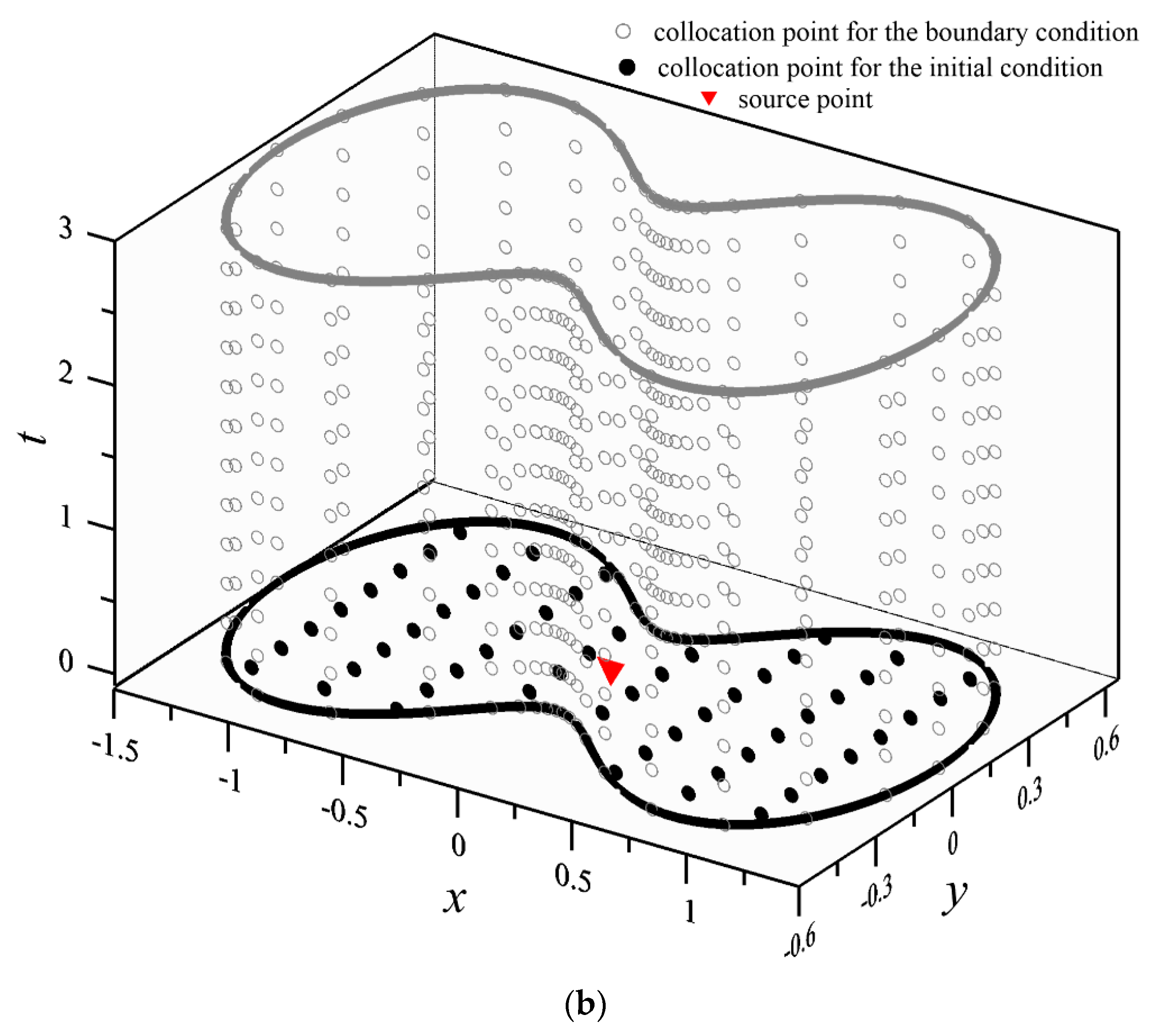
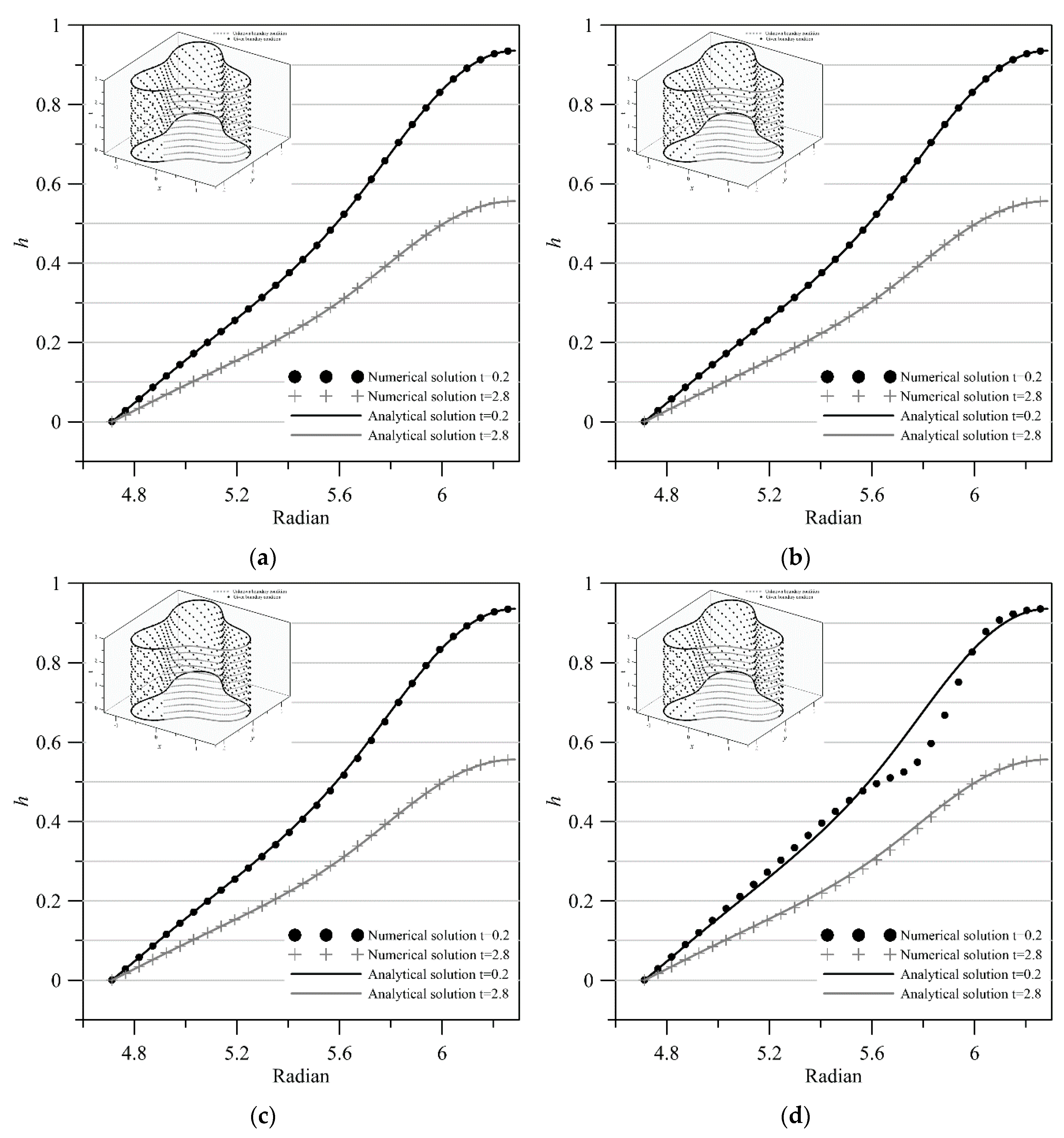
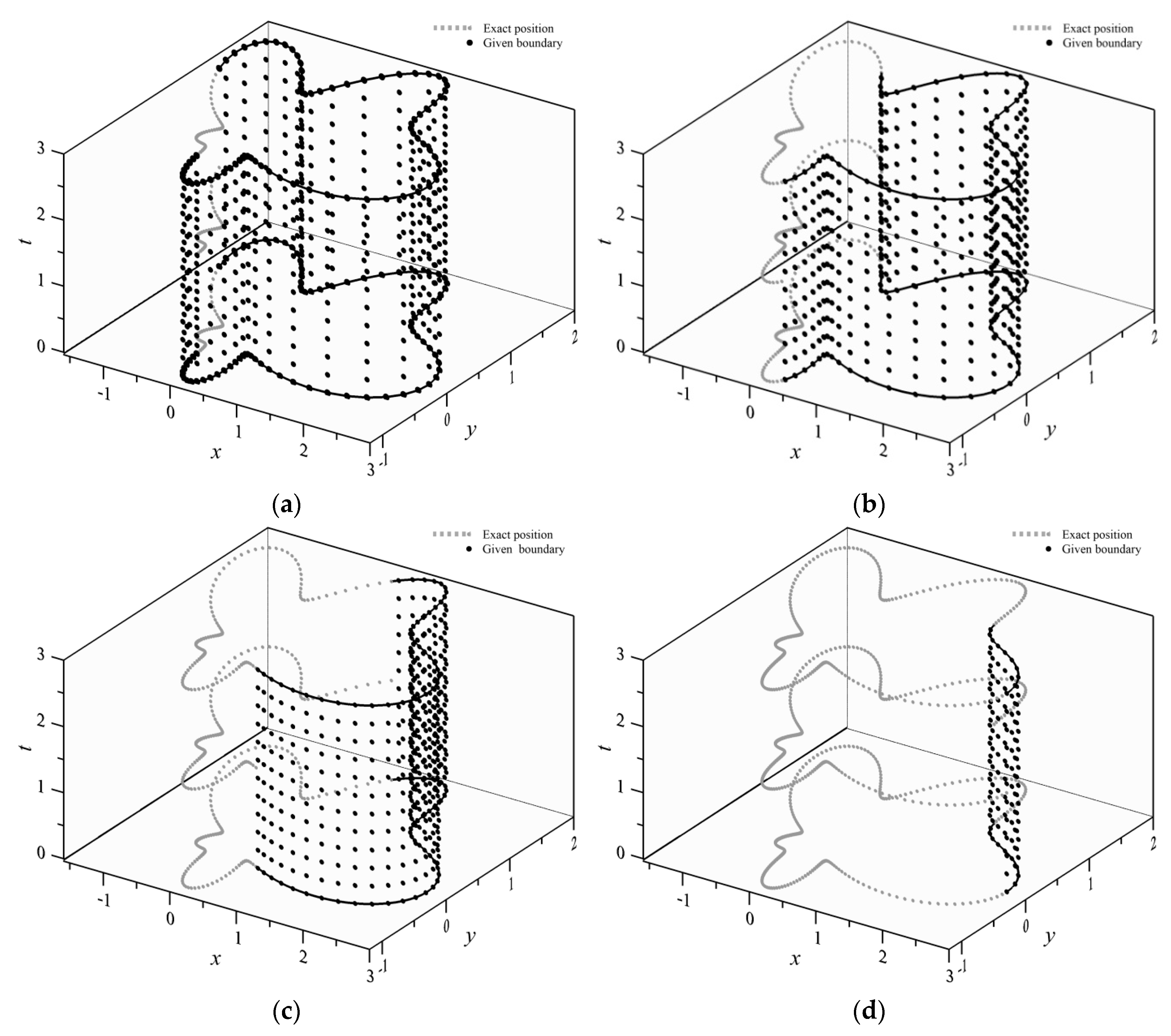
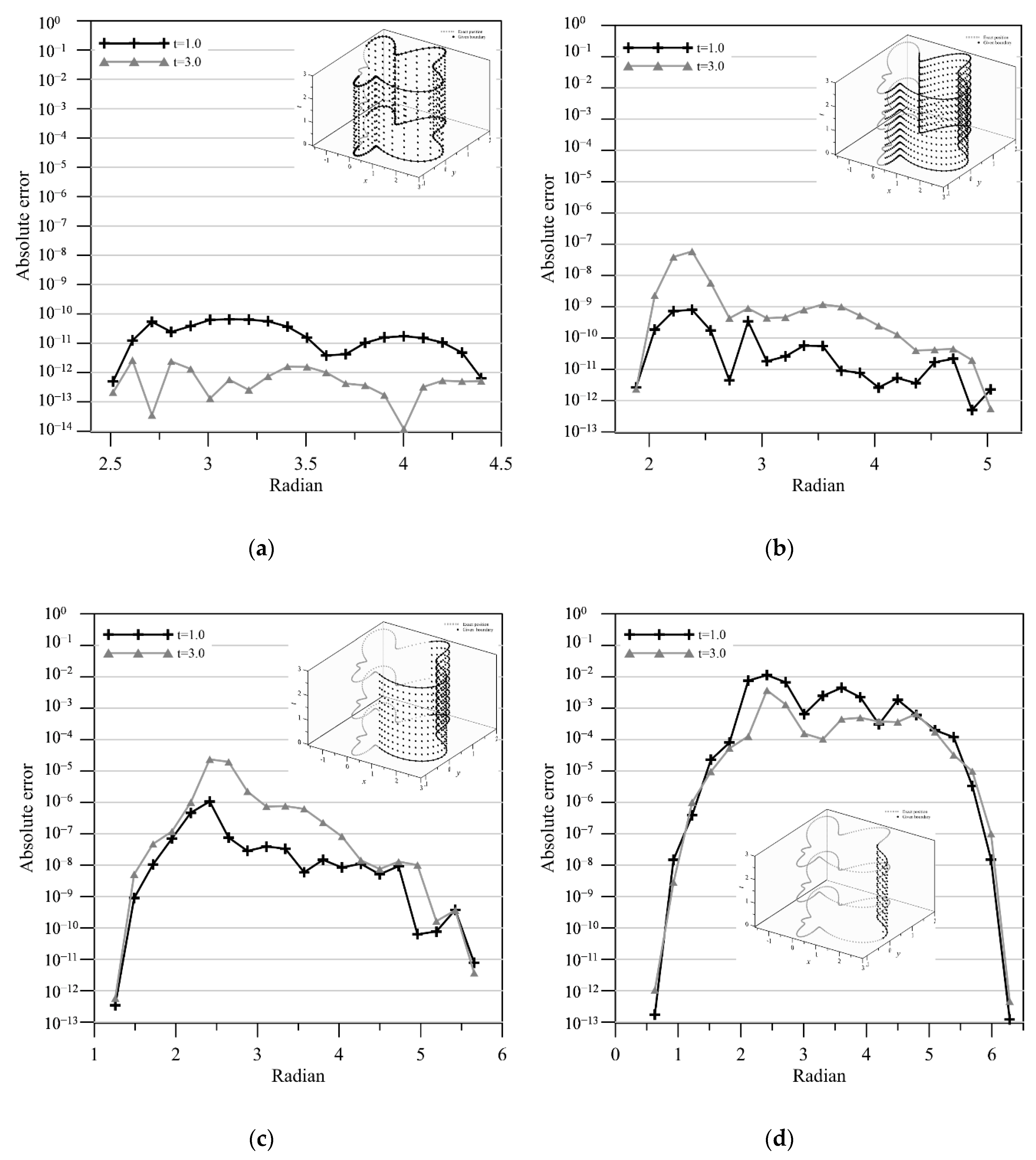
4.1. An Inverse Transient Groundwater Problem—A Cassini-like Boundary
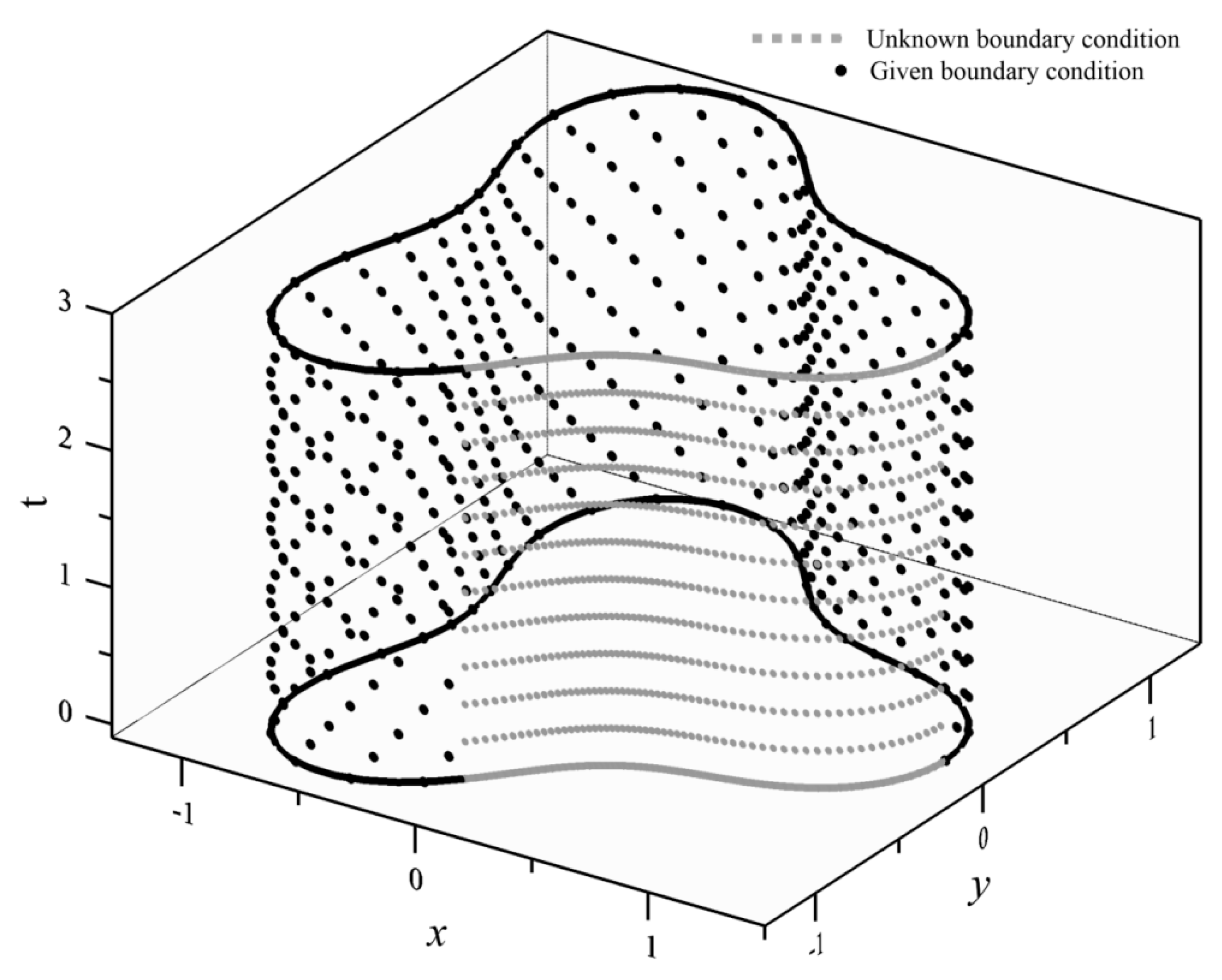
4.2. A Boundary Detection Problem—An Amoeba-like Boundary
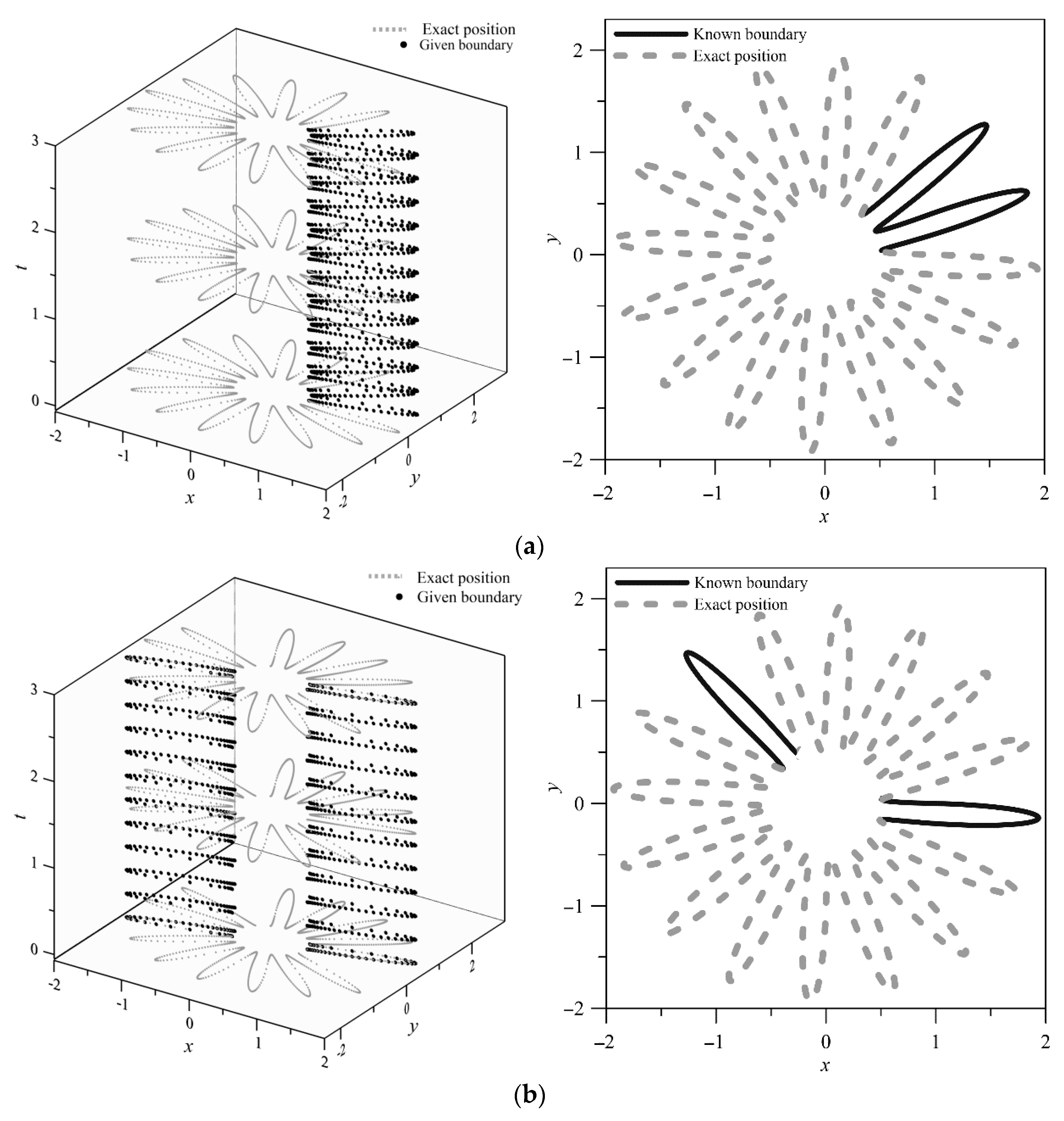
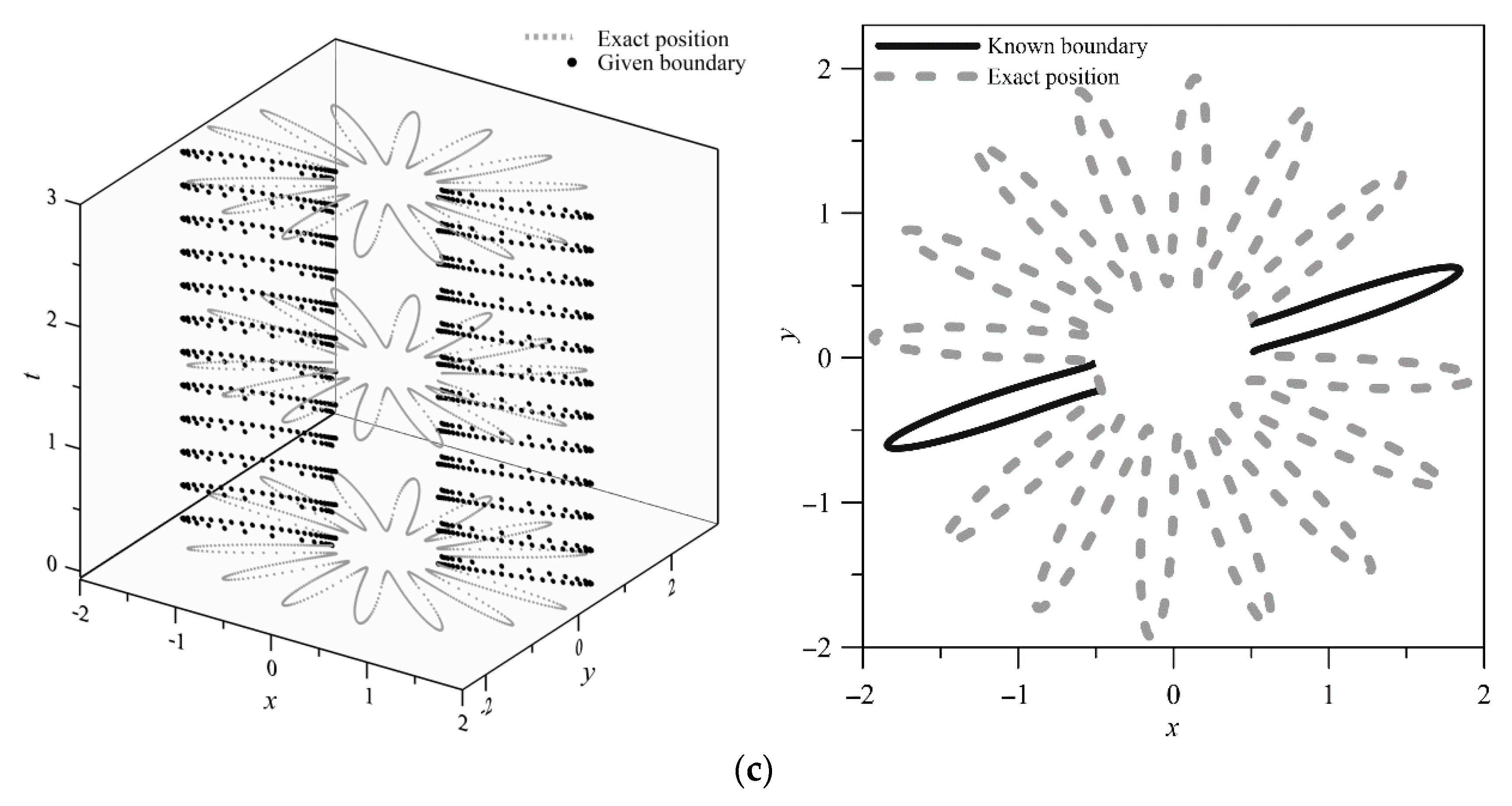
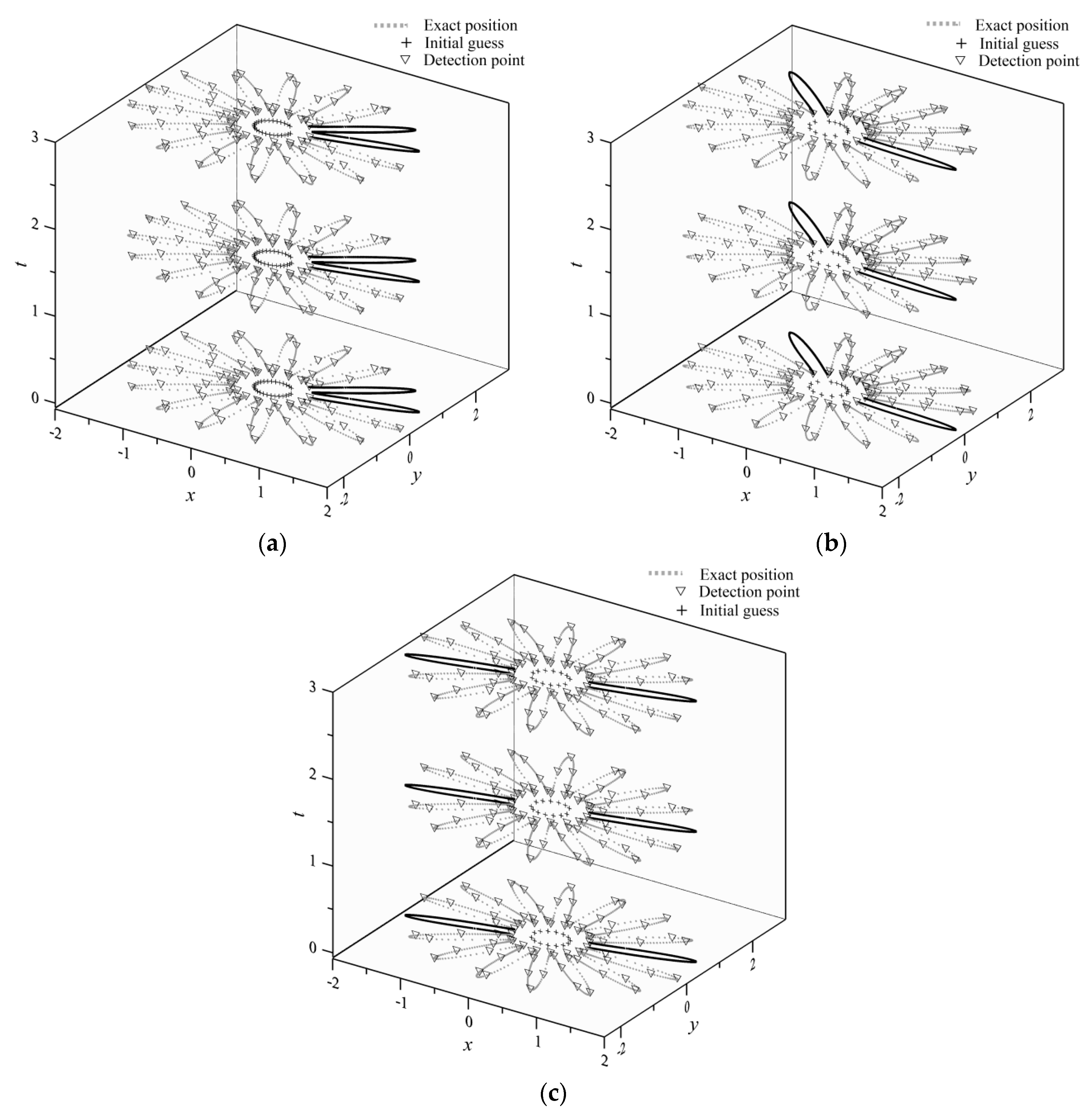
4.3. A Boundary Detection Problem—A Flower-like Boundary
5. Conclusions
- (1)
- For modeling of the two-dimensional transient groundwater inverse problems, an innovative concept, that the collocation points are placed on the space–time boundaries, is presented. Both the initial and boundary data are regarded as boundary conditions on the space–time boundary. Using the space–time collocation, the initial value problem (IVP) for solving the transient groundwater equation is considered to be a problem of the inverse boundary value where the time marching for the IVP can be avoided.
- (2)
- Previous studies depict that the Trefftz method is limited to linear and stationary problems. This study demonstrates that we solved transient groundwater inverse problems using the space–time meshfree method utilizing Trefftz functions with very high accuracy. The iterative scheme of the FTIM is utilized to deal with the system of nonlinear algebraic equations, which is resulted from spatial discretization of the space–time collocation Trefftz method. The advantages of the proposed meshfree method for solving inverse problems are also presented. Accurate approximations are yielded in which inaccessible boundary may be recovered, even 7/8 portion of the overall space–time boundaries are inaccessible.
- (3)
- The approximations of the transient groundwater boundary detection problem in two dimensions were developed. The geometric shape of inaccessible parts of the domain remains unknown and is obtained by solving the nonlinear equation formulated from the Trefftz functions and the coefficients. The fictitious time integration method was successfully applied for the solution of the nonlinearity. Highly accurate results for the two-dimensional transient groundwater boundary detection problem were obtained using the proposed space–time meshfree method.
Author Contributions
Funding
Conflicts of Interest
References
- Azaiez, M.; Ben Abda, A.; Ben Abdallah, J. Revisiting the Dirichlet-to-Neumann solver for data completion and application to some inverse problems. Math. Mech. 2005, 1, 106–121. [Google Scholar]
- Ling, L.; Takeuchi, T. Boundary control for inverse Cauchy problems of the Laplace equations. CMES-Comp. Model. Eng. Sci. 2008, 29, 45–54. [Google Scholar]
- Thomas, A.; Majumdar, P.; Eldho, T.I.; Rastogi, A.K. Simulation optimization model for aquifer parameter estimation using coupled meshfree point collocation method and cat swarm optimization. Eng. Anal. Bound. Elem. 2018, 91, 60–72. [Google Scholar] [CrossRef]
- Fan, C.M.; Chan, H.-F.; Kuo, C.-L.; Yeih, W. Numerical solutions of boundary detection problems using modified collocation Trefftz method and exponentially convergent scalar homotopy algorithm. Eng. Anal. Bound. Elem. 2012, 36, 2–8. [Google Scholar] [CrossRef]
- Irsa, J.; Zhang, Y. A direct method of parameter estimation for steady state flow in heterogeneous aquifers with unknown boundary conditions. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Ku, C.Y.; Liu, C.-Y.; Xiao, J.-E.; Yeih, W.; Fan, C.-M. A spacetime meshless method for modeling subsurface flow with a transient moving boundary. Water 2019, 11, 2595. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Fan, C.M.; Hua, Q.; Gu, Y. Localized MFS for the inverse Cauchy problems of two-dimensional Laplace and biharmonic equations. Appl. Math. Comput. 2020, 364, 124658. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.; Wu, W.; Wang, H.; Wang, Y. A novel localized collocation solver based on Trefftz basis for potential-based inverse electromyography. Appl. Math. Comput. 2020, 390, 125604. [Google Scholar] [CrossRef]
- Ku, C.Y.; Xiao, J.E.; Huang, W.P.; Yeih, W.; Lui, C.-Y. On solving two-dimensional inverse heat conduction problems using the multiple source meshless method. Appl. Sci. 2019, 9, 2629. [Google Scholar] [CrossRef] [Green Version]
- Li, P.W. Space–time generalized finite difference nonlinear model for solving unsteady Burgers’ equations. Appl. Math. Lett. 2020, 114, 106896. [Google Scholar] [CrossRef]
- Solyaev, Y.O.; Lurie, S.A. Trefftz collocation method for two-dimensional strain gradient elasticity. Int. J. Numer. Methods Eng. 2020. [Google Scholar] [CrossRef]
- Zhao, W.; Hon, Y.C.; Stoll, M. Numerical simulations of nonlocal phase-field and hyperbolic nonlocal phase-field models via localized radial basis functions-based pseudo-spectral method (LRBF-PSM). Appl. Math. Comput. 2018, 337, 514–534. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X. Variational multiscale interpolating element-free Galerkin method for the nonlinear Darcy–Forchheimer model. Comput. Math. Appl. 2020, 79, 363–377. [Google Scholar] [CrossRef]
- Huybrechs, D.; Olteanu, A.E. An oversampled collocation approach of the wave based method for Helmholtz problems. Wave Motion. 2019, 87, 92–105. [Google Scholar] [CrossRef] [Green Version]
- Kołodziej, J.A.; Grabski, J.K. Many names of the Trefftz method. Eng. Anal. Bound. Elem. 2018, 96, 169–178. [Google Scholar] [CrossRef]
- Piltner, R. Some remarks on Trefftz type approximations. Eng. Anal. Bound. Elem. 2019, 101, 102–112. [Google Scholar] [CrossRef]
- Fu, Z.J.; Yang, L.W.; Zhu, H.Q.; Xu, W.Z. A semi-analytical collocation Trefftz scheme for solving multi-term time fractional diffusion-wave equations. Eng. Anal. Bound. Elem. 2019, 98, 137–146. [Google Scholar] [CrossRef]
- Trefftz, E. Ein gegenstück zum ritzschen verfahren. In Proceedings of the 2nd International Congress for Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 131–137. [Google Scholar]
- Li, Z.C.; Lu, Z.Z.; Hu, H.Y.; Cheng, H.D. Trefftz and Collocation Methods; WIT Press: Southampton, UK, 2008. [Google Scholar]
- Liu, Y.C.; Fan, C.M.; Yeih, W.; Ku, C.-Y.; Chu, C.-L. Numerical solutions of two-dimensional Laplace and biharmonic equations by the localized Trefftz method. Eng. Anal. Bound. Elem. 2020. [Google Scholar] [CrossRef]
- Borkowski, M.; Moldovan, I.D. On rank-deficiency in direct Trefftz method for 2D Laplace problems. Eng. Anal. Bound. Elem. 2019, 106, 102–115. [Google Scholar] [CrossRef]
- Liu, C.S.; Atluri, S.N. A fictitious time integration method (FTIM) for solving mixed complementarity problems with applications to non-linear optimization. CMES-Comp. Model. Eng. Sci. 2008, 34, 155–178. [Google Scholar]
- Ku, C.Y.; Yeih, W.; Liu, C.S.; Chi, C.C. Applications of the fictitious time integration method using a new time-like function. CMES 2009, 43, 173. [Google Scholar]
| Noise Level | |||||
|---|---|---|---|---|---|
| MAE | |||||
| RMSE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ku, C.-Y.; Hong, L.-D.; Liu, C.-Y. Solving Transient Groundwater Inverse Problems Using Space–Time Collocation Trefftz Method. Water 2020, 12, 3580. https://doi.org/10.3390/w12123580
Ku C-Y, Hong L-D, Liu C-Y. Solving Transient Groundwater Inverse Problems Using Space–Time Collocation Trefftz Method. Water. 2020; 12(12):3580. https://doi.org/10.3390/w12123580
Chicago/Turabian StyleKu, Cheng-Yu, Li-Dan Hong, and Chih-Yu Liu. 2020. "Solving Transient Groundwater Inverse Problems Using Space–Time Collocation Trefftz Method" Water 12, no. 12: 3580. https://doi.org/10.3390/w12123580
APA StyleKu, C.-Y., Hong, L.-D., & Liu, C.-Y. (2020). Solving Transient Groundwater Inverse Problems Using Space–Time Collocation Trefftz Method. Water, 12(12), 3580. https://doi.org/10.3390/w12123580







