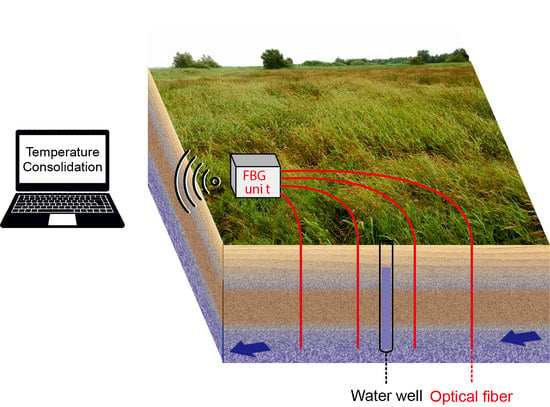
Temperature and Consolidation Sensing Near Drinking Water Wells Using Fiber Bragg Grating Sensors
Abstract
1. Introduction
2. Materials and Methods
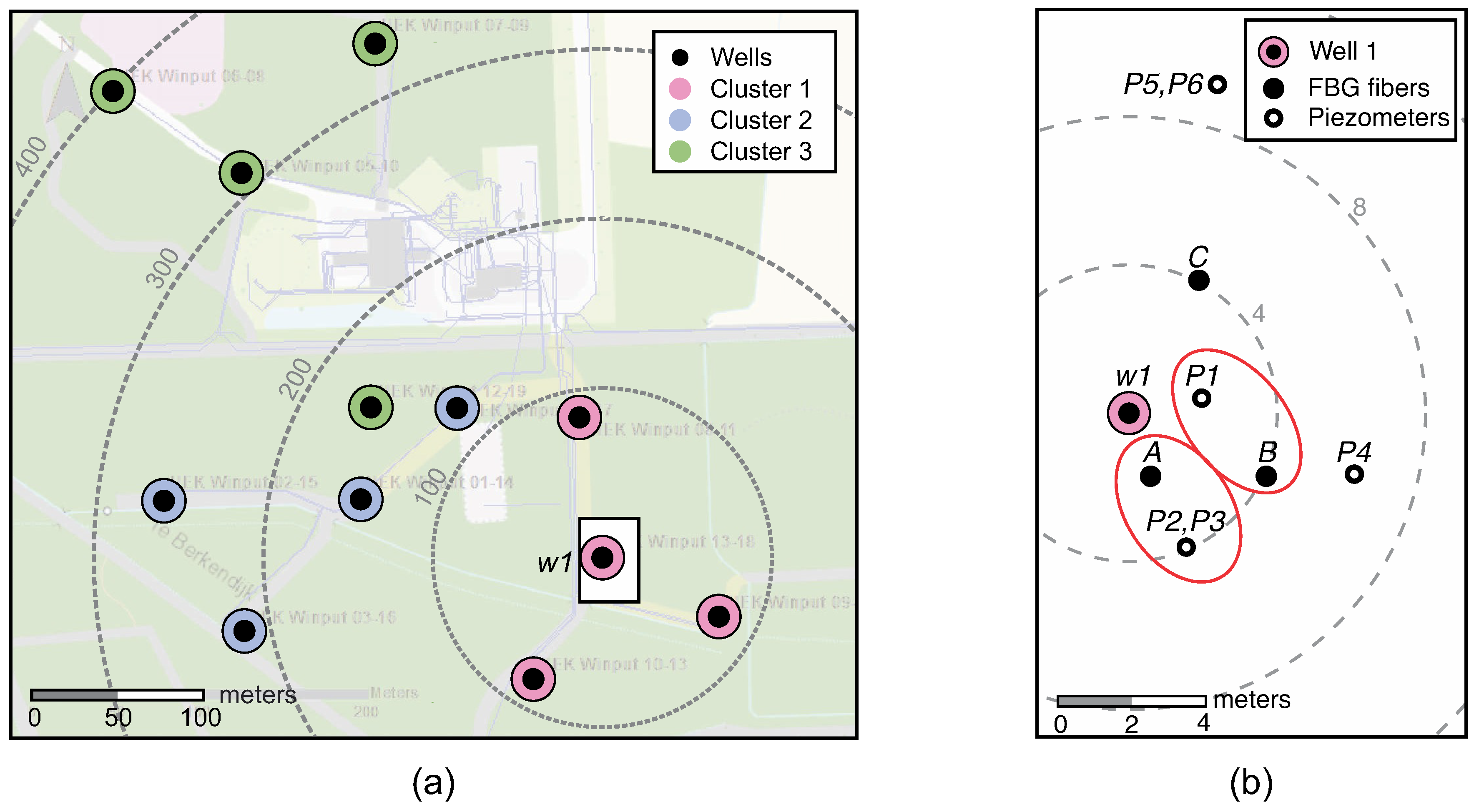
2.1. Experimental Site and Sensor Installation
- FBG sensors: consolidation and temperature
- reference divers: pressure and temperature
- weather station: atmospheric pressure
- flowmeter: horizontal flowrate in well
- status of 12 wells: on/off
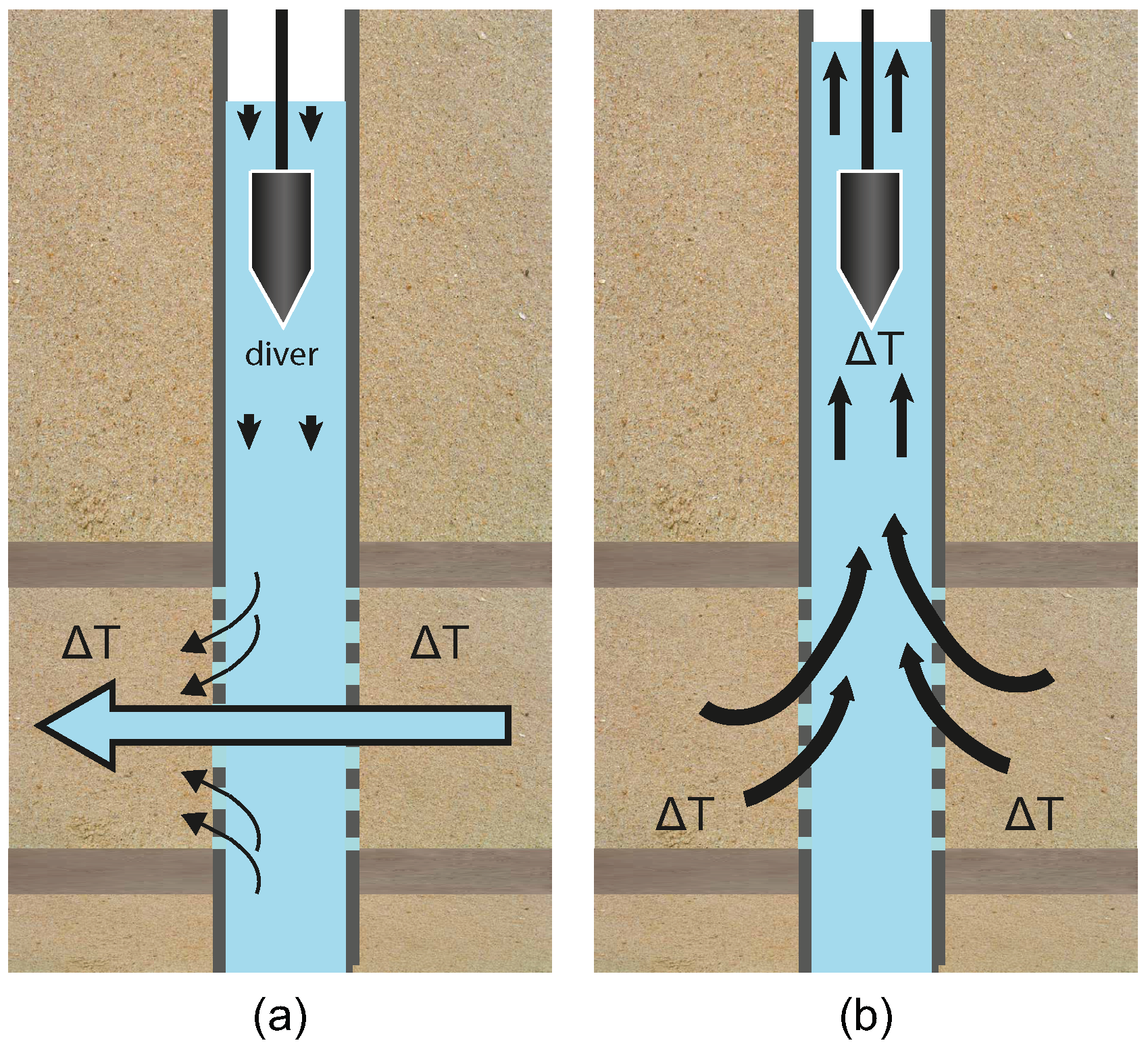
2.2. Pressure Sensing
2.3. Consolidation Models and Temperature Sensing
- —time shifted output values
- —time shifted input values
- —error term
- —model coefficients
- —backward time shift in the output
- —backward time shift in the input
- —number of input samples that occur before the input affects the output, also called the dead time in the system.
- and
- .
3. Results and Discussion
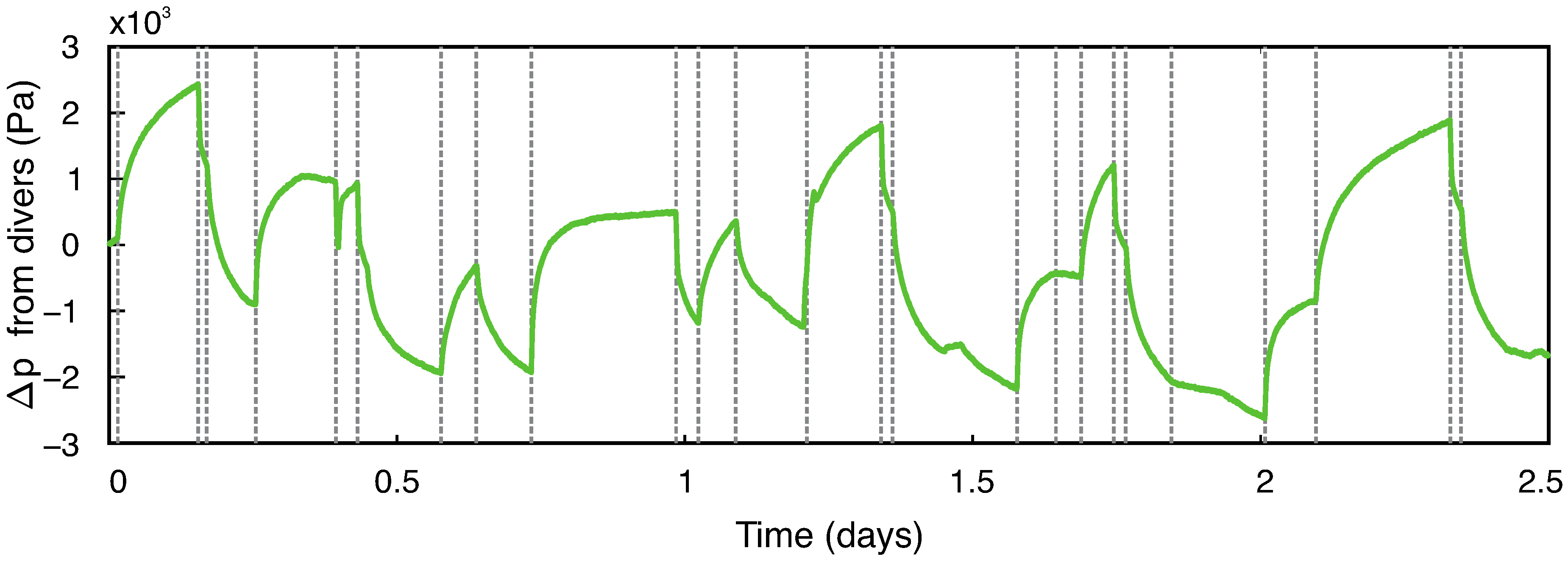
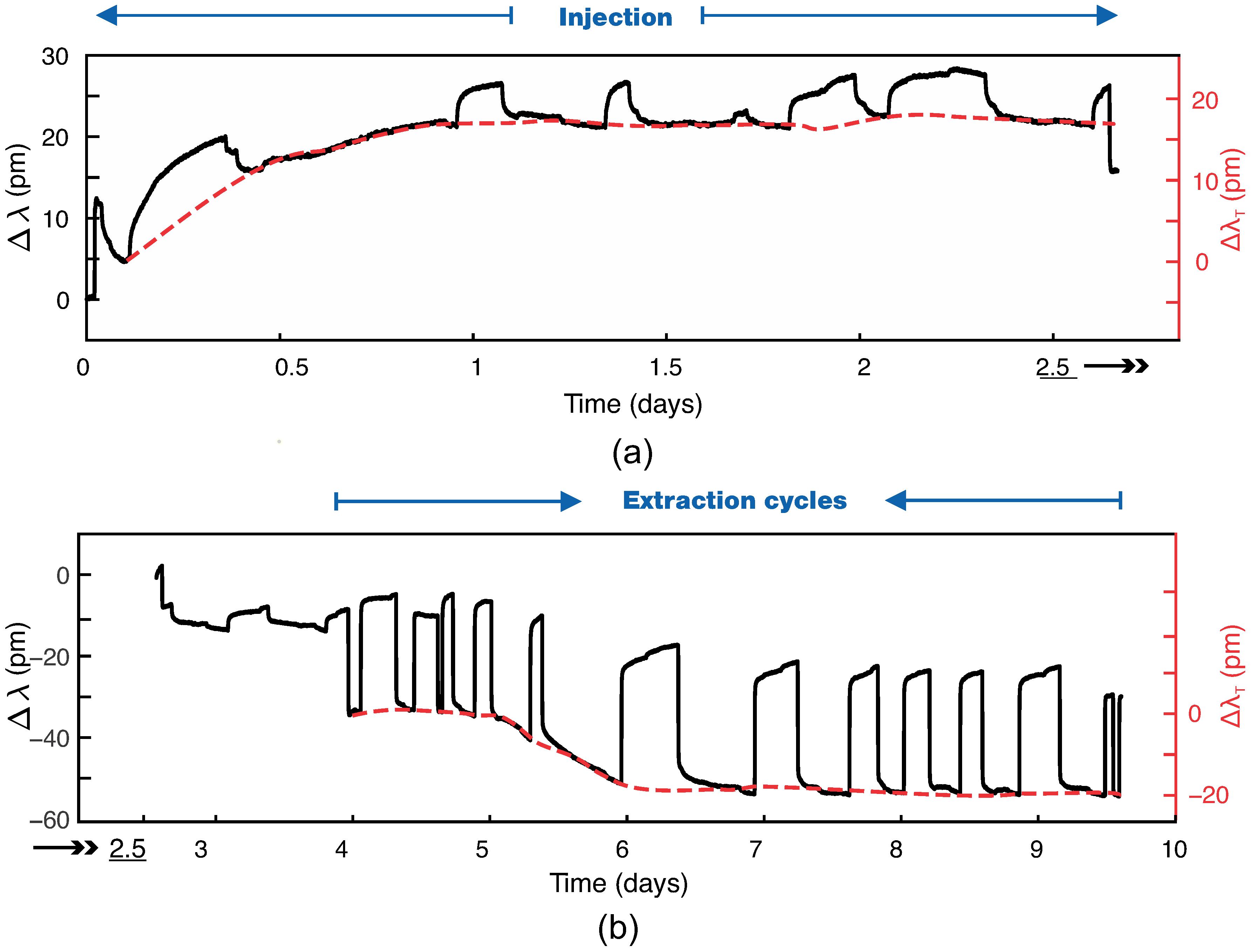
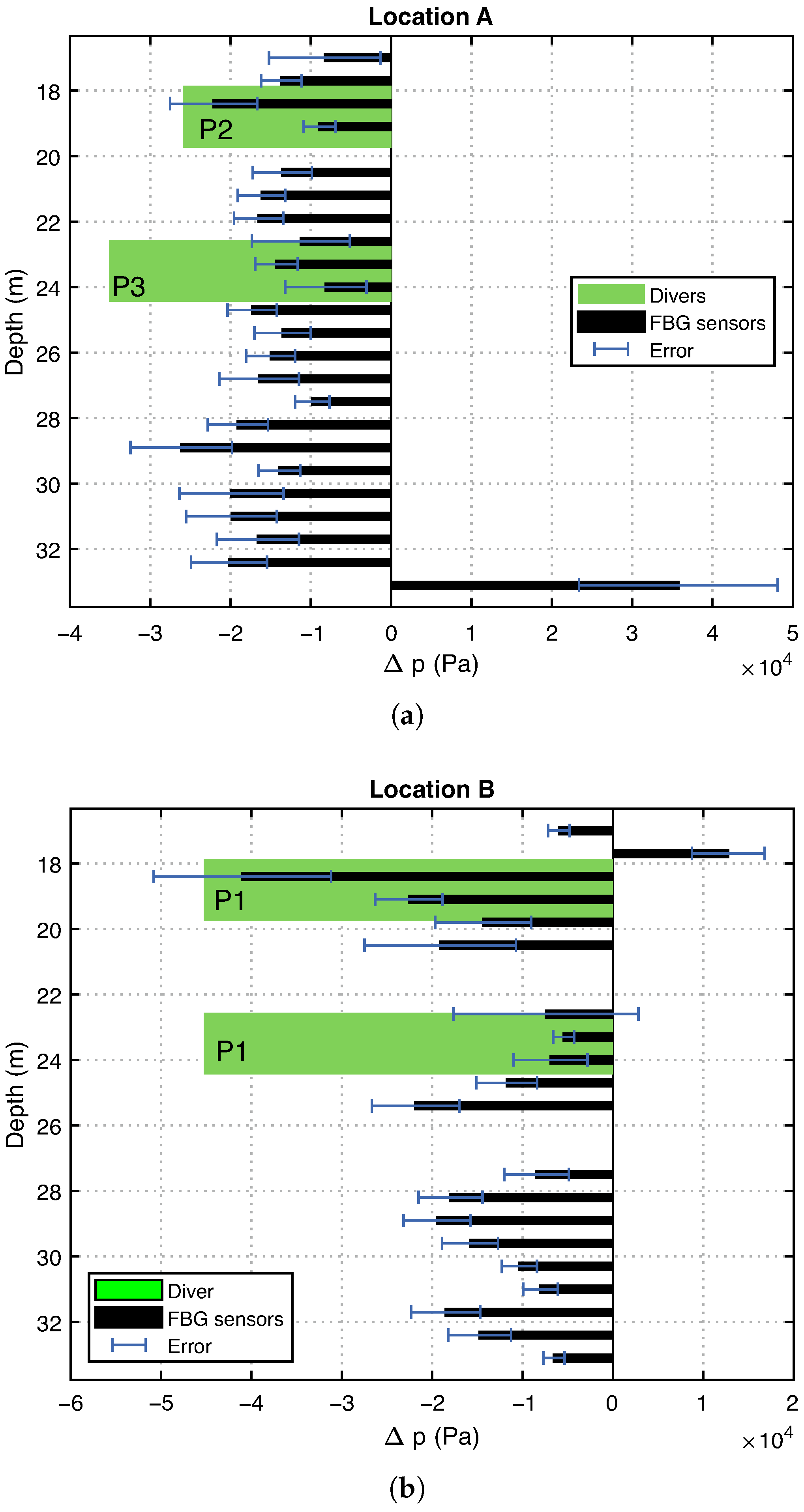
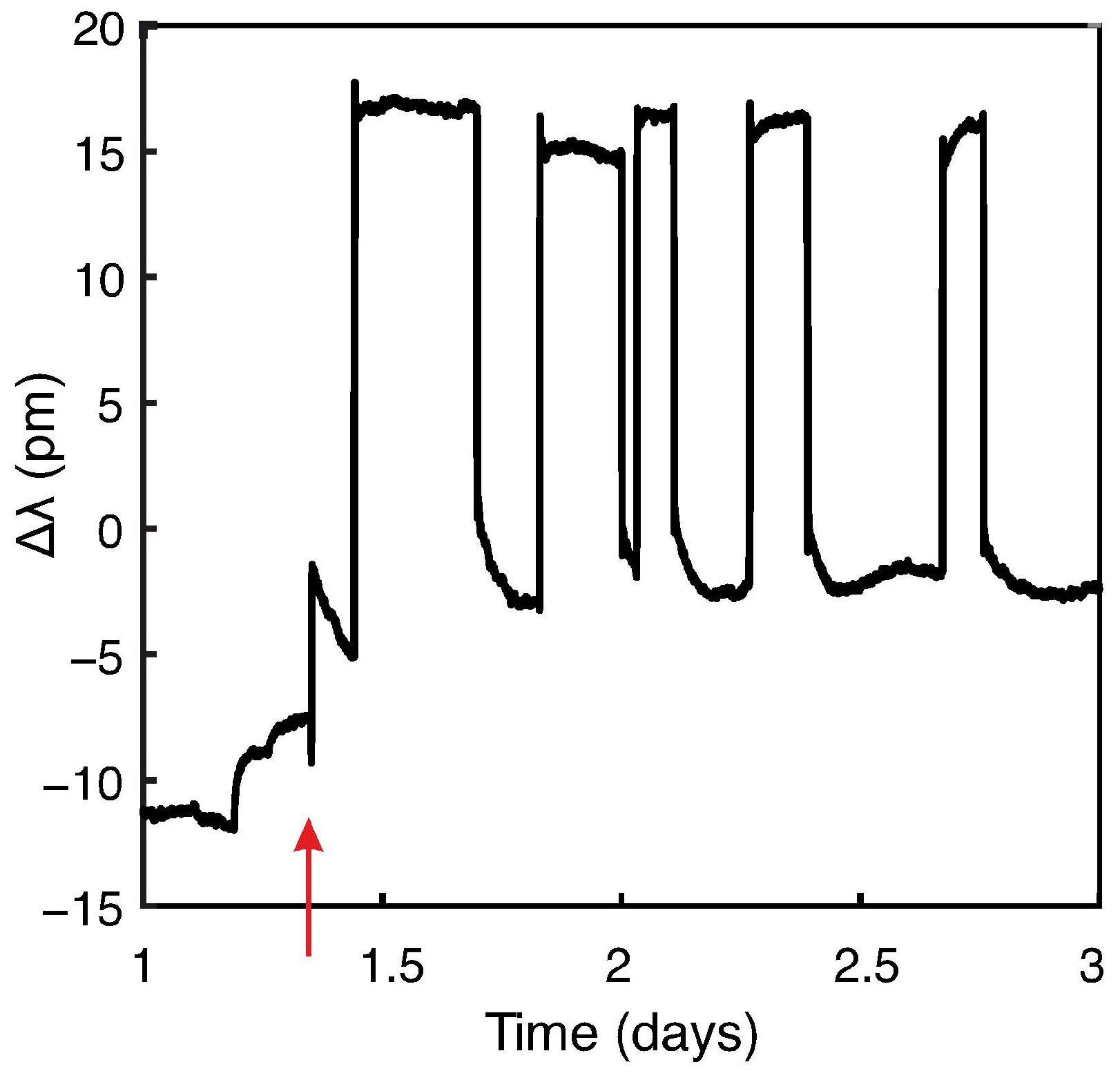
3.1. Pressure (FBG Sensors vs. Divers)
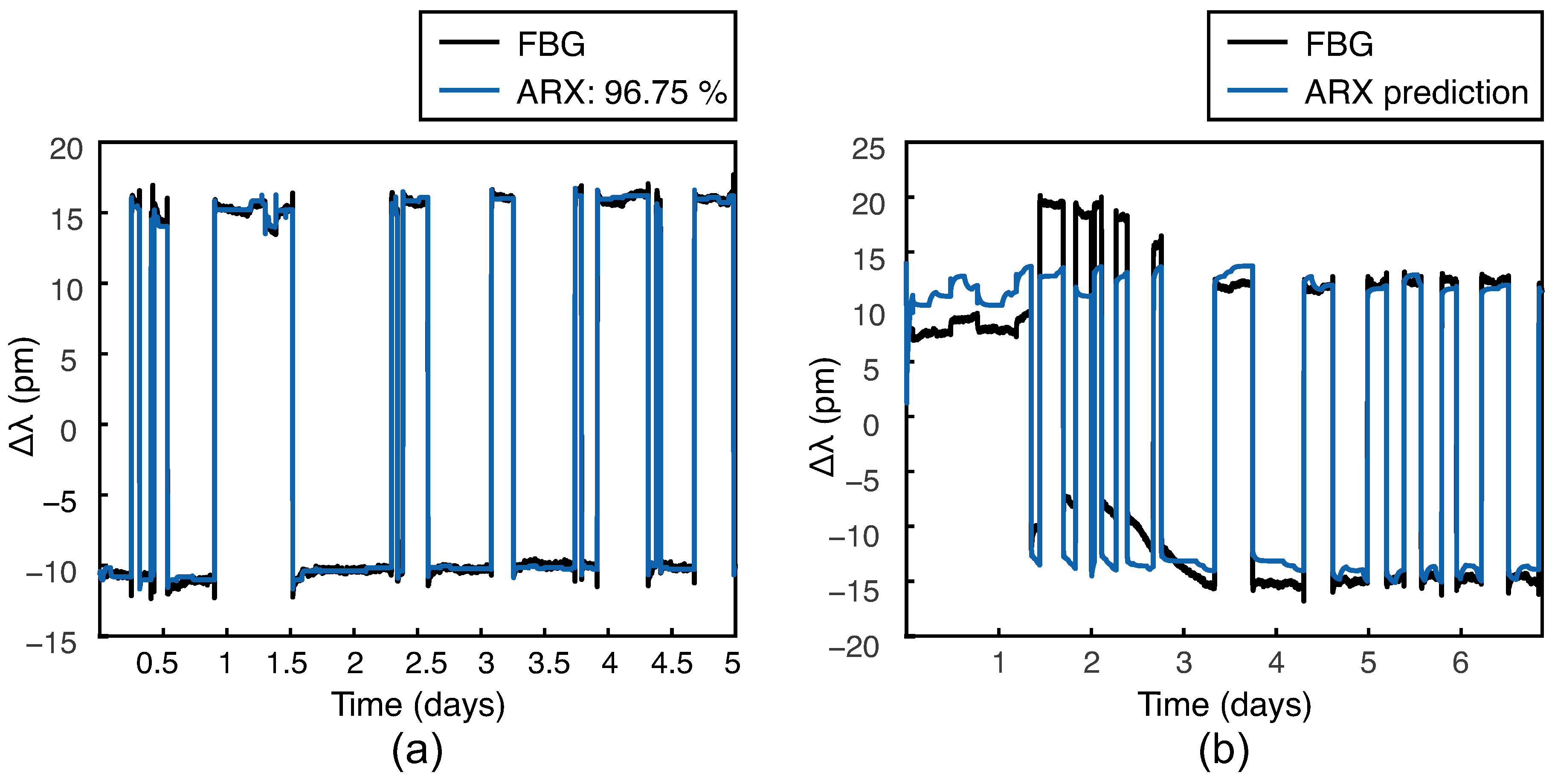
3.2. Consolidation Models
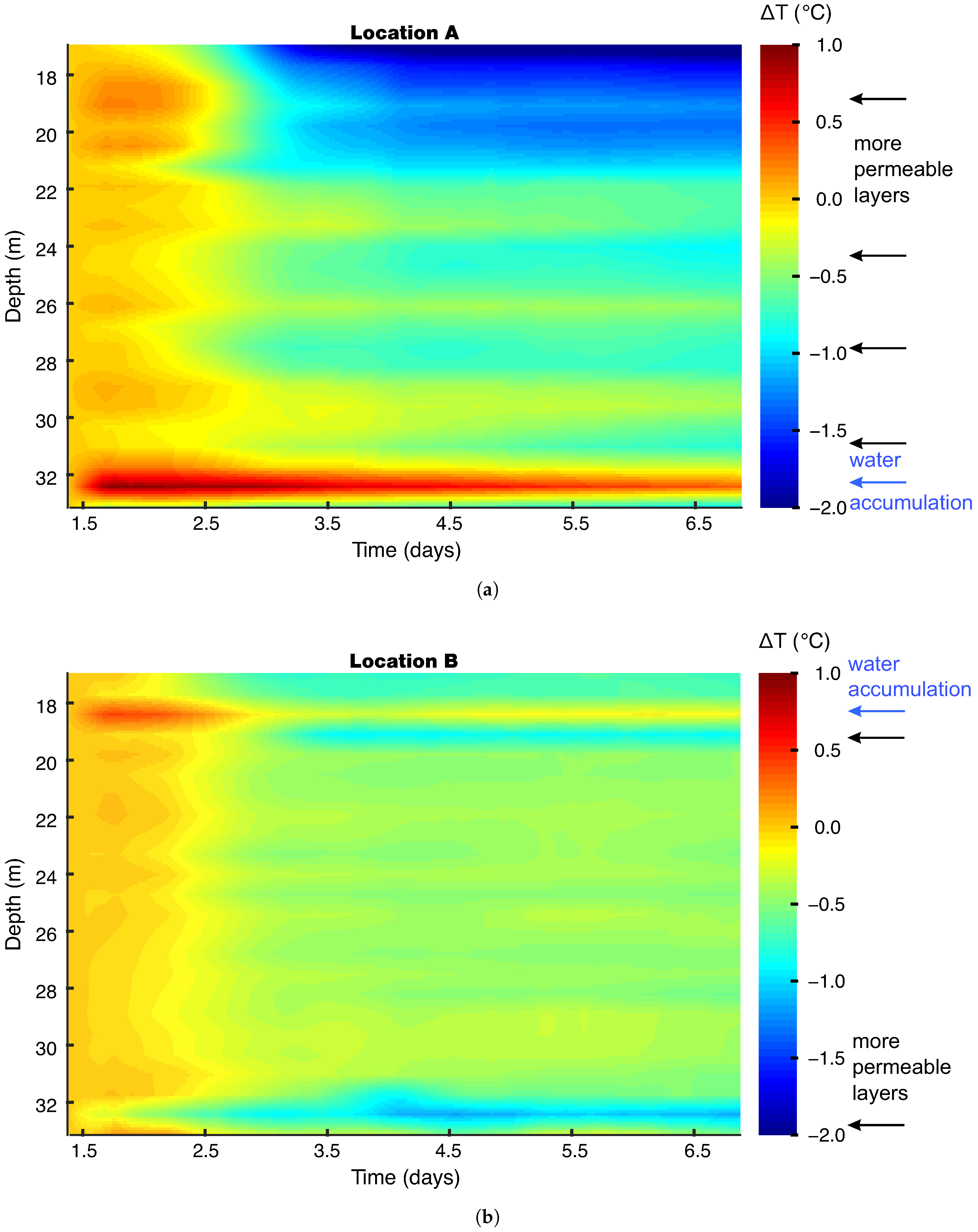
3.3. Temperature (FBG Sensors)
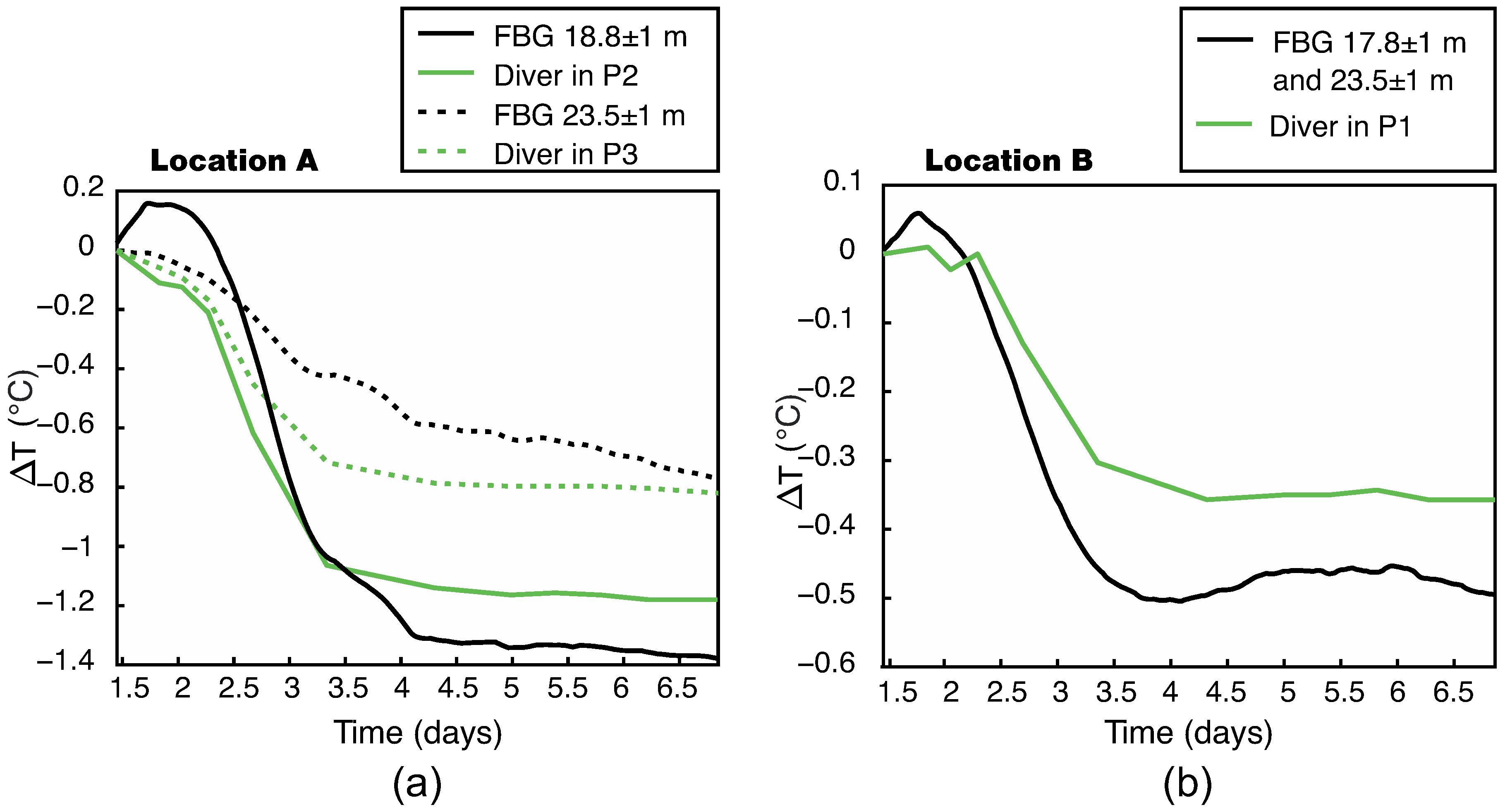
3.4. Temperature (FBG Sensors vs. Divers)
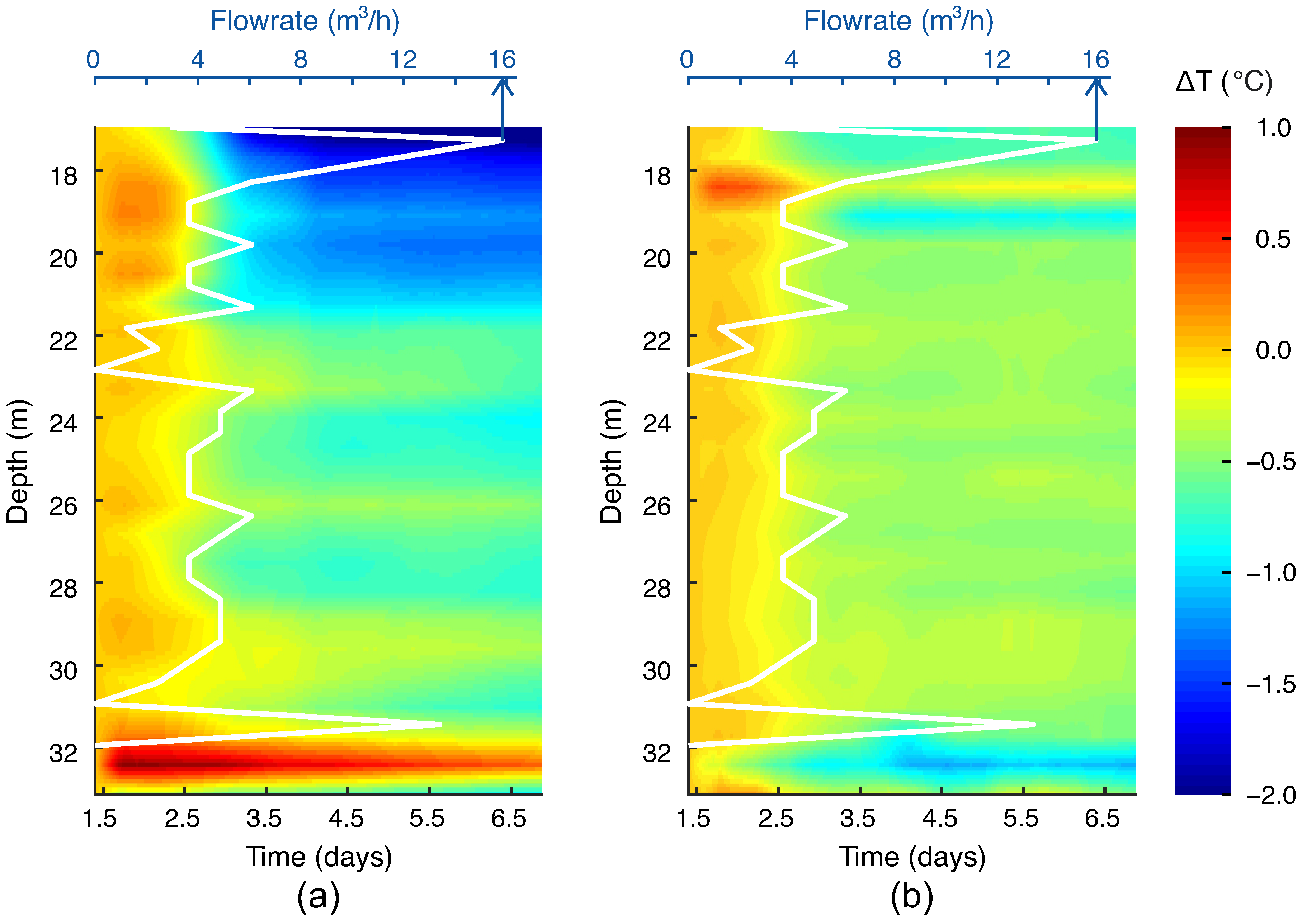
3.5. Temperature (FBG Sensors vs. Well Flowrate)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boak, R. Technical Review: Practical Guidelines for Test Pumping in Water Wells; Technical Report; International Committee of the Red Cross: Geneva, Switzerland, 2011. [Google Scholar]
- Chen, X.; Goeke, J.; Ayers, J.F.; Summerside, S. Observation well network design for pumping tests in unconfined aquifers. J. Am. Water Resour. Assoc. 2003, 39, 17–32. [Google Scholar] [CrossRef]
- Walton, W. Groundwater Pumping Tests; Taylor & Francis: Abingdon-on-Thames, UK, 1990. [Google Scholar]
- van Beek, C.K. Cause and Prevention of Clogging of Wells Abstracting Groundwater from Unconsolidated Aquifers. Ph.D. Thesis, VU Amsterdam, Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Harou, J.J.; Lund, J.R. Ending groundwater overdraft in hydrologic-economic systems. Hydrogeol. J. 2008, 16, 1039–1055. [Google Scholar] [CrossRef]
- Du, Z.; Ge, L.; Ng, A.H.M.; Zhu, Q.; Zhang, Q.; Kuang, J.; Dong, Y. Long-term subsidence in Mexico City from 2004 to 2018 revealed by five synthetic aperture radar sensors. Land Degrad. Dev. 2019, 30, 1785–1801. [Google Scholar] [CrossRef]
- Loáiciga, H.A. Consolidation Settlement in Aquifers Caused by Pumping. J. Geotech. Geoenviron. Eng. 2012, 139, 1191–1204. [Google Scholar] [CrossRef]
- Shen, S.L.; Xu, Y.S. Numerical evaluation of land subsidence induced by groundwater pumping in Shanghai. Can. Geotech. J. 2011, 48, 1378–1392. [Google Scholar] [CrossRef]
- Lienau, P.J. Data Acquisition for Low-Temperature Geothermal Well Tests and Long-Term Monitoring; Technical Report; U.S. Department of Energy: Idaho Falls, ID, USA, 1992. [CrossRef]
- Paillet, F. Borehole flowmeter applications in irregular and large-diameter boreholes. J. Appl. Geophys. 2004, 55, 39–59. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, W. A review of regional groundwater flow modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef]
- Selker, J.S.; Thévenaz, L.; Huwald, H.; Mallet, A.; Luxemburg, W.; van de Giesen, N.; Stejskal, M.; Zeman, J.; Westhoff, M.; Parlange, M.B. Distributed fiber-optic temperature sensing for hydrologic systems. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Campanella, C.E.; Cuccovillo, A.; Campanella, C.; Yurt, A.; Passaro, V.M. Fibre Bragg Grating based strain sensors: Review of technology and applications. Sensors 2018, 18, 3115. [Google Scholar] [CrossRef]
- Huang, J.Y.; Roosbroeck, J.V.; Vlekken, J.; Daerden, E.; Martinez, A.B.; Geernaert, T.; Berghmans, F.; Hoe, B.V.; Lindner, E.; Caucheteur, C. Packaged FBG based optical fiber sensor for simultaneous pressure and temperature monitoring. In Fiber Optic Sensors and Applications XV; Mendez, A., Baldwin, C.S., Du, H.H., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10654, pp. 93–99. [Google Scholar] [CrossRef]
- Ameen, O.F.; Younus, M.H.; Aziz, M.S.; Azmi, A.I.; Ibrahim, R.K.R.; Ghoshal, S.K.; Raja Ibrahim, R.K.; Ghoshal, S.K. Graphene diaphragm integrated FBG sensors for simultaneous measurement of water level and temperature. Sens. Actuators A Phys. 2016, 252, 225–232. [Google Scholar] [CrossRef]
- Dinia, L.; Mangini, F.; Muzi, M.; Frezza, F. FBG multifunctional pH sensor-monitoring the pH rain in cultural heritage. Acta IMEKO 2018, 7, 24–30. [Google Scholar] [CrossRef]
- Bellas, M.; Voulgaridis, G. Study of the major landslide at the community of Ropoto, Central Greece, mitigation and FBG early warning system design. Innov. Infrastruct. Solut. 2018, 3, 1–14. [Google Scholar] [CrossRef]
- Wang, M.; Chen, J.; Wei, H.; Song, B.; Xiao, W. Investigation on seismic damage model test of a high concrete gravity dam based on application of FBG strain sensor. Complexity 2019, 2019. [Google Scholar] [CrossRef]
- Monsberger, C.; Klug, F.; Lienhart, W. Performance assessment of a fiber Bragg grating sensor network inside a hydro power dam using optical backscatter reflectometry. In Fiber Optic Sensors and Applications XIV; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10208, p. 102080R. [Google Scholar] [CrossRef]
- Qiao, X.; Shao, Z.; Bao, W.; Rong, Q. Fiber Bragg Grating Sensors for the Oil Industry. Sensors 2017, 17, 429. [Google Scholar] [CrossRef] [PubMed]
- Alemohammad, H.; Liang, R.; Yilman, D.; Azhari, A.; Mathers, K.; Chang, C.; Chan, B.; Pope, M.A. Fiber optic sensors for harsh environments: Environmental, hydrogeological, and chemical sensing applications. In Proceedings of the 26th International Conference on Optical Fiber Sensors, Lausanne, Switzerland, 24–28 September 2018. [Google Scholar] [CrossRef]
- Gu, K.; Shi, B.; Liu, C.; Jiang, H.; Li, T.; Wu, J. Investigation of land subsidence with the combination of distributed fiber optic sensing techniques and microstructure analysis of soils. Eng. Geol. 2018, 240, 34–47. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, H.; Su, J.; Shi, B.; Jiang, Y.; Gu, K. Application of distributed fiber optic sensing technique in land subsidence monitoring. J. Civ. Struct. Health Monit. 2015, 5, 587–597. [Google Scholar] [CrossRef]
- Van Halem, D.; de Vet, W.; Verberk, J.; Amy, G.; van Dijk, H. Characterization of accumulated precipitates during subsurface iron removal. Appl. Geochem. 2011, 26, 116–124. [Google Scholar] [CrossRef]
- Drusová, S.; Wagterveld, R.M.; Wexler, A.D.; Offerhaus, H.L. Dynamic consolidation measurements in a well field using fiber Bragg grating sensors. Sensors 2019, 19, 4403. [Google Scholar] [CrossRef]
- Zanotti, C.; Rotiroti, M.; Sterlacchini, S.; Cappellini, G.; Fumagalli, L.; Stefania, G.A.; Nannucci, M.S.; Leoni, B.; Bonomi, T. Choosing between linear and nonlinear models and avoiding overfitting for short and long term groundwater level forecasting in a linear system. J. Hydrol. 2019, 578, 124015. [Google Scholar] [CrossRef]
- Varouchakis Emmanouil, A. Modeling of temporal groundwater level variations based on a Kalman filter adaptation algorithm with exogenous inputs. J. Hydroinf. 2017, 19, 191–206. [Google Scholar] [CrossRef]
- Keesman, K.J. System Identification An Introduction; Springer: London, UK, 2019; Volume 53, pp. 1689–1699. [Google Scholar] [CrossRef]
- Kashyap, R. Fiber Bragg Gratings; Electronics & Electrical; Elsevier Science: Philadelphia, PA, USA, 1999. [Google Scholar]
- Smits, K.M.; Sakaki, T.; Limsuwat, A.; Illangasekare, T.H. Thermal Conductivity of Sands under Varying Moisture and Porosity in Drainage–Wetting Cycles. Vadose Zone J. 2010, 9, 172. [Google Scholar] [CrossRef]
- Dos Santos, E.C.; De Mendonça Silva, J.C.; Duarte, H.A. Pyrite Oxidation Mechanism by Oxygen in Aqueous Medium. J. Phys. Chem. C 2016, 120, 2760–2768. [Google Scholar] [CrossRef]
- Drusová, S.; Offerhaus, H.L.; Wagterveld, R.M.; Keesman, K.J. Simultaneous temperature and consolidation sensing near drinking water wells using fiber-optic sensors. 4TU.ResearchData Collect. 2020. [Google Scholar] [CrossRef]
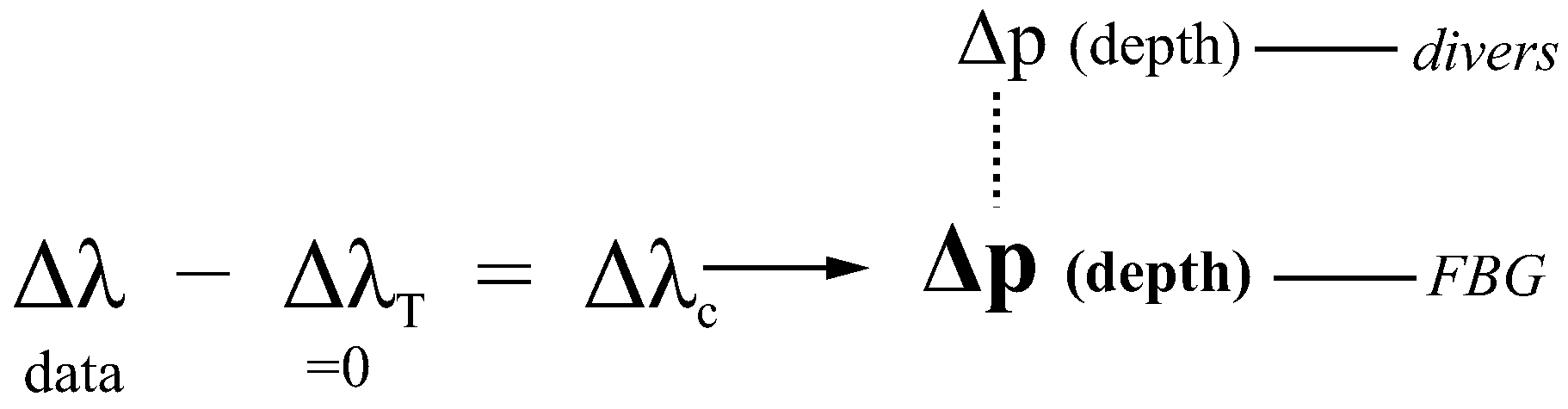
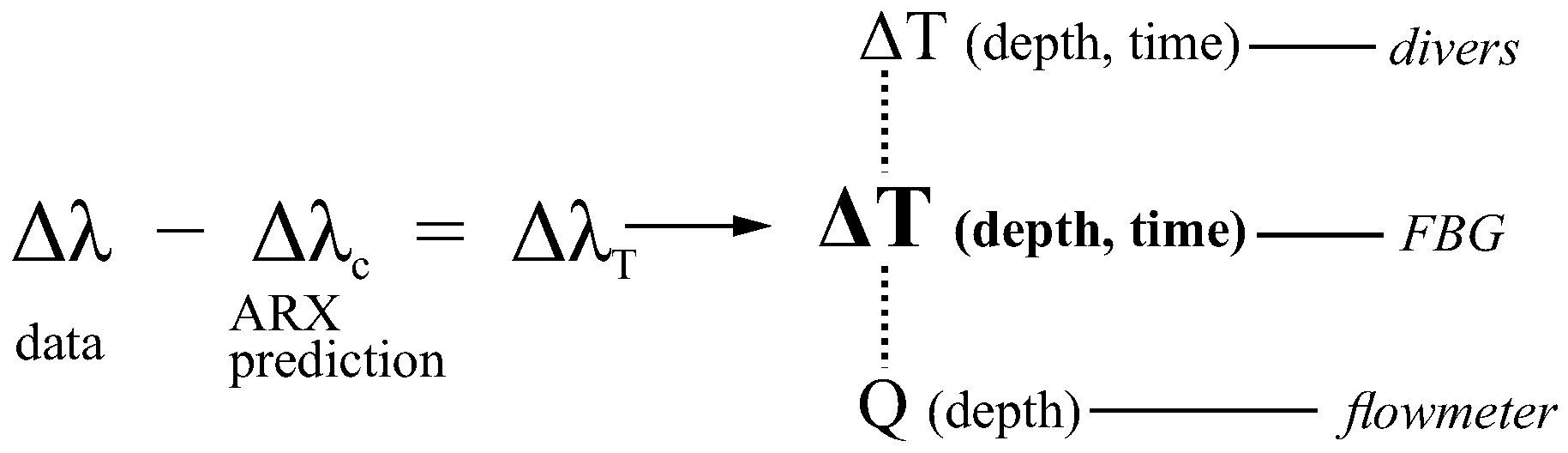
| Output | Input Well | ||
|---|---|---|---|
| na | 6 | ||
| nb | 8 | 2 | |
| nk | 0 | 1 | |
| Depth (m) | 17.0 | 17.7 | 18.4 | 19.1 | 19.8 | 20.5 | 21.2 | 21.9 | |
| A | RMSE training (%) | 88.4 | 94.0 | 94.6 | 92.1 | 73.7 | 89.8 | 90.7 | 94.5 |
| RMSE validation (%) | 86.8 | 91.8 | 92.7 | 89.4 | 71.8 | 86.5 | 88.2 | 92.0 | |
| B | RMSE training (%) | 92.7 | 91.2 | 96.7 | 96.5 | 90.9 | 91.4 | 91.8 | 35.1 |
| RMSE validation (%) | 80.9 | 75.1 | 89.2 | 86.7 | 79.5 | 75.8 | −111.9 | 1.1 | |
| Depth (m) | 22.6 | 23.3 | 24.0 | 24.7 | 25.4 | 26.1 | 26.8 | 27.5 | |
| A | RMSE training (%) | 94.1 | 94.6 | 89.0 | 92.3 | 92.8 | 95.0 | 94.0 | 88.5 |
| RMSE validation (%) | 92.4 | 92.2 | 89.1 | 87.3 | 90.2 | 91.5 | 91.6 | 86.7 | |
| B | RMSE training (%) | 89.5 | 89.6 | 86.7 | 93.2 | 96.0 | 35.4 | 69.4 | 85.5 |
| RMSE validation (%) | 87.0 | 72.8 | 76.3 | 78.0 | 91.5 | 0.7 | 22.8 | 76.6 | |
| Depth (m) | 28.2 | 28.9 | 29.6 | 30.3 | 31.0 | 31.7 | 32.4 | 33.1 | |
| A | RMSE training (%) | 95.1 | 96.4 | 94.7 | 89.4 | 92.7 | 87.7 | 92.1 | 89.5 |
| RMSE validation (%) | 93.5 | 92.5 | 93.0 | 90.4 | 89.8 | 82.1 | 88.5 | 86.3 | |
| B | RMSE training (%) | 96.3 | 96.5 | 95.6 | 94.4 | 90.0 | 94.0 | 90.1 | 87.7 |
| RMSE validation (%) | 93.2 | 93.0 | 91.9 | 89.1 | 77.2 | 80.6 | 71.9 | 80.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drusová, S.; Wagterveld, R.M.; Keesman, K.J.; Offerhaus, H.L. Temperature and Consolidation Sensing Near Drinking Water Wells Using Fiber Bragg Grating Sensors. Water 2020, 12, 3572. https://doi.org/10.3390/w12123572
Drusová S, Wagterveld RM, Keesman KJ, Offerhaus HL. Temperature and Consolidation Sensing Near Drinking Water Wells Using Fiber Bragg Grating Sensors. Water. 2020; 12(12):3572. https://doi.org/10.3390/w12123572
Chicago/Turabian StyleDrusová, Sandra, R. Martijn Wagterveld, Karel J. Keesman, and Herman L. Offerhaus. 2020. "Temperature and Consolidation Sensing Near Drinking Water Wells Using Fiber Bragg Grating Sensors" Water 12, no. 12: 3572. https://doi.org/10.3390/w12123572
APA StyleDrusová, S., Wagterveld, R. M., Keesman, K. J., & Offerhaus, H. L. (2020). Temperature and Consolidation Sensing Near Drinking Water Wells Using Fiber Bragg Grating Sensors. Water, 12(12), 3572. https://doi.org/10.3390/w12123572