Impact of Input Filtering and Architecture Selection Strategies on GRU Runoff Forecasting: A Case Study in the Wei River Basin, Shaanxi, China
Abstract
1. Introduction
2. Methodology
2.1. Preprocessing
2.1.1. Principal Component Analysis (PCA) Denoising
2.1.2. Normalization
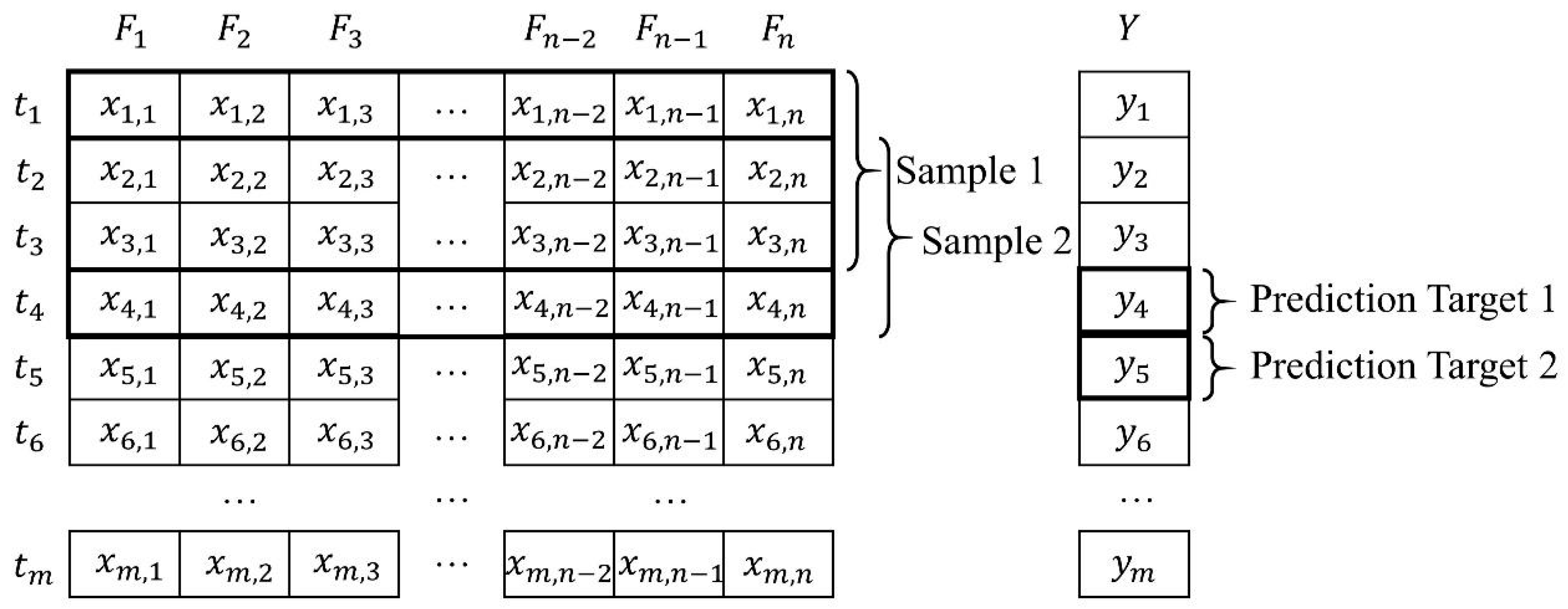
2.1.3. Sliding Window Sampling
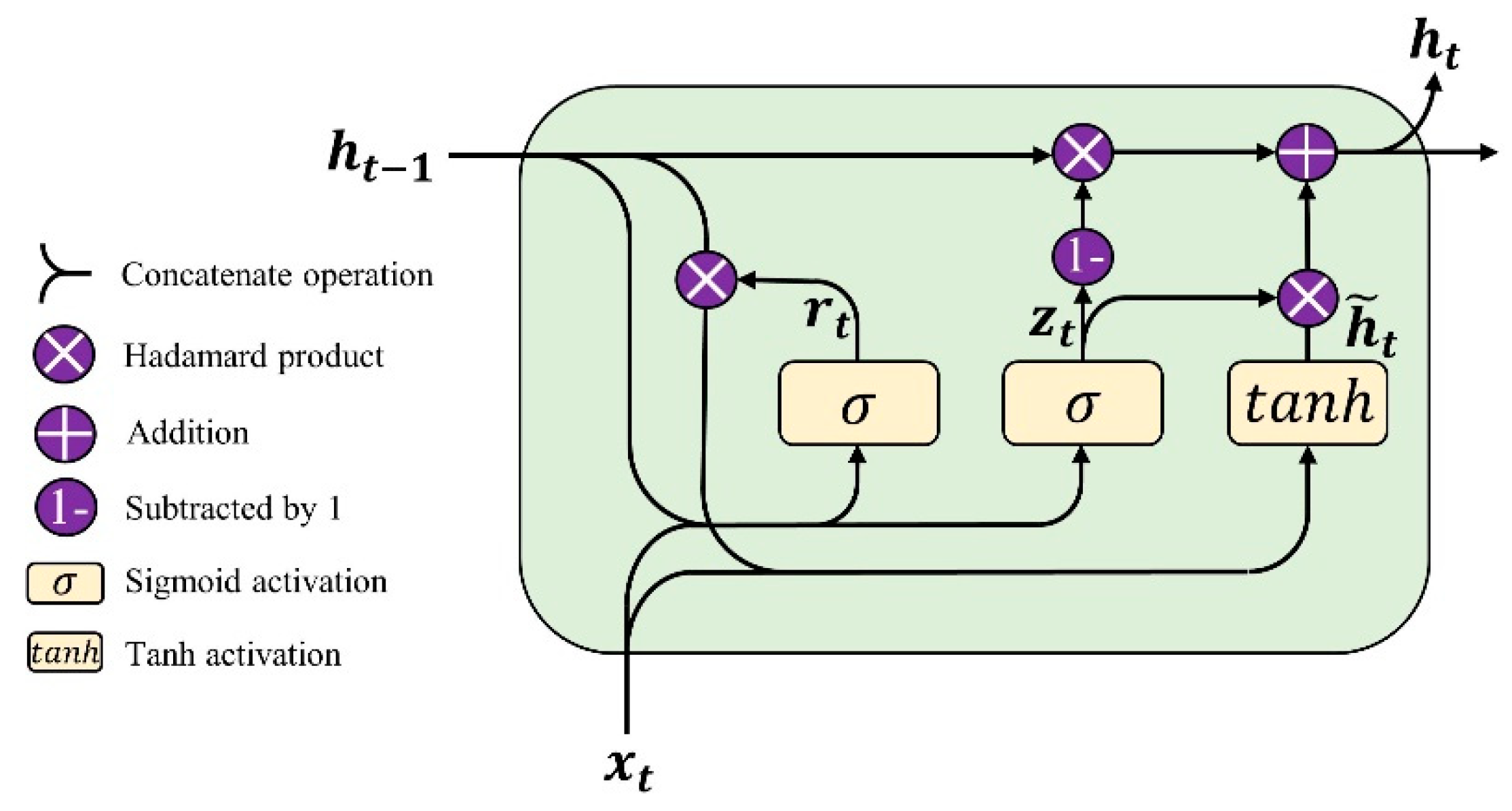
2.2. Gated Recurrent Unit (GRU)
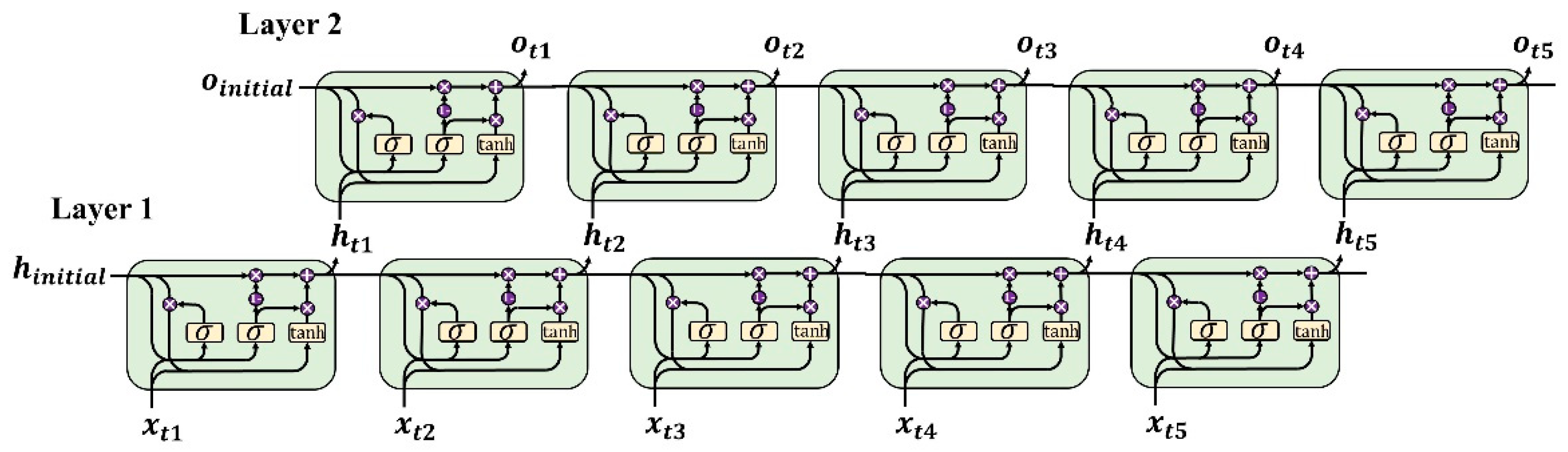
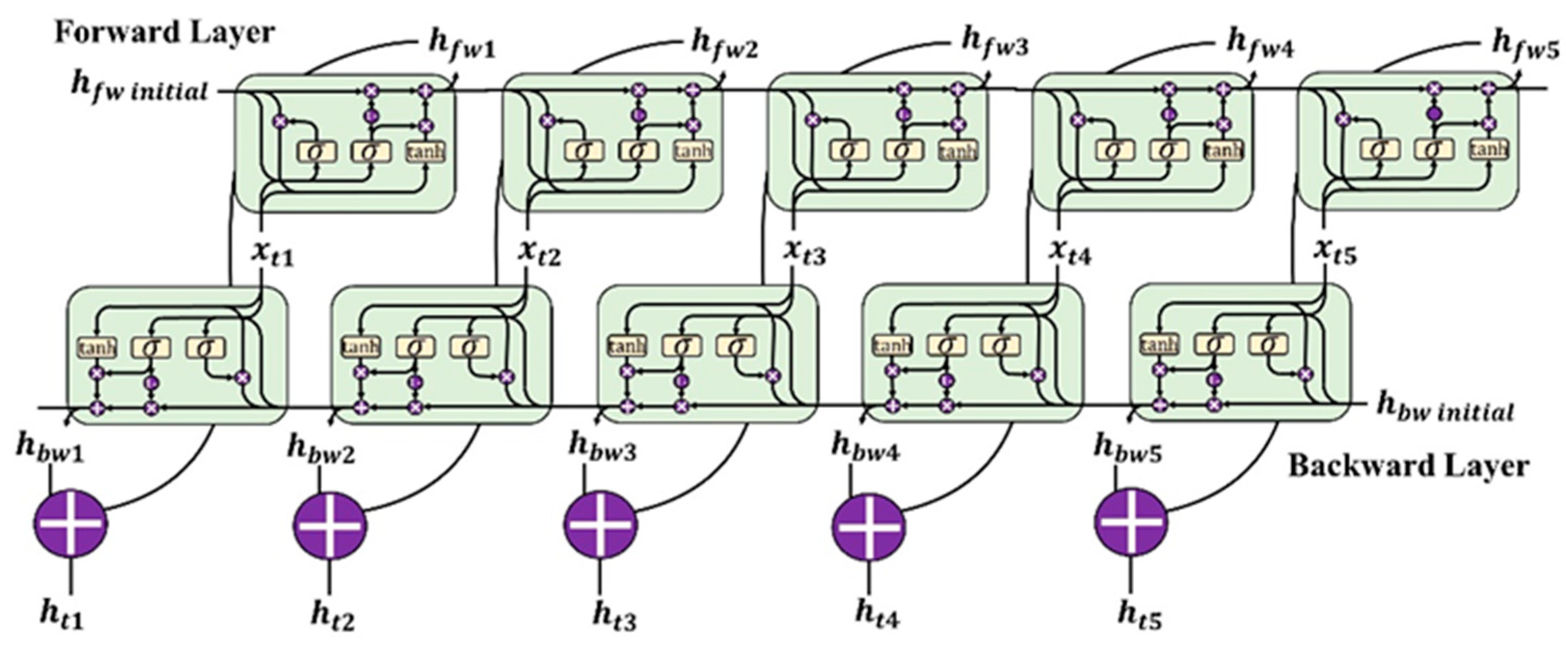
2.3. Stacked and Bi-Directional GRU (bi-GRU)
2.4. Model Evaluation
3. Case Study and Materials
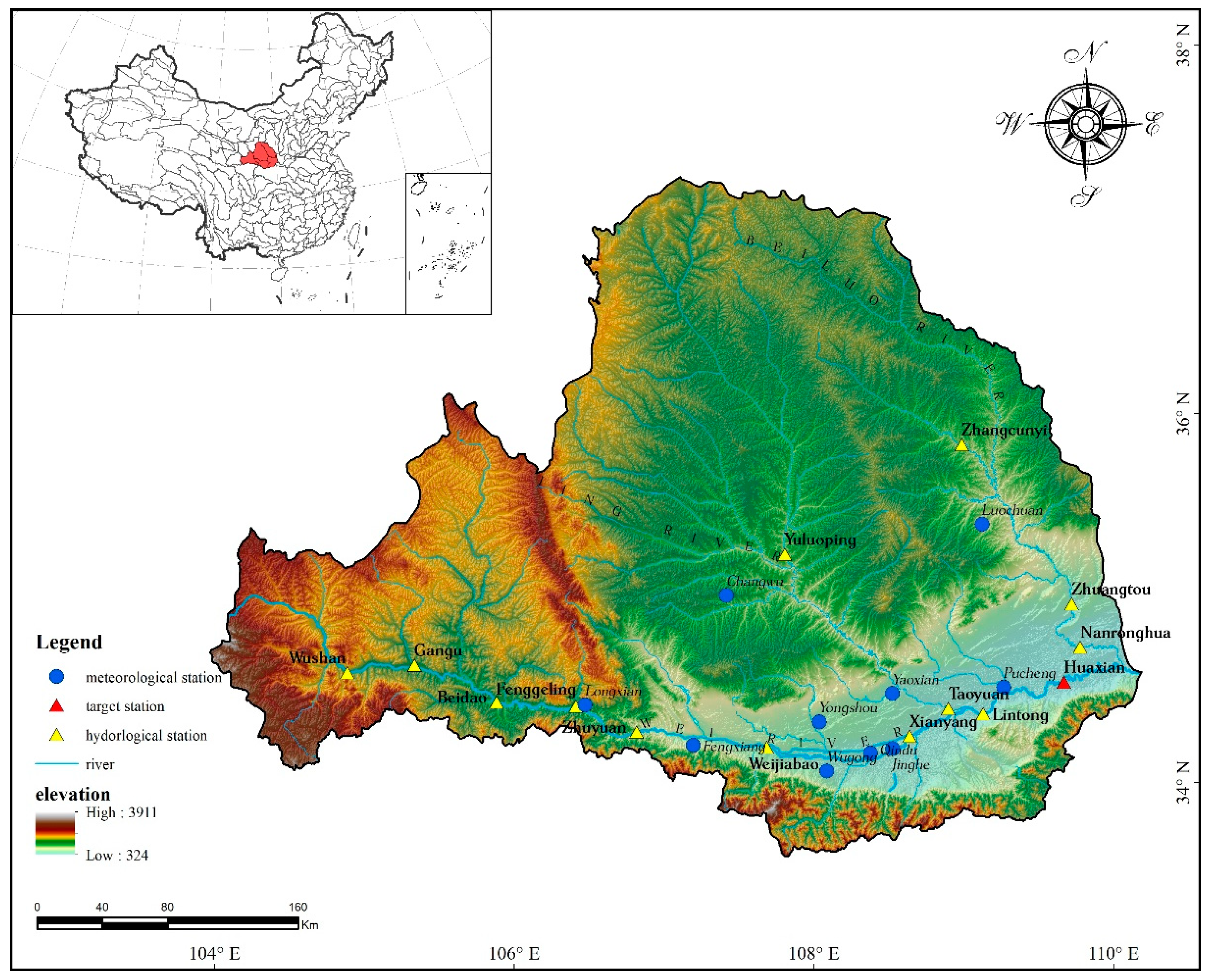
3.1. Research Area and Data
3.2. Scenarios and Traning Process
3.3. PCA Denoised Data
4. Results and Discussions
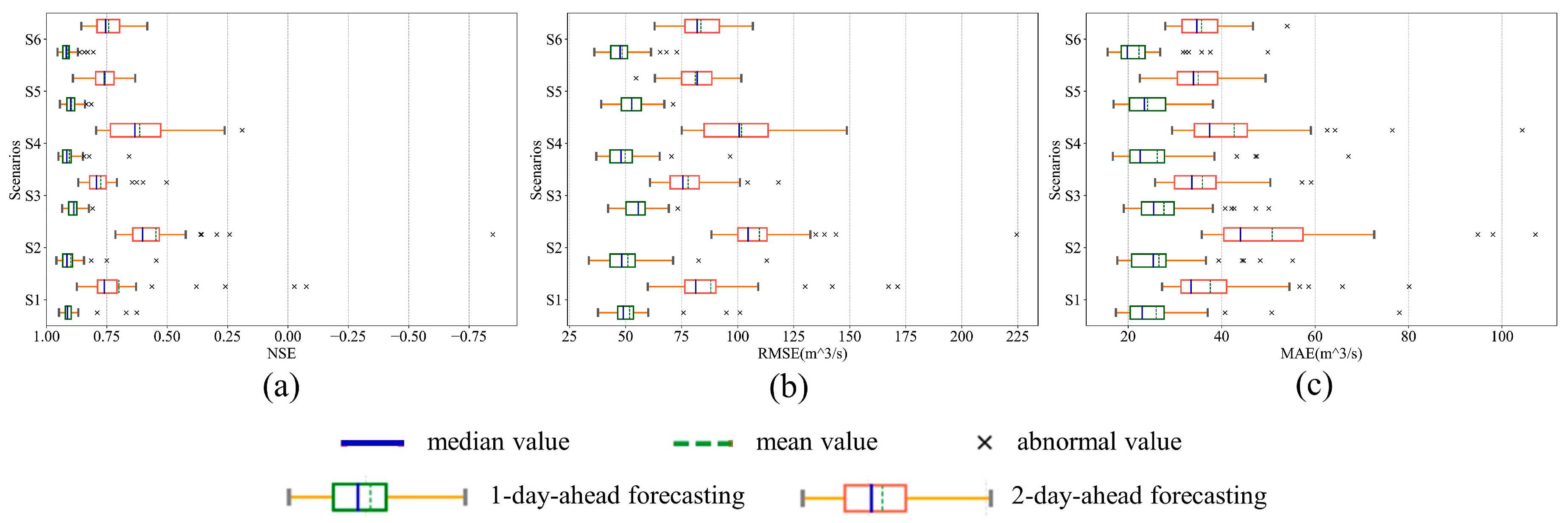
4.1. Robustness Evaluation
4.1.1. Overall Evaluation
4.1.2. Time Step Standard Deviation of the Evaluation Metrics
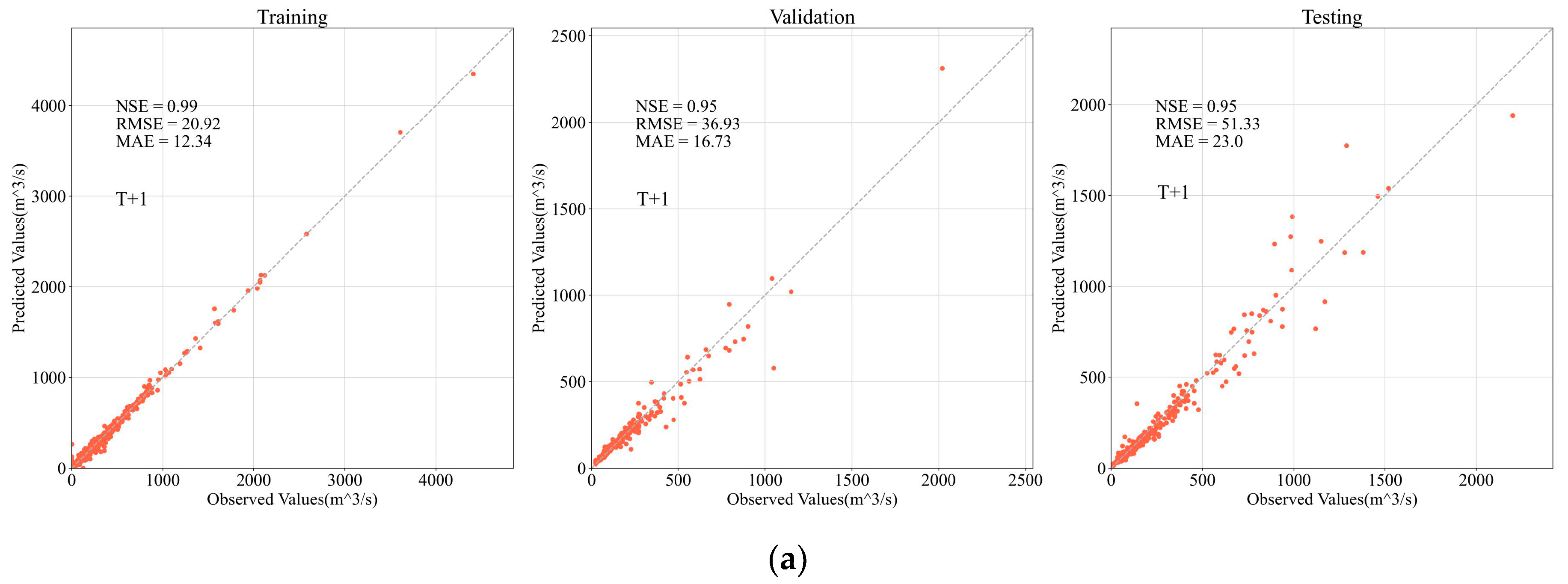
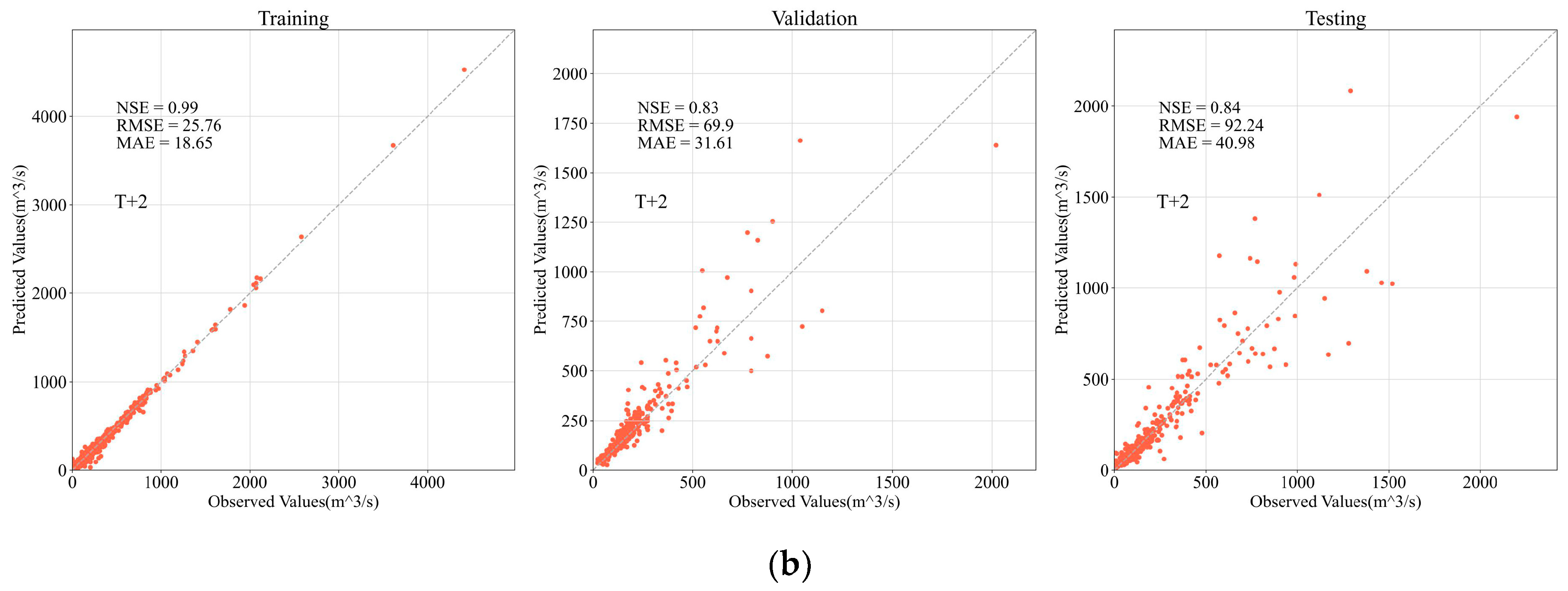
4.2. Accuracy Evaluation
4.2.1. Overall Evaluation
4.2.2. Accuracy of Flood Peak Forecasts
4.3. Recommendations Based on the Evaluation Results
5. Conclusions
- Based on the premise that the rainfall data is sufficient, its inclusion can enhance the model’s robustness when the hyperparameters vary. Additionally, when the lead time increases, this enhancement effect becomes more pronounced. For optimized accuracy, the rainfall data has a negative impact on the forecasts with a short lead time but is valuable for the forecasts with a longer one in either the overall forecasting process or the flood peak forecasting process. Therefore, the rainfall data is recommended to be included in long-lead-time forecasts.
- Though a relative high relevance to the prediction target, the runoff data at the adjacent tributary introduces noise that significantly hinders the robustness of the model and will increase the difficulty of the optimization of hyperparameters. Nevertheless, this runoff data also contains valuable information for the flood peak forecasts with a short lead time and, thus, the exclusion of it should be carefully considered according to the purpose of use. For the forecasts with a more extended lead time, this data acts as noise and should be excluded.
- The model uses PCA denoising as the input filtering strategy has comparable robustness to the model that uses well manually filtered data as the input. Thus, it can reduce much effort in the data filtering stage. Meanwhile, the model with PCA denoising operation can provide accurate forecasts, especially for the flood peak forecasts when the lead time increases. Thus, the PCA denoising can be an efficient substitution for the manual input filtering process and is recommended to be considered as an alternative preprocessing method in the future.
- Despite a slightly lower time-step robustness, the bi-directional architecture has higher prediction accuracy than the single directional architecture for runoff forecasting, therefore, it is suggested to be utilized.
Author Contributions
Funding
Conflicts of Interest
References
- Narbondo, S.; Gorgoglione, A.; Crisci, M.; Chreties, C. Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions. Water 2020, 12, 528. [Google Scholar] [CrossRef]
- Navas, R.; Alonso, J.; Gorgoglione, A.; Vervoort, R.W. Identifying Climate and Human Impact Trends in Streamflow: A Case Study in Uruguay. Water 2019, 11, 1433. [Google Scholar] [CrossRef]
- Nazari-Sharabian, M.; Taheriyoun, M.; Ahmad, S.; Karakouzian, M.; Ahmadi, A. Water Quality Modeling of Mahabad Dam Watershed–Reservoir System under Climate Change Conditions, Using SWAT and System Dynamics. Water 2019, 11, 394. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward Improved Predictions in Ungauged Basins: Exploiting the Power of Machine Learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Ahmed, U.; Mumtaz, R.; Anwar, H.; Shah, A.A.; Irfan, R. Efficient Water Quality Prediction Using Supervised Machine Learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef]
- Liang, J.; Li, W.; Bradford, S.A.; Šimůnek, J. Physics-Informed Data-Driven Models to Predict Surface Runoff Water Quantity and Quality in Agricultural Fields. Water 2019, 11, 200. [Google Scholar] [CrossRef]
- Busico, G.; Colombani, N.; Fronzi, D.; Pellegrini, M.; Tazioli, A.; Mastrocicco, M. Evaluating SWAT model performance, considering different soils data input, to quantify actual and future runoff susceptibility in a highly urbanized basin. J. Environ. Manag. 2020, 266, 110625. [Google Scholar] [CrossRef]
- Duan, Y.; Meng, F.; Liu, T.; Huang, Y.; Luo, M.; Xing, W.; De Maeyer, P. Sub-Daily Simulation of Mountain Flood Processes Based on the Modified Soil Water Assessment Tool (SWAT) Model. Int. J. Environ. Res. Public Health 2019, 16, 3118. [Google Scholar] [CrossRef]
- Fereidoon, M.; Koch, M.; Brocca, L. Predicting Rainfall and Runoff Through Satellite Soil Moisture Data and SWAT Modelling for a Poorly Gauged Basin in Iran. Water 2019, 11, 594. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, M.; Takeuchi, K.; Ishidaira, H. Improved version of BTOPMC model and its application in event-based hydrologic simulations. J. Geogr. Sci. 2007, 17, 73–84. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, X.; Zhang, X.; Zhou, H.; Zhang, Z. A Flood Forecasting Model that Considers the Impact of Hydraulic Projects by the Simulations of the Aggregate reservoir’s Retaining and Discharging. Water Resour. Manag. 2017, 31, 1031–1045. [Google Scholar] [CrossRef]
- Paparrizos, S.; Maris, F. Hydrological simulation of Sperchios River basin in Central Greece using the MIKE SHE model and geographic information systems. Appl. Water Sci. 2017, 7, 591–599. [Google Scholar] [CrossRef]
- Xevi, E.; Christiaens, K.; Espino, A.; Sewnandan, W.; Mallants, D.; Sørensen, H.; Feyen, J. Calibration, Validation and Sensitivity Analysis of the MIKE-SHE Model Using the Neuenkirchen Catchment as Case Study. Water Resour. Manag. 1997, 11, 219–242. [Google Scholar] [CrossRef]
- Tan, M.L.; Ramli, H.P.; Tam, T.H. Effect of DEM Resolution, Source, Resampling Technique and Area Threshold on SWAT Outputs. Water Resour. Manag. 2018, 32, 4591–4606. [Google Scholar] [CrossRef]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Souag-Gamane, D.; Ahmed, A.N.; Sammen, S.S.; Kisi, O.; Huang, Y.F.; El-Shafie, A. Rainfall-runoff modelling using improved machine learning methods: Harris hawks optimizer vs. particle swarm optimization. J. Hydrol. 2020, 589, 125133. [Google Scholar] [CrossRef]
- Parisouj, P.; Mohebzadeh, H.; Lee, T. Employing Machine Learning Algorithms for Streamflow Prediction: A Case Study of Four River Basins with Different Climatic Zones in the United States. Water Resour. Manag. 2020, 34, 4113–4131. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Fu, D.; Shi, X.; Tang, B.; Qi, H. Snowmelt-Driven Streamflow Prediction Using Machine Learning Techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1743. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Deo, R.C.; Kim, S.; Hasanpour Kashani, M.; Karimi, V.; Izadkhah, M. Development and evaluation of the cascade correlation neural network and the random forest models for river stage and river flow prediction in Australia. Soft Comput. 2020, 24, 12079–12090. [Google Scholar] [CrossRef]
- Orellana-Alvear, J.; Celleri, R.; Rollenbeck, R.; Muñoz, P.; Contreras, P.; Bendix, J. Assessment of Native Radar Reflectivity and Radar Rainfall Estimates for Discharge Forecasting in Mountain Catchments with a Random Forest Model. Remote Sens. 2020, 12, 1986. [Google Scholar] [CrossRef]
- Song, T.; Ding, W.; Wu, J.; Liu, H.; Zhou, H.; Chu, J. Flash Flood Forecasting Based on Long Short-Term Memory Networks. Water 2020, 12, 109. [Google Scholar] [CrossRef]
- Poonia, V.; Tiwari, H.L. Rainfall-runoff modeling for the Hoshangabad Basin of Narmada River using artificial neural network. Arab. J. Geosci. 2020, 13, 1–10. [Google Scholar] [CrossRef]
- Ali, S.; Shahbaz, M. Streamflow forecasting by modeling the rainfall–streamflow relationship using artificial neural networks. Model. Earth Syst. Environ. 2020, 6, 1645–1656. [Google Scholar] [CrossRef]
- Wagena, M.B.; Goering, D.; Collick, A.S.; Bock, E.; Fuka, D.R.; Buda, A.; Easton, Z.M. Comparison of short-term streamflow forecasting using stochastic time series, neural networks, process-based, and Bayesian models. Environ. Model. Softw. 2020, 126, 104669. [Google Scholar] [CrossRef]
- Unnikrishnan, P.; Jothiprakash, V. Hybrid SSA-ARIMA-ANN Model for Forecasting Daily Rainfall. Water Resour. Manag. 2020, 34, 3609–3623. [Google Scholar] [CrossRef]
- Saha, A.; Singh, K.N.; Ray, M.; Rathod, S. A hybrid spatio-temporal modelling: An application to space-time rainfall forecasting. Theor. Appl. Climatol. 2020, 1–12. [Google Scholar] [CrossRef]
- Ghamariadyan, M.; Imteaz, M.A. A wavelet artificial neural network method for medium-term rainfall prediction in Queensland (Australia) and the comparisons with conventional methods. Int. J. Climatol. 2020, 2020, 1–21. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Souag-Gamane, D.; Kisi, O. Artificial intelligence models versus empirical equations for modeling monthly reference evapotranspiration. Environ. Sci. Pollut. Res. 2020, 27, 30001–30019. [Google Scholar] [CrossRef]
- Ferreira, L.B.; Da Cunha, F.F. New approach to estimate daily reference evapotranspiration based on hourly temperature and relative humidity using machine learning and deep learning. Agric. Water Manag. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Han, Z.; Dian, Y.; Xia, H.; Zhou, J.; Jian, Y.; Yao, C.; Wang, X.; Li, Y. Comparing Fully Deep Convolutional Neural Networks for Land Cover Classification with High-Spatial-Resolution Gaofen-2 Images. ISPRS Int. J. Geo-Inf. 2020, 9, 478. [Google Scholar] [CrossRef]
- Collazos-Huertas, D.F.; Alvarez-Meza, A.M.; Acosta-Medina, C.D.; Castaño-Duque, G.A.; Castellanos-Dominguez, G. CNN-based framework using spatial dropping for enhanced interpretation of neural activity in motor imagery classification. Brain Inform. 2020, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Xia, G.; Member, S. Mining Deep Semantic Representations for Scene Classification of High-Resolution Remote Sensing Imagery. IEEE Trans. Big Data. 2020, 6, 522–536. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic routing between capsules. Adv. Neural Inf. Process. Syst. 2017, 30, 3857–3867. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Jang, B.; Kim, M.; Harerimana, G.; Kang, S.U.; Kim, J.W. Bi-LSTM Model to Increase Accuracy in Text Classification: Combining Word2vec CNN and Attention Mechanism. Appl. Sci. 2020, 10, 5841. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, X.; Zhang, W.; Liu, S.; Zhang, Y. A Bi-Directional LSTM-CNN Model with Attention for Aspect-Level Text Classification. Future Internet 2018, 10, 116. [Google Scholar] [CrossRef]
- Jelodar, H.; Wang, Y.; Orji, R.; Huang, H. Deep Sentiment Classification and Topic Discovery on Novel Coronavirus or COVID-19 Online Discussions: NLP Using LSTM Recurrent Neural Network Approach. IEEE J. Biomed. Health Inform. 2020, 24, 1. [Google Scholar] [CrossRef]
- Zou, Q.; Xiong, Q.; Li, Q.; Yi, H.; Yu, Y.; Wu, C. A water quality prediction method based on the multi-time scale bidirectional long short-term memory network. Environ. Sci. Pollut. Res. 2020, 27, 16853–16864. [Google Scholar] [CrossRef]
- Liu, D.R.; Lee, S.J.; Huang, Y.; Chiu, C.J. Air pollution forecasting based on attention-based LSTM neural network and ensemble learning. Expert Syst. 2020, 37, 1–16. [Google Scholar] [CrossRef]
- Song, C.; Zhang, H. Study on turbidity prediction method of reservoirs based on long short term memory neural network. Ecol. Model. 2020, 432, 109210. [Google Scholar] [CrossRef]
- Wang, C.; Qi, Y.; Zhu, G. Deep learning for predicting the occurrence of cardiopulmonary diseases in Nanjing, China. Chemosphere 2020, 257, 127176. [Google Scholar] [CrossRef] [PubMed]
- Goluguri, N.V.R.R.; Devi, K.S.; Srinivasan, P. Rice-net: An efficient artificial fish swarm optimization applied deep convolutional neural network model for identifying the Oryza sativa diseases. Neural Comput. Appl. 2020, 1–16. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing (EMNLP 2014), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar] [CrossRef]
- Wang, C.; Du, W.; Zhu, Z.; Yue, Z. The real-time big data processing method based on LSTM or GRU for the smart job shop production process. J. Algorithms Comput. Technol. 2020, 14, 1–9. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. Exploring the best sequence LSTM modeling architecture for flood prediction. Neural Comput. Appl. 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, Y.; Zhu, Y.; Feng, J.; Wang, S. Complexity to Forecast Flood: Problem Definition and Spatiotemporal Attention LSTM Solution. Complexity 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Chen, X.; Huang, J.; Han, Z.; Gao, H.; Liu, M.; Li, Z.; Liu, X.; Li, Q.; Qi, H.; Huang, Y. The importance of short lag-time in the runoff forecasting model based on long short-term memory. J. Hydrol. 2020, 589, 125359. [Google Scholar] [CrossRef]
- Okkan, U.; Kirdemir, U. Towards a hybrid algorithm for the robust calibration of rainfall-runoff models. J. Hydroinform. 2020, 22, 876–899. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. High temporal resolution rainfall–runoff modeling using long-short-term-memory (LSTM) networks. Neural Comput. Appl. 2020, 6. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. Predictions for COVID-19 with deep learning models of LSTM, GRU and Bi-LSTM. Chaos Solitons Fractals 2020, 140, 110212. [Google Scholar] [CrossRef] [PubMed]
- Atef, S.; Eltawil, A.B. Assessment of stacked unidirectional and bidirectional long short-term memory networks for electricity load forecasting. Electr. Power Syst. Res. 2020, 187, 106489. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, Q.; Wan, X.; Li, X.; Wang, Y.; Wang, W. Comprehensive ecological risk assessment for semi-arid basin based on conceptual model of risk response and improved TOPSIS model-a case study of Wei River Basin, China. Sci. Total Environ. 2020, 719, 137502. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Jiang, J.; Zheng, Y.; Hong, Y.; Chung, E.S.; Shamseldin, A.Y.; Wei, Y.; Wang, X. Robustness analysis of storm water quality modelling with LID infrastructures from natural event-based field monitoring. Sci. Total Environ. 2021, 753, 142007. [Google Scholar] [CrossRef] [PubMed]
- Geng, D.; Zhang, H.; Wu, H. Short-Term Wind Speed Prediction Based on Principal Component Analysis and LSTM. Appl. Sci. 2020, 10, 4416. [Google Scholar] [CrossRef]
- Bhagat, S.K.; Tiyasha, T.; Awadh, S.M.; Tung, T.M.; Jawad, A.H.; Yaseen, Z.M. Prediction of sediment heavy metal at the Australian Bays using newly developed hybrid artificial intelligence models. Environ. Pollut. 2021, 268, 115663. [Google Scholar] [CrossRef]
- Arozi, M.; Caesarendra, W.; Ariyanto, M.; Munadi, M.; Setiawan, J.D.; Glowacz, A. Pattern Recognition of Single-Channel sEMG Signal Using PCA and ANN Method to Classify Nine Hand Movements. Symmetry 2020, 12, 541. [Google Scholar] [CrossRef]
- Huang, C.J.; Shen, Y.; Chen, Y.H.; Chen, H.C. A novel hybrid deep neural network model for short-term electricity price forecasting. Int. J. Energy Res. 2020, 1–22. [Google Scholar] [CrossRef]
- Crisóstomo de Castro Filho, H.; Abílio de Carvalho Júnior, O.; Ferreira de Carvalho, O.L.; Pozzobon de Bem, P.; dos Santos de Moura, R.; Olino de Albuquerque, A.; Rosa Silva, C.; Guimarães Ferreira, P.H.; Fontes Guimarães, R.; Trancoso Gomes, R.A. Rice crop detection using LSTM, Bi-LSTM, and machine learning models from Sentinel-1 time series. Remote Sens. 2020, 12, 2655. [Google Scholar] [CrossRef]
- Duan, L.; Wang, W.; Sun, Y.; Zhang, C.; Sun, Y. Hydrogeochemical Characteristics and Health Effects of Iodine in Groundwater in Wei River Basin. Expo. Health 2020, 12, 369–383. [Google Scholar] [CrossRef]
- Zeng, G.; Jiang, R.; Huang, G.; Xu, M.; Li, J. Optimization of wastewater treatment alternative selection by hierarchy grey relational analysis. J. Environ. Manag. 2007, 82, 250–259. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Xu, Z.; Qiu, L.; Zhao, W. Distributed rainfall-runoff simulation for an unclosed river basin with complex river system: A case study of lower reach of the Wei River, China. J. Flood Risk Manag. 2016, 9, 169–177. [Google Scholar] [CrossRef]
- Müller, E.N.; van Schaik, L.; Blume, T.; Bronstert, A.; Carus, J.; Fleckenstein, J.H.; Fohrer, N.; Gerke, H.H.; Graeff, T.; Hesse, C.; et al. Herausforderungen der ökohydrologischen Forschung in Deutschland. Hydrol. Wasserbewirtsch. 2014, 58, 221–240. [Google Scholar] [CrossRef]
- Deb, P.; Kiem, A.S.; Willgoose, G. Mechanisms influencing non-stationarity in rainfall-runoff relationships in southeast Australia. J. Hydrol. 2019, 571, 749–764. [Google Scholar] [CrossRef]
- Chen, X.; He, J.; Wu, X.; Yan, W.; Wei, W. Sleep staging by bidirectional long short-term memory convolution neural network. Futur. Gener. Comput. Syst. 2020, 109, 188–196. [Google Scholar] [CrossRef]
- Grimaldi, S.; Nardi, F.; Piscopia, R.; Petroselli, A.; Apollonio, C. Continuous hydrologic modelling for design simulation in small and ungauged basins: A step forward and some tests for its practical use. J. Hydrol. 2020, 125664. [Google Scholar] [CrossRef]
- Petroselli, A.; Grimaldi, S. Design hydrograph estimation in small and fully ungauged basins: A preliminary assessment of the EBA4SUB framework. J. Flood Risk Manag. 2018, 11, S197–S210. [Google Scholar] [CrossRef]
- Piscopia, R.; Petroselli, A.; Grimaldi, S. A software package for predicting design-flood hydrographs in small and ungauged basins. J. Agric. Eng. 2015, 46, 74–84. [Google Scholar] [CrossRef]
- Nguyen, M.D.; Pham, B.T.; Ho, L.S.; Ly, H.B.; Le, T.T.; Qi, C.; Le, V.M.; Le, L.M.; Prakash, I.; Son, L.H.; et al. Soft-computing techniques for prediction of soils consolidation coefficient. Catena 2020, 195, 104802. [Google Scholar] [CrossRef]
- Canchala, T.; Alfonso-Morales, W.; Carvajal-Escobar, Y.; Cerón, W.L.; Caicedo-Bravo, E. Monthly rainfall anomalies forecasting for southwestern Colombia using artificial neural networks approaches. Water 2020, 12, 2628. [Google Scholar] [CrossRef]
- Premjith, B.; Kumar, M.A.; Soman, K.P. Neural Machine Translation System for English to Indian Language Translation Using MTIL Parallel Corpus. J. Intell. Syst. 2019, 28, 387–398. [Google Scholar] [CrossRef]
- Shahmohammadi, H.; Dezfoulian, M.H.; Mansoorizadeh, M. Paraphrase detection using LSTM networks and handcrafted features. Multimed. Tools Appl. 2020, 1–14. [Google Scholar] [CrossRef]
- Kwak, G.; Ahn, C.P.H.; Park, K.L.N. Potential of Bidirectional Long Short-Term Memory Networks for Crop Classification with Multitemporal Remote Sensing Images. Korean J. Remote Sens. 2020, 36, 515–525. [Google Scholar]

| Stations | Sub-Basin | Distance (Km) | Max (m3/s) | Mean (m3/s) | Grey Relation | R |
|---|---|---|---|---|---|---|
| Huaxian | W | 0.0 | 4410.0 | 171.7 | 1.000 | 1.000 |
| Nanronghua | B.L. | 23.5 | 250.0 | 12.5 | 0.993 | 0.763 |
| Zhuangtou | B.L. | 49.4 | 440.0 | 15.5 | 0.993 | 0.757 |
| Lintong | W | 53.3 | 4570.0 | 182.0 | 0.996 | 0.888 |
| Taoyuan | J | 72.8 | 906.0 | 32.7 | 0.993 | 0.703 |
| Xianyang | W | 100.3 | 2890.0 | 94.9 | 0.995 | 0.809 |
| Zhangcunyi | B.L. | 158.5 | 147.0 | 2.8 | 0.990 | 0.409 |
| Weijiabao | W | 186.7 | 1830.0 | 64.9 | 0.992 | 0.727 |
| Yuluoping | J | 188.8 | 687.0 | 10.1 | 0.990 | 0.194 |
| Zhuyuan | W | 263.9 | 59.5 | 2.0 | 0.992 | 0.536 |
| Fenggeling | W | 299.8 | 114.0 | 3.7 | 0.993 | 0.545 |
| Beidao | W | 348.2 | 959.0 | 22.8 | 0.991 | 0.365 |
| Gangu | W | 398.5 | 90.7 | 0.6 | 0.987 | 0.098 |
| Wushan | W | 439.6 | 699.0 | 12.1 | 0.991 | 0.274 |
| Stations | Sub-Basin | Distance (Km) | Max (mm) | Mean (mm) | Grey Relation | R |
|---|---|---|---|---|---|---|
| Pucheng | W | 37.3 | 60.8 | 1.4 | 0.979 | 0.114 |
| Yaoxian | W | 105.6 | 69.0 | 1.6 | 0.979 | 0.120 |
| Luochuan | B.L. | 109.1 | 107.5 | 1.7 | 0.979 | 0.096 |
| Jinghe | W | 115.2 | 117.3 | 1.5 | 0.979 | 0.109 |
| Qindu | W | 126.3 | 158.5 | 1.5 | 0.979 | 0.093 |
| Yongshou | W | 151.9 | 100.1 | 1.6 | 0.979 | 0.106 |
| Wugong | W | 155.3 | 101.4 | 1.7 | 0.979 | 0.124 |
| Changwu | J | 213.7 | 142.2 | 1.6 | 0.980 | 0.089 |
| Fengxiang | W | 232.6 | 76.2 | 1.7 | 0.979 | 0.097 |
| Longxian | W | 296.9 | 214.6 | 1.6 | 0.980 | 0.094 |
| Prediction Target | Scenario | RNN Cell | Pre-Processing | Hydrological Stations (Runoff Data) | Meteorological Stations (Rainfall Data) |
|---|---|---|---|---|---|
| T + 1 | S1 | GRU | MMN | all included | all included |
| S2 | GRU | MMN | all included | all excluded | |
| S3 | GRU | MMN | B.L. excluded | all included | |
| S4 | GRU | MMN | B.L. excluded | all excluded | |
| S5 | GRU | PCA + MAN | all included | all included | |
| S6 | bi-GRU | PCA + MAN | all included | all included | |
| T + 2 | S1 | GRU | MMN | all included | all included |
| S2 | GRU | MMN | all included | all excluded | |
| S3 | GRU | MMN | B.L. excluded | all included | |
| S4 | GRU | MMN | B.L. excluded | all excluded | |
| S5 | GRU | PCA + MAN | all included | all included | |
| S6 | bi-GRU | PCA + MAN | all included | all included |
| Num. of Layers | Input Time Steps | Num. of Hidden Units | ||
|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | ||
| 1 | 5~10 | 1 | - | - |
| 2 | 10, 20, 30 | 1 | - | |
| 3 | 10, 20, 30, 40 | 10 | 1 | |
| Prediction Target | Scenario | NSE | RMSE (m3/s) | MAE (m3/s) |
|---|---|---|---|---|
| T + 1 | S1 | 0.045 | 9.552 | 7.790 |
| S2 | 0.046 | 10.225 | 7.355 | |
| S3 | 0.023 | 5.634 | 6.849 | |
| S4 | 0.037 | 8.915 | 8.325 | |
| S5 | 0.023 | 5.713 | 4.693 | |
| S6 | 0.028 | 7.409 | 5.436 | |
| T + 2 | S1 | 0.116 | 15.080 | 7.983 |
| S2 | 0.148 | 15.370 | 13.799 | |
| S3 | 0.061 | 10.062 | 6.825 | |
| S4 | 0.110 | 14.560 | 10.106 | |
| S5 | 0.057 | 9.825 | 5.762 | |
| S6 | 0.068 | 11.105 | 5.143 |
| Prediction Target | Scenario | NSE | RMSE (m3/s) | MAE (m3/s) |
|---|---|---|---|---|
| T + 1 | S1 | 0.937 | 50.088 | 24.089 |
| S2 | 0.945 | 47.449 | 21.276 | |
| S3 | 0.927 | 54.695 | 28.848 | |
| S4 | 0.951 | 44.132 | 19.868 | |
| S5 | 0.941 | 48.402 | 24.178 | |
| S6 | 0.946 | 46.511 | 20.147 | |
| T + 2 | S1 | 0.835 | 82.436 | 38.032 |
| S2 | 0.745 | 98.346 | 42.062 | |
| S3 | 0.836 | 81.469 | 39.625 | |
| S4 | 0.801 | 89.179 | 37.733 | |
| S5 | 0.828 | 84.130 | 39.014 | |
| S6 | 0.836 | 81.069 | 36.293 |
| Lead Time | Case (Year/Month/Day) | Flow (m3/s) | Relative Error (%) | |||||
|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | |||
| T + 1 | 2012/9/3 | 2020 | 16.75 | 4.12 | 13.94 | 14.48 | 4.30 | 17.95 |
| 2013/7/24 | 2200 | 9.97 | 8.75 | 2.63 | 11.81 | 24.40 | 1.81 | |
| 2014/9/17 | 1520 | 6.77 | 7.44 | 31.15 | 1.22 | 9.32 | 7.19 | |
| Mean | - | 11.17 | 6.77 | 15.90 | 9.17 | 12.68 | 8.99 | |
| T + 2 | 2012/9/3 | 2020 | 38.85 | 57.00 | 18.58 | 17.83 | 14.66 | 18.89 |
| 2013/7/24 | 2200 | 35.74 | 54.11 | 46.29 | 26.52 | 16.18 | 11.80 | |
| 2014/9/17 | 1520 | 19.63 | 31.87 | 11.23 | 33.44 | 33.64 | 32.70 | |
| Mean | - | 31.41 | 47.66 | 25.37 | 25.93 | 21.49 | 21.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Liu, Y.; Yue, Q.; Zheng, Y.; Yao, X.; Yu, J. Impact of Input Filtering and Architecture Selection Strategies on GRU Runoff Forecasting: A Case Study in the Wei River Basin, Shaanxi, China. Water 2020, 12, 3532. https://doi.org/10.3390/w12123532
Wang Q, Liu Y, Yue Q, Zheng Y, Yao X, Yu J. Impact of Input Filtering and Architecture Selection Strategies on GRU Runoff Forecasting: A Case Study in the Wei River Basin, Shaanxi, China. Water. 2020; 12(12):3532. https://doi.org/10.3390/w12123532
Chicago/Turabian StyleWang, Qianyang, Yuan Liu, Qimeng Yue, Yuexin Zheng, Xiaolei Yao, and Jingshan Yu. 2020. "Impact of Input Filtering and Architecture Selection Strategies on GRU Runoff Forecasting: A Case Study in the Wei River Basin, Shaanxi, China" Water 12, no. 12: 3532. https://doi.org/10.3390/w12123532
APA StyleWang, Q., Liu, Y., Yue, Q., Zheng, Y., Yao, X., & Yu, J. (2020). Impact of Input Filtering and Architecture Selection Strategies on GRU Runoff Forecasting: A Case Study in the Wei River Basin, Shaanxi, China. Water, 12(12), 3532. https://doi.org/10.3390/w12123532




