Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China
Abstract
:1. Introduction
- How does COSIPY perform in modeling the observed SMB variability of Urumqi Glacier No. 1?
- Can the implementation of locally more specific bare-ice albedos improve performance?
- Can modeled MB variations explain discharge variability downstream, and how strong is the influence of Urumqi Glacier No. 1 on the variance of runoff from the catchment?
2. Materials and Methods
2.1. COSIPY
2.2. Albedo Parameterization
2.3. Atmospheric Forcing of COSIPY
2.4. Observation Data for Model Validation
3. Results
3.1. Surface Mass Balance Modeling
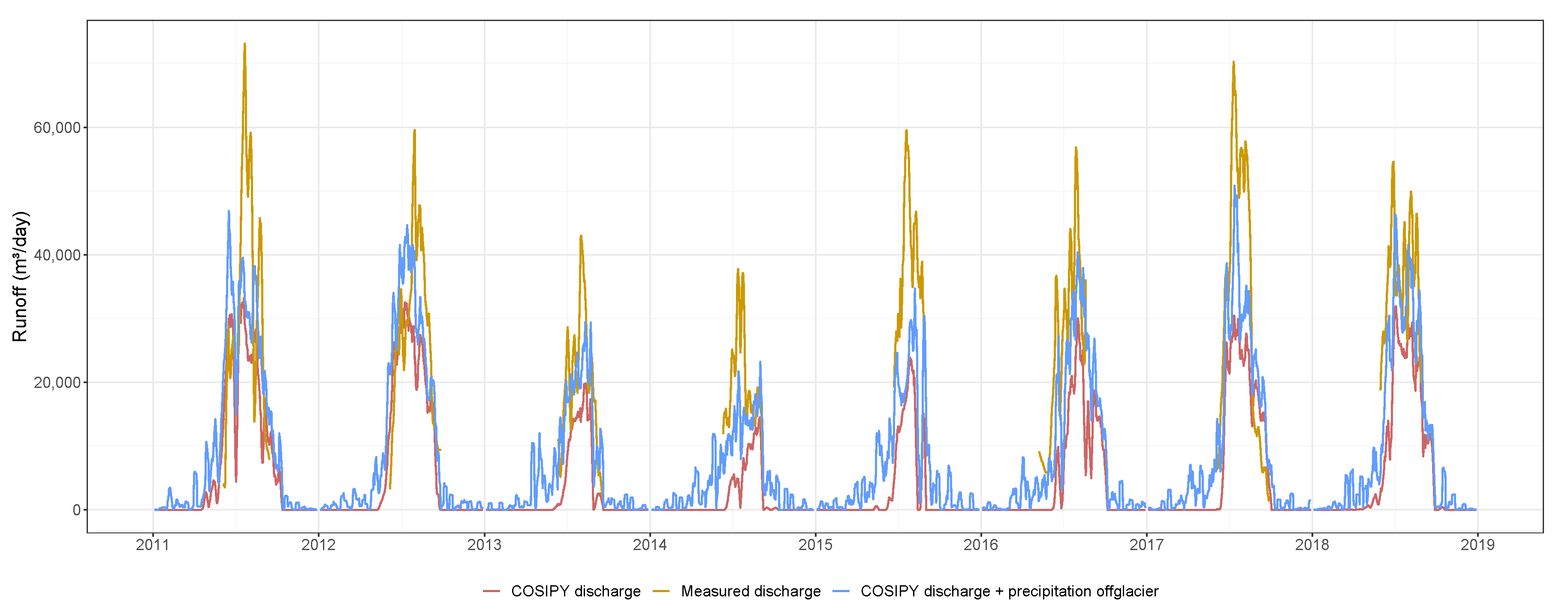
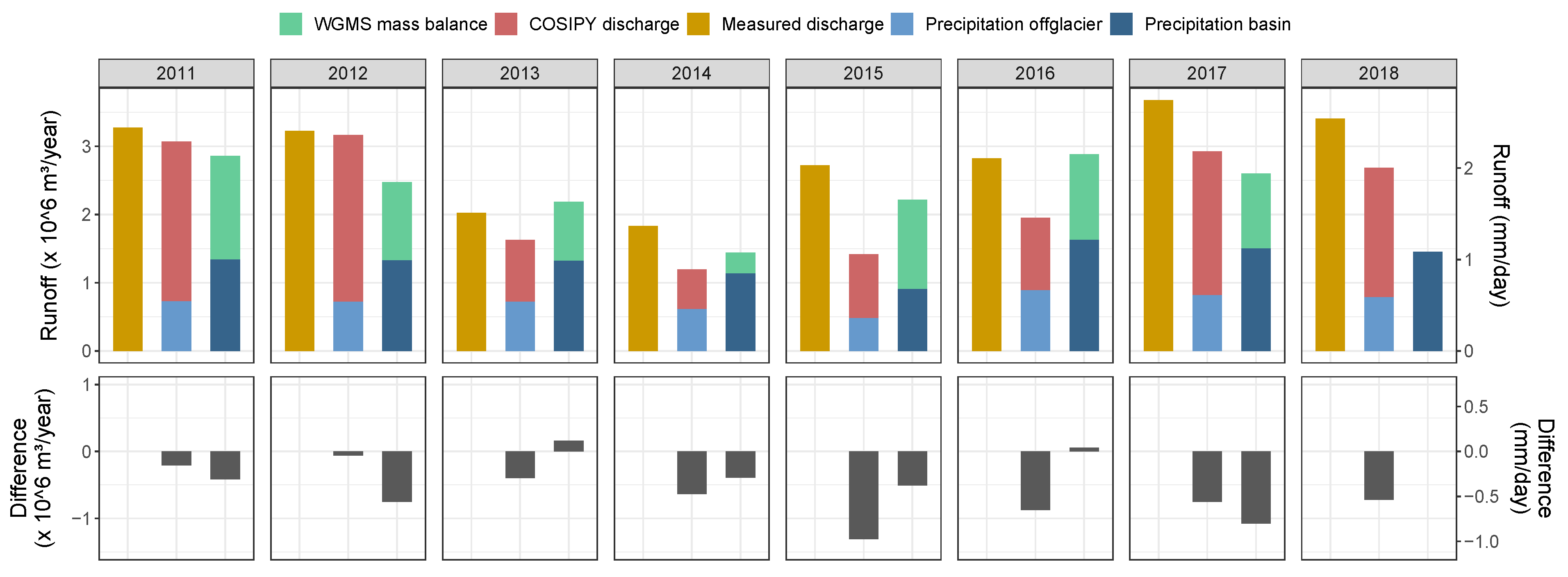
3.2. Discharge Derived from Glacier Mass Balance Modeling and Estimation of Catchment Runoff
4. Discussion
4.1. Surface Mass Balance Modeling and Associated Uncertainties
4.2. Albedo Parameterization and Associated Uncertainties
4.3. Approximation of Discharge and Associated Uncertainties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms |
| AWS Automatic weather station. |
| COSIMA COupled Snowpack and Ice surface energy and MAss balance model. |
| COSIPY COupled Snowpack and Ice surface energy and mass balance model in PYthon. |
| DEM Digital elevation model. |
| ECMWF European Centre for Medium-Range Weather Forecasts. |
| ERA5 ECMWF Reanalysis 5 th Generation. |
| MB Mass balance. |
| MBE Mean bias error. |
| RGI 6.0 Randolph Glacier Inventory 6.0. |
| RMSE Root mean squared error. |
| SEB Surface energy balance. |
| SLA Snow line altitude. |
| SMB Surface mass balance. |
| SRTM Shuttle Radar Topography Mission. |
| UG1 Urumqi Glacier No. 1. |
| USGS U.S. Geological Survey. |
| WGMS World Glacier Monitoring Service. |
| List of constants | |||
| Symbol | Description | Unit | Default Value |
| Latent heat of fusion | 3.34 × 105 | ||
| Latent heat of sublimation | 2.849 × 106 | ||
| Latent heat of vaporization | 2.514 × 106 | ||
| Zero temperature | K | 273.16 | |
| List of symbols | ||
| Symbol | Description | Unit |
| F | Energy flux | |
| G | Solar radiation | |
| N | Cloud cover fraction | - |
| Surface pressure | ||
| Ground heat flux | ||
| Latent heat flux | ||
| Energy available for surface melt | ||
| Sensible heat flux | ||
| Relative humidity in 2 m | % | |
| RRR | Precipitation | mm |
| SF | Mass gain by snowfall | |
| Air temperature at 2 m | K | |
| Surface temperature | K | |
| U10 | WS10 component in direction x | |
| U2 | Wind speed at 2 m | |
| V10 | WS10 component in direction y | |
| Volumetric fraction of ice | - | |
| Liquid water content | - | |
| Albedo | - | |
| Firn albedo | - | |
| Fresh snow albedo | - | |
| Bare ice albedo | - | |
| Density of ice | ||
| Density of fresh snow | ||
| Landsat spectral band number | - | |
| Water vapor pressure of the air | hPa | |
| Water vapor pressure at the surface | hPa | |
| Incoming longwave radiation | ||
| Outgoing longwave radiation | ||
| Incoming shortwave radiation | ||
| Subsurface temperature | K | |
| Temperature lapse rate | ||
References
- Kong, Y.; Pang, Z. Evaluating the sensitivity of glacier rivers to climate change based on hydrograph separation of discharge. J. Hydrol. 2012, 434, 121–129. [Google Scholar] [CrossRef]
- Huss, M.; Sold, L.; Hoelzle, M.; Stokvis, M.; Salzmann, N.; Farinotti, D.; Zemp, M. Towards remote monitoring of sub-seasonal glacier mass balance. Ann. Glaciol. 2013, 54, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.; Li, H.; Duan, Z.; Ren, Z.; Meng, X.; Pan, X. Modelling glacier variation and its impact on water resource in the Urumqi Glacier No. 1 in Central Asia. Sci. Total Environ. 2018, 644, 1160–1170. [Google Scholar] [CrossRef] [PubMed]
- Pelto, M.S. Skykomish River, Washington: Impact of ongoing glacier retreat on streamflow. Hydrol. Process. 2011, 25, 3356–3363. [Google Scholar] [CrossRef]
- Huss, M. Present and future contribution of glacier storage change to runoff from macroscale drainage basins in Europe. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Koboltschnig, G.R.; Schöner, W. The relevance of glacier melt in the water cycle of the Alps: The example of Austria. Hydrol. Earth Syst. Sci. 2011, 15, 2039–2048. [Google Scholar] [CrossRef] [Green Version]
- Bliss, A.; Hock, R.; Radić, V. Global response of glacier runoff to twenty-first century climate change. J. Geophys. Res. Earth Surf. 2014, 119, 717–730. [Google Scholar] [CrossRef]
- Carturan, L.; De Blasi, F.; Cazorzi, F.; Zoccatelli, D.; Bonato, P.; Borga, M.; Dalla Fontana, G. Relevance and Scale Dependence of Hydrological Changes in Glacierized Catchments: Insights from Historical Data Series in the Eastern Italian Alps. Water 2019, 11, 89. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Luo, Y.; Sun, L. Quantifying future changes in glacier melt and river runoff in the headwaters of the Urumqi River, China. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Bershaw, J.; Lechler, A.R. The isotopic composition of meteoric water along altitudinal transects in the Tian Shan of Central Asia. Chem. Geol. 2019, 516, 68–78. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z.; Wang, W.; Wang, W. Rapid decrease of observed mass balance in the Urumqi Glacier No. 1, Tianshan Mountains, central Asia. Quat. Int. 2014, 349, 135–141. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Zhang, M.; Wang, F.; Li, H. Observed changes in streamflow at the headwaters of the Urumqi River, eastern Tianshan, central Asia. Hydrol. Process. 2010. [Google Scholar] [CrossRef]
- Ye, B.; Yang, D.; Jiao, K.; Han, T.; Jin, Z.; Yang, H.; Li, Z. The Urumqi River source Glacier No. 1, Tianshan, China: Changes over the past 45 years. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Han, T.; Ding, Y.; Ye, B.; Liu, S.; Jiao, K. Mass-balance characteristics of Ürümqi glacier No. 1, Tien Shan, China. Ann. Glaciol. 2006, 43, 323–328. [Google Scholar] [CrossRef] [Green Version]
- Mingjie, G.; Tianding, H.; Baisheng, Y.; Keqin, J. Characteristics of melt water discharge in the Glacier No. 1 basin, headwater of Urumqi River. J. Hydrol. 2013, 489, 180–188. [Google Scholar] [CrossRef]
- Li, Z.; Li, H.; Chen, Y. Mechanisms and simulation of accelerated shrinkage of continental glaciers: A case study of Urumqi Glacier No. 1 in eastern Tianshan, Central Asia. J. Earth Sci. 2011, 22, 423–430. [Google Scholar] [CrossRef]
- Li, Z.; Yongping, S.; Huilin, L.; Zhiwen, D.; Liwei, W. Response of the Melting Urumqi Glacier No. 1 in Eastern Tianshan to Climate Change. Adv. Clim. Chang. Res. 2008, 4, 67–72. [Google Scholar]
- Takeuchi, N.; Li, Z. Characteristics of Surface Dust on Ürümqi Glacier No. 1 in the Tien Shan Mountains, China. Arct. Antarct. Alp. Res. 2008, 40, 744–750. [Google Scholar] [CrossRef]
- WGMS. Glacier Mass Balance Bulletin; No. 12 (20 ed.; Vol. 12, ICSU(WDS)/IUGG(IACS)/UNEP/ UNESCO/WMO; World Glacier Monitoring Service: Zurich, Switzerland, 2013. [Google Scholar] [CrossRef]
- Yuan, F.; Hao, Z.; Berndtsson, R.; Jiang, P.; Yasuda, H. The Mass Balance of Glacier No. 1 at the Headwaters of the Urumqi River in Relation to Northern Hemisphere Teleconnection Patterns. Water 2016, 8, 100. [Google Scholar] [CrossRef] [Green Version]
- Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Mölg, T.; Bolch, T.; Vorogushyn, S.; Güntner, A. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
- Che, Y.; Zhang, M.; Li, Z.; Wei, Y.; Nan, Z.; Li, H.; Wang, S.; Su, B. Energy balance model of mass balance and its sensitivity to meteorological variability on Urumqi River Glacier No.1 in the Chinese Tien Shan. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, P.; Li, Z.; Li, H.; Zhang, Z.; Xu, L.; Yue, X. Glaciers in Xinjiang, China: Past Changes and Current Status. Water 2020, 12, 2367. [Google Scholar] [CrossRef]
- Scherler, D.; Bookhagen, B.; Strecker, M.R. Spatially variable response of Himalayan glaciers to climate change affected by debris cover. Nat. Geosci. 2011, 4, 156–159. [Google Scholar] [CrossRef]
- Sagredo, E.; Lowell, T. Climatology of Andean glaciers: A framework to understand glacier response to climate change. Glob. Planet. Chang. 2012, 86-87, 101–109. [Google Scholar] [CrossRef]
- Adhikari, S.; Marshall, S.J. Influence of high-order mechanics on simulation of glacier response to climate change: Insights from Haig Glacier, Canadian Rocky Mountains. Cryosphere 2013, 7, 1527–1541. [Google Scholar] [CrossRef] [Green Version]
- Hock, R.; Holmgren, B. A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden. J. Glaciol. 2005, 51, 25–36. [Google Scholar] [CrossRef] [Green Version]
- Bolch, T.; Kulkarni, A.; Kaab, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The State and Fate of Himalayan Glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [Green Version]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Hammerle, A.; Niedrist, G.; Scholz, K.; Tomelleri, E.; Zhao, P. On the energy balance closure and net radiation in complex terrain. Agric. For. Meteorol. 2016, 226-227, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Mölg, T.; Maussion, F.; Yang, W.; Scherer, D. The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier. Cryosphere 2012, 6, 1445–1461. [Google Scholar] [CrossRef] [Green Version]
- Maussion, F.; Gurgiser, W.; Großhauser, M.; Kaser, G.; Marzeion, B. ENSO influence on surface energy and mass balance at Shallap Glacier, Cordillera Blanca, Peru. Cryosphere 2015, 9, 1663–1683. [Google Scholar] [CrossRef] [Green Version]
- Sauter, T.; Arndt, A.; Schneider, C. COSIPY v1.3—An open-source coupled snowpack and ice surface energy and mass balance model. Geosci. Model Dev. 2020. [Google Scholar] [CrossRef]
- Oerlemans, J.; Giesen, R.; Van Den Broeke, M. Retreating alpine glaciers: Increased melt rates due to accumulation of dust (Vadret da Morteratsch, Switzerland). J. Glaciol. 2009, 55, 729–736. [Google Scholar] [CrossRef] [Green Version]
- Qu, B.; Ming, J.; Kang, S.C.; Zhang, G.S.; Li, Y.W.; Li, C.D.; Zhao, S.Y.; Ji, Z.M.; Cao, J.J. The decreasing albedo of the Zhadang glacier on western Nyainqentanglha and the role of light-absorbing impurities. Atmos. Chem. Phys. 2014, 14, 11117–11128. [Google Scholar] [CrossRef] [Green Version]
- Brun, F.; Dumont, M.; Wagnon, P.; Berthier, E.; Azam, M.F.; Shea, J.M.; Sirguey, P.; Rabatel, A.; Ramanathan, A. Seasonal changes in surface albedo of Himalayan glaciers from MODIS data and links with the annual mass balance. Cryosphere 2015, 9, 341–355. [Google Scholar] [CrossRef] [Green Version]
- Mernild, S.H.; Malmros, J.K.; Yde, J.C.; Wilson, R.; Knudsen, N.T.; Hanna, E.; Fausto, R.S.; As, D.V. Albedo decline on Greenland’s Mittivakkat Gletscher in a warming climate. Int. J. Climatol. 2015, 35, 2294–2307. [Google Scholar] [CrossRef]
- Hoffman, M.J.; Fountain, A.G.; Liston, G.E. Distributed modeling of ablation (1996–2011) and climate sensitivity on the glaciers of Taylor Valley, Antarctica. J. Glaciol. 2016, 62, 215–229. [Google Scholar] [CrossRef] [Green Version]
- Machguth, H.; Paul, F.; Hoelzle, M.; Haeberli, W. Distributed glacier mass-balance modelling as an important component of modern multi-level glacier monitoring. Ann. Glaciol. 2006, 43, 335–343. [Google Scholar] [CrossRef] [Green Version]
- Fitzgerald, P.W.; Bamber, J.L.; Ridley, J.K.; Rougier, J.C. Exploration of parametric uncertainty in a surface mass balance model applied to the Greenland ice sheet: Exploration of Parametric Uncertainty. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Bergstrom, A.; Gooseff, M.; Myers, M.; Doran, P.T. The seasonal evolution of albedo across glaciers and the surrounding landscape of the Taylor Valley, Antarctica. Remote Sens. 2019. [Google Scholar] [CrossRef] [Green Version]
- Jonsell, U.; Hock, R.; Holmgren, B. Spatial and temporal variations in albedo on Storglaciären, Sweden. J. Glaciol. 2003, 49, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Naegeli, K.; Huss, M.; Hoelzle, M. Change detection of bare-ice albedo in the Swiss Alps. Cryosphere 2019, 13, 397–412. [Google Scholar] [CrossRef] [Green Version]
- Collier, E.; Maussion, F.; Nicholson, L.I.; Mölg, T.; Immerzeel, W.W.; Bush, A.B.G. Impact of debris cover on glacier ablation and atmosphere-glacier feedbacks in the Karakoram. Cryosphere 2015, 9, 1617–1632. [Google Scholar] [CrossRef] [Green Version]
- Ming, J.; Du, Z.; Xiao, C.; Xu, X.; Zhang, D. Darkening of the mid-Himalaya glaciers since 2000 and the potential causes. Environ. Res. Lett. 2012, 7, 014021. [Google Scholar] [CrossRef] [Green Version]
- Ming, J.; Xiao, C.; Wang, F.; Li, Z.; Li, Y. Grey Tienshan Urumqi Glacier No.1 and light-absorbing impurities. Environ. Sci. Pollut. Res. 2016, 23, 9549–9558. [Google Scholar] [CrossRef] [Green Version]
- Yue, X.; Zhao, J.; Li, Z.; Zhang, M.; Fan, J.; Wang, L.; Wang, P. Spatial and temporal variations of the surface albedo and other factors influencing Urumqi Glacier No. 1 in Tien Shan, China. J. Glaciol. 2017, 63, 899–911. [Google Scholar] [CrossRef] [Green Version]
- Naegeli, K.; Huss, M. Sensitivity of mountain glacier mass balance to changes in bare-ice albedo. Ann. Glaciol. 2017, 58, 119–129. [Google Scholar] [CrossRef] [Green Version]
- Naegeli, K.; Damm, A.; Huss, M.; Schaepman, M.; Hoelzle, M. Imaging spectroscopy to assess the composition of ice surface materials and their impact on glacier mass balance. Remote Sens. Environ. 2015, 168, 388–402. [Google Scholar] [CrossRef]
- Huintjes, E.; Sauter, T.; Schröter, B.; Maussion, F.; Yang, W.; Kropáček, J.; Buchroithner, M.; Scherer, D.; Kang, S.; Schneider, C. Evaluation of a Coupled Snow and Energy Balance Model for Zhadang Glacier, Tibetan Plateau, Using Glaciological Measurements and Time-Lapse Photography. Arct. Antarct. Alp. Res. 2015, 47, 573–590. [Google Scholar] [CrossRef]
- Sauter, T.; Arndt, A. COSIPY v1.3. 2020. Available online: https://github.com/cryotools/cosipy (accessed on 17 November 2020).
- Consortium, R.G.I. Randolph Glacier Inventory 6.0; Digital Media: Denver, CO, USA, 2017. [Google Scholar] [CrossRef]
- Oerlemans, J. Glaciers and Climate Change; Google-Books-ID: OJHXK91Ci1AC; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Coléou, C.; Lesaffre, B. Irreducible water saturation in snow: Experimental results in a cold laboratory. Ann. Glaciol. 1998, 26, 64–68. [Google Scholar] [CrossRef] [Green Version]
- Hantel, M.; Ehrendorfer, M.; Haslinger, A. Climate sensitivity of snow cover duration in Austria. Int. J. Climatol. 2000, 20, 615–640. [Google Scholar] [CrossRef]
- Vionnet, V.; Brun, E.; Morin, S.; Boone, A.; Faroux, S.; Le Moigne, P.; Martin, E.; Willemet, J.M. The detailed snowpack scheme Crocus and its implementation in SURFEX v7.2. Geosci. Model Dev. 2012, 5, 773–791. [Google Scholar] [CrossRef] [Green Version]
- Huintjes, E. Energy and Mass Balance Modelling for Glaciers on the Tibetan Plateau: Extension, Validation and Application of a Coupled Snow and Energy Balance Model. Ph.D. Thesis, Publikationsserver der RWTH Aachen University, Aachen, Germany, 2014. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Oerlemans, J.; Knap, W.H. A 1 year record of global radiation and albedo in the ablation zone of Morteratschgletscher, Switzerland. J. Glaciol. 1998, 44, 231–238. [Google Scholar] [CrossRef] [Green Version]
- Claverie, M.; Vermote, E.F.; Franch, B.; Masek, J.G. Evaluation of the Landsat-5 TM and Landsat-7 ETM+ surface reflectance products. Remote Sens. Environ. 2015, 169, 390–403. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- USGS. U.S. Geological Survey. Earth Explorer. 2020. Available online: https://earthexplorer.usgs.gov/ (accessed on 17 November 2020).
- Fugazza, D.; Senese, A.; Azzoni, R.S.; Maugeri, M.; Maragno, D.; Diolaiuti, G.A. New evidence of glacier darkening in the Ortles-Cevedale group from Landsat observations. Glob. Planet. Chang. 2019, 178, 35–45. [Google Scholar] [CrossRef]
- Liang, S. Narrowband to broadband conversions of land surface albedo I Algorithms. Remote Sens. Environ. 2000, 76, 213–238. [Google Scholar] [CrossRef]
- Naegeli, K.; Damm, A.; Huss, M.; Wulf, H.; Schaepman, M.; Hoelzle, M. Cross-Comparison of Albedo Products for Glacier Surfaces Derived from Airborne and Satellite (Sentinel-2 and Landsat 8) Optical Data. Remote Sens. 2017, 9, 110. [Google Scholar] [CrossRef] [Green Version]
- Knap, W.H.; Reijmer, C.H.; Oerlemans, J. Narrowband to broadband conversion of Landsat TM glacier albedos. Int. J. Remote Sens. 1999, 20, 2091–2110. [Google Scholar] [CrossRef]
- Wang, J.; Ye, B.; Cui, Y.; He, X.; Yang, G. Spatial and temporal variations of albedo on nine glaciers in western China from 2000 to 2011: The Variations of Albedo on Nine Glaciers in Western China. Hydrol. Process. 2014, 28, 3454–3465. [Google Scholar] [CrossRef]
- Pope, E.L.; Willis, I.C.; Pope, A.; Miles, E.S.; Arnold, N.S.; Rees, W.G. Contrasting snow and ice albedos derived from MODIS, Landsat ETM+ and airborne data from Langjökull, Iceland. Remote Sens. Environ. 2016, 175, 183–195. [Google Scholar] [CrossRef] [Green Version]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers; Google-Books-ID: Jca2v1u1EKEC; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- ECMWF. Copernicus Climate Change Service. 2020. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 17 November 2020).
- Stull, R. Practical Meteorology; OCLC: 955055316; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Brock, B.W.; Willis, I.C.; Sharp, M.J. Measurement and parameterization of aerodynamic roughness length variations at Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2006, 52, 281–297. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, P.A.; González-Rouco, J.F.; Montávez, J.P.; García-Bustamante, E.; Navarro, J.; Dudhia, J. Analysis of the long-term surface wind variability over complex terrain using a high spatial resolution WRF simulation. Clim. Dyn. 2013, 40, 1643–1656. [Google Scholar] [CrossRef]
- Shea, J.; Wagnon, P.; Immerzeel, W.; Biron, R.; Brun, F.; Pellicciotti, F. A comparative high-altitude meteorological analysis from three catchments in the Nepalese Himalaya. Int. J. Water Resour. Dev. 2015, 31, 174–200. [Google Scholar] [CrossRef] [Green Version]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth’s land surface areas. Sci. Data 2017, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferreira, M.; Santos, A.; Lucio, P. Short-term forecast of wind speed through mathematical models. Energy Rep. 2019, 5, 1172–1184. [Google Scholar] [CrossRef]
- Ramon, J.; Lledó, L.; Torralba, V.; Soret, A.; Doblas-Reyes, F.J. What global reanalysis best represents near-surface winds? Q. J. R. Meteorol. Soc. 2019, 145, 3236–3251. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.; Li, Z.; Jin, S.; Xu, C.; Deng, H.; Zhang, M. Runoff Changes from Urumqi Glacier No. 1 over the Past 60 Years, Eastern Tianshan, Central Asia. Water 2020, 12, 1286. [Google Scholar] [CrossRef]
- Wang, P.; Li, Z.; Li, H.; Wang, W.; Yao, H. Comparison of glaciological and geodetic mass balance at Urumqi Glacier No. 1, Tian Shan, Central Asia. Glob. Planet. Chang. 2014, 114, 14–22. [Google Scholar] [CrossRef]
- WGMS. Fluctuations of Glaciers Database; World Glacier Monitoring Service (WGMS): Zurich, Switzerland, 2019. [Google Scholar] [CrossRef]
- Ostrem, G.; Brugman, M. Glacier Mass-Balance Measurements—A Manual for Field and Office Work; Technical Report 4; Geographisches Institut Universität Zurich: Zurich, Switzerland, 1991. [Google Scholar]
- TGS. The Annual Report; Technical Report; Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Carturan, L.; Cazorzi, F.; De Blasi, F.; Dalla Fontana, G. Air temperature variability over three glaciers in the Ortles–Cevedale (Italian Alps): Effects of glacier fragmentation, comparison of calculation methods, and impacts on mass balance modeling. Cryosphere 2015, 9, 1129–1146. [Google Scholar] [CrossRef] [Green Version]
- Petersen, L.; Pellicciotti, F. Spatial and temporal variability of air temperature on a melting glacier: Atmospheric controls, extrapolation methods and their effect on melt modeling, Juncal Norte Glacier, Chile: Temperature Variability over a Glacier. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Petersen, L.; Pellicciotti, F.; Juszak, I.; Carenzo, M.; Brock, B. Suitability of a constant air temperature lapse rate over an Alpine glacier: Testing the Greuell and Böhm model as an alternative. Ann. Glaciol. 2013, 54, 120–130. [Google Scholar] [CrossRef] [Green Version]
- Greuell, W.; Knap, W.H.; Smeets, P.C. Elevational changes in meteorological variables along a midlatitude glacier during summer. J. Geophys. Res. Atmos. 1997, 102, 25941–25954. [Google Scholar] [CrossRef]
- Greuell, W.; Böhm, R. 2 m temperatures along melting mid-latitude glaciers, and implications for the sensitivity of the mass balance to variations in temperature. J. Glaciol. 1998, 44, 9–20. [Google Scholar] [CrossRef] [Green Version]
- Shea, J.M.; Moore, R.D. Prediction of spatially distributed regional-scale fields of air temperature and vapor pressure over mountain glaciers. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.Y.; Kim, J.; Boo, K.O.; Shim, S.; Kim, Y. Intercomparison of precipitation datasets for summer precipitation characteristics over East Asia. Clim. Dyn. 2019, 52, 3005–3022. [Google Scholar] [CrossRef] [Green Version]
- Cogley, J.G. Geodetic and direct mass-balance measurements: Comparison and joint analysis. Ann. Glaciol. 2009, 50, 96–100. [Google Scholar] [CrossRef] [Green Version]
- Andreassen, L.M.; Elvehøy, H.; Kjøllmoen, B.; Engeset, R.V. Reanalysis of long-term series of glaciological and geodetic mass balance for 10 Norwegian glaciers. Cryosphere 2016, 10, 535–552. [Google Scholar] [CrossRef] [Green Version]
- Soruco, A.; Vincent, C.; Francou, B.; Ribstein, P.; Berger, T.; Sicart, J.; Wagnon, P.; Arnaud, Y.; Favier, V.; Lejeune, Y. Mass balance of Glaciar Zongo, Bolivia, between 1956 and 2006, using glaciological, hydrological and geodetic methods. Ann. Glaciol. 2009, 50, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Klok, E.J.; Greuell, W.; Oerlemans, J. Temporal and spatial variation of the surface albedo of Morteratschgletscher, Switzerland, as derived from 12 Landsat images. J. Glaciol. 2003, 49, 491–502. [Google Scholar] [CrossRef] [Green Version]
- Arnold, N.S.; Rees, W.G.; Hodson, A.J.; Kohler, J. Topographic controls on the surface energy balance of a high Arctic valley glacier. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Azzoni, R.S.; Senese, A.; Zerboni, A.; Maugeri, M.; Smiraglia, C.; Diolaiuti, G.A. Estimating ice albedo from fine debris cover quantified by a semi-automatic method: The case study of Forni Glacier, Italian Alps. Cryosphere 2016, 10, 665–679. [Google Scholar] [CrossRef] [Green Version]
- Jepsen, S.M.; Adams, E.E.; Priscu, J.C. Sediment Melt-Migration Dynamics in Perennial Antarctic Lake Ice. Arct. Antarct. Alp. Res. 2010, 42, 57–66. [Google Scholar] [CrossRef]
- Greuell, W. Melt-water accumulation on the surface of the greenland ice sheet: Effect on albedo and mass balance. Geogr. Ann. Ser. A Phys. Geogr. 2000, 82, 489–498. [Google Scholar] [CrossRef]
- Paul, F.; Machguth, H.; Kääb, A. On the impact of glacier albedo under conditions of extreme glacier melt: The summer of 2003 in the ALPS. EARSeL eProc. 2005, 4, 139–149. [Google Scholar]
- Oerlemans, J. The Microclimate of Valley Glaciers. In Igitur, Utrecht Publishing & Archiving Services; Archiving Services; Universiteitsbibliotheek Utrecht: Utrecht, The Netherlands, 2010; p. 138. [Google Scholar]
- Fugazza, D.; Senese, A.; Azzoni, R.S.; Maugeri, M.; Diolaiuti, G.A. Spatial distribution of surface albedo at the Forni Glacier (Stelvio National Park, Central Italian Alps). Cold Reg. Sci. Technol. 2016, 125, 128–137. [Google Scholar] [CrossRef]
- Nolin, A.W.; Phillippe, J.; Jefferson, A.; Lewis, S.L. Present-day and future contributions of glacier runoff to summertime flows in a Pacific Northwest watershed: Implications for water resources: Late Summer Glacier Runoff in a Pacific NW Watershed. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Frenierre, J.L.; Mark, B.G. A review of methods for estimating the contribution of glacial meltwater to total watershed discharge. Prog. Phys. Geogr. Earth Environ. 2014, 38, 173–200. [Google Scholar] [CrossRef]
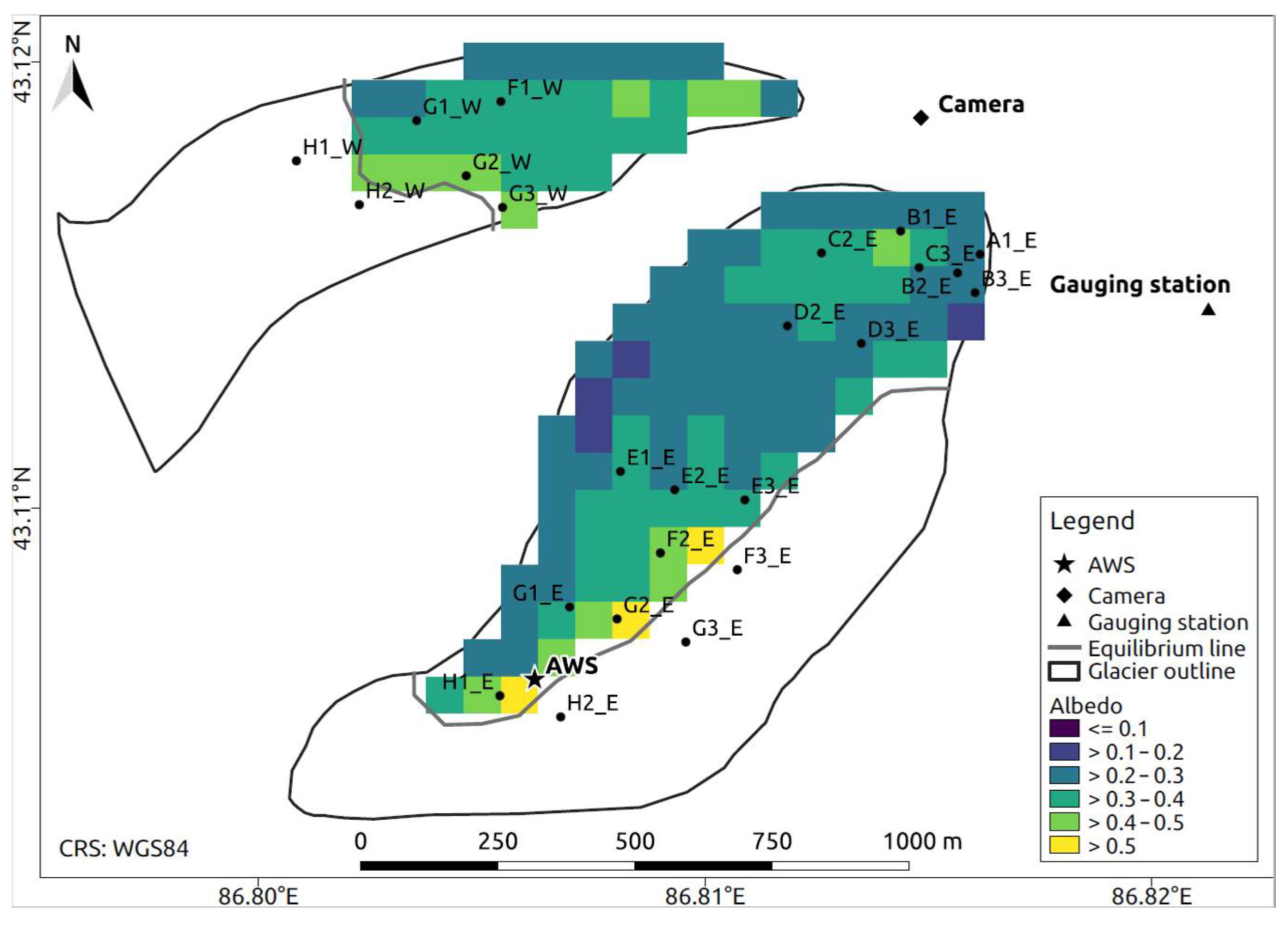
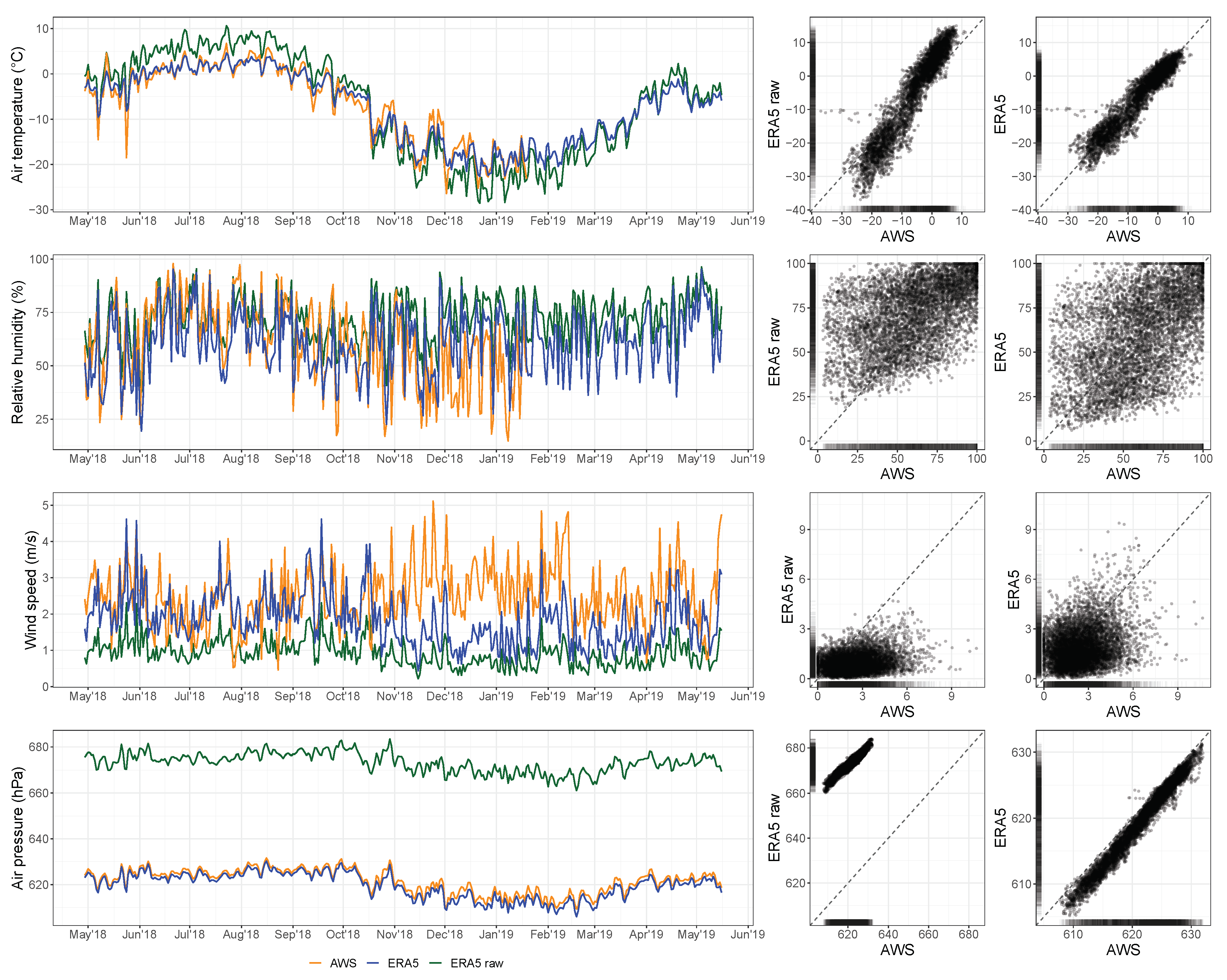
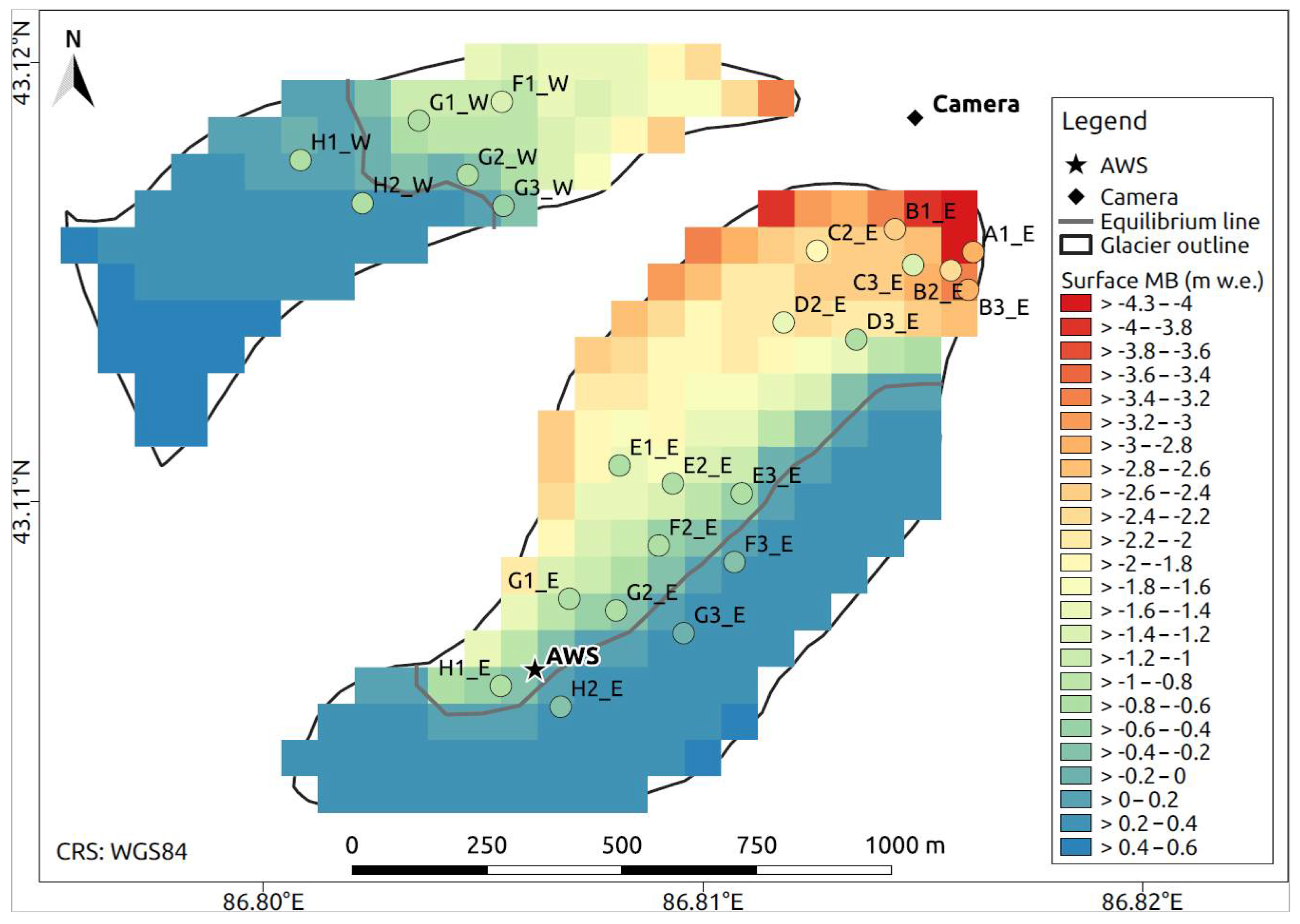
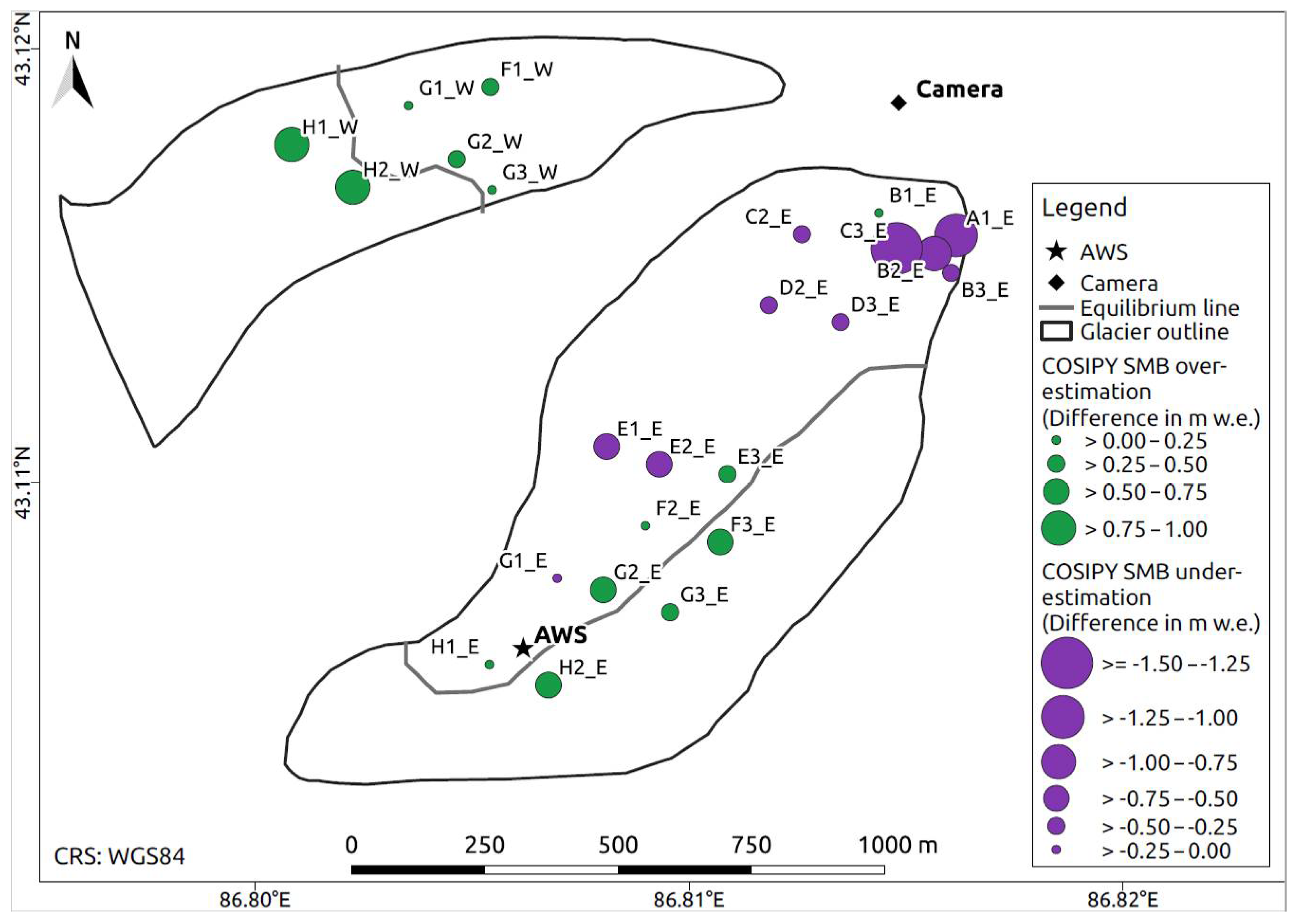
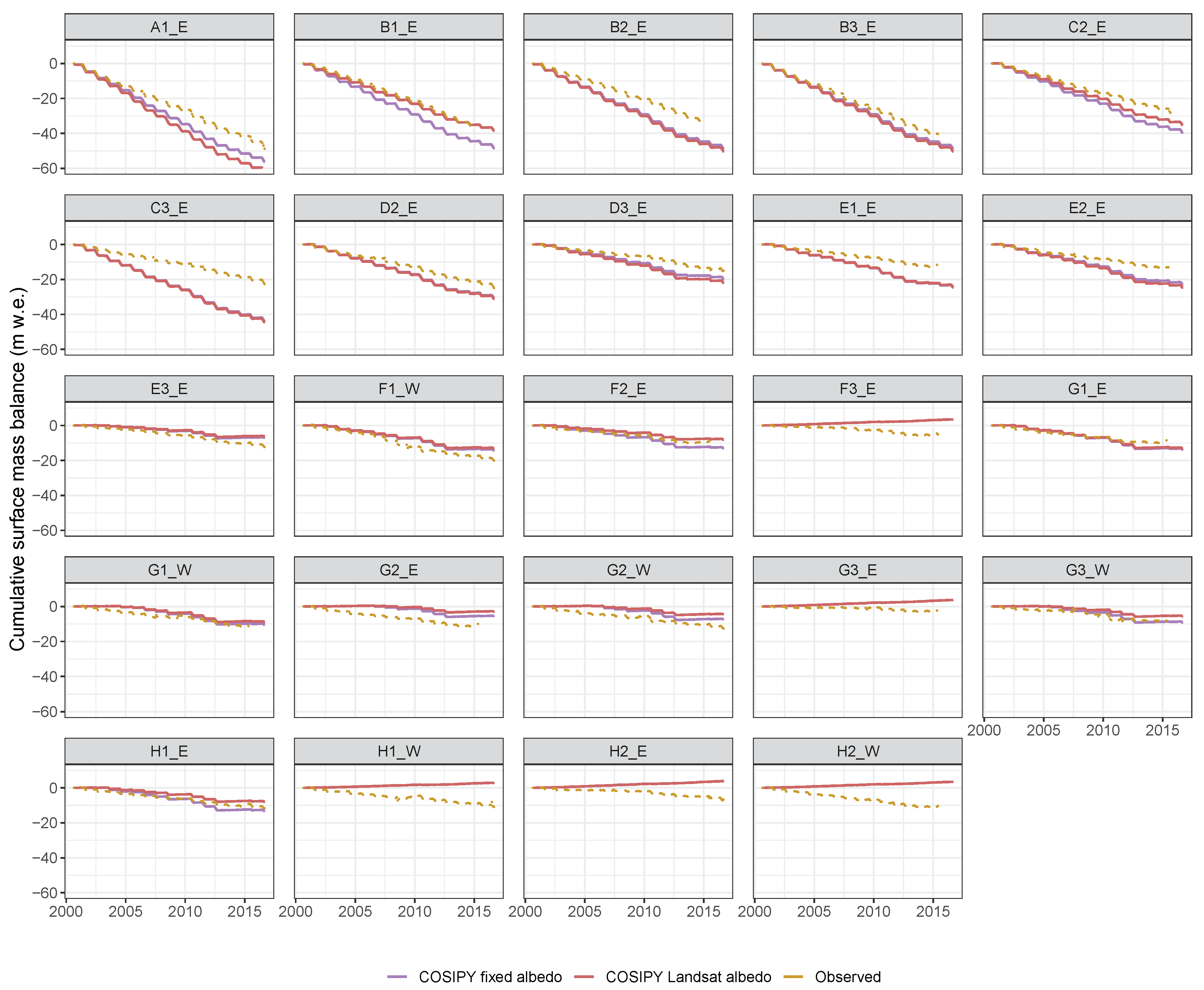

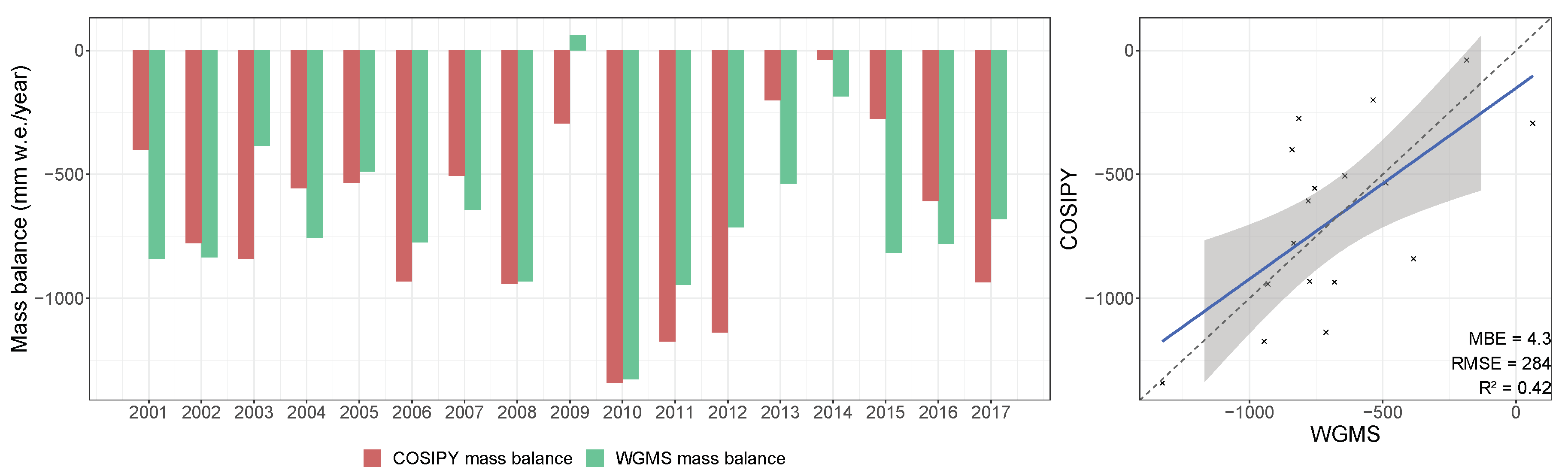

| Data Set | Period | Time Step | Function/Purpose |
|---|---|---|---|
| Digital elevation model (SRTM) | - | static | Modeling |
| Glacier outline (RGI 6.0) | 2007 | static | Modeling |
| ERA5 | 2000–2020 | hourly | Model forcing |
| AWS | April 2018–May 2019 | hourly | Downscaling |
| Landsat 7 | 2 September 2012 | - | Albedo parameterization |
| Landsat 7 | 5 September 2013 | - | Albedo parameterization |
| Landsat 7 | 27 July 2016 | - | Albedo parameterization |
| Landsat 8 | 4 August 2016 | - | Albedo parameterization |
| Landsat 8 | 13 August 2019 | - | Albedo parameterization |
| Ablation stakes | August 2000–September 2014 (2016) | monthly, in summer | Model validation |
| Time-lapse photography | 1 July 2018–29 December 2018 | 1–2 per day | Model validation |
| Discharge measurements | 2011–2018 | daily, in summer | Model validation |
| Variable | Description | Unit |
|---|---|---|
| Surface pressure | hPa | |
| Air temperature | K | |
| Relative humidity | % | |
| G | Incoming solar radiation | W m |
| Wind speed | m s | |
| Total precipitation | mm | |
| N | Cloud cover fraction | − |
| Variable | Downscaling Approach ERA5 Data to AWS | Spatial Integration Approach from AWS to Distributed Fields on Glacier |
|---|---|---|
| Air pressure | Barometric formula | Barometric formula |
| Air temperature | Quantile mapping | Lapse rate |
| Cloud cover fraction N | - | - |
| Incoming shortwave radiation | - | Radiation modeling [30] |
| Relative humidity | Quantile mapping | - |
| Total precipitation | - | - |
| Wind speed | Logarithmic wind profile, Scaling factor of 2 | - |
| Raw | Downscaled | ||||
|---|---|---|---|---|---|
| Variable | RMSE | MBE | RMSE | MBE | R2 |
| (day) | |||||
| (day) | |||||
| (day) | |||||
| (day) | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thiel, K.; Arndt, A.; Wang, P.; Li, H.; Li, Z.; Schneider, C. Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China. Water 2020, 12, 3297. https://doi.org/10.3390/w12123297
Thiel K, Arndt A, Wang P, Li H, Li Z, Schneider C. Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China. Water. 2020; 12(12):3297. https://doi.org/10.3390/w12123297
Chicago/Turabian StyleThiel, Kira, Anselm Arndt, Puyu Wang, Huilin Li, Zhongqin Li, and Christoph Schneider. 2020. "Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China" Water 12, no. 12: 3297. https://doi.org/10.3390/w12123297
APA StyleThiel, K., Arndt, A., Wang, P., Li, H., Li, Z., & Schneider, C. (2020). Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China. Water, 12(12), 3297. https://doi.org/10.3390/w12123297





