Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Observation Data
2.2. Trend Analysis Methods
2.2.1. Innovative Trend Analysis (ITA)
2.2.2. Traditional Trend Analysis Methods
2.3. Pearson’s Correlation
3. Results and Discussions
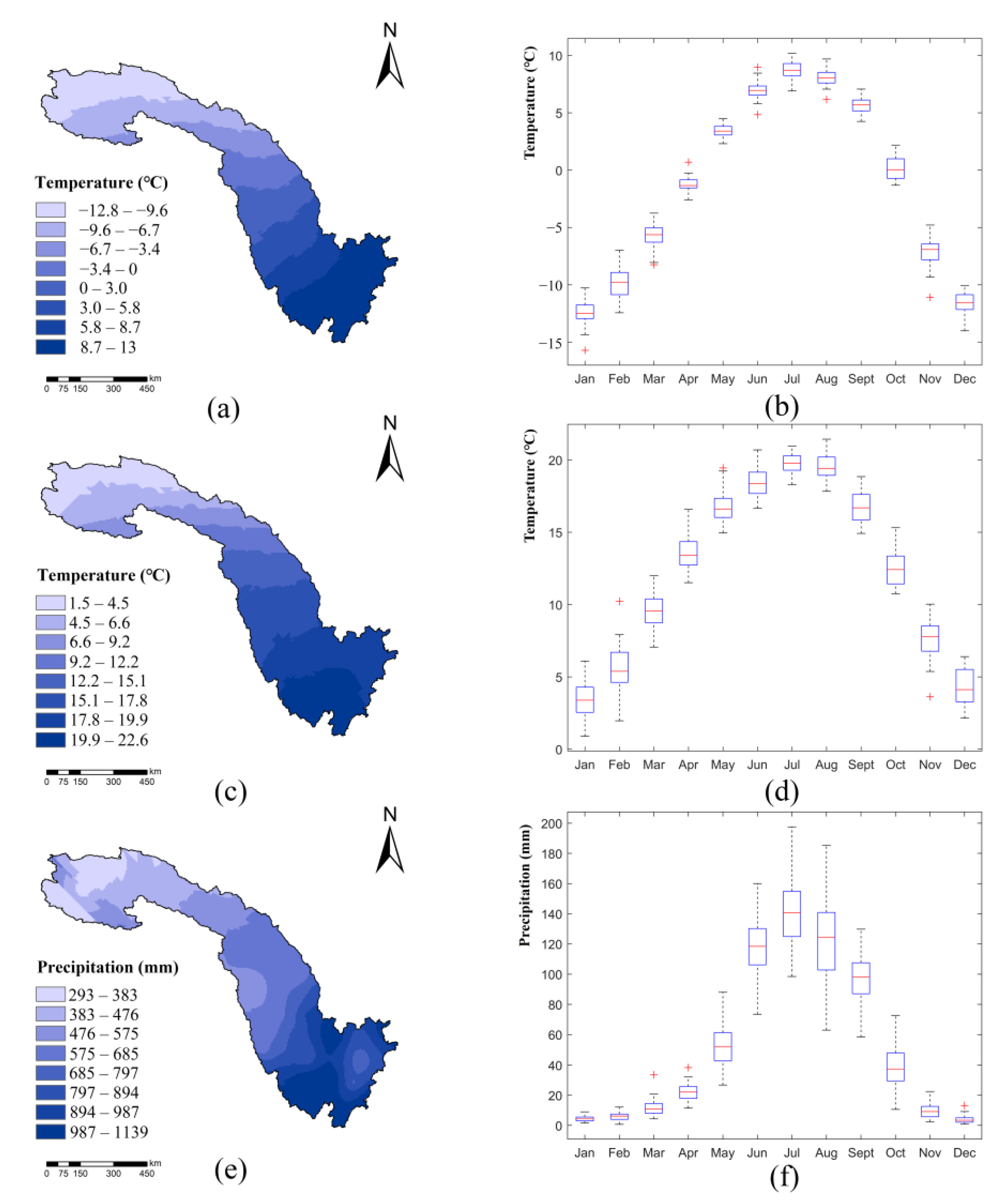
3.1. Temperature Trends
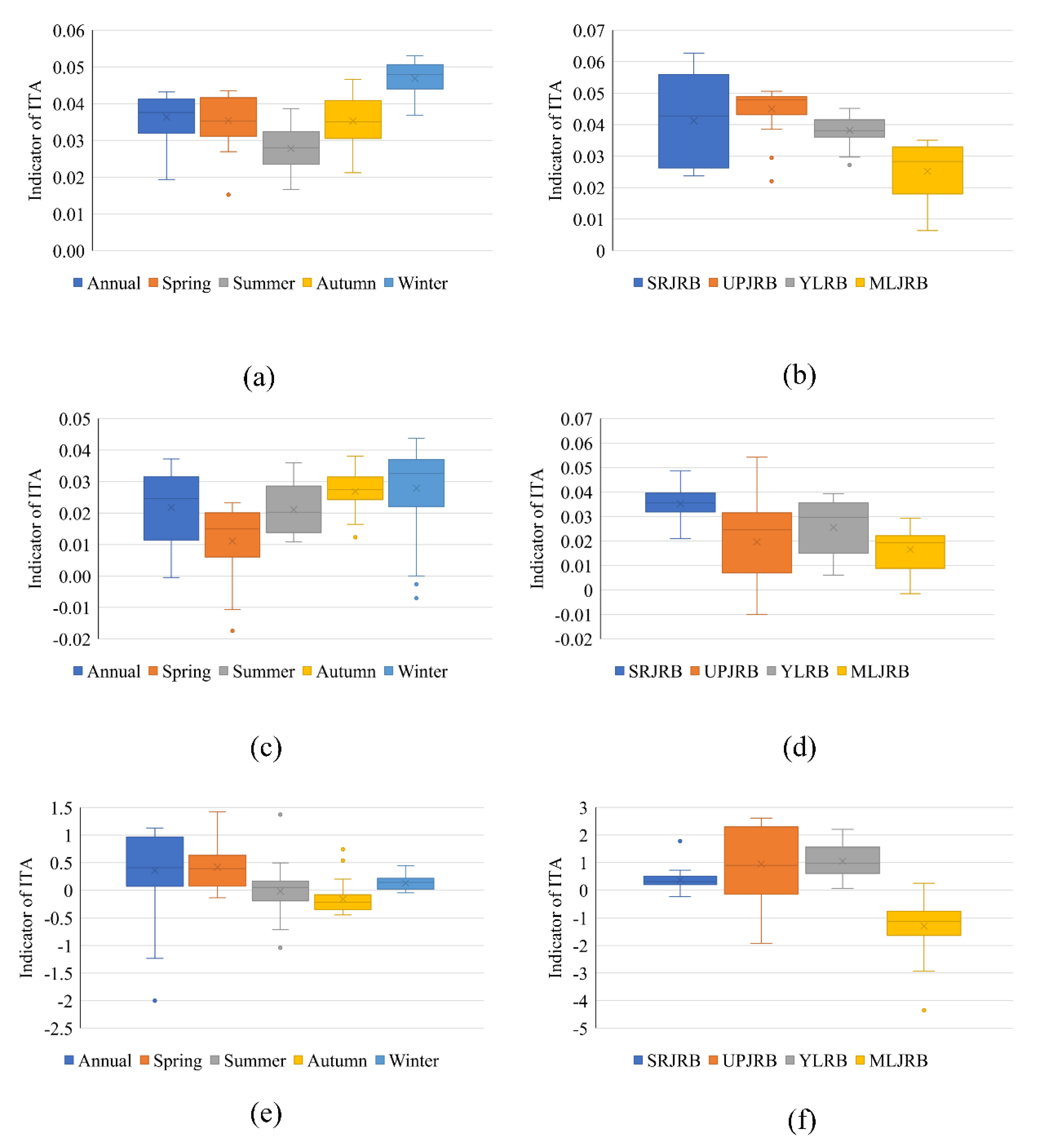
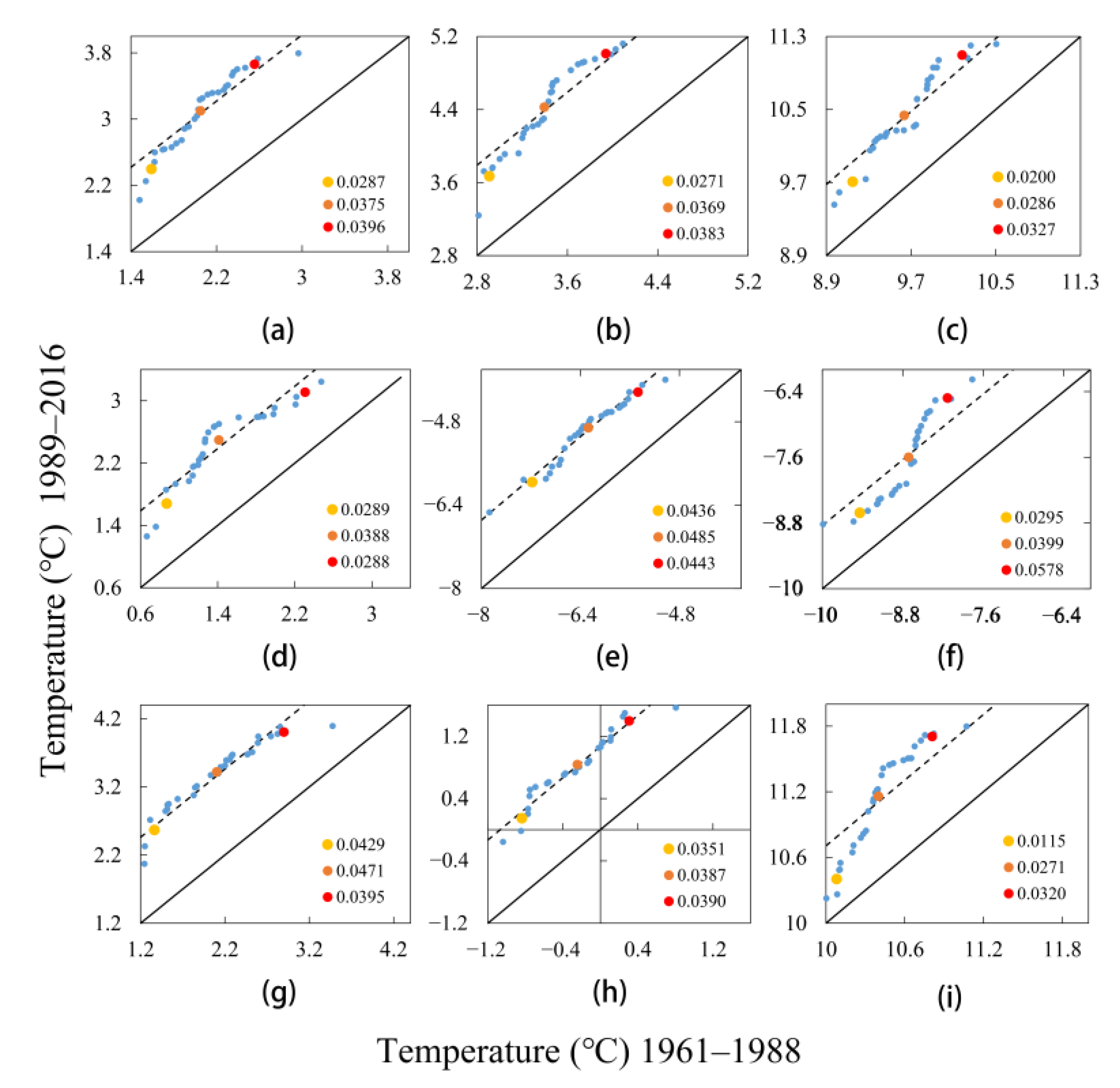
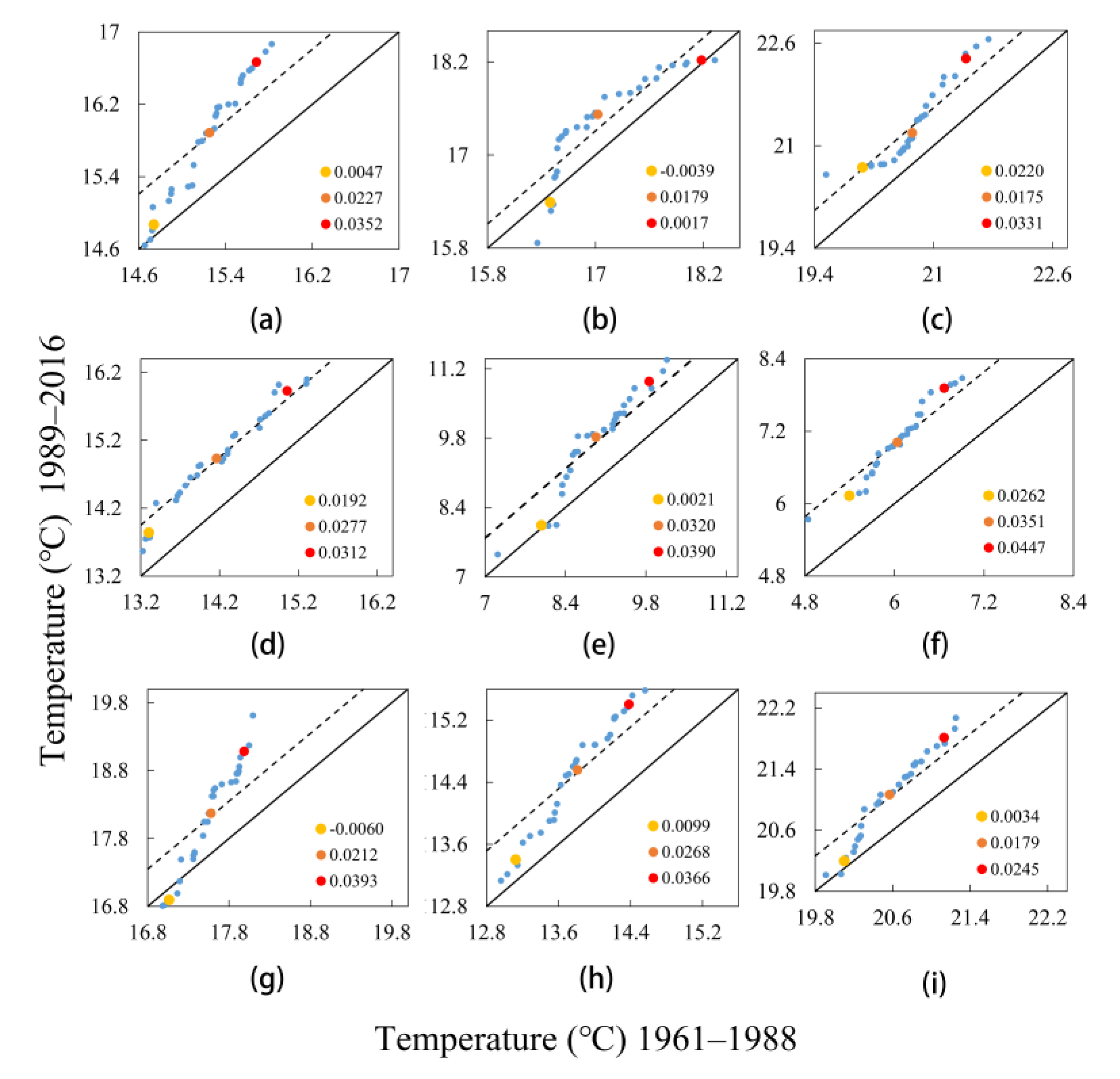
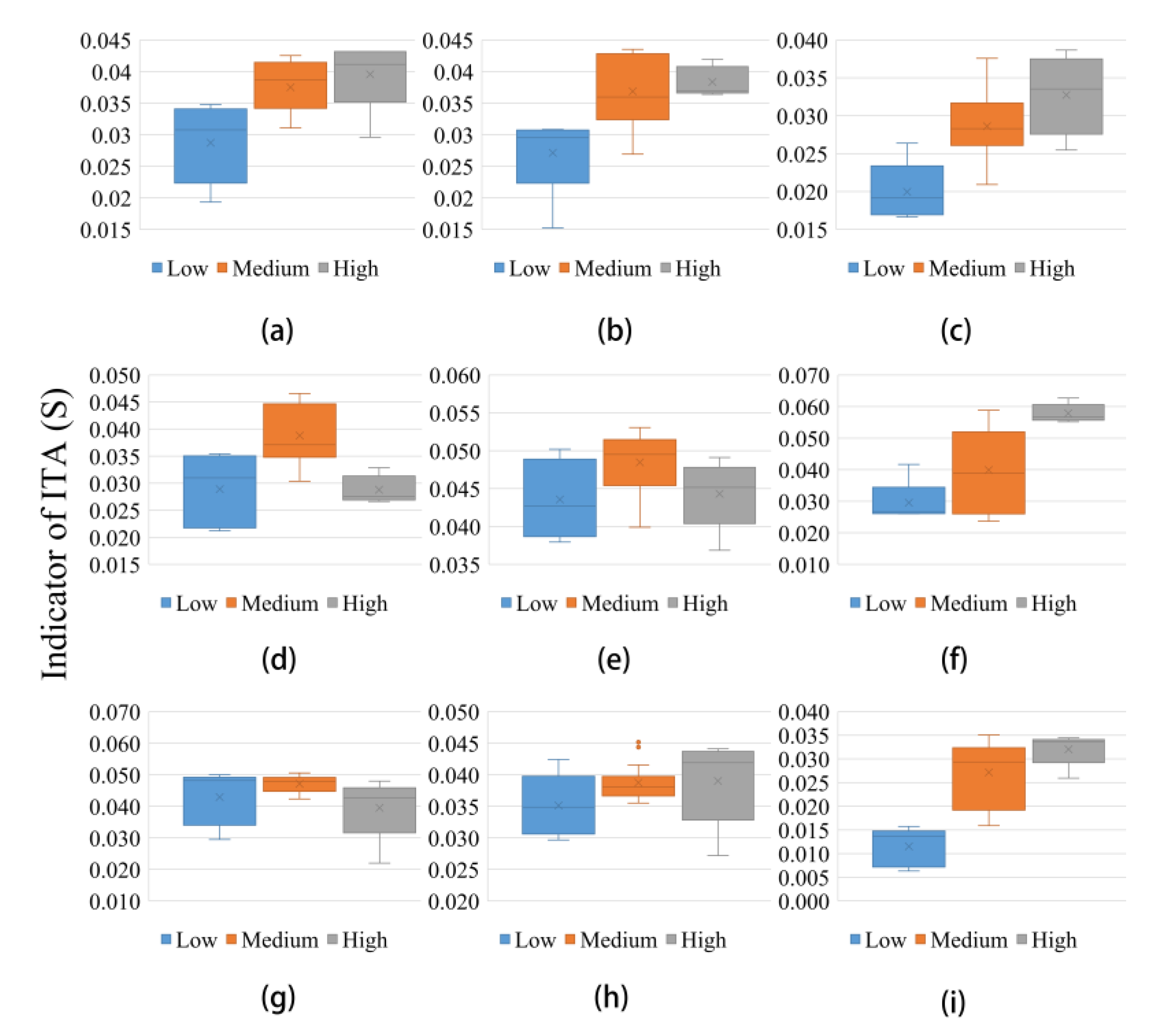
3.1.1. Annual and Seasonal Trends
3.1.2. Spatial Patterns of Trends
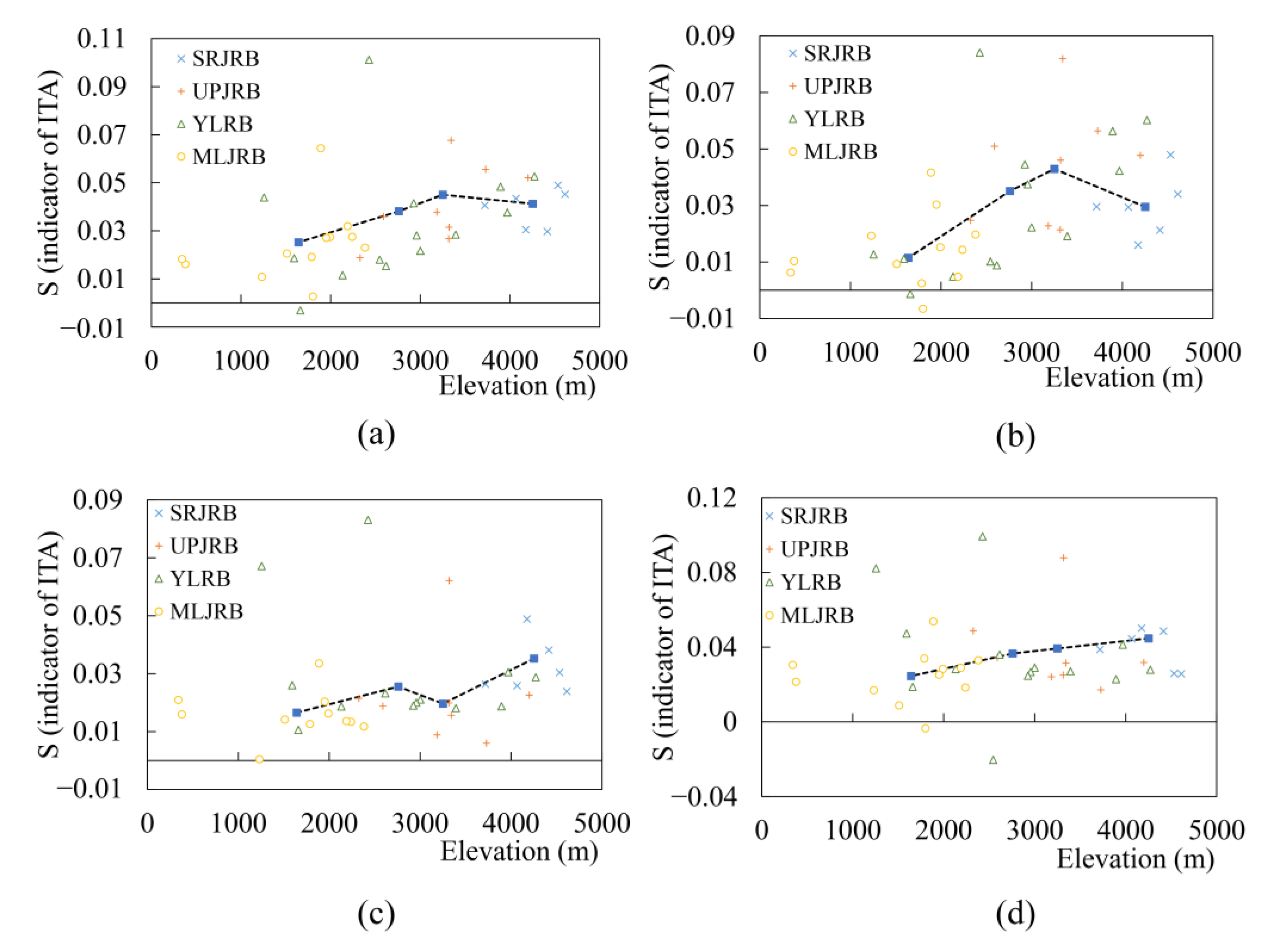
3.1.3. Potential Impacts of Temperature Trends
3.2. Precipitation Trends
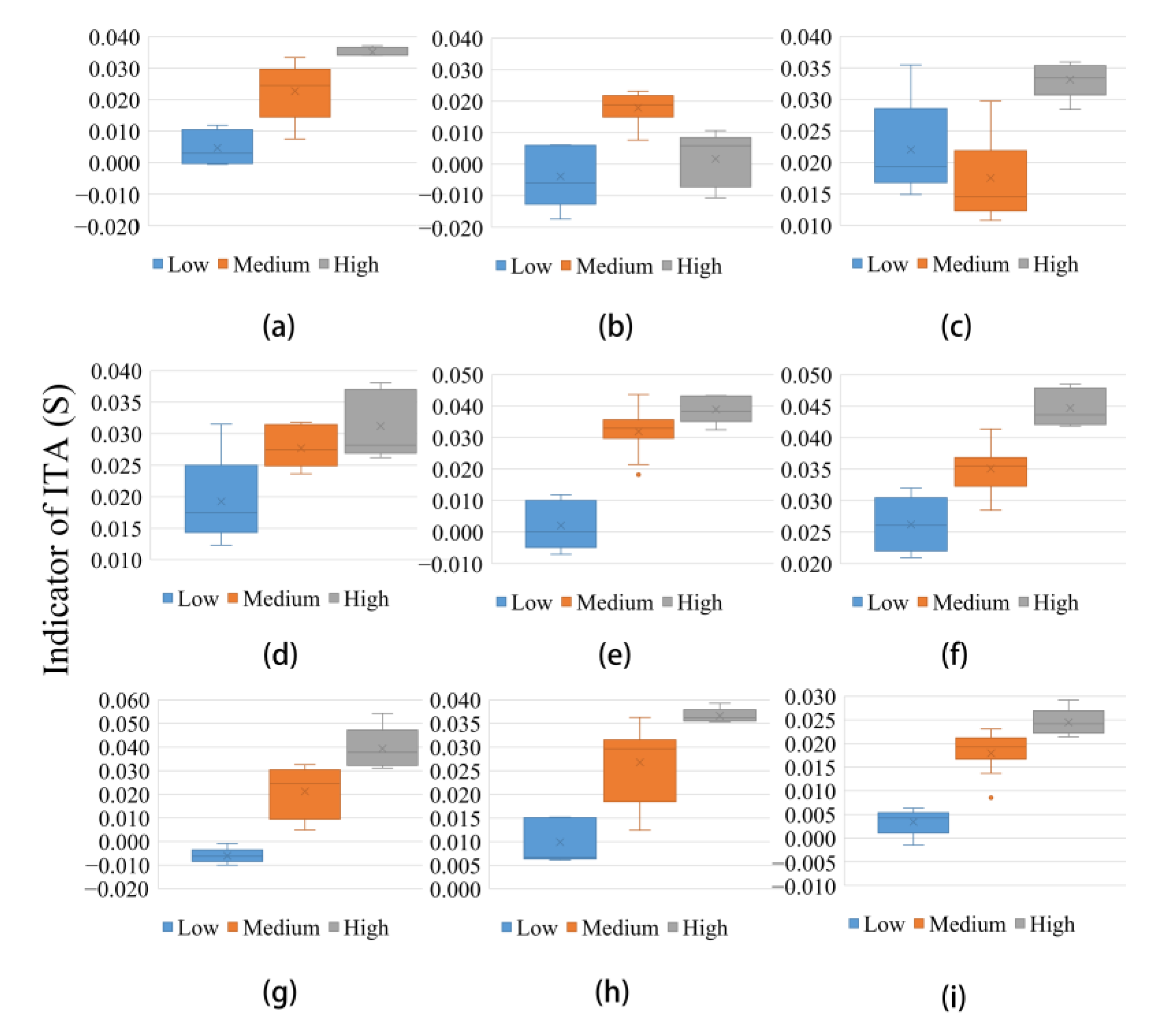
3.2.1. Annual and Seasonal Trends
3.2.2. Spatial Patterns of Precipitation Trends
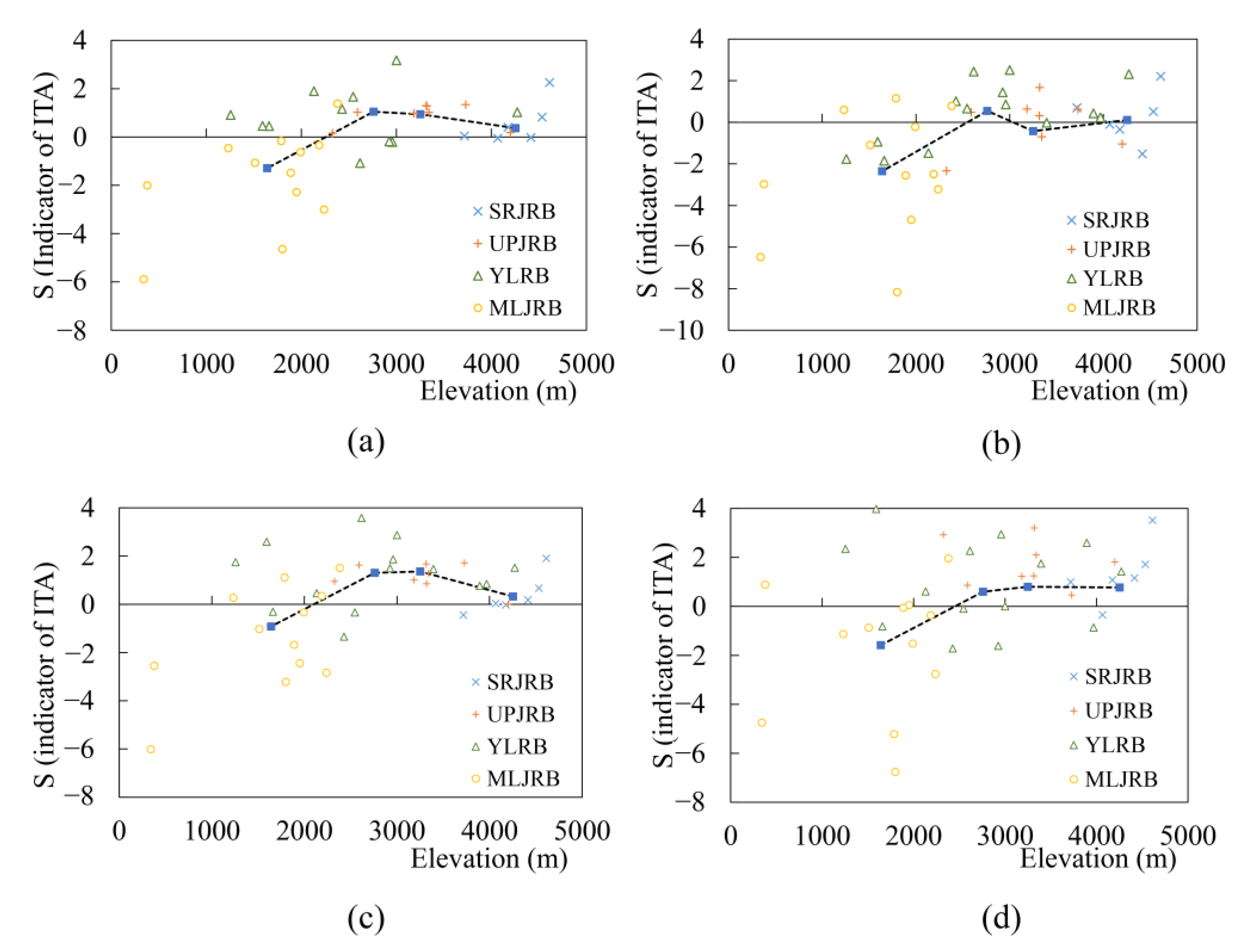
3.2.3. Potential Impact of Precipitation Trends
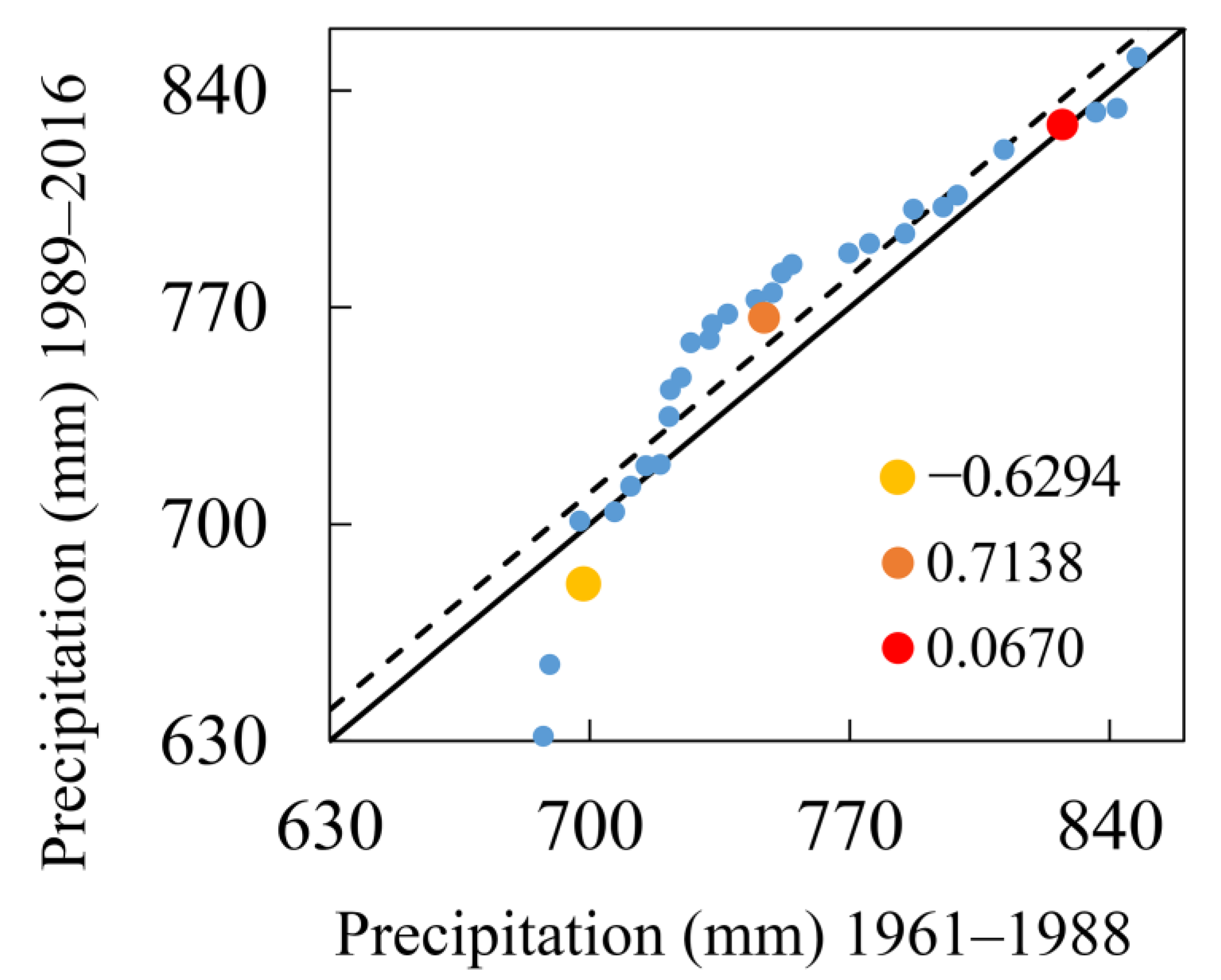
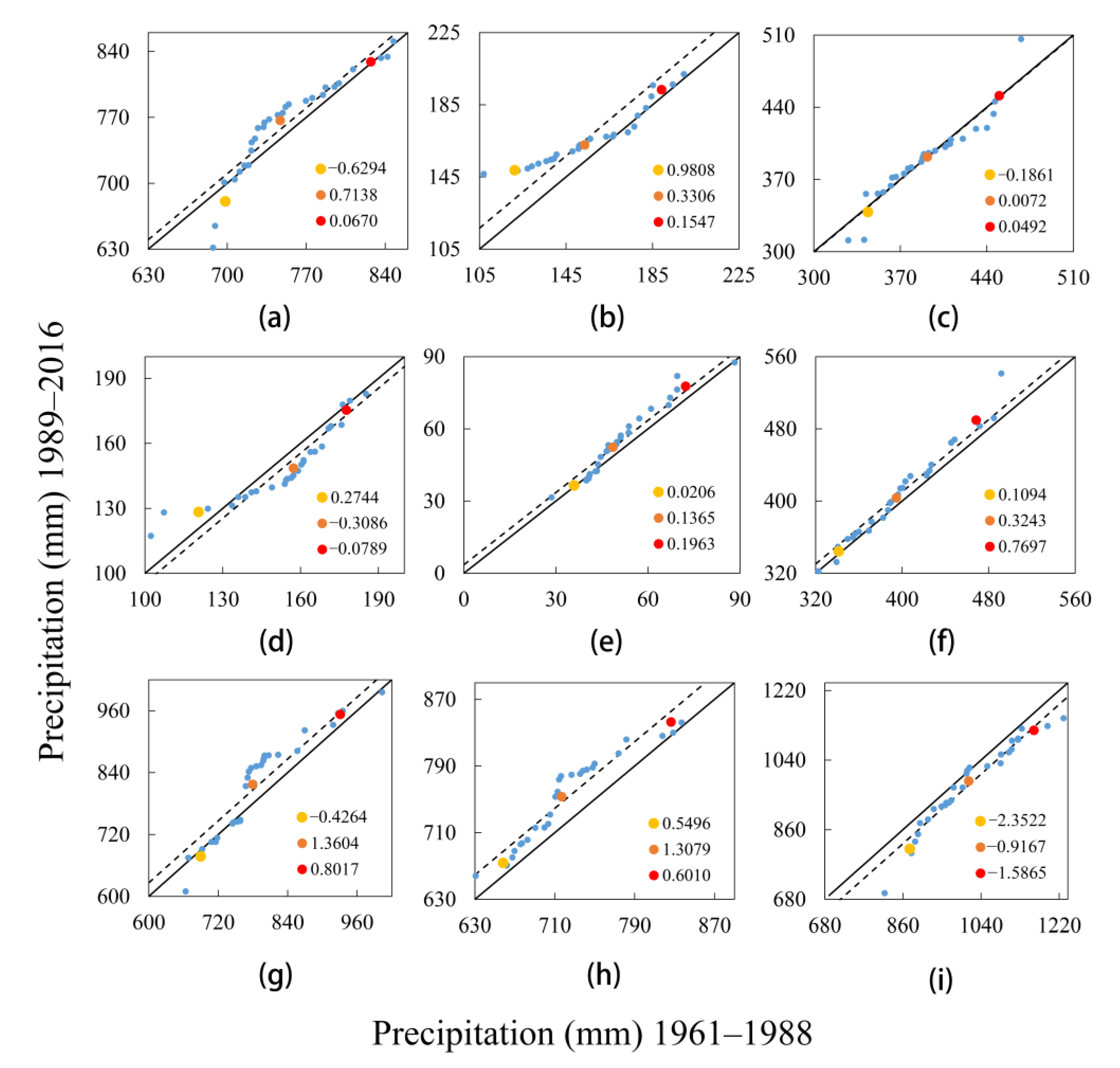
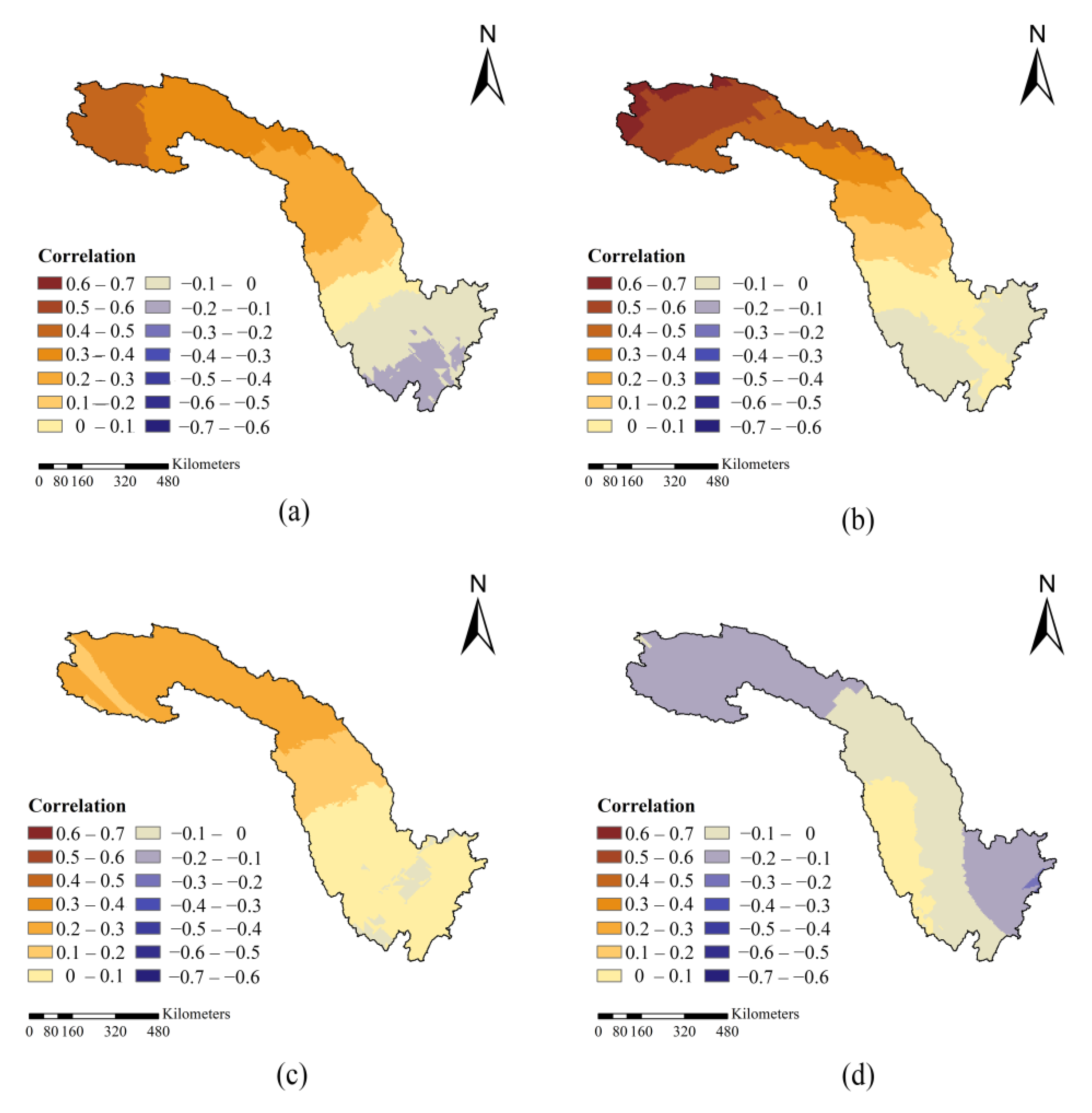
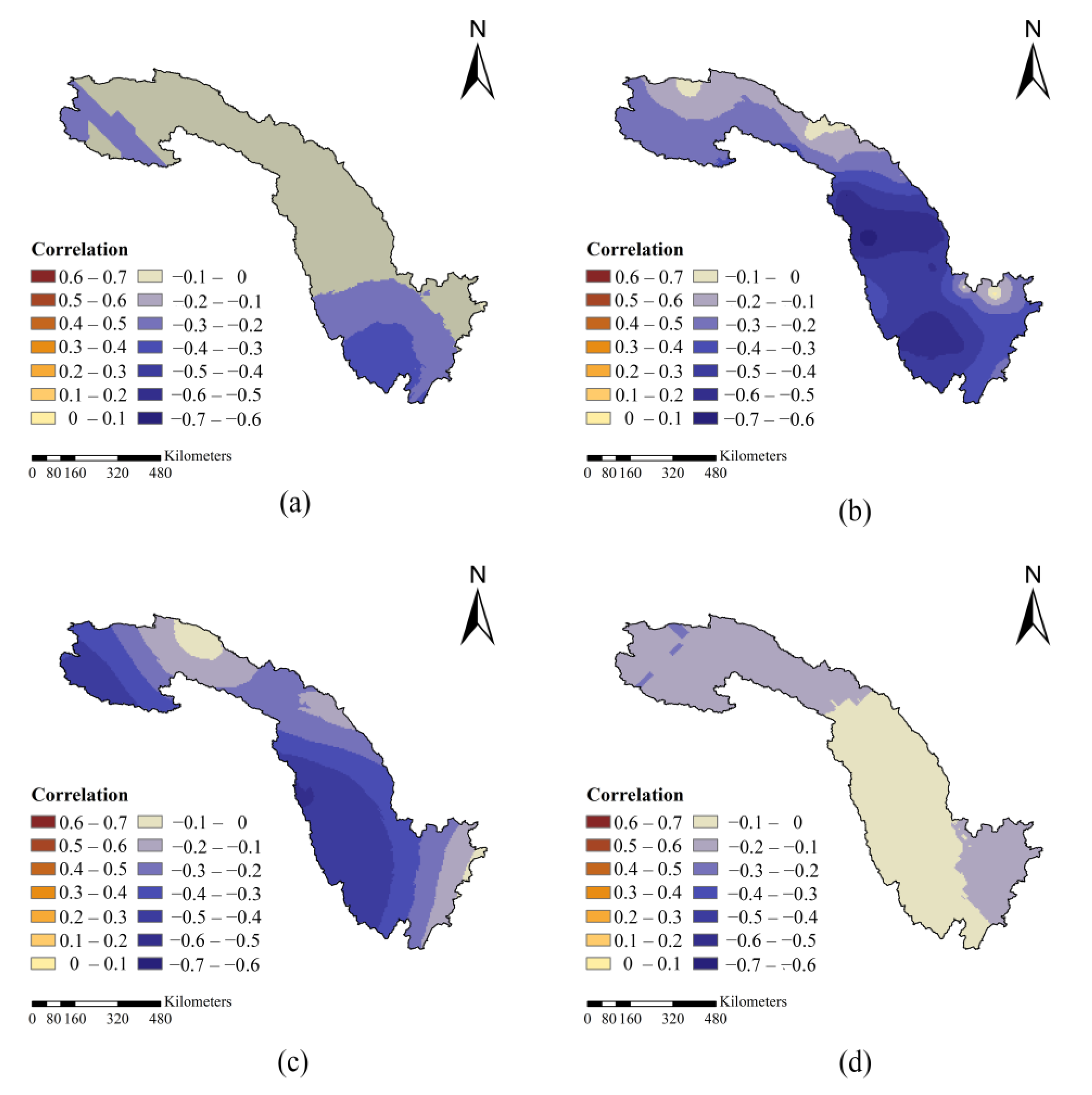
3.3. Relationship between Air Temperature and Precipitation
4. Conclusions
- (1)
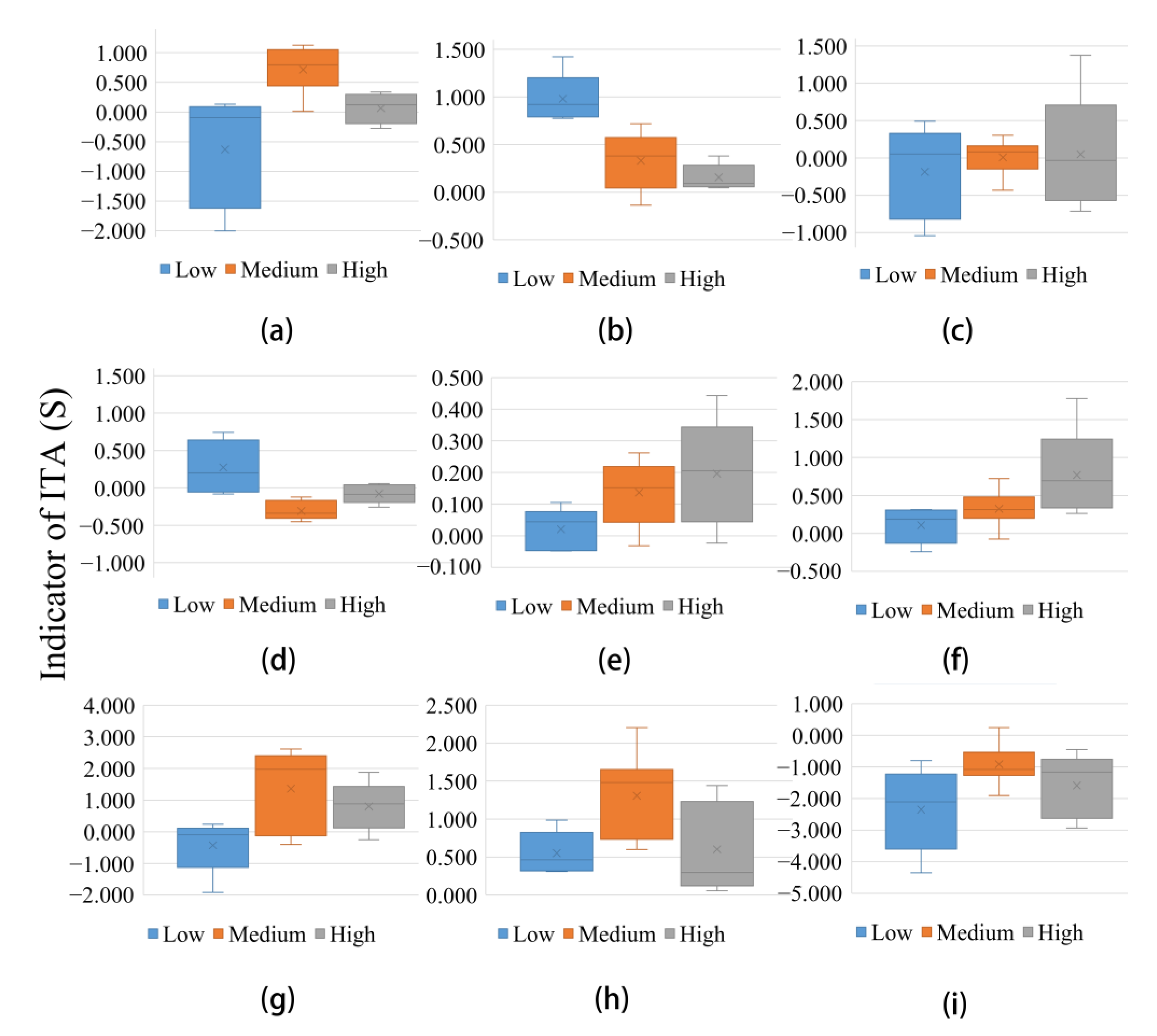
- Annual and seasonal temperatures showed significant increasing trends over the JRB at a 99% confidence level. Subcategory (low, medium, and high) results indicate that the increasing trends of Tmin were consistent, whereas those of the “high” category of Tmax were more obvious than for the other categories. In addition, the variation ranges of annual, summer, and autumn temperatures tended to decrease, whereas the opposite was true for spring and winter. Sub-basin results indicate that high elevation areas showed a larger increase in Tmin than lower elevation areas.
- (2)
- The annual precipitation showed an increasing trend in the JRB according to the ITA; however, a significant decreasing trend was present in the “low” categories at a 99% confidence level, whereas no trend occurred in the “high” precipitation categories. There were no consistent trends for seasonal precipitation, and the “low” category of summer precipitation showed a decreasing trend, whereas there was an increasing trend for the “high” category of spring precipitation. In terms of spatial patterns, the precipitation in the MLJRB showed a decreasing trend, whereas other sub-basins showed an increasing trend. Further analyses show that the impact of elevation on different categories of precipitation was distinctive where the elevation was >2000 m.
- (3)
- The present study additionally examined the correlation between temperature and precipitation in the JRB. For the SRJRB, strong positive correlations occurred between precipitation and the minimum temperature in spring, summer, and autumn, whereas the opposite dynamic was observed for the relationship between precipitation and the maximum temperature in the MLJRB. The combined change in temperature and precipitation will pose new challenges for water resource management, agriculture, and economic development in the JRB.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Sharma, C.S.; Panda, S.N.; Pradhan, R.P.; Singh, A.; Kawamura, A. Precipitation and temperature changes in eastern India by multiple trend detection methods. Atmos. Res. 2016, 180, 211–225. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Barnett, T.; Adam, J.; Lettenmaier, D. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Oki, T.; Kanae, S. Global Hydrological Cycles and World Water Resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef]
- Bo, L.; Qi, H.; Wang, W.; Zeng, X.; Zhai, J. Variation of actual evapotranspiration and its impact on regional water resources in the Upper Reaches of the Yangtze River. Quat. Int. 2011, 244, 185–193. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Zhang, Z.; Chen, Y.D.; Liu, C.L.; Lin, H. Spatial and temporal variability of precipitation maxima during 1960–2005 in the Yangtze River basin and possible association with large-scale circulation. J. Hydrol. 2008, 353, 215–227. [Google Scholar] [CrossRef]
- Şen, Z. Partial trend identification by change-point successive average methodology (SAM). J. Hydrol. 2019, 571, 288–299. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Tabari, H.; Wang, J.; Wang, Q.; Song, S.; Hu, Z. Innovative trend analysis of annual and seasonal rainfall in the Yangtze River Delta, eastern China. Atmos. Res. 2020, 231, 104673. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: Oxford, UK, 1975; Available online: https://psycnet.apa.org/record/1948-15040-000 (accessed on 15 September 2020).
- Arnone, E.; Pumo, D.; Viola, F.; Noto, L.V. Rainfall Statistic Changes in Sicily. Hydrol. Earth Syst. Sci. 2013, 17, 2449–2458. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Su, B.D.; Jiang, T.; Jin, W.B. Recent trends in observed temperature and precipitation extremes in the Yangtze River basin, China. Theor. Appl. Climatol. 2006, 83, 139–151. [Google Scholar] [CrossRef]
- Chowdhury, R.K.; Beecham, S.; Boland, J.; Piantadosi, J. Understanding South Australian rainfall trends and step changes. Int. J. Climatol. 2015, 35, 348–360. [Google Scholar] [CrossRef]
- Jones, J.R.; Schwartz, J.S.; Ellis, K.N.; Hathaway, J.M.; Jawdy, C.M. Temporal variability of precipitation in the Upper Tennessee Valley. J. Hydrol. Reg. Stud. 2015, 3, 125–138. [Google Scholar] [CrossRef]
- Sabzevari, A.A.; Zarenistanak, M.; Tabari, H.; Moghimi, S. Evaluation of precipitation and river discharge variations over southwestern Iran during recent decades. J. Earth. Syst. Sci. 2015, 124, 335–352. [Google Scholar] [CrossRef]
- Wu, H.; Qian, H. Innovative trend analysis of annual and seasonal rainfall and extreme values in Shaanxi, China, since the 1950s. Int. J. Climatol. 2017, 37, 2582–2592. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Şen, Z. Trend Identification Simulation and Application. J. Hydrol. Eng. 2014, 19, 635–642. [Google Scholar] [CrossRef]
- Şen, Z. Innovative trend significance test and applications. Theor. Appl. Climatol. 2017, 127, 939–947. [Google Scholar] [CrossRef]
- Sonali, P.; Kumar, D.N. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Kisi, O. An innovative method for trend analysis of monthly pan evaporations. J. Hydrol. 2015, 527, 1123–1129. [Google Scholar] [CrossRef]
- Öztopal, A.; Şen, Z. Innovative Trend Methodology Applications to Precipitation Records in Turkey. Water Resour. Manag. 2017, 31, 727–737. [Google Scholar] [CrossRef]
- Wu, H.; Li, X.; Qian, H. Detection of Anomalies and Changes of Rainfall in the Yellow River Basin, China, through Two Graphical Methods. Water 2018, 10, 15. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Application of the Innovative Trend Analysis Method for the Trend Analysis of Rainfall Anomalies in Southern Italy. Water Resour. Manag. 2018, 32, 4971–4983. [Google Scholar] [CrossRef]
- Elouissi, A.; Sen, Z.; Habi, M. Algerian rainfall innovative trend analysis and its implications to Macta watershed. Arab. J. Geosci. 2016, 9, 303. [Google Scholar] [CrossRef]
- Güçlü, Y.S. Improved visualization for trend analysis by comparing with classical Mann-Kendall test and ITA. J. Hydrol. 2020, 584, 124674. [Google Scholar] [CrossRef]
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Nguyen, P.; Thorstensen, A.; Sorooshian, S.; Hsu, K.; Aghakouchak, A.; Ashouri, H.; Tran, H.; Braithwaite, D. Global Precipitation Trends across Spatial Scales Using Satellite Observations. Bull. Amer. Meteor. Soc. 2018, 99, 689–697. [Google Scholar] [CrossRef]
- Ren, L.; Arkin, P.; Smith, T.M.; Shen, S.S. Global precipitation trends in 1900–2005 from a reconstruction and coupled model simulations. J. Geophys. Res. Atmos. 2013, 118, 1679–1689. [Google Scholar] [CrossRef]
- Cui, L.; Wang, L.; Lai, Z.; Tian, Q.; Liu, W.; Li, J. Innovative trend analysis of annual and seasonal air temperature and rainfall in the Yangtze River Basin, China during 1960–2015. J. Atmos. Sol. Terr. Phys. 2017, 164, 48–59. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X. Long-term trend analysis for temperature in the Jinsha River Basin in China. Theor. Appl. Climatol. 2012, 109, 591–603. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Liu, Z.; Wang, D. Trend Analysis of Precipitation in the Jinsha River Basin in China. J. Hydrometeorol. 2013, 14, 290–303. [Google Scholar] [CrossRef]
- Li, D.; Lu, X.X.; Yang, X.; Chen, L.; Lin, L. Sediment load responses to climate variation and cascade reservoirs in the Yangtze River: A case study of the Jinsha River. Geomorphology 2018, 322, 41–52. [Google Scholar] [CrossRef]
- Peng, T.; Zhang, C.; Zhou, J.Z. Intra- and Inter-Annual Variability of Hydrometeorological Variables in the Jinsha River Basin, Southwest China. Sustainability 2019, 11, 5142. [Google Scholar] [CrossRef]
- Zhang, P.; Cai, Y.; Yang, W.; Yi, Y.; Yang, Z. Climatic and anthropogenic impacts on water and sediment generation in the middle reach of the Jinsha River Basin. River Res. Appl. 2020, 36, 338–350. [Google Scholar] [CrossRef]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M.; Dozier, J. Climatic and Hydrologic Changes in the Tien Shan, Central Asia. J. Clim. 1997, 10, 1393–1404. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Guo, X.; Chen, D. Does summer precipitation trend over and around the Tibetan Plateau depend on elevation? Int. J. Climatol. 2017, 37, 1278–1284. [Google Scholar] [CrossRef]
- Du, M.; Liu, J.; Li, Y.; Zhang, F.; Tang, Y. Are high altitudinal regions warming faster than lower elevations on the Tibetan Plateau? Int. J. Glob. Warm. 2019, 18, 363–384. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Pepin, N.; Flügel, W.A.; Yan, Y.; Behrawan, H.; Huang, J. Relationship between temperature trend magnitude, elevation and mean temperature in the Tibetan Plateau from homogenized surface stations and reanalysis data. Glob. Planet. Chang. 2010, 71, 124–133. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.C.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Berardy, A.; Chester, M.V. Climate change vulnerability in the food, energy, and water nexus: Concerns for agricultural production in Arizona and its urban export supply. Environ. Res. Lett. 2017, 12, 035004. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; Pu, J.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Change 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Kang, S.; Eltahir, E.A.B. Impact of irrigation on regional climate over Eastern China. Geophys. Res. Lett. 2019, 46, 5499–5505. [Google Scholar] [CrossRef]
- Yin, R.; Xiang, Q. An integrative approach to modeling land-use changes: Multiple facets of agriculture in the Upper Yangtze basin. Sustain. Sci. 2010, 5, 9. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Wang, J.; Zhao, Y.; Xu, C. Impacts of Climate Change and Land-Use Change on Hydrological Extremes in the Jinsha River Basin. Water 2019, 11, 1398. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Yu, J.; Liu, C. Decadal Climatic Variability, Trends, and Future Scenarios for the North China Plain. J. Clim. 2009, 22, 2111–2123. [Google Scholar] [CrossRef]
- Oyler, J.W.; Dobrowski, S.Z.; Ballantyne, A.P.; Klene, A.E.; Running, S.W. Artificial amplification of warming trends across the mountains of the western United States. Geophys. Res. Lett. 2015, 42, 153–161. [Google Scholar] [CrossRef]
- Swed, F.S.; Eisenhart, C. Tables for Testing Randomness of Grouping in a Sequence of Alternatives. Ann. Math. Stat. 1943, 14, 66–87. [Google Scholar] [CrossRef]
- Caloiero, T.; Filice, E.; Coscarelli, R.; Pellicone, G. A Homogeneous Dataset for Rainfall Trend Analysis in the Calabria Region (Southern Italy). Water 2020, 12, 2541. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Ullah, S.; You, Q.; Ali, A.; Ullah, W.; Jan, M.A.; Zhang, Y.; Xie, W.; Xie, X. Observed changes in maximum and minimum temperatures over China- Pakistan economic corridor during 1980–2016. Atmos. Res. 2019, 216, 37–51. [Google Scholar] [CrossRef]
- Guan, Y.; Zhang, X.; Zheng, F.; Wang, B. Trends and variability of daily temperature extremes during 1960–2012 in the Yangtze River Basin, China. Glob. Planet. Chang. 2015, 124, 79–94. [Google Scholar] [CrossRef]
- Ren, Y.; Ren, G.; Sun, X.; Shrestha, A.B.; You, Q.; Zhan, Y.; Rajbhandari, R.; Zhang, P.; Wen, K. Observed changes in surface air temperature and precipitation in the Hindu Kush Himalayan region over the last 100-plus years. Adv. Clim. Chang. Res. 2017, 8, 148–156. [Google Scholar] [CrossRef]
- Kang, S.C.; Zhang, Y.J.; Qin, D.H.; Ren, J.W.; Zhang, Q.G.; Grigholm, B.; Mayewski, P.A. Recent temperature increase recorded in an ice core in the source region of Yangtze River. Chin. Sci. Bull. 2007, 52, 825–831. [Google Scholar] [CrossRef]
- Liang, E.Y.; Shao, X.M.; Xu, Y. Tree-ring evidence of recent abnormal warming on the southeast Tibetan Plateau. Theor. Appl. Climatol. 2009, 98, 9–18. [Google Scholar] [CrossRef]
- Harlan, S.L.; Ruddell, D.M. Climate change and health in cities: Impacts of heat and air pollution and potential co-benefits from mitigation and adaptation. Curr. Opin. Environ. Sustain. 2011, 3, 126–134. [Google Scholar] [CrossRef]
- Jhajharia, D.; Dinpashoh, Y.; Kahya, E.; Singh, V.P.; Fakheri-Fard, A. Trends in reference evapotranspiration in the humid region of northeast India. Hydrol. Process. 2012, 26, 421–435. [Google Scholar] [CrossRef]
- O’Neal, M.R.; Nearing, M.A.; Vining, R.C.; Southworth, J.; Pfeifer, R.A. Climate change impacts on soil erosion in Midwest United States with changes in crop management. Catena 2005, 61, 165–184. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.G.; Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Mamassis, N. A comparison of local and aggregated climate model outputs with observed data. Hydro. Sci. J. 2010, 55, 1094–1110. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Efstratiadis, A.; Mamassis, N.; Christofides, A. On the credibility of climate predictions. Hydro. Sci. J. 2010, 53, 671–684. [Google Scholar] [CrossRef]
- Li, J.; Wu, W.; Ye, X. Innovative trend analysis of main agriculture natural hazards in China during 1989–2014. Nat. Hazards 2018, 95, 677–720. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.; Gao, R. Temporal and spatial variation of precipitation in the Hengduan Mountains region in China and its relationship with elevation and latitude. Atmos. Res. 2018, 213, 1–16. [Google Scholar] [CrossRef]
- Ullah, S.; You, Q.; Ullah, W.; Ali, A. Observed changes in precipitation in China-Pakistan economic corridor during 1980–2016. Atmos. Res. 2018, 210, 1–14. [Google Scholar] [CrossRef]
- Álvarez-Rodríguez, J.; Llasat, M.C.; Estrela, T. Analysis of geographic and orographic influence in Spanish monthly precipitation. Int. J. Climatol. 2017, 37, 350–362. [Google Scholar] [CrossRef]
- He, C.; He, X.; Fu, L. China’s South-to-North Water Transfer Project: Is it Needed? Geogr. Compass 2010, 4, 1312–1323. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Relationships between precipitation and surface temperature. Geophys. Res. Lett. 2005, 32, L14703. [Google Scholar] [CrossRef]
- Isaac, G.A.; Stuart, R.A. Temperature–Precipitation Relationships for Canadian Stations. J. Clim. 1992, 5, 822–830. [Google Scholar] [CrossRef]
- Mann, M.; Zhang, Z.; Hughes, M.; Bradley, R.; Miller, S.; Rutherford, S.; Ni, F. Proxy-based Reconstructions of Hemispheric and Global Surface Temperature Variations over the Past Two Millennia. Proc. Natl. Acad. Sci. USA 2008, 105, 13252–13257. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.; Charles, S.P.; Viney, N.R.; Chen, S.; Wu, J.Q. Impacts of climate variability on stream-flow in the Yellow River. Hydrol. Process. 2007, 21, 3431–3439. [Google Scholar] [CrossRef]
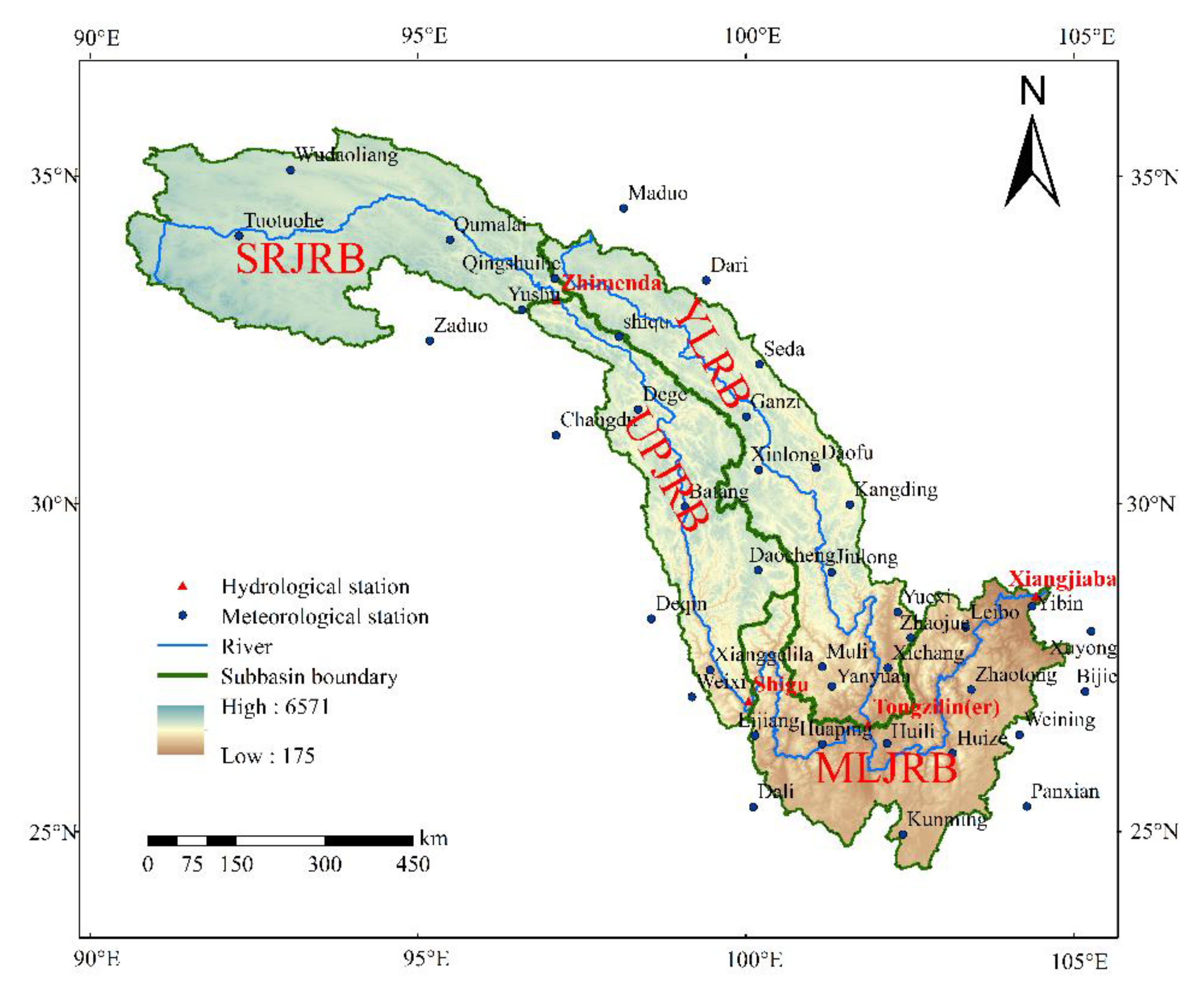
| Sub-Basin | Station | Latitude (°N) | Longitude (°E) | Elevation (m) |
|---|---|---|---|---|
| SRJRB 1 | Wudaoliang | 35.13 | 93.05 | 4612 |
| Tuotuohe | 34.13 | 92.26 | 4533 | |
| Zaduo | 32.53 | 95.17 | 4066 | |
| Qumalai | 34.07 | 95.48 | 4175 | |
| Yushu | 33.00 | 96.58 | 3717 | |
| Qingshuihe | 33.48 | 97.08 | 4415 | |
| UPJRB 2 | Shiqu | 32.59 | 98.06 | 4200 |
| Changdu | 31.09 | 97.10 | 3315 | |
| Dege | 31.48 | 98.35 | 3184 | |
| Batang | 30.00 | 99.06 | 2589 | |
| Daocheng | 29.03 | 100.18 | 3728 | |
| Deqin | 28.29 | 98.55 | 3319 | |
| Xianggelila | 27.51 | 99.45 | 3342 | |
| Weixi | 27.10 | 99.17 | 2326 | |
| YLRB 3 | Maduo | 34.55 | 98.13 | 4272 |
| Dari | 33.45 | 99.39 | 3968 | |
| Ganzi | 31.37 | 100.00 | 3394 | |
| Seda | 32.17 | 100.20 | 3894 | |
| Daofu | 30.59 | 101.07 | 2957 | |
| Xinlong | 30.56 | 100.19 | 3000 | |
| Kangding | 30.03 | 101.58 | 2616 | |
| Muli | 27.56 | 101.16 | 2427 | |
| Jiulong | 29.00 | 101.30 | 2925 | |
| Yuexi | 28.39 | 102.31 | 1660 | |
| Zhaojue | 28.00 | 102.51 | 2132 | |
| Leibo | 28.16 | 103.35 | 1256 | |
| Yanyuan | 27.26 | 101.31 | 2545 | |
| Xichang | 27.54 | 102.16 | 1591 | |
| MLJRB 4 | Yibin | 28.48 | 104.36 | 341 |
| Zhaotong | 27.21 | 103.43 | 1950 | |
| Lijiang | 26.51 | 100.13 | 2381 | |
| Huaping | 26.38 | 101.16 | 1231 | |
| Huili | 26.39 | 102.15 | 1787 | |
| Huize | 26.24 | 103.15 | 2188 | |
| Weining | 26.52 | 104.17 | 2238 | |
| Dali | 25.42 | 100.11 | 1991 | |
| Kunming | 25 | 102.39 | 1888 | |
| Panxian | 25.43 | 104.28 | 1800 | |
| Xuyong | 28.10 | 105.26 | 378 | |
| Bijie | 27.18 | 105.17 | 1511 |
| Factors | Tmin | Tmax | Precipitation | |||
|---|---|---|---|---|---|---|
| b | Z | b | Z | b | Z | |
| Annual | 0.037 | 8.064 ** | 0.024 | 4.813 ** | 0.315 | 0.657 |
| Spring | 0.038 | 8.001 ** | 0.018 | 3.046 ** | 0.278 | 1.491 |
| Summer | 0.027 | 6.113 ** | 0.022 | 4.969 ** | −0.060 | −0.163 |
| Autumn | 0.036 | 6.707 ** | 0.031 | 4.658 ** | −0.205 | −1.237 |
| Winter | 0.047 | 7.470 ** | 0.033 | 4.332 ** | 0.112 | 1.039 |
| SRJRB 1 | 0.040 | 6.481 ** | 0.033 | 6.212 ** | 0.695 | 1.703 |
| UPJRB 2 | 0.047 | 7.937 ** | 0.024 | 4.318 ** | 0.210 | 0.177 |
| YLRB 3 | 0.036 | 7.343 ** | 0.030 | 5.025 ** | 1.088 | 2.113 * |
| MLJRB 4 | 0.027 | 6.651 ** | 0.019 | 4.163 ** | −0.900 | −0.855 |
| Factors | Series | Slope S | Standard Deviation | Correlation | Slope Standard Deviation | Sig. Level 95% | Sig. Level 99% |
|---|---|---|---|---|---|---|---|
| Tmin | Annual | 0.036 ** | 0.6524 | 0.9576 | 0.0009 | 0.0018 | 0.0023 |
| Spring | 0.035 ** | 0.6562 | 0.9643 | 0.0008 | 0.0016 | 0.0022 | |
| Summer | 0.028 ** | 0.5822 | 0.9626 | 0.0008 | 0.0015 | 0.0020 | |
| Autumn | 0.035 ** | 0.7104 | 0.9251 | 0.0013 | 0.0026 | 0.0034 | |
| Winter | 0.047 ** | 0.8966 | 0.9778 | 0.0009 | 0.0018 | 0.0023 | |
| SRJRB | 0.041 ** | 0.8703 | 0.9362 | 0.0015 | 0.0029 | 0.0038 | |
| UPJRB | 0.045 ** | 0.8287 | 0.9475 | 0.0013 | 0.0025 | 0.0033 | |
| YLSB | 0.038 ** | 0.6849 | 0.9617 | 0.0009 | 0.0018 | 0.0023 | |
| MLJRB | 0.025 ** | 0.5156 | 0.9421 | 0.0008 | 0.0016 | 0.0022 | |
| Tmax | Annual | 0.022 ** | 0.5948 | 0.9857 | 0.0005 | 0.0009 | 0.0012 |
| Spring | 0.011 ** | 0.6550 | 0.8800 | 0.0015 | 0.0030 | 0.0040 | |
| Summer | 0.021 ** | 0.6207 | 0.9427 | 0.0010 | 0.0020 | 0.0026 | |
| Autumn | 0.027 ** | 0.7641 | 0.9829 | 0.0007 | 0.0013 | 0.0017 | |
| Winter | 0.028 ** | 0.9318 | 0.9629 | 0.0012 | 0.0024 | 0.0031 | |
| SRJRB | 0.035 ** | 0.7257 | 0.9811 | 0.0007 | 0.0013 | 0.0017 | |
| UPJRB | 0.020 ** | 0.6568 | 0.9804 | 0.0006 | 0.0012 | 0.0016 | |
| YLSB | 0.026 ** | 0.6955 | 0.9866 | 0.0005 | 0.0011 | 0.0014 | |
| MLJRB | 0.017 ** | 0.5316 | 0.9839 | 0.0005 | 0.0009 | 0.0012 | |
| Pr | Annual | 0.358 ** | 48.9034 | 0.9257 | 0.0900 | 0.1764 | 0.2321 |
| Spring | 0.415 ** | 20.9512 | 0.9545 | 0.0302 | 0.0778 | 0.0591 | |
| Summer | −0.020 | 37.7991 | 0.9534 | 0.0551 | 0.1080 | 0.1422 | |
| Autumn | −0.164 ** | 18.5630 | 0.9256 | 0.0342 | 0.0670 | 0.0882 | |
| Winter | 0.127 ** | 13.7122 | 0.9786 | 0.0135 | 0.0265 | 0.0349 | |
| SRJRB | 0.365 ** | 47.1670 | 0.9879 | 0.0350 | 0.0687 | 0.0904 | |
| UPJRB | 0.942 ** | 90.4367 | 0.9373 | 0.1529 | 0.2996 | 0.3944 | |
| YLSB | 1.046 ** | 60.8229 | 0.9600 | 0.0821 | 0.1609 | 0.2118 | |
| MLJRB | −1.293 ** | 276.1900 | 0.9500 | 0.4168 | 0.8170 | 1.0754 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Jia, W.; Sarukkalige, R.; Fu, G.; Meng, Q.; Wang, Q. Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China. Water 2020, 12, 3293. https://doi.org/10.3390/w12113293
Dong Z, Jia W, Sarukkalige R, Fu G, Meng Q, Wang Q. Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China. Water. 2020; 12(11):3293. https://doi.org/10.3390/w12113293
Chicago/Turabian StyleDong, Zengchuan, Wenhao Jia, Ranjan Sarukkalige, Guobin Fu, Qing Meng, and Qin Wang. 2020. "Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China" Water 12, no. 11: 3293. https://doi.org/10.3390/w12113293
APA StyleDong, Z., Jia, W., Sarukkalige, R., Fu, G., Meng, Q., & Wang, Q. (2020). Innovative Trend Analysis of Air Temperature and Precipitation in the Jinsha River Basin, China. Water, 12(11), 3293. https://doi.org/10.3390/w12113293







