Taking into Account both Explicit Conduits and the Unsaturated Zone in Karst Reservoir Hybrid Models: Impact on the Outlet Hydrograph
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Hybrid Model and the Considered Karst Specificities
2.2. Flow Equations and Model Parameters
2.3. Simulations and Evaluation Criteria
- Peak flow (maximum discharge value); in some cases, several local extrema are identified;
- Time after the event until peak flow;
- Discharge duration;
- Third order moment (skewness), which describes the shape of distribution;
- Fourth order moment (kurtosis), which is a flattening coefficient.
3. Results and Discussion
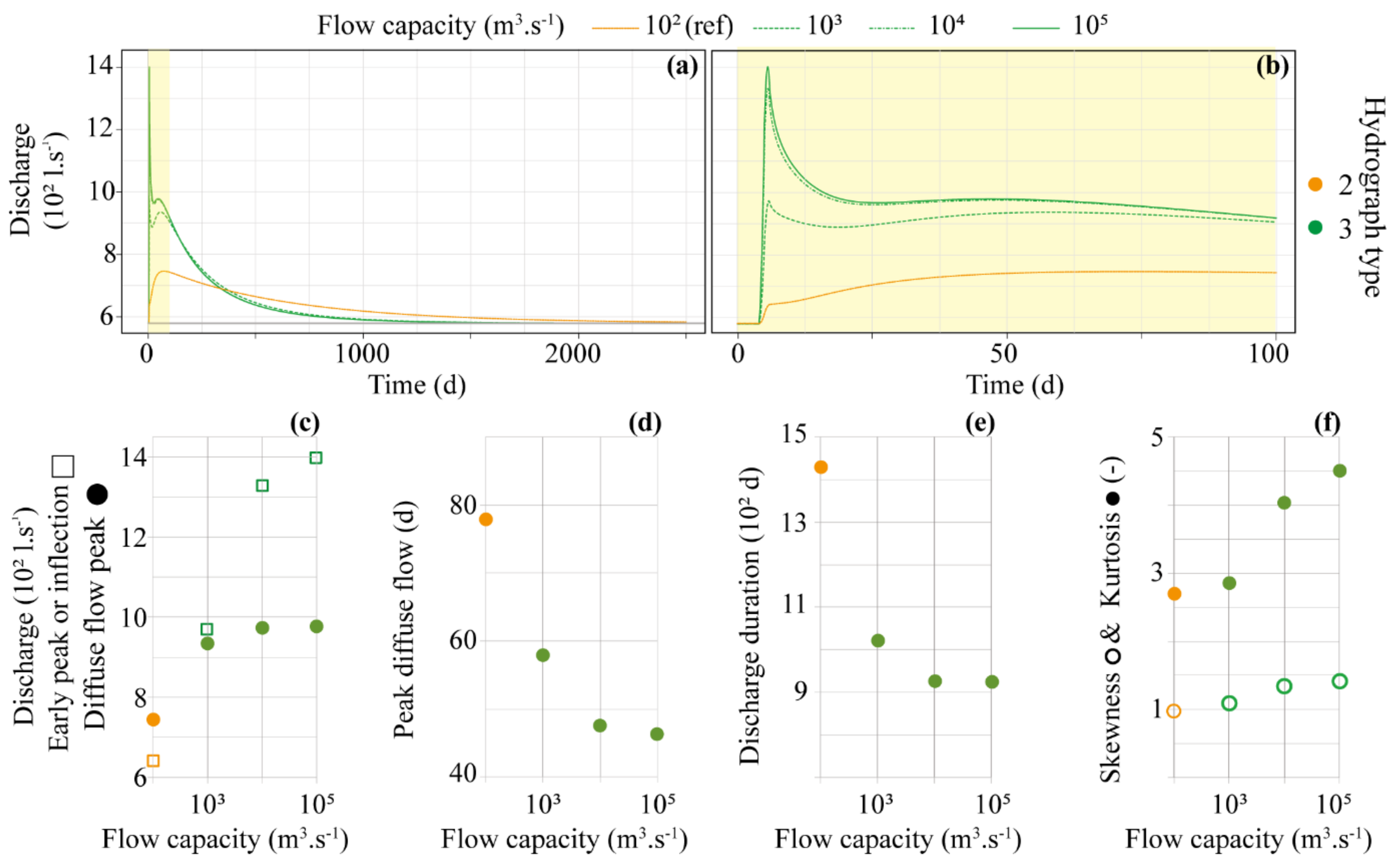
3.1. Overview of Simulation Results and Hydrograph Typology
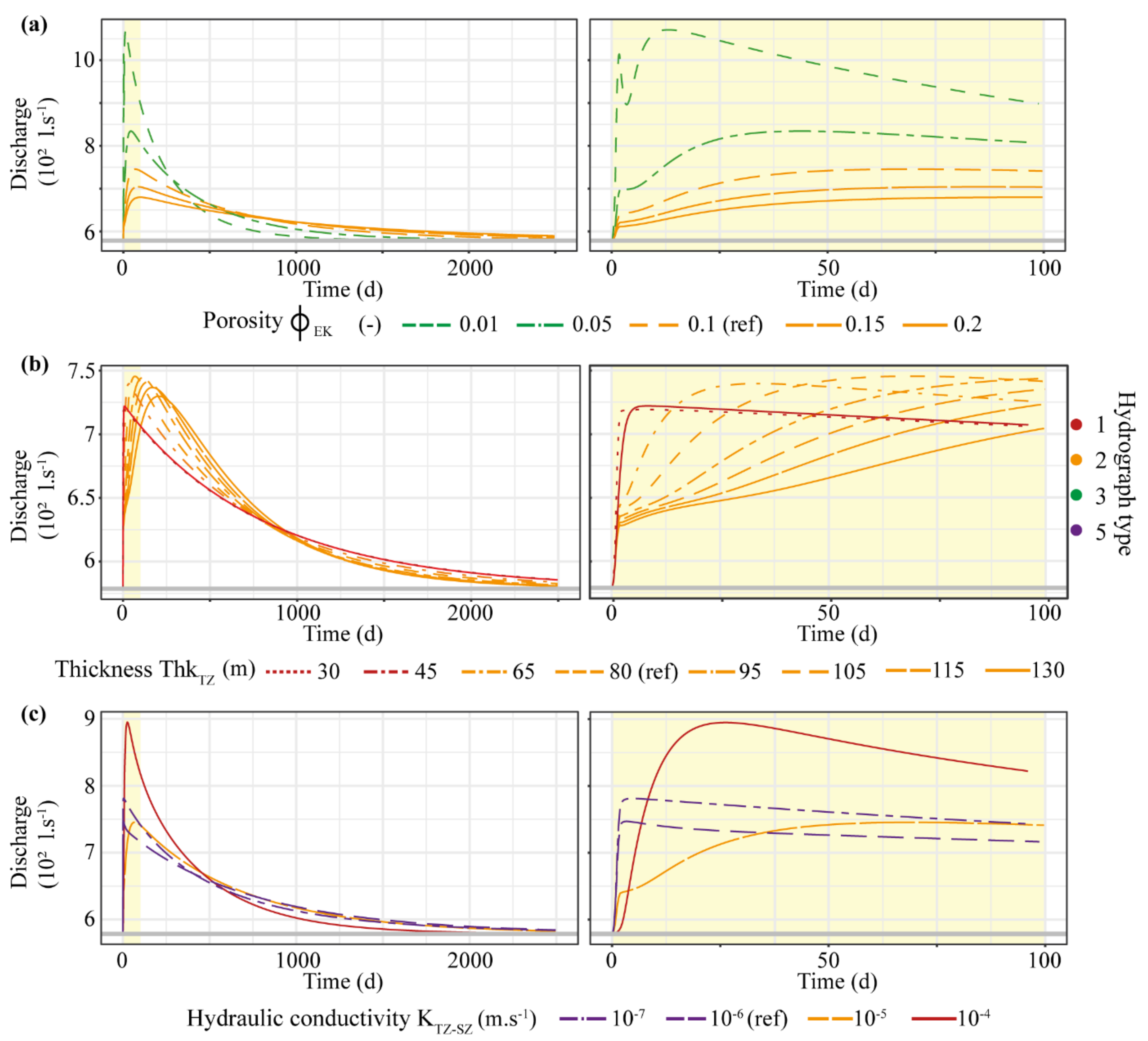
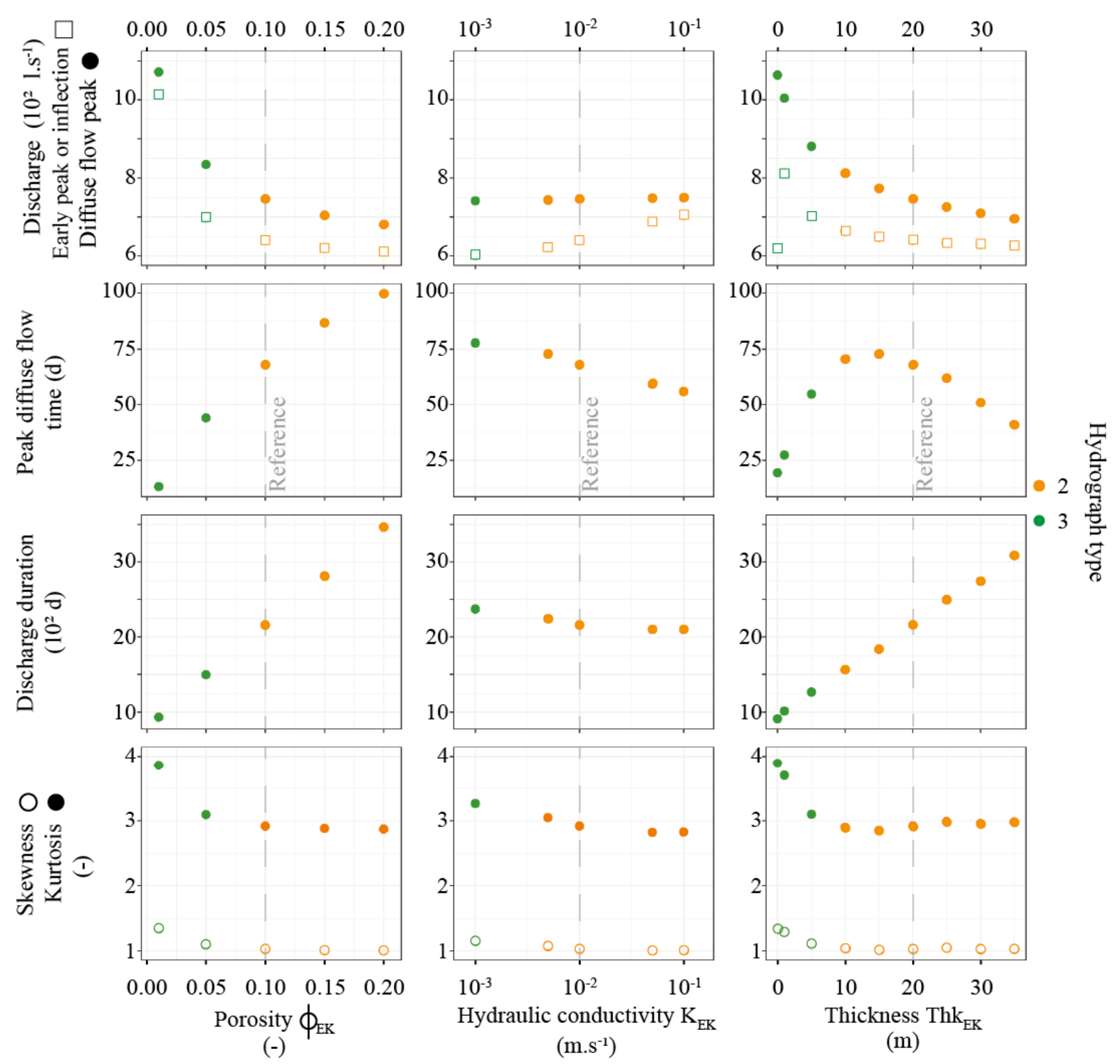
3.1.1. The Role of Epikarst Parameters
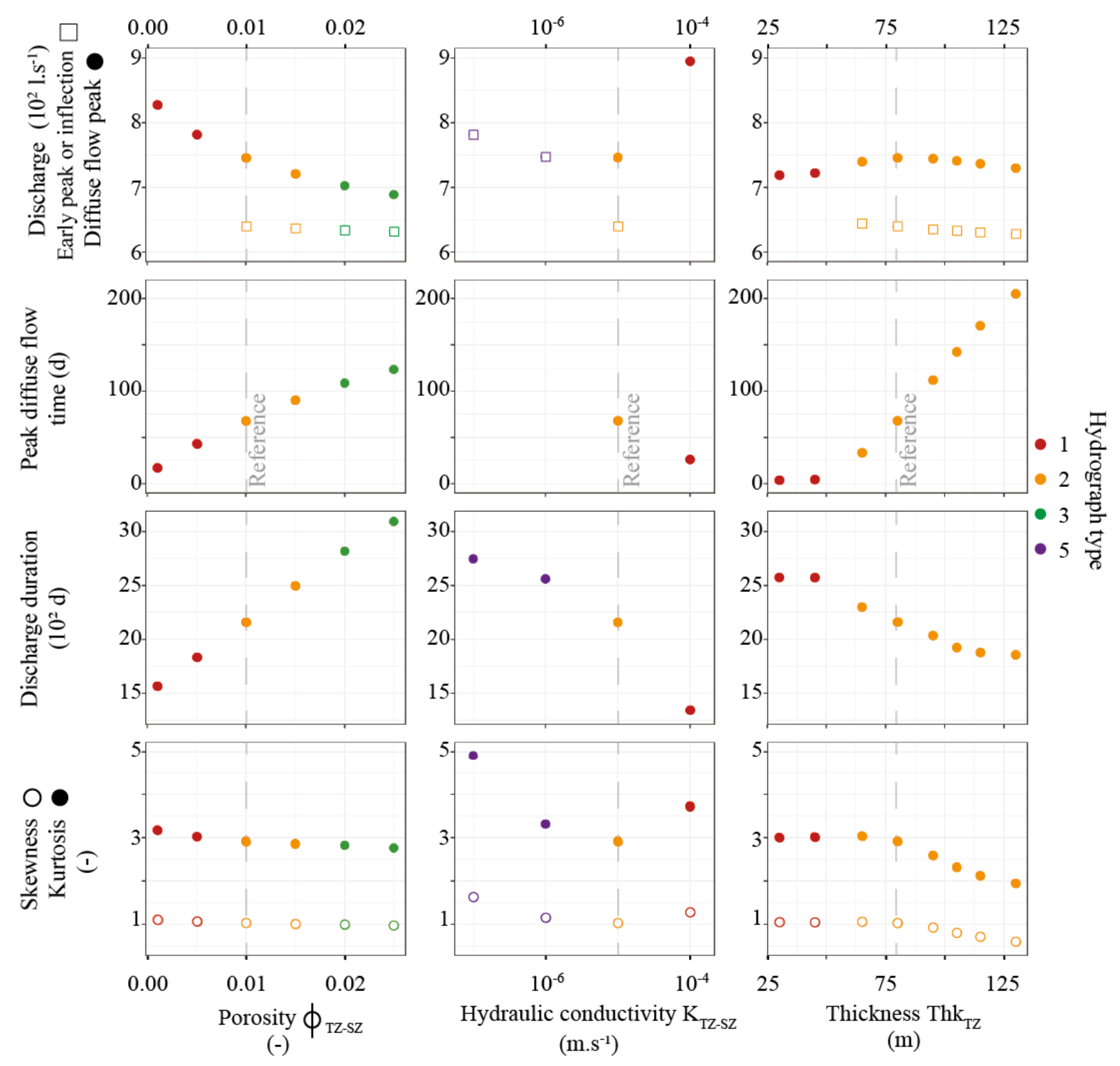
3.1.2. The Role of Transmission and Saturated Zones Parameters
4. Evaluation of Models
4.1. Model Assumptions
4.2. Scaling Issues
4.3. Evaluation of Models Outputs
4.3.1. The Need of Hydrographs Descriptors
4.3.2. Matching Model Outputs with Field Measurements
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ford, D.C.; Williams, P.W. Karst Hydrogeology and Geomorphology; John Wiley & Sons: Chichester, UK, 2007. [Google Scholar]
- Burchette, T.P. Carbonate rocks and petroleum reservoirs: A geological perspective from the industry. Geol. Soc. Lond. Spec. Publ. 2012, 370, 17. [Google Scholar] [CrossRef]
- Cornaton, F.; Perrochet, P. Analytical 1D dual-porosity equivalent solutions to 3D discrete single-continuum models. Application to karstic spring hydrograph modelling. J. Hydrol. 2002, 262, 165–176. [Google Scholar] [CrossRef][Green Version]
- Kaufmann, G. Modelling karst geomorphology on different time scales. Geomorphology 2009, 106, 62–77. [Google Scholar] [CrossRef]
- Kovacs, A.; Perrochet, P.; Kiraly, L.; Jeannin, P.Y. A quantitative method for the characterisation of karst aquifers based on spring hydrograph analysis. J. Hydrol. 2005, 303, 152–164. [Google Scholar] [CrossRef]
- Liedl, R.; Sauter, M.; Huckinghaus, D.; Clemens, T.; Teutsch, G. Simulation of the development of karst aquifers using a coupled continuum pipe flow model. Water Resour. Res. 2003, 39, 11. [Google Scholar] [CrossRef]
- Oehlmann, S.; Geyer, T.; Licha, T.; Birk, S. Influence of aquifer heterogeneity on karst hydraulics and catchment delineation employing distributive modeling approaches. Hydrol. Earth Syst. Sci. 2013, 17, 4729–4742. [Google Scholar] [CrossRef]
- Geyer, T.; Birk, S.; Liedl, R.; Sauter, M. Quantification of temporal distribution of recharge in karst systems from spring hydrographs. J. Hydrol. 2008, 348, 452–463. [Google Scholar] [CrossRef]
- Király, L. Modelling karst aquifers by the combined discrete channel and continuum approach. Bull. Cent. Hydrogéol. 1998, 16, 77–98. [Google Scholar]
- Bonacci, O. Karst springs hydrographs as indicators of karst aquifers. Hydrol. Sci. J. 1993, 38, 51–62. [Google Scholar] [CrossRef]
- Eisenlohr, L.; Bouzelboudjen, M.; Kiraly, L.; Rossier, Y. Numerical versus statistical modelling of natural response of a karst hydrogeological system. J. Hydrol. 1997, 202, 244–262. [Google Scholar] [CrossRef]
- Felton, G.K.; Currens, J.C. Peak flow-rate and recession-curve characteristics of a karst spring in the inner Bluegrass, Central Kentucky. J. Hydrol. 1994, 162, 99–118. [Google Scholar] [CrossRef]
- Jukic, D.; Denic-Jukic, V. Nonlinear kernel functions for karst aquifers. J. Hydrol. 2006, 328, 360–374. [Google Scholar] [CrossRef]
- Kovács, A.; Perrochet, P. A quantitative approach to spring hydrograph decomposition. J. Hydrol. 2008, 352, 16–29. [Google Scholar] [CrossRef]
- Mangin, A. Contribution à L’étude Hydrodynamique des Aquifères Karstiques. Ph.D. Thesis, Université de Dijon, Dijon, France, 1975. [Google Scholar]
- Padilla, A.; Pulido-Bosch, A.; Mangin, A. Relative importance of baseflow and quickflow from hydrographs of karst spring. Ground Water 1994, 32, 267–277. [Google Scholar] [CrossRef]
- Doummar, J.; Sauter, M.; Geyer, T. Simulation of flow processes in a large scale karst system with an integrated catchment model (Mike She)-Identification of relevant parameters influencing spring discharge. J. Hydrol. 2012, 426, 112–123. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Mace, R.E.; Barrett, M.E.; Smith, B. Can we simulate regional groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs Edwards aquifer, USA. J. Hydrol. 2003, 276, 137–158. [Google Scholar] [CrossRef]
- Tritz, S.; Guinot, V.; Jourde, H. Modelling the behaviour of a karst system catchment using non-linear hysteretic conceptual model. J. Hydrol. 2011, 397, 250–262. [Google Scholar] [CrossRef]
- Xu, Z.X.; Hu, B.X.; Davis, H.; Kish, S. Numerical study of groundwater flow cycling controlled by seawater/freshwater interaction in a coastal karst aquifer through conduit network using CFPv2. J. Contam. Hydrol. 2015, 182, 131–145. [Google Scholar] [CrossRef][Green Version]
- Bakalowicz, M. The epikarst, the skin of karst. In Special Publication 9: Epikarst; Jones, W.K., Culver, D.C., Herman, J.S., Eds.; Karst Waters Institute: Leesburg, VA, USA, 2004; pp. 16–22. [Google Scholar]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- Klimchouk, A.B. Towards defining, delimiting and classifying epikarst: Its origin, processes and variants of geomorphic evolution. In Special Publication 9: Epikarst; Jones, W.K., Culver, D.C., Herman, J.S., Eds.; Karst Waters Institute: Leesburg, VA, USA, 2004; pp. 23–35. [Google Scholar]
- Williams, P.W. The role of the epikarst in karst and cave hydrogeology: A review. Int. J. Speleol. 2008, 37, 1–10. [Google Scholar] [CrossRef]
- Dal Soglio, L.; Danquigny, C.; Mazzilli, N.; Emblanch, C.; Massonnat, G. Modelling the matrix-conduit exchanges in both epikarst and transmission zone of karst systems. J. Water 2020, 11. [Google Scholar]
- Smart, C.C.; Ford, D.C. Structure and function of a conduit aquifer. Can. J. Earth Sci. 1986, 23, 919–929. [Google Scholar] [CrossRef]
- Williams, P.W. Subcutaneous hydrology and the development of doline and cockpit karst. Z. Geomorphol. Stuttg. 1985, 29, 463–482. [Google Scholar]
- Carrière, S.D.; Chalikakis, K.; Danquigny, C.; Clément, R.; Emblanch, C. Feasibility and Limits of Electrical Resistivity Tomography to Monitor Water Infiltration Through Karst Medium During a Rainy Event. In Hydrogeological and Environmental Investigations in Karst Systems; Andreo, B., Carrasco, F., Durán, J.J., Jiménez, P., LaMoreaux, J.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 1, pp. 45–55. [Google Scholar]
- Carriere, S.D.; Chalikakis, K.; Danquigny, C.; Davi, H.; Mazzilli, N.; Ollivier, C.; Emblanch, C. The role of porous matrix in water flow regulation within a karst unsaturated zone: An integrated hydrogeophysical approach. Hydrogeol. J. 2016, 24, 1905–1918. [Google Scholar] [CrossRef]
- Mazzilli, N.; Boucher, M.; Chalikakis, K.; Legchenko, A.; Jourde, H.; Champollion, C. Contribution of magnetic resonance soundings for characterizing water storage in the unsaturated zone of karst aquifers. Geophysics 2016, 81, WB49–WB61. [Google Scholar] [CrossRef]
- Watlet, A.; Van Camp, M.J.; Francis, O.; Poulain, A.; Hallet, V.; Triantafyllou, A.; Delforge, D.; Quinif, Y.; Van Ruymbeke, M.; Kaufmann, O. Surface and subsurface continuous gravimetric monitoring of groundwater recharge processes through the karst vadose zone at Rochefort Cave (Belgium). In Proceedings of the American Geophysical Union Fall Meeting, New Orleans, LA, USA, 11–15 December 2017; p. G51B-0743. [Google Scholar]
- Barbel-Perineau, A.; Barbiero, L.; Danquigny, C.; Emblanch, C.; Mazzilli, N.; Babic, M.; Simler, R.; Valles, V. Karst flow processes explored through analysis of long-term unsaturated-zone discharge hydrochemistry: A 10-year study in Rustrel, France. Hydrogeol. J. 2019, 27, 1711–1723. [Google Scholar] [CrossRef]
- Lastennet, R.; Mudry, J. Role of karstification and rainfall in the behavior of a heterogeneous karst system. Environ. Geol. 1997, 32, 114–123. [Google Scholar] [CrossRef]
- Moore, P.J.; Martin, J.B.; Screaton, E.J. Geochemical and statistical evidence of recharge, mixing, and controls on spring discharge in an eogenetic karst aquifer. J. Hydrol. 2009, 376, 443–455. [Google Scholar] [CrossRef]
- Charlier, J.B.; Bertrand, C.; Mudry, J. Conceptual hydrogeological model of flow and transport of dissolved organic carbon in a small Jura karst system. J. Hydrol. 2012, 460, 52–64. [Google Scholar] [CrossRef]
- Emblanch, C.; Zuppi, G.M.; Mudry, J.; Blavoux, B.; Batiot, C. Carbon 13 of TDIC to quantify the role of the unsaturated zone: The example of the Vaucluse karst systems (Southeastern France). J. Hydrol. 2003, 279, 262–274. [Google Scholar] [CrossRef]
- Celle-Jeanton, H.; Emblanch, C.; Mudry, J.; Charmoille, A. Contribution of time tracers (Mg2+, TOC, delta C-13(TDIC), NO3-) to understand the role of the unsaturated zone: A case study-Karst aquifers in the Doubs valley, eastern France. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, J.C.; Jiang, G.H.; Liu, L.; Reimann, T.; Sauter, M. Modelling spring discharge and solute transport in conduits by coupling CFPv2 to an epikarst reservoir for a karst aquifer. J. Hydrol. 2019, 569, 587–599. [Google Scholar] [CrossRef]
- Clemens, T.; Huckinghaus, D.; Liedl, R.; Sauter, M. Simulation of the development of karst aquifers: Role of the epikarst. Int. J. Earth Sci. 1999, 88, 157–162. [Google Scholar] [CrossRef]
- Mudarra, M.; Andreo, B. Relative importance of the saturated and the unsaturated zones in the hydrogeological functioning of karst aquifers: The case of Alta Cadena (Southern Spain). J. Hydrol. 2011, 397, 263–280. [Google Scholar] [CrossRef]
- Perrin, K.; Jeannin, P.Y.; Zwahlen, F. Epikarst storage in a karst aquifer: A conceptual model based on isotopic data, Milandre test site, Switzerland. J. Hydrol. 2003, 279, 106–124. [Google Scholar] [CrossRef]
- Pronk, M.; Goldscheider, N.; Zopfi, J.; Zwahlen, F. Percolation and Particle Transport in the Unsaturated Zone of a Karst Aquifer. Ground Water 2009, 47, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Falcone, R.A.; Falgiani, A.; Parisse, B.; Petitta, M.; Spizzico, M.; Tallini, M. Chemical and isotopic (delta O-18 parts per thousand, delta H-2 parts per thousand, delta C-13 parts per thousand, Rn-222) multi-tracing for groundwater conceptual model of carbonate aquifer (Gran Sasso INFN underground laboratory—Central Italy). J. Hydrol. 2008, 357, 368–388. [Google Scholar] [CrossRef]
- Contractor, D.N.; Jenson, J.W. Simulated effect of vadose infiltration on water levels in the Northern Guam Lens Aquifer. J. Hydrol. 2000, 229, 232–254. [Google Scholar] [CrossRef]
- de Rooij, R.; Perrochet, P.; Graham, W. From rainfall to spring discharge: Coupling conduit flow, subsurface matrix flow and surface flow in karst systems using a discrete-continuum model. Adv. Water Resour. 2013, 61, 29–41. [Google Scholar] [CrossRef]
- Kaufmann, G. Modelling unsaturated flow in an evolving karst aquifer. J. Hydrol. 2003, 276, 53–70. [Google Scholar] [CrossRef]
- Kordilla, J.; Sauter, M.; Reimann, T.; Geyer, T. Simulation of saturated and unsaturated flow in karst systems at catchment scale using a double continuum approach. Hydrol. Earth Syst. Sci. 2012, 16, 3909–3923. [Google Scholar] [CrossRef]
- Pardo-Iguzquiza, E.; Dowd, P.; Bosch, A.P.; Luque-Espinar, J.A.; Heredia, J.; Duran-Valsero, J.J. A parsimonious distributed model for simulating transient water flow in a high-relief karst aquifer. Hydrogeol. J. 2018, 26, 2617–2627. [Google Scholar] [CrossRef]
- Roulier, S.; Baran, N.; Mouvet, C.; Stenemo, F.; Morvan, X.; Albrechtsen, H.J.; Clausen, L.; Jarvis, N. Controls on atrazine leaching through a soil-unsaturated fractured limestone sequence at Brevilles, France. J. Contam. Hydrol. 2006, 84, 81–105. [Google Scholar] [CrossRef] [PubMed]
- Abusaada, M.; Sauter, M. Studying the Flow Dynamics of a Karst Aquifer System with an Equivalent Porous Medium Model. Ground Water 2013, 51, 641–650. [Google Scholar] [CrossRef] [PubMed]
- Gallegos, J.J.; Hu, B.X.; Davis, H. Simulating flow in karst aquifers at laboratory and sub-regional scales using MODFLOW-CFP. Hydrogeol. J. 2013, 21, 1749–1760. [Google Scholar] [CrossRef]
- Ghasemizadeh, R.; Hellweger, F.; Butscher, C.; Padilla, I.; Vesper, D.; Field, M.; Alshawabkeh, A. Review: Groundwater flow and transport modeling of karst aquifers, with particular reference to the North Coast Limestone aquifer system of Puerto Rico. Hydrogeol. J. 2012, 20, 1441–1461. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.X. Examining a coupled continuum pipe-flow model for groundwater flow and solute transport in a karst aquifer. Acta Carsologica 2010, 39, 347–359. [Google Scholar] [CrossRef]
- Peleg, N.; Gvirtzman, H. Groundwater flow modeling of two-levels perched karstic leaking aquifers as a tool for estimating recharge and hydraulic parameters. J. Hydrol. 2010, 388, 13–27. [Google Scholar] [CrossRef]
- Saller, S.P.; Ronayne, M.J.; Long, A.J. Comparison of a karst groundwater model with and without discrete conduit flow. Hydrogeol. J. 2013, 21, 1555–1566. [Google Scholar] [CrossRef]
- Larocque, M.; Banton, O.; Ackerer, P.; Razack, M. Determining karst transmissivities with inverse modeling and an equivalent porous media. Ground Water 1999, 37, 897–903. [Google Scholar] [CrossRef]
- Kuniansky, E.L. Simulating Groundwater Flow in Karst Aquifers with Distributed Parameter Models—Comparison of Porous-Equivalent Media and Hybrid Flow Approaches; Scientific Investigations Report 2016-5116; US Geological Survey: Reston, VA, USA, 2016.
- Jeannin, P.Y. Modeling flow in phreatic and epiphreatic karst conduits in the Holloch cave (Muotatal, Switzerland). Water Resour. Res. 2001, 37, 191–200. [Google Scholar] [CrossRef]
- Teutsch, G.; Sauter, M. Groundwater modeling in karst terranes: Scale effects, data acquisition and field validation. In Proceedings of the Third Conference on Hydrogeology, Ecology, Monitoring, and Management of Ground Water in Karst Terranes, Nashville, TN, USA, 4–6 December 1991; pp. 17–35. [Google Scholar]
- Worthington, S.R.H. Diagnostic hydrogeologic characteristics of a karst aquifer (Kentucky, USA). Hydrogeol. J. 2009, 17, 1665–1678. [Google Scholar] [CrossRef]
- Malenica, L.; Gotovac, H.; Kamber, G.; Simunovic, S.; Allu, S.; Divic, V. Groundwater Flow Modeling in Karst Aquifers: Coupling 3D Matrix and 1D Conduit Flow via Control Volume Isogeometric AnalysisExperimental Verification with a 3D Physical Model. Water 2018, 10, 32. [Google Scholar] [CrossRef]
- Wong, D.L.Y.; Doster, F.; Geiger, S.; Kamp, A. Partitioning Thresholds in Hybrid Implicit-Explicit Representations of Naturally Fractured Reservoirs. Water Resour. Res. 2020, 56, 16. [Google Scholar] [CrossRef]
- Binet, S.; Joigneaux, E.; Pauwels, H.; Alberic, P.; Flehoc, C.; Bruand, A. Water exchange, mixing and transient storage between a saturated karstic conduit and the surrounding aquifer: Groundwater flow modeling and inputs from stable water isotopes. J. Hydrol. 2017, 544, 278–289. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, J.C.; Jiang, G.H. Modeling the hydrological behavior of a karst spring using a nonlinear reservoir-pipe model. Hydrogeol. J. 2015, 23, 901–914. [Google Scholar] [CrossRef]
- Giese, M.; Reimann, T.; Bailly-Comte, V.; Marechal, J.C.; Sauter, M.; Geyer, T. Turbulent and Laminar Flow in Karst Conduits Under Unsteady Flow Conditions: Interpretation of Pumping Tests by Discrete Conduit-Continuum Modeling. Water Resour. Res. 2018, 54, 1918–1933. [Google Scholar] [CrossRef]
- Diersch, H.-J. FEFLOW. Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: Berlin/Heidelberg, Germany, 2014; p. 996. [Google Scholar] [CrossRef]
- Shoemaker, W.B.; Kuniansky, E.L.; Birk, S.; Bauer, S.; Swain, E.D. Documentation of a conduit flow process (CFP) for MODFLOW-2005. In Techniques and Methods; US Geological Survey: Reston, VA, USA, 2007; p. 6. [Google Scholar]
- Palmer, A.N. Origin and morphology of limestone caves. Geol. Soc. Am. Bull. 1991, 103, 1–21. [Google Scholar] [CrossRef]
- Trefry, M.G.; Muffels, C. Feflow: A finite-element ground water flow and transport modeling tool. Ground Water 2007, 45, 525–528. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Huang, Z.-Q.; Yao, J.; Wang, Y.-Y. An Efficient Numerical Model for Immiscible Two-Phase Flow in Fractured Karst Reservoirs. Commun. Comput. Phys. 2013, 13, 540–558. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Al-fares, W.; Bakalowicz, M.; Guerin, R.; Dukhan, M. Analysis of the karst aquifer structure of the Lamalou area (Herault, France) with ground penetrating radar. J. Appl. Geophys. 2002, 51, 97–106. [Google Scholar] [CrossRef]
- Bakalowicz, M. La zone d’infiltration des aquifères karstiques. Méthodes d’étude, structure et fonctionnement. Hydrogéologie 1995, 4, 3–21. [Google Scholar]
- Jeannin, P.-Y. Structure et Comportement Hydraulique des Aquifères Karstiques; University of Neuchâtel: Neuchâtel, Switzerland, 1996. [Google Scholar]
- Petrella, E.; Falasca, A.; Celico, F. Natural-gradient tracer experiments in epikarst: A test study in the Acqua dei Faggi experimental site, southern Italy. Geofluids 2008, 8, 159–166. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.-f.; Xue, X.; Zhang, Z.; Wei, L. Estimation of baseflow recession constants and effective hydraulic parameters in the karst basins of southwest China. Hydrol. Res. 2012, 43, 102–112. [Google Scholar] [CrossRef]
- Daher, W.; Pistre, S.; Kneppers, A.; Bakalowicz, M.; Najem, W. Karst and artificial recharge: Theoretical and practical problems: A preliminary approach to artificial recharge assessment. J. Hydrol. 2011, 408, 189–202. [Google Scholar] [CrossRef]
- Chang, Y.; Wu, J.C.; Liu, L. Effects of the conduit network on the spring hydrograph of the karst aquifer. J. Hydrol. 2015, 527, 517–530. [Google Scholar] [CrossRef]
- Sauter, M. Quantification and Forecasting of Regional Groundwater Flow and Transport in a Karst Aquifer (Gallusquelle, Malm, SW Germany). Ph.D. Thesis, University of Tubingen, Tubingen, Germany, 1992. [Google Scholar]
- Worthington, S.R.H. A comprehensive strategy for understanding flow in carbonate aquifer. In Karst Modeling: Special Publication 5; Palmer, A.N., Palmer, M.V., Sasowsky, I.D., Eds.; The Karst Waters Institute: Charles Town, WV, USA, 1999; pp. 30–37. [Google Scholar]
- Granger, D.E.; Fabel, D.; Palmer, A.N. Pliocene-Pleistocene incision of the Green River, Kentucky, determined from radioactive decay of cosmogenic Al-26 and Be-10 in Mammoth Cave sediments. Geol. Soc. Am. Bull. 2001, 113, 825–836. [Google Scholar] [CrossRef]
- Lastennet, R.; Mudry, J. Impact of an exceptional storm episode on the functioning of karst system-the case of the 22/9/92 storm at Vaison-La-Romaine (Vaucluse, France). Comptes Rendus Acad. Des. Sci. Ser. 1995, 320, 953–959. [Google Scholar]
- Marechal, J.C.; Ladouche, B.; Dorfliger, N. Karst flash flooding in a Mediterranean karst, the example of Fontaine de Nimes. Eng. Geol. 2008, 99, 138–146. [Google Scholar] [CrossRef]
- Marsaud, B. Structure et Fonctionnement de la Zone Noyée des Karsts à Partir des Résultats Expérimentaux. Ph.D. Thesis, Université Paris XI, Orsay, France, 1996. [Google Scholar]
- Padilla, A.; Pulido-Bosch, A. Simple procedure to simulate karstic aquifers. Hydrol. Process. 2008, 22, 1876–1884. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Rainfall–runoff relations for karstic springs. Part I: Convolution and spectral analyses. J. Hydrol. 2000, 238, 123–148. [Google Scholar] [CrossRef]
- Labat, D.; Mangin, A.; Ababou, R. Rainfall-runoff relations for karstic springs: Multifractal analyses. J. Hydrol. 2002, 256, 176–195. [Google Scholar] [CrossRef]
- Mangin, A. Pour une meilleure connaissance des systèmes hydrologiques à partir des analyses corrélatoire et spectrale. J. Hydrol. 1984, 67, 25–43. [Google Scholar] [CrossRef]
- Sivelle, V.; Labat, D.; Mazzilli, N.; Massei, N.; Jourde, H. Dynamics of the Flow Exchanges between Matrix and Conduits in Karstified Watersheds at Multiple Temporal Scales. Water 2019, 11, 15. [Google Scholar] [CrossRef]
- Blavoux, B.; Mudry, J.; Puig, J.-M. Bilan, fonctionnement et protection du système karstique de la Fontaine de Vaucluse (sud-est de la France). Geodin. Acta 1992, 5, 153–172. [Google Scholar] [CrossRef]
- Fleury, P.; Plagnes, V.; Bakalowicz, M. Modelling of the functioning of karst aquifers with a reservoir model: Application to Fontaine de Vaucluse (South of France). J. Hydrol. 2007, 345, 38–49. [Google Scholar] [CrossRef]
- Ollivier, C.; Lecomte, Y.; Chalikakis, K.; Mazzilli, N.; Danquigny, C.; Emblanch, C. A QGIS Plugin Based on the PaPRIKa Method for Karst Aquifer Vulnerability Mapping. Groundwater 2019, 57, 201–204. [Google Scholar] [CrossRef]
- Ollivier, C.; Mazzilli, N.; Olioso, A.; Chalikakis, K.; Carriere, S.D.; Danquigny, C.; Emblanch, C. Karst recharge-discharge semi distributed model to assess spatial variability of flows. Sci. Total Environ. 2020, 703, 20. [Google Scholar] [CrossRef]
- Reimann, T.; Geyer, T.; Shoemaker, W.B.; Liedl, R.; Sauter, M. Effects of dynamically variable saturation and matrix-conduit coupling of flow in karst aquifers. Water Resour. Res. 2011, 47, 19. [Google Scholar] [CrossRef]
- Jeannin, P.Y.; Marechal, J.C. Lois de pertes de charge dans les conduits karstiques: Base théorique et observations; Laws of head loss in karst conduits: Theoretical basis and observations. Bull. Hydrogéol. 1995, 14, 149–176. [Google Scholar]
- Danquigny, C.; Massonnat, G.; Mermoud, C.; Rolando, J.-P. Intra- and Inter-Facies Variability of Multi-Physics Data in Carbonates. New Insights from Database of ALBION R&D Project. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 11 November 2019; p. 11. [Google Scholar]
- Massonnat, G.; Danquigny, C.; Rolando, J.-P. Permeability Upscaling in Carbonates. An Integrated Case Study From the Albion R&D Project. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 11 November 2019; p. 8. [Google Scholar]
- Starnoni, M.; Pokrajac, D. On the concept of macroscopic capillary pressure in two-phase porous media flow. Adv. Water Resour. 2020, 135, 9. [Google Scholar] [CrossRef]
- Misaghian, N.; Assareh, M.; Sadeghi, M. An upscaling approach using adaptive multi-resolution upgridding and automated relative permeability adjustment. Comput. Geosci. 2018, 22, 261–282. [Google Scholar] [CrossRef]
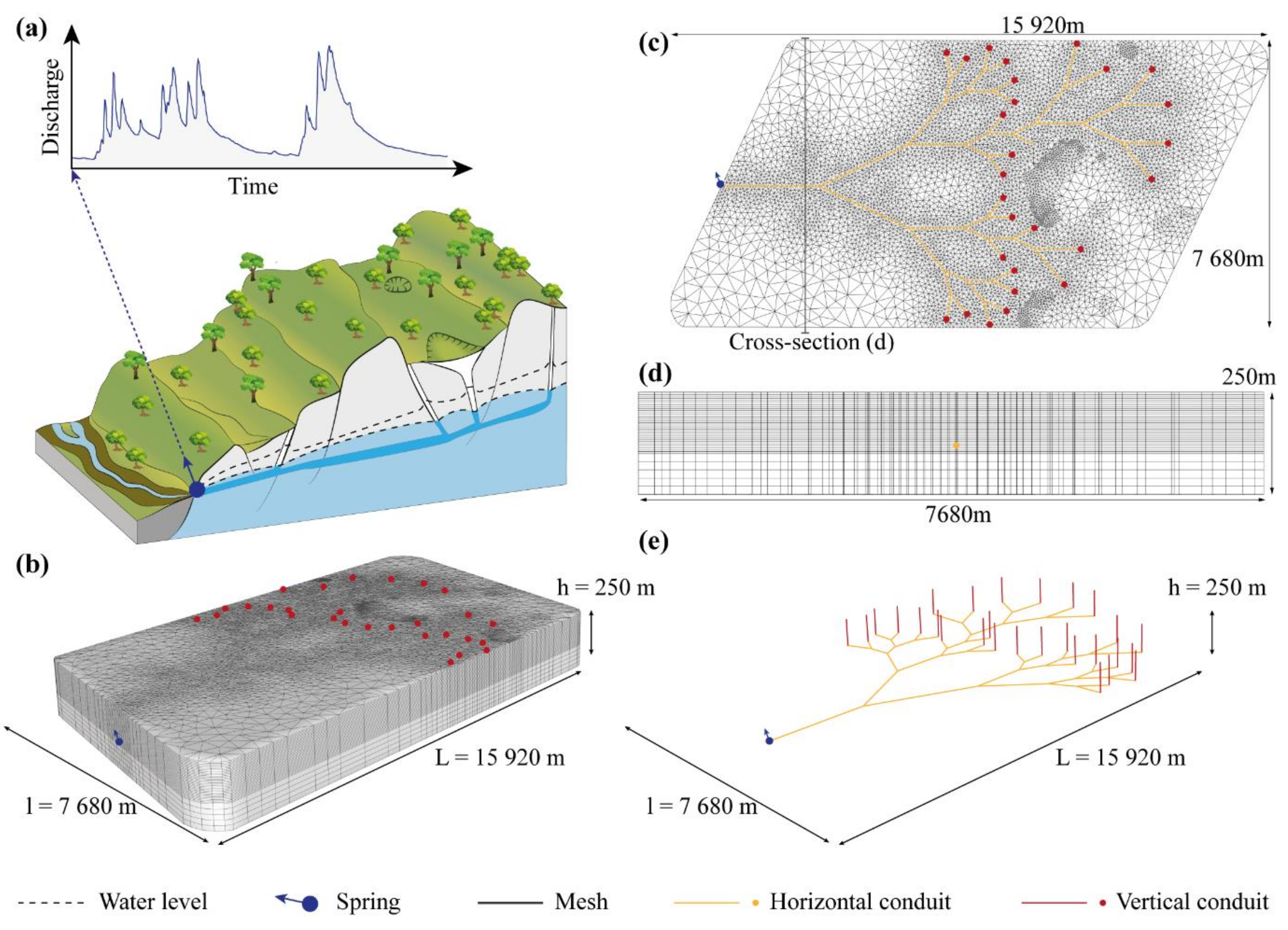
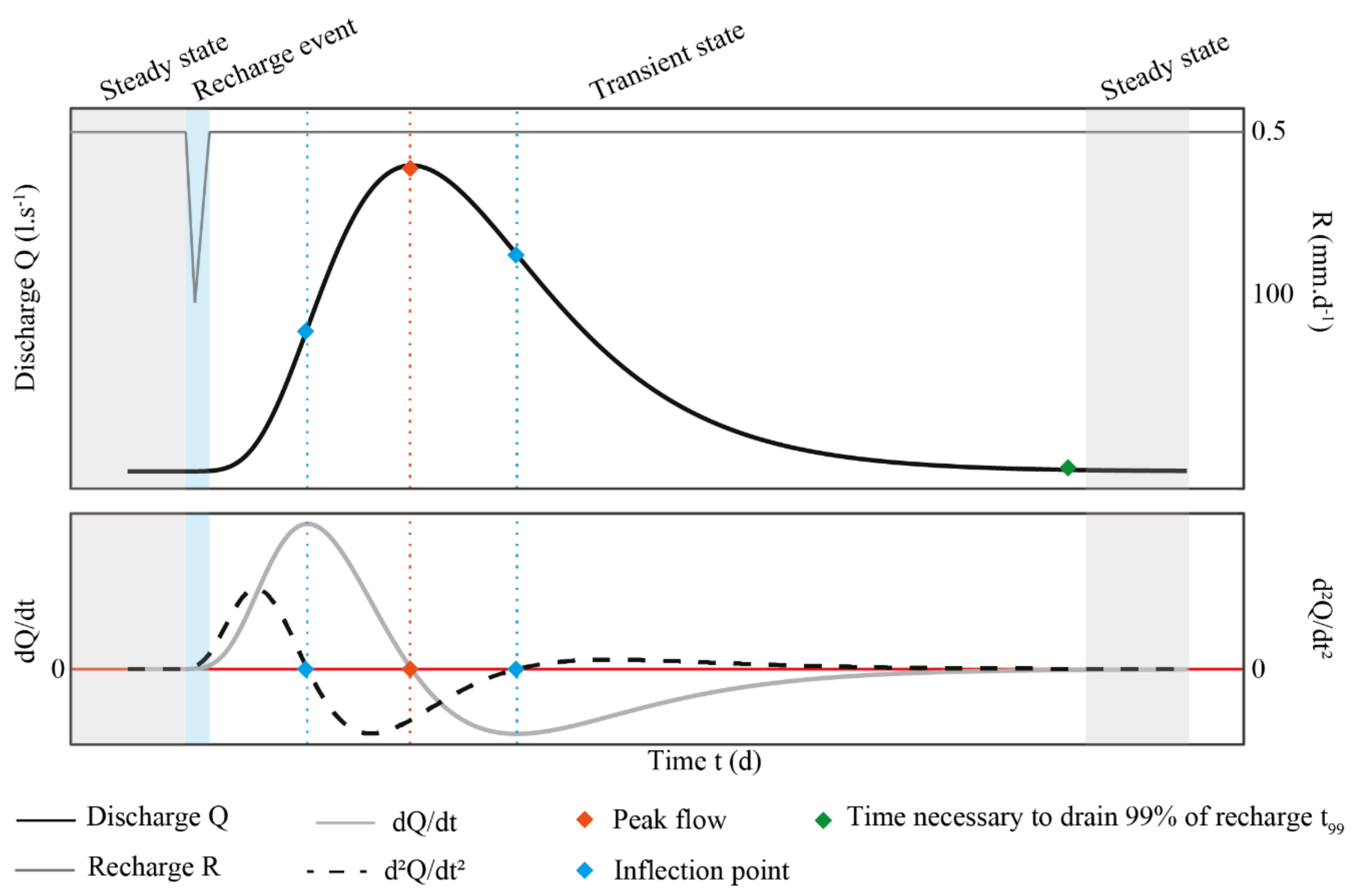
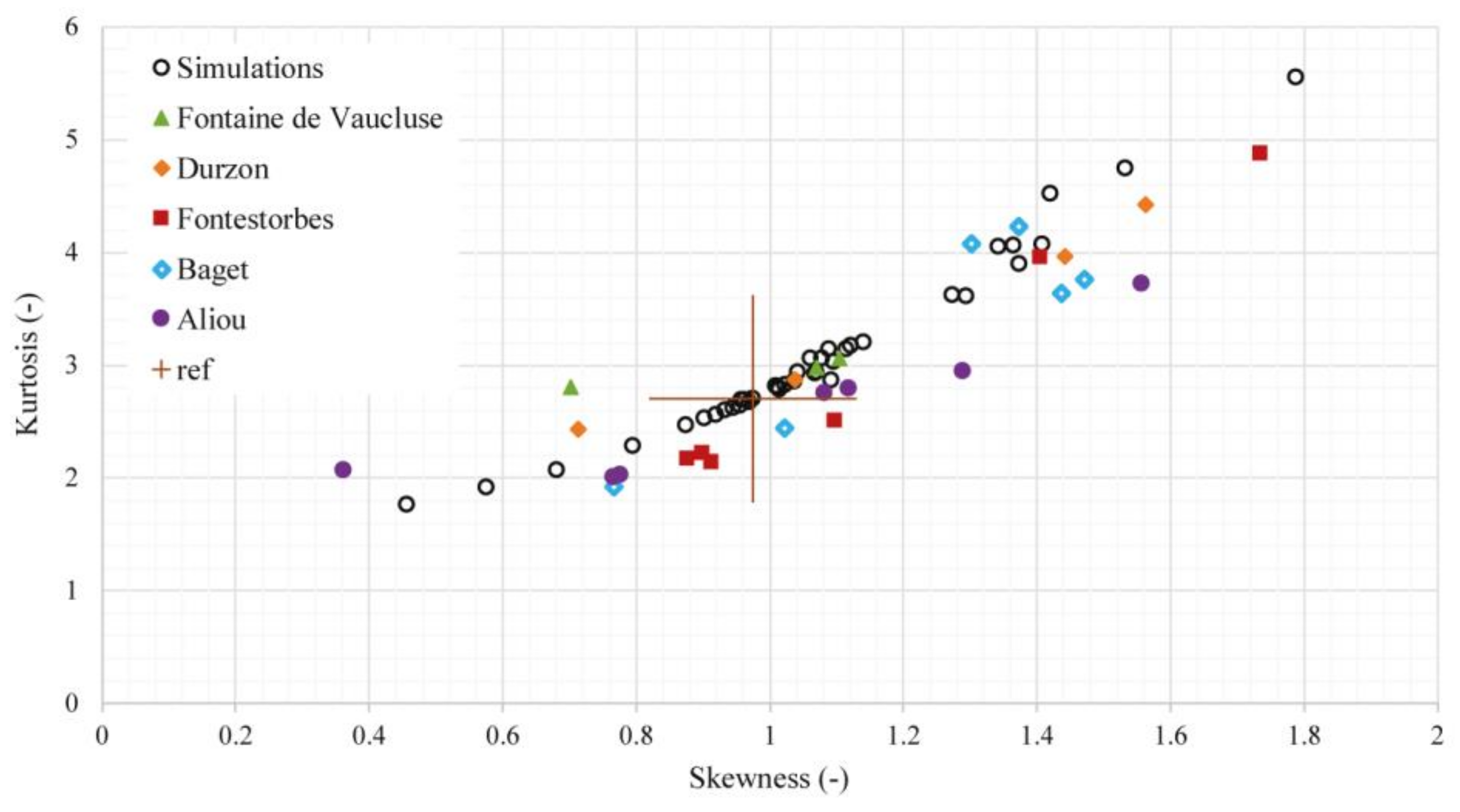
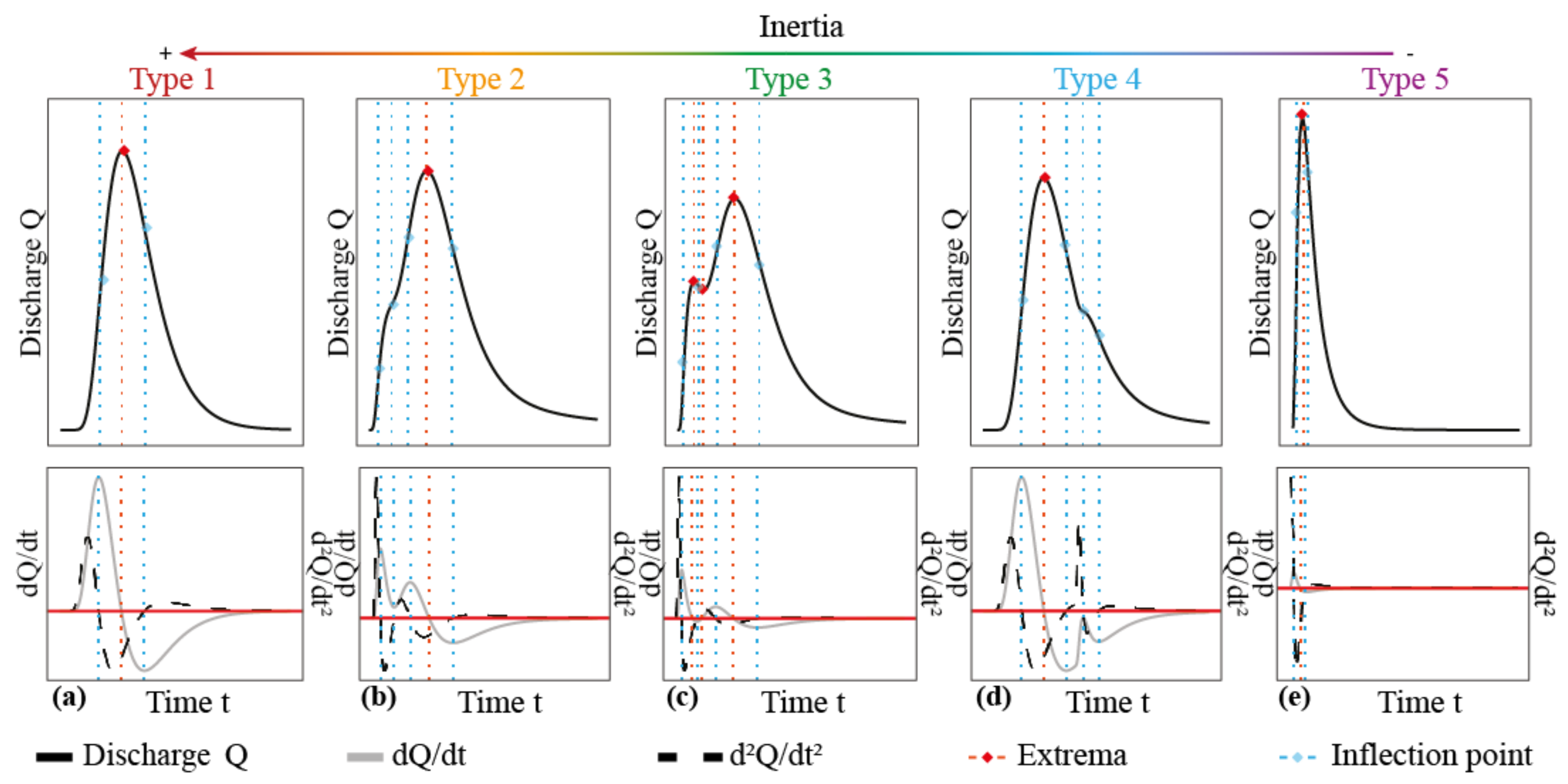
| Subsystem | Property (Units) | Values and Ranges of Values 1 from Literature | Model’s Values and Range of Values Min–Ref–Max |
|---|---|---|---|
| Epikarst (EK) | Thickness ThkEK (m) | (0; >30) [24] (few meters; 10−15) [23] (3; 10) [1] (8; 12) [73] | 0–20–35 |
| Porosity ϕEK (-) | (0.05; 0.1) [24,74] (0.1; 0.3) [27] >0.2 [1] | 0.01–0.1–0.25 | |
| Horizontal 2 hydraulic conductivity KEK (m·s−1) | (10−7; 10−4) [41] 10−5 [39] (5 × 10−5; 10−3) [75] (2 × 10−4; 2 × 10−3) [76] 10−3 [77] >1000 * KTZ-SZ [78] | 10−5–10−2–10−1 | |
| Transmission and saturated zones (TZ–SZ) | Thickness ThkTZ (m) | depending on the field site, usually tens of meters, <20; <50 [77] up to 700 [32] | 30–80–130 |
| Porosity ϕTZ-SZ (-) | (0.004; 0.01) [1] 0.005 [79] (0.01; 0.02) [80] (0.024; 0.3) [81] | 0.005–0.01–0.025 | |
| Horizontal 2 hydraulic conductivity KTZ-SZ (m·s−1) | (10−10; 7 × 10−5) [81] (10−7 [46]; 10−6 [1,47]) [75] (5 × 10−7; 5 × 10−6 [39]) [9] (10−6 [1,47]; 10−4 [79]) [80] (10−5; 103) [17] | 10−7–10−5–10−3 | |
| Conduit (C) | Diameter D (m) | (0.08; 15) [64] (2; 10) [60] | Flow Capacity AC * KC (m3·s−1) 10−2–10−1–101 |
| Section AC (m2) | (<1; >100) [82] | ||
| Hydraulic conductivity KC (m·s−1) | (6 × 10−5; 4 × 10−1) [81] (10−1; 10) [17,75] (3; 10) [80] 10 [9,47] | ||
| Van Genuchten Model | Coefficient α (m−1) | (3.28 × 10−3; 6.23 × 10−1) [44] 3.65 × 10−2 [47,49] 10−2 [17,46] | 3.65 × 10−2 |
| Empirical parameter n (-) | (0.01; 3) [44] 1.83 [47,49] 2 [17,46] | 1.83 | |
| Residual water content θr (-) or Residual water saturation Sr (-) | θr = Sr = 0 [46] θr ∈(0.01; 0.05) [44] Sr = 0.05 [47] θr = 0.171 [17] | Sr = 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dal Soglio, L.; Danquigny, C.; Mazzilli, N.; Emblanch, C.; Massonnat, G. Taking into Account both Explicit Conduits and the Unsaturated Zone in Karst Reservoir Hybrid Models: Impact on the Outlet Hydrograph. Water 2020, 12, 3221. https://doi.org/10.3390/w12113221
Dal Soglio L, Danquigny C, Mazzilli N, Emblanch C, Massonnat G. Taking into Account both Explicit Conduits and the Unsaturated Zone in Karst Reservoir Hybrid Models: Impact on the Outlet Hydrograph. Water. 2020; 12(11):3221. https://doi.org/10.3390/w12113221
Chicago/Turabian StyleDal Soglio, Lucie, Charles Danquigny, Naomi Mazzilli, Christophe Emblanch, and Gérard Massonnat. 2020. "Taking into Account both Explicit Conduits and the Unsaturated Zone in Karst Reservoir Hybrid Models: Impact on the Outlet Hydrograph" Water 12, no. 11: 3221. https://doi.org/10.3390/w12113221
APA StyleDal Soglio, L., Danquigny, C., Mazzilli, N., Emblanch, C., & Massonnat, G. (2020). Taking into Account both Explicit Conduits and the Unsaturated Zone in Karst Reservoir Hybrid Models: Impact on the Outlet Hydrograph. Water, 12(11), 3221. https://doi.org/10.3390/w12113221






