Abstract
Water availability is increasingly stressed in cities across the world due to population growth, which increases demands, and climate change, which can decrease supply. Novel water markets and water supply paradigms are emerging to address water shortages in the urban environment. This research develops a new peer-to-peer non-potable water market that allows households to capture, use, sell, and buy rainwater within a network of water users. A peer-to-peer non-potable water market, as envisioned in this research, would be enabled by existing and emerging technologies. A dual reticulation system, which circulates non-potable water, serves as the backbone for the water trading network by receiving water from residential rainwater tanks and distributing water to households for irrigation purposes. Prosumer households produce rainwater by using cisterns to collect and store rainwater and household pumps to inject rainwater into the network at sufficiently high pressures. The smart water grid would be enabled through an array of information and communication technologies that provide capabilities for automated and real-time metering of water flow, control of infrastructure, and trading between households. The goal of this manuscript is to explore and test the hydraulic feasibility of a micro-trading system through an agent-based modeling approach. Prosumer households are represented as agents that store rainwater and pump rainwater into the network; consumer households are represented as agents that withdraw water from the network for irrigation demands. An all-pipe hydraulic model is constructed and loosely coupled with the agent-based model to simulate network hydraulics. A set of scenarios are analyzed to explore how micro-trading performs based on the level of irrigation demands that could realistically be met through decentralized trading; pressure and energy requirements at prosumer households; pressure and water quality in the pipe network.
1. Introduction
Urban water utility systems around the world are increasingly pressured by limited water resources, growing urban demand, and impacts from climate change. The United Nations projects that, by 2025, 1.8 billion people will be living in regions with absolute water scarcity, and two-thirds of the world population could be living under water-stressed conditions [1]. Supply-side strategies for urban water management are limited in water-scarce regimes, because they require large investments to construct new infrastructure and develop new resources. Demand-side strategies, on the other hand, extend existing resources by reducing demands through conservation campaigns, pricing strategies, and restrictions. Demand-side strategies that rely on continued demand reduction, however, are ultimately limited by hardened demands that cannot be reduced further. As water scarcity in urban centers increases with population growth and climate change, new technologies, advanced management strategies, and diverse water sources must emerge to create new efficiencies in water supply and use. Innovative programs can utilize new technologies and data that have emerged as part of smart cities initiatives [2]. For example, smart meters provide capabilities to collect sub-hourly water flow and consumption data in real-time [3], and automated control systems operate infrastructure components remotely and efficiently [4,5,6].
This manuscript explores a novel management strategy for improving water efficiency in urban areas by supplementing non-potable purposes of the total demand using alternative water sources. A smart water grid is presented here as a water network that is shared by multiple diverse users, who can either produce or consume water. The concept presented in this manuscript builds on an existing dual reticulation system, which pumps non-potable reclaimed water back to a community via a second parallel pipe network and reduces demands for high quality treated water, as compared with a conventional urban water cycle (Figure 1a,b). We propose that the existing non-potable water network can be used as a smart water grid to facilitate micro-trading, where households can exchange water within a peer-to-peer network. Households generate water through rainwater harvesting, putting rainwater “back on the grid” by pumping water into the non-potable water infrastructure system, and purchase water from neighbors by withdrawing water from the pipe network. Smart technologies, such as smart meters, blockchain, smart contracts, and automated infrastructure, would provide the necessary capabilities to allow real-time trading within a smart water grid. Within a smart city paradigm, a rainwater micro-trading program re-envisions the urban water cycle by allowing households to act as prosumers, who produce and sell water within their community (Figure 1c). By allowing households to trade rainwater, a new efficiency is introduced in the water cycle that offsets requirements to treat and pump reclaimed water from a centralized facility. This offset can create energy savings and save reclaimed water for use in other non-potable applications.
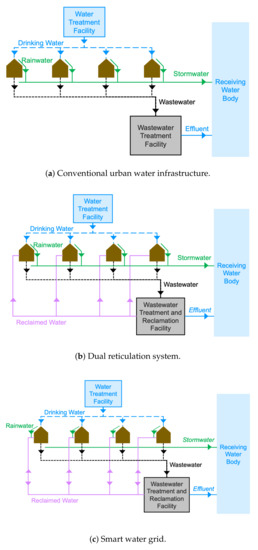
Figure 1.
(a) Conventional urban drinking water, wastewater, and stormwater systems. (b) A dual
reticulation system closes the loop in the urban water cycle by treating wastewater and providing it for
non-potable household uses. Effluent flows from the wastewater facility are reduced. (c) A smart water
grid increases water efficiency in the urban water cycle by allowing households to contribute rainwater
to the dual reticulation system. Effluent and stormwater flows are reduced.
In the energy sector, micro-trading has been demonstrated as a viable market for decentralized resource production, in which households can generate energy through solar photovoltaic cells, store energy in batteries, and sell and transmit excess energy to neighbors through existing power distribution infrastructure [7,8]. Micro-trading water has a number of nuanced constraints that may limit its adoption by utilities and community members. For example, new infrastructure at households is needed to enable storage, sensing, treatment, and trading water, and household participation may vary based on climate and economics. The research presented in this manuscript focuses on the performance of centralized infrastructure and takes a simulation-based approach to evaluate the effects on water savings, energy savings, nodal pressure, and water quality. Reclaimed water networks are designed to maintain pressures and flows, and performance of a smart water grid may decrease due to new flows associated with produced water. The ability of prosumers to contribute water to a non-potable water network is facilitated by household-level pump systems, and the introduction of these decentralized flows into a pipe network affects flows and pressures in the network. High pressures in the network can limit the contribution of water from households that must overcome pressure heads through small pumps, and low pressures may emerge in times of low production and high demands. This research also evaluates savings in energy and water associated with a smart water grid. Micro-trading can reduce demands for produced reclaimed water, resulting in water savings. The energy required to run household pumps across a network, however, must be compared with the energy requirements of treating and pumping water from a centralized facility.
The goal of this manuscript is to explore the feasibility of a smart water grid based on the performance of the centralized infrastructure and energy demands. This research develops a simulation framework that couples agent-based modeling and hydraulic models to test energy consumption, water consumption, and nodal water pressure in a smart water grid. Agent-based models simulate the individual behaviors and interactions of a population of agents to explore emergent system-level dynamics [9,10]. Agent-based modeling has been applied in water resources management to simulate a population of water consumers as agents with the purpose of exploring the emergence of system-level performance due to micro-level interactions [11]. A few studies couple agent-based models with hydraulic simulation to explore how changes in household demands affect system-level performance, such as pressure and flow directions [12,13,14]. Further, agent-based modeling has been applied to simulate markets for trading natural resources [11,15,16,17], and recent research applied agent-based modeling to simulate how households trade solar generated energy in a peer-to-peer energy market [8]. In the formulation developed in this research, consumer households are simulated as agents that exert irrigation demands, and prosumer households are simulated as agents that store rainwater, and pump rainwater into a pipe network. A hydraulic model is developed of a reclaimed water network that serves a small community of non-potable water consumers and prosumers. Output from the agent-based model specifies flows into and out of the water network at each node, and these outputs are used as negative and positive demand patterns for the hydraulic model. The modeling framework is applied for an illustrative case study that was developed based on realistic infrastructure data. Water consumption, nodal pressure, and energy consumption are evaluated for the network of water users for scenarios with and without micro-trading. System performance is tested for 126 scenarios across different climates and concentrations of prosumers to explore how precipitation and participation affect feasibility. The results demonstrate that a smart water grid is feasible, generating energy and water savings that vary in magnitude based on local climate and the level of community participation.
2. Background
2.1. Dual Reticulation Networks
Only a fraction of water used for urban purposes needs to be potable quality, and reclaimed water can serve as an alternative water source for non-potable applications [18]. Reclaimed water is wastewater that has been treated to levels lower than potable water quality and can be used for nonpotable applications, including washing, cooling, gardening, toilet flushing, and lawn irrigation [19]. Reclaimed water can be provided to a large group of consumers through a dual reticulation system, which includes two parallel pipe networks: the primary water network distributes potable water, and the secondary network conveys reclaimed water [20]. A centralized utility typically manages water reclamation programs to ensure that treatment standards are met and to distribute reclaimed water. Dual reticulation programs have been implemented in cities in the United States, Japan, and Australia [21]. Reclaimed water products can help conserve high-quality water produced by utilities for essential purposes.
Dual reticulation systems impose high capital costs, but costs can be offset by a reduction in demands that are exerted on aquifers and surface water sources, leading to improved ecosystem health and drought resilience [22]. While it is difficult to quantify the externalities in a cost-benefit analysis of non-potable water systems [23,24], dual reticulation systems can offset the use of potable water, creating savings in utility energy costs for water treatment [25]. Energy savings can be sufficient to offset the capital costs required for building a dual pipe infrastructure [26]. Dual reticulation systems may also create benefits by reducing the need for infrastructure investment for the main potable system [27] and systematically encouraging conservation by adding new value to water. The cost-benefit analysis of dual reticulation systems, however, can vary widely based on the characteristics of a location, such as infrastructure design, topography, energy sources, quality of source water, and existing infrastructure [28]. The distance between users and a water reclamation plant and the amount of uphill pumping can limit the feasibility of dual systems. A study of four U.S. cities that recycle water found that there were significant economic barriers to implementing dual-reticulation systems. Challenges were cited, including diminishing returns, due to the lack of additional large consumers of nonpotable water near the treatment plant; commitments to return treated effluent for instream flows; more efficient options for selling recycled water for cooling and industrial processes; lack of clear and convergent regulations around water reuse programs [22].
2.2. Rainwater Harvesting Systems
Rainwater harvesting systems can be installed at the household level to capture roof runoff, providing an alternative source to meet non-potable water demands [29]. Harvesting rainwater is a millennia-old agricultural practice, with increasing implementation in modern cities with large population demands, including in Adelaide and Addis Ababa [29,30]. Rainwater harvesting is used widely because it provides easy collection with low cost, treatment, and maintenance requirements [31]. Captured rainwater can be applied on-site or on a larger scale for community purposes, and communal rainwater tanks may be economically feasible [32]. Rainwater harvesting may be feasible for individual users, subject to the specific water demand and roof area [31,33], but its economic feasibility may be limited for some households because it does not provide a continuous supply of water and needs to be supplemented with other sources [34]. As an alternative source, however, rainwater can provide significant volumes of water, and it is estimated that up to 80% of rainfall could be harvested from urban rooftops in the U.S. [35]. For example, a study of California water indicates that recycling irrigation runoff water (priced at ($0.43–1.21 per 1000 gallons) was a cost-effective alternative to using the region’s municipal water ($2.39–2.91 per 1000 gallons) [36]. Rainwater harvesting has other benefits, and it can reduce stormwater infrastructure costs by reducing peak flows. Liang et al. [37] showed that implementing smart rainwater harvesting systems reduces peak system flows by 35% to 85%.
There are practical limitations and costs that prevent the transition to the wide-scale use of rainwater infrastructure. Rainwater harvesting is shown to have long payback periods before benefits outweigh costs, with economic returns that are very sensitive to local policy, water quality concerns, and government rebates [38,39]. Grants from local initiatives and environmental agencies can reduce capital costs. For example, rebates of $0.50 per gallon of installed tank capacity were used to incentivize rainwater harvesting in Barbados [38]. The costs and benefits indicate that green infrastructure solutions have market value and should be strongly considered, though the economics of purchasing tanks and pumps, as required in the smart water grid, may need economic incentives to encourage wide-spread adoption. The system that is proposed in this research creates a new efficiency in the use of rainwater by providing the means to share rainwater within a community and creating a reliable source of non-potable flows by integrating rainwater harvesting within a reclaimed water reticulation system.
2.3. Micro-Trading in Water Markets and Smart Technologies
Economists have argued that scarce water can be allocated more efficiently through water markets, rather than through centralized control [40]. Large-scale water rights markets have been operating for decades among utilities and agricultural users [41], and new markets that trade conserved water are emerging as a strategy for demand-side management to create value and new incentives around conservation activities [42,43]. Decentralization of water services is seen as an approach to support a sustainable future for urban water management [44,45], where water can be supplied or treated at small-scale plants, rather than at centralized locations. Efficiencies may be gained through decentralized systems because water or wastewater does not need to be transported over long distances, and resources can be re-used to meet demands on-site. A few studies explore decentralized markets for water supply that allow for trading among households. Haddad [46] proposed a cap-and-trade water program among residential end-users, where a cap is used to grant each customer with use-rights to available water. Water conservationists could sell or rent unused use-rights, and customers would be heavily penalized for using water in excess of their use-rights. Water customers would call a toll free number to execute transfers through a specially-trained broker. Haddad’s micro-trading system was criticized based on the complexities of making initial allocation of use-rights to users; expected sizeable transaction costs; lack of household expertise and willingness to engage in a market; impact of a water-use market on economic development in the area [47,48]. More recently, a decentralized water supply system was developed in Western Australia, in which consumers contribute recycled water, including stormwater and greywater, to a groundwater resource through garden bores [49]. By contributing recycled water, consumers become prosumers and gain credits in their water use accounts. The program is enabled through smart meters, which record water consumption and contributions at 10-minute intervals, and the shallow aquifer provides a pathway in the urban water cycle among households and utility.
The viability of micro-trading has been enabled by the emergence of blockchain technology in water markets. Blockchain technology is an information and communications technology (ICT) capable of addressing some of the challenges in implementing peer-to-peer markets [50]. A blockchain is a distributed ledger that provides a platform for digital transactions without a trusted third-party organization [51,52]. Data structures are both immutable and cryptographically verifiable, promising security, accuracy, authentication and traceability of transactions [53]. Blockchain can also reduce transaction costs associated with third-party brokers, though some fees may be necessary to maintain a critical centralized infrastructure [8]. Smart contracts can be used with blockchain, where smart contracts work as simple scripts encoded on the blockchain that contain predefined directions for automating workflows on recorded data and finalizing the settlement of financial transactions between buyers and sellers [54]. Smart contracts automate micro-trading to allow for rapid reconciliation between consumers and prosumers and reduce the time and associated cost of trading, which may increase participation. As an emerging technology, blockchain has applications in water resources management, supporting data sharing among utilities with assurances of confidentiality and commercial sensitivity; linking flowmeter sensor data with water resources mapping, billing, and operations; facilitating trading and tracking of water credits among large-scale users; allowing households to buy water in a market of competitive water providers; serving as a stable currency to enhance security of water supply [55,56,57]. Blockchain provides a ledger system that can support peer-to-peer markets for micro-trading water, and a few examples exist to date. Melbourne, Australia, has proposed a rainwater micro-trading program that would be under-girded by blockchain technologies [55]. The program would assign apartments with a quota of free rainwater from a communal tank, and excess rainwater would be conveyed to a large water recycling plant to supply treated water for non-drinking uses [58,59]. In another example, a proof-of-concept model was developed to simulate blockchain-enabled trading of virtual water among homes, where water could be sold by low-consuming households to households that want to exceed a daily limit on water consumption [60]. Similar to Haddad’s cap-and-trade system [46], customers would trade water rights. Whereas Haddad’s program would allow customers to trade water on a monthly or seasonal basis, the market proposed by Alcarria et al. [60] relies on smart meters, blockchain, and smart contracts, and the functionality of these technologies would allow customers to make daily decisions about trading water.
The smart water grid proposed in this research would rely on smart connected technologies, similar to the systems described above. Smart water meters are needed to record the exact flow rate and time of consumed and produced water. Water that is available during times of peak demands is inherently of higher value than water that is available at times of low demand. Prosumers can invest in large tanks to store water and release it during periods of high consumption, and precise meters are needed to record high resolution of trades. Automated infrastructure components, such as digitally operated pumps and valves, are needed to update flows into the network from prosumers when a trade is negotiated. Blockchain and smart contract technologies are needed to support micro-trading. Unlike other micro-trading systems described above, however, the smart water grid relies on a centralized pipe network to convey traded rainwater among households, and the focus of this research in on a feasibility analysis to explore how the hydraulics of the pipe network would be affected by decentralized buying and selling of rainwater. The feasibility of a smart water grid will also be affected by the availability and functionality of smart technologies, including blockchain and smart contracts, and the effects of benefits and costs of infrastructure, new technologies, and water and energy savings on market efficiency. While market efficiency and smart technologies are not included in the modeling framework that is described in this research, they should be explored in future research to further test the feasibility of the smart water grid.
2.4. Agent-Based Modeling for Water Infrastructure
Agent-based modeling simulates the behaviors and micro-interactions of a population of autonomous and heterogenous agents to model and study system-level phenomena [9,10]. Agent-based modeling has been applied to simulate a range of water resources planning problems by representing water users, stakeholders, and decision-makers as agents to capture decisions and behaviors around water use, water supply, wastewater services, and stormwater runoff [11]. Agent-based models have been applied to represent a population of residential water users that adapt their water consumption based on economics, climate, policies, and social influence [61,62,63,64,65,66,67,68,69,70,71]. These models simulate household decisions to use water and reduce consumption by adopting water-efficient technologies and restricting water use. Some frameworks couple agent-based modeling with the water supply system to capture feedback between the availability of water resources and decisions to conserve water [64,65,66,67,70]. Other agent-based models couple a population of agents with the hydraulic simulation of a water distribution system to evaluate how network flows are impacted by changing demands. Models capture water use changes during a water supply contamination event, based on exposure to the contaminant, communication from public officials, and social influence of peers [12,13,72,73,74,75,76,77]. Another set of studies uses agent-based modeling coupled with hydraulic simulation to evaluate how flows in a reclaimed water network and a potable water network change as customers adopt or resist water reuse programs [14,27,78]. Agent-based modeling has also been applied to model trading within natural resource markets, where agents use cost information to seek trades, negotiate, and adapt their preferences for trading permits with other agents. A few modeling studies couple an agent-based model with a water quality simulation model to assess water quality impacts of permit-trading strategies on river and estuary systems [11,15]. Other agent-based models capture the decisions of polluters to bid and sell permits in an emissions market, and these models are applied to assess the effect of trading on air quality [16,17]. More recently, an agent-based modeling was applied to simulate peer-to-peer markets by modeling households as agents that buy and sell energy in a residential smart energy grid [8]. In the research presented in this manuscript, agent-based modeling is loosely coupled with hydraulic simulation modeling to assess network performance metrics that are affected by agent behaviors to trade water. A simple market is simulated, where consumer agents buy rainwater when it is needed for irrigation, and prosumer agents meet demands when they have rainwater that is stored. The price of rainwater is not considered in this simulation, because the focus of the model is on the hydraulic feasibility of the network when trades are made. Additional research is needed to develop cost information and simulate how households make decisions to participate, bid, and execute micro-trades in a rainwater market.
3. Agent-Based Modeling Framework
The modeling framework presented in this research loosely couples an agent-based model with a hydraulic simulation model (Figure 2). The agent-based model represents households as either consumers, which purchase water and withdraw it from the system, or prosumers, which pump collected rainwater into the network when a buyer has committed to purchase the water. Prosumer water input and consumer demands are used to modify an input file for the hydraulic simulation, which calculates water flows and pressures in the pipe network based on production and consumption of water at households. The agent-based model is described following the Overview Design Details (ODD) protocol [79]. The ODD protocol provides a clear and succinct approach to describe agent-based models by describing purpose, entities, state variables, and scales as part of the Overview; process overview and design concepts as part of the Design; input, initialization, implementation, and submodels as part of the Details.
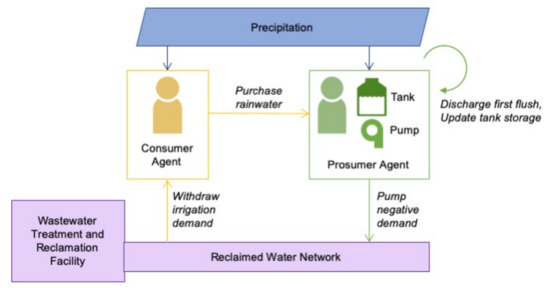
Figure 2.
Agent-based modeling framework couples consumer and prosumer agents with a reclaimed water network. Image credit: Water Tank by Carlos Ochoa from the Noun Project.
3.1. Overview
3.1.1. Purpose
The purpose of the agent-based model is to simulate rainwater trading among consumer and prosumer agents facilitated through a reclaimed water network and to evaluate how water resources, energy consumption, and hydraulic performance of the network are affected by micro-trading.
3.1.2. Entities, State Variables, and Scales
Agents represent individual prosumer and consumer households. Each consumer agent is assigned a lawn area to calculate irrigation demand and is assigned a time of day for exerting demand. Prosumer agents are each assigned a rainwater tank volume capacity, a catchment area, and a small pump with a given exit pipe diameter, length, and roughness coefficient to add harvested rainwater to the hydraulic network. Parameters are used as input to the model (Table 1). State variables are updated dynamically (Table 2). For each prosumer, tank storage is updated due to precipitation, flushing requirements, and water released into the network. The model operates on an hourly time scale.

Table 1.
Parameters for consumer and prosumer agents.

Table 2.
State variables for consumer and prosumer agents.
Three system-level state variables are used to represent the depth of hourly precipitation (), total precipitation depth over the preceding 24-h period (), and the time step at which rain begins ().
3.1.3. Process Overview and Scheduling
The following steps are executed at each hourly time step, t, of the simulation. The execution time step is labeled . The agent-based model requires hourly precipitation () as input.
Step 1. Update system-level state variables. Based on the value of , the values for and are updated. The precipitation over the preceding 24-h period () is a binary variable that takes a value of one if there is a precipitation greater than zero in 24-h period before the execution time:
where t is the time step and is the current execution time step. Rain time, , is the first time step when the precipitation is greater than zero if the precipitation over the preceding 24-h period is zero.
Step 2. Prosumer agents update rainwater storage values. Each prosumer agent g calculates rainwater storage volume, , at time t based on the runoff from the roof catchment and the volume of water flushed for the first flush diversion:
where A is the roof area; V is the capacity of the rainwater tank; is the volume of water flushed from the rainwater tank at time step t for agent g. Prosumers can accumulate a maximum volume of water equivalent to the capacity of the rainwater tank (); any excess volume is released as runoff. If no precipitation falls in the previous 24 h before a distinct rain event begins, the prosumer agent is required to discard a first flush volume. The volume of rainwater that should be flushed () ensures that a prosumer agent flushes a volume equal to after the rain event begins, where F is the required first flush rate, and A is the roof area. The agent can flush the total volume () over multiple time steps, if needed.
Step 3. Consumer agents exert irrigation demands. If no precipitation fell in the previous 24 h (), each consumer agent c exerts a daily irrigation demand () at time step . The hourly demand exerted by each consumer agent c is assigned using Equation (5):
The value of is calculated to initialize the model, as described in Section 3.4.1.
Step 4. Prosumer and consumer agents trade rainwater. Each consumer agent with non-zero demand at time step t is randomly paired with a prosumer agent with . A consumer agent c receives traded water () from prosumer agent g up to its demand, . If the consumer agent has a non-zero volume of unmet demand, it is randomly matched with other prosumer agents until the total volume of traded water it receives is equal to or until no prosumers have stored rainwater. For time steps when prosumers cannot meet consumer demands, consumer demands are met using water that was reclaimed through the centralized treatment plant. The flow () that a prosumer pumps into the network at each time step is the sum of traded water () that is purchased by consumer agents.
where is the number of consumers that prosumer g supplies at time step t. The total volume of water purchased by consumer agent c is supplemented by flows from the centralized system () at time step t to meet its demand:
where is the number of prosumers that sell water to consumer agent c at time step t.
Step 5. Increase time step. In this step, . The agent-based model is executed to simulate trades for a total of T time steps to simulate a one-month period. If the simulation time is reached (e.g., ) go to Step 6. Otherwise, go to Step 1.
Step 6. Execute hydraulic simulation model. The dataset of negative demands ( for all prosumers) and positive demands ( for all consumers) are used as input for the hydraulic simulation model. Section 3.4.2 details the method for running the hydraulic simulation model.
Step 7. Calculate hydraulic effects and energy consumption for the infrastructure system. Methods for calculating energy consumption and water age are described in Section 3.4.3 and Section 3.4.4, respectively.
3.2. Design Concepts
3.2.1. Decision-Making
Agents use simple heuristics to make decisions. Prosumer agents are uniformly sampled to meet consumer water demands until consumer water demands are met or no prosumers have rainwater remaining in their tanks. Consumer agents do not use information about network location, amount of available water, or cost associated with purchasing water to select a prosumer agent for trading. Prosumers are simple reactive agents and release water when matched with consumer agents.
3.2.2. Stochasticity
There is little stochasticity in consumer and prosumer behaviors. Households in the network are randomly assigned as consumer and prosumer agents, and consumer agents select among prosumers with uniform probability to buy water.
3.2.3. Sensing
Consumer agents know the volume of water that is stored by each prosumer agent, and both consumer and prosumer agents have exact information about precipitation depths.
3.2.4. Interaction
Consumer and prosumer agents exchange water directly. Trades are not constrained by spatial location, and any prosumer agent can trade with any consumer agent. Consumer agents do not interact with other consumer agents, and prosumer agents do not interact with other prosumer agents.
3.3. Details: Initialization, Input, and Implementation
The agent-based model is initialized with 2016 households, using a pre-specified ratio of prosumers to consumers. Parameter values are specified in Table 1. Values for the first flush volume as reported in the literature (e.g., Gikas and Tsihrintzis [83]), and rainwater harvesting regulations [84,85], vary in the range of 0.11–1.02 L/m2. The value used in the prosumer model represents a conservative estimate of first flush. All tanks are empty at the beginning of the simulation, and the number of hours since the previous flush is set to 24, which forces prosumer agents to flush tanks before beginning trades. Each prosumer agent is assigned a household pump model, with a pump efficiency of 75%. Consumer households are each assigned a time of day to irrigate their lawns (), derived from the diurnal irrigation pattern for dual-reticulated systems reported by Willis et al. [80]. For each discrete value of , Figure 3 specifies the number of consumer agents that are randomly selected from the pool of consumer agents without replacement and assigned the selected value for . For example, if the consumer agent pool consists of 100 agents, then for 21 randomly selected agents. The agent-based model requires hourly precipitation data as input, which are needed to calculate demands and trades at hourly intervals.
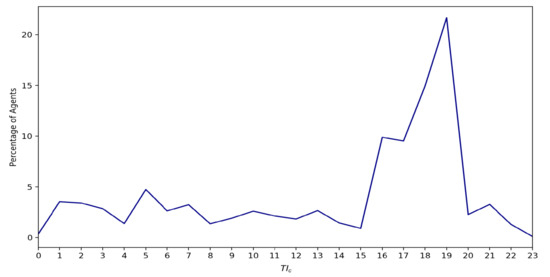
Figure 3.
Consumer agents are assigned a value for using the distribution of values shown here.
The agent-based model is implemented in Multi-Agent Simulator Of Neighborhoods (MASON) [86], a Java-based discrete-event multi-agent simulation library. The code is published by Ramsey [87]. The output from MASON was used to create input for the hydraulic simulation submodel, which is described below.
3.4. Details: Submodels
3.4.1. Consumer Daily Irrigation Demand Submodel
The consumer daily demand volume, , is calculated using the outdoor water demand model [88].
where f is an irrigation factor indicating frequency of watering; L is the irrigable lawn area (m2); k is a crop coefficient; is evapotranspiration (mm/month); r is effective rainfall (mm/month); is the number of days per month. Effective rainfall represents the precipitation that penetrates the soil and thereby reduces the water demand of plants. It is calculated as a function of total measured monthly rainfall (mm/month) [88], as:
The monthly demand value is converted and reported as a daily demand. The irrigation factor (f) is set at 1.0, because it is assumed all households that opt to connect to the system are frequent irrigators. The crop coefficient (k) is set as 0.7 to represent lawn. The value of L (irrigable lawn area) is calculated as
where the household density is (unit per m2), roof area is represented as A (m2), and the ratio of unpaved land is U (dimensionless).
3.4.2. Hydraulic Simulation Submodel
The pipe network is simulated using EPANET, which is a software application that calculates the movement and fate of drinking water constituents within water distribution systems [89]. Each household (consumer or prosumer agent) is represented in the network using three nodes: one node represents the street-level metered connection to the non-potable water network; a second node represents the irrigation demand node; a third node represents the negative demand node that allows a household to contribute rainwater to the network. The negative demand node represents an onsite rainwater harvesting tank and a pump that is used to put rainwater back into the network. The dataset of negative demands, or positive flows into the network (), are placed at negative demand nodes, corresponding to each prosumer and time step. The dataset of positive demands () are placed at irrigation demand nodes, corresponding to each consumer and time step. Demands are used to modify the EPANET input file, and the hydraulic model is run for a one-month period to calculate network flows and pressure values.
3.4.3. Energy Consumption Submodel
Energy requirements for the water infrastructure network are based on three energy components: energy consumed by prosumers to pump rainwater into the network (), energy used to pump water from the centralized treatment plant (), and energy required to treat wastewater (). The total energy required by the system () is the sum of the three components. Energy is reported in kilowatt hours (kWh).
The energy consumed by the prosumers to pump water into the network is calculated as:
where is the specific weight of water (kN/m3); is the flow rate of pumped water from prosumer g, as defined above (m3/s); is the pressure head at the negative demand node for prosumer g at time step t, which is the head required by the pump (m); G is the number of prosumers in the system; T is the number of simulated time steps; is the time step, or one hour in this application.
The energy consumed to pump water from the centralized system is calculated as:
where is the flow rate of water pumped from the reservoir to the system (m3/s); corresponds to the head (m) gained by the pump at time step t.
The volume of reclaimed water that is offset by rainwater contributions can result in energy savings through a reduction in the volume of water that must be treated. Treating water to high standards is energy intensive, and supplementing the reclaimed water network with rainwater decreases the volume of wastewater that water treatment facilities need to process for household consumption. The energy required to treat wastewater can vary based on influent water quality, facility hydraulics, and treatment processes employed, and a value of 0.343 kWh/m3 is adopted in this study [25]. The energy required to treat wastewater is calculated as:
where is the total volume of treated water that is pumped into the system over the simulated time; is the unit energy required to treat wastewater (0.343 kWh/m3).
3.4.4. Water Age Submodel
The water age of the system is a surrogate metric for water quality [90]. Water age is calculated using water quality calculations in EPANET, which are executed at small time steps to reduce error. The weighted water age is calculated using Equation (14) at consumer nodes across the network.
where is the weighted average water age above the limit for the system (hours). The acceptable limit for water age () is 48 h [90]. represents the water age at consumer node c and time step t, reported in hours. The binary variable represents if the water age at node c and time step t exceeds the limit, where if the water age is greater than the limit, and otherwise. The time step for calculating water quality is 15 min, and the total number of time steps () is 2880 for simulation of a 30-day month.
4. Virtual Network: Wolfpack City
“Wolfpack City” was developed as a virtual non-potable water distribution network (Figure 4) with realistic hydraulic design parameters and is used in this research to simulate a micro-trading program. It is assumed that each household receives potable water to meet high-quality end uses via a separate potable water system that is not modeled in this framework; simulations for Wolfpack City are specifically for non-potable water supply and demand. Wolfpack City represents a population of 2016 households, which exert irrigation demands based on rainfall and evapotranspiration. One demand is exerted as a constant flow (0.0078 m3/s or 125 GPM) to represent an industrial demand, such as a cooling process.
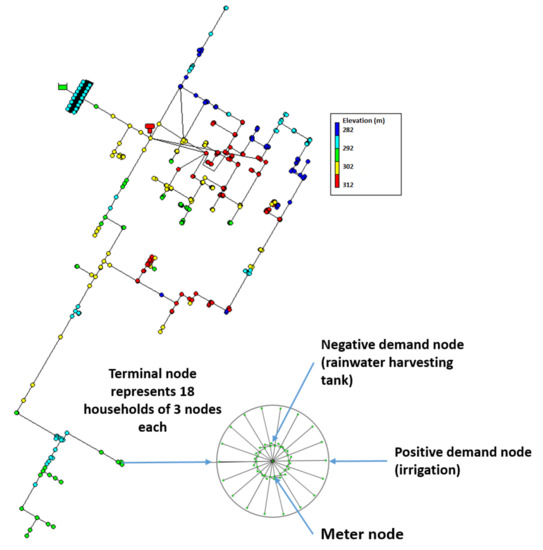
Figure 4.
Wolfpack City water model. Each terminal node represents 18 households, which are represented using three nodes each: a meter node, positive demand node, and negative demand node.
4.1. Non-Potable Network System
Household elevations in Wolfpack City range from 282 to 312 m (Figure 4). The source represented by a reservoir with a head of 297 m is a reclaimed water treatment plant and pumps water to the network using a set of pumps and a tank. The pump station includes a main pump and eight additional parallel pumps that are controlled by the water level of the tank. The main pump delivers up to 0.0227 m3/s and a gained head of around 56 m. The parallel pumps operate to meet the intermittent demand exerted by consumers and deliver up to 0.050 m3/s each. The pump efficiency is simulated as 75%. The tank is initialized at full capacity.
4.2. Climate Data
Local climate data are needed to initialize rainwater harvesting tank storage and irrigation demand values for Wolfpack City. We selected the location of Wolfpack City based on the maximum potential rainwater yield at various locations across the U.S. using Equation (15) [91]:
where Y is maximum potential rainwater harvesting yield; C is a runoff coefficient, assigned a value of 0.75 [91]; is land area; is the percentage of land cover which is rooftop; is average annual precipitation. The percentage rooftop is calculated based on land area, housing density, and average roof size [81,92]. We estimated the potential rainwater harvesting yield at 10 locations that are spread across regions of the U.S. using publicly available land cover data [92] and thirty year precipitation averages [93]. Cities that were included in the analysis are Baltimore, Maryland; Branson, Missouri; Dallas, Texas; Denver, Colorado; Fargo, North Dakota; Phoenix, Arizona; Raleigh, North Carolina; San Diego, California; Seattle, Washington. Cities that report the highest value for Y are Seattle (24.1 million m3, Dallas (13.5 million m3), and Phoenix, Arizona (12.2 million m3). The values for each city are shown in Appendix A (Table A1).
Seattle, Washington, was selected as a climate region for Wolfpack City, and observations of precipitation and evapotranspiration in April 2020 are used to create climate scenarios. The data used in this study were recorded at USGS Station 12113346 for Springbook Creek at Orillia, WA [92]. Over April 2020, evapotranspiration was recorded as 281.25 mm/month. Seattle’s household density () is 721 housing units/km2, and other parameters needed for the agent-based model, such as roof size and ratio of unpaved land to total land area, are determined using national averages (Table 1) [81,92]. Using Equation (10), consumer irrigable lawn area () is calculated as 494.9 m2.
4.3. Modeling Scenarios
A set of scenarios are developed to explore the performance of the smart water grid for variations in model characteristics. This analysis explores changes in the number of households that join the market as prosumers to assess how many prosumers are needed to meet demands exerted by consumers. The participation of households as prosumers varies from 0% to 100% of the total number of households by increments of 5%. Households are randomly assigned as prosumer and consumer agents to meet the scenario definition. This analysis also explores changes in precipitation, as precipitation is expected to affect the amount of rainwater traded. Higher depths of rainfall and more frequent precipitation events lead to greater volumes of water stored, but reduce the amount of water needed for irrigation, as consumers do not exert demands immediately following precipitation events. Precipitation scenarios are explored where the depth of rainfall at each hourly time step is multiplied by a factor of 0.5, 1.0, 2.0, 3.0, 4.0, and 5.0. The total number of time steps with precipitation greater than zero is held constant to maintain consistency across simulations; for example, if 5.0 mm is recorded during the first hour of Seattle’s April 2020 precipitation data, then a total of 15.0 mm falls during that time step in a scenario with a precipitation factor of . Evapotranspiration () values are held constant throughout all scenarios. According to the Blaney–Criddle equation, is correlated with temperature, wind, and daylight hours, which we assume as constant across all precipitation scenarios [94]. A total of 126 scenarios (six precipitation settings and 20 prosumer settings) are generated, and scenarios are labeled as the percentage of households that participate as prosumers in the market and the factor used to adjust rainfall depths. Each scenario was simulated over the one-month horizon using MASON, which required approximately 40 s to run using a 3.1 GHz Dual-Core Intel Core i5. Output from the agent-based model was used to create the input file depicting the demands of that scenario for EPANET, which required approximately 6.7 min when run using a 2.9 GHz 4-Core Intel Xeon W-2102.
5. Results
The results presented below demonstrate the dynamics of water storage, water consumption, energy consumption, and hydraulic performance for an example scenario. Subsequently, the performance of the ABM and the network across all scenarios are reported and explored.
5.1. Scenario
Scenario simulates rainfall using Seattle’s April 2020 precipitation data (), and 20% of agents (403 of 2016 total agents) are initialized as prosumers. The time series plots of precipitation, irrigation demands and volume of traded rainwater pumped into the network are shown in Figure 5. The simulated horizon includes six distinct rainfall events of varying volumes, followed by a reduction in immediate irrigation demands. The reduction in irrigation demands represents that consumers do not exert irrigation demands within 24 h of a rainfall event. Traded rainwater injections into the reclaimed water network spike after this 24 h period. The highest peaks in irrigation demand each day correspond with the irrigation patterns shown in Figure 3, peaking at hour 19 (or 7:00 p.m.) each day. A total of 525 m3 of harvested rainwater are pumped into the system during the simulation, which is the equivalent of the daily water demand exerted by 141 consumer households (8.7% of consumers). The volume of rainwater that is traded is a small fraction (less than 1%) of the total volume of water consumed, as shown in Table 3. The flows of water produced at the treatment plant and consumed at nodes for Scenario are simulated using EPANET (Figure 6), demonstrating that the network satisfies exerted demands without significant excess production; the difference in water produced and water consumed is 7% of the water consumed (Table 3). For this scenario, six of the nine pumps are turned on to meet demands. The centralized system maintains a minimum production volume when consumer demands are zero to meet the constant demand of 0.0079 m3/s (or 20,477 m3 over the one-month period).
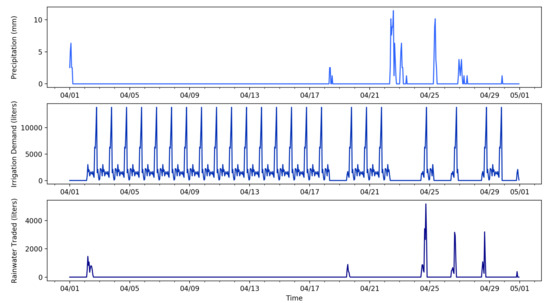
Figure 5.
Precipitation, irrigation demand volume, and traded rainwater volume for Scenario .

Table 3.
Metrics reported for Scenarios and .
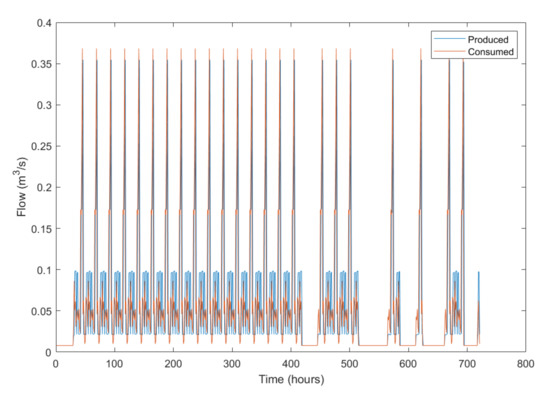
Figure 6.
EPANET output reports flow of water produced by the treatment facility and flow of water consumed at nodes for Scenario .
The energy consumed for system-level pumping, reclaimed water treatment, and prosumer pumping for Scenario are calculated and compared with the energy required for Scenario (no prosumers) in Table 3 to allow for the examination of energy savings between scenarios with and without rainwater trading. The energy consumed by prosumers for household-level pumping increases by 41 kWh when 20% of households function as prosumers, compared with Scenario . Residential demands are 20% lower in Scenario , due to the number of consumers that switch to prosumers. The increase in energy for household pumping corresponds to a decrease in energy consumed by system-level pumping and treatment. There is a decrease of 2409 kWh in energy consumed by system-level pumps for Scenario , and a total reduction in energy consumption of 11% when compared with Scenario . Unit energy consumed is calculated as the total energy required per unit volume of water produced by both centralized and decentralized processes (Table 3). Unit energy provides an assessment of the energy efficiency of the system. The unit energy for Scenarios and are the same value (0.37 kWh/m3), and the the addition of 403 prosumers to the network does not impact energy efficiency of meeting demands.
Pressure is affected by reductions in consumer demands and the injection of water at terminal nodes through household-level pumping. The maximum pressure in the network occurs when no demands are exerted and is the same value for Scenarios and . As shown in Table 3, the minimum pressure when 20% of households are prosumers is slightly increased, compared to Scenario . The distribution of pressures at a time step with low pressures is shown in Figure 7. The time step shown is 9 p.m. on a day that is preceded by 24 h without rainfall, and pressures remain at or near the minimum (7 m). In the central area of the city, elevations cover a 30 m range, and the pressures are around 20 m at nodes that are located at high elevations. The southern section of the network is at a lower elevation, and pressures remain in the range of 25–35 m during this period of relatively low pressure.
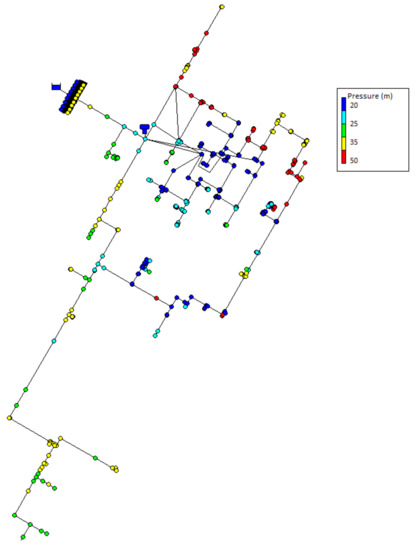
Figure 7.
Lowest nodal pressures for Scenario at 9:00 p.m. on a day with no rainfall in the previous 24 h.
Water age is calculated for Scenarios and using Equation (14), calculated over all irrigation nodes, and is reported to explore water quality. It is expected that the water age of Scenario would be higher than the water age of Scenario , because the injection of water at households may increase the residence time of water in the system, and there are fewer agents consuming water in the network. The water age of Scenario is marginally less than the water age of Scenario (a difference of less than 1 h). This difference may be due to the process of calculation. The water age is calculated only at consumer nodes, and there are fewer households acting as consumers in Scenario , leading to a marginal reduction in water age. In addition, the age of water entering the system due to household-level pumping is initialized at zero hours, which does not account for the time that the water resides in the household-level rainwater harvesting tank.
5.2. Performance Analysis across All Scenarios
The total volume of traded rainwater, total number of trades, and percentage of irrigation demand met for each of the 126 scenarios (six levels of precipitation and 21 levels of prosumers) are shown in Figure 8. For all scenarios where no agents are prosumers (0%) or all households are prosumers (100%), no trades occur because of the homogeneity of agents. For all other scenarios, an increase in rainfall volume corresponds to an increase in volumes of trades (Figure 8a) and number of trades (Figure 8b). During higher precipitation volume scenarios, prosumer agents can harvest higher volumes of rainwater, which allows some consumer agents to satisfy demands through trading. For higher precipitation, the peaks in volume and number of trades correspond with lower percentages of prosumer agents. During scenarios with precipitation volume , for example, the maximum volume of traded rainwater corresponds with a prosumer ratio of 80%, compared to 50% for precipitation volume . This is because for lower rainfall depths, a higher number of prosumers are needed to participate in the market to offset the demand exerted by a consumer. The highest number of trades occur for scenarios with precipitation volume . Consumer agents buy rainwater from multiple prosumers at each time step to meet demands, leading to a high number of trades (Figure 8b). At low precipitation depth, , the number of trades is relatively low, because prosumer agents are unable to harvest higher volumes of rainwater, resulting in reduced ability to trade. The volume of rainwater that is traded decreases for higher numbers of prosumer agents because fewer agents are consumers to exert demands. The system does not meet total irrigation demands for any of the 126 scenarios (Figure 8c), however, because irrigation demands of consumers are substantially higher than harvested rainwater volumes. Across all precipitation volumes, the highest percentage of demand that is met through trading occurs when 95% of agents are prosumers.
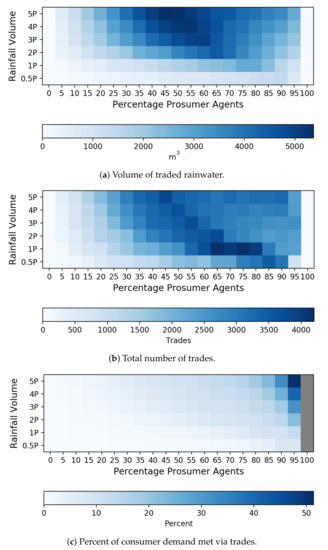
Figure 8.
Total volume of traded rainwater (m3), total number of trades, and total percentage of
irrigation demand satisfied by traded rainwater across 126 scenarios of varying rainfall depth and
percentage of prosumer agents.
EPANET simulations were used to evaluate energy consumption, pressure, and water age. The amount of energy consumed by household-level pumping (Figure 9a) follows the same pattern as the volume of traded rainwater (Figure 8a) with the highest consumption of energy at high rainfall depths and around 50% prosumers. Scenarios with lower percentages of prosumer agents and low rainfall volumes require more system-level energy consumption (Figure 9b). System-level energy is orders of magnitude greater than energy consumed by household-level pumping, and there is a large reduction in system-level energy requirements for higher numbers of prosumers. This trend emerges because prosumer agents do not irrigate, which reduces the energy requirements of pumping from decentralized locations. Energy consumed for treatment is high for this system, approximately twice the energy required for pumping. Treating wastewater to non-potable standards is an energy-intensive activity, and these numbers reflect that cost. In this research, we assume that the volume of wastewater is treated to match the unmet demands in the systems, and the energy cost of treating excess wastewater that is not needed for reuse is not included in this framework. However, wastewater that is released to the environment or used for other recycling purposes would also need to be treated, and a holistic assessment of the interconnections between water, wastewater, and reclaimed water systems may use an alternative approach to holistically account for energy costs. Based on the sum of energy requirements for the smart water grid system (Figure 9d), a higher number of prosumers leads to higher savings in energy.
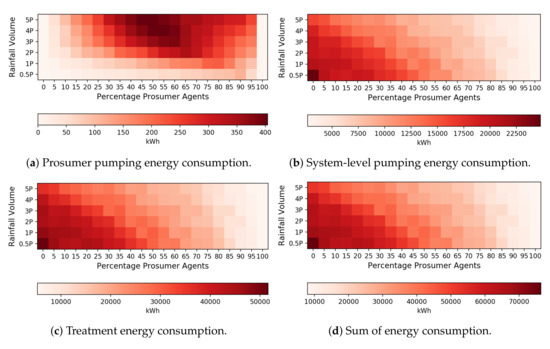
Figure 9.
Energy consumption for (a) prosumers for pumping water at households, (b) system-level
pumping, (c) treatment of water at the treatment plant, and (d) the sum of energy consumption for
prosumers, system-level pumping, and water treatment.
The system’s unit energy is calculated as the energy consumed by three processes (household-level pumping, system-level pumping, and treatment) per unit volume of water produced by the centralized system and prosumer pumping (Figure 10). Unit energy is used to represent the efficiency of the system in meeting demands. For scenarios of high percentages of prosumers and high precipitation depths, the water contributed by prosumers reduces the amount of water required by the centralized system, leading to higher energy efficiency. For example, unit energy generally increases across scenarios, which corresponds with the reduction in treatment and pumping energy shown in Figure 9b,c. Household-level pumps inject water in the network at peak demand times, which offsets the need to use the additional pumps that operate in parallel to the main pump. As a result, the number of pumps that operate to provide water from the centralized system decreases with increasing numbers of prosumers (nine pumps are needed for 0–5% prosumers; seven pumps: 10–15%; six pumps: 20–25%; five pumps: 30–40%; four pumps: 45–60%; three pumps: 65–80%; two pumps: 85–95%; one pump: 100%). Further, pumping water from terminal nodes in the network requires less energy than pumping from the centralized treatment plant, as there is less head loss to overcome when the water is pumped from near-by terminal nodes.
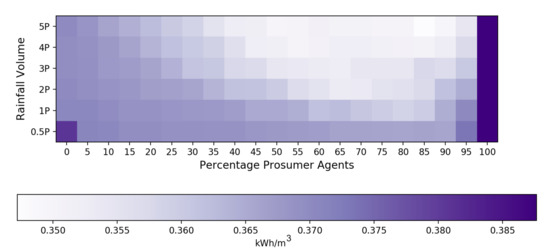
Figure 10.
Energy consumed per unit volume of water produced. Energy is calculated as the sum of all three energy expenditures: Household-level pumping, centralized pumping, and treatment. Produced water is calculated as the sum of water produced by the centralized system and the water produced by prosumer agents.
Unit energy does not increase monotonically across the scenarios, however, because of the infrastructure complexities of water production. For some scenarios, water production exceeds demands on the centralized system by up to 18%, while in others, water production drops to 91% of the demand exerted on the centralized system (that is, total demand minus the demands that are met by household-level pumping). In cases where the water demanded exceeds the water produced by the centralized system, the water storage tanks meet the remaining demand because they are initialized at full capacity. At 80% prosumers, the system reaches a minimum unit energy, and, subsequently, the energy required per unit volume increases with increasing percentages of prosumers. This trend mirrors the change in volume of traded rainwater across scenarios of increasing numbers of prosumers, shown in Figure 8a, which reaches a peak at 80% prosumers for the scenario. When consumers comprise less than 20% of agents, they demand less water than prosumers produce when tanks are full. Because low volumes of water are traded and the bulk of demand is at the constant demand, which is met by the centralized system, the system requires higher unit energy. Higher precipitation depths (, , , and scenarios) lead to improved energy efficiency because prosumers can produce more water to offset demands. Increasing the volume of water that can be provided by prosumers increases benefits to both water and energy savings through the smart water grid.
The minimum and maximum pressure across all consumer irrigation nodes and over all time steps are reported for each scenario. The minimum pressure across the scenarios varies between 5.0 and 30 m of head (Figure 11), while the maximum pressure is approximately the same at around 50 m for all scenarios. The minimum pressure is low at high numbers of consumers (low percentage of prosumers). Scenarios where the minimum pressure values fall below 7 m (approximately 10 psi) may be considered as infeasible because the pressure is not high enough to meet irrigation purposes. For rainfall scenarios, scenarios are infeasible until the percentage of prosumer agents reaches around 30%. When the number of prosumers is lower than 30%, consumers require a large volume of water from the centralized system, and pressures in the central part of the system drop to values less than 7 m. With higher precipitation depths, the amount of water that is provided by prosumer agents increases, resulting in relatively higher minimum pressure values. For higher precipitation scenarios, prosumers contribute high volumes of water, leading to increasing pressure. For example, for rainfall scenarios, approximately 15% of agents need to be prosumers to ensure a feasible system.
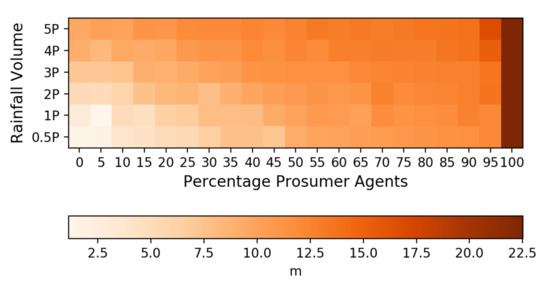
Figure 11.
Minimum head (m) across consumer nodes for all scenarios.
As the number of prosumers increases, there are benefits in energy savings and meeting pressure requirements, as shown above. There is, however, an expected drop in water quality based on the residence time of water in the network. As the system has intermittent consumption for irrigation purposes, water age increases in scenarios with high precipitation values and high percentages of prosumers (Figure 12). Water age values represent the average number of hours exceeding the water age requirement of 48 h, and this number is between 20 and 30 h when the percentage of prosumers is less than 80%. The effect on water age does not grow significantly until the percentage of prosumers reaches 80%, and water age increases dramatically with additional prosumers. Tradeoffs among water age, energy consumption, and pressure may govern how a water micro-trading market should be designed. Results show for scenarios, that water saving is at a maximum at 80%; unit energy is minimum at 80%; pressure requirements constrain the network to function only if 30% or more households join as prosumers; water age requirements may constrain the percentage of prosumers to less than 80%.
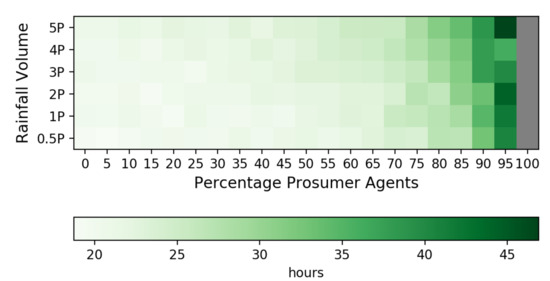
Figure 12.
Water age calculated for all scenarios using Equation (14).
6. Discussion
This study proposes and tests the hydraulic feasibility of a smart water grid for micro-trading rainwater through a peer-to-peer non-potable water market that allows residential households to capture, use, sell, and buy rainwater within a network of water users. In this research, we explore the impact of the depth of rainfall and the distribution of consumers and prosumers on the performance metrics that are used to evaluate the hydraulic feasibility of the smart water grid. In related research, an agent-based modeling framework was developed to explore how the numbers of prosumers and consumers affect performance of a peer-to-peer household-level energy trading market, and results demonstrated that the presence of too many prosumers in the market led to market inefficiencies [8]. In the smart water grid, however, the volume of water that is required by consumers for irrigation is much higher than the volume of water that is produced by prosumers. Prosumers could not completely satisfy consumer demands for any of the simulated scenarios, and production from the centralized system was required to meet demands.
The volume of water that is produced by prosumers drives the performance of the smart water grid, with respect to both water and energy savings. The total volume of traded water increases and the energy required to pump demands decreases for scenarios with higher numbers of prosumers and higher rainfall depths, leading to a more energy efficient system. The energy requirements at households to pump water from rainwater tanks is lower than the energy required at the system level to pump the same volume of water from the water treatment plant. Pumping water from the central treatment plant requires the operation of extra parallel pumps, which are not needed when prosumers contribute water to the system. In addition, water that is pumped into the network at terminal nodes by prosumers does not need to overcome headlosses or elevation losses when consumer nodes are located nearby. Energy savings are also associated with treating smaller volumes of wastewater to nonpotable standards. In this model, the efficiencies of household pumps and systems were assumed to be equal (75%). Household pumps, however, may more realistically have lower efficiency than large pumps, which would change the analysis of energy consumption. The model developed in this research does not account for energy requirements of onsite treatment that could be required at prosumer households to treat rainwater. It is expected, however, that treatment of rainwater to meet nonpotable standards would require much less energy than treatment of wastewater. Pressure and water quality constraints are also explored in this research, as they are affected by increased trading and show tradeoffs based on the number of prosumers. For the simulations conducted in this research, consumer and prosumer agents are assigned randomly at nodes across the network, and the results are specific to one random realization. Further research can explore how clustering of consumer or prosumer agents at nodes in the network could affect pressure, energy, and water age through multiple realizations of initializing consumer and prosumer agents.
In this research, rainfall and evapotranspiration the data that are used to simulate demands are from the Seattle, WA, USA area, and we explore how higher precipitation can lead to a more efficient market. The modeling framework presented in this manuscript uses the theoretical outdoor water demand model, which may overestimate the amount of water required by households. Other climates may lead to differences in rainwater exchanges, and new methods for estimating irrigation may be needed to more accurately represent household behaviors.
6.1. Smart Technologies
The system that is conceptualized in this research would be possible through smart technologies that can record and account for water flows and peer-to-peer transactions in real-time. Smart water flow meters are needed to sense and record water contributed to and withdrawn from the water network at each household on sub-hourly time steps. AMI that includes smart water flow sensors can allow urban water managers to accurately and continuously account for non-potable water use and pumping [95]. Blockchain technologies can be applied to create a ledger to record transactions between peers, and smart contracts can be built on top of a distributed ledger to facilitate the settlement of water trades. Automated valves and pumps would be needed to automatically execute trades by releasing water at the household into the network. The integration of these technologies creates a smart water grid that enables new water and energy savings through decentralized water sources. These technologies were not modeled as functioning entities in this framework, and future research can explore how these technologies would be adopted and would function in a smart water grid. Introducing this array of new technologies can create new vulnerabilities to failure that may occur due to internet disruption, power outages, and malfunctioning controllers. Fail-safe protocols and technological solutions are needed to account for loss of water or trades that are not fulfilled.
6.2. Semi-Centralized Infrastructure
The smart water grid is a semi-centralized system and relies on both decentralized and centralized infrastructure to provide diverse sources of non-potable water. A pre-existing dual reticulation system is required as part of the envisioned system to circulate non-potable water that is generated at lower water quality for end uses such as irrigation and flushing toilets. Constructing a secondary pipe network within an existing water supply system is typically cost-prohibitive, and implementation of the smart water grid may be better incorporated into new systems, such as the network that is conceptualized for Fisherman’s Bend near Melbourne, Australia [59]. A smart water grid for micro-trading rainwater could also be implemented using a shared aquifer [49] or water trucks to provide conveyance of traded water. Micro-trading rainwater can also use a water rights structure, where households buy the rights to use rainwater from a community source. Rainwater harvesting provides a sustainable source of water by recycling runoff; however, rainwater is an unreliable source, and it is likely that rainwater would be unavailable at times when irrigation water is needed most, such as during droughts. By taking a semi-decentralized approach that incorporates rainwater tanks into a reclaimed water network, diverse sources are utilized to meet potable demands. Diverse portfolios of water sources can lead to reliable water supply systems [96], and the smart water grid would meet demands during low rainfall by circulating reclaimed water and reusing rainwater when it is available. Other benefits of decentralized water management associated with a smart water grid may include offsetting household energy costs [97] and reducing stormwater flows [37].
6.3. Peer-to-Peer Markets and Cost-Benefit Analysis
Criticisms of Haddad’s early depiction of micro-trading [46] argued that households may not have the expertise, interest, or time to trade water [47]. Haddad argued that households regularly make complex decisions around finances and could readily bid on water prices [48]. A smart water grid would involve transaction costs and costs associated with rainwater tanks and smart meters, creating considerable economic barriers. Research around a peer-to-peer energy trading market found that households were engaged in bidding on energy, but they became disengaged due to the structure of transaction costs that created market inefficiency [8]. The buy-in for consumers to invest in rainwater cisterns and pumps could contribute to challenges in implementing a smart grid, as researchers have demonstrated that the payback period of rainwater harvesting systems alone can be 20–30 years [31,98]. Water resources are projected to become increasingly scarce [1], however, and a study conducted in India suggests that people, particularly in drought-prone areas, may be willing to invest in rainwater harvesting systems or other creative and environmentally-friendly water alternatives [99]. As described above, rainwater harvesting alone provides an intermittent source of water, and the cost-benefit analysis of purchasing a rainwater harvesting tank and pump to join a smart grid would be altered, because participants are granted access to continuous water supply. It is expected that micro-trading could function as an efficient market in a water-scarce urban environment. Further analysis is needed to explore the cost and benefits associated with the economics of the infrastructure and participation in the water market. The agent-based model can be extended in further research to capture economic decisions of households to join the market and to buy and sell water. New modeling mechanisms can be included in the framework to capture the interplay among demands, climate, trading adaptations, and infrastructure performance.
6.4. Water Quality
Water reuse programs have historically been challenged in garnering public support, due to the “yuck factor”, or perception that treated wastewater is dirty or unsafe [100,101]. Water quality of water withdrawn through the smart water grid should be managed to mitigate public health risks and enhance positive perceptions of water quality. The quality of rainwater is generally accepted as high enough for irrigation and toilet flushing, especially when first flushing is used to remove contaminants that are washed off of roofs [38,83]. The quality of harvested water is expected to degrade, however, as the water moves through a pipe network and is stored in a tank. We include a first flush diversion that would improve the quality of water entering the network, but further research is needed to better represent the quality of water that is pumped from rainwater harvesting tanks and the fate and transport of contaminants in the network. Filtration and treatment systems can be installed at the point-of-entry, and research is needed to explore how to enhance household expertise in the operation and maintenance of treatment technology. For example, new research explores how real time control of the operation of biofilters can improve microbial removal from stormwater [102].
7. Conclusions
Smart water sensors can be integrated with water distribution infrastructure, distributed ledger technology, smart contracts, and automated control to support novel decentralized water markets to improve water savings in urban environments. This research demonstrates how a semi-decentralized water supply system can create water and energy savings by deploying existing smart city technologies and decentralized infrastructure within a centralized reclaimed water distribution system. In this research, we report the feasibility of a reclaimed water system that is augmented by prosumers, who pump harvested rainwater into the network at decentralized nodes. We construct an all-pipe hydraulic model for a hypothetical community to simulate demands exerted for non-potable uses at households and to evaluate hydraulics in the dual reticulation network. An agent-based modeling approach is developed to simulate household behaviors, including storing, pumping, trading, and withdrawing non-potable water. The agent-based model is loosely coupled with hydraulic modeling, and negative and positive demands of prosumers and consumers are used to modify input to the pipe network model. The simulation framework is applied using climate parameters for a location in the northwest U.S., which was selected based on the potential yield expected from rainwater harvesting, and a theoretical outdoor water demand model is used to simulate irrigation demands at households. Multiple scenarios are explored to demonstrate the feasibility of peer-to-peer non-potable water trading, and tradeoffs among the volume of traded water, energy savings, satisfaction of pressure constraints, and water quality are explored. The smart water grid is a complex system, and energy outcomes emerge based on reductions in the volume of water required by households, the volume of water provided by prosumers, and the dynamics of centralized water distribution infrastructure. The water and energy efficiency of scenarios depends on the reduction in the volume of water that is provided by the centralized system through traded rainwater. Higher volumes of water produced by prosumers increases both water and energy savings. Analysis demonstrates that there is a lower bound on the number of households that should participate as prosumers to meet pressure requirements, and an upper bound on prosumers to protect water quality. This research develops a novel water management system designed to further the use of decentralized infrastructure and smart city technologies in improving the sustainability of the built environment.
Author Contributions
Conceptualization: E.Z.B.; methodology: E.R., J.P., M.A.K.F., J.M.; formal analysis: E.R., E.Z.B., J.P.; data curation: M.D., E.R., J.P., M.A.K.F.; writing—original draft preparation: E.R., E.Z.B., M.D., M.A.K.F., J.P.; writing—review and editing: E.Z.B., E.R.; resources: E.Z.B., J.M.; supervision: E.Z.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by North Carolina State University through a 2019 University of Adelaid—NC State Starter Grant.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Maximum potentialrainwater harvesting yield values for 10 U.S. cities.
Table A1.
Maximum potentialrainwater harvesting yield values for 10 U.S. cities.
| City | State | LA (km2) | RT (%) | Pann (cm) | Y (million m3) |
|---|---|---|---|---|---|
| Baltimore | Maryland | 209.6 | 19.7% | 29.1 | 12.0 |
| Branson | Missouri | 53.4 | 2.2% | 28.3 | 0.3 |
| Dallas | Texas | 881.9 | 8.2% | 18.7 | 13.5 |
| Denver | Colorado | 396.3 | 10.1% | 29.4 | 11.7 |
| Fargo | North Dakota | 126.4 | 5.5% | 13.7 | 1.0 |
| Phoenix | Arizona | 1338.2 | 6.1% | 14.8 | 12.2 |
| Raleigh | North Carolina | 370.1 | 6.6% | 29.4 | 7.2 |
| San Diego | California | 842.2 | 8.5% | 8.8 | 6.3 |
| Seattle | Washington | 217.4 | 19.8% | 56.0 | 24.1 |
| Tulsa | Oklahoma | 509.6 | 5.1% | 27.7 | 7.2 |
References
- United Nations. UN-Water Annual Report 2015; Technical Report; United Nations: Geneva, Switzerland, 2015. [Google Scholar]
- Berglund, E.Z.; Monroe, J.G.; Ahmed, I.; Noghabaei, M.; Do, J.; Pesantez, J.E.; Fasaee, M.A.K.; Bardaka, E.; Han, K.; Proestos, G.T.; et al. Smart Infrastructure: A Vision for the Role of the Civil Engineering Profession in Smart Cities. J. Infrastruct. Syst. 2020, 26, 03120001. [Google Scholar] [CrossRef]
- Giurco, D.P.; White, S.B.; Stewart, R.A. Smart Metering and Water End-Use Data: Conservation Benefits and Privacy Risks. Water 2018, 2, 461. [Google Scholar] [CrossRef]
- Palleti, V.R.; Kurian, V.; Narasimhan, S.; Rengaswamy, R. Actuator network design to mitigate contamination effects in water distribution networks. Comput. Chem. Eng. 2018, 108, 194–205. [Google Scholar] [CrossRef]
- Page, P.R.; Zulu, S.; Mothetha, M.L. Remote real-time pressure control via a variable speed pump in a specific water distribution system. J. Water Supply Res. Technol. 2019, 68, 20–28. [Google Scholar] [CrossRef]
- Munir, M.; Bajwa, I.; Cheema, S. An intelligent and secure smart watering system using fuzzy logic and blockchain. Comput. Electr. Eng. 2019, 77, 109–119. [Google Scholar] [CrossRef]
- Hansen, P.; Morrison, G.; Zaman, A.; Liu, X. Smart technology needs smarter management: Disentangling the dynamics of digitalism in the governance of shared solar energy in Australia. Energy Res. Soc. Sci. 2020, 60, 1–13. [Google Scholar] [CrossRef]
- Monroe, J.; Hansen, P.; Sorell, M.; Berglund, E.Z. Agent-Based Model of a Blockchain Enabled Peer-to-Peer Energy Market: Application for a Neighborhood Trial in Perth, Australia. Smart Cities 2020, 3, 53. [Google Scholar] [CrossRef]
- Holland, J.H. Hidden Order: How Adaptation Builds Complexity; Basic Books: New York, NY, USA, 1995. [Google Scholar]
- Holland, J.H. Emergence: From Chaos to Order; OUP: Oxford, UK, 2000. [Google Scholar]
- Berglund, E.Z. Using agent-based modeling for water resources planning and management. J. Water Resour. Plan. Manag. 2015, 141, 04015025. [Google Scholar] [CrossRef]
- Zechman, E.M. Agent-based modeling to simulate contamination events and evaluate threat management strategies in water distribution systems. Risk Anal. 2011, 31, 758–772. [Google Scholar] [CrossRef] [PubMed]
- Shafiee, M.E.; Zechman, E.M. An agent-based modeling framework for sociotechnical simulation of water distribution contamination events. J. Hydroinf. 2013, 15, 862. [Google Scholar] [CrossRef]
- Kandiah, V.; Berglund, E.; Binder, A. Cellular Automata Modeling Framework for Urban Water Reuse Planning and Management. J. Water Resour. Plan. Manag. 2016, 142, 04016054. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Yu, H.; Dong, Z.; Zhang, B. Trade-offs in designing water pollution trading policy with multiple objectives: A case study in the Tai Lake basin, China. Environ. Sci. Policy 2013, 33, 295–307. [Google Scholar] [CrossRef]
- Huang, H.; Ma, H. An agent-based model for an air emissions cap and trade program; A case study in Taiwan. J. Environ. Manag. 2016, 183, 613–621. [Google Scholar] [CrossRef]
- Peng, Z.S.; Zhang, Y.L.; Shi, G.M.; Chen, X.H. Cost and effectiveness of emissions trading considering exchange rates based on an agent-based model analysis. J. Clean. Prod. 2019, 219, 75–85. [Google Scholar] [CrossRef]
- Okun, D.A. Distributing reclaimed water through dual systems. J. Am. Water Work. Assoc. 1997, 89, 52–64. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. 2012 Guidelines for Water Reuse; Technical Report EPA/600/R-12/618; Office of Wastewater Management, Office of Water: Washington, DC, USA, 2012. [Google Scholar]
- Grigg, N.; Rogers, P.; Edmiston, S. Dual Water Systems: Characterization and Performance for Distribution of Reclaimed Water; Technical Report 4333; Water Research Foundation: Denver, CO, USA, 2013. [Google Scholar]
- Hambly, A.C.; Henderson, R.K.; Baker, A.; Stuetz, R.; Khan, S. Cross-connection detection in Australian dual reticulation systems by monitoring inherent fluorescent organic matter. Environ. Technol. Rev. 2012, 1, 67–80. [Google Scholar] [CrossRef]
- Hess, D.; Collins, B. Recycling water in U.S. cities: Understanding preferences for aquifer recharging and dual-reticulation systems. Water Policy 2019, 21, 1207–1223. [Google Scholar] [CrossRef]
- Grant, S.; Saphores, J.; Feldman, D.; Hamilton, A.; Fletcher, T.; Cook, P.; Stewardson, M.; Sanders, B.; Levin, L.; Ambrose, R.; et al. Taking the ‘waste’ out of ‘wastewater’ for human water security and ecosystem sustainability. Science 2012, 337, 681–686. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Hernandez-Sancho, F.; Sala-Garrido, R. Economic feasibility study for new technological alternatives in wastewater treatment processes: A review. Water Sci. Technol. 2012, 65, 898–906. [Google Scholar] [CrossRef] [PubMed]
- Barker, Z.; Stillwell, A.; Berglund, E. Scenario Analysis of Energy and Water Trade-Offs in the Expansion of a Dual Water System. J. Water Resour. Plan. Manag. 2016, 142, 05016012. [Google Scholar] [CrossRef]
- Stillwell, A.; Twomey, K.; Osborne, R.; Greene, D.; Pedersen, D.; Webber, M. An integrated energy, carbon, water, and economic analysis of reclaimed water use in urban settings: A case study of Austin, Texas. J. Water Reuse Desalination 2011, 1, 208–223. [Google Scholar] [CrossRef]
- Kandiah, V.; Berglund, E.Z.; Binder, A.R. An agent-based modeling approach to project adoption of water reuse and evaluate expansion plans within a sociotechnical water infrastructure system. Sustain. Cities Soc. 2019, 46, 101412. [Google Scholar] [CrossRef]
- Kavvada, O.; Horvath, A.; Stokes-Draut, J.; Hendrickson, T.; Eisenstein, W.; Nelson, K. Assessing location and scale of urban nonpotable water reuse systems for life-cycle energy consumption and greenhouse gas emissions. Environ. Sci. Technol. 2016, 50, 13184–13194. [Google Scholar] [CrossRef]
- Bawden, T. Water sensitive urban design technical manual for the greater Adelaide region. Aust. Plan. 2009, 46, 8–9. [Google Scholar] [CrossRef]
- Herslund, L.; Backhaus, A.; Fryd, O.; Jørgensen, G.; Jensen, M.; Limbumba, T.; Yeshitela, K. Conditions and opportunities for green infrastructure—Aiming for green, water-resilient cities in Addis Ababa and Dar es Salaam. Landsc. Urban Plan. 2018, 180, 319–327. [Google Scholar] [CrossRef]
- Imteaz, M.; Paudel, U.; Ahsan, A.; Santos, C. Climatic and spatial variability of potential rainwtaer savings for a large coastal city. Resour. Conserv. Recycl. 2015, 105, 143–147. [Google Scholar] [CrossRef]
- Cook, S.; Sharma, A.; Chong, M. Performance analysis of a communal residential rainwater system: A case study in Brisbane, Australia. J. Water Resour. Manag. 2013, 27, 4865–4876. [Google Scholar] [CrossRef]
- Berwanger, H.; Ghisi, E. Investment feasibility analysis of rainwater harvesting in the city of Itapiranga, Brazil. Int. J. Sustain. Hum. Dev. 2014, 2, 104–114. [Google Scholar]
- Jung, K.; Lee, T.; Choi, B.; Hong, S. Rainwater harvesting system for continuous water supply to the regions with high seasonal rainfall variations. Water Resour. Manag. 2015, 29, 961–972. [Google Scholar] [CrossRef]
- Lee, J.; Bae, K.H.; Younos, T. Conceptual framework for decentralized green water-infrastructure systems. Water Environ. J. 2018, 32, 112–117. [Google Scholar] [CrossRef]
- Pitton, B.; Hall, C.; Haver, D. A cost analysis for using recycled irrigation runoff water in container nursery production: A Southern California nursery case study. Irrig. Sci. 2018, 36, 217–226. [Google Scholar] [CrossRef]
- Liang, R.; Di Matteo, M.; Maier, H.R.; Thyer, M.A. Real-Time, Smart Rainwater Storage Systems: Potential Solution to Mitigate Urban Flooding. Water 2019, 11, 2428. [Google Scholar] [CrossRef]
- Campisano, A.; Butler, D.; Ward, S.; Burns, M.; Friedler, E.; Debusk, K.; Han, M. Urban rainwater harvesting systems: Research, implementation and future perspectives. Water Resour. 2017, 115, 195–209. [Google Scholar] [CrossRef]
- Imteaz, A.; Moniruzzaman, M. Spatial variability of reasonable government rebates for rainwater tank T installations: A case study for Sydney. Resour. Conserv. Recycl. 2018, 133, 112–119. [Google Scholar] [CrossRef]
- Grafton, R.; Libecap, G.; McGlenno, S.; Landry, C.; O’Brien, B. An integrated assessment of water markets: A cross-country comparison. Rev. Environ. Econ. Policy 2011, 5, 219–239. [Google Scholar] [CrossRef]
- Garrick, D.; Whitten, S.; Coggan, A. Understanding the evolution and performance of water markets and allocation policy: A transaction costs analysis framework. Ecol. Econ. 2013, 88, 195–205. [Google Scholar] [CrossRef]
- Rinaudo, J.; Calatrava, J.; Byans, M.D. Tradable water saving certificates to improve urban water use efficiency: An ex-ante evaluation in a French case study. Aust. J. Agric. Resour. Econ. 2016, 60, 422–441. [Google Scholar] [CrossRef]
- Gonzales, P.; Ajami, N.; Sun, Y. Coordinating water conservation efforts through tradable credits: A proof of concept for drought response in the San Francisco Bay area. Water Resour. Res. 2017, 53, 7662–7677. [Google Scholar] [CrossRef]
- Leigh, N.; Lee, H. Sustainable and Resilient Urban Water Systems: The Role of Decentralization and Planning. Sustainability 2019, 11, 918. [Google Scholar] [CrossRef]
- Sharma, A.K.; Burn, S.; Gardner, T.; Gregory, A. Role of decentralized systems in the transition of urban water systems. Water Sci. Technol. 2010, 10, 577–583. [Google Scholar]
- Haddad, B. Economic Incentives for Water Conservation on the Monterey Peninsula: The Market Proposal. J. Am. Water Resour. Assoc. 2000, 36, 1–15. [Google Scholar] [CrossRef]
- Agthe, D.E.; Billings, R.B. Discussion “Economic Incentives for Water Conservation on the Monterey Peninsula: The Market Proposal” by Brent M. Haddad. J. Am. Water Resour. Assoc. 2000, 36, 931–932. [Google Scholar] [CrossRef]
- Haddad, B. Reply to Discussion by Donald E. Agthe and R. Bruce Billings “Economic Incentives for Water Conservation on the Monterey Peninsula: The Market Proposal”. J. Am. Water Resour. Assoc. 2000, 36, 933–934. [Google Scholar] [CrossRef]
- Fornarelli, R.; Anda, M.; Dallas, S.; Schmack, M.; Dawood, F.; Byrne, J.; Morrison, G.; Fox-Reynolds, K. Enabling residential hybrid water systems through a water credit–debit system. Water Supply 2019, 19, 2131–2139. [Google Scholar] [CrossRef]
- Mengelkamp, E.; Notheisen, B.; Beer, C.; Dauer, S.; Daueri, D.; Weinhardt, C. A blockchain-based smart grid: Towards sustainable local energy markets. Comput. Sci. 2018, 33, 207–214. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: www.bitcoin.org (accessed on 31 October 2020).
- Xu, X.; Weber, I.; Staples, M.; Zhu, L.; Bosch, J.; Bass, L.; Pautasso, C.; Rimba, P. A taxonomy of blockchain-based systems for architecture design. In Proceedings of the IEEE International Conference on Software Architecture (ICSA), Gothenburg, Sweden, 3–7 April 2017; pp. 243–252. [Google Scholar]
- Andoni, M.; Robu, V.; Flynn, D.; Abram, S.; Geach, D.; Jenkins, D.; McCallum, P.; Peacock, A. Blockchain technology in the energy sector: A systematic review of challenges and opportunities. Renew. Sustain. Energy Rev. 2019, 100, 143–174. [Google Scholar] [CrossRef]
- Christidis, K.; Devetsikiotis, M. Blockchains and Smart Contracts for the Internet of Things. IEEE 2016, 4, 2292–2303. [Google Scholar] [CrossRef]
- Aquatech. Blockchain’s Potential to Disrupt water Supply Remains Divisive. 2018. Available online: https://www.aquatechtrade.com/news/utilities/blockchains-potential-to-disrupt-water-supply-remains-divisive/ (accessed on 31 October 2020).
- Sobrinho, R.; Garcia, J.; Maia, A.; Romeiro, A. Blockchain technology and complex flow systems as opportunities for water governance innovation. Rev. Bras. Inov. 2019, 18, 157–176. [Google Scholar]
- Pee, S.J.; Nang, J.H.; Jang, J.W. A Simple Blockchain-based Peer-to-Peer Water Trading System Leveraging Smart Contracts. In Proceedings of the International Conference Internet Computing and Internet of Things, Las Vegas, NV, USA, 30 July–2 August 2018; pp. 63–68. [Google Scholar]
- Carey, A. Future Melbourne Residents Could Trade in Rainwater to Cut down on Bills. 2017. Available online: https://www.theage.com.au/national/victoria/future-melbourne-residents-could-trade-in-rainwater-to-cut-down-on-bills-20170905-gyb5mj.html (accessed on 31 October 2020).
- South East Water. Fishermans Bend: A Water Sensitive Community. 2020. Available online: https://southeastwater.com.au/CurrentProjects/Projects/Pages/Fishermans-Bend.aspx (accessed on 31 October 2020).
- Alcarria, R.; Bordel, B.; Robles, T.; Martín, D.; Ángel Manso-Callejo, M. A Blockchain-Based Authorization System for Trustworthy Resource Monitoring and Trading in Smart Communities. Sensors 2018, 18, 3561. [Google Scholar] [CrossRef]
- Athanasiadis, I.N.; Mentes, A.K.; Mitkas, P.A.; Mylopoulos, Y.A. A hybrid agent-based model for estimating residential water demand. Simulation 2005, 81, 175–187. [Google Scholar] [CrossRef]
- Schwarz, N.; Ernst, A. Agent-based modeling of the diffusion of environmental innovations—An empirical approach. Technol. Forecast. Soc. Chang. 2009, 76, 497–511. [Google Scholar] [CrossRef]
- Galán, J.M.; López-Paredes, A.; Del Olmo, R. An agent-based model for domestic water management in Valladolid metropolitan area. Water Resour. Res. 2009, 45, W05401. [Google Scholar] [CrossRef]
- Giacomoni, M.; Kanta, L.; Zechman, E. Complex adaptive systems approach to simulate the sustainability of water resources and urbanization. J. Water Resour. Plan. Manag. 2013, 139, 554–564. [Google Scholar] [CrossRef]
- Kanta, L.; Zechman, E. Complex Adaptive Systems Framework to Assess Supply-Side and Demand-Side Management for Urban Water Resources. J. Water Resour. Plan. Manag. 2014, 140, 75–85. [Google Scholar] [CrossRef]
- Giacomoni, M.; Berglund, E. A Complex Adaptive Simulation Framework for Evaluating Adaptive Demand Management for Urban Water Resources Sustainability. J. Water Resour. Plan. Manag. 2015, 141, 04015024. [Google Scholar] [CrossRef]
- Kanta, L.; Berglund, E.Z. Exploring tradeoffs in demand-side and supply-side management of urban water resources using agent-based modeling and evolutionary computation. Systems 2015, 3, 287. [Google Scholar] [CrossRef]
- Koutiva, I.; Makropoulos, C. Modelling domestic water demand: An agent-based approach. Environ. Model. Softw. 2016, 79, 35–54. [Google Scholar] [CrossRef]
- Koutiva, I.; Makropoulos, C. Exploring the effects of domestic water management measures to water conservation attitudes using agent based modelling. Water Sci. Technol. Water Supply 2017, 17, 552–560. [Google Scholar] [CrossRef]
- Mashhadi Ali, A.; Shafiee, M.E.; Berglund, E.Z. Agent-based modeling to simulate the dynamics of urban water supply: Climate, population growth, and water shortages. Sustain. Cities Soc. 2017, 28, 420–434. [Google Scholar] [CrossRef]
- Darbandsari, P.; Kerachian, R.; Malakpour-Estalaki, S. An Agent-based behavioral simulation model for residential water demand management: The case-study of Tehran, Iran. Simul. Model. Pract. Theory 2017, 78, 51–72. [Google Scholar] [CrossRef]
- Zechman, E.M. Integrating evolution strategies and genetic algorithms with agent-based modeling for flushing a contaminated water distribution system. J. Hydroinf. 2013, 15, 798. [Google Scholar] [CrossRef]
- Shafiee, M.E.; Berglund, E.Z. Agent-based modeling and evolutionary computation for disseminating public advisories about hazardous material emergencies. Comput. Environ. Urban Syst. 2016, 57, 12–25. [Google Scholar] [CrossRef]
- Shafiee, M.E.; Berglund, E.Z. Complex Adaptive Systems Framework to Simulate the Performance of Hydrant Flushing Rules and Broadcasts during a Water Distribution System Contamination Event. J. Water Resour. Plan. Manag. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Shafiee, M.E.; Berglund, E.Z.; Lindell, M.K. An Agent-based Modeling Framework for Assessing the Public Health Protection of Water Advisories. Water Resour. Manag. 2018, 32, 2033–2059. [Google Scholar] [CrossRef]
- Monroe, J.; Ramsey, E.; Berglund, E. Allocating countermeasures to defend water distribution systems against terrorist attack. Reliab. Eng. Syst. Saf. 2018, 1–15. [Google Scholar] [CrossRef]
- Strickling, H.; DiCarlo, M.F.; Shafiee, M.E.; Berglund, E. Simulation of Containment and Wireless Emergency Alerts within Targeted Pressure Zones for Water Contamination Management. Sustain. Cities Soc. 2019, 101820. [Google Scholar] [CrossRef]
- Kandiah, V.; Ar, B.; Berglund, E. An Empirical Agent-Based Model to Simulate the Adoption of Water Reuse Using the Social Amplification of Risk Framework. Risk Anal. 2017, 10, 2005–2022. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; Bastiansen, F.; Eliassen, S.; Ginot, V.; Giske, J.; Goss-Custard, J.; Gr, T.; Heinz, S.K.; Huse, G.; et al. A standard protocol for describing individual-based and agent-based models. Ecol. Model. 2006, 198, 115–126. [Google Scholar] [CrossRef]
- Willis, R.; Stewart, R.; Williams, P.; Hacker, C.; Emmonds, S.; Capati, G. Residential potable and recycled water end uses in a dual reticulated supply system. Desalination 2011, 272, 201–211. [Google Scholar] [CrossRef]
- NAHB. Cost of Constructing a Home. 2010. Available online: https://www.nahbclassic.org/generic.aspx?genericContentID=248306 (accessed on 31 October 2020).
- Duraplas. Available online: https://www.duraplas.com.au/ (accessed on 31 October 2020).
- Gikas, G.D.; Tsihrintzis, V.A. Assessment of water quality of first-flush roof runoff and harvested rainwater. J. Hydrol. 2012, 466–467, 115–126. [Google Scholar] [CrossRef]
- Texas Water Development Board. The Texas Manual on Rainwater Harvesting; Technical Report; Texas Water Development Board: Austin, TX, USA, 2005. [Google Scholar]
- Lawson, S.; LaBranche-Tucker, A.; Otto-Wack, H.; Hall, R.; Sojka, B.; Crawford, E.; Crawford, D.; Brand, C. Virginia Rainwater Harvesting Manual; Technical Report; Cabell Brand Center: Salem, VA, USA, 2009. [Google Scholar]
- Luke, S. Multiagent Simulation and the MASON Library; George Mason University: Fairfax, VI, USA, 2019. [Google Scholar]
- Ramsey, L. RainwaterABM. 2020. Available online: https://github.com/evramsey/RainwaterABM (accessed on 31 October 2020).
- Jacobs, H.; Haarhoff, J. Structure and data requirements of an end-use model for residential water demand and return flow. Water SA 2004, 30, 293–304. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2 Users Manual, 2nd ed.; US Environmental Protection Agency: Cincinnati, OH, USA, 2000. [Google Scholar]
- Marchi, A.; Salomons, E.; Ostfeld, A.; Kapelan, Z.; Simpson, A.R.; Zecchin, A.C.; Maier, H.R.; Wu, Z.Y.; Elsayed, S.M.; Song, Y.; et al. Battle of the Water Networks II. J. Water Resour. Plan. Manag. 2014, 140, 04014009. [Google Scholar] [CrossRef]
- Bhattacharya, A. Harvesting Rainwater: Catch Water Where It Falls; Working Papers id:2349; eSocialScience: New Delhi, India, 2009. [Google Scholar]
- United States Geological Service. USGS 12113346 Springbrook Creek at Orillia, WA. 2020. Available online: https://waterdata.usgs.gov/usa/nwis/uv?12113346 (accessed on 31 October 2020).
- PRISM Climate Group-Oregon State University. 2004. Available online: http://prism.oregonstate.edu (accessed on 31 October 2020).
- Doorenbos, J.; Pruitt, W. Guidelines for predicting crop water requirements. FAO Irrig. Drain. Pap. 1977, 24, 144. [Google Scholar]
- Beal, C.D.; Flynn, J. Toward the digital water age: Survey and case studies of Australian water utility smart-metering programs. Util. Policy 2015, 32, 29–37. [Google Scholar] [CrossRef]
- Boryczko, K.; Rak, J. Method for Assessment of Water Supply Diversification. Resources 2020, 9, 87. [Google Scholar] [CrossRef]
- Grubic, T.; Vara, L.; Hu, Y.; Tewari, A. Micro-generation technologies and consumption of resources: A complex systems’ exploration. J. Clean. Prod. 2020, 247, 119091. [Google Scholar] [CrossRef]
- Paudel, U.; Imteaz, M. Spatial Variability of Reasonable Government Rebates for Rainwater Tank Installations: A Case Study for Adelaide. In Sustainability Perspectives: Science, Policy and Practice; Khaiter, P., Erechtchoukova, M., Eds.; Springer: New York, NY, USA, 2019; Chapter 13. [Google Scholar]
- Ramsey, E.; Berglund, E.; Goyal, R. The Impact of Demographic Factors, Beliefs, and Social Influences on Residential Water Consumption and Implications for Non-Price Policies in Urban India. Water 2017, 9, 844. [Google Scholar] [CrossRef]
- Dolnicar, S.; Hurlimann, A.; Brun, B. What affects public acceptance of recycled and desalinated water? Water Res. 2011, 45, 933–943. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Cuerva, L.; Berglund, E.; Binder, A. Public Perceptions of Water Shortages, Conservation Behaviors, and Support for Water Reuse in the U.S. Resour. Conserv. Recycl. 2016, 113, 106–111. [Google Scholar] [CrossRef]
- Shen, P.; Deletic, A.; Bratieres, K.; McCarthy, D. Real time control of biofilters delivers stormwater suitable for harvesting and reuse. Water Res. 2020, 169, 115257. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).