Buckley–Leverett Theory for Two-Phase Immiscible Fluids Flow Model with Explicit Phase-Coupling Terms
Abstract
:1. Introduction
2. Mathematical Formulation
3. Buckley–Leverett Theory
3.1. Buckley–Leverett Equations
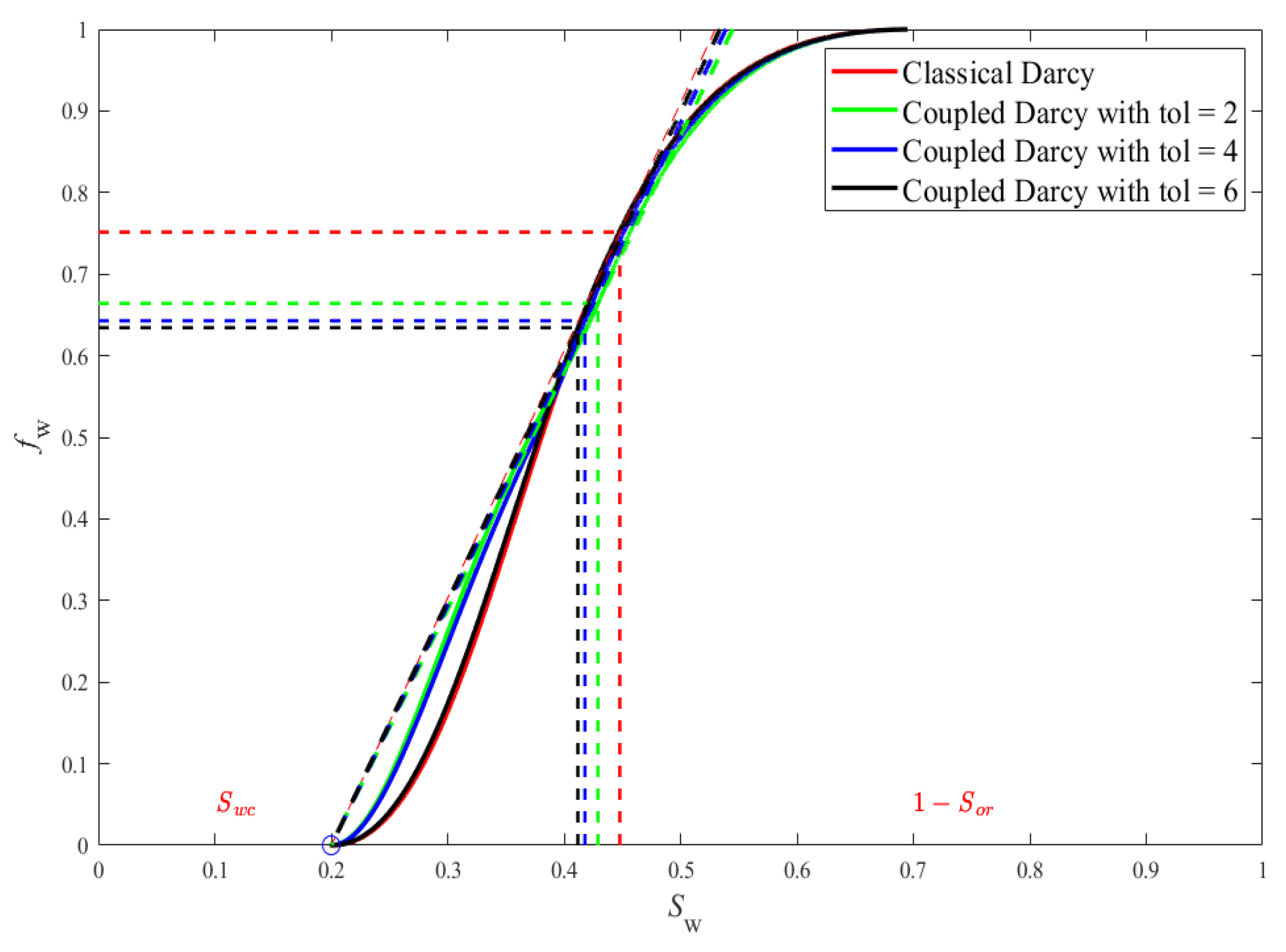
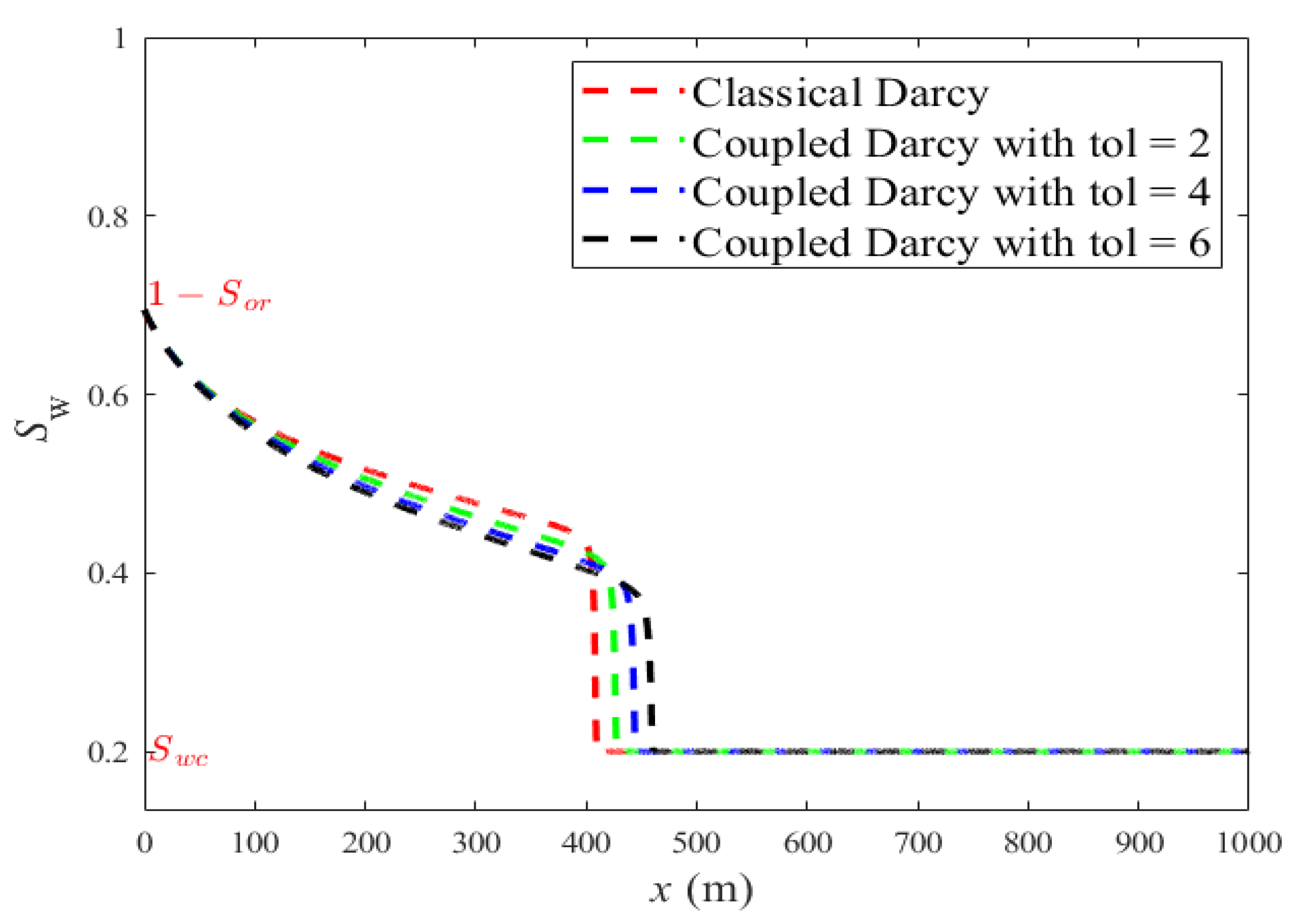
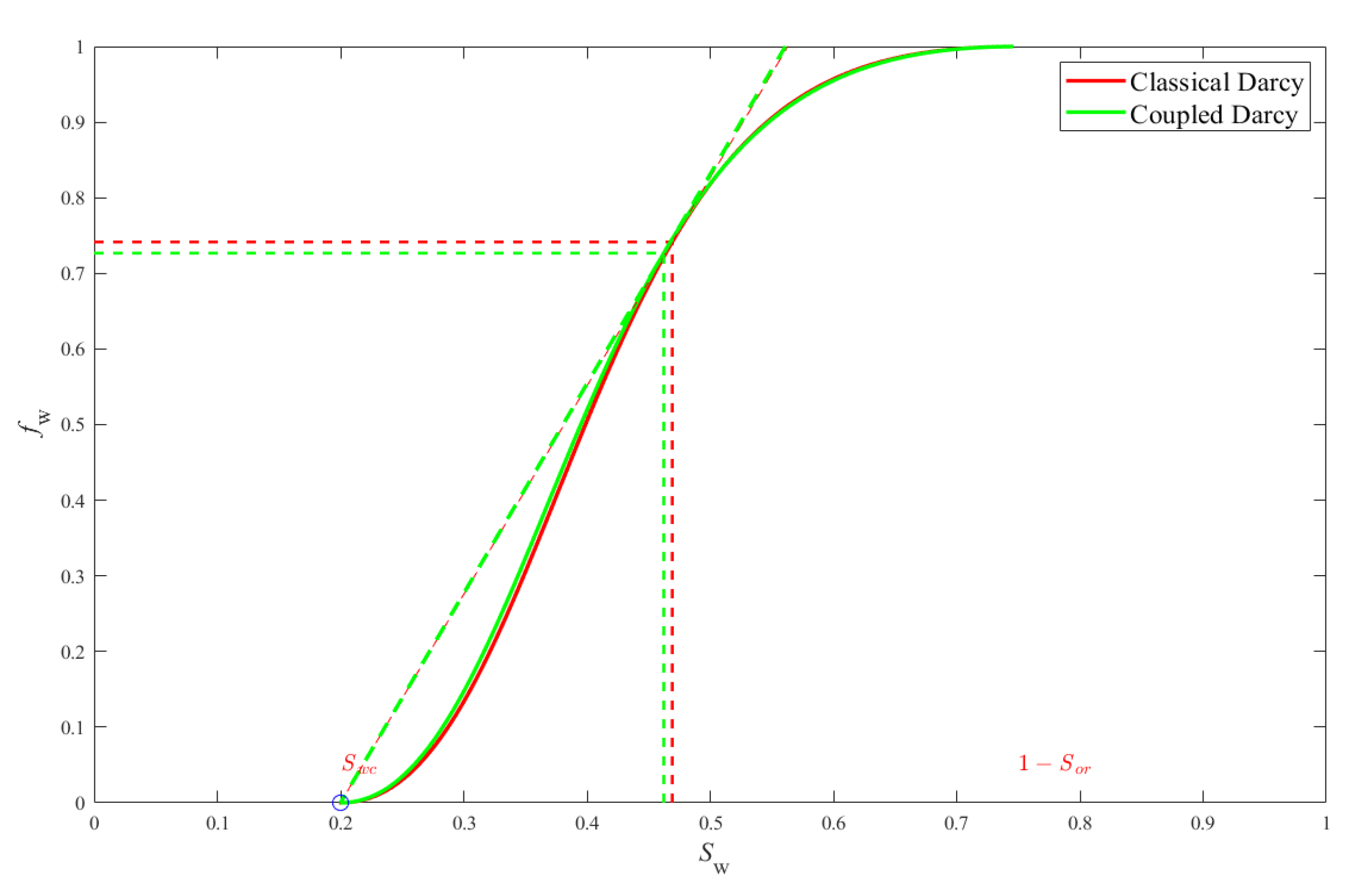
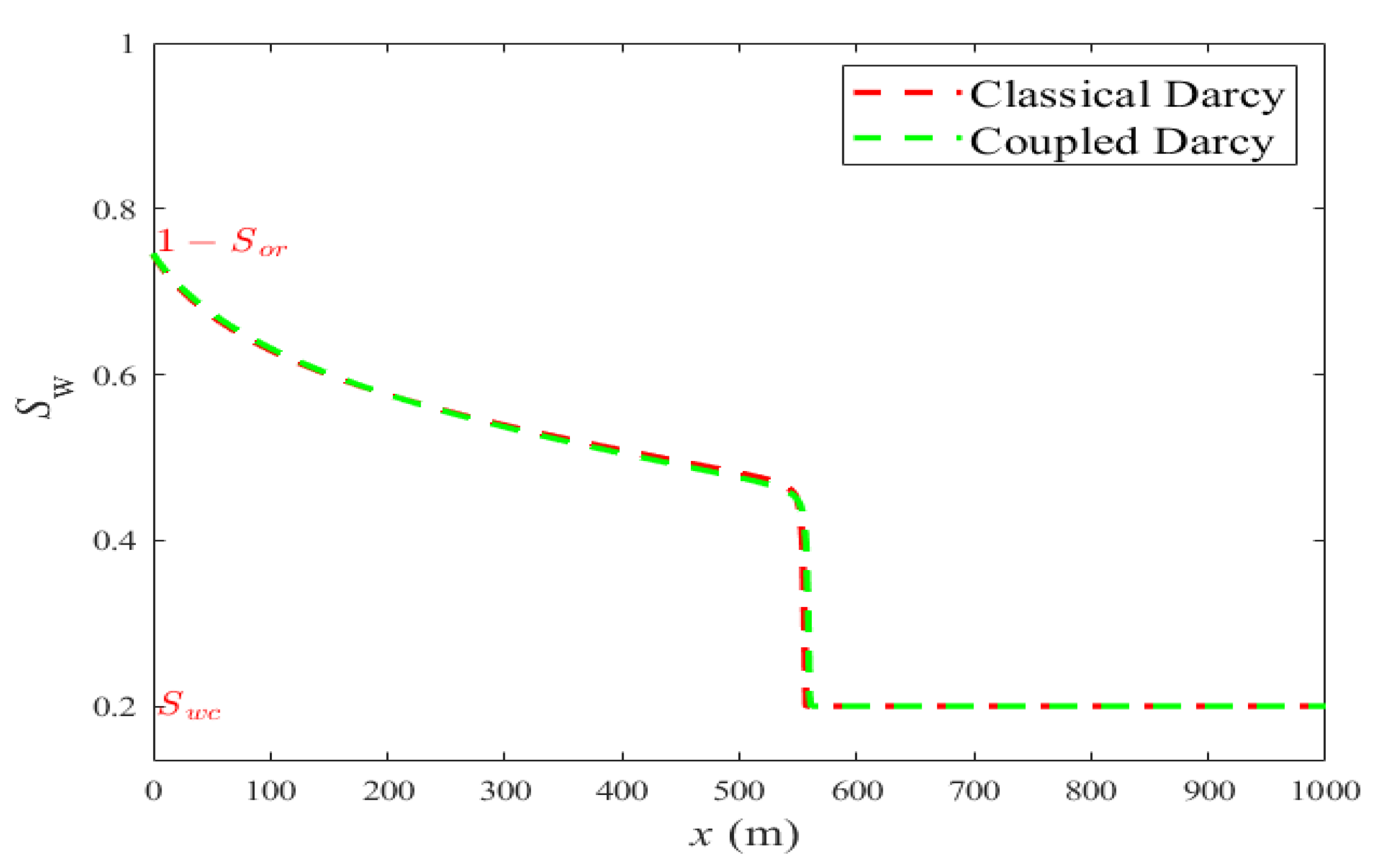
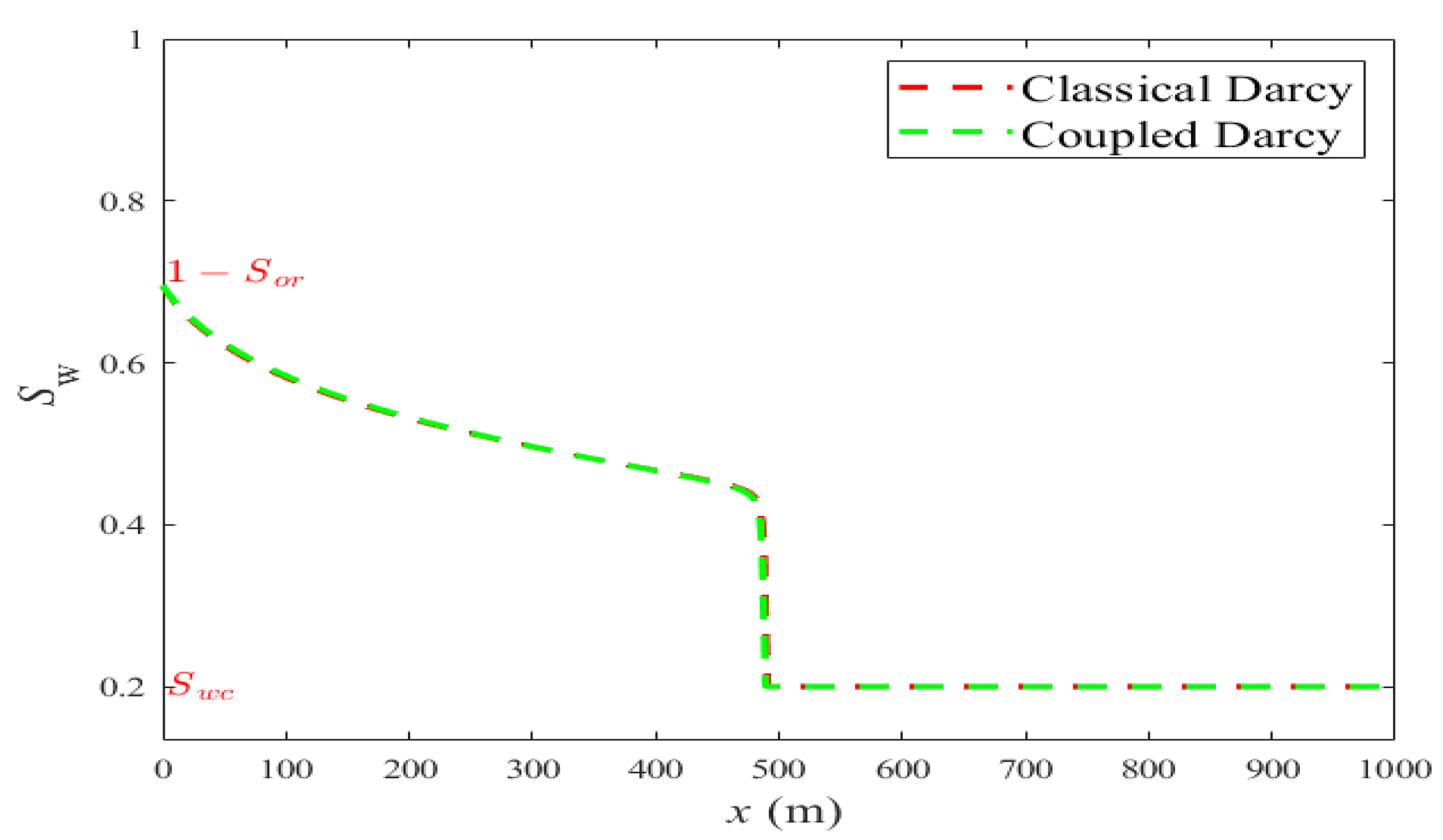
- Comparison: classical Darcy’s system vs coupled system with (see (19))
- Effect of non-symmetric coupling: coupled system with (we refer to as tolerance). For more examples, see (see (20))
- (a)
- First set of data
Parameters Value Unit Length of formation, L 1000.0 [m] Cross-area of reservoir, A [m] Absolute permeability, k 2.96 [m] Oil phase viscosity, 5 [Pa.s] Water phase viscosity, [Pa.s] Oil density, 0.8 [kg/m] Water density, [kg/m] Initial water injection rate, 400 [m/s] Porosity, 0.30 [-] Residual oil saturation, 0.25 [-] Connate water saturation, 0.20 [-] Maximal relative permeability for oil, 0.8 [-] Maximal relative permeability for water, 0.5 [-] Power index of water relative permeability 2.00 [-] Power index of oil relative permeability, 2.00 [-] Power index of first coupling term , 2.00 [-] Power index of second coupling term , , 2.00 [-] - (b)
- Second set of data
Parameters Value Unit Length of formation, L 3280 [ft] Cross-area of reservoir, A [ft] Absolute permeability, k 300 [mD] Oil phase viscosity, 5 [cP] Water phase viscosity, 1 [cP] Oil density, 22.653 [kg/ft] Water density, 28.316 [kg/ft] Initial water injection rate, 2515.924 [bbl/s] Porosity, 0.30 [-] Residual oil saturation, 0.25 [-] Connate water saturation, 0.20 [-] Maximal relative permeability for oil, 0.8 [-] Maximal relative permeability for water, 0.5 [-] Power index of water relative permeability 2.00 [-] Power index of oil relative permeability, 2.00 [-] Power index of first coupling term , 2.00 [-] Power index of second coupling term , , 2.00 [-]
- The case of , we choose
- The case of we choose:
3.2. Numerical Results
| Classical Darcy | Tolerance | Tolerance | Tolerance |
| days | days | days | days |
| Classical Darcy | Coupled Darcy with |
| days | days |
4. Discussion
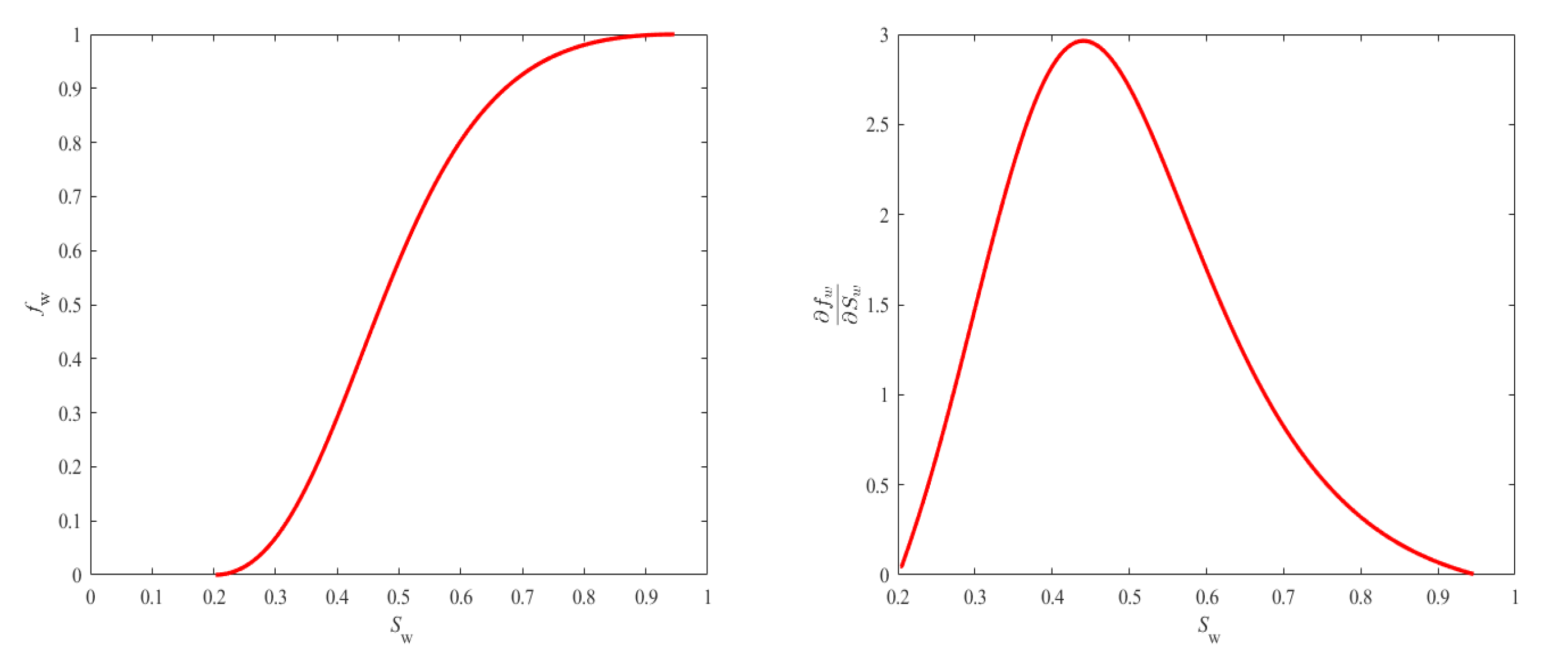
4.1. On the Fractional Flow
4.2. Solution of Coupled System by a Decoupling Approach
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; The Mapple Press Company: York, PA, USA, 1946. [Google Scholar]
- Kalaydjian, F. A macroscopic description of multiphase flow in porous media involving spacetime evolution of fluid/fluid interface. Transp. Porous Media 1987, 2, 537. [Google Scholar] [CrossRef]
- Kalaydjian, F. Origin and quantification of coupling between relative permeabilities for two-phase flows in porous media. Transp. Porous Media 1990, 5, 215. [Google Scholar] [CrossRef]
- Danis, M.; Quintard, M. Modélisation d’un écoulement diphasique dans une succession de pores. Rev. Inst. Français Pétrole 1984, 39, 37. [Google Scholar] [CrossRef]
- Rothman, D.H. Macroscopic laws for immiscible two-phase flow in porous media: Results from numerical experiments. J. Geophys. Res. Solid Earth 1990, 95, 8663. [Google Scholar] [CrossRef]
- Rose, W. Measuring transport coefficients necessary for the description of coupled two-phase flow of immiscible fluids in porous media. Transp. Porous Media 1988, 3, 163–171. [Google Scholar] [CrossRef]
- Rose, W. Petroleum reservoir engineering at the crossroads (Ways of thinking). Iran Petrol. Inst. Bull. 1972, 46, 23–27. [Google Scholar]
- Rose, W. Second thoughts on Darcy’s law. Iran Pet. Inst. Bull. 1974, 48, 25–30. [Google Scholar]
- De Gennes, P.G. Theory of slow biphasic flows in porous media. Phys. Chem. Hydrol. 1983, 4, 175–185. [Google Scholar]
- De la Cruz, V.; Spanos, T.J.T. Mobilization of oil ganglia. AIChE J. 1983, 29, 854–858. [Google Scholar] [CrossRef]
- Auriault, J.L.; Sanchez-Palencia, E. Remarques sur la loi de Darcy pour les écoulements biphasiques en milieu poreux. Z Theor. Appl. Mech. 1986, 141–156. [Google Scholar]
- Whitaker, S. Flow in porous media II: The governing equations for immiscible, two-phase flow. Transp. Porous Media 1986, 1, 105–125. [Google Scholar] [CrossRef]
- Spanos, T.J.T.; de la Cruz, V.; Hube, J.; Sharma, R.C. An analysis of Buckley–Leverett theory. J. Can. Petrol. Technol. 1986, 25, 71–75. [Google Scholar] [CrossRef]
- Kalaydjian, E.; Legait, B. Ecoulement lent à contre-courant de deux fluides non miscibles dans un capillaire présentant un rétrécissement. C.R. Acad. Sci. Paris. Ser. H 1987, 304, 869–872. [Google Scholar]
- Spanos, T.J.T.; de la Cruz, V.; Hube, J. An analysis of the theoretical foundations of relative permeability curves. AOSTRA J. Res. 1988, 4, 181. [Google Scholar]
- Kalaydjian, F.; Legait, B. Effets de la géométrie des pores et de la mouillabilité sur le déplacement diphasique à contre-courant en capillaire et en milieu poreux. Rev. Phys. Appl. 1988, 23, 1071–1081. [Google Scholar] [CrossRef]
- Rose, W. Attaching new meanings to the Equations of Buckley and Leverett. J. Pet. Sci. Eng. 1988, 1, 223–228. [Google Scholar] [CrossRef]
- Dullien, F.; Dong, M. Experimental determination of the flow transport coefficients in the coupled equations of two-phase flow in porous media. Transp. Porous Media 1996, 25, 97–120. [Google Scholar] [CrossRef]
- Pasquier, S.; Quintard, M.; Davit, Y. Modeling two-phase flow of immiscible fluids in porous media: Buckley–Leverett theory with explicit coupling terms. Phys. Rev. Fluids 2017, 2, 104101. [Google Scholar] [CrossRef] [Green Version]
- Buckley, S.E.; Leverett, M.C. Mechanism of fluid displacement in sands. Trans. AIME 1942, 146, 107–116. [Google Scholar] [CrossRef]
- Welge, H.J. A simplified method for computing oil recovery by gas or water drive. J. Pet. Technol. 1952, 4, 91–98. [Google Scholar] [CrossRef]
- Sheldon, J.W.; Cardwell, W.T., Jr. One-dimensional incompressible noncapillary two-phase fluid flow in a porous medium. Pet. Trans. AIME 1959, 216, 290–296. [Google Scholar] [CrossRef]
- McWhorter, D.B.; Sunada, D.K. Exact integral solutions for two-phase flow. Water Resour. Res. 1990, 26, 399–413. [Google Scholar] [CrossRef]
- Guérillot, D.; Kalaydjian, F. Application du Formalisme par Pression Globale a L’etude du Couplage Entre lois de Darcy Pour les Ecoulements Diphasiques en Milieu Poreux (Application of the Global Pressure Concept to the Study of Coupling between Generalized Darcy’s Laws for Two-Phase Flow in Porous Media Comptes Rendus); Serie II; Academie des Sciences: Paris, France, 1988; Volume 306, pp. 853–858. [Google Scholar]
- Chavent, G.; Cohen, G.; Jaffre, J.; Eyard, R.; Guerillot, D.R.; Weill, L. Discontinuous and Mixed Finite Elements for Two-Phase Incompressible Flow. SPE Reserv. Eng. 1990, 5, 567–575. [Google Scholar] [CrossRef]
- Willhite, G.P. Waterflooding; Society of Petroleum Engineers: Richardson, TX, USA, 1986. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media. In Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1964; p. 3. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guérillot, D.; Kadiri, M.; Trabelsi, S. Buckley–Leverett Theory for Two-Phase Immiscible Fluids Flow Model with Explicit Phase-Coupling Terms. Water 2020, 12, 3041. https://doi.org/10.3390/w12113041
Guérillot D, Kadiri M, Trabelsi S. Buckley–Leverett Theory for Two-Phase Immiscible Fluids Flow Model with Explicit Phase-Coupling Terms. Water. 2020; 12(11):3041. https://doi.org/10.3390/w12113041
Chicago/Turabian StyleGuérillot, Dominique, Mostafa Kadiri, and Saber Trabelsi. 2020. "Buckley–Leverett Theory for Two-Phase Immiscible Fluids Flow Model with Explicit Phase-Coupling Terms" Water 12, no. 11: 3041. https://doi.org/10.3390/w12113041
APA StyleGuérillot, D., Kadiri, M., & Trabelsi, S. (2020). Buckley–Leverett Theory for Two-Phase Immiscible Fluids Flow Model with Explicit Phase-Coupling Terms. Water, 12(11), 3041. https://doi.org/10.3390/w12113041






