Age of Water Particles as a Diagnosis of Steady-State Flows in Shallow Rectangular Reservoirs
Abstract
1. Introduction
- Persson [27] applied a 2D depth-averaged model to estimate the residence time distribution in ponds of various layouts, based on the advection–diffusion equation for a tracer. The results revealed that a subsurface berm or an island placed in front of the inlet reduces short-circuiting, and improves the effective volume and degree of mixing;
- Sonnenwald et al. [6] used a 3D computational model to obtain residence time distributions for vegetated storm water treatment ponds, showing that the presence of vegetation results in residence times close to those of plug flow conditions;
- By means of tracer studies with laboratory-scale models, Guzman et al. [3] evaluated the residence time distribution for 54 topographies of storm water detention ponds and treatment wetlands, to compare the hydraulic performances of the various designs.
2. Data and Method
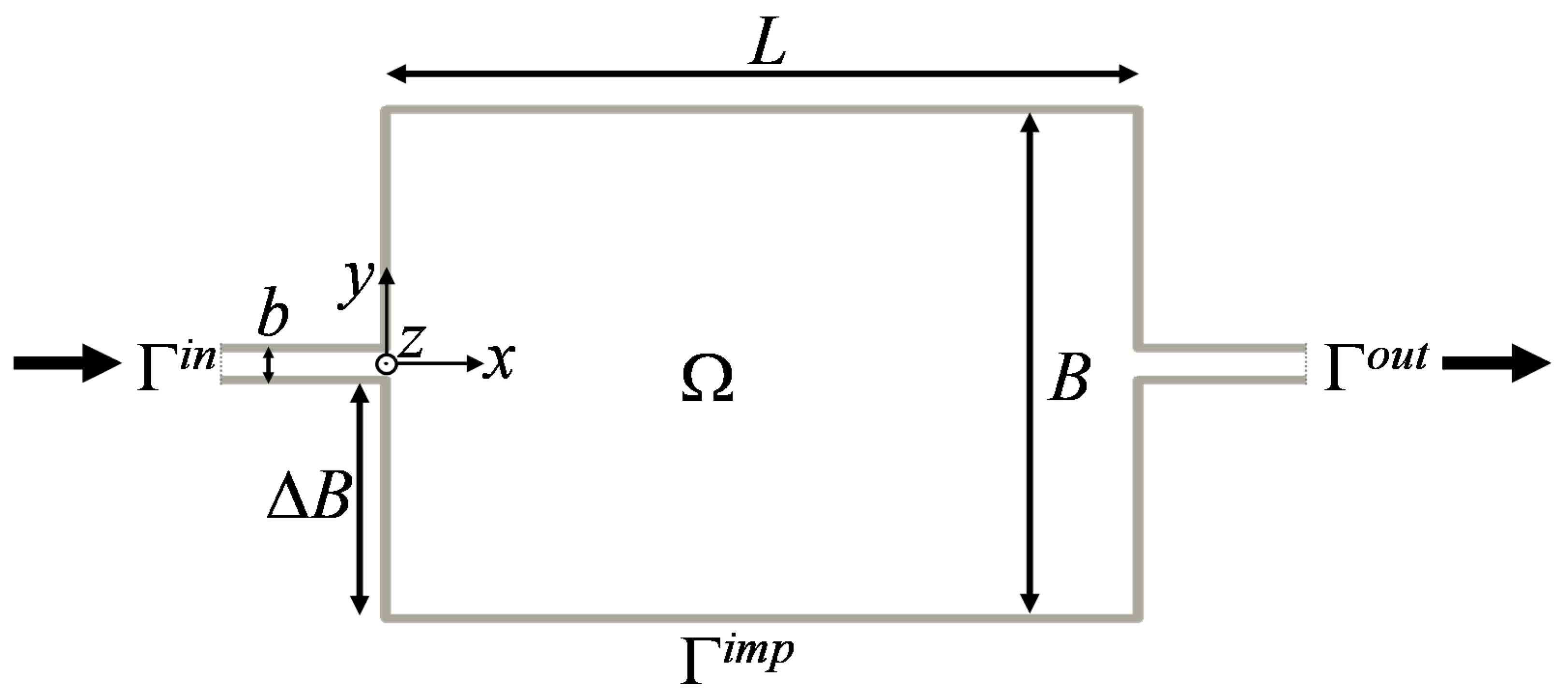
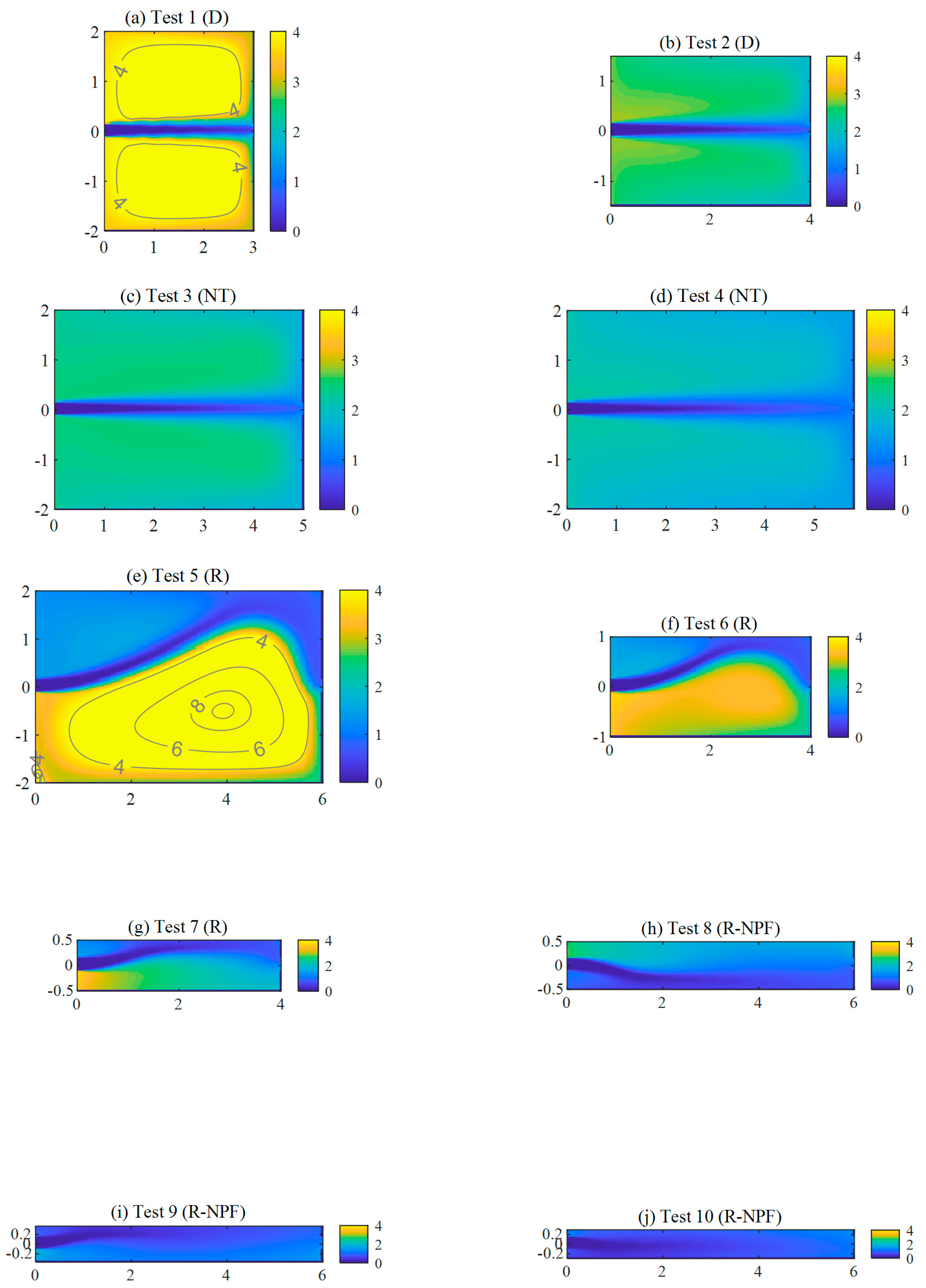
2.1. Characteristics of the Considered Reservoirs
2.2. Flow Model and Computed Flow Fields
2.3. Water Age Distribution Function
2.4. Mathematical Properties of the Mean Water Age
- The solution is unique;
- a(x) is non-negative;
- The value of the mean age on the incoming boundary is not zero, unless diffusion is zero. Indeed, on Γin, there is a mixture of water particles that are entering the domain and particles that have been moving for some time in the domain and were brought back to the incoming boundary by diffusion;
- The maximum of the mean age is not necessarily on the outgoing boundary Γout, but it may be located inside the domain of interest. This contrasts with a one-dimensional setting, in which the maximum of mean age occurs at the outgoing boundary because there is only one path from the reservoir inlet to the outlet;
- On the outgoing boundary Γout, the average value of the mean age satisfies:
2.5. Computational Procedure
3. Results
3.1. Model Verification: Prismatic Channel
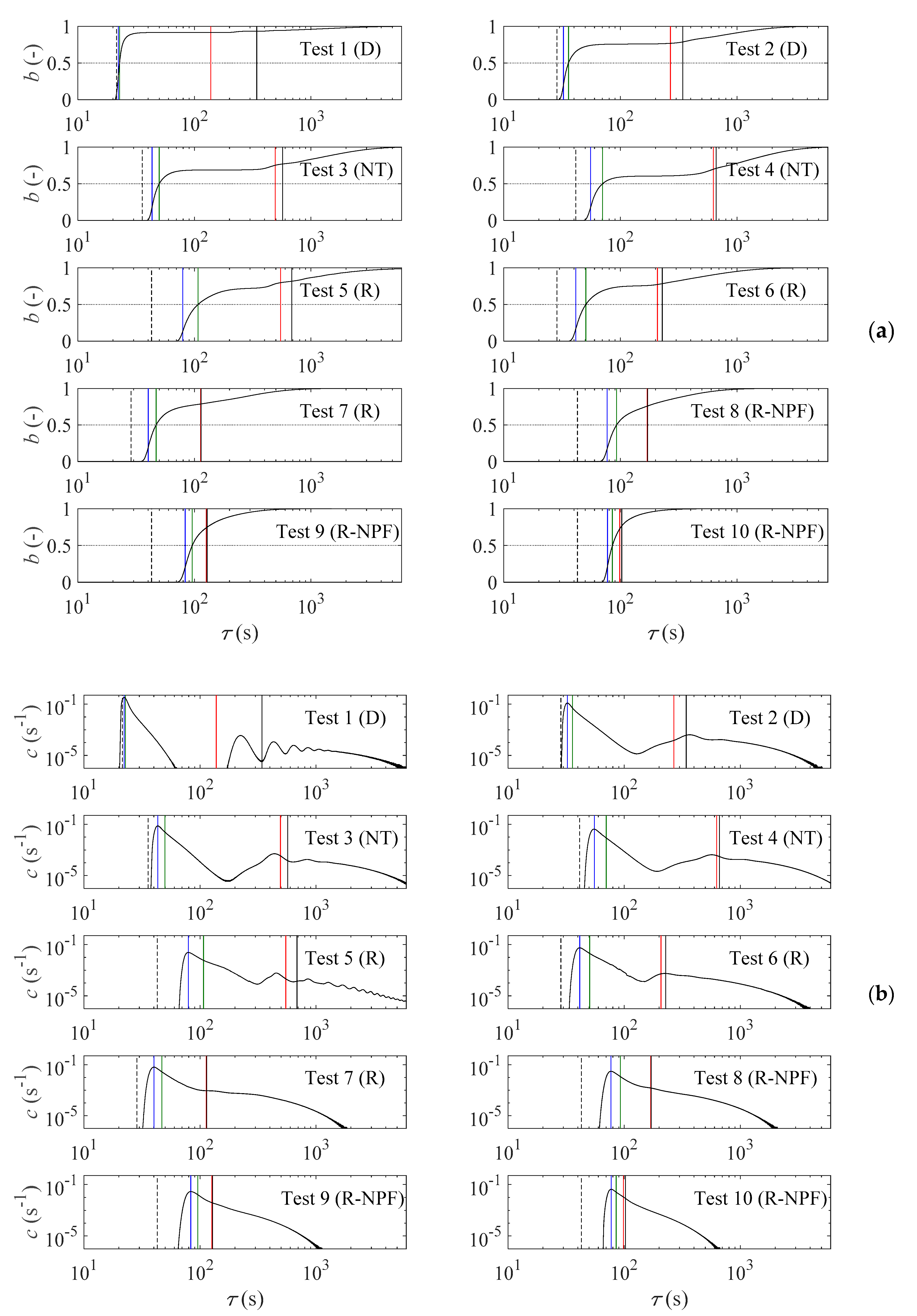
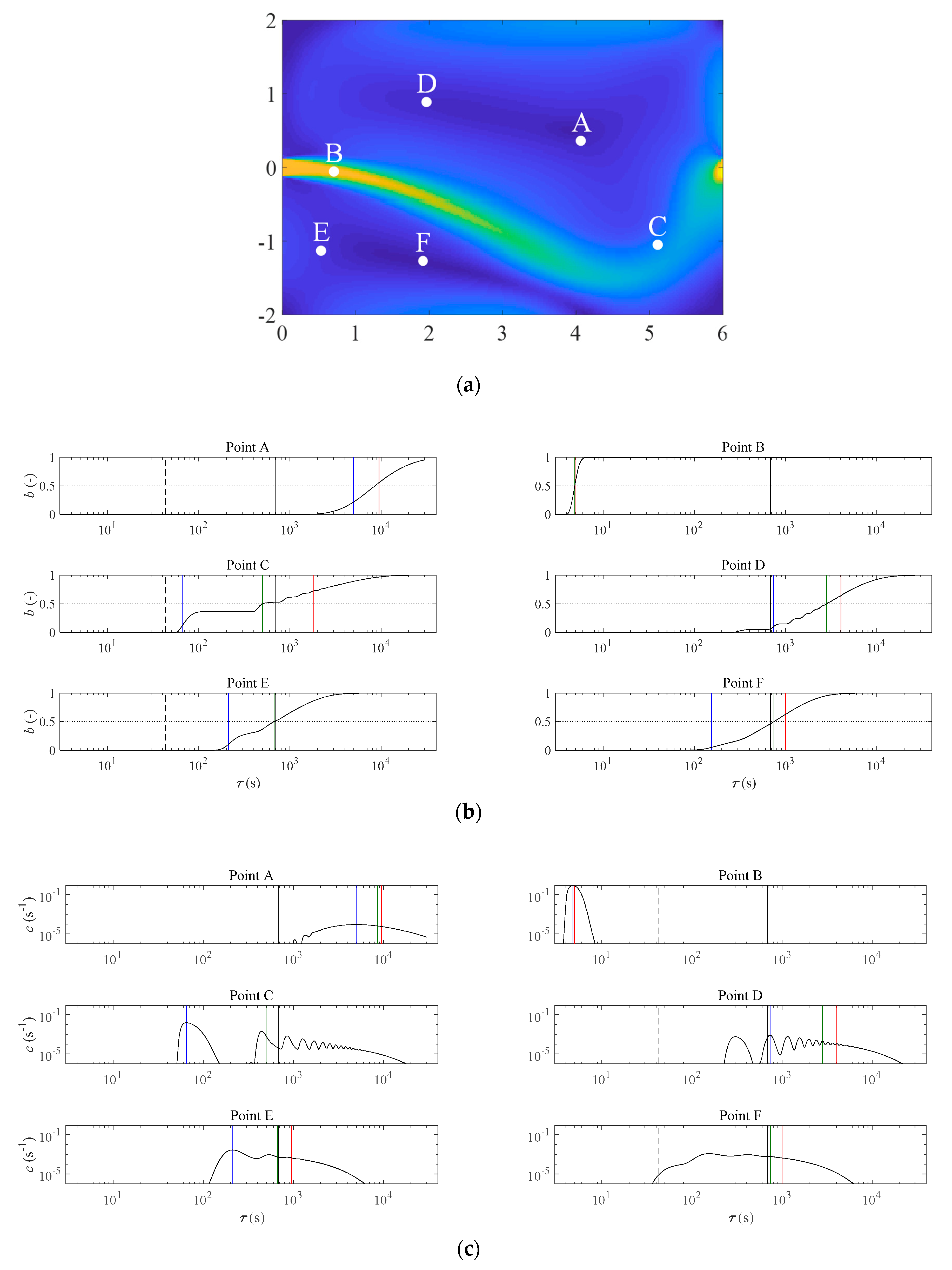
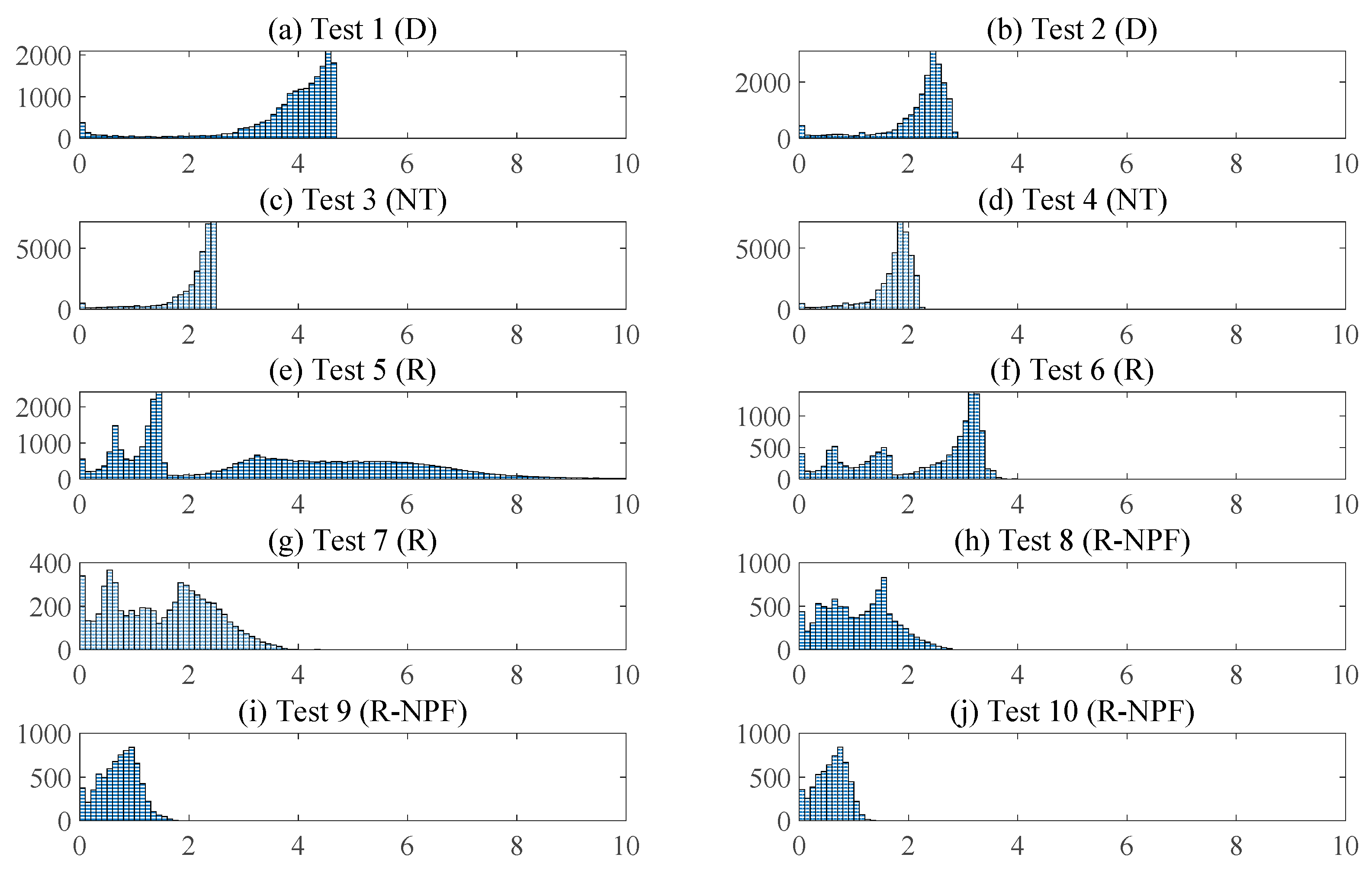
3.2. Distribution of Water Age at Reservoir Outlet
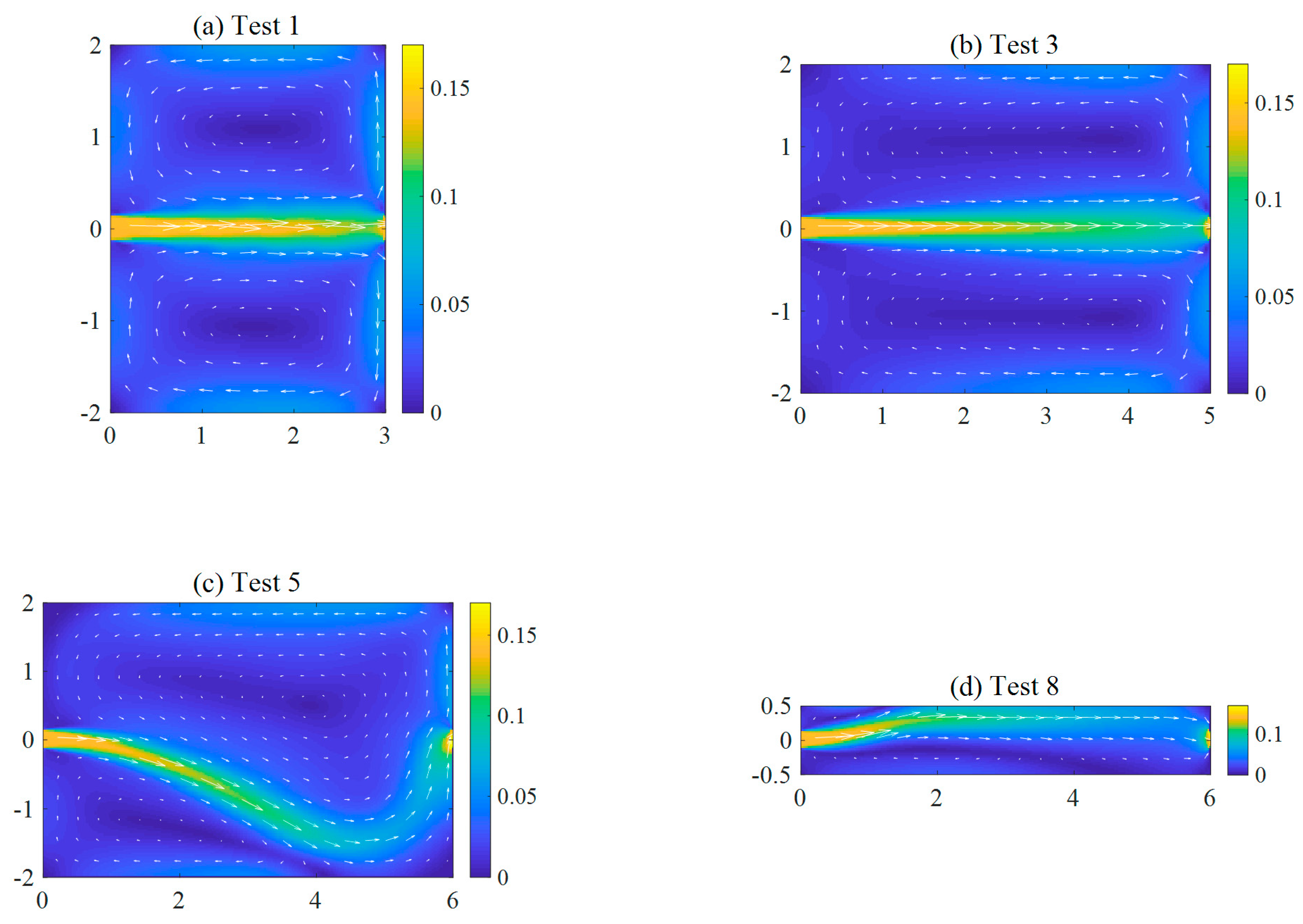
- In the nearly-plug-flow configurations (Tests 8, 9 and 10), the water age distribution at the outlet is unimodal, but strongly skewed towards the higher values of τ;
- Looking sequentially at the results obtained for Tests 7, 6 and 5, all corresponding to configurations with a reattached jet, it appears that the water age distribution at the outlet shifts gradually from a unimodal to a bimodal distribution;
- In all cases with a detached jet, the water age distribution at the outlet is bimodal (Tests 4, 3 and 2), or even multimodal in the case of Test 1.
- V/Q, which would correspond to the transit time through the reservoir in the case of a perfect plug flow all over the reservoir;
- L/(Q/Sin), would be equal to the transit time through the reservoir if the jet at the inlet was not diffused at all in the crosswise direction.
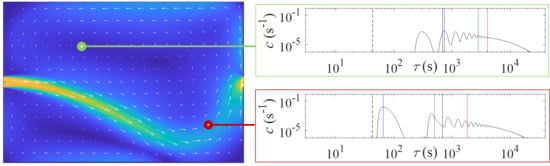
3.3. Distribution of Water Age within the Reservoirs
3.4. Mean Age in the Reservoirs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brink, I.C.; Kamish, W. Associations between stormwater retention pond parameters and pollutant (Suspended solids and metals) removal efficiencies. Water SA 2018, 44, 45–53. [Google Scholar] [CrossRef]
- Dominic, J.A.; Aris, A.Z.; Sulaiman, W.N.A.; Tahir, W.Z.W.M. Discriminant analysis for the prediction of sand mass distribution in an urban stormwater holding pond using simulated depth average flow velocity data. Environ. Monit. Assess. 2016, 188, 1–15. [Google Scholar] [CrossRef]
- Guzman, C.B.; Cohen, S.; Xavier, M.; Swingle, T.; Qiu, W.; Nepf, H. Island topographies to reduce short-circuiting in stormwater detention ponds and treatment wetlands. Ecol. Eng. 2018, 117, 182–193. [Google Scholar] [CrossRef]
- MoayeriKashani, M.; Hin, L.S.; Ibrahim, S. Experimental investigation of fine sediment deposition using particle image velocimetry. Environ. Earth Sci. 2017, 76, 655. [Google Scholar] [CrossRef]
- Sebastian, C.; Becouze-Lareure, C.; Lipeme Kouyi, G.; Barraud, S. Event-based quantification of emerging pollutant removal for an open stormwater retention basin—Loads, efficiency and importance of uncertainties. Water Res. 2014, 72, 239–250. [Google Scholar] [CrossRef] [PubMed]
- Sonnenwald, F.; Guymer, I.; Stovin, V. Computational fluid dynamics modelling of residence times in vegetated stormwater ponds. Proc. Inst. Civ. Eng. Water Manag. 2018, 171, 76–86. [Google Scholar] [CrossRef]
- Stovin, V.R.; Saul, A.J. Computational fluid dynamics and the design of sewage storage chambers. Water Environ. J. 2000, 14, 103–110. [Google Scholar] [CrossRef]
- Isenmann, G.; Dufresne, M.; Vazquez, J.; Mose, R. Bed turbulent kinetic energy boundary conditions for trapping efficiency and spatial distribution of sediments in basins. Water Sci. Technol. 2017, 76, 2032–2043. [Google Scholar] [CrossRef]
- Liu, X.; Xue, H.; Hua, Z.; Yao, Q.; Hu, J. Inverse calculation model for optimal design of rectangular sedimentation tanks. J. Environ. Eng. 2013, 139, 455–459. [Google Scholar] [CrossRef]
- Tarpagkou, R.; Pantokratoras, A. CFD methodology for sedimentation tanks: The effect of secondary phase on fluid phase using DPM coupled calculations. Appl. Math. Model. 2013, 37, 3478–3494. [Google Scholar] [CrossRef]
- Zhang, J.-M.; Lee, H.P.; Khoo, B.C.; Peng, K.Q.; Zhong, L.; Kang, C.-W.; Ba, T. Shape effect on mixing and age distributions in service reservoirs. J. Am. Water Works Assoc. 2014, 106, E481–E491. [Google Scholar] [CrossRef]
- Oca, J.; Masalo, I. Design criteria for rotating flow cells in rectangular aquaculture tanks. Aquac. Eng. 2007, 36, 36–44. [Google Scholar] [CrossRef]
- Camnasio, E.; Orsi, E.; Schleiss, A. Experimental study of velocity fields in rectangular shallow reservoirs. J. Hydraul. Res. 2011, 49, 352–358. [Google Scholar] [CrossRef]
- Dufresne, M.; Dewals, B.J.; Erpicum, S.; Archambeau, P.; Pirotton, M. Classification of flow patterns in rectangular shallow reservoirs. J. Hydraul. Res. 2010, 48, 197–204. [Google Scholar] [CrossRef]
- Kantoush, S.A.; De Cesare, G.; Boillat, J.L.; Schleiss, A.J. Flow field investigation in a rectangular shallow reservoir using UVP, LSPIV and numerical modelling. Flow Meas. Instrum. 2008, 19, 139–144. [Google Scholar] [CrossRef]
- Peltier, Y.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Dewals, B. Experimental investigation of meandering jets in shallow reservoirs. Environ. Fluid Mech. 2014, 14, 699–710. [Google Scholar] [CrossRef]
- Choufi, L.; Kettab, A.; Schleiss, A.J. Bed roughness effect on flow field in rectangular shallow reservoir. [Effet de la rugosité du fond d’un réservoir rectangulaire à faible profondeur sur le champ d’écoulement]. Houille Blanche 2014, 5, 83–92. [Google Scholar]
- Camnasio, E.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Dewals, B. Prediction of mean and turbulent kinetic energy in rectangular shallow reservoirs. Eng. Appl. Comput. Fluid Mech. 2014, 8, 586–597. [Google Scholar] [CrossRef]
- Camnasio, E.; Erpicum, S.; Orsi, E.; Pirotton, M.; Schleiss, A.J.; Dewals, B. Coupling between flow and sediment deposition in rectangular shallow reservoirs. J. Hydraul. Res. 2013, 51, 535–547. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Haun, S.; Rüther, N. Three-dimensional numerical modelling of flow field in shallow reservoirs. Proc. Inst. Civ. Eng. Water Manag. 2016, 169, 229–244. [Google Scholar] [CrossRef]
- Peltier, Y.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Dewals, B. Can meandering flows in shallow rectangular reservoirs be modeled with the 2D shallow water equations? J. Hydraul. Eng. 2015, 141, 04015008. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modeling free-surface flow in rectangular shallow basins by using lattice boltzmann method. J. Hydraul. Eng. 2012, 137, 1680–1685. [Google Scholar] [CrossRef]
- Schleiss, A.J.; Franca, M.J.; Juez, C.; De Cesare, G. Reservoir sedimentation. J. Hydraul. Res. 2016, 54, 595–614. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- Monsen, N.E.; Cloern, J.E.; Lucas, L.V.; Monismith, S.G. A comment on the use of flushing time, residence time, and age as transport time scales. Limnol. Oceanogr. 2002, 47, 1545–1553. [Google Scholar] [CrossRef]
- Takeoka, H. Fundamental concepts of exchange and transport time scales in a coastal sea. Cont. Shelf Res. 1984, 3, 311–326. [Google Scholar] [CrossRef]
- Persson, J. The hydraulic performance of ponds of various layouts. Urban Water 2000, 2, 243–250. [Google Scholar] [CrossRef]
- Delhez, E.J.M.; Campin, J.-M.; Hirst, A.C.; Deleersnijder, E. Toward a general theory of the age in ocean modelling. Ocean Model. 1999, 1, 17–27. [Google Scholar] [CrossRef]
- Goltsman, A.; Saushin, I. Flow pattern of double-cavity flow at high Reynolds number. Phys. Fluids 2019, 31, 065101. [Google Scholar] [CrossRef]
- Peltier, Y.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Dewals, B. Meandering jets in shallow rectangular reservoirs: POD analysis and identification of coherent structures. Exp. Fluids 2014, 55, 1740. [Google Scholar] [CrossRef]
- Chu, V.H.; Liu, F.; Altai, W. Friction and confinement effects on a shallow recirculating flow. J. Environ. Eng. Sci. 2004, 3, 463–475. [Google Scholar] [CrossRef]
- Dufresne, M.; Dewals, B.J.; Erpicum, S.; Archambeau, P.; Pirotton, M. Numerical investigation of flow patterns in rectangular shallow reservoirs. Eng. Appl. Comput. Fluid Mech. 2011, 5, 247–258. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. Trans. Asme 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Campin, J.-M.; Delhez, E.J.M. The concept of age in marine modelling I. Theory and preliminary model results. J. Mar. Syst. 2001, 28, 229–267. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Dewals, B. Mathematical Properties of the Position-Dependent, Steady-State Water Age in a Shallow Reservoir; Working Note; Université Catholique de Louvain: Louvain-la-Neuve, Belgium, 2020; p. 18. Available online: http://hdl.handle.net/2078.1/230041 (accessed on 4 October 2020).
- Deleersnijder, E.; Draoui, I.; Lambrechts, J.; Legat, V.; Mouchet, A. Consistent boundary conditions for age calculations. Water 2020, 12, 1274. [Google Scholar] [CrossRef]
- Varni, M.; Carrera, J. Simulation of groundwater age distributions. Water Resour. Res. 1998, 34, 3271–3281. [Google Scholar] [CrossRef]
- Cornaton, F.; Perrochet, P. Groundwater age, life expectancy and transit time distributions in advective-dispersive systems; 2. Reservoir theory for sub-drainage basins. Adv. Water Resour. 2006, 29, 1292–1305. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R. Sediment transport time scales and trapping efficiency in a Tidal river. J. Geophys. Res. Earth Surf. 2017, 122, 2042–2063. [Google Scholar] [CrossRef]
- Gong, W.; Shen, J. A model diagnostic study of age of river-borne sediment transport in the tidal York River Estuary. Environ. Fluid Mech. 2010, 10, 177–196. [Google Scholar] [CrossRef]
- Liu, W.-C.; Chen, W.-B.; Hsu, M.-H. Using a three-dimensional particle-tracking model to estimate the residence time and age of water in a tidal estuary. Comput. Geosci. 2011, 37, 1148–1161. [Google Scholar] [CrossRef]
- Arega, F.; Badr, A.W. Numerical age and residence-time mapping for a small tidal creek: Case study. J. Waterw. Port Coast. Ocean Eng. 2010, 136, 226–237. [Google Scholar] [CrossRef]
- Spivakovskaya, D.; Heemink, A.W.; Milstein, G.N.; Schoenmakers, J.G.M. Simulation of the transport of particles in coastal waters using forward and reverse time diffusion. Adv. Water Resour. 2005, 28, 927–938. [Google Scholar] [CrossRef]
- Scott, C.F. Particle tracking simulation of pollutant discharges. J. Environ. Eng. 1997, 123, 919–927. [Google Scholar] [CrossRef]
- Heemink, A.W. Stochastic modelling of dispersion in shallow water. Stoch. Hydrol. Hydraul. 1990, 4, 161–174. [Google Scholar] [CrossRef]
- Zahabi, H.; Torabi, M.; Alamatian, E.; Bahiraei, M.; Goodarzi, M. Effects of geometry and hydraulic characteristics of shallow reservoirs on sediment entrapment. Water 2018, 10, 1725. [Google Scholar] [CrossRef]

| Persson [27] | Sonnenwald et al. [6] | Guzman et al. [3] | Zhang et al. [11] | Present Study | |
|---|---|---|---|---|---|
| Modeling approach | 2D | 3D | Lab | 3D | 2D |
| Considered layouts | 13 | 4 × 3 | 45+ | 3 | 10 |
| Full domain considered (i.e., no a priori assumption of symmetric flow) | ✓ | ✓ | ✓ | ✓ | |
| Residence time distribution (at the outlet) | ✓ | ✓ | ✓ | ✓ | |
| Mean water age throughout the reservoir | ✓ | ✓ | |||
| Age distribution throughout the reservoir | ✓ |
| Test ID | L (m) | B (m) | SF (−) | Type of Flow Pattern | Test ID in Camnasio et al. [18] |
|---|---|---|---|---|---|
| 1 | 3 | 4 | 3.6 | Detached jet (D) | 5 |
| 2 | 4 | 3 | 5.8 | Detached jet (D) | 6 |
| 3 | 5 | 4 | 6.0 | Near-transition (NT) | 4 |
| 4 | 5.8 | 4 | 6.9 | Near-transition (NT) | 2 |
| 5 | 6 | 4 | 7.2 | Reattached jet (R) | 1 |
| 6 | 4 | 2 | 7.6 | Reattached jet (R) | 7 |
| 7 | 4 | 1 | 12.5 | Reattached jet (R) | 8 |
| 8 | 6 | 1 | 18.8 | Reattached nearly-plug-flow (R-NPF) | 9 |
| 9 | 6 | 0.75 | 24.0 | Reattached nearly-plug-flow (R-NPF) | 10 |
| 10 | 6 | 0.6 | 29.7 | Reattached nearly-plug-flow (R-NPF) | 11 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dewals, B.; Archambeau, P.; Bruwier, M.; Erpicum, S.; Pirotton, M.; Adam, T.; Delhez, E.; Deleersnijder, E. Age of Water Particles as a Diagnosis of Steady-State Flows in Shallow Rectangular Reservoirs. Water 2020, 12, 2819. https://doi.org/10.3390/w12102819
Dewals B, Archambeau P, Bruwier M, Erpicum S, Pirotton M, Adam T, Delhez E, Deleersnijder E. Age of Water Particles as a Diagnosis of Steady-State Flows in Shallow Rectangular Reservoirs. Water. 2020; 12(10):2819. https://doi.org/10.3390/w12102819
Chicago/Turabian StyleDewals, Benjamin, Pierre Archambeau, Martin Bruwier, Sebastien Erpicum, Michel Pirotton, Tom Adam, Eric Delhez, and Eric Deleersnijder. 2020. "Age of Water Particles as a Diagnosis of Steady-State Flows in Shallow Rectangular Reservoirs" Water 12, no. 10: 2819. https://doi.org/10.3390/w12102819
APA StyleDewals, B., Archambeau, P., Bruwier, M., Erpicum, S., Pirotton, M., Adam, T., Delhez, E., & Deleersnijder, E. (2020). Age of Water Particles as a Diagnosis of Steady-State Flows in Shallow Rectangular Reservoirs. Water, 12(10), 2819. https://doi.org/10.3390/w12102819