Multi-Indicator Evaluation for Extreme Precipitation Events in the Past 60 Years over the Loess Plateau
Abstract
1. Introduction
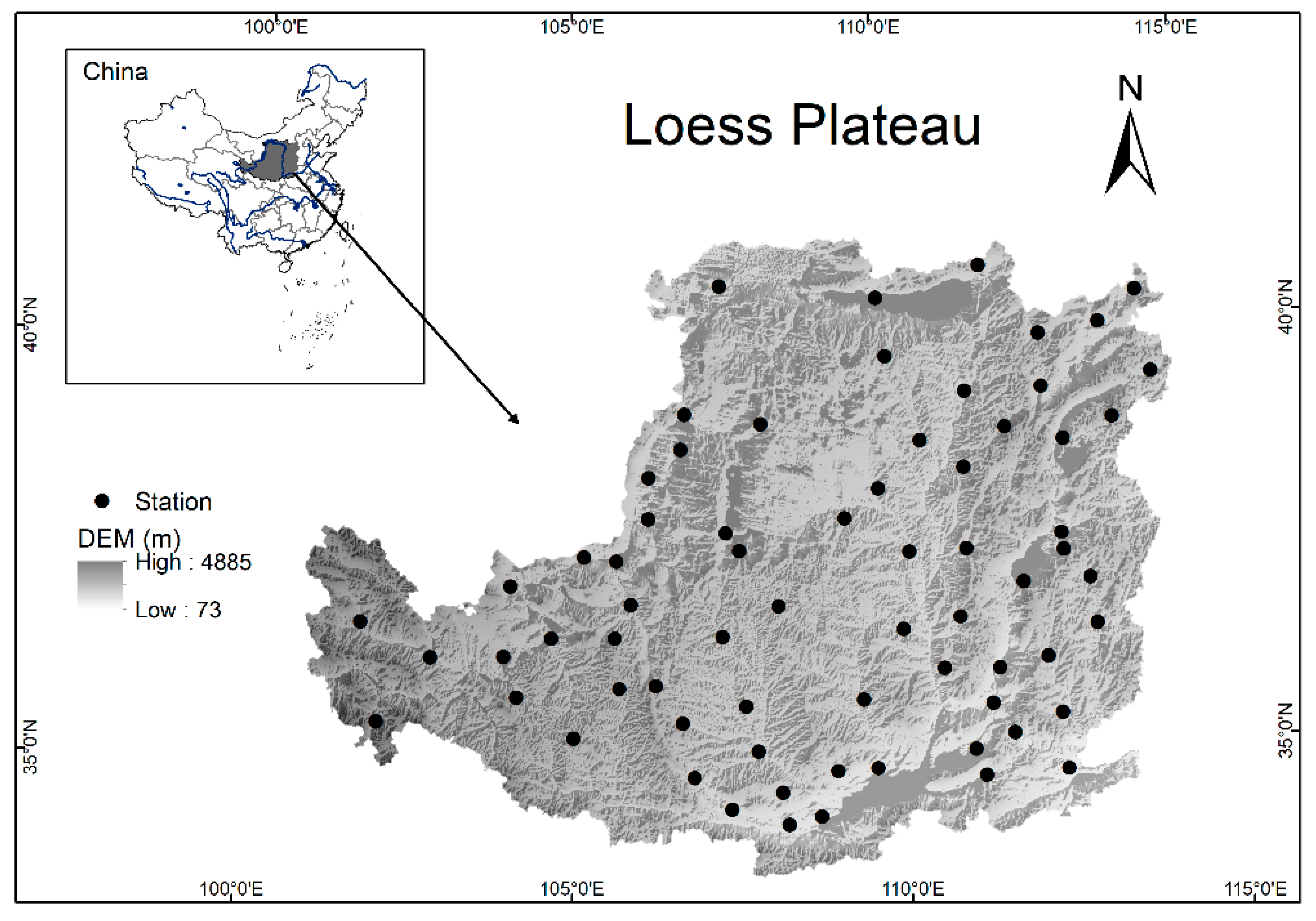
2. Study Area and Data
3. Method
3.1. Marginal Distribution and Univariate Return Period
3.2. Construction of Joint Distribution of Extreme Precipitation Indicators
3.3. Bivariate Return Periods of Extreme Precipitation Indicators
4. Method Application and Results Analyses
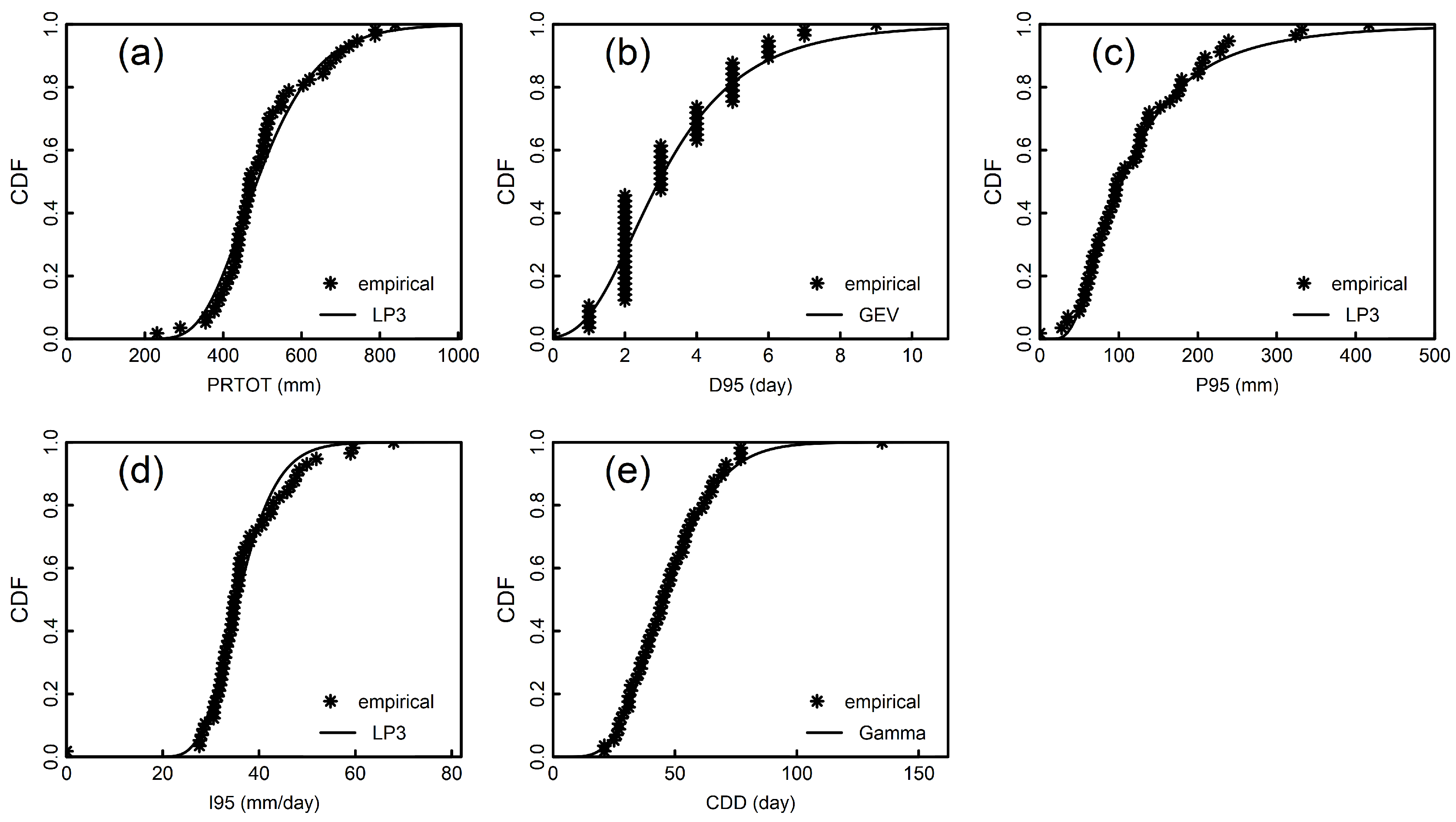
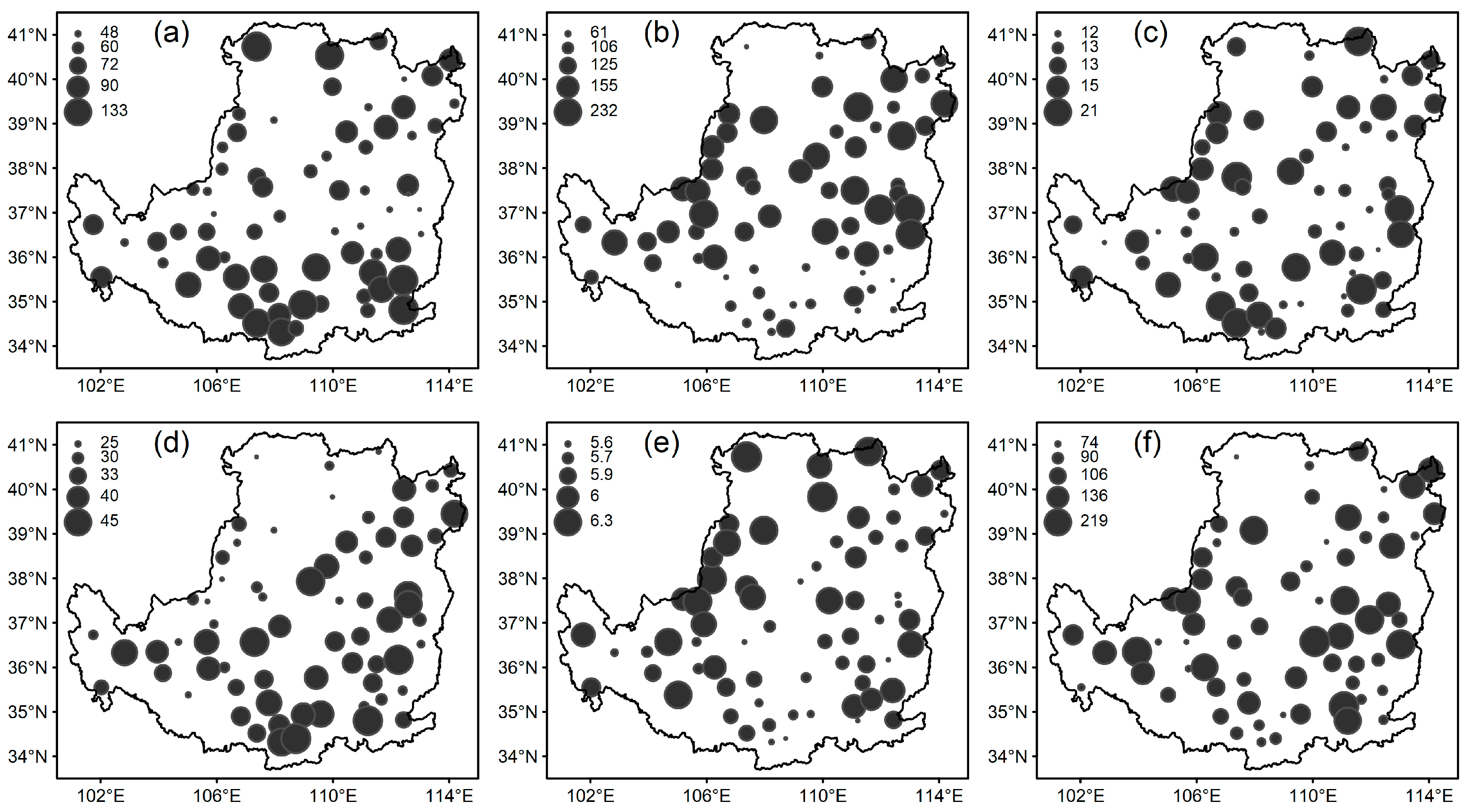
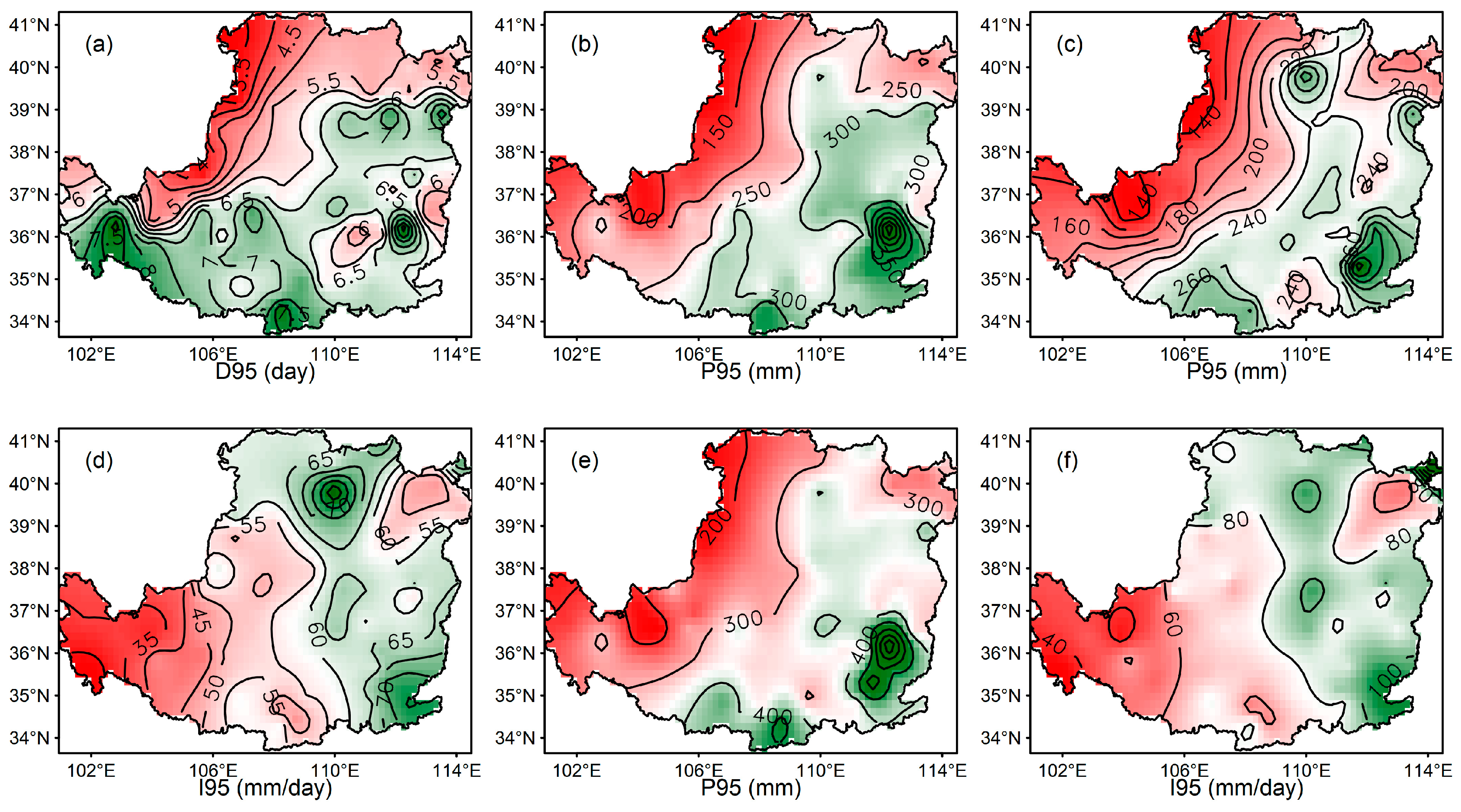
4.1. Univariate Analysis
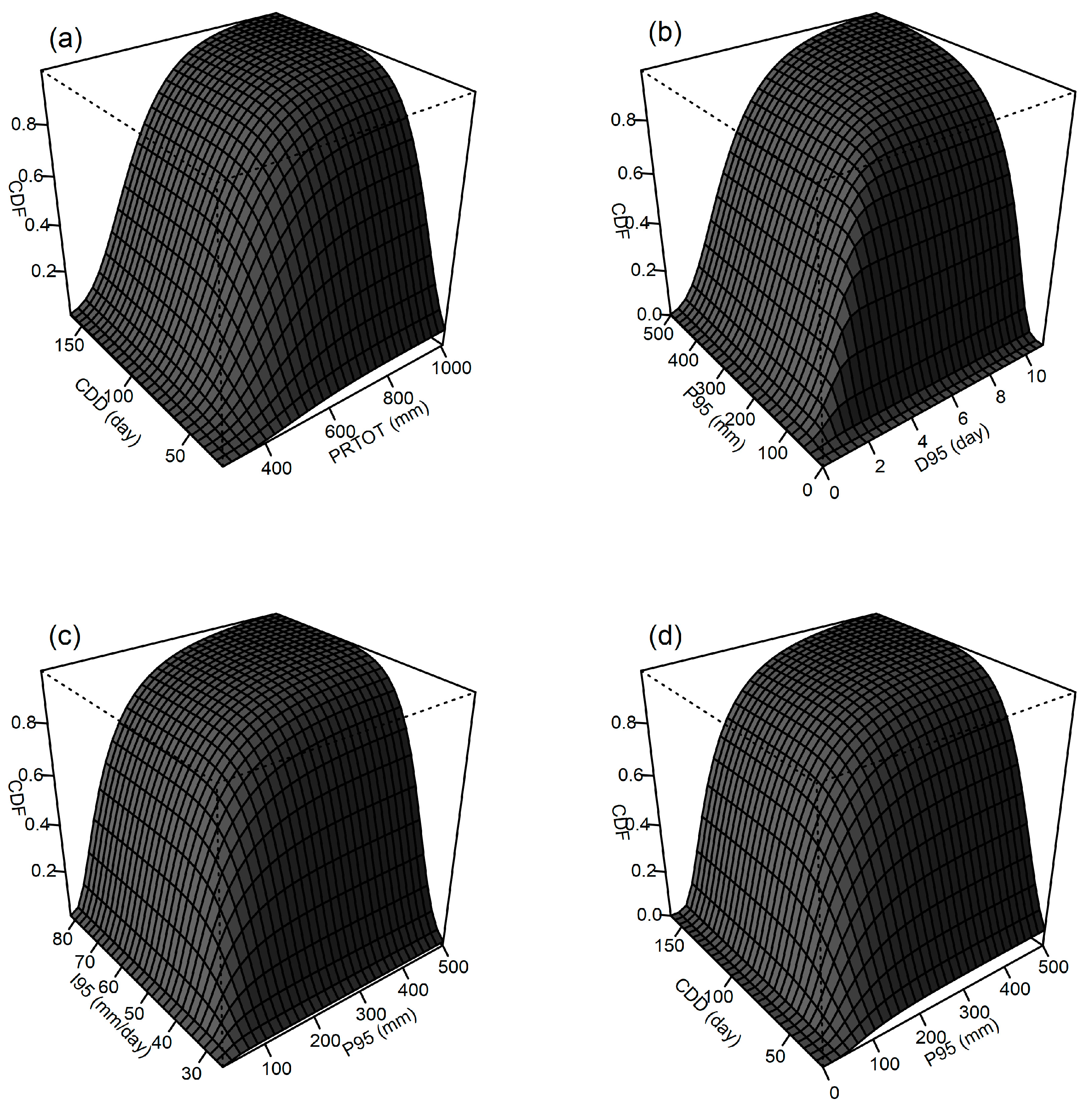
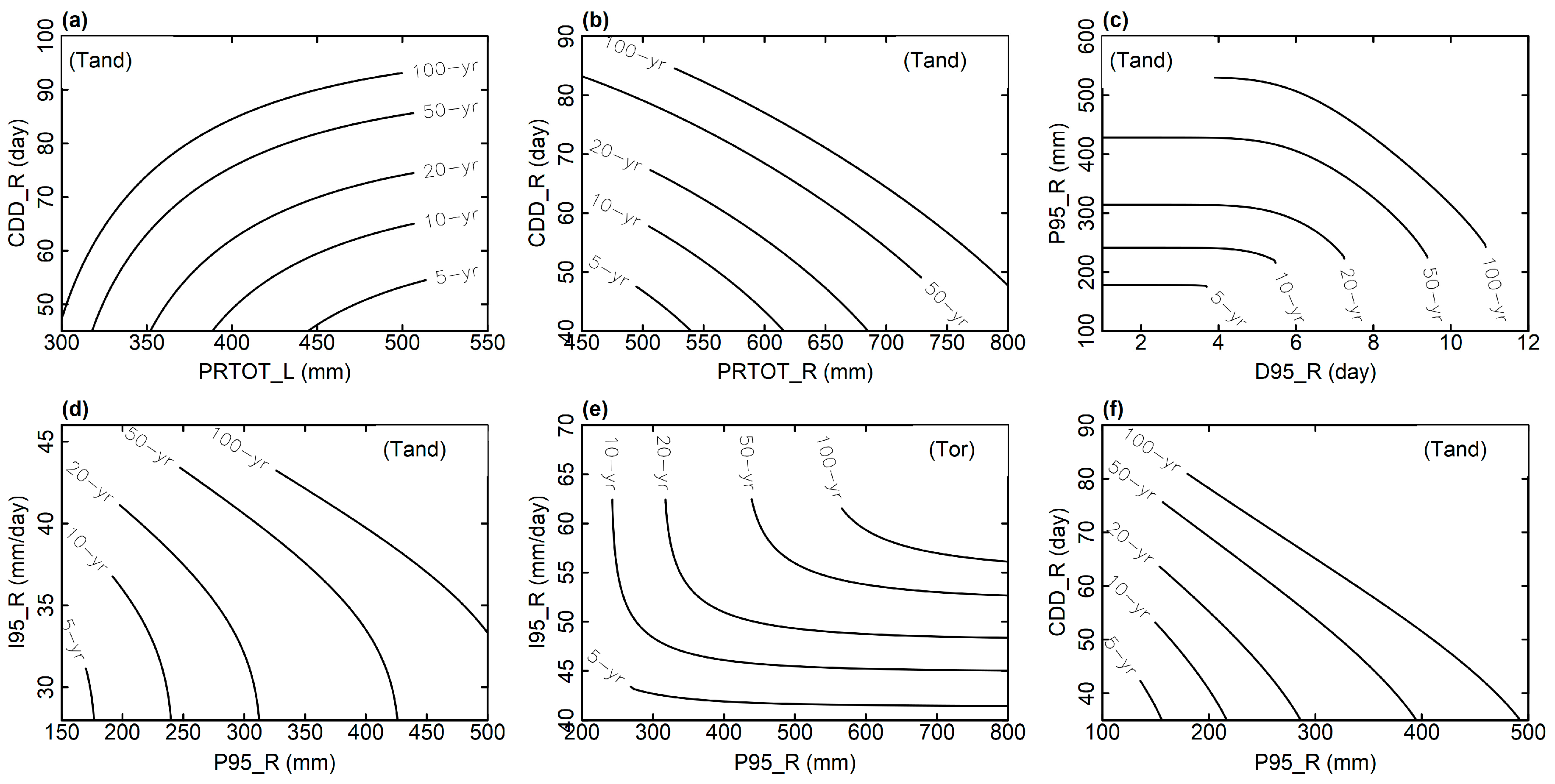
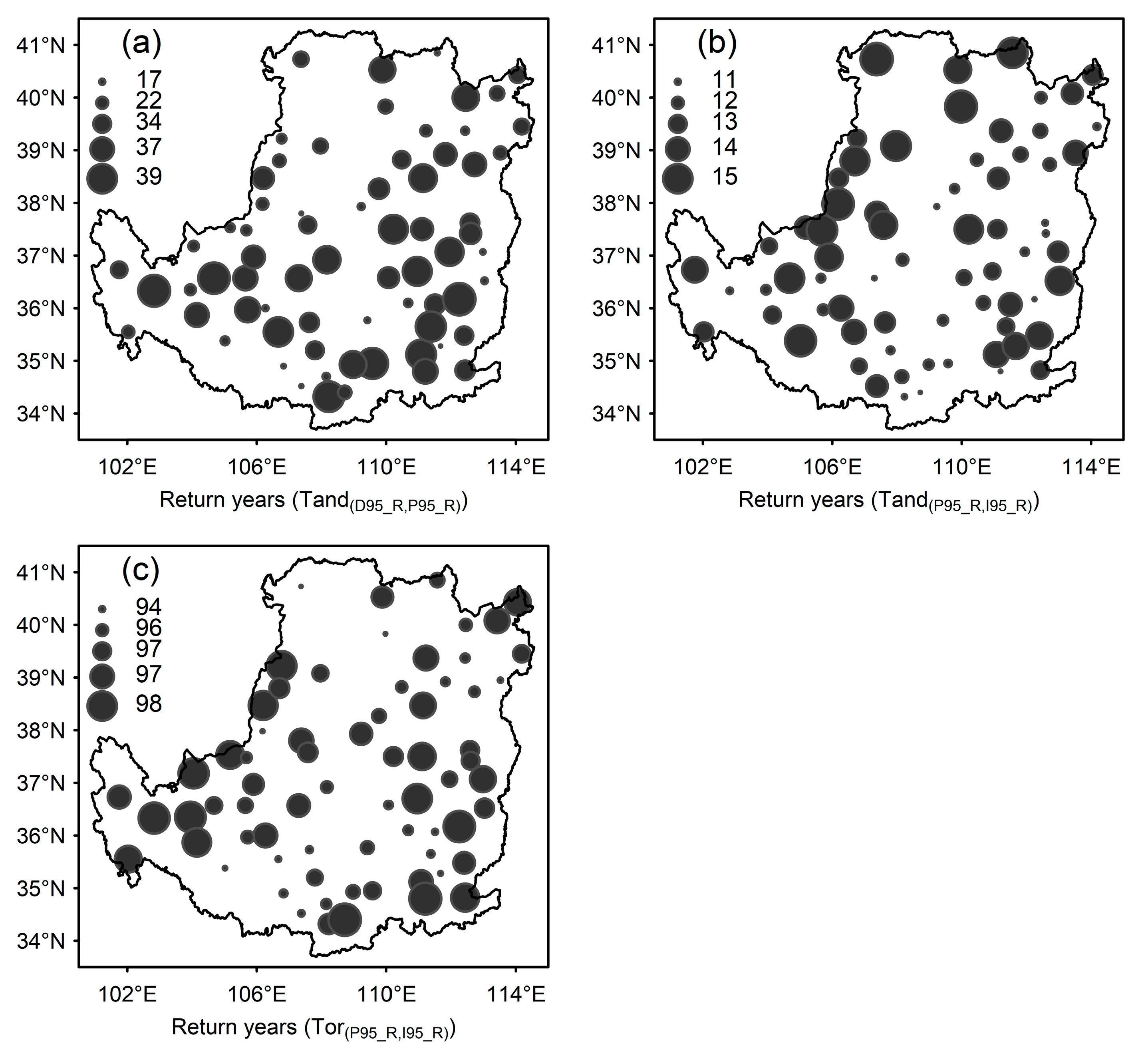
4.2. Bivariate Analysis
5. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Climate Change 2007: The Physical Science Basis; Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007.
- Climate Change 2014: Impacts, Adaptation, and Vulnerability; Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014.
- Emori, S. Dynamic and thermodynamic changes in mean and extreme precipitation under changed climate. Geophys. Res. Lett. 2005, 32, L17706. [Google Scholar] [CrossRef]
- Barros, V.; Stocker, T.F. Managing the risks of extreme events and disasters to advance climate change adaptation: Special report of the Intergovernmental Panel on Climate Change. J. Clin. Microbiol. Metab. 2012, 18, 586–599. [Google Scholar]
- Lu, W.; Qin, X.; Jun, C. A parsimonious framework of evaluating WSUD features in urban flood mitigation. J. Environ. Inf. 2019, 33, 17–27. [Google Scholar] [CrossRef]
- Chang, L.-C.; Chang, F.-J. Intelligent control for modelling of real-time reservoir operation. Hydrol. Process. 2010, 15, 1621–1634. [Google Scholar] [CrossRef]
- Jhong, B.C.; Tung, C.P. Evaluating future joint probability of precipitation extremes with a copula-based assessing approach in climate change. Water Resour. Manag. 2018, 32, 4253–4274. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Wehner, M. Changes in temperature and precipitation extremes in the CMIP5 ensemble. Clim. Chang. 2013, 119, 345–357. [Google Scholar] [CrossRef]
- Caesar, J.; Alexander, L.V.; Trewin, B.; Tse-ring, K.; Sorany, L.; Vuniyayawa, V.; Keosavang, N.; Shimana, A.; Htay, M.M.; Karmacharya, J.; et al. Changes in temperature and precipitation extremes over the Indo-Pacific region from 1971 to 2005. Int. J. Climatol. 2011, 31, 791–801. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Aguilar, E.; Pepin, N.; Flügel, W.-A.; Yan, Y. Changes in daily climate extremes in China and their connection to the large scale atmospheric circulation during 1961–2003. Clim. Dyn. 2011, 36, 2399–2417. [Google Scholar] [CrossRef]
- Zhai, P.; Zhang, X.; Wan, H.; Pan, X. Trends in total precipitation and frequency of daily precipitation extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Wang, C.; Ren, X.; Li, Y. Analysis of extreme precipitation characteristics in low mountain areas based on three-dimensional copulas—Taking Kuandian County as an example. Theo. Appl. Climato. 2017, 128, 169–179. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.D.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major us cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Madadgar, S.; Aghakouchak, A.; Farahmand, A.; Davis, S.J. Probabilistic estimates of drought impacts on agricultural production. Geophys. Res. Lett. 2017, 44, 7799–7807. [Google Scholar] [CrossRef]
- Zhang, D.D.; Yan, D.H.; Lu, F.; Wang, Y.C.; Feng, J. Copula-based risk assessment of drought in Yunnan province, China. Nat. Hazards 2015, 75, 2199–2220. [Google Scholar] [CrossRef]
- Rana, A.; Moradkhani, H.; Qin, Y. Understanding the joint behavior of temperature and precipitation for climate change impact studies. Theo. Appl. Clim. 2016, 129, 1–19. [Google Scholar] [CrossRef]
- Jeong, D.I.; Sushama, L.; Khaliq, M.N.; René, R. A copula-based multivariate analysis of canadian rcm projected changes to flood characteristics for northeastern Canada. Clim. Dyn. 2014, 42, 2045–2066. [Google Scholar] [CrossRef]
- Qian, L.; Wang, H.; Dang, S.; Wang, C.; Jiao, Z.; Zhao, Y. Modelling bivariate extreme precipitation distribution for data-scarce regions using gumbel-hougaard copula with maximum entropy estimation. Hydrol. Process. 2017, 32, 212–227. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Multivariate real-time assessment of droughts via copula-based multi-site hazard trajectories and fans. J. Hydrol. 2015, 526, 101–115. [Google Scholar] [CrossRef]
- Volpi, E.; Fiori, A. Hydraulic structures subject to bivariate hydrological loads: Return period, design, and risk assessment. Water Resour. Res. 2014, 50, 885–897. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, W.W.; Huang, G.H.; Huang, K.; Li, Y.P.; Kong, X.M. Bivariate hydrologic risk analysis based on a coupled entropy-copula method for the Xiangxi River in the Three Gorges Reservoir area, China. Theor. Appl. Clim. 2016, 125, 381–397. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Singh, V.P.; Xu, C.Y. Copula-based spatio-temporal patterns of precipitation extremes in China. Int. J. Clim. 2013, 33, 1140–1152. [Google Scholar] [CrossRef]
- Goswami, U.P.; Hazra, B.; Kumar, G.M. Copula-based probabilistic characterization of precipitation extremes over north sikkim himalaya. Atmos. Res. 2018, 212, 273–284. [Google Scholar] [CrossRef]
- Wang, L.; Cheung, K.K.W.; Chi-Yung, T.; Tai, A.P.K.; Li, Y. Evaluation of the regional climate model over the loess plateau of China. Int. J. Climatol. 2018, 38, 35–54. [Google Scholar] [CrossRef]
- Xin, Z.; Yu, X.; Li, Q.; Lu, X.X. Spatiotemporal variation in rainfall erosivity on the Chinese loess plateau during the period 1956–2008. Regional Environ. Chang. 2011, 11, 149–159. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z. Quantitative estimation of the impact of climate change on actual evapotranspiration in the yellow river basin, China. J. Hydrol. 2010, 395, 226–234. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.L.; Liu, W.Z.; Jiang, D.J. Spatially downscaling gcms outputs to project changes in extreme precipitation and temperature events on the loess plateau of China during the 21st century. Global Planet. Chang. 2012, 82, 0–73. [Google Scholar] [CrossRef]
- Nolan, S.; Unkovich, M.; Yuying, S.; Lingling, L.; Bellotti, W. Farming systems of the loess plateau, Gansu province, China. Agric. Ecosyst. Environ. 2008, 124, 13–23. [Google Scholar] [CrossRef]
- Liang, W.; Bai, D.; Wang, F.; Fu, B.; Yan, J.; Wang, S.; Yang, Y.; Long, D.; Feng, M. Quantifying the impacts of climate change and ecological restoration on streamflow changes based on a budyko hydrological model in China’s Loess Plateau. Water Resour. Res. 2015, 51, 6500–6519. [Google Scholar] [CrossRef]
- Wang, X.L. Accounting for autocorrelation in detecting mean shifts in climate data series using the penalized maximal t or f test. J. Appl. Meteorol. Climatol. 2008, 47, 2423–2444. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Peng, S.; Zhang, Z.; Xing, W.; An, G.; Yong, B. Spatial and temporal characteristics of changes in precipitation during 1957–2007 in the haihe river basin, China. Stochastic Environ. Res. Risk Assess. 2011, 25, 881–895. [Google Scholar] [CrossRef]
- Sun, C.X.; Huang, G.H.; Fan, Y.; Zhou, X.; Lu, C.; Wang, X.Q. Drought occurring with hot extremes: Changes under future climate change on Loess Plateau, China. Earth’s Future 2019, 7, 587–604. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Gringorten, I.I. A plotting rule for extreme probability paper. J. Geophys. Res. 1963, 68, 813–814. [Google Scholar] [CrossRef]
- Sklar, K. Fonctions dé repartition á n dimensions et leurs marges. Publications de l’Institut de Statistique de l’Universite dé Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Sraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: A case study of the litija station on the sava river. Hydrol. Process. 2015, 29, 225–238. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, G.; Wang, X.; Fan, Y.; Cheng, G. A coupled dynamical-copula downscaling approach for temperature projections over the canadian prairies. Clim. Dyn. 2018, 51, 2413–2431. [Google Scholar] [CrossRef]
- Salvadori, G.; de Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40, 1–17. [Google Scholar] [CrossRef]
- Egrioglu, E.; Aladag, C.; Basaran, M. A new approach based on the optimization of the length of intervals in fuzzy time series. J. Intell. Fuzzy Syst. 2011, 22, 15–19. [Google Scholar] [CrossRef]
- Bürger, G.; Murdock, T.Q.; Werner, A.T.; Sobie, S.R.; Cannon, A.J. Downscaling Extremes—An Intercomparison of Multiple Statistical Methods for Present Climate. J. Clim. 2012, 2, 4366–4388. [Google Scholar]
- Shivam, G.; Goyal, M.K.; Sarma, A.K. Index-based study of future precipitation changes over subansiri river catchment under changing climate. J. Environ. Inf. 2019, 34, 1–14. [Google Scholar] [CrossRef]

| Indices | Abbreviations | Definitions | Unit |
|---|---|---|---|
| PRTOT | PRTOT | The amount of annual total precipitation | mm |
| Number of extreme heavy precipitation days | D95 | Number of days with precipitation exceeding the 95th percentile of precipitation series (daily precipitation ≥1 mm) during 1971–2000. | days |
| The amount of extreme heavy precipitation | P95 | Annual total amount of precipitation with daily precipitation exceeding the 95th percentile of precipitation series during 1971–2000 | mm |
| The intensity of extreme heavy precipitation | I95 | Mean daily precipitation intensity of extreme heavy precipitation | mm/day |
| Consecutive dry days | CDD | Maximum number of consecutive dry days (days with precipitation <1 mm) | days |
| Indices | Marginal Distribution | a | b | α | K-S Test | RMSE | AIC | |
|---|---|---|---|---|---|---|---|---|
| T | p value | |||||||
| PRTOT | LP III | 118.81 | 44.46 | 3.52 | 0.10 | 0.63 | 0.0458 | −339.14 |
| D95 | GEV | 0.11 | 1.52 | 2.38 | 0.17 | 0.10 | 0.0655 | −299.34 |
| P95 | LP III | 26.73 | 8.47 | 1.53 | 0.05 | 0.99 | 0.0194 | −435.49 |
| I95 | LP III | 163.79 | 72.20 | 1.31 | 0.11 | 0.53 | 0.0485 | −332.81 |
| CDD | Gamma | 7.59 | 0.16 | 0.05 | 0.99 | 0.0521 | −471.51 | |
| ID | Combinations | Return Periods (years) | Variables (X, Y) |
|---|---|---|---|
| 1 | {PRTOT_L, CDD_R} | T{X ≤ x and Y > y} | PRTOT, CDD |
| 2 | {PRTOT_R, CDD_R} | T{X > x and Y > y} | PRTOT, CDD |
| 3 | {D95_R, P95_R} | T{X > x and Y > y} | D95, P95 |
| 4 | {P95_R, I95_R} | T{X > x and Y > y} | P95, I95 |
| 5 | {P95_R or I95_R} | T{X > x or Y > y} | P95, I95 |
| 6 | {P95_R, CDD_R} | T{X > x and Y > y} | P95, CDD |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Huang, G.; Fan, Y. Multi-Indicator Evaluation for Extreme Precipitation Events in the Past 60 Years over the Loess Plateau. Water 2020, 12, 193. https://doi.org/10.3390/w12010193
Sun C, Huang G, Fan Y. Multi-Indicator Evaluation for Extreme Precipitation Events in the Past 60 Years over the Loess Plateau. Water. 2020; 12(1):193. https://doi.org/10.3390/w12010193
Chicago/Turabian StyleSun, Chaoxing, Guohe Huang, and Yurui Fan. 2020. "Multi-Indicator Evaluation for Extreme Precipitation Events in the Past 60 Years over the Loess Plateau" Water 12, no. 1: 193. https://doi.org/10.3390/w12010193
APA StyleSun, C., Huang, G., & Fan, Y. (2020). Multi-Indicator Evaluation for Extreme Precipitation Events in the Past 60 Years over the Loess Plateau. Water, 12(1), 193. https://doi.org/10.3390/w12010193






