A Clustered, Decentralized Approach to Urban Water Management
Abstract
1. Introduction
2. Methods
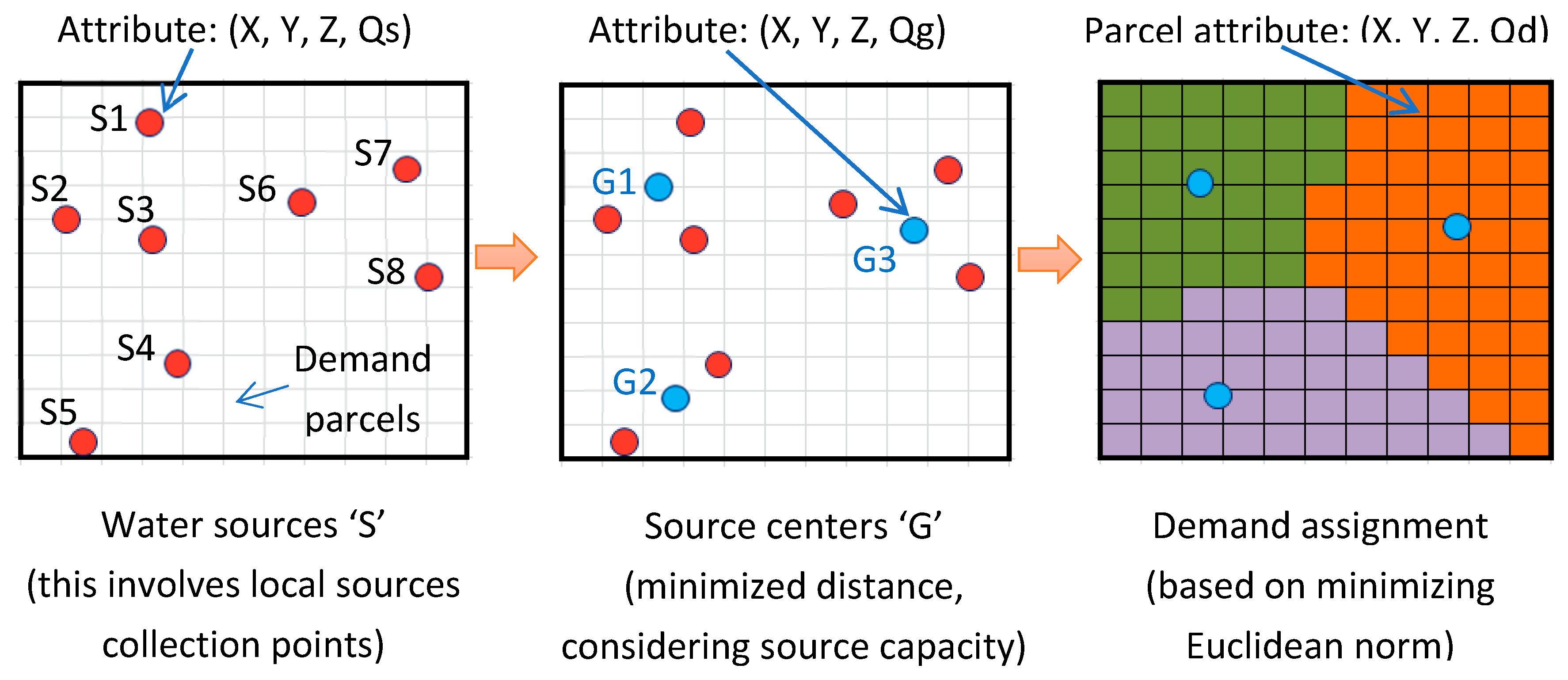
2.1. Proposed Water Supply System Clustering Method
2.2. Source-Demand Distance
2.3. Intra-Cluster Demand and Topographic Homogeneity
2.4. Minimization of Source-Demand Distance
2.5. Identification of Source Centers: Water Source Clustering
2.6. Assignment of Demand Parcel to the Nearest Source
2.7. Maximization Intra-Cluster Homogeneity and Connectivity
2.8. K-means for Clustering WSS
2.9. Intra-Cluster Parcels Connectivity
3. Results of Cluster Analysis Application to Arua, Uganda
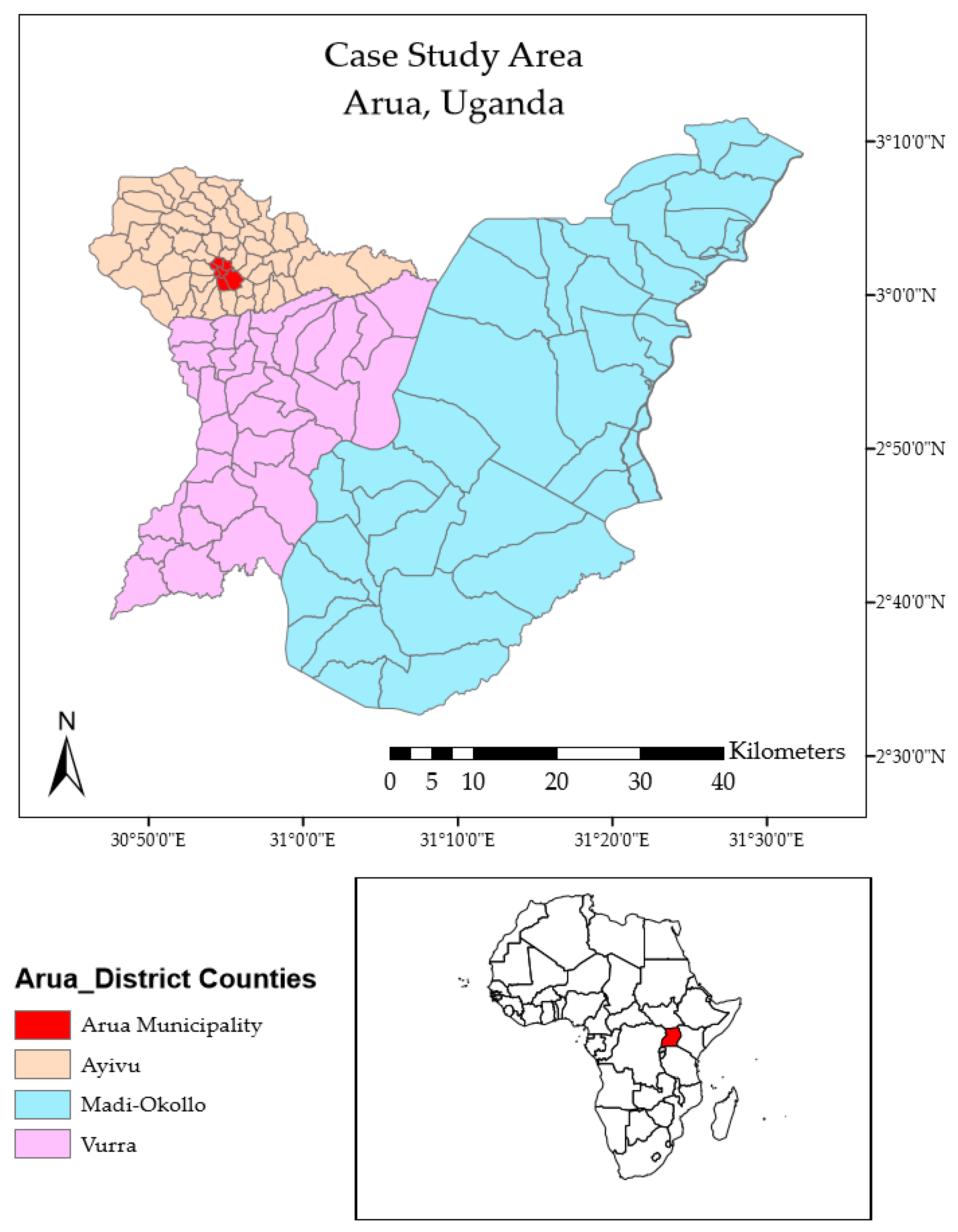
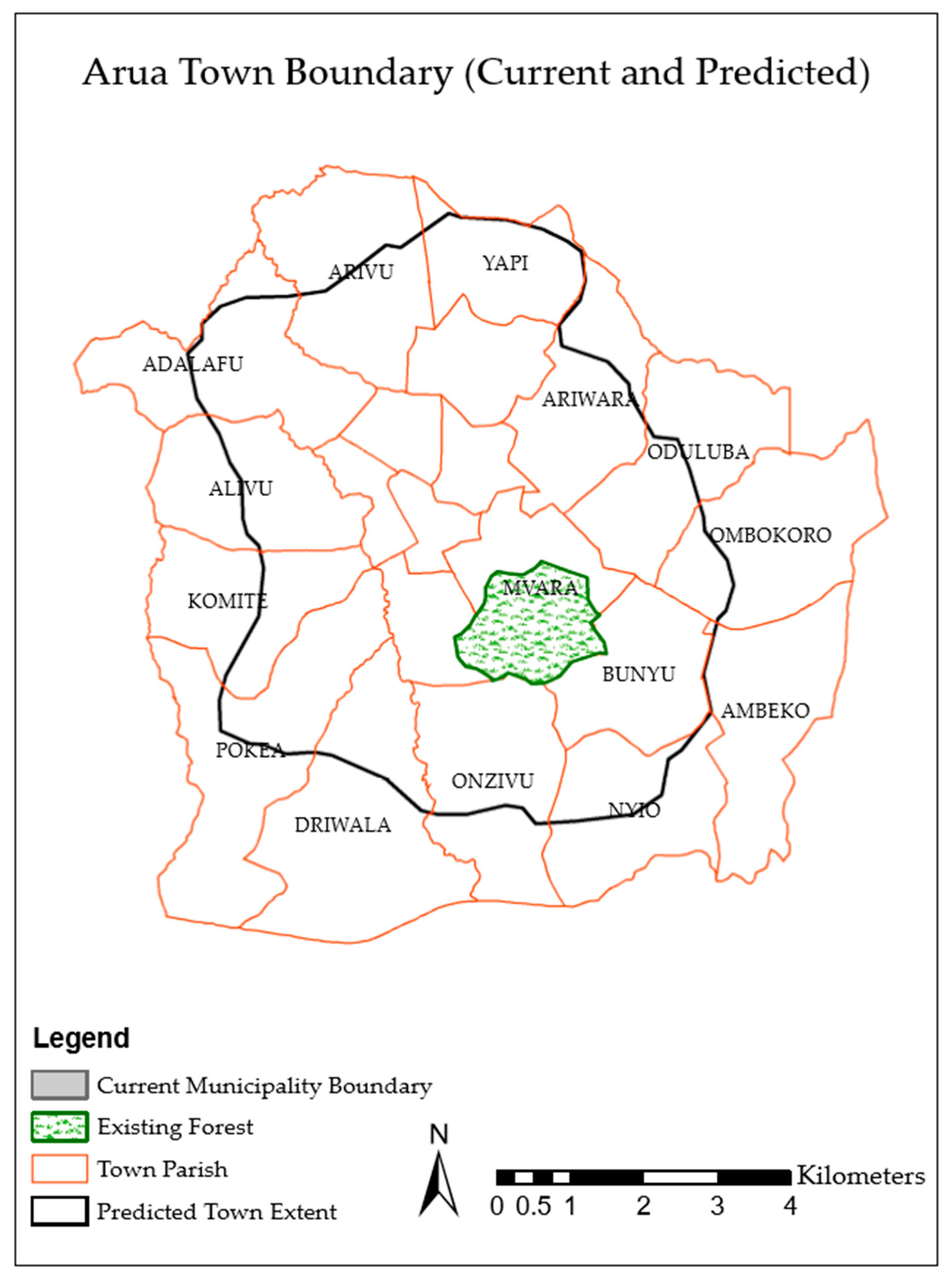
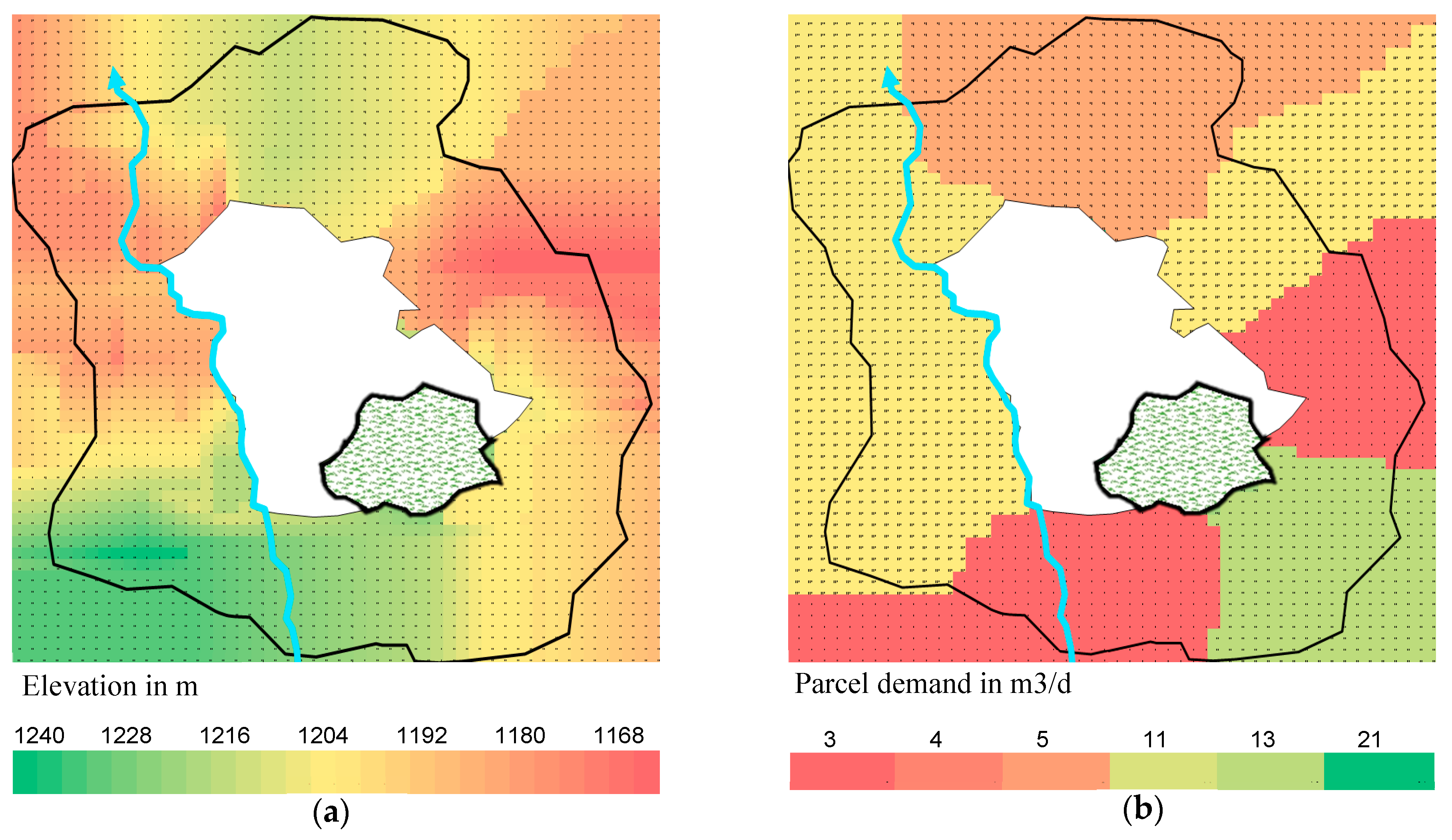
3.1. General Description of the Area
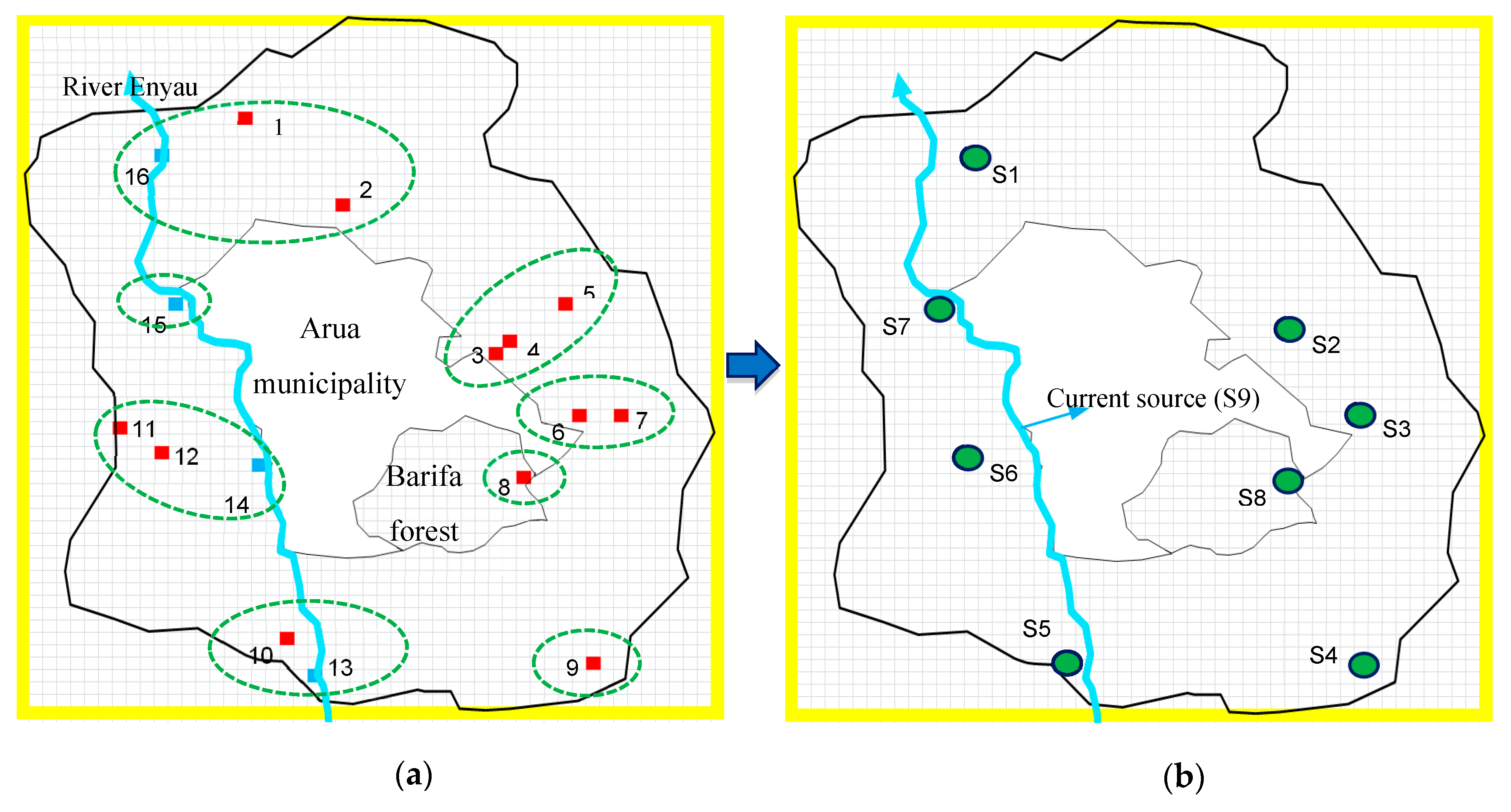
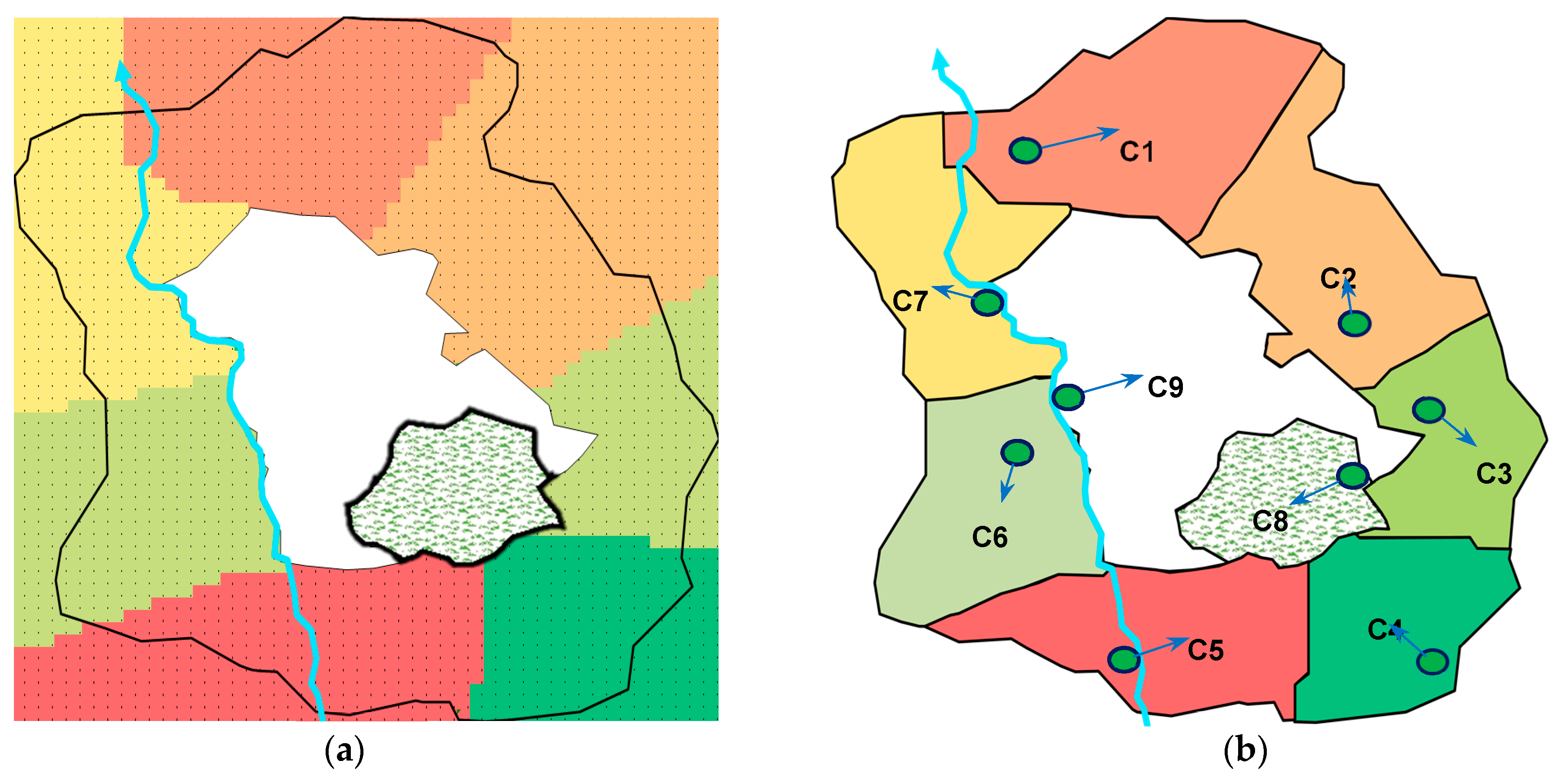
3.2. Application of the Proposed Clustering Method and Results
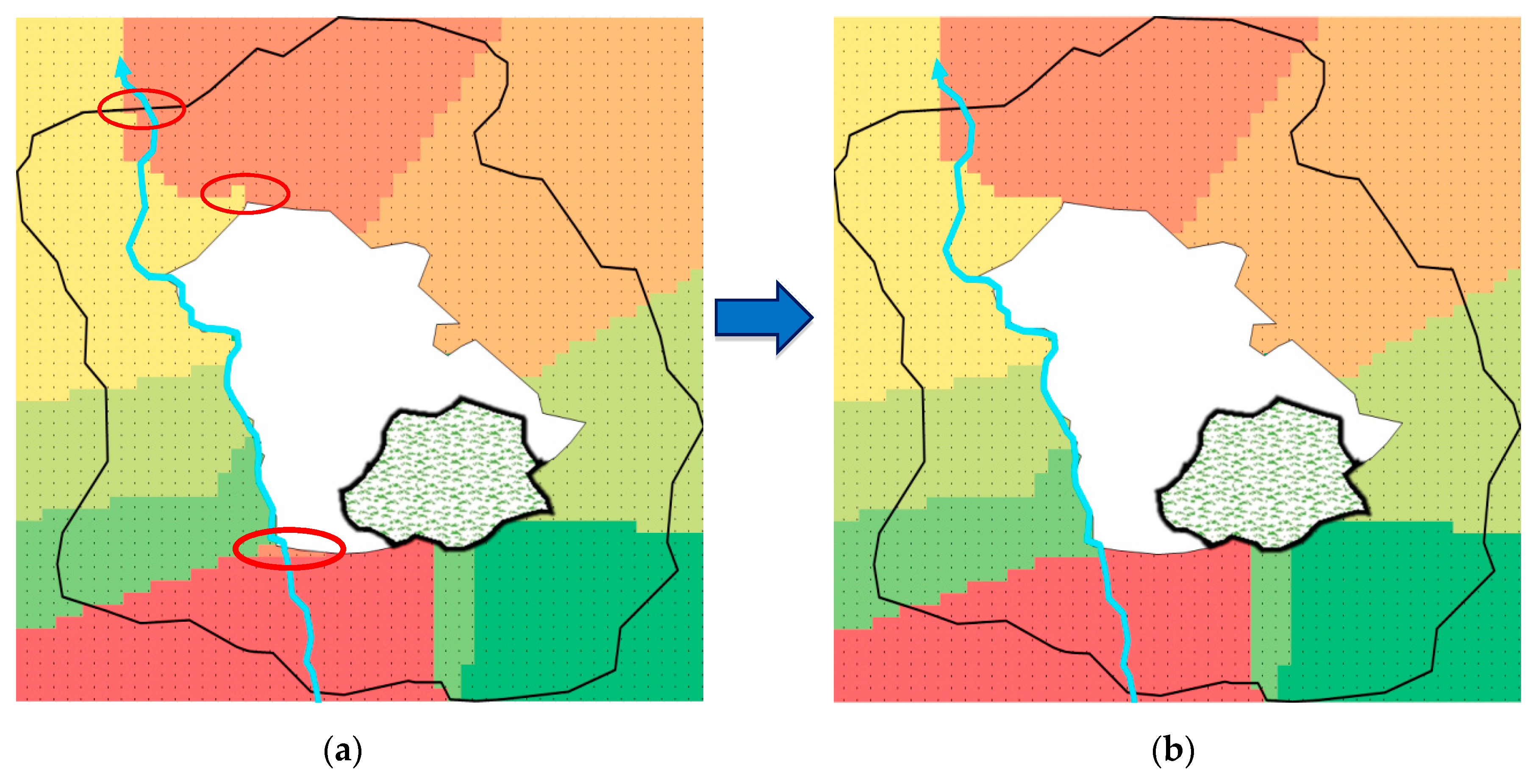
3.3. Source-Demand Distance minimization
3.4. Maximizing Homogeneity and Connectivity Analysis
4. Discussion
4.1. Performance Analysis
4.2. Method for Power Usage Analysis
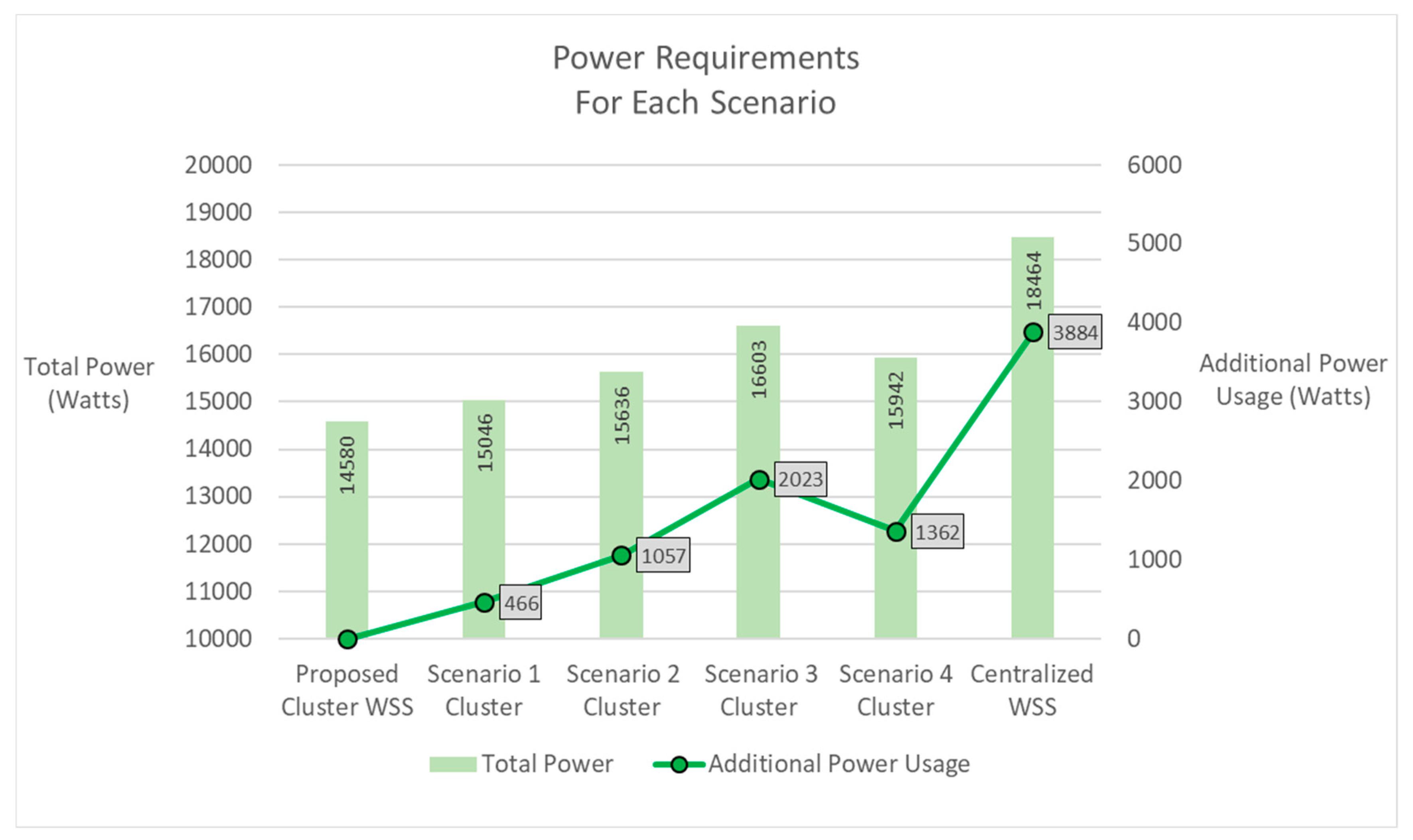
4.3. Power Usage-Scenario Analysis
4.4. Water Security and Resiliency
4.5. Future Research
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- United Nations Educational, Scientific and Cultural Organization (UNESCO). Water A Shared Responsibility: The United Nations World Water Development Report 2; Berghahn Books: New York, NY, USA, 2006. [Google Scholar]
- Poplak, R. What’s Actually behind Cape Town’s Water Crisis. The Atlantic. 15 February 2018. Available online: https://www.theatlantic.com/international/archive/2018/02/cape-town-water-crisis/553076/ (accessed on 13 August 2019).
- Masih, N.; Slater, J. As A Major Indian City Runs Out of Water, 9 Million People Pray for Rain. The Washington Post. 28 June 2019. Available online: https://www.washingtonpost.com/world/2019/06/28/major-indian-city-runs-out-water-million-people-pray-rain/?noredirect=on (accessed on 13 August 2019).
- Bairoch, P.; Goertz, G. Factors of urbanisation in the nineteenth century developed countries: A descriptive and economic analysis. Urban Stud. 1986, 23, 285–305. [Google Scholar] [CrossRef]
- Webster, M.; Jacobsen, M.; Vairavamoorthy, K. The Future of Water in African Cities: Why Waste Water; International Bank for Reconstruction and Development/International Development Association (World Bank): Washington, DC, USA, 2012. [Google Scholar]
- Valerie, N. New Approach in Decentralized Water Infrastructure; Coalition of Alternative Wastewater Treatment: Gloucester, MA, USA, 2008; Available online: https://www.csu.edu/cerc/researchreports/documents/NewApproachesInDecentralizedWaterInfrastructure2008.pdf (accessed on 14 August 2019).
- Grigg, N.S. Total Water Management: Practices for a Sustainable Future; American Water Works Association: Denver, CO, USA, 2008. [Google Scholar]
- Bieker, S.; Cornel, P.; Wagner, M. Semicentralised supply and treatment systems: Integrated infrastructure solutions for fast growing urban areas. Water Sci. Technol. 2010, 61, 2905–2913. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Wang, X. Cost-benefit evaluation of a decentralized water system for wastewater reuse and environmental protection. Water Sci. Technol. 2009, 59, 1515–1522. [Google Scholar] [CrossRef] [PubMed]
- Verstraete, W.; Van de Caveye, P.; Diamantis, V. Maximum use of resources present in domestic “used water”. Bioresour. Technol. 2009, 100, 5537–5545. [Google Scholar] [CrossRef] [PubMed]
- Newman, P. Sustainable urban water systems in rich and poor cities--steps towards a new approach. Water Sci. Technol. 2001, 43, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Cornel, P.; Meda, A.; Bieker, S. Wastewater as a source of energy, nutrients and service water. Treatise Water Sci. 2011, 3, 92. [Google Scholar]
- Kluge, T.; Libbe, J. Transformation of Network Infrastructure–Strategies for Communities: The Example Water; Difu-Beitrage zur Stadtforschung: Berlin, Germany, 2006. [Google Scholar]
- Böhm, H.R.; Schramm, S.; Bieker, S.; Zeig, C.; Anh, T.H.; Thanh, N.C. The semicentralized approach to integrated water supply and treatment of solid waste and wastewater—A flexible infrastructure strategy for rapidly growing urban regions: The case of Hanoi/Vietnam. Clean Technol. Environ. Policy 2011, 13, 617–623. [Google Scholar] [CrossRef]
- Weber, B.; Cornel, P.; Wagner, M. Semi-centralized supply and treatment systems for (fast growing) urban areas. Water Sci. Technol. 2007, 55, 349–356. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chen, R.; Zhang, Q.; Li, K. Optimized plan of centralized and decentralized wastewater reuse systems for housing development in the urban area of Xi’an, China. Water Sci. Technol. 2008, 58, 969–975. [Google Scholar] [CrossRef] [PubMed]
- Tsegaye, S.; Eckart, J.; Vairavamoorthy, K. Urban water management in cities of the future: Emerging areas in developing countries. In On the Water Front; Lundqvist, J., Ed.; SIWI: Stockholm, Sweden, 2012; pp. 42–48. [Google Scholar]
- Maliva, R.G.; Missimer, T.M. Aquifer Storage and Recovery and Managed Aquifer Recharge Using Wells: Planning, Hydrogeology, Design, and Operation; Schlumberger: Houston, TX, USA, 2010. [Google Scholar]
- GAUFF Consulting Engineers. Arua Emergency Water Supply Project: Inception Report. GAUFF Consulting Engineers. 2011. Available online: http://www.amk.rwth-aachen.de/uploads/media/RECLAIM_WATER_ Publishable_Final_Activity_Report.pdf (accessed on 15 July 2012).
- Herrera, M.; Canu, S.; Karatzoglou, A.; Perez-García, R.; Izquierdo, J. An approach to water supply clusters by semi-supervised learning. In Proceedings of the International Congress on Environmental Modelling and Software 190, Ottawa, ON, Canada, 5–8 July 2010. [Google Scholar]
- Puust, R.; Kapelan, Z.; Savic, D.A.; Koppel, T. A review of methods for leakage management in pipe networks. Urban Water J. 2010, 7, 25–45. [Google Scholar] [CrossRef]
- Wang, Y.; Zayed, T.; Moselhi, O. Prediction models for annual break rates of water mains. J. Perform. Constr. Facil. 2009, 23, 47–54. [Google Scholar] [CrossRef]
- Celebi, M.E.; Celiker, F.; Kingravi, H.A. On Euclidean norm approximations. Pattern Recognit. 2010, 44, 278–283. [Google Scholar] [CrossRef]
- Barni, M.; Bartolini, F.; Buti, F.; Cappellini, V. Optimum linear approximation of the Euclidean norm to speed up vector median filtering. In Proceedings of the 2nd IEEE International Conference on Image Processing (ICIP’95), Washington, DC, USA, 23–26 October 1995. [Google Scholar]
- BMBF. Final report of Sino-German Research Project. In Semicentralized Supply and Disposal Systems for Fast Growing Urban Regions in China; German Federal Ministry of Science and Technology: Berlin, Germany, 2006. [Google Scholar]
- Andersen, K.D.; Christiansen, E.; Conn, A.R.; Overton, M.L. An efficient primal-dual interior-point method for minimizing a sum of Euclidean norms. SIAM J. Sci. Comput. 2000, 22, 243–262. [Google Scholar] [CrossRef]
- Dopp, K.A.; Godfrey, N. Legislative Redistricting-Compactness and Population Density Fairness. 2011. Available online: https://ssrn.com/abstract=1945879 or http://dx.doi.org/10.2139/ssrn.1945879 (accessed on 14 August 2019).
- D’Agostino, M.; Dardanoni, V. What’s so special about Euclidean distance? Soc. Choice Welf. 2009, 33, 211–233. [Google Scholar] [CrossRef]
- Singh, K.; Malik, D.; Sharma, N. Evolving limitations in K-means algorithm in data mining and their removal. Int. J. Comput. Eng. Manag. 2011, 12, 105–109. [Google Scholar]
- Al-Saleh, M.F.; Yousif, A.E. Properties of the standard deviation that are rarely mentioned in classrooms. Aust. J. Stat. 2009, 38, 193–202. [Google Scholar] [CrossRef]
- Uganda Bureau of Statistics (UBOS). Mid-Year Projected Population for Town Councils; Uganda Bureau of Statistics (UBOS): Kampala, Uganda, 2011. [Google Scholar]
- COWATER. District Town Sewerage, Sanitation Feasibility Study: Arua Master Plan, National; Water and Sewerage Corporation: Arua, Uganda, 2005. [Google Scholar]
- Jung, Y.T.; Narayanan, N.C.; Cheng, Y.-L. Cost comparison of centralized and decentralized wastewater management systems using optimization model. J. Environ. Manag. 2018, 213, 90–97. [Google Scholar] [CrossRef] [PubMed]
- Hunter. The Handbook of Technical Irrigation Information. A Complete Reference Source for the Professional. 2015. Available online: https://www.hunterindustries.com/sites/default/files/tech_handbook_of_technical_irrigation_information.pdf (accessed on 30 August 2019).
- UMEME. The Electricity End-User Retail Base Tariffs for 2019 as Set and Announced by The Electricity Regulatory Authority; UMEME: Kampala, Uganda, 2018. [Google Scholar]
- Marlow, D.R.; Moglia, M.; Cook, S.; Beale, D.J. Towards sustainable urban water management: A critical reassessment. Water Res. 2013, 47, 7150–7161. [Google Scholar] [CrossRef] [PubMed]
- Sapkota, M.; Arora, M.; Malano, H.; Moglia, M.; Sharma, A.; George, B.; Pamminger, F. An overview of hybrid water supply systems in the context of urban water management: Challenges and opportunities. Water 2015, 7, 153–174. [Google Scholar] [CrossRef]
- Werbeloff, L.; Brown, R. Working towards sustainable urban water management: The vulnerability blind spot. Water Sci. Technol. 2011, 64, 2362–2369. [Google Scholar] [CrossRef] [PubMed]




| Source Group | Source no. | Water Source-Center Location | |
|---|---|---|---|
| X (m) | Y (m) | ||
| 1 | 1 | 1992 | 6772 |
| 2 | |||
| 16 | |||
| 2 | 3 | 5461 | 4650 |
| 4 | |||
| 5 | |||
| 3 | 6 | 6181 | 3600 |
| 7 | |||
| 4 | 9 | 6150 | 600 |
| 5 | 10 | 3110 | 510 |
| 13 | |||
| 6 | 11 | 2062 | 3108 |
| 12 | |||
| 14 | |||
| 7 | 15 | 1650 | 4950 |
| Forest (8) | 8 | 5400 | 2850 |
| Municipality (9) | 2400 | 3150 | |
| Proposed Cluster WSS | Scenario 1 Cluster | Scenario 2 Cluster | Scenario 3 Cluster | Scenario 4 Cluster | Centralized WSS | |
|---|---|---|---|---|---|---|
| Cluster Number | Power Per Cluster (W) | Power Per Cluster (W) | Power Per Cluster (W) | Power Per Cluster (W) | Power Per Cluster (W) | Power for Centralized (W) |
| 1 | 852.14 | 804.53 | 739.50 | 934.16 | 956.58 | 18,463.78 |
| 2 | 2967.08 | 3497.88 | 3990.10 | 4420.44 | 4742.18 | |
| 3 | 1154.50 | 971.45 | 820.32 | 868.80 | 941.99 | |
| 4 | 4597.13 | 4296.83 | 4435.66 | 4472.43 | 2986.95 | |
| 5 | 460.32 | 398.16 | 366.06 | 526.45 | 587.94 | |
| 6 | 4545.88 | 5074.51 | 5183.64 | 5124.28 | 5089.55 | |
| 7 | 2.46 | 2.38 | 101.09 | 256.46 | 636.46 | |
| Total Power | 14,579.51 | 15,045.74 | 15,636.38 | 16,603.01 | 15,941.65 | 18,463.78 |
| Additional Power Usage | 0.00 | 466.23 | 1056.87 | 2023.50 | 1362.14 | 3884.27 |
| US$ Per Year | $23,659 | $24,416 | $25,374 | $26,943 | $25,870 | $29,962 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsegaye, S.; Missimer, T.M.; Kim, J.-Y.; Hock, J. A Clustered, Decentralized Approach to Urban Water Management. Water 2020, 12, 185. https://doi.org/10.3390/w12010185
Tsegaye S, Missimer TM, Kim J-Y, Hock J. A Clustered, Decentralized Approach to Urban Water Management. Water. 2020; 12(1):185. https://doi.org/10.3390/w12010185
Chicago/Turabian StyleTsegaye, Seneshaw, Thomas M. Missimer, Jong-Yeop Kim, and Jason Hock. 2020. "A Clustered, Decentralized Approach to Urban Water Management" Water 12, no. 1: 185. https://doi.org/10.3390/w12010185
APA StyleTsegaye, S., Missimer, T. M., Kim, J.-Y., & Hock, J. (2020). A Clustered, Decentralized Approach to Urban Water Management. Water, 12(1), 185. https://doi.org/10.3390/w12010185






