Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation
Abstract
1. Introduction
2. Study Area and Data Source
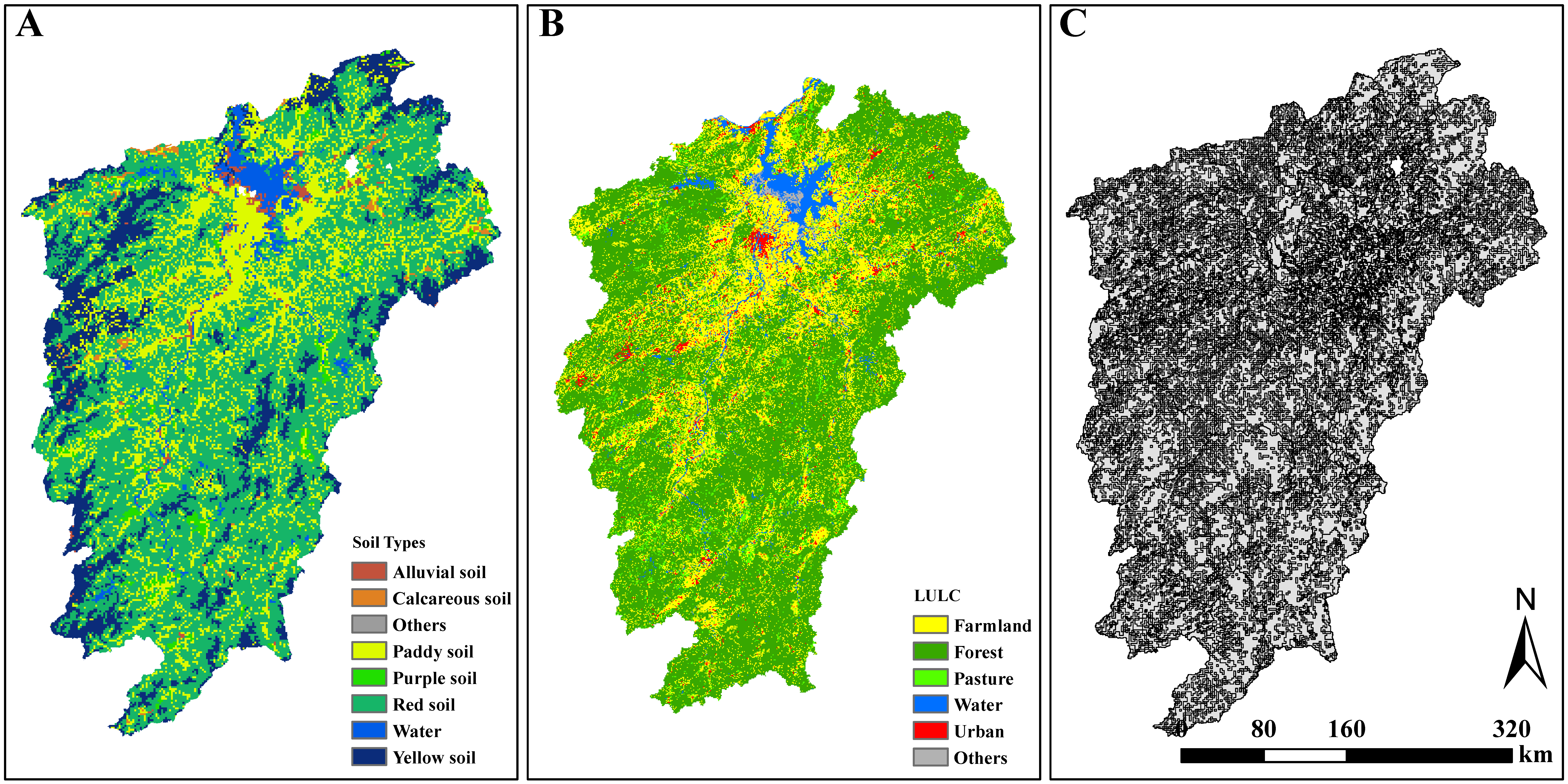
2.1. Study Area
2.2. Data Source
2.3. Data Pre-Processing
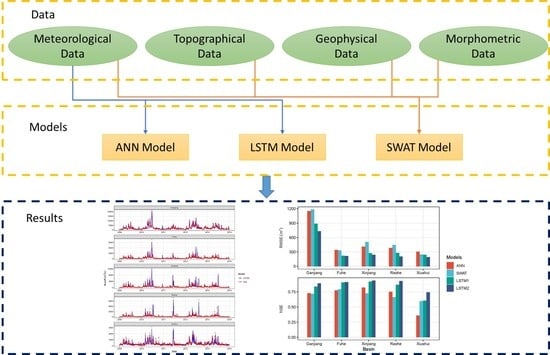
3. Methodology
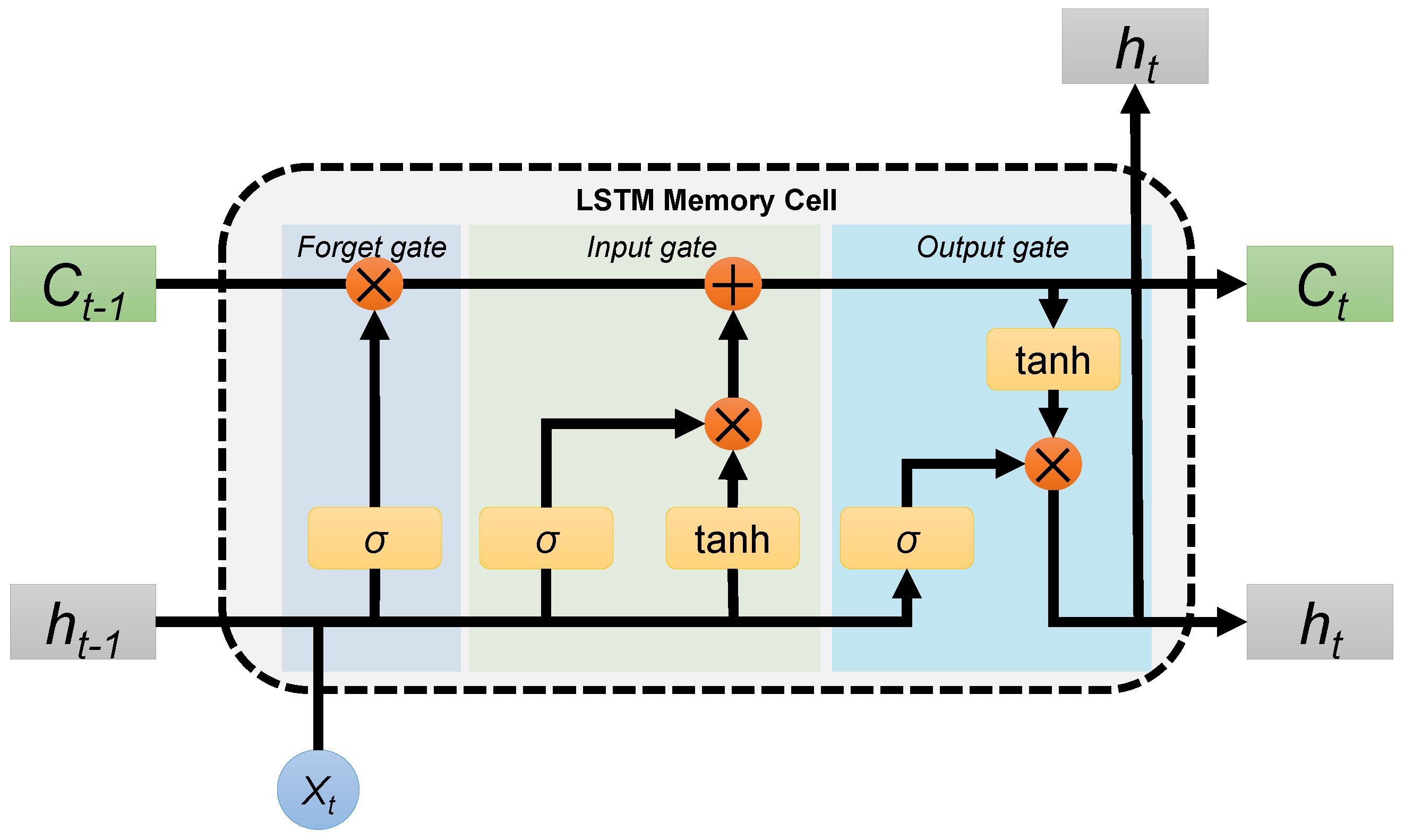
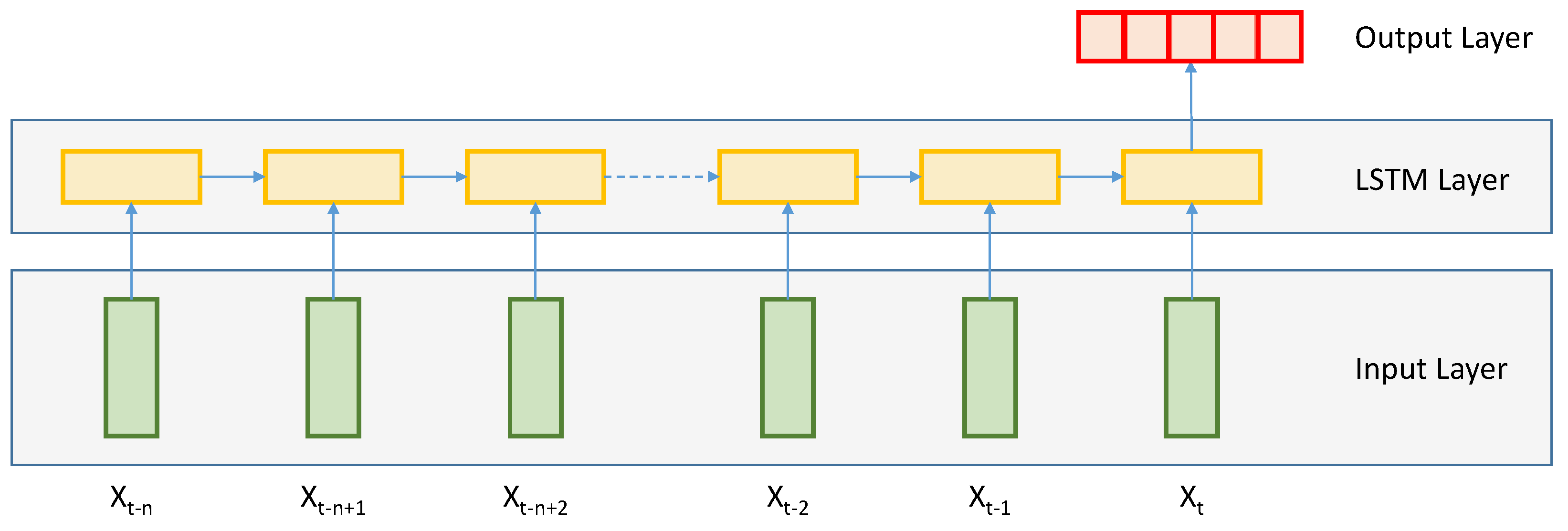
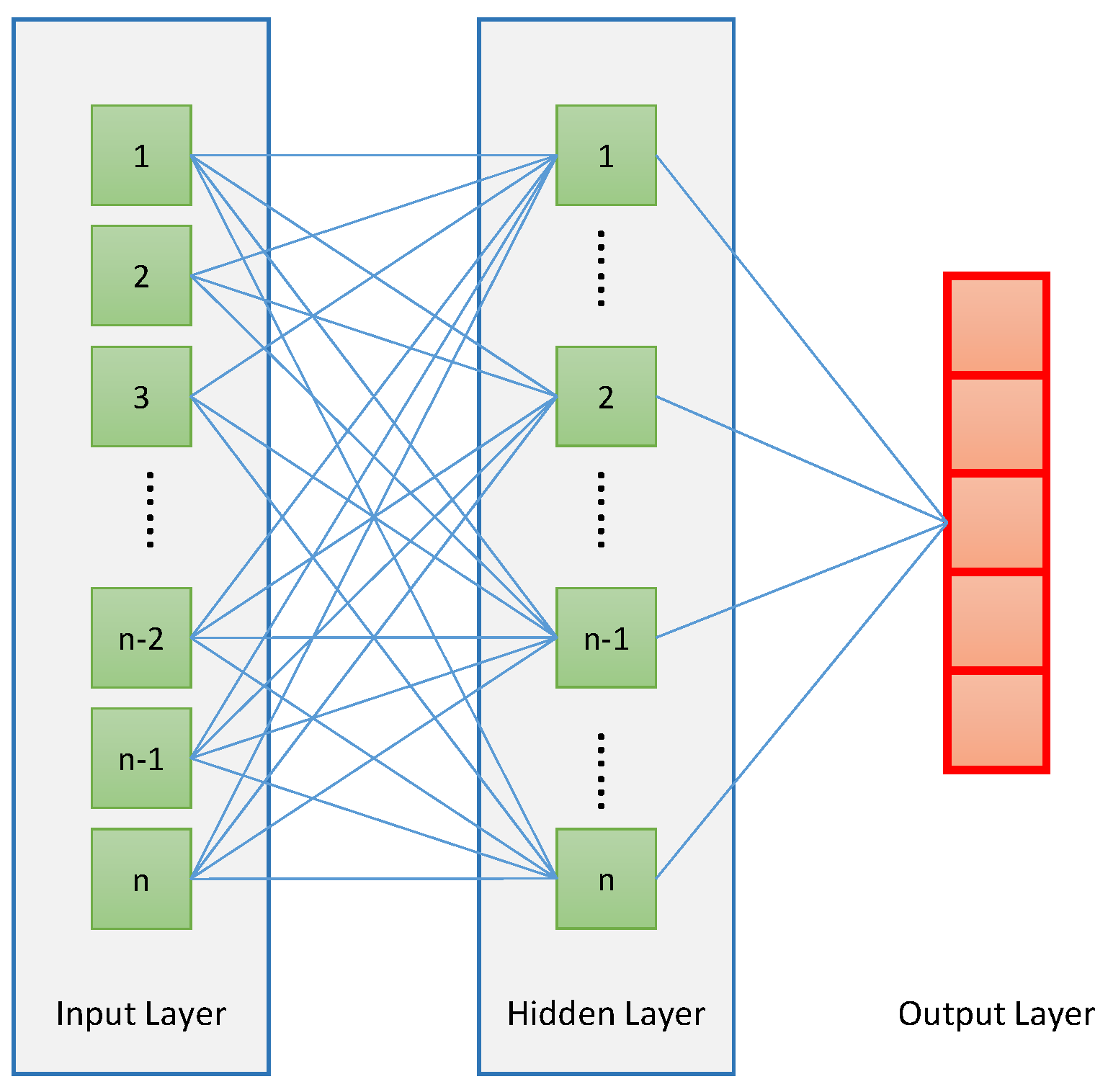
3.1. Long Short Term Memory Network
3.2. LSTM Setup
3.3. ANN Setup
3.4. Tuning Procedure for LSTM
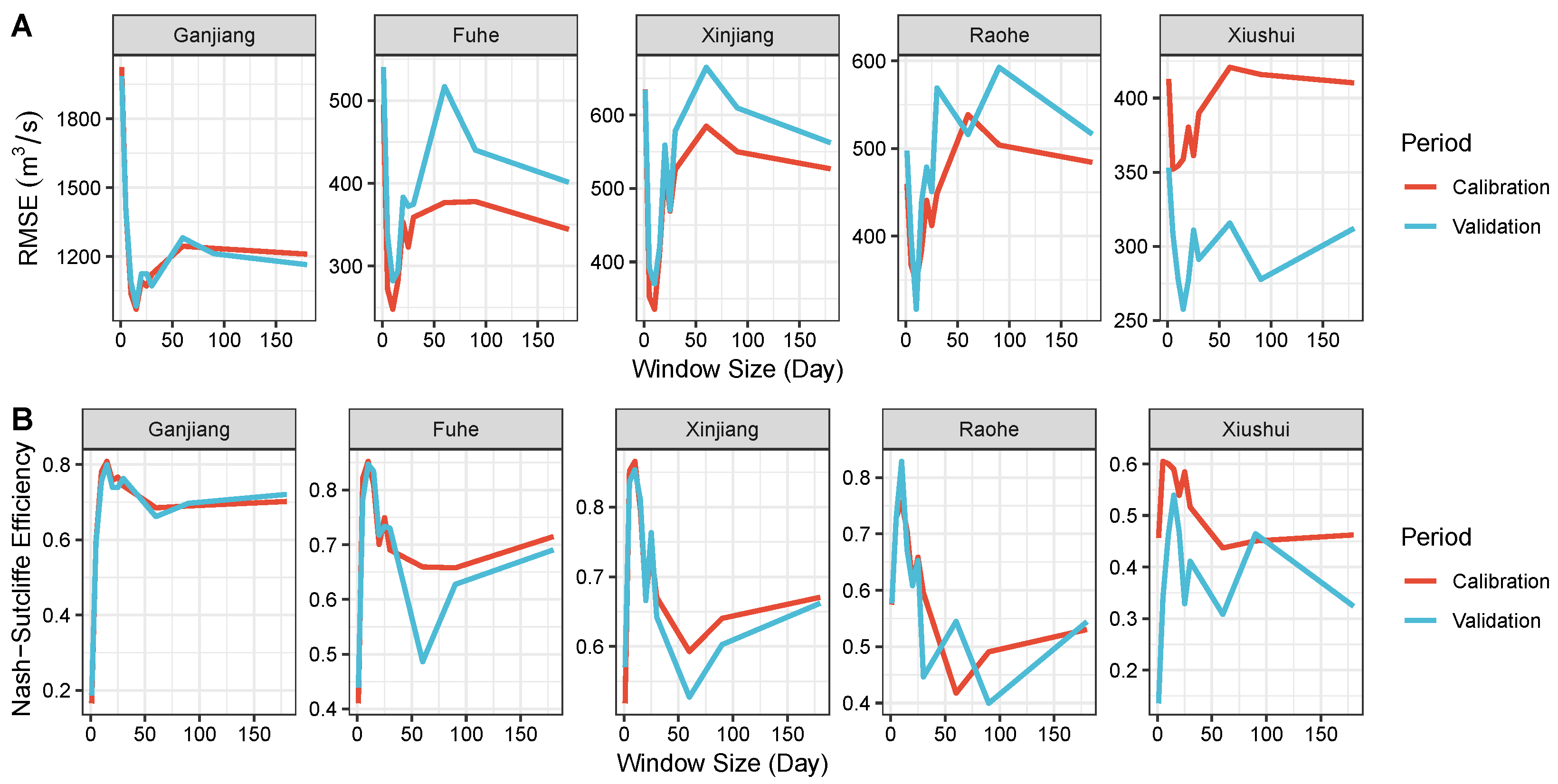
3.4.1. Tuning for Window Size
3.4.2. Tuning for Hyperparameters
3.5. Evaluation Metrics
3.6. Hydrological Model
4. Results
4.1. Effect of the Window Size
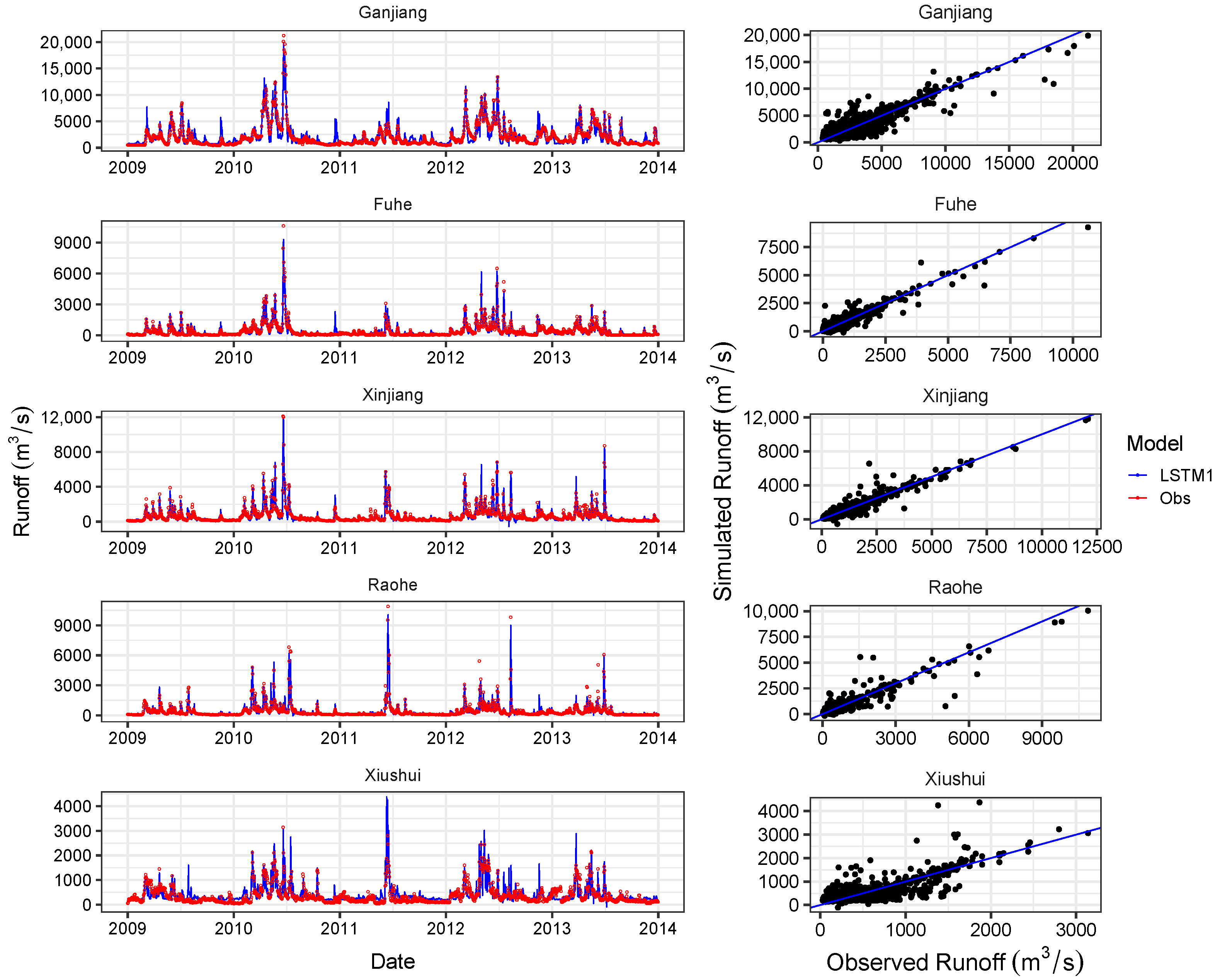
4.2. Overall Performance of LSTMs
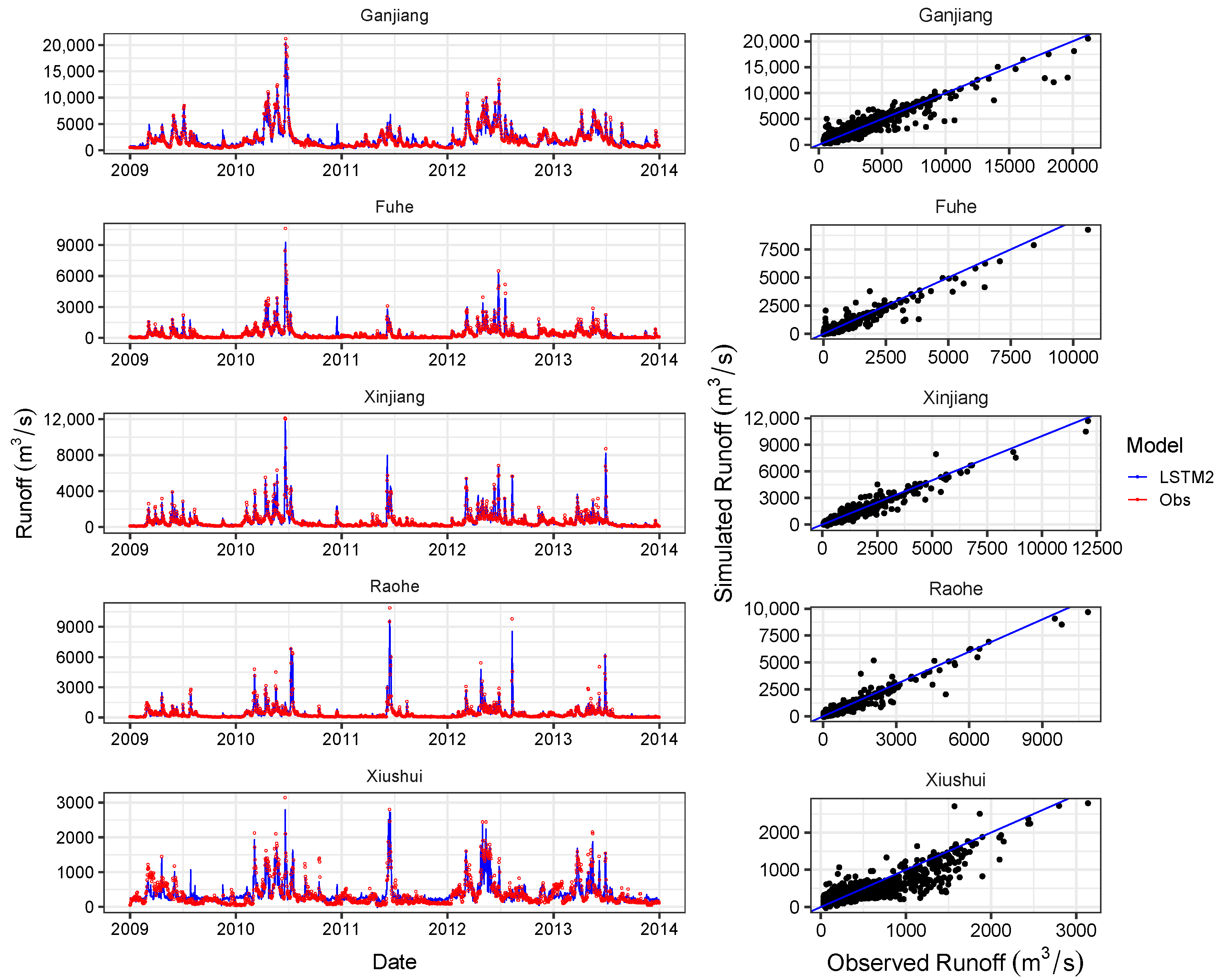
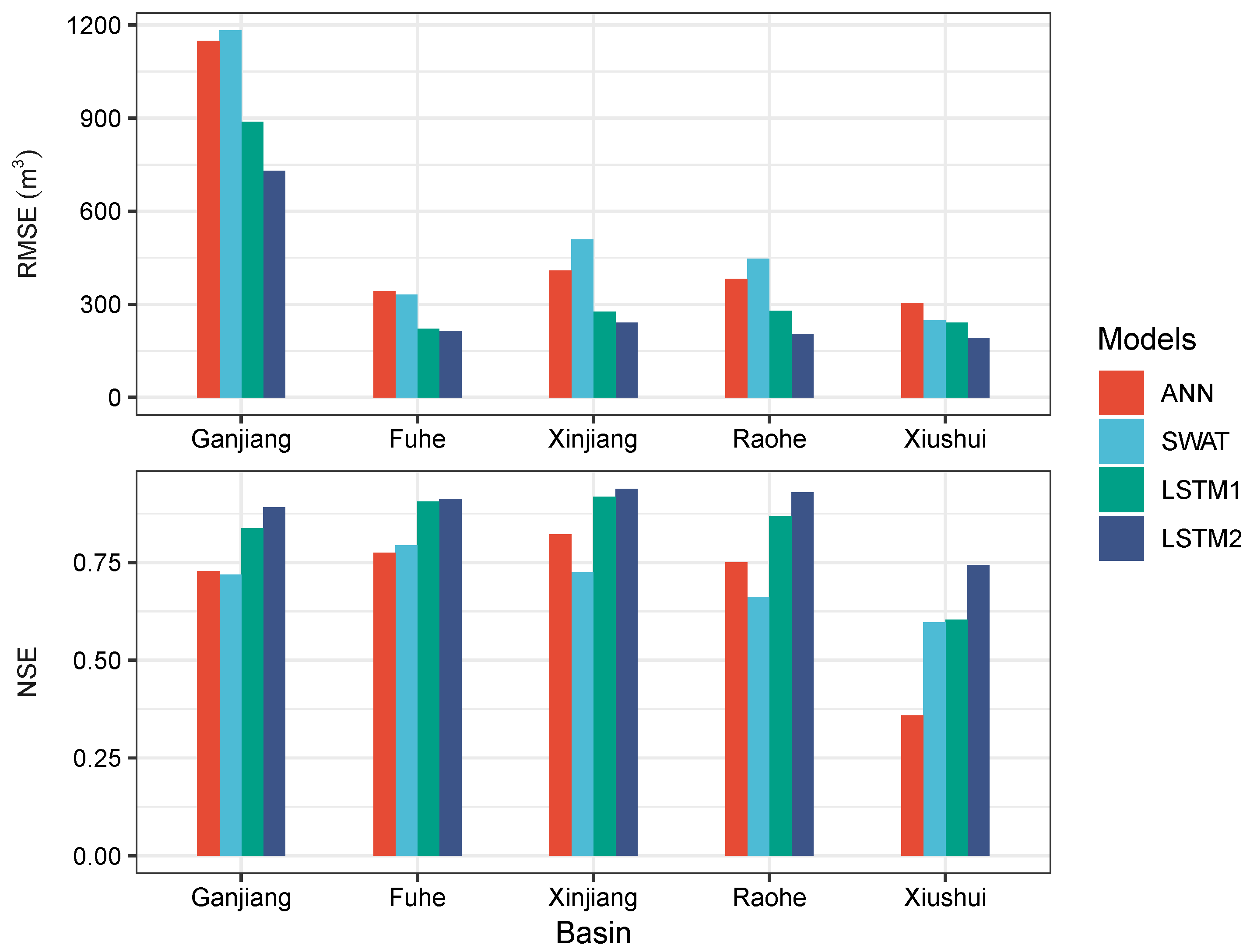
4.3. Comparison of Simulation Capability with Other Models
5. Discussion
5.1. Potential Factors that Influence Runoff Simulation
5.2. Limitations and Uncertainties of Neural Network
5.3. Implications for Regional Water Resources Management
6. Conclusions
- The performance of the proposed LSTM model is strongly affected by the widow size. A window in improper large size will dramatically deteriorate the model performance. In terms of PYLB, better model performance can be achieved by increasing the window size when it is less than 15 days. When the window size is between 15 and 60 days, the model performance will remain stable as the window size increase. A window size of 15 days might be appropriate for both accuracy and computational efficiency.
- The proposed LSTM model can achieve desirable results (where the NSE ranged from 0.60 to 0.92 for the test period) with precipitation data as the only input. And the performance can be improved simply by feeding the model with more meteorological variables (where NSE ranged from 0.74 to 0.94 for the test period). In addition, the LSTM model with more meteorological variables is able to capture the peak values of runoff more precisely.
- The comparison results with the ANN and the SWAT showed that the the proposed LSTM model scored the best in most cases even in regions with sparse meteorological stations. The application of LSTMs and its further development have therefore a high potential to extend data-based modeling approaches in the field of hydrology.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LSTM | Long Short Term Memory |
| ANN | Artificial Neural Network |
| PYLB | Poyang Lake Basin |
| RMSE | root mean square error |
| NSE | Nash-Sutcliffe Efficiency |
References
- Yang, H.B.; Yang, D.W. Derivation of climate elasticity of runoff to assess the effects of climate change on annual runoff. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. Assessing the differences in sensitivities of runoff to changes in climatic conditions across a large basin. J. Hydrol. 2011, 406, 234–244. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-Runoff modelling using Long-Short-Term-Memory (LSTM) networks. Hydrol. Earth Syst. Sci. Discuss. 2018, 2018, 1–26. [Google Scholar] [CrossRef]
- Lee, H.; McIntyre, N.; Wheater, H.; Young, A. Selection of conceptual models for regionalisation of the rainfall-runoff relationship. J. Hydrol. 2005, 312, 125–147. [Google Scholar] [CrossRef]
- Kan, G.; Li, J.; Zhang, X.; Ding, L.; He, X.; Liang, K.; Jiang, X.; Ren, M.; Li, H.; Wang, F.; et al. A new hybrid data-driven model for event-based rainfall–runoff simulation. Neural Comput. Appl. 2017, 28, 2519–2534. [Google Scholar] [CrossRef]
- Nash, L.L.; Gleick, P.H. Sensitivity of streamflow in the Colorado basin to climatic changes. J. Hydrol. 1991, 125, 221–241. [Google Scholar] [CrossRef]
- Revelle, R.R.; Waggoner, P.E. Effects of a Carbon Dioxide-Induced Climatic Change on Water Supplies in 7 the Western United States. Month 1983, 419, 432. [Google Scholar]
- Schaake, J.C.; Waggoner, P. From climate to flow. In Climate Change and US Water Resources; OSTI: Oak Ridge, TN, USA, 1990; pp. 177–206. [Google Scholar]
- Vogel, R.M.; Wilson, I.; Daly, C. Regional regression models of annual streamflow for the United States. J. Irrig. Drain. Eng. 1999, 125, 148–157. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhang, Q.; Werner, A.D.; Yao, J. Investigating a complex lake-catchment-river system using artificial neural networks: Poyang Lake (China). Hydrol. Res. 2015, 46, 912. [Google Scholar] [CrossRef]
- Maniquiz, M.C.; Lee, S.; Kim, L.H. Multiple linear regression models of urban runoff pollutant load and event mean concentration considering rainfall variables. J. Environ. Sci. 2010, 22, 946–952. [Google Scholar] [CrossRef]
- Behzad, M.; Asghari, K.; Eazi, M.; Palhang, M. Generalization performance of support vector machines and neural networks in runoff modeling. Expert Syst. Appl. 2009, 36, 7624–7629. [Google Scholar] [CrossRef]
- Parkin, G.; Birkinshaw, S.; Younger, P.; Rao, Z.; Kirk, S. A numerical modelling and neural network approach to estimate the impact of groundwater abstractions on river flows. J. Hydrol. 2007, 339, 15–28. [Google Scholar] [CrossRef]
- Del Frate, F.; Ferrazzoli, P.; Schiavon, G. Retrieving soil moisture and agricultural variables by microwave radiometry using neural networks. Remote Sens. Environ. 2003, 84, 174–183. [Google Scholar] [CrossRef]
- Shoaib, M.; Shamseldin, A.Y.; Khan, S.; Khan, M.M.; Khan, Z.M.; Sultan, T.; Melville, B.W. A comparative study of various hybrid wavelet feedforward neural network models for runoff forecasting. Water Resour. Manag. 2018, 32, 83–103. [Google Scholar] [CrossRef]
- Fang, K.; Shen, C.; Kifer, D.; Yang, X. Prolongation of SMAP to spatiotemporally seamless coverage of continental US using a deep learning neural network. Geophys. Res. Lett. 2017, 44, 11–30. [Google Scholar] [CrossRef]
- Shen, C. A trans-disciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Chollet, F.; Allaire, J.J. Deep Learning with R; Manning Publications Company: Shelter Island, NY, USA, 2018. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.R.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Montreal, QC, Canada, 2014; pp. 3104–3112. [Google Scholar]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, B. Poyang Lake-Hydrology Biology Deposit Wetland Development and Rehabilitation; China Science and Technology University Press: Heifei, China, 1997; pp. 146–233. [Google Scholar]
- Shankman, D.; Liang, Q. Landscape Changes and Increasing Flood Frequency in China’s Poyang Lake Region. Prof. Geogr. 2003, 55, 434–445. [Google Scholar] [CrossRef]
- Tan, Z.; Tao, H.; Jiang, J.; Zhang, Q. Influences of Climate Extremes on NDVI (Normalized Difference Vegetation Index) in the Poyang Lake Basin, China. Wetlands 2015, 35, 1033–1042. [Google Scholar] [CrossRef]
- Fan, H.; Xu, L.; Tao, H.; Feng, W.; Cheng, J.; You, H. Accessing the Difference in the Climate Elasticity of Runoff across the Poyang Lake Basin, China. Water 2017, 9, 135. [Google Scholar] [CrossRef]
- Ye, X.C.; Zhang, Q.; Liu, J.; Li, X.H.; Xu, C.Y. Distinguishing the relative impacts of climate change and human activities on variation of streamflow in the Poyang Lake catchment, China. J. Hydrol. 2013, 494, 83–95. [Google Scholar] [CrossRef]
- LeCun, Y.A.; Bottou, L.; Orr, G.B.; Müller, K.R. Efficient backprop. In Neural Networks: Tricks of the Trade; Springer: Berlin, Germany, 2012; pp. 9–48. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory; MIT Press: Cambridge, MA, USA, 1997; Volume 9, pp. 1735–1780. [Google Scholar]
- Kawakami, K. Supervised Sequence Labelling with Recurrent Neural Networks. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2008. [Google Scholar]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Jacobs, R.A. Increased rates of convergence through learning rate adaptation. Neural Netw. 1988, 1, 295–307. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Zhang, X.S. A distributed non-point source pollution model: Calibration and validation in the Yellow River Basin. J. Environ. Sci. 2004, 16, 646–650. [Google Scholar]
- Gassman, P.W.; Sadeghi, A.M.; Srinivasan, R. Applications of the SWAT model special section: Overview and insights. J. Environ. Qual. 2014, 43, 1–8. [Google Scholar] [CrossRef]
- Schuol, J.; Abbaspour, K. Calibration and uncertainty issues of a hydrological model (SWAT) applied to West Africa. Adv. Geosci. 2006, 9, 137–143. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Technical Report; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Guo, H.; Hu, Q.; Jiang, T. Annual and seasonal streamflow responses to climate and land-cover changes in the Poyang Lake basin, China. J. Hydrol. 2008, 355, 106–122. [Google Scholar] [CrossRef]
- Chen, Y.; Takeuchi, K.; Xu, C.; Chen, Y.; Xu, Z. Regional climate change and its effects on river runoff in the Tarim Basin, China. Hydrol. Process. 2006, 20, 2207–2216. [Google Scholar] [CrossRef]
- Lu, B.; Li, K.; Zhang, H.; Wang, W.; Gu, H. Study on the optimal hydropower generation of Zhelin reservoir. J. Hydro-Environ. Res. 2013, 7, 270–278. [Google Scholar] [CrossRef]
- Allaire, J.; Tang, Y. Tensorflow: R Interface to ‘TensorFlow’; R Package Version 1.10; The Comprehensive R Archive Network: Vienna, Austria, 2018. [Google Scholar]
- Allaire, J.; Chollet, F. Keras: R Interface to ‘Keras’; R Package Version 2.2.4; The Comprehensive R Archive Network: Vienna, Austria, 2018. [Google Scholar]
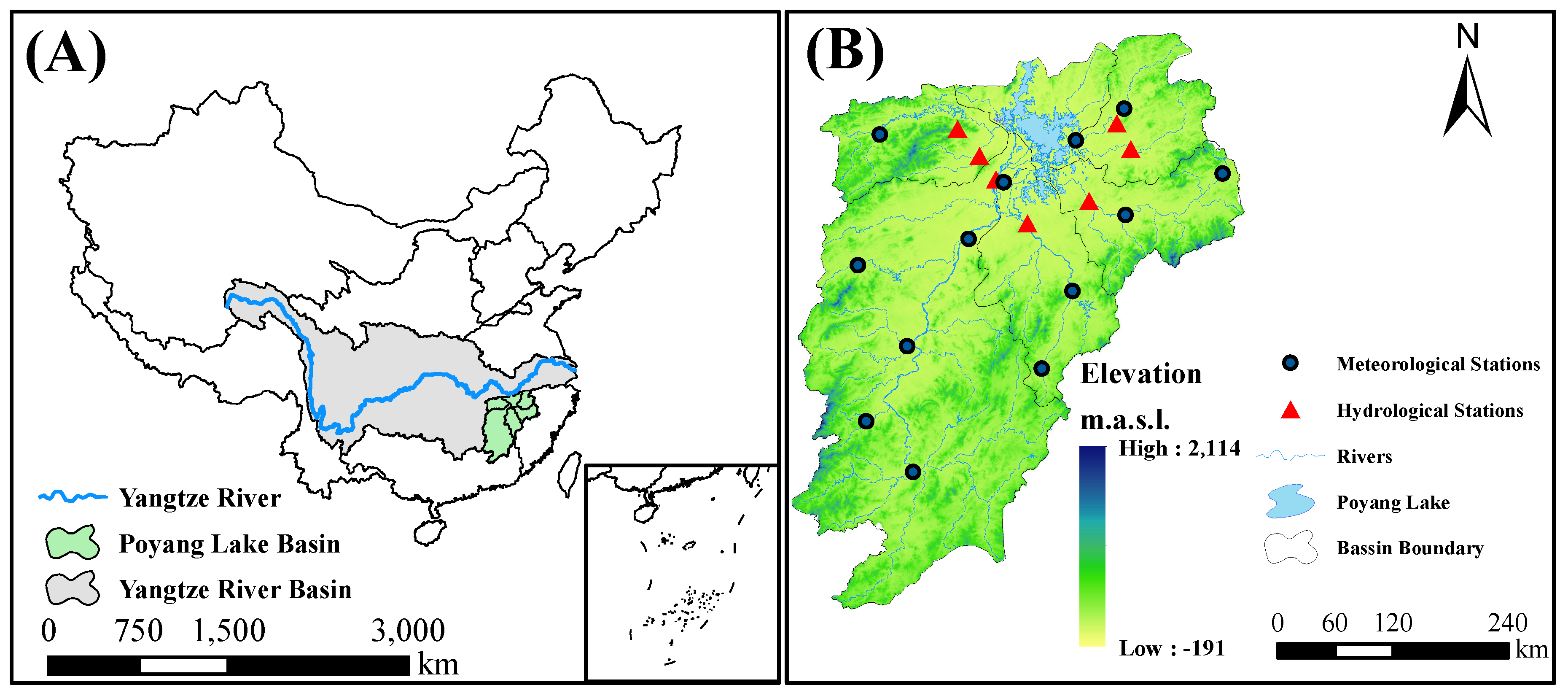
| Hydrological Station | Location | Coordinates | Gauged Area (km) |
|---|---|---|---|
| Qiujin | Xiushui | 115.41 E, 29.10 N | 9914 |
| Wanjiabu | Xiushui (Liaohe tributary) | 115.65 E, 28.85 N | 3548 |
| Waizhou | Ganjiang | 115.83 E, 28.63 N | 80,948 |
| Lijiadu | Fuhe | 116.17 E, 28.22 N | 15,811 |
| Meigang | Xinjiang | 116.82 E, 28.43 N | 15,535 |
| Hushan | Raohe (Le’an tributary) | 117.27 E, 28.92 N | 6374 |
| Dufengken | Raohe (Changjiang tributary) | 117.12 E, 29.16 N | 5013 |
| Model | LSTM1 | LSTM2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Period | Calibration Period | Validation Period | Calibration Period | Validation Period | ||||
| Metrics | NSE | RMSE | NSE | RMSE | NSE | RMSE | NSE | RMSE |
| Ganjiang | 0.86 | 834.63 | 0.84 | 888.09 | 0.91 | 667.71 | 0.89 | 729.95 |
| Fuhe | 0.91 | 192.26 | 0.91 | 221.60 | 0.92 | 177.87 | 0.91 | 213.89 |
| Xinjiang | 0.92 | 258.20 | 0.92 | 276.36 | 0.94 | 230.78 | 0.94 | 240.18 |
| Raohe | 0.86 | 264.37 | 0.87 | 278.77 | 0.91 | 212.95 | 0.93 | 204.10 |
| Xiushui | 0.73 | 293.72 | 0.60 | 240.41 | 0.83 | 230.79 | 0.74 | 192.16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation. Water 2020, 12, 175. https://doi.org/10.3390/w12010175
Fan H, Jiang M, Xu L, Zhu H, Cheng J, Jiang J. Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation. Water. 2020; 12(1):175. https://doi.org/10.3390/w12010175
Chicago/Turabian StyleFan, Hongxiang, Mingliang Jiang, Ligang Xu, Hua Zhu, Junxiang Cheng, and Jiahu Jiang. 2020. "Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation" Water 12, no. 1: 175. https://doi.org/10.3390/w12010175
APA StyleFan, H., Jiang, M., Xu, L., Zhu, H., Cheng, J., & Jiang, J. (2020). Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation. Water, 12(1), 175. https://doi.org/10.3390/w12010175