Numerical Investigation of Vortex Induced Vibration for Submerged Floating Tunnel under Different Reynolds Numbers
Abstract
1. Introduction
2. Numerical Model
2.1. Governing Equation and Turbulence Model
2.2. Motion Response of SFT
2.3. Calculation Model and Boundary Conditions
3. Numerical Dispersion and Grid Update
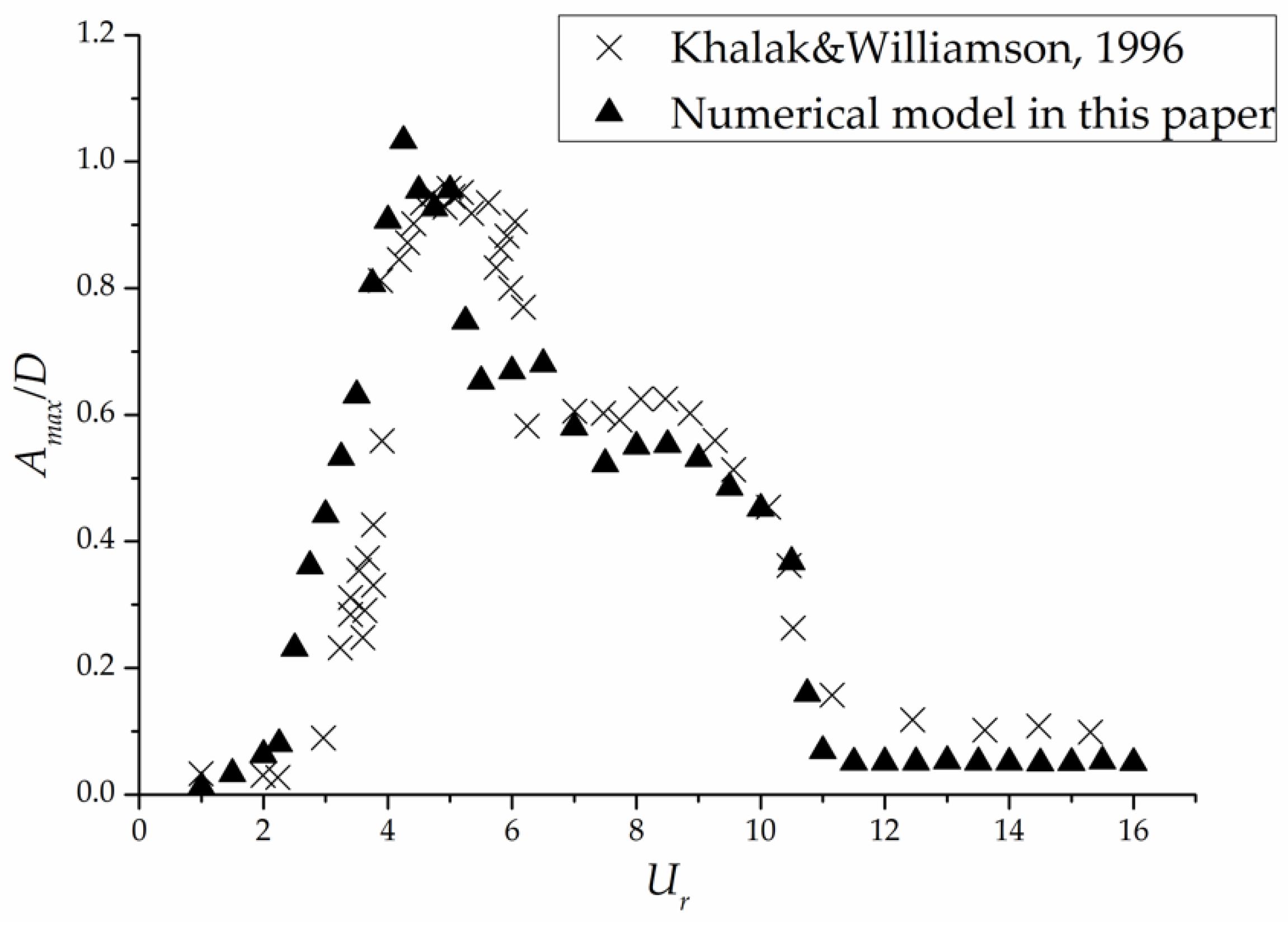
4. Model Validation
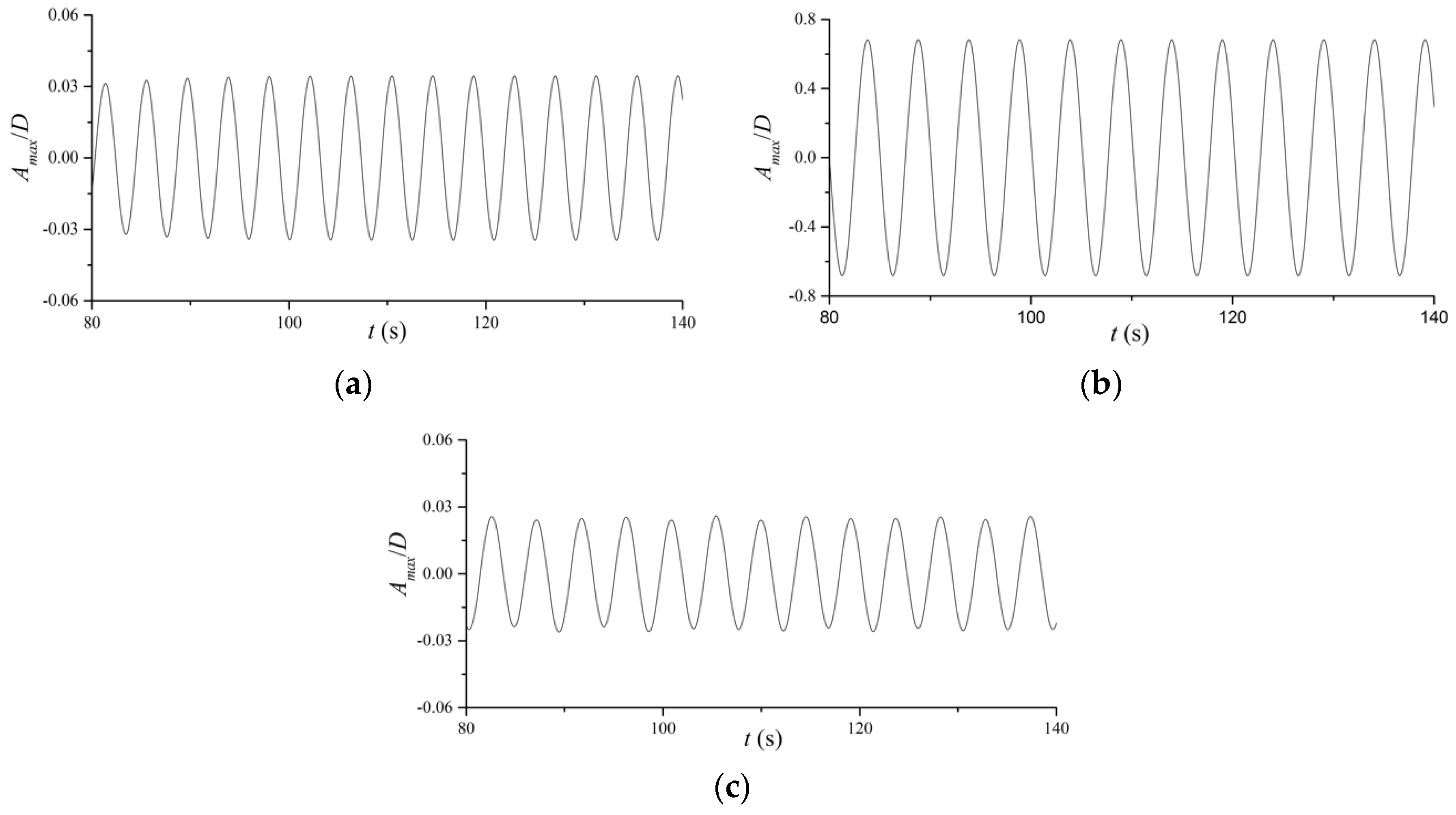
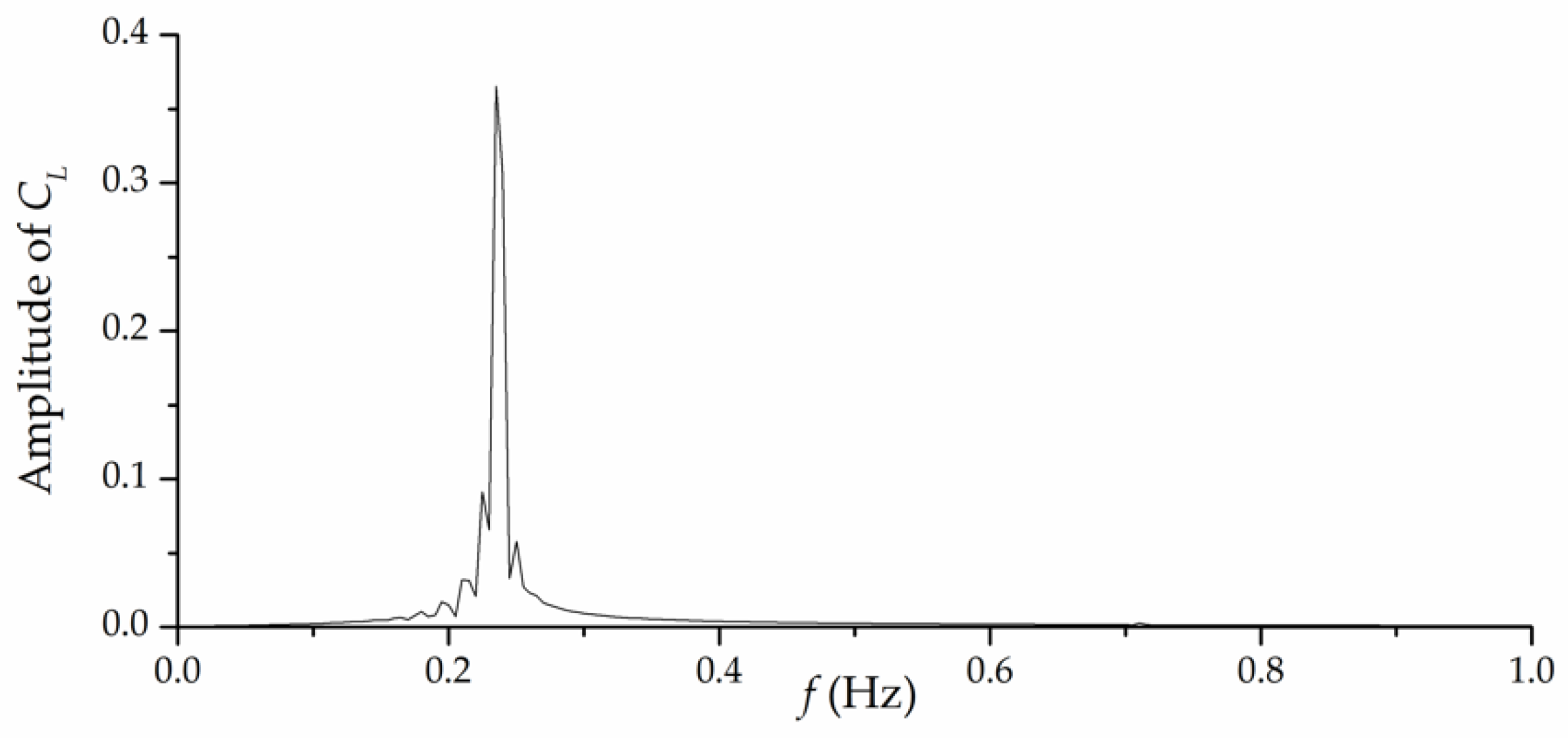
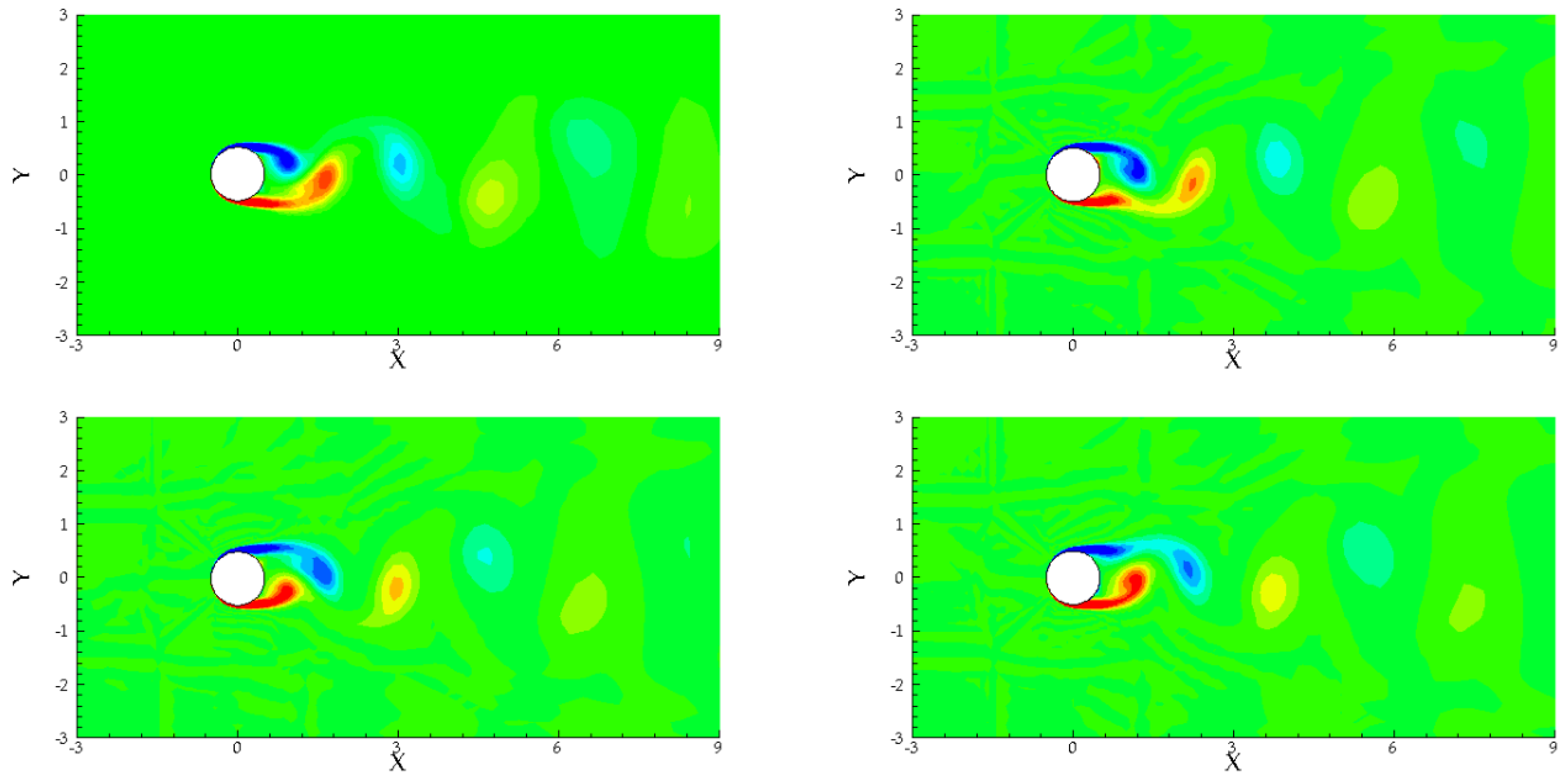
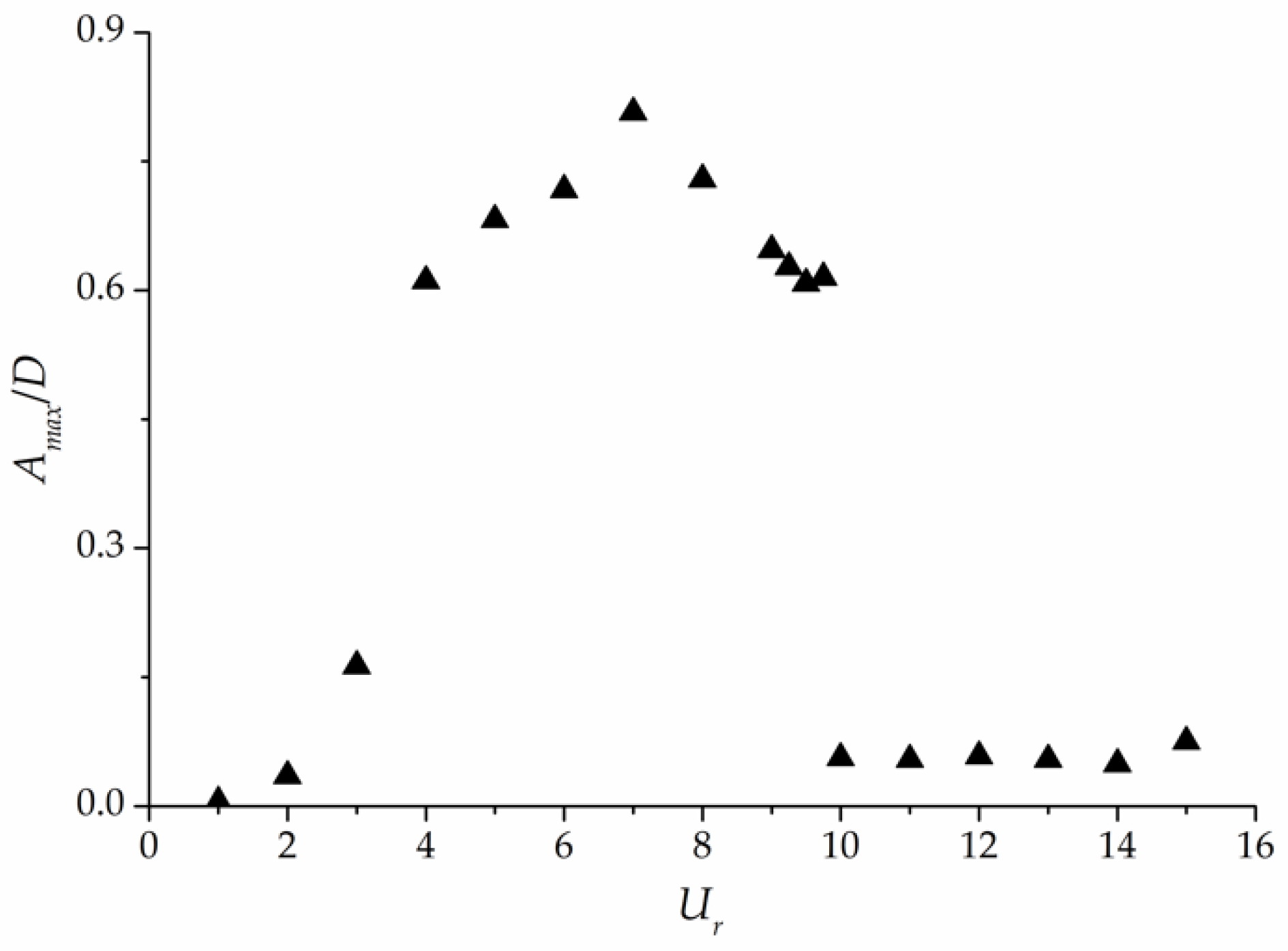
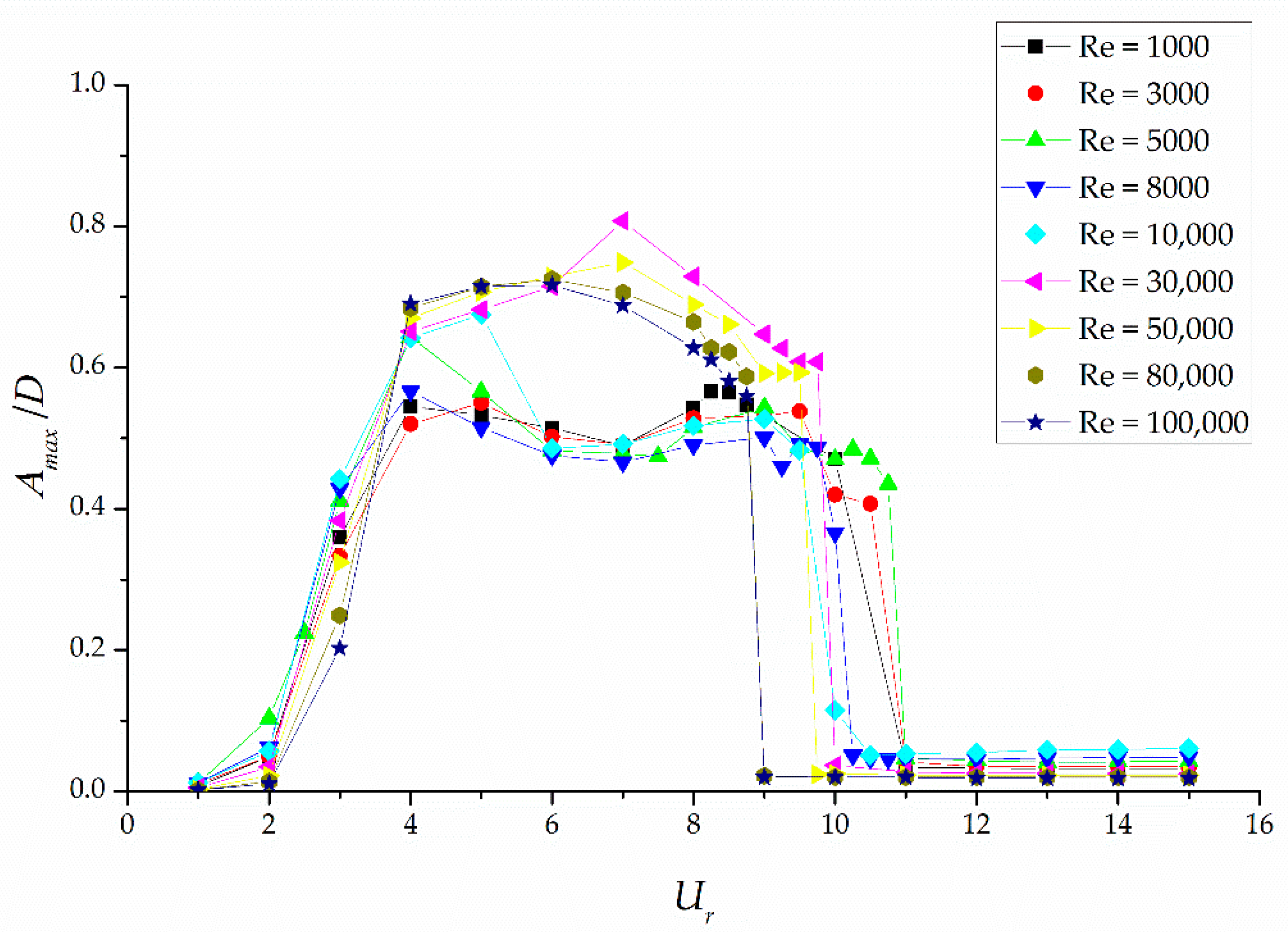
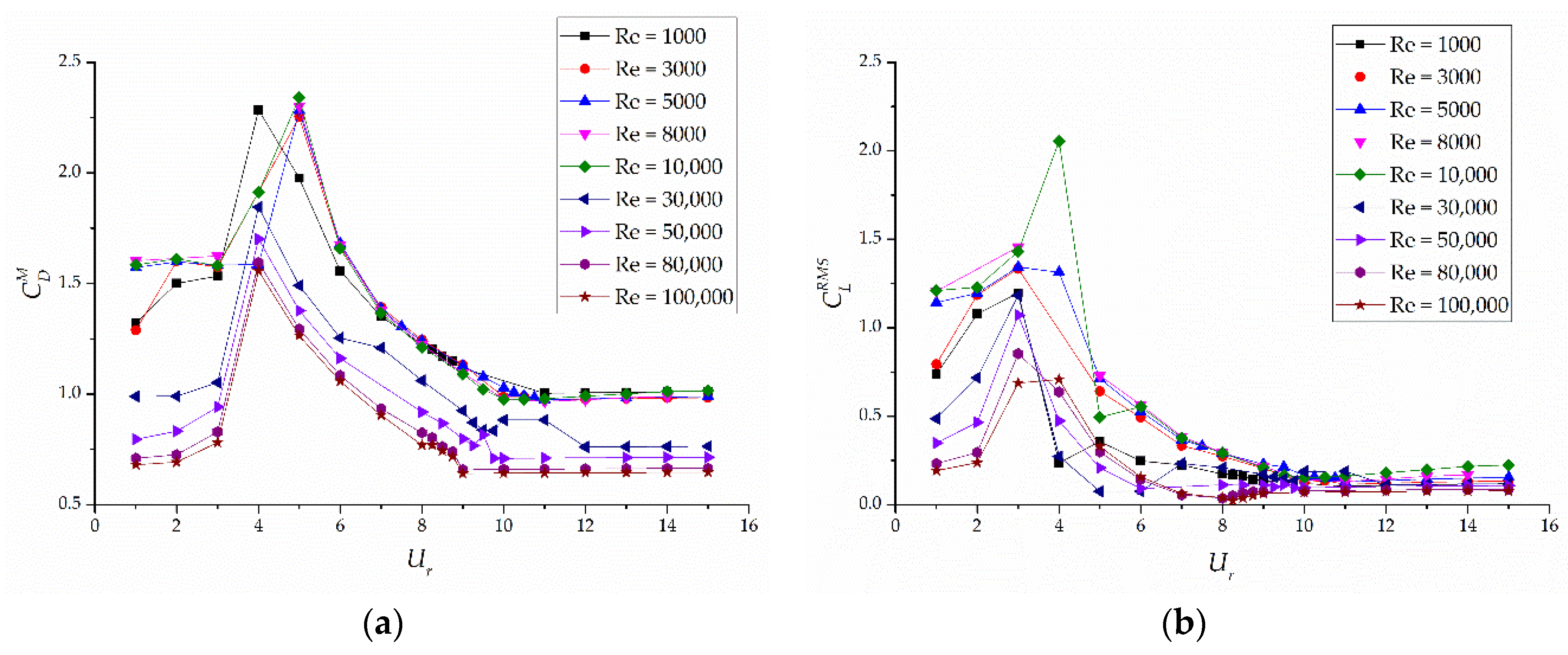
5. Example Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mai, J.T. The Study of Responses of a Submerged Floating Tunnel Subjected to the Wave and Current. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2005. [Google Scholar]
- Wang, G.D. Numerical Analysis and Experiment Research of Submerged Floating Tunnel Subjected to the Wave and Current Effects. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2008. [Google Scholar]
- Long, X. Dynamic Response of Submerged Floating Tunnel with Different Buoyancy-Weight Ratios under Wave and Current Loads. Master’s Thesis, Chinese Academy of Sciences, Beijing, China, 2009. [Google Scholar]
- Luo, G.; Zhou, X.J.; Li, D.F.; Zhang, C. Analysis on characteristics of flow passing submerged floating tunnels of different sections. J. China Railw. Soc. 2013, 35, 115–120. [Google Scholar]
- Luo, G.; Zhou, X.J.; Zhang, C.; Shen, Q. Numerical simulation analysis on rational cross-section of submerged floating tunnel. Railw. Eng. 2012, 12, 32–36. [Google Scholar]
- Morse, T.L.; Williamson, C.H.K. Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 2009, 634, 5–39. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C.H.K. Critical mass in vortex-induced vibration of a cylinder. Eur. J. Mech. B Fluids 2004, 23, 17–27. [Google Scholar] [CrossRef]
- Yan, B.; Luo, M.; Bai, W. An experimental and numerical study of plunging wave impact on a box-shape structure. Mar. Struct. 2019, 66, 272–287. [Google Scholar] [CrossRef]
- Luo, M.; Reeve, D.E.; Shao, S.D.; Karunarathna, H.; Lin, P.; Cai, H. Consistent Particle Method simulation of solitary wave impinging on and overtopping a seawall. Eng. Anal. Bound. Elem. 2019, 103, 160–171. [Google Scholar] [CrossRef]
- Zheng, X.G.; Chen, R.D.; Luo, M.; Kazemi, E.; Liu, X.N. Dynamic hydraulic jump and retrograde sedimentation in an open channel induced by sediment supply: Experimental study and SPH simulation. J. Mt. Sci. 2019, 16, 1913–1927. [Google Scholar] [CrossRef]
- Feng, C.C. The Measurement of Vortex Induced Effected in Flow Past Stationary and Oscillating Circular and d-Section Cylinder. Ph.D. Thesis, University of British Columbia, Vancouver, SC, Canada, 1968. [Google Scholar]
- Khalak, A.; Williamson, C.H.K. Dynamics of a hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 1996, 10, 455–472. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C.H.K. Investigation of relative effects of mass and damping in vortex-induced vibration of a circular cylinder. J. Wind Eng. Ind. Aerodyn. 1997, 69, 341–350. [Google Scholar] [CrossRef]
- Govardhan, R.; Williamson, C.H.K. Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 2000, 420, 85–130. [Google Scholar] [CrossRef]
- Lu, X.Y.; Dalton, C. Calculation of the timing of vortex formation from an oscillating cylinder. J. Fluids Struct. 1996, 10, 527–541. [Google Scholar] [CrossRef]
- Dong, S.; Karniadakis, G.E. DNS of flow past a stationary and oscillating cylinder at Re = 10000. J. Fluids Struct. 2005, 20, 519–531. [Google Scholar] [CrossRef]
- Ge, F.; Long, X.; Wang, L.; Hong, Y. Flow-induced vibrations of long circular cylinders modeled by coupled nonlinear oscillators. Sci. China Ser. G Phys. Mech. Astron. 2009, 52, 1086–1093. [Google Scholar] [CrossRef]
- Kang, L.; Ge, F.; Hong, Y.S. A numerical study on responses of submerged floating structures undergoing vortex-induced vibration and seismic excitation. Procedia Eng. 2016, 166, 91–98. [Google Scholar] [CrossRef]
- Su, Z.B.; Sun, S.N. Vortex-Induced Dynamic Response of Submerged Floating Tunnel Tether Based on Wake Oscillator Model. Adv. Mater. Res. 2014, 919, 1262–1265. [Google Scholar] [CrossRef]
- Chen, Z.; Xiang, Y.Q.; Lin, H.; Yang, Y. Coupled vibration analysis of submerged floating tunnel system in wave and current. Appl. Sci. 2018, 8, 1311. [Google Scholar] [CrossRef]
- Liu, M.M.; Lu, L.; Teng, B.; Zhao, M.; Tang, G.Q. Numerical modeling of local scour and forces for submarine pipeline under surface waves. Coast. Eng. 2016, 116, 275–288. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Palm, J.; Eskilsson, C.; Paredes, G.M.; Bergdahl, L. Coupled mooring analysis for floating wave energy converters using CFD: Formulation and validation. Int. J. Mar. Energy 2016, 16, 83–99. [Google Scholar] [CrossRef]
- Brooks, A.N.; Hughes, T.J.R. Streamline Upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Johnson, A.A.; Tezduyar, T.E. Mesh update strategies in parallel finite element computations of flow problems with moving boundaries and interfaces. Comput. Methods Appl. Mech. Eng. 1994, 119, 73–94. [Google Scholar] [CrossRef]
- Mochida, A.; Murakami, S. On turbulent vortex shedding flow past 2D square cylinder predicted by CFD. J. Wind Eng. Ind. Aerodyn. 1995, 54–55, 191–211. [Google Scholar]
- Kim, D.H.; Yang, K.S.; Senda, M. Large eddy simulation of turbulent flow past a square cylinder confined in a channel. Comput. Fluids 2004, 33, 81–96. [Google Scholar] [CrossRef]
- Guilmineau, E.; Queutey, P. Numerical simulation of vortex-induced vibration of a circular cylinder with low mass-damping in a turbulent flow. J. Fluids Struct. 2004, 19, 449–466. [Google Scholar] [CrossRef]
- Tang, G.Q.; Lu, L.; Teng, B.; Liu, M.M. Numerical simulation of vortex-induced vibration with three-step finite element method and Arbitrary Lagrangian-Eulerian formulation. Adv. Mech. Eng. 2013, 5, 1–14. [Google Scholar] [CrossRef]
- Lu, L.; Guo, X.L.; Tang, G.Q.; Liu, M.M.; Chen, C.Q.; Xie, Z.H. Numerical investigation of flow-induced rotary oscillation of circular cylinder with rigid splitter plate. Phys. Fluids 2016, 28, 093604. [Google Scholar] [CrossRef]
- Gopalkrishnan, R. Vortex-Induced Forces on Oscillating Bluff Cylinders. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1993. [Google Scholar]
- Zhao, M.; Cheng, L.; Teng, B.; Dong, G. Hydrodynamic forces on dual cylinders of different diameters in steady currents. J. Fluids Struct. 2007, 23, 59–83. [Google Scholar] [CrossRef]
- Song, J.N. Experimental Investigation and Numerical Simulation by a Discrete Vortex Method on VIV of Marine Risers. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]




| β* | α1 | β1 | σk1 | σω1 | α2 | β2 | σk2 | σω2 |
|---|---|---|---|---|---|---|---|---|
| 0.09 | 5/9 | 3/40 | 0.85 | 0.5 | 0.44 | 0.0828 | 1.0 | 0.856 |
| Boundary Division | Element | Nodes | Dismin/D | Ymax/D | fn | |||
|---|---|---|---|---|---|---|---|---|
| Mesh 1 | 80 | 18,200 | 18,490 | 0.0045 | 0.7166 | 1.295 | 0.148 | 0.173 |
| Mesh 2 | 120 | 21,900 | 22,300 | 0.0045 | 0.7284 | 1.325 | 0.187 | 0.172 |
| Mesh 3 | 160 | 25,600 | 25,970 | 0.0040 | 0.7292 | 1.332 | 0.214 | 0.172 |
| Mesh 4 | 200 | 29,300 | 29,710 | 0.0038 | 0.7293 | 1.335 | 0.224 | 0.172 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, R.; Liu, M.; Geng, B.; Jin, X.; Zhang, H.; Liu, Y. Numerical Investigation of Vortex Induced Vibration for Submerged Floating Tunnel under Different Reynolds Numbers. Water 2020, 12, 171. https://doi.org/10.3390/w12010171
Jin R, Liu M, Geng B, Jin X, Zhang H, Liu Y. Numerical Investigation of Vortex Induced Vibration for Submerged Floating Tunnel under Different Reynolds Numbers. Water. 2020; 12(1):171. https://doi.org/10.3390/w12010171
Chicago/Turabian StyleJin, Ruijia, Mingming Liu, Baolei Geng, Xin Jin, Huaqing Zhang, and Yong Liu. 2020. "Numerical Investigation of Vortex Induced Vibration for Submerged Floating Tunnel under Different Reynolds Numbers" Water 12, no. 1: 171. https://doi.org/10.3390/w12010171
APA StyleJin, R., Liu, M., Geng, B., Jin, X., Zhang, H., & Liu, Y. (2020). Numerical Investigation of Vortex Induced Vibration for Submerged Floating Tunnel under Different Reynolds Numbers. Water, 12(1), 171. https://doi.org/10.3390/w12010171






