Pump Efficiency Analysis for Proper Energy Assessment in Optimization of Water Supply Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Brief Summary of the Granados System
- If < CE1 ⇒Diameter is preferable to .
- If > CE1 ⇒Diameter is preferable to .
- If .
- If .
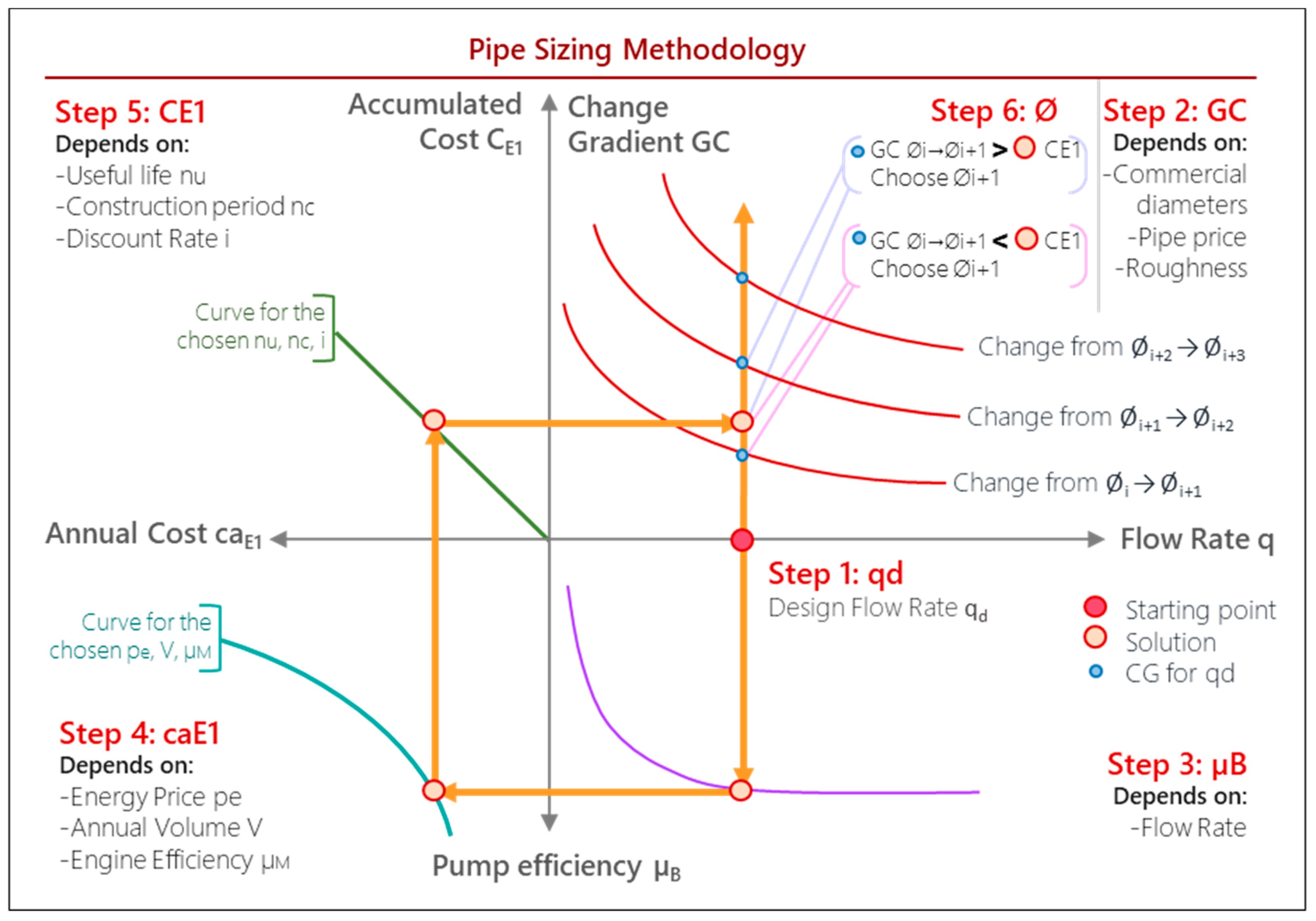
2.2. Methodology
- Split case pumps: CP/CPI/CPR series.
- Horizontal pumps (normalized in the European Union): RNI/RN series.
- Multistage horizontal pumps: APM series.
- Vertical pumps: VS/VG series.
- Submersible vertical pumps: SVA/SVH series.
3. Results and Discussion
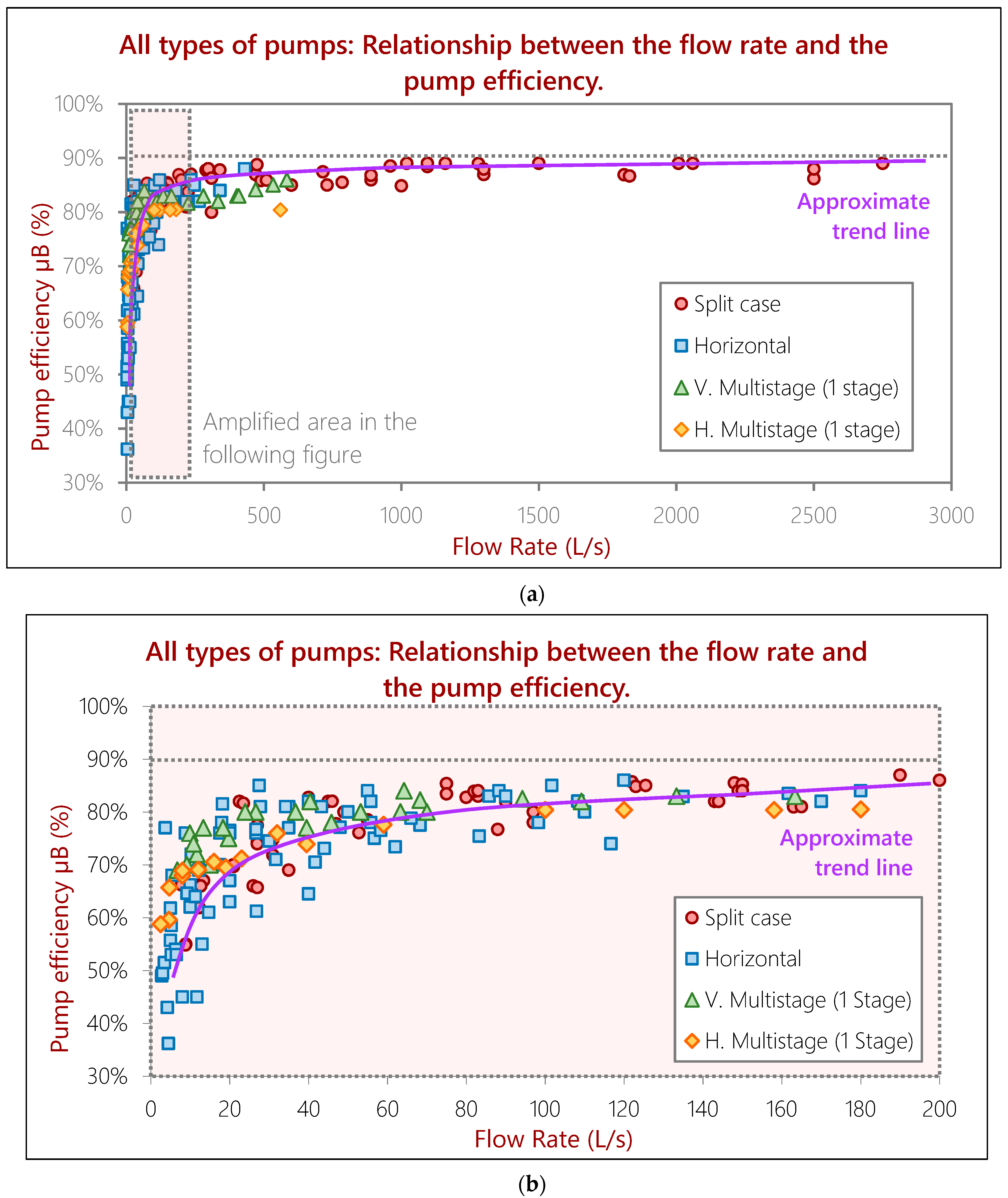
- Split case pumps are, in general, the ones that provide the best performance for flow rates over 500 L/s.
- Between 100 L/s and 500 L/s, both split case and horizontal offer the best results.
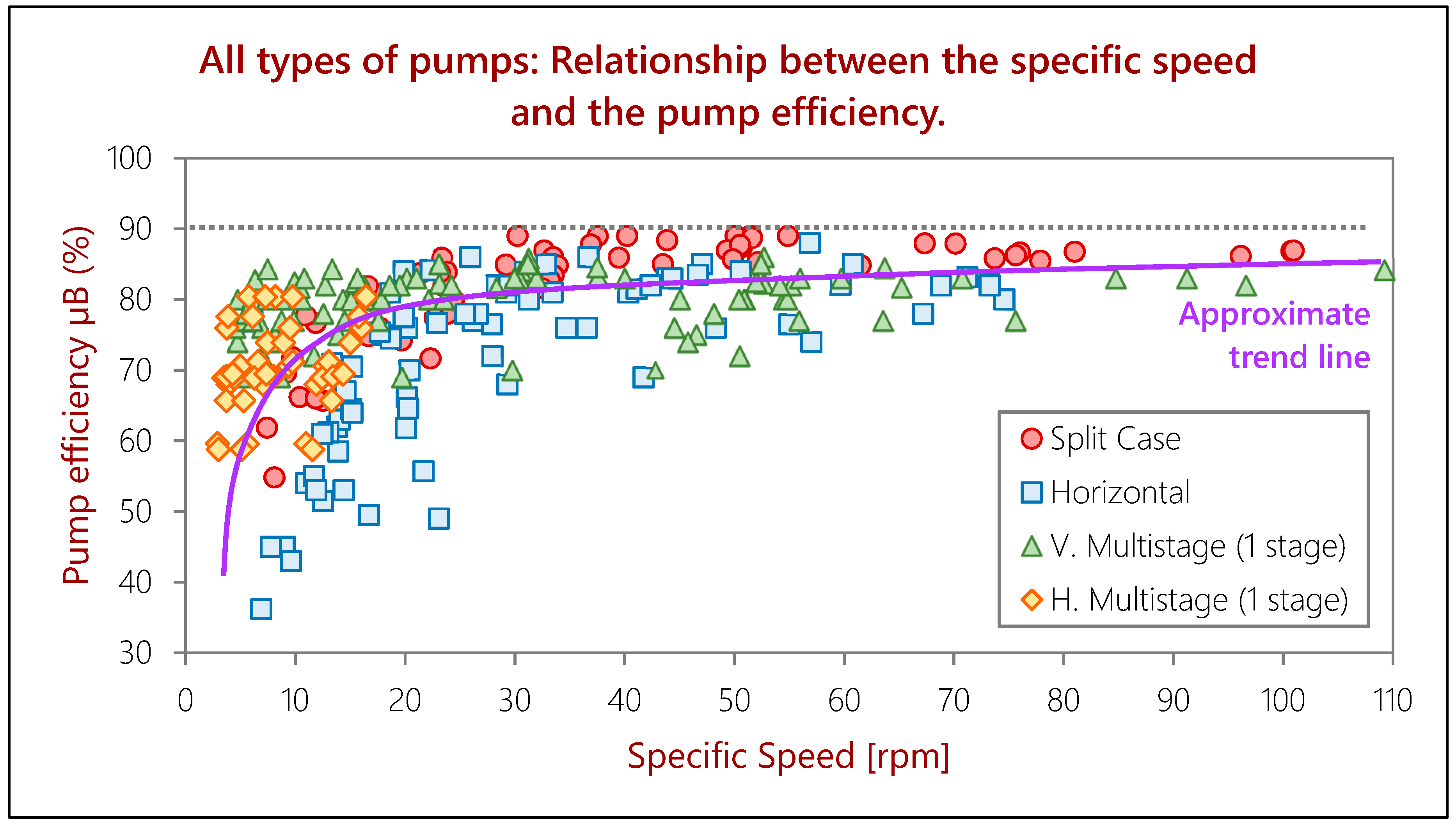
- Under 100 L/s, the distribution is very heterogeneous and disperse, but as a general rule, there is always a horizontal pump that can provide the best efficiency (but also the lowest, due to the dispersion). Vertical pumps also show great performances, but they can generally be exceeded by a horizontal model.
- Vertical multistage pumps always give a better efficiency than horizontal multistage pumps.
- For small flow rates, the differences between the pump efficiency among models are very high. Different models can almost double other pump’s efficiency, meaning that the energy cost can be almost twice as much if the pump is not well selected. This is why the pump analysis is more complicated for small discharge values.
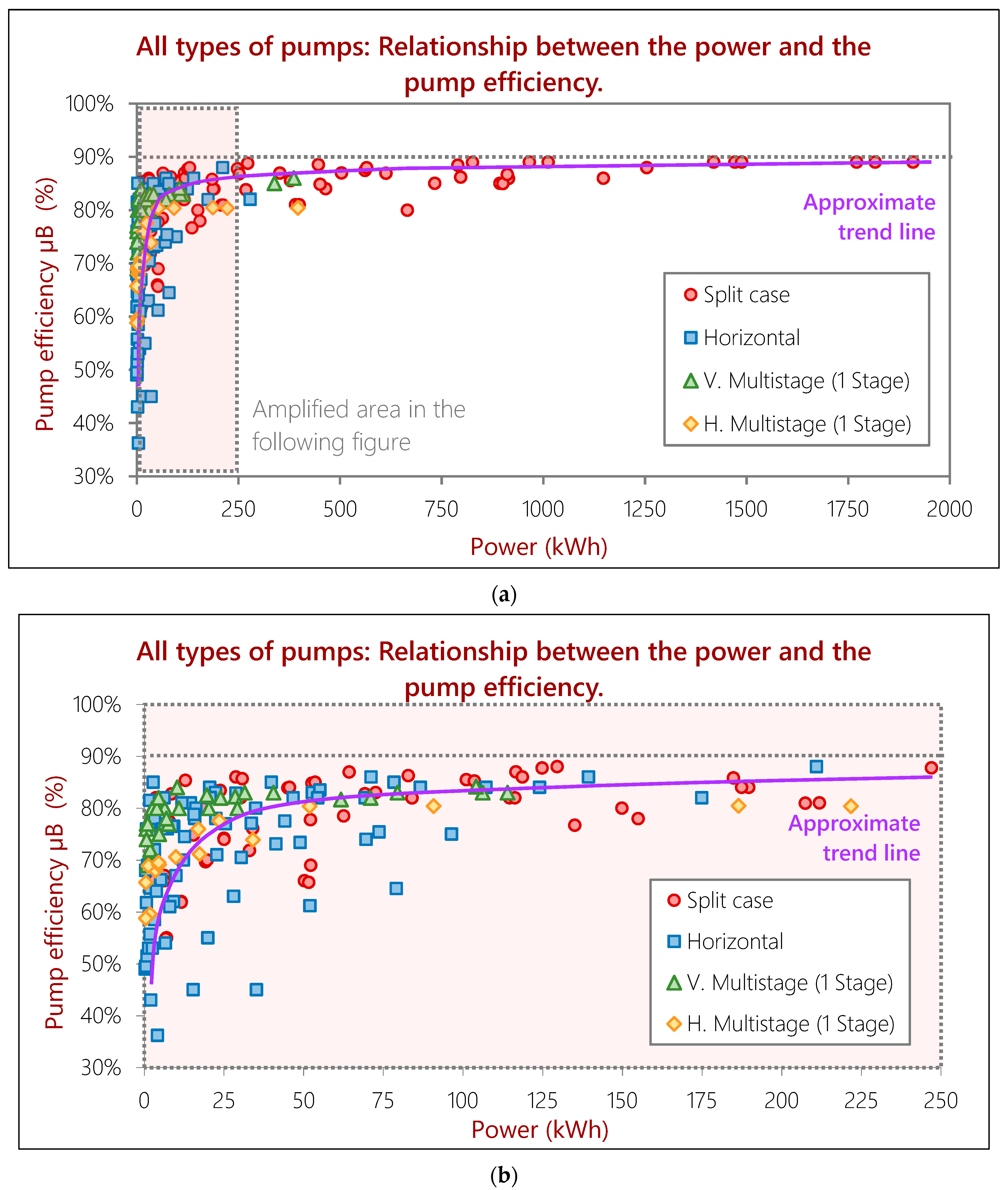
- There is a relationship between the pump efficiency and the required power for the optimum operating point.
- The relation seems to be clearer from 400 kW and on, and values greater than 80% efficiency can be expected.
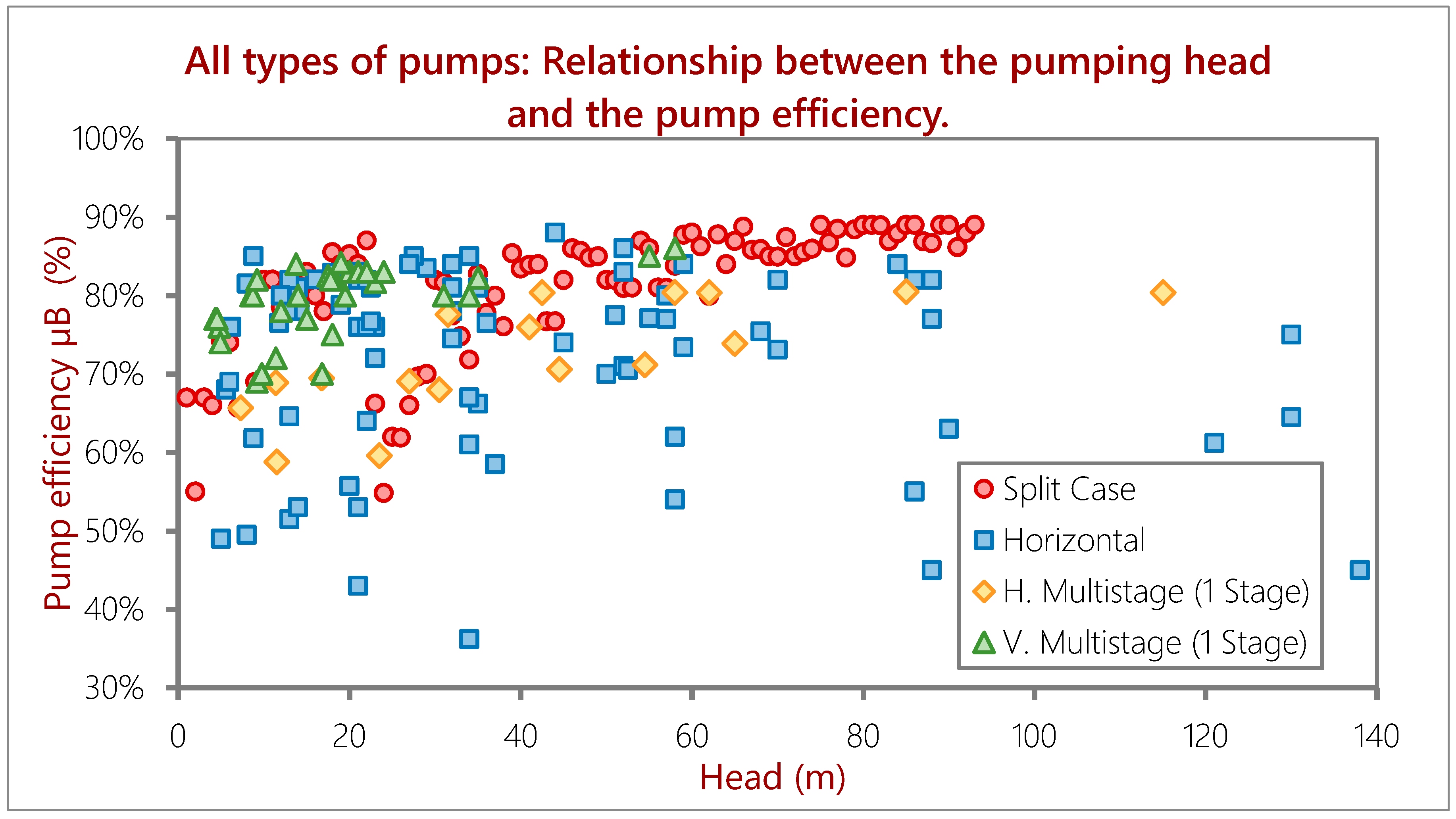
- This relationship seems to be weaker than the existing one between the flow rate and the pump efficiency. The interpreted reason for this fact is that, since the power is calculated from the flow rate and the pumping height, the good relationship that the flow rate transfers to the power is weakened by the poor bond that the pumping head and efficiency have. The authors of [3] had already presented similar conclusions. In their work, they empirically proved that the cost of pumping depended on power; which indeed agrees with these results.
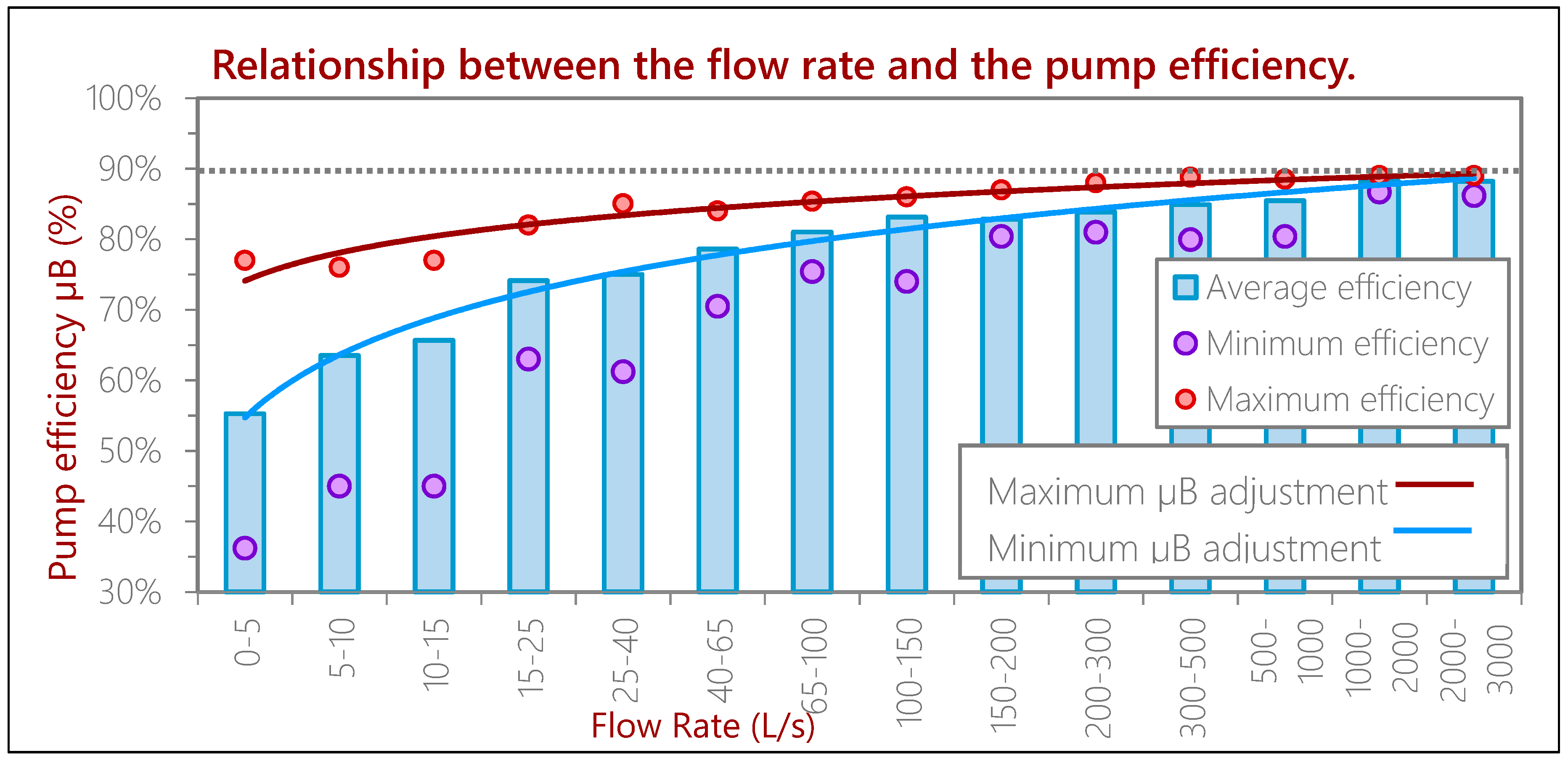
3.1. Relationship between the Flow Rate and the Pump Efficiency
3.2. Application of the Pump Efficiency Curves to the Granados System
- Calculate the design demand flow rate of the hydraulic drive.
- Calculate the change gradient curves for a commercial series of diameters with Equation (2).Since the aim is to compare the construction costs to those of the energy, excavation costs also must be considered and added to these figures.
- Calculate the expected pump efficiency using the average pump efficiency equation (Equation (7)).It is always more conservative to use the average pump efficiency equation rather than the maximum one, nevertheless this one can also be used but it would require a much more exhaustive pump search.
- Calculate the annual energy cost for one meter height Ca
- E1 using Equation (3).At this point, different alternatives might be considered for various energy prices, etc.
- Calculate the total accumulated energy cost for one meter height CE1 with Equations (3) and (4).
- Compare the change gradient and the energy cost CE1 and select the pipe diameter: when < CE1 select the wider diameter ; but when > CE1 select diameter . When = CE1, it is always preferable to build a bigger diameter , in case energy price, discount rate, etc. change.
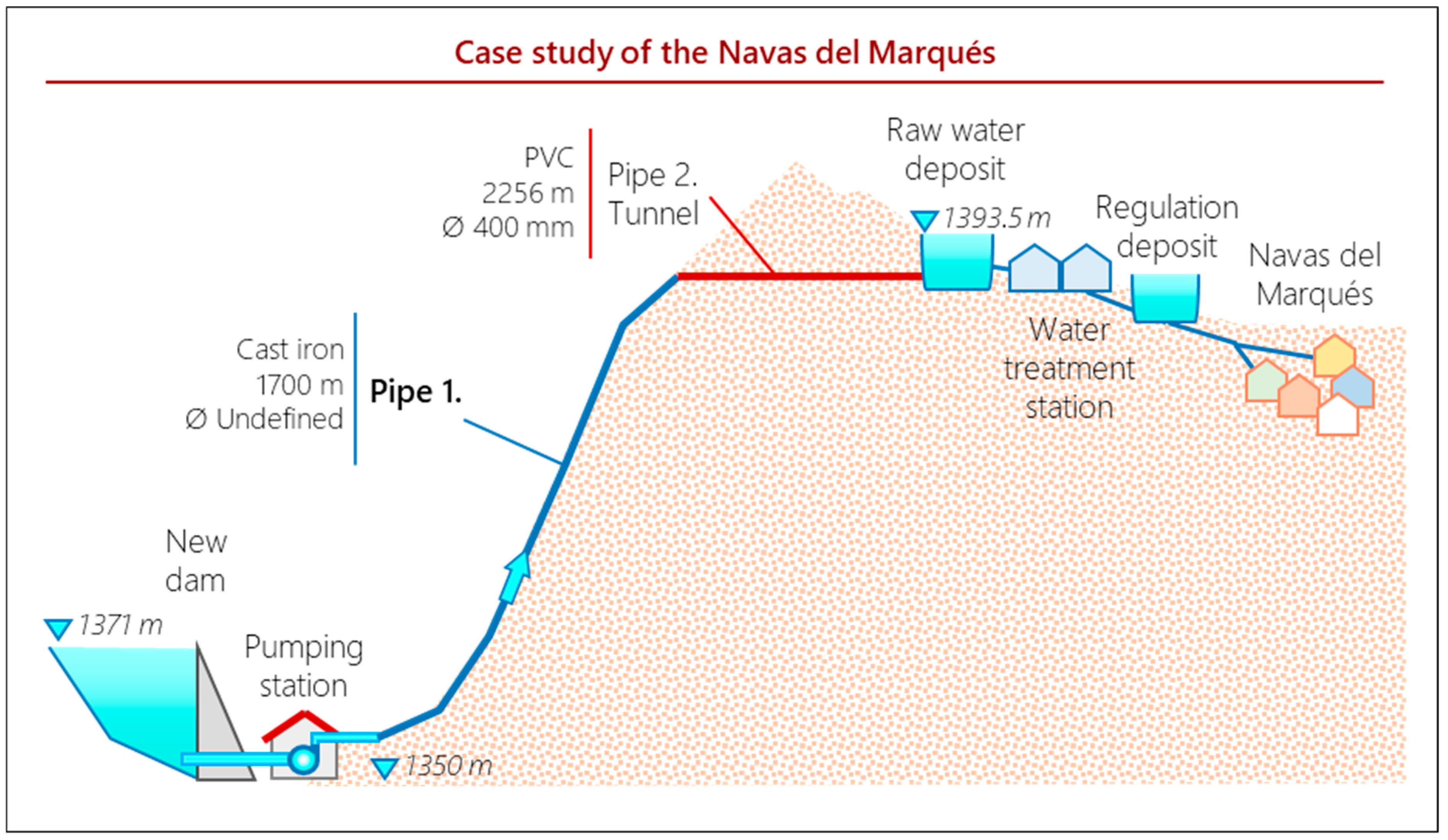
3.3. Case Study: Navas del Marqués
- New dam.
- New pumping station.
- New pipe replacing the first part of the water drive. There was a tunnel section from the previous water supply system that will remain as it was.
- New raw water deposit, previous to the water treatment station.
- New regulation deposit, after the water treatment station.
- New distribution network.
- Design flow rate: 0.164 m3/s.
- Annual volume of water: 1.5 hm3/year.
- Pipe diameters and the correspondent prices. These are compiled in Table 2.
- Energy price: 0.072 €/kWh.
- Duration of the construction period: 30 months.
- Although it is not specified in the project, pump engine efficiency is fixed at 94%.
- The design discharge flow is the one used by the original project which is q = 0.164 m3/s.
- For the calculation of the change gradients, the material for the pipe is ductile cast iron. Two different studies have been elaborated for two different pipe prices. Firstly, the pipe prices used in the project have been considered. Secondly, we used the pipe prices proposed by the Canal de Isabel II. Canal de Isabel II is the public authority in charge of the integral water supply of Madrid, Spain, and they published the average pipe prices they use in their infrastructure. Since the Tagus Hydrographic Confederation is also a public company, these prices have also been considered for a sensitivity analysis. On the other hand, it must be kept in mind that the prices used for the change gradient include that of the full construction cost (including excavation, joining, etc.). Table 2 shows the pipe prices and the change gradients.
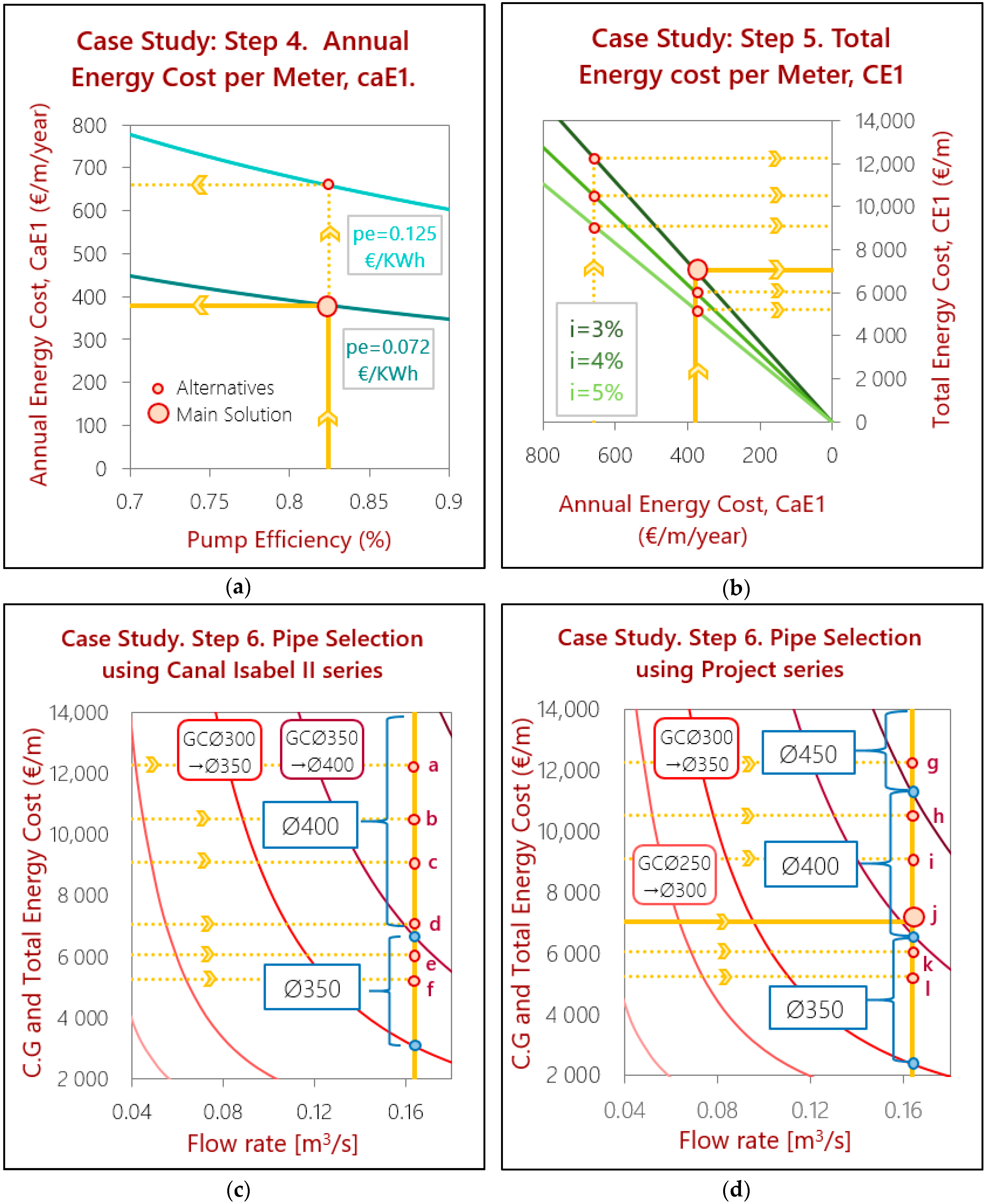
- Using Equations (7) and (8), the average pump efficiency obtained is 82.44% and the maximum value is 86.52%. This same result can be obtained from Figure 6a with the design flow rate q = 0.164 m3/s.
- The calculation of the annual energy cost per meter has been made for different values of the energy price. Engine efficiency was fixed at 94% and the demanded annual volume of the project is 1.5 hm3. Energy prices used for the calculations are 0.072 €/kWh, which, using Equation (3), gives an annual energy cost of 380 €/m/year; and also 0.125 €/kWh, for which CaE1 is 659 €/m/year.This will allow a sensibility analysis to see how robust the design is against energy price changes. The first price, 0.072 €/kWh, corresponds to the energy price used in the project, and the second alternative, 0.125 €/kWh, corresponds to a higher energy price. These results can be seen in Figure 9a.
- Once the annual unit pumping cost is obtained, the total accumulated cost is calculated using Equation (3). We assume a life span for the cast iron pipe of 31 years. Likewise, the duration of the expected construction period according to the project is 30 months, which corresponds to 2.5 years. We analyzed the sensibility of the design for the discount rate. In this line we adopt three values of the flow rate, where i equals 3%, 4% and 5%. With all this, the results obtained in each situation of energy prices and discount rate are shown in Table 3 below and in Figure 9b.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sanchis, R.; Díaz-Madroñero, M.; López-Jiménez, P.A.; Pérez-Sánchez, M. Solution Approaches for the Management of the Water Resources in Irrigation Water Systems with Fuzzy Costs. Water 2019, 11, 2432. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef]
- Kim, J.H.; Mays, L.W. Optimal rehabilitation model for water-distribution systems. J. Water Resour. Plan. Manag. 1994, 120, 674–692. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Scenario-based robust optimization of regional water and wastewater infrastructure. J. Water Resour. Plan. Manag. 2012, 139, 325–338. [Google Scholar] [CrossRef]
- Dziedzic, R.; Karney, B.W. Cost gradient–based assessment and design improvement technique for water distribution networks with varying loads. J. Water Resour. Plan. Manag. 2015, 142, 04015043. [Google Scholar] [CrossRef]
- Samani, H.M.; Mottaghi, A. Optimization of water distribution networks using integer linear programming. J. Hydraul. Eng. 2006, 132, 501–509. [Google Scholar] [CrossRef]
- Costa, A.; De Medeiros, J.; Pessoa, F. Optimization of pipe networks including pumps by simulated annealing. Braz. J. Chem. Eng. 2000, 17, 887–896. [Google Scholar] [CrossRef]
- Vamvakeridou-Lyroudia, L.; Walters, G.; Savic, D. Fuzzy multiobjective optimization of water distribution networks. J. Water Resour. Plan. Manag. 2005, 131, 467–476. [Google Scholar] [CrossRef]
- Spiliotis, M.; Tsakiris, G. Minimum cost irrigation network design using interactive fuzzy integer programming. J. Irrig. Drain. Eng. 2007, 133, 242–248. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, J.; Gao, J.-L.; Wu, W.-Y. Multi-objective optimization of water supply network rehabilitation with non-dominated sorting genetic algorithm-II. J. Zhejiang Univ. Sci. A 2008, 9, 391–400. [Google Scholar] [CrossRef]
- Roshani, E.; Filion, Y. Event-based approach to optimize the timing of water main rehabilitation with asset management strategies. J. Water Resour. Plan. Manag. 2013, 140, 04014004. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A. An adaptive heuristic cross-entropy algorithm for optimal design of water distribution systems. Eng. Optim. 2007, 39, 413–428. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A.; Salomons, E. Cross entropy multiobjective optimization for water distribution systems design. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, A.R.; Maier, H.R. Multi-objective genetic algorithm optimisation of water distribution systems accounting for sustainability. Proc. Water Down Under 2008, 2008, 1750. [Google Scholar]
- Wu, W.; Simpson, A.R.; Maier, H.R. Accounting for greenhouse gas emissions in multiobjective genetic algorithm optimization of water distribution systems. J. Water Resour. Plan. Manag. 2009, 136, 146–155. [Google Scholar] [CrossRef]
- Wu, W.; Maier, H.R.; Simpson, A.R. Single-objective versus multiobjective optimization of water distribution systems accounting for greenhouse gas emissions by carbon pricing. J. Water Resour. Plan. Manag. 2009, 136, 555–565. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, A.R.; Maier, H.R. Sensitivity of optimal tradeoffs between cost and greenhouse gas emissions for water distribution systems to electricity tariff and generation. J. Water Resour. Plan. Manag. 2011, 138, 182–186. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, A.R.; Maier, H.R.; Marchi, A. Incorporation of variable-speed pumping in multiobjective genetic algorithm optimization of the design of water transmission systems. J. Water Resour. Plan. Manag. 2011, 138, 543–552. [Google Scholar] [CrossRef]
- Stokes, C.S.; Simpson, A.R.; Maier, H.R. A computational software tool for the minimization of costs and greenhouse gas emissions associated with water distribution systems. Environ. Model. Softw. 2015, 69, 452–467. [Google Scholar] [CrossRef]
- Stokes, C.S.; Maier, H.R.; Simpson, A.R. Effect of storage tank size on the minimization of water distribution system cost and greenhouse gas emissions while considering time-dependent emissions factors. J. Water Resour. Plan. Manag. 2015, 142, 04015052. [Google Scholar] [CrossRef]
- Reed, P.M.; Hadka, D.; Herman, J.D.; Kasprzyk, J.R.; Kollat, J.B. Evolutionary multiobjective optimization in water resources: The past, present, and future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Carrasco, F.J.M.; de Marcos, L.G. Dimensionamiento y Optimización de Obras Hidráulicas, 4th ed.; Garceta Grupo Editorial: Malaga, Spain, 2013. (In Spanish) [Google Scholar]
- Granados, A. Problemas de Obras Hidráulicas; Escuela de Ingenieros de Caminos, Canales y Puertos. Servicio de Publicaciones: Madrid, Spain, 1995. (In Spanish) [Google Scholar]
- Ostfeld, A. Optimal design and operation of multiquality networks under unsteady conditions. J. Water Resour. Plan. Manag. 2005, 131, 116–124. [Google Scholar] [CrossRef]
- Gessler, J.; Walski, T.M. Water Distribution System Optimization; Army Engineer Waterways Experiment Station Vicksburg Ms Environmental Lab: Washington, DC, USA, 1985. [Google Scholar]
- Alperovits, E.; Shamir, U. Design of optimal water distribution systems. Water Resour. Res. 1977, 13, 885–900. [Google Scholar] [CrossRef]
- Featherstone, R.E.; El-Jumaily, K.K. Optimal diameter selection for pipe networks. J. Hydraul. Eng. 1983, 109, 221–234. [Google Scholar] [CrossRef]
- Dandy, G.; Hewitson, C. Optimizing hydraulics and water quality in water distribution networks using genetic algorithms. In Building Partnerships, Joint Conference on Water Resource Engineering and Water Resources Planning and Management 2000, Minneapolis, MN, USA, 30 July–2 August 2000; Hotchkiss, R.H., Glade, M., Eds.; ASCE: Reston, VA, USA, 2000; pp. 1–10. [Google Scholar]
- Tsakiris, G.; Spiliotis, M. Fuzzy linear programming for problems of water allocation under uncertainty. Eur. Water 2004, 7, 25–37. [Google Scholar]
- Gonçalves, G.M.; Gouveia, L.; Pato, M.V. An improved decomposition-based heuristic to design a water distribution network for an irrigation system. Ann. Oper. Res. 2014, 219, 141–167. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M.; Savić, D. Using real options in the optimal design of water distribution networks. J. Water Resour. Plan. Manag. 2014, 141, 04014052. [Google Scholar] [CrossRef]
- Schwartz, R.; Housh, M.; Ostfeld, A. Least-cost robust design optimization of water distribution systems under multiple loading. J. Water Resour. Plan. Manag. 2016, 142, 04016031. [Google Scholar] [CrossRef]
- Ostfeld, A.; Tubaltzev, A. Ant colony optimization for least-cost design and operation of pumping water distribution systems. J. Water Resour. Plan. Manag. 2008, 134, 107–118. [Google Scholar] [CrossRef]
- Vicente, D.; Garrote, L.; Sánchez, R.; Santillán, D. Pressure management in water distribution systems: Current status, proposals, and future trends. J. Water Resour. Plan. Manag. 2015, 142, 04015061. [Google Scholar] [CrossRef]
- Capelo, B.; Pérez-Sánchez, M.; Fernandes, J.F.; Ramos, H.M.; López-Jiménez, P.A.; Branco, P.C. Electrical behaviour of the pump working as turbine in off grid operation. Appl. Energy 2017, 208, 302–311. [Google Scholar] [CrossRef]
- Tsakiris, G.; Spiliotis, M. Uncertainty in the analysis of urban water supply and distribution systems. J. Hydroinform. 2017, 19, 823–837. [Google Scholar] [CrossRef][Green Version]
- Fu, G.; Kapelan, Z.; Reed, P. Reducing the complexity of multiobjective water distribution system optimization through global sensitivity analysis. J. Water Resour. Plan. Manag. 2011, 138, 196–207. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.-J.; López-Jiménez, P.A. Huella energética del agua en función de los patrones de consumo en redes de distribución. Ingeniería Agua 2017, 21, 197–212. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. Modified affinity laws in hydraulic machines towards the best efficiency line. Water Resour. Manag. 2018, 32, 829–844. [Google Scholar] [CrossRef]
- Cabreros, J.M. Proyecto de Presa Navas del Marqués; Tajo, C.H.d., Ed.; Ministerio de Medio Ambiente: Ávila, Spain, 1999. (In Spanish)

| Pump Efficiency for Each Flow Rate Interval | ||||||
|---|---|---|---|---|---|---|
| Interval Number | Flow Rate Range | Pump Efficiency | ||||
| Minimum | Maximum | Average | Average | Maximum | Minimum | |
| q (L/s) | q (L/s) | q (L/s) | µB (%) | µB (%) | µB (%) | |
| 1 | 0 | 5 | 2.5 | 55.3% | 77.0% | 36.2% |
| 2 | 5 | 10 | 7.5 | 63.5% | 76.0% | 45.0% |
| 3 | 10 | 15 | 12.5 | 65.7% | 77.0% | 45.0% |
| 4 | 15 | 25 | 20 | 74.2% | 82.0% | 63.0% |
| 5 | 25 | 40 | 32.5 | 75.0% | 85.0% | 61.2% |
| 6 | 40 | 65 | 52.5 | 78.6% | 84.0% | 70.5% |
| 7 | 65 | 100 | 82.5 | 81.0% | 85.4% | 75.4% |
| 8 | 100 | 150 | 125 | 83.1% | 86.0% | 74.0% |
| 9 | 150 | 200 | 175 | 82.8% | 87.0% | 80.4% |
| 10 | 200 | 300 | 250 | 83.9% | 88.0% | 81.0% |
| 11 | 300 | 500 | 400 | 84.9% | 88.8% | 79.9% |
| 12 | 500 | 1000 | 750 | 85.5% | 88.5% | 80.4% |
| 13 | 1000 | 2000 | 1500 | 88.3% | 89.0% | 86.7% |
| 14 | 2000 | 3000 | 2500 | 88.2% | 89.0% | 86.2% |
| Change Gradients | ||||
|---|---|---|---|---|
| Pipe Diameter | Canal de Isabel II | Project Diameters | ||
| Construction Cost | Change Gradient | Construction Cost | Change Gradient | |
| mm | €/m | €/m | €/m | €/m |
| 60 | 55 | 0.11 | ||
| 80 | 64 | 0.26 | ||
| 100 | 69 | 2.11 | ||
| 125 | 79 | 4.84 | ||
| 150 | 86 | 30 | 103 1 | 36 |
| 200 | 105 | 233 | 127 | 256 |
| 250 | 134 | 796 | 159 | 1044 |
| 300 | 161 | 3070 | 194 | 2373 |
| 350 | 197 | 6670 | 221 | 6593 |
| 400 | 227 | 15,972 | 252 | 11,226 |
| 450 | 260 | 33,781 | 295 | 64,309 |
| 500 | 295 | 98,565 | 341 | 76,920 |
| 600 | 378 | 405 | ||
| Pipe Selection | ||||||
|---|---|---|---|---|---|---|
| Annual Unit Energy Cost | Total Unit Energy Cost | Selected Diameter | ||||
| Energy Price | CaE1 | i | fa | CE1 | Canal Isabel II Pipes | Project Pipes |
| €/m/year | % | €/m | mm | mm | ||
| 0.125 €/kWh | 659 | 3 | 18.6 | 12,248 | (a) 400 * | (g) 450 |
| 4 | 15.9 | 10,513 | (b) 400 | (h) 400 | ||
| 5 | 13.8 | 9100 | (c) 400 | (i) 400 | ||
| 0.072 €/kWh | 380 | 3 | 18.6 | 7055 | (d) 400 | (j) 400 |
| 4 | 15.9 | 6056 | (e) 350 | (k) 350 | ||
| 5 | 13.8 | 5242 | (f) 350 | (l) 350 | ||
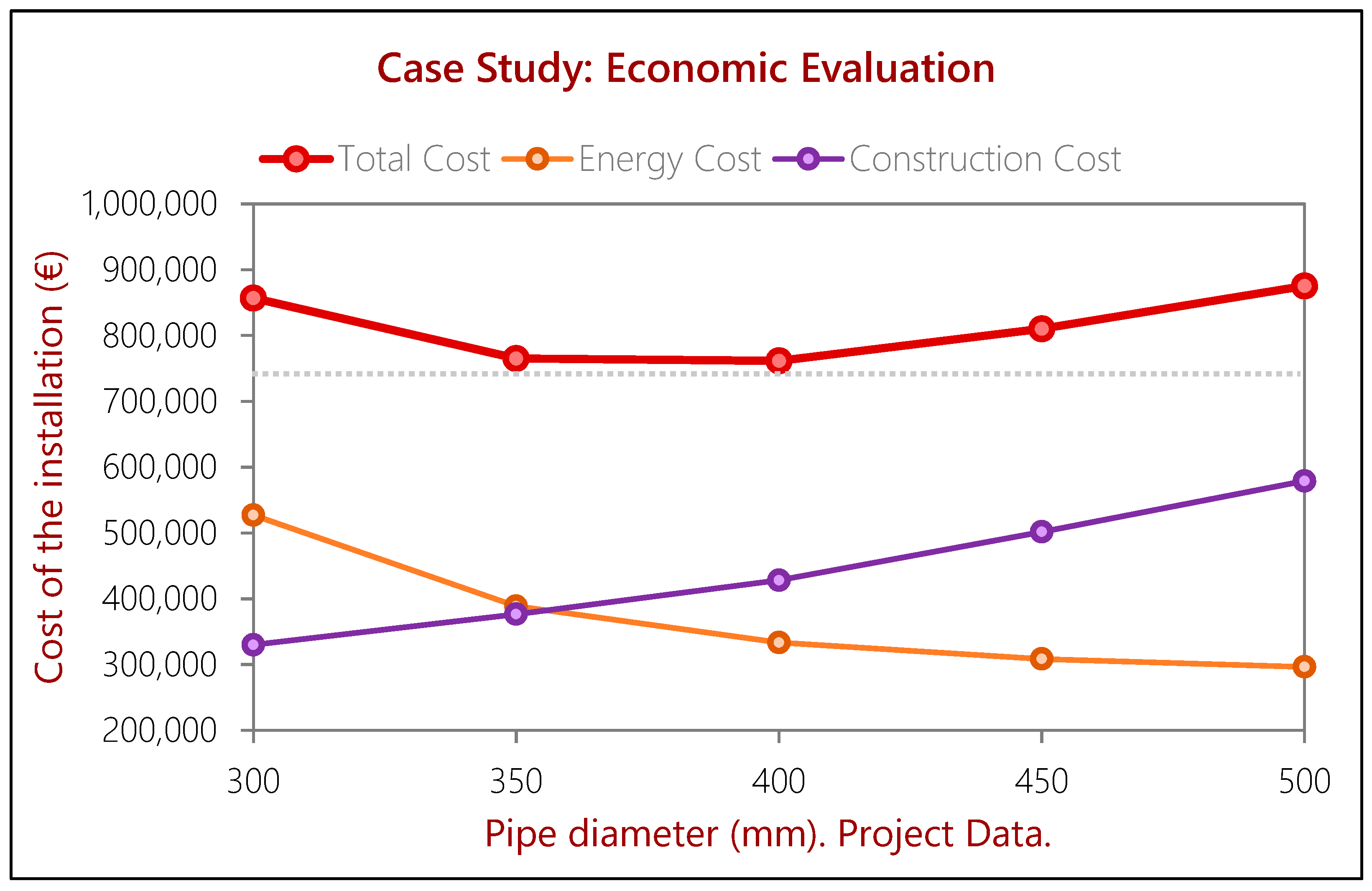
| Economic Evaluation | |||||
|---|---|---|---|---|---|
| Diameter | Construction Costs | Head Loss | Annual Cost | i = 3% | Total Cost |
| Ø | ∆h | caE | CE | ||
| (mm) | € | (m) | (€/year) | (€) | (€) |
| 300 | 329,886 | 35.01 | 28,374 | 527,076 | 856,962 |
| 350 | 376,444 | 15.39 | 20,922 | 388,646 | 765,091 |
| 400 | 428,121 | 7.55 | 17,946 | 333,353 | 761,474 |
| 450 | 501,646 | 4.03 | 16,609 | 308,516 | 810,162 |
| 500 | 578,985 | 2.30 | 15,951 | 296,302 | 875,288 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martin-Candilejo, A.; Santillán, D.; Garrote, L. Pump Efficiency Analysis for Proper Energy Assessment in Optimization of Water Supply Systems. Water 2020, 12, 132. https://doi.org/10.3390/w12010132
Martin-Candilejo A, Santillán D, Garrote L. Pump Efficiency Analysis for Proper Energy Assessment in Optimization of Water Supply Systems. Water. 2020; 12(1):132. https://doi.org/10.3390/w12010132
Chicago/Turabian StyleMartin-Candilejo, Araceli, David Santillán, and Luis Garrote. 2020. "Pump Efficiency Analysis for Proper Energy Assessment in Optimization of Water Supply Systems" Water 12, no. 1: 132. https://doi.org/10.3390/w12010132
APA StyleMartin-Candilejo, A., Santillán, D., & Garrote, L. (2020). Pump Efficiency Analysis for Proper Energy Assessment in Optimization of Water Supply Systems. Water, 12(1), 132. https://doi.org/10.3390/w12010132







