A Continuous Drought Probability Monitoring System, CDPMS, Based on Copulas
Abstract
1. Introduction
2. Materials and Methods
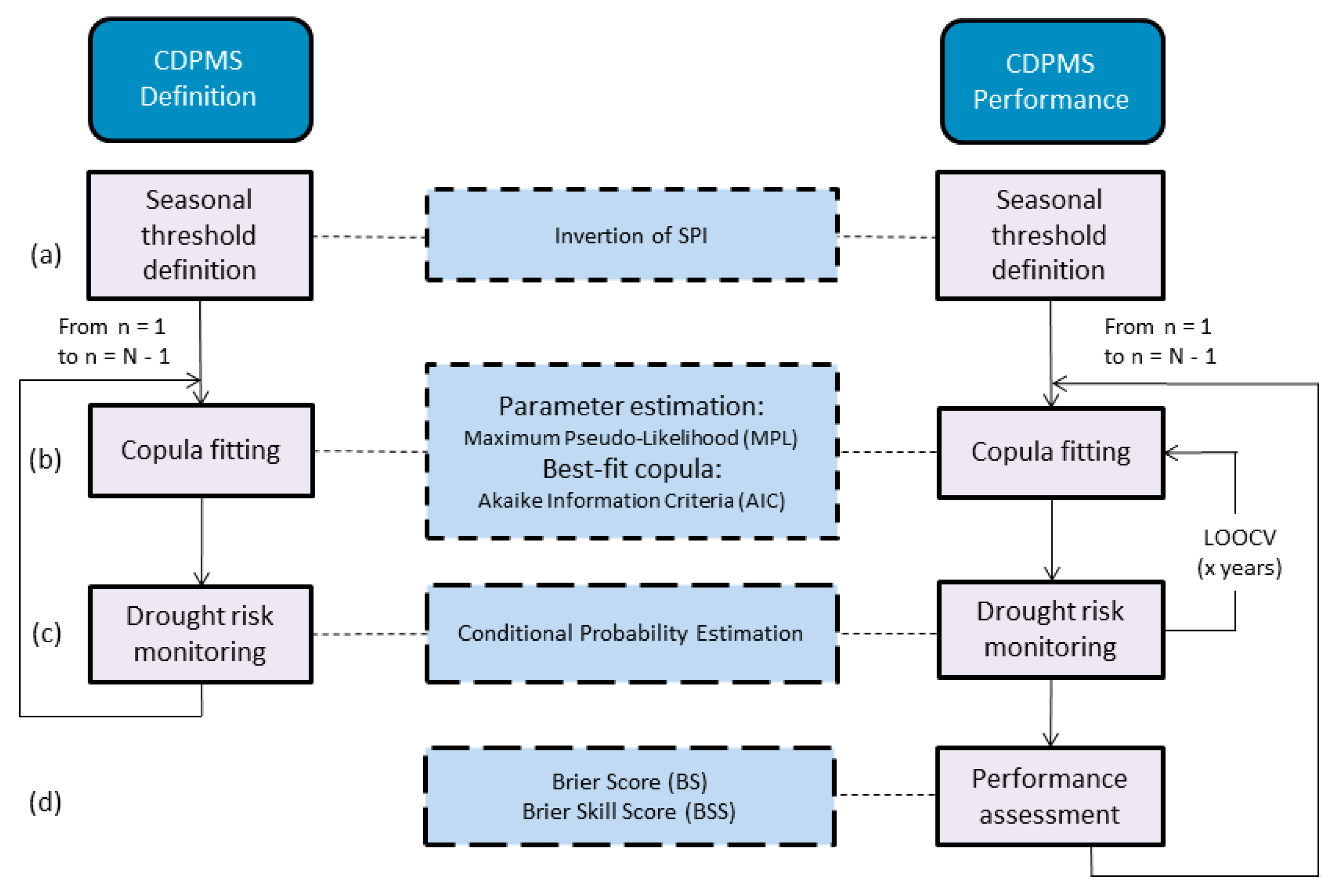
2.1. CDPMS Definition
2.1.1. Seasonal Threshold Definition
2.1.2. Copula Fitting
2.1.3. Conditional Probability
2.2. CDPMS Performance Assessment
2.2.1. Brier Score (BS)
2.2.2. Brier Skill Score (BSS)
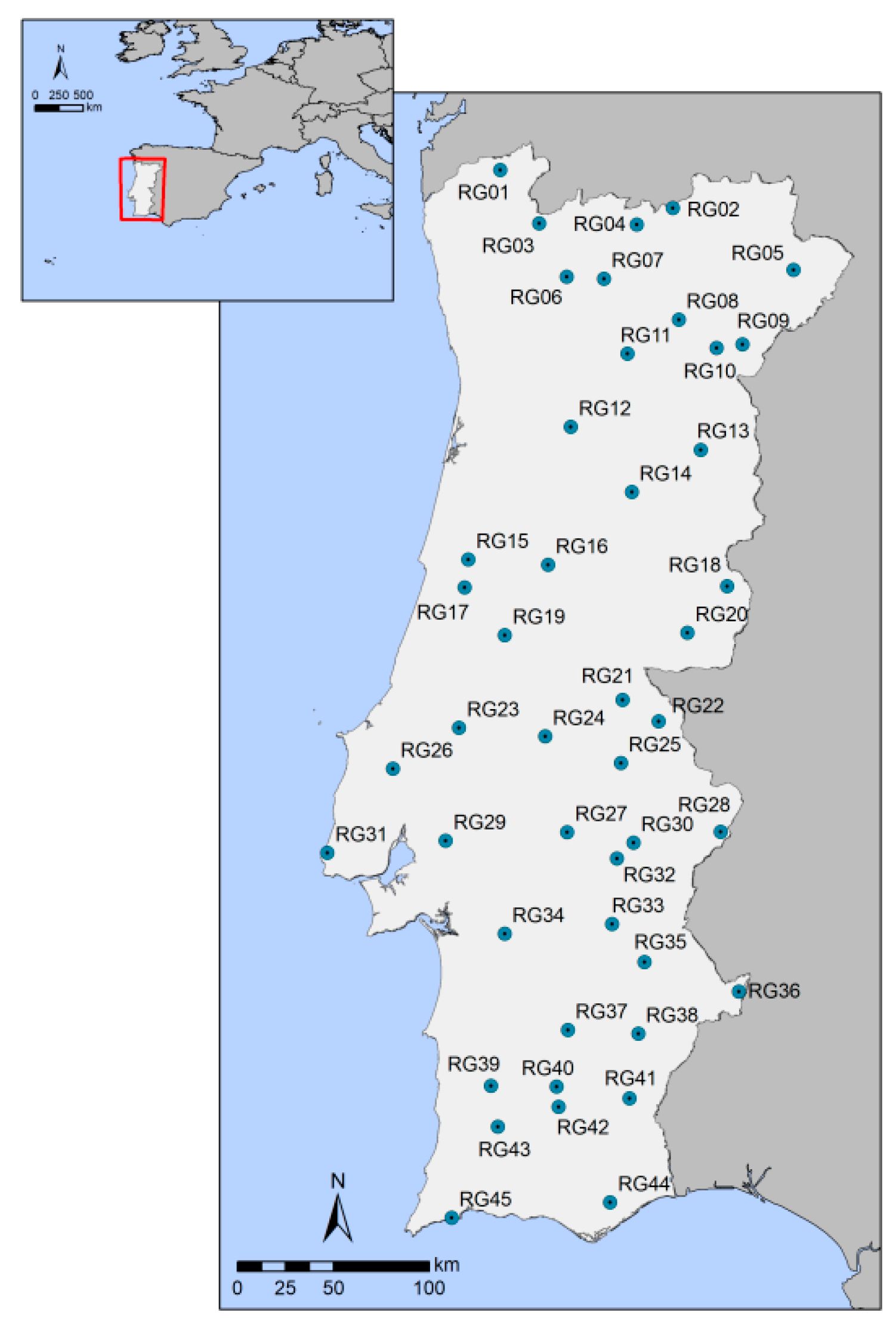
3. Precipitation Data
4. CDPMS for Mainland Portugal: Definition and Performance
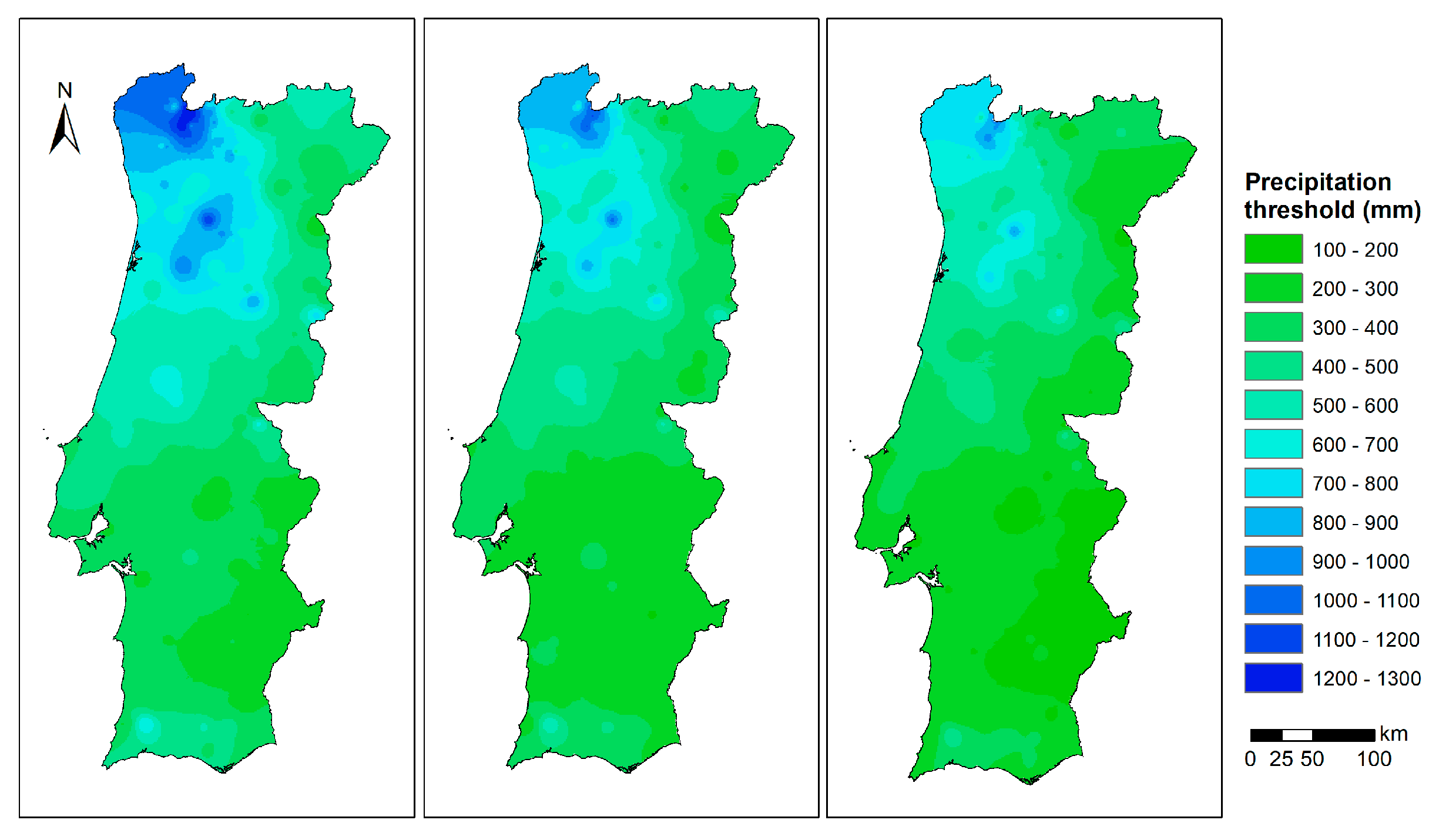
4.1. Precipitation Thresholds for Drought Recognition
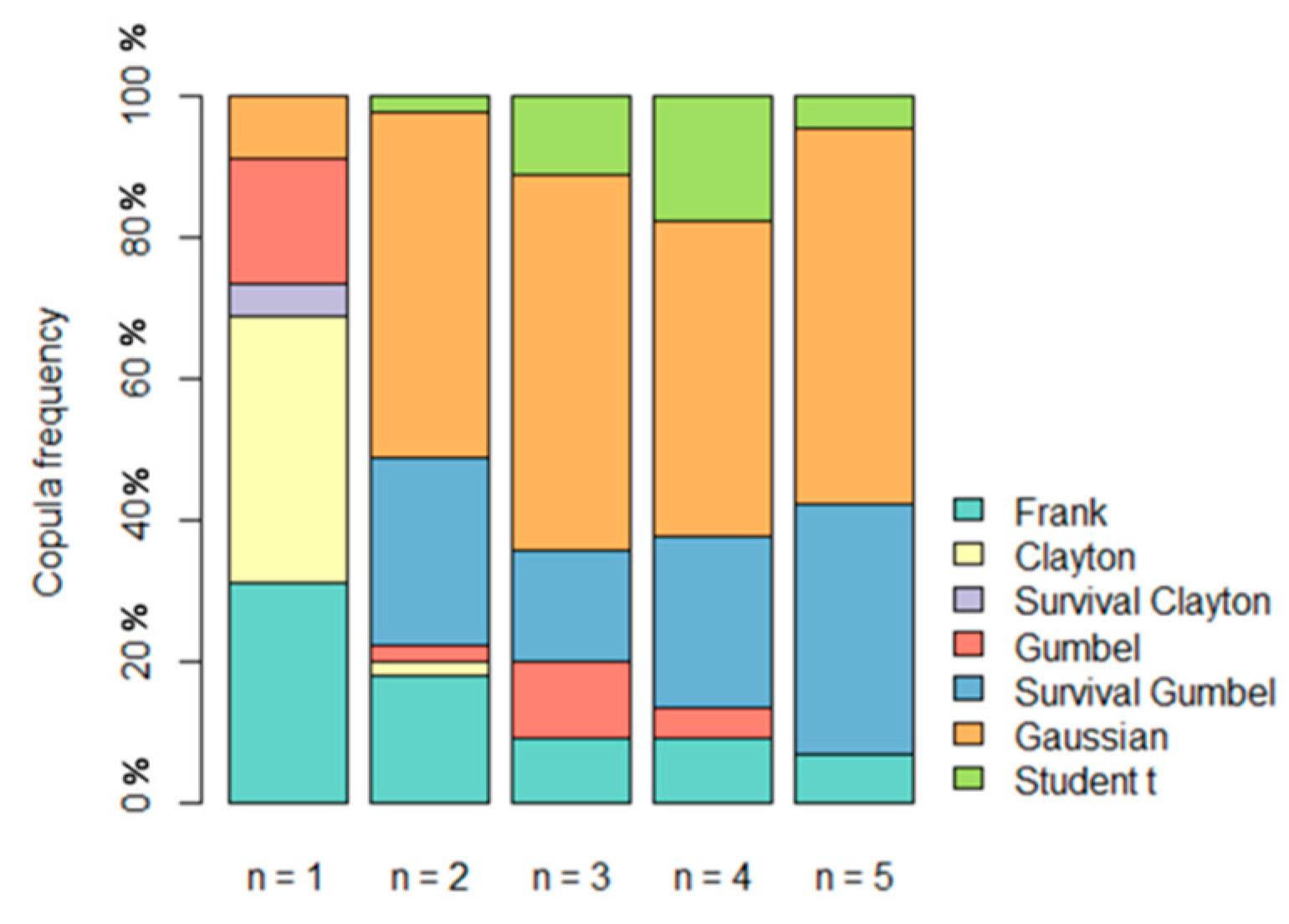
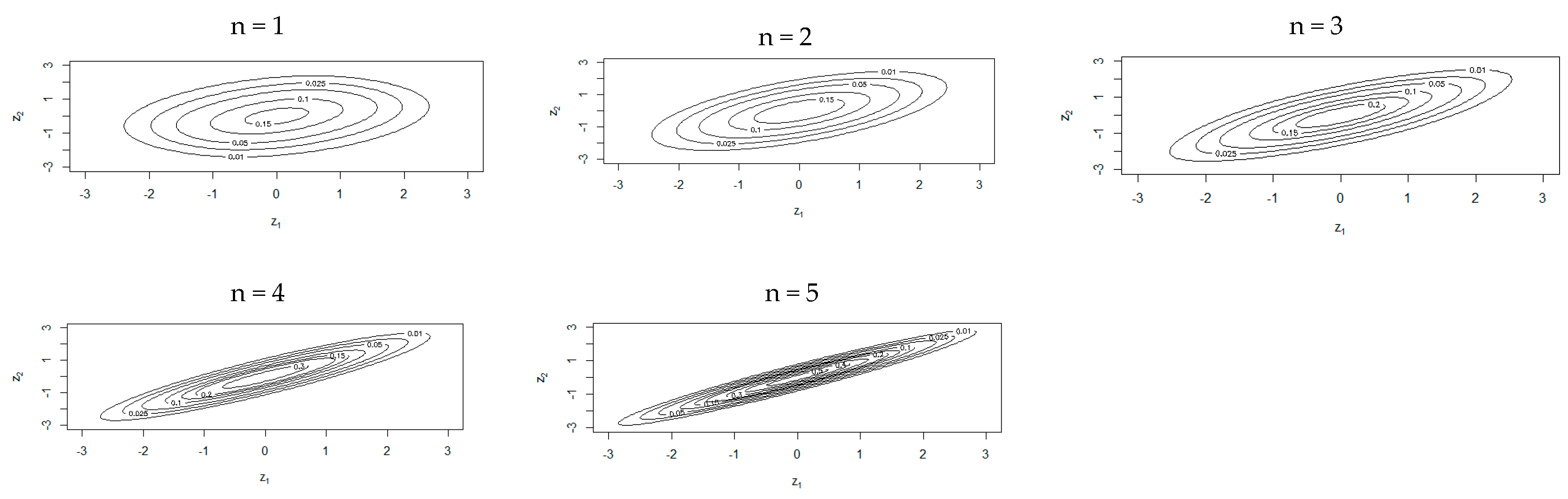
4.2. Copula Fitting
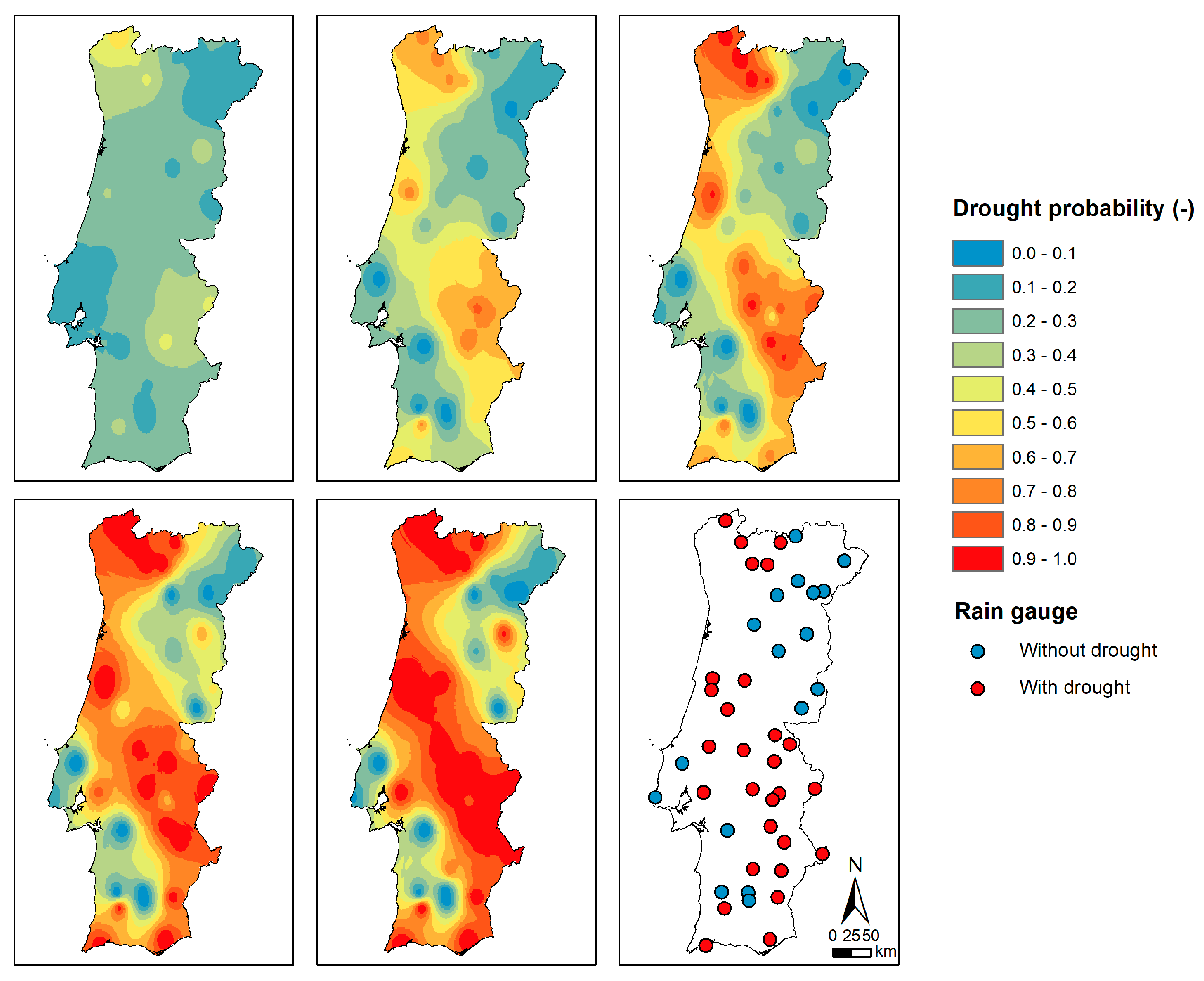
4.3. Drought Risk Monitoring
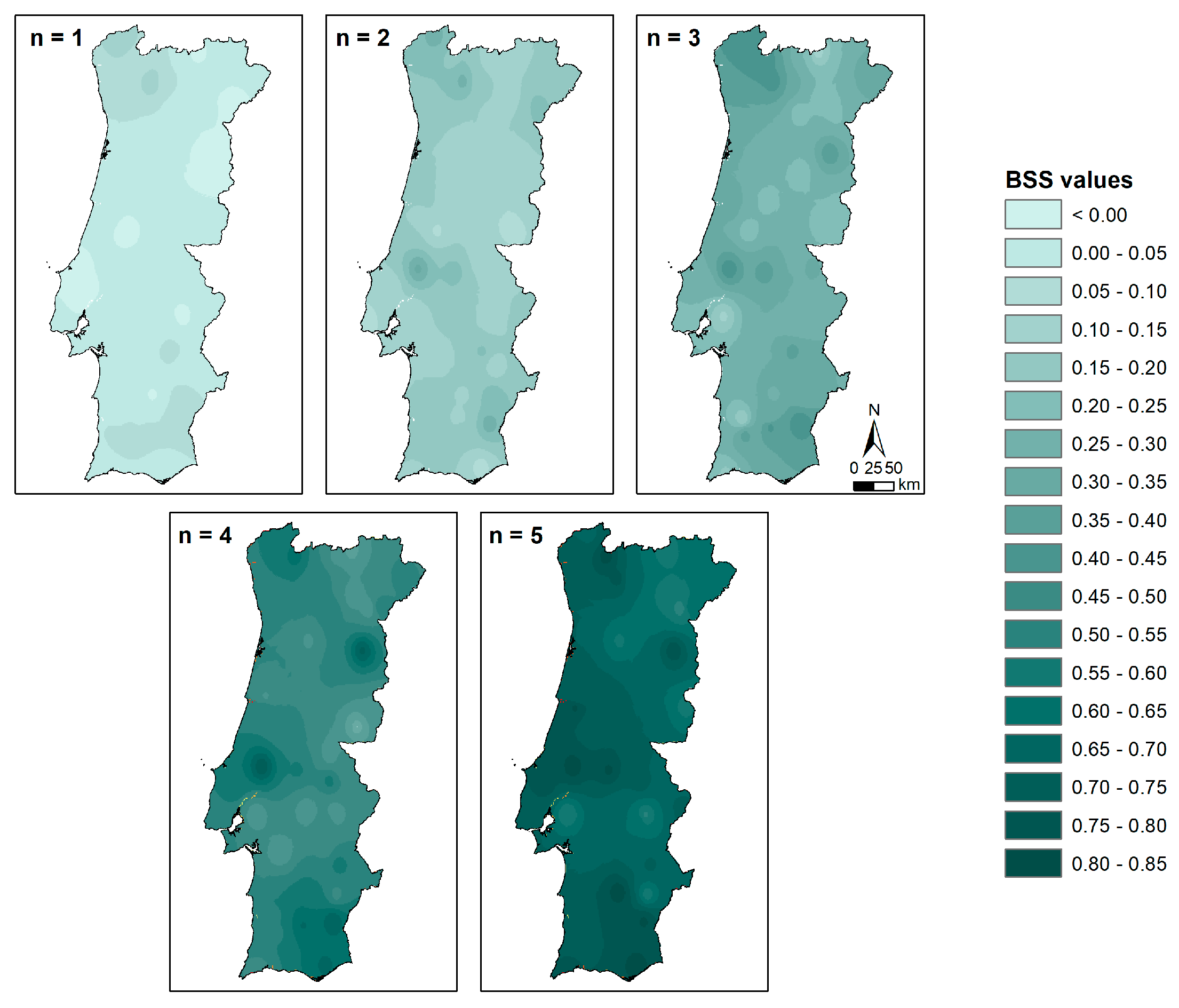
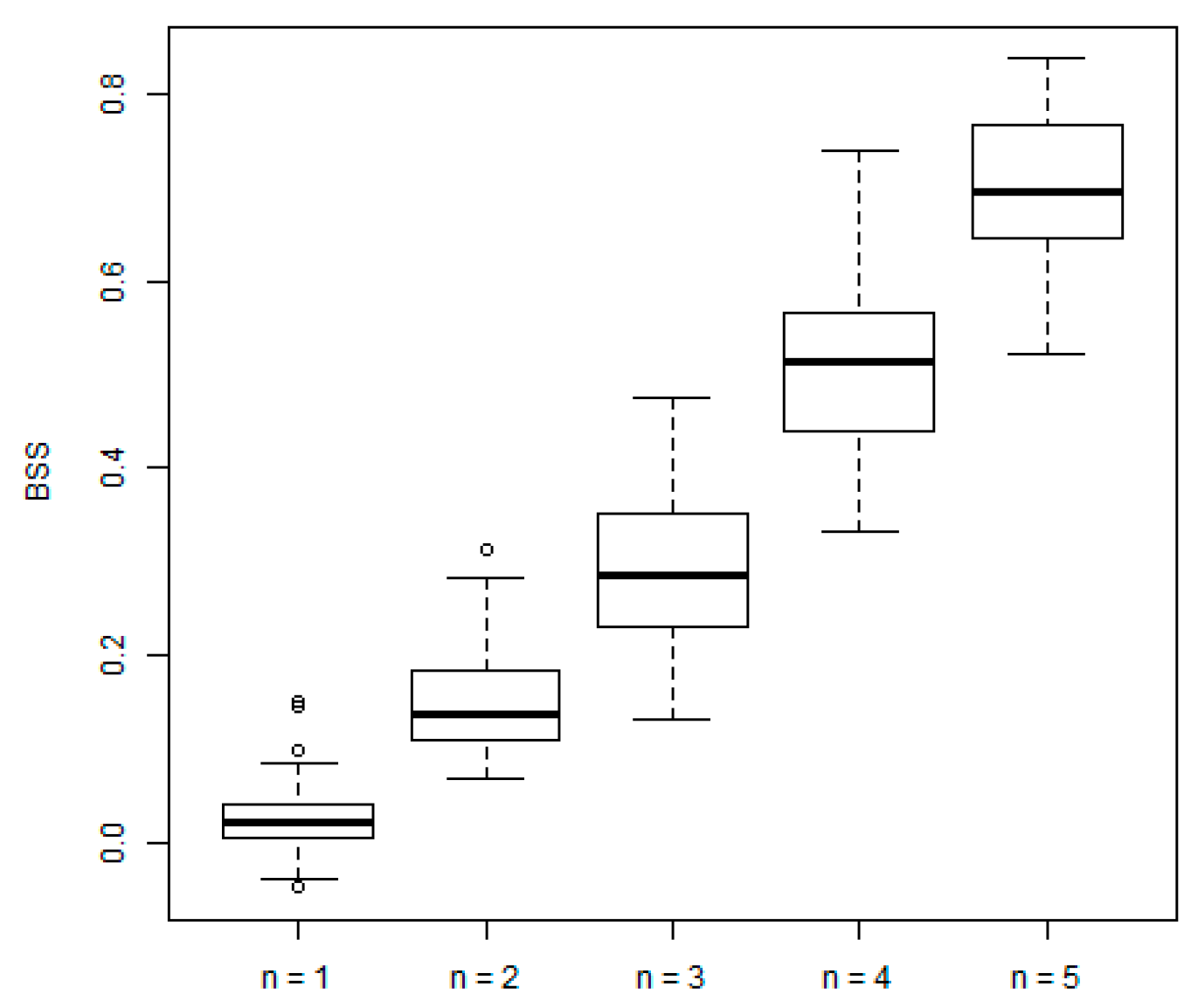
4.4. CDPMS Performance Assessment
5. CDRMS Applied to a Single Site
5.1. CDRMS Development for Santa Marta da Montanha
5.2. CDRMS Application—Drought Risk Monitoring
6. Discussion and Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Wilhite, D.A.; Glantz, M.H. Understanding: The Drought Phenomenon: The Role of Definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The quantification of drought: An evaluation of drought indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- European Commision. Report on the Review of the European Water Scarcity and Droughts Policy; European Commision: Brussels, Belgium, 2012. [Google Scholar]
- Heim, R.R. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Genest, C.; Favre, A.-C. Everything You always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. IDF Curves Using the Frank Archimedean Copula. J. Hydrol. Eng. 2007, 12, 651–662. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Mishra, A.K.; Guo, J. Drought analysis using copulas. J. Hydrol. Eng. 2013, 18, 797–808. [Google Scholar] [CrossRef]
- Lazoglou, G.; Anagnostopoulou, C. Joint distribution of temperature and precipitation in the Mediterranean, using the Copula method. Theor. Appl. Climatol. 2019, 135, 1399–1411. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Review of dependence modeling in hydrology and water resources. Prog. Phys. Geogr. 2016, 40, 549–578. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A. Pair-copula constructions of multiple dependence Projektpartner Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Xu, X.; Lei, H. Copula based drought frequency analysis considering the spatio-temporal variability in Southwest China. J. Hydrol. 2015, 527, 630–640. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Li, J.; Feng, P. Three-dimensional identification of hydrological drought and multivariate drought risk probability assessment in the Luanhe River basin, China. Theor. Appl. Climatol. 2019. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Li, Y.; Song, S.; Javed, T.; Yao, N. Probabilistic modelling of drought events in China via 2-dimensional joint copula. J. Hydrol. 2018, 559, 373–391. [Google Scholar] [CrossRef]
- Montaseri, M.; Amirataee, B.; Rezaie, H. New approach in bivariate drought duration and severity analysis. J. Hydrol. 2018, 559, 166–181. [Google Scholar] [CrossRef]
- Kao, S.C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Chang, J.; Li, Y.; Wang, Y.; Yuan, M. Copula-based drought risk assessment combined with an integrated index in the Wei River Basin, China. J Hydrol. 2016, 540, 824–834. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Ren, L.; Yong, B.; Singh, V.P.; Yuan, F.; Jiang, S.; Yang, X. On the mechanisms of two composite methods for construction of multivariate drought indices. Sci. Total Environ. 2019, 647, 981–991. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Can, I. Application of copulas for regional bivariate frequency analysis of meteorological droughts in Turkey. Nat. Hazards 2016. [Google Scholar] [CrossRef]
- Shin, J.Y.; Chen, S.; Lee, J.-H.; Kim, T.-W. Investigation of drought propagation in South Korea using drought index and conditional probability. Terr. Atmos. Ocean. Sci. 2018, 29, 231–241. [Google Scholar] [CrossRef]
- Portela, M.M.; dos Santos, J.F.F.; Naghettini, M.; Matos, J.P.; Silva, A.T. Superfícies de limiares de precipitação para identificação de secas em Portugal continental: Uma aplicação complementar do Índice de Precipitação Padronizada, SPI. Rev. Recur. Hídricos. 2012, 33, 5–23. [Google Scholar] [CrossRef]
- Dos Santos, J.F.F.; Portela, M.M.; Naghettini, M.; Matos, J.P.; Silva, A.T. Precipitation thresholds for drought recognition: A complementary use of the standardized precipitation index, SPI. River Basin Manag. 2013. [Google Scholar] [CrossRef]
- Dos Santos, J.F.F. Drought Analysis in Mainland Portugal: Spatial Distribution, Frequency and Hindcasting. Ph.D. Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2012. [Google Scholar]
- Agnew, C. Using the SPI to identify drought. Drought Netw. News 2000, 12, 5–12. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006; pp. 1–656. [Google Scholar]
- Ayantobo, O.O.; Li, Y.; Song, S. Multivariate drought frequency analysis using four-variate symmetric and asymmetric archimedean copula functions. Water Resour. Manag. 2019, 33, 103–127. [Google Scholar] [CrossRef]
- Zhang, Q.; Xiao, M.; Singh, V.P.; Chen, X. Copula-based risk evaluation of hydrological droughts in the East River basin, China. Stoch. Environ. Res. Risk Assess. 2013. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Copula-based stochastic uncertainty analysis of satellite precipitation products. J Hydrol. 2019, 570, 739–754. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Dependence Concepts; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Genest, C.; Ghoudi, K.; Rivest, L.P. A semiparametric estimation procedure of dependence parameters in multivariate families of distributions. Biometrika 1995, 82, 543–552. [Google Scholar] [CrossRef]
- Brechmann, E.C.; Schepsmeier, U. Modeling Dependence with C- and D-Vine Copulas: The R Package CDVine. J. Stat. Softw. 2013, 52. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; pp. 2–676. [Google Scholar]
- Klein, B.; Meissner, D.; Kobialka, H.-U.; Reggiani, P. Predictive Uncertainty Estimation of Hydrological Multi-Model Ensembles Using Pair-Copula Construction. Water 2016, 8, 125. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Zhang, X. Statistical prediction of the severity of compound dry-hot events based on El Niño-Southern Oscillation. J. Hydrol. 2019. [Google Scholar] [CrossRef]
- Portela, M.M.; Zeleňáková, M.; dos Santos, J.F.F.; Purcz, P.; Silva, A.T.; Hlavatá, H. A comprehensive drought analysis in Slovakia using SPI. Eur Water. 2015, 51, 15–31. [Google Scholar]
- Russo, A.C.; Gouveia, C.M.; Trigo, R.M.; Liberato, M.L.R.; DaCamara, C.C. The influence of circulation weather patterns at different spatial scales on drought variability in the Iberian Peninsula. Front. Environ. Sci. 2015, 3, 1–15. [Google Scholar] [CrossRef]
- Trigo, R.M.; DaCamara, C.C. Circulation weather types and their influence on the precipitation regime in Portugal. Int. J. Climatol. 2000, 20, 1559–1581. [Google Scholar] [CrossRef]
- Trigo, R.M.; Valente, M.A.; Trigo, I.F.; Miranda, P.M.A.; Ramos, A.M.; Paredes, D.; García-Herrera, R. The impact of North Atlantic wind and cyclone trends on European precipitation and significant wave height in the Atlantic. Ann. N Y Acad. Sci. 2008, 1146, 212–234. [Google Scholar] [CrossRef] [PubMed]
- Trigo, R.M.; Pozo-Vázquez, D.; Osborn, T.J.; Castro-Díez, Y.; Gámiz-Fortis, S.; Esteban-Parra, M.J. North Atlantic oscillation influence on precipitation, river flow and water resources in the Iberian Peninsula. Int. J. Climatol. 2004, 24, 925–944. [Google Scholar] [CrossRef]
- Cortesi, N.; Gonzalez-Hidalgo, J.C.; Trigo, R.M.; Ramos, A.M. Weather types and spatial variability of precipitation in the Iberian Peninsula. Int. J. Climatol. 2014, 34, 2661–2677. [Google Scholar] [CrossRef]
- Santos, J.F.; Portela, M.M.; Pulido-Calvo, I. Spring drought prediction based on winter NAO and global SST in Portugal. Hydrol. Process. 2014, 28, 1009–1024. [Google Scholar] [CrossRef]
- Del Valle García Valdecasas Ojeda, M.M. Climate-Change Projections in the Iberian Peninsula: A Study on the Hydrological Impacts. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2018. [Google Scholar]
- Silva, A.T. Nonstationarity and Uncertainty of Extreme Hydrological Events. Ph.D. Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2018. [Google Scholar]

| Drought Class | Probability | SPI Value |
|---|---|---|
| Moderate Drought | 0.20 | Less than −0.84 |
| Severe Drought | 0.10 | Less than −1.28 |
| Extreme Drought | 0.05 | Less than −1.65 |
| Class | Family | Parameter Range | |
|---|---|---|---|
| Archimedean | Gumbel | ||
| Archimedean | Frank | ||
| Archimedean | Clayton | ||
| Meta-Elliptical | Gaussian | ||
| Meta-Elliptical | t Student |
| Name | Code | ID | Lat (°) | Long (°) |
|---|---|---|---|---|
| Merufe | 01G03UG | RG01 | 42.0180 | −8.3890 |
| Travancas | 03N01G | RG02 | 41.8280 | −7.3056 |
| Leonte | 03I03UG | RG03 | 41.7650 | −8.1470 |
| Soutelo (Chaves) | 03L02UG | RG04 | 41.7530 | −7.5348 |
| Campo de Víboras | 04R03UG | RG05 | 41.5240 | −6.5580 |
| Cabeceiras de Basto | 04J06UG | RG06 | 41.5127 | −7.9792 |
| Santa Marta da Montanha | 04K02G | RG07 | 41.5008 | −7.7460 |
| Folgares | 06N01C | RG08 | 41.3032 | −7.2828 |
| Carviçais | 06P02UG | RG09 | 41.1790 | −6.8900 |
| Moncorvo | 06O04UG | RG10 | 41.1650 | −7.0510 |
| Adorigo | 07L01U | RG11 | 41.1460 | −7.6070 |
| Pindelo dos Milagres | 09J02U | RG12 | 40.8060 | −7.9630 |
| Freixedas | 09O02U | RG13 | 40.6880 | −7.1630 |
| Gouveia | 11L01UG | RG14 | 40.4940 | −7.5930 |
| Santo Varão | 12F02C | RG15 | 40.1840 | −8.6020 |
| Góis | 13I01G | RG16 | 40.1568 | −8.1133 |
| Soure | 13F01G | RG17 | 40.0521 | −8.6250 |
| Penha Garcia | 13O01UG | RG18 | 40.0420 | −7.0180 |
| Alvaiázere | 15G01UG | RG19 | 39.8270 | −8.3810 |
| Ladoeiro | 14N02UG | RG20 | 39.8269 | −7.2660 |
| Nisa | 16L03UG | RG21 | 39.5160 | −7.6690 |
| Castelo de Vide | 17M01G | RG22 | 39.4116 | −7.4525 |
| Pernes | 17F01UG | RG23 | 39.3910 | −8.6630 |
| Bemposta | 17I02UG | RG24 | 39.3490 | −8.1410 |
| Alter do Chão | 18L01UG | RG25 | 39.2182 | −7.6844 |
| Pragança | 18C01G | RG26 | 39.1990 | −9.0640 |
| Pavia | 20I01G | RG27 | 38.8965 | −8.0136 |
| Caia (Monte Caldeiras) | 20O02UG | RG28 | 38.8873 | −7.0898 |
| Santo Estevão | 20E02UG | RG29 | 38.8600 | −8.7460 |
| Estremoz | 20L01G | RG30 | 38.8416 | −7.6159 |
| Colares (Sarrazola) | 21A01C | RG31 | 38.8020 | −9.4570 |
| Évora−Monte | 21K02UG | RG32 | 38.7690 | −7.7161 |
| São Manços | 23K01UG | RG33 | 38.4605 | −7.7505 |
| Barragem de Pego do Altar | 23G01C | RG34 | 38.4196 | −8.3952 |
| Amieira | 24L01C | RG35 | 38.2793 | −7.5605 |
| Barrancos | 25P01UG | RG36 | 38.1321 | −7.0013 |
| Santa Vitória | 26I01UG | RG37 | 37.9645 | −8.0227 |
| Serpa | 26L01UG | RG38 | 37.9426 | −7.6038 |
| Relíquias | 27G01G | RG39 | 37.7030 | −8.4825 |
| Castro Verde | 27I01G | RG40 | 37.6976 | −8.0933 |
| Mértola | 28L01UG | RG41 | 37.6371 | −7.6619 |
| Rosário (Almodôvar) | 28I02U | RG42 | 37.6020 | −8.0810 |
| Barragem de Mira | 28G01C | RG43 | 37.5101 | −8.4433 |
| Santa Catarina (Tavira) | 31K01UG | RG44 | 37.1487 | −7.7847 |
| Valverde | 31E03C | RG45 | 37.0820 | −8.7180 |
| Rain Gauge ID | Drought Intensity | Rain Gauge ID | Drought Intensity | ||||
|---|---|---|---|---|---|---|---|
| Moderate | Severe | Extreme | Moderate | Severe | Extreme | ||
| RG01 | 745.2 | 550.6 | 411.7 | RG23 | 379.6 | 288.8 | 218.2 |
| RG02 | 429.9 | 351.9 | 297.6 | RG24 | 307.4 | 226.9 | 165.0 |
| RG03 | 1250.0 | 933.9 | 701.4 | RG25 | 269.9 | 190.0 | 126.2 |
| RG04 | 338.9 | 272.4 | 228.7 | RG26 | 442.1 | 357.1 | 294.9 |
| RG05 | 252.7 | 212.2 | 189.9 | RG27 | 245.4 | 181.4 | 132.1 |
| RG06 | 624.0 | 467.6 | 350.5 | RG28 | 228.6 | 169.4 | 122.5 |
| RG07 | 774.4 | 614.7 | 500.8 | RG29 | 272.3 | 208.9 | 160.4 |
| RG08 | 250.9 | 197.3 | 158.8 | RG30 | 281.6 | 208.1 | 151.8 |
| RG09 | 290.0 | 221.5 | 172.2 | RG31 | 371.7 | 309.3 | 263.1 |
| RG10 | 225.0 | 175.0 | 137.3 | RG32 | 265.6 | 201.5 | 152.4 |
| RG11 | 280.2 | 223.0 | 182.2 | RG33 | 238.9 | 178.1 | 130.7 |
| RG12 | 601.4 | 479.3 | 393.2 | RG34 | 269.6 | 214.9 | 174.6 |
| RG13 | 311.6 | 232.8 | 170.6 | RG35 | 256.2 | 202.4 | 162.6 |
| RG14 | 517.3 | 419.1 | 345.1 | RG36 | 260.6 | 204.4 | 160.0 |
| RG15 | 446.4 | 361.0 | 294.2 | RG37 | 251.9 | 197.7 | 155.9 |
| RG16 | 557.5 | 449.0 | 364.9 | RG38 | 237.9 | 182.4 | 140.6 |
| RG17 | 415.4 | 320.1 | 246.6 | RG39 | 311.3 | 242.3 | 191.1 |
| RG18 | 383.7 | 310.8 | 255.6 | RG40 | 267.9 | 215.7 | 175.7 |
| RG19 | 586.6 | 468.6 | 378.5 | RG41 | 184.5 | 146.8 | 120.9 |
| RG20 | 288.6 | 234.7 | 194.2 | RG42 | 284.4 | 223.2 | 176.3 |
| RG21 | 331.5 | 256.7 | 199.4 | RG43 | 292.3 | 225.8 | 173.2 |
| RG22 | 370.7 | 284.5 | 221.8 | RG44 | 318.5 | 239.5 | 180.3 |
| RG45 | 289.5 | 229.0 | 182.3 | ||||
| Rain Gauge ID | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | Average |
|---|---|---|---|---|---|---|
| RG01 | 0.15 | 0.27 | 0.46 | 0.57 | 0.69 | 0.43 |
| RG02 | −0.02 | 0.10 | 0.13 | 0.37 | 0.55 | 0.23 |
| RG03 | 0.05 | 0.19 | 0.47 | 0.63 | 0.83 | 0.44 |
| RG04 | 0.04 | 0.10 | 0.25 | 0.44 | 0.65 | 0.30 |
| RG05 | 0.00 | 0.18 | 0.35 | 0.51 | 0.65 | 0.34 |
| RG06 | 0.15 | 0.27 | 0.44 | 0.55 | 0.77 | 0.44 |
| RG07 | 0.06 | 0.18 | 0.35 | 0.52 | 0.66 | 0.35 |
| RG08 | 0.04 | 0.11 | 0.23 | 0.41 | 0.56 | 0.27 |
| RG09 | −0.03 | 0.25 | 0.27 | 0.53 | 0.62 | 0.33 |
| RG10 | 0.01 | 0.16 | 0.22 | 0.41 | 0.52 | 0.27 |
| RG11 | 0.02 | 0.14 | 0.22 | 0.53 | 0.64 | 0.31 |
| RG12 | 0.01 | 0.13 | 0.28 | 0.44 | 0.59 | 0.29 |
| RG13 | −0.03 | 0.14 | 0.39 | 0.71 | 0.79 | 0.40 |
| RG14 | 0.00 | 0.11 | 0.23 | 0.52 | 0.66 | 0.30 |
| RG15 | 0.02 | 0.19 | 0.32 | 0.44 | 0.70 | 0.33 |
| RG16 | 0.01 | 0.11 | 0.23 | 0.50 | 0.73 | 0.32 |
| RG17 | 0.02 | 0.13 | 0.31 | 0.54 | 0.81 | 0.36 |
| RG18 | 0.00 | 0.12 | 0.23 | 0.44 | 0.58 | 0.27 |
| RG19 | −0.02 | 0.09 | 0.21 | 0.50 | 0.70 | 0.29 |
| RG20 | 0.01 | 0.07 | 0.21 | 0.33 | 0.65 | 0.25 |
| RG21 | 0.01 | 0.10 | 0.29 | 0.42 | 0.74 | 0.31 |
| RG22 | 0.00 | 0.13 | 0.31 | 0.47 | 0.69 | 0.32 |
| RG23 | 0.01 | 0.31 | 0.44 | 0.74 | 0.83 | 0.47 |
| RG24 | 0.03 | 0.23 | 0.38 | 0.56 | 0.81 | 0.40 |
| RG25 | 0.02 | 0.15 | 0.30 | 0.57 | 0.73 | 0.35 |
| RG26 | −0.05 | 0.12 | 0.25 | 0.60 | 0.78 | 0.34 |
| RG27 | 0.03 | 0.17 | 0.30 | 0.41 | 0.67 | 0.32 |
| RG28 | 0.03 | 0.18 | 0.29 | 0.47 | 0.72 | 0.34 |
| RG29 | 0.02 | 0.10 | 0.14 | 0.41 | 0.55 | 0.24 |
| RG30 | −0.04 | 0.11 | 0.27 | 0.40 | 0.54 | 0.25 |
| RG31 | 0.03 | 0.07 | 0.24 | 0.51 | 0.73 | 0.32 |
| RG32 | 0.05 | 0.15 | 0.25 | 0.49 | 0.62 | 0.31 |
| RG33 | 0.08 | 0.21 | 0.37 | 0.48 | 0.67 | 0.36 |
| RG34 | 0.01 | 0.13 | 0.27 | 0.41 | 0.68 | 0.30 |
| RG35 | 0.01 | 0.11 | 0.32 | 0.57 | 0.71 | 0.34 |
| RG36 | 0.04 | 0.19 | 0.29 | 0.54 | 0.68 | 0.35 |
| RG37 | −0.01 | 0.14 | 0.29 | 0.57 | 0.84 | 0.36 |
| RG38 | 0.07 | 0.24 | 0.31 | 0.48 | 0.57 | 0.33 |
| RG39 | 0.04 | 0.17 | 0.15 | 0.54 | 0.71 | 0.32 |
| RG40 | 0.03 | 0.13 | 0.31 | 0.61 | 0.80 | 0.37 |
| RG41 | 0.10 | 0.28 | 0.47 | 0.70 | 0.81 | 0.47 |
| RG42 | 0.07 | 0.16 | 0.42 | 0.66 | 0.78 | 0.42 |
| RG43 | 0.08 | 0.20 | 0.37 | 0.54 | 0.70 | 0.38 |
| RG44 | 0.03 | 0.08 | 0.35 | 0.66 | 0.82 | 0.39 |
| RG45 | 0.01 | 0.14 | 0.19 | 0.47 | 0.76 | 0.32 |
| Average | 0.03 | 0.16 | 0.30 | 0.51 | 0.70 | 0.34 |
| Family | Parameters | Kendall’s Tau | AIC | p-Value | |||
|---|---|---|---|---|---|---|---|
| Model | Empirical | ||||||
| n = 1 | Frank | 1.75 | - | 0.19 | 0.19 | −6.16 | <0.05 |
| n = 2 | Gaussian | 0.60 | - | 0.41 | 0.40 | −37.86 | <0.05 |
| n = 3 | t Student | 0.76 | 30.00 | 0.55 | 0.53 | −75.34 | <0.05 |
| n = 4 | Gaussian | 0.91 | - | 0.72 | 0.72 | −161.84 | <0.05 |
| n = 5 | Gaussian | 0.96 | - | 0.83 | 0.83 | −251.14 | <0.05 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pontes Filho, J.D.; Portela, M.M.; Marinho de Carvalho Studart, T.; Souza Filho, F.d.A. A Continuous Drought Probability Monitoring System, CDPMS, Based on Copulas. Water 2019, 11, 1925. https://doi.org/10.3390/w11091925
Pontes Filho JD, Portela MM, Marinho de Carvalho Studart T, Souza Filho FdA. A Continuous Drought Probability Monitoring System, CDPMS, Based on Copulas. Water. 2019; 11(9):1925. https://doi.org/10.3390/w11091925
Chicago/Turabian StylePontes Filho, João Dehon, Maria Manuela Portela, Ticiana Marinho de Carvalho Studart, and Francisco de Assis Souza Filho. 2019. "A Continuous Drought Probability Monitoring System, CDPMS, Based on Copulas" Water 11, no. 9: 1925. https://doi.org/10.3390/w11091925
APA StylePontes Filho, J. D., Portela, M. M., Marinho de Carvalho Studart, T., & Souza Filho, F. d. A. (2019). A Continuous Drought Probability Monitoring System, CDPMS, Based on Copulas. Water, 11(9), 1925. https://doi.org/10.3390/w11091925






