Physical Experiment and Modeling of the Transport and Deposition of Polydisperse Particles in Stormwater: Effects of a Depth-Dependent Initial Filter Coefficient
Abstract
1. Introduction
2. Materials and Methods
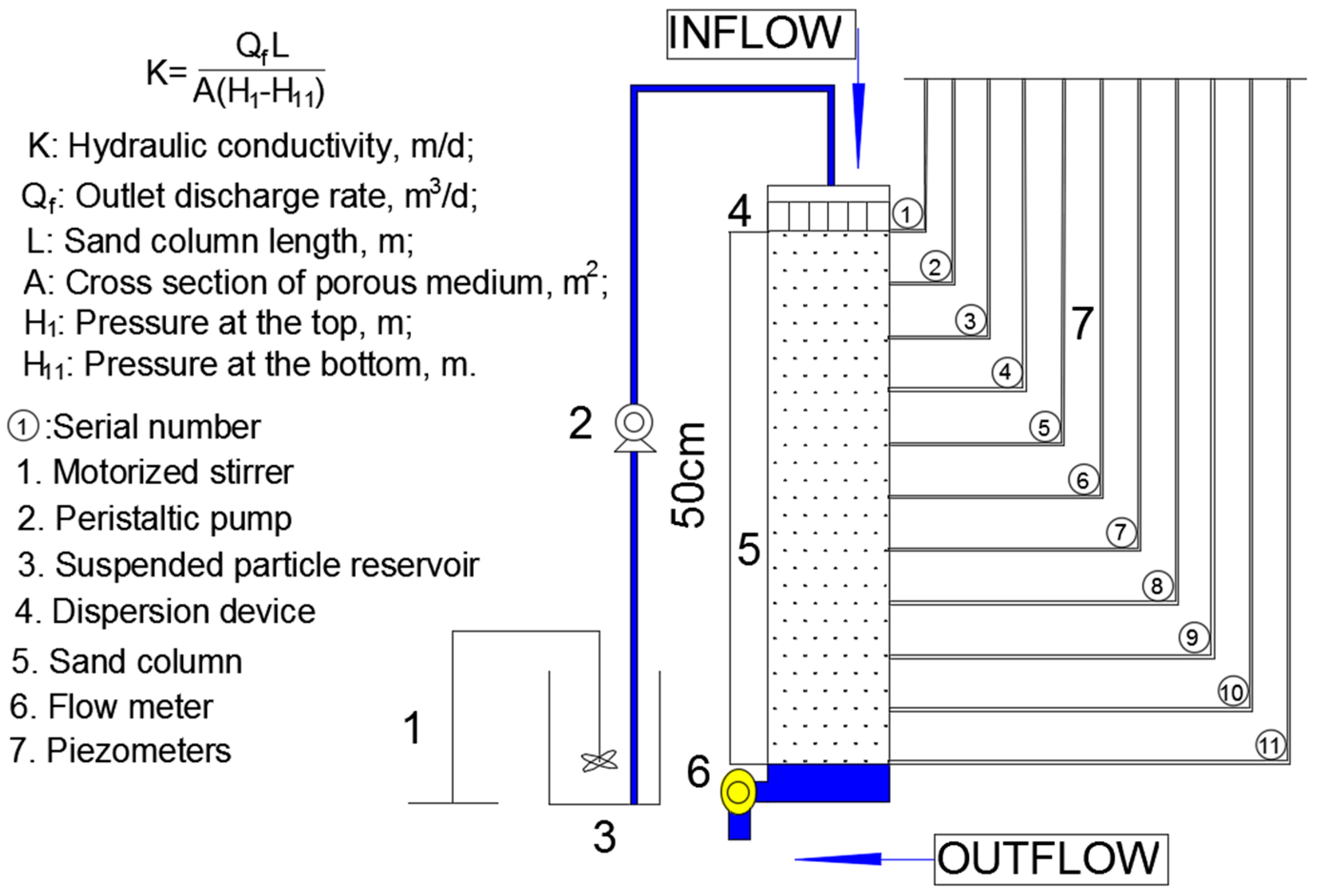
2.1. Design of the Sand Column
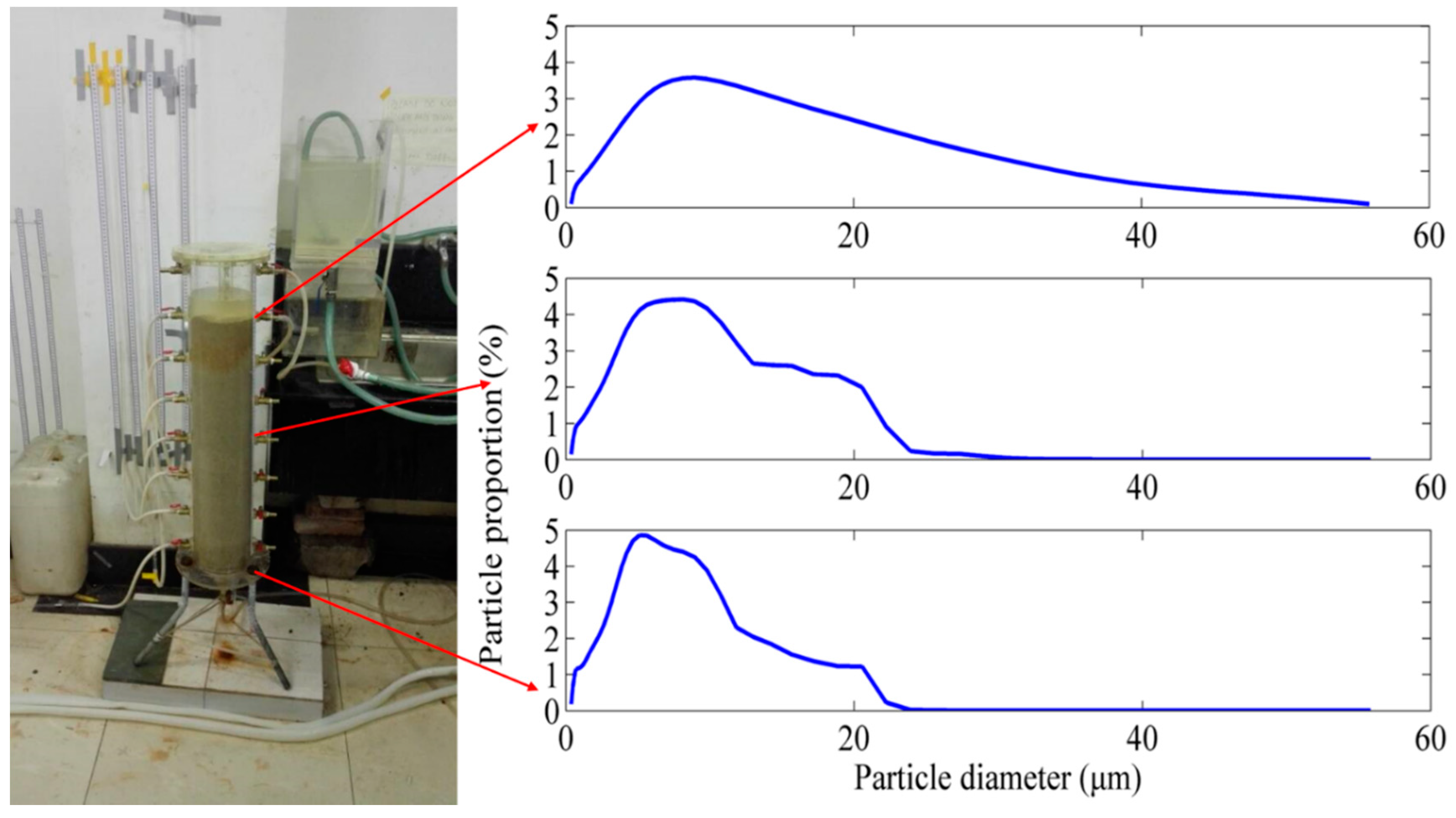
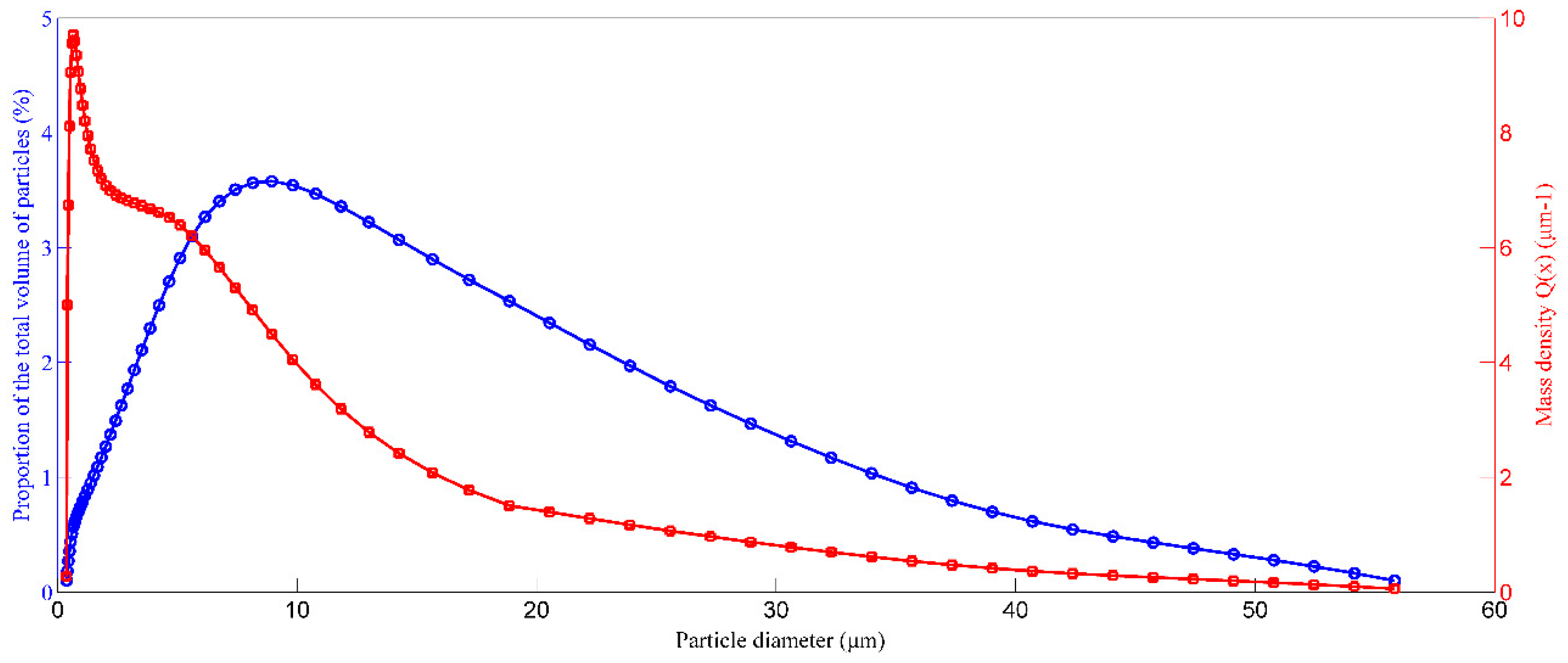
2.2. Characteristics of Suspended Particles (SP) and Porous Medium
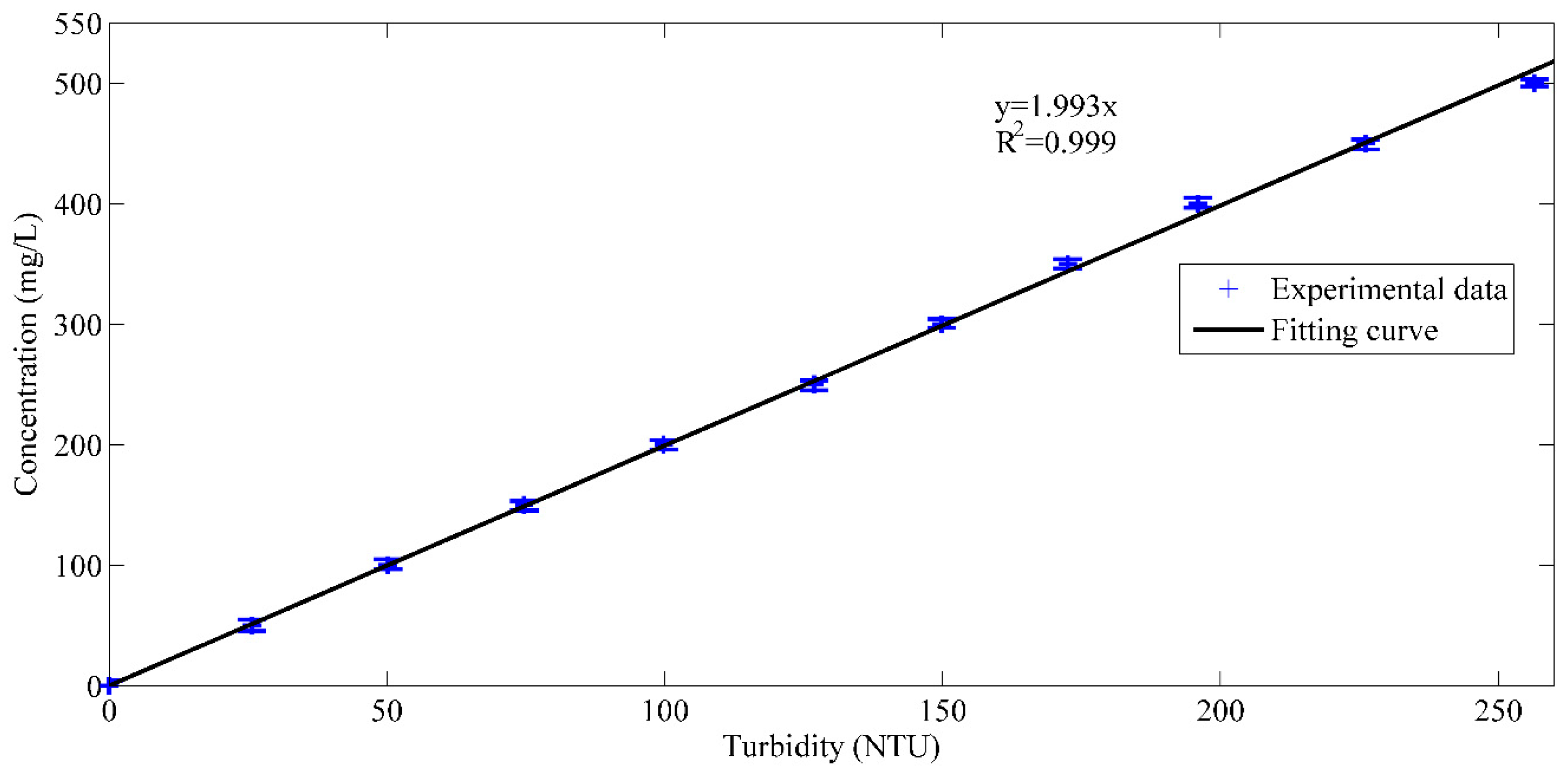
2.3. Experimental Procedures
3. Modelling Aspects
4. Results
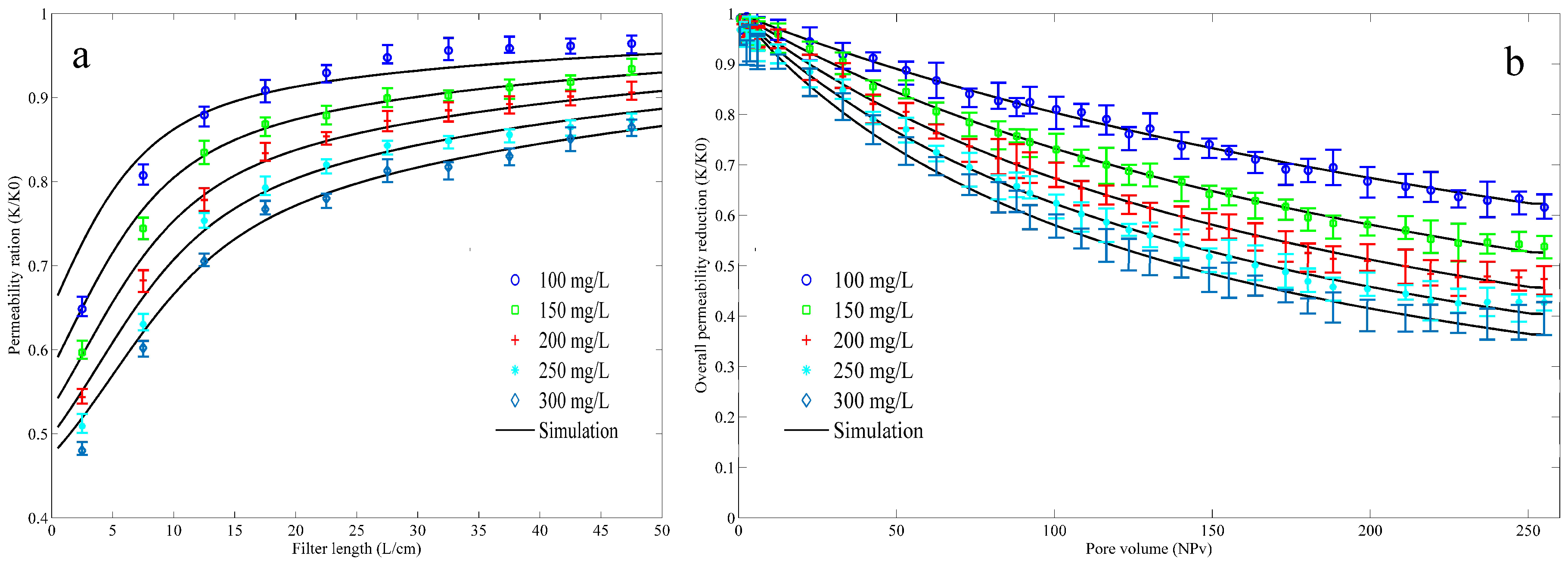
4.1. SP Transport and Retention in the Porous Medium
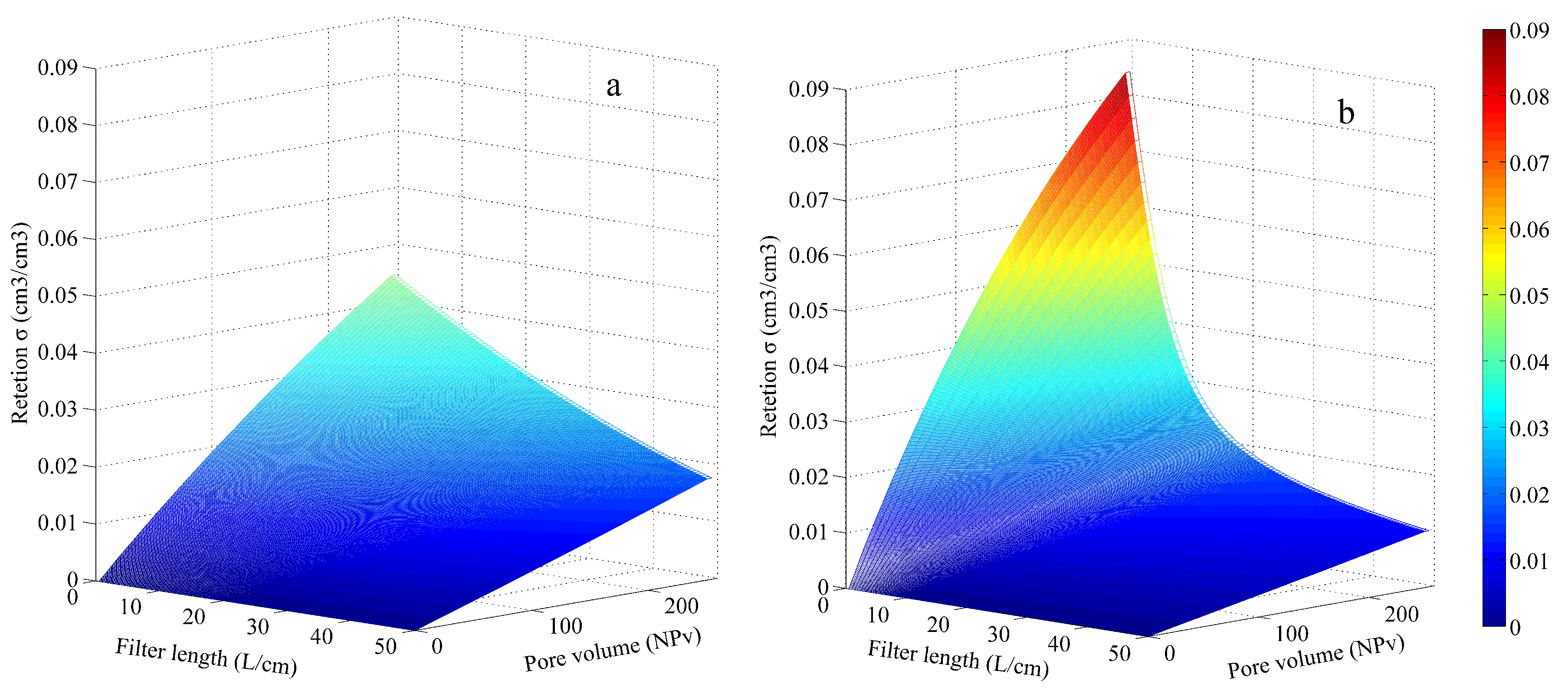
4.2. Spatial Distribution of Deposition
5. Discussion
5.1. The Deviation of a Hyper-Exponential Retention Profile
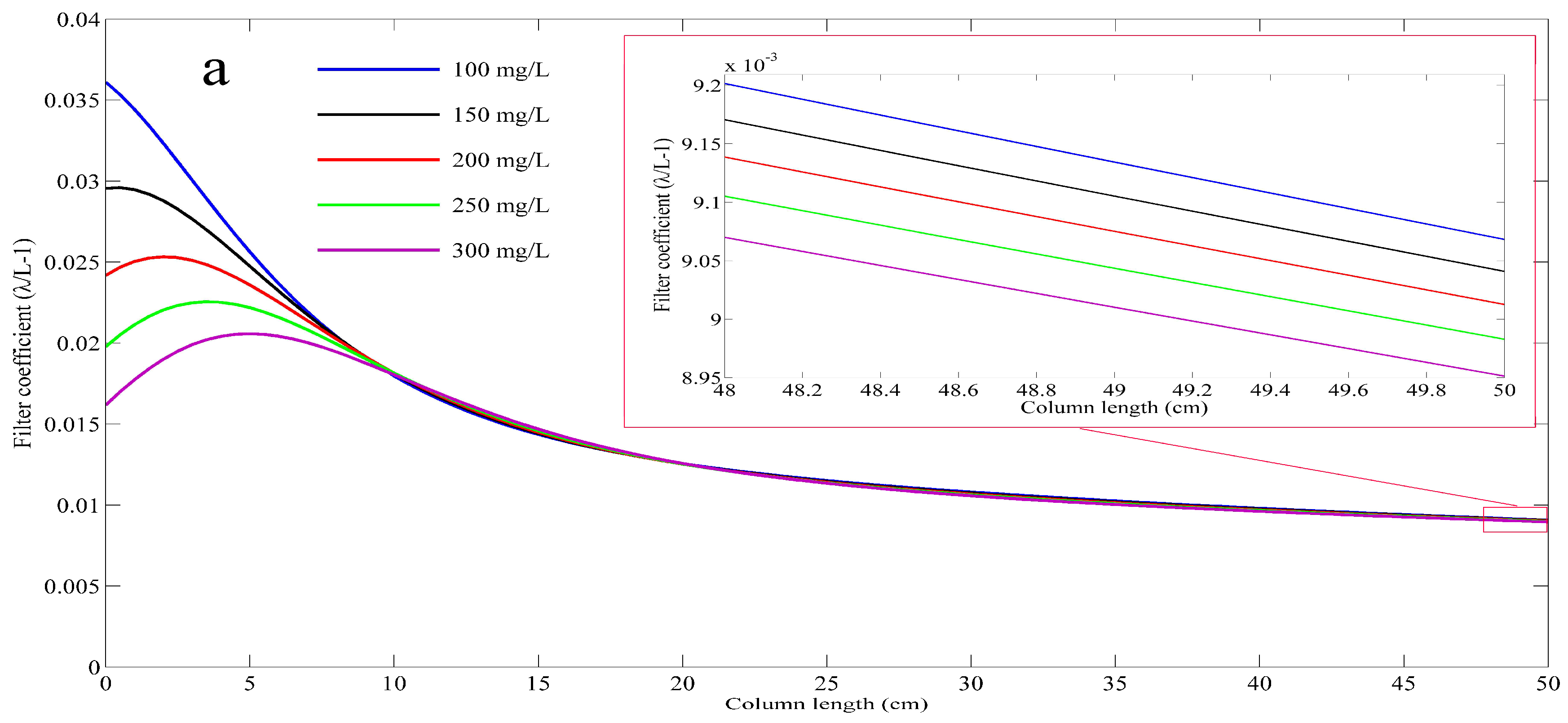
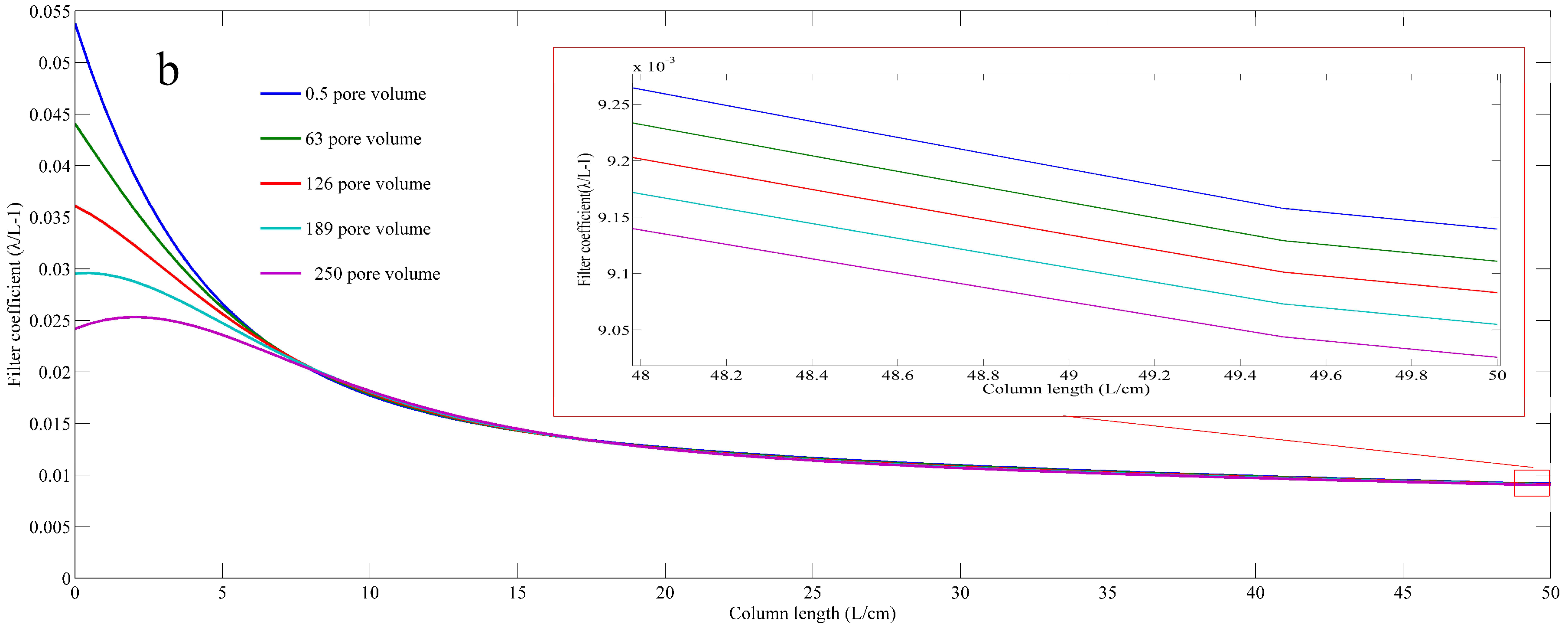
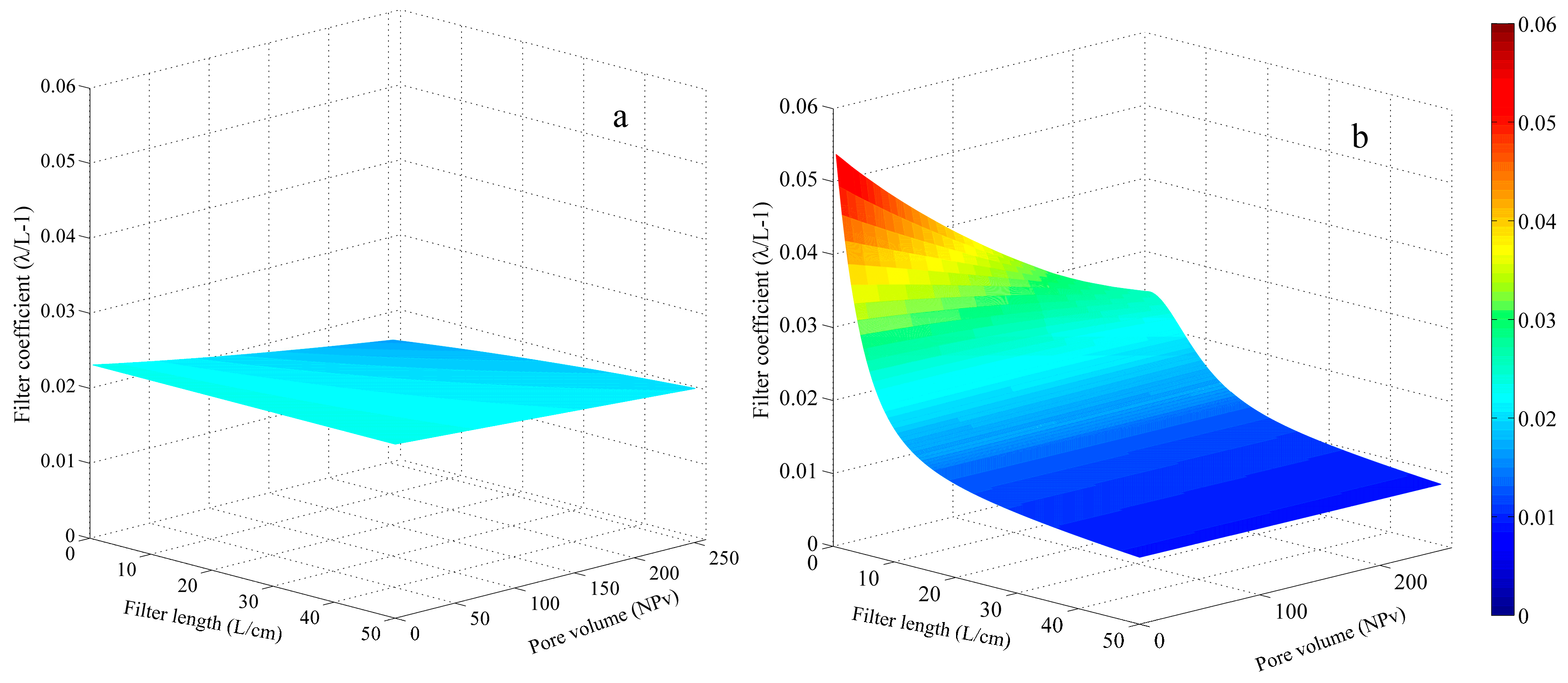
5.2. Spatial and Temporal Evolution of Filter Coefficient
5.3. Uneven Permeability of the Porous Medium
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C | Suspended particles concentration |
| Cin | Influent particle concentration |
| Cout | Effluent particle concentration |
| d | Particle diameter |
| L | Depth of filter bed |
| Lc | Characteristic length of filter bed |
| ϕ | the porosity of filter medium |
| p(d) | Capture probability function |
| P(d) | Standard capture probability function |
| Q(d) | Mass density function |
| t | Time |
| u | Filtration velocity |
| λ0 | Initial equivalent filter coefficient |
| λ0 (z) | Initial filter coefficient at location z |
| σ | Deposited particle mass per unit of bed volume |
| σm | Maximum possible value of σ |
Appendix A
Appendix B
References
- Kandra, H.S.; Mccarthy, D.; Fletcher, T.D.; Deletic, A. Assessment of clogging phenomena in granular filter media used for stormwater treatment. J. Hydrol. 2014, 512, 518–527. [Google Scholar] [CrossRef]
- Dillon, P. Future management of aquifer recharge. Hydrogeol. J. 2005, 13, 313–316. [Google Scholar] [CrossRef]
- Kandra, H.S.; Deletic, A.; Mccarthy, D. Assessment of impact of filter design variables on clogging in stormwater filters. Water Resour. Manag. 2014, 28, 1873–1885. [Google Scholar] [CrossRef]
- Voisin, J.; Cournoyer, B.; Vienney, A.; Mermillod-Blondin, F. Aquifer recharge with stormwater runoff in urban areas: Influence of vadose zone thickness on nutrient and bacterial transfers from the surface of infiltration basins to groundwater. Sci. Total Environ. 2018, 637–638, 1496–1507. [Google Scholar] [CrossRef] [PubMed]
- Jegatheesan, V.; Vigneswaran, S. The effect of concentration on the early stages of deep bed filtration of submicron particles. Water Res. 1997, 31, 2910–2913. [Google Scholar] [CrossRef]
- Sansalone, J.; Kuang, X.; Ying, G.; Ranieri, V. Filtration and clogging of permeable pavement loaded by urban drainage. Water Res. 2012, 46, 6763–6774. [Google Scholar] [CrossRef]
- Blazejewski, R.; Murat-Blazejewska, S. Soil clogging phenomena in constructed wetlands with subsurface flow. Water Sci. Technol. 1997, 35, 183–188. [Google Scholar] [CrossRef]
- Dillon, P.; Pavelic, P.; Massmann, G.; Barry, K.; Correll, R. Enhancement of the membrane filtration index (MFI) method for determining the clogging potential of turbid urban stormwater and reclaimed water used for aquifer storage and recovery. Desalination 2001, 140, 153–165. [Google Scholar] [CrossRef]
- Dechesne, M.; Barraud, S.; Bardin, J.P. Indicators for hydraulic and pollution retention assessment of stormwater infiltration basins. J. Environ. Manag. 2004, 71, 371–380. [Google Scholar] [CrossRef]
- Yong, C.F.; Mccarthy, D.T.; Deletic, A. Predicting physical clogging of porous and permeable pavements. J. Hydrol. 2013, 481, 48–55. [Google Scholar] [CrossRef]
- AI-Isawi, R.; Scholz, M.; Wang, Y.; Sani, A. Clogging of vertical-flow constructed wetlands treating urban wastewater contaminated with a diesel spill. Environ. Sci. Pollut. Res. 2015, 22, 12779–12803. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.Y.; Lu, M.Z.; Bian, H.F. Effects of clogging on hydraulic behavior in a vertical-flow constructed wetland system: A modelling approach. Ecol. Eng. 2017, 109, 41–47. [Google Scholar] [CrossRef]
- Siriwardene, N.; Deletic, A.; Fletcher, T.D. Clogging of stormwater gravel infiltration systems and filters: Insights from a laboratory study. Water Res. 2007, 41, 1433–1440. [Google Scholar] [CrossRef] [PubMed]
- Bouwer, H. Artificial recharge of groundwater: Hydrogeology and engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef]
- Siriwardene, N.R.; Deletic, A.; Fletcher, T.D. Modeling of sediment transport through stormwater gravel filters over their lifespan. Environ. Sci. Technol. 2007, 41, 8099–8103. [Google Scholar] [CrossRef] [PubMed]
- Schubert, J. Hydraulic aspects of riverbank filtration-field studies. J. Hydrol. 2002, 266, 145–161. [Google Scholar] [CrossRef]
- Mays, C.M.; Hunt, J.R. Hydrodynamic aspects of particle clogging in porous media. Environ. Sci. Technol. 2005, 39, 577–584. [Google Scholar] [CrossRef]
- Mays, D.C. Contrasting clogging in granular media filters, soils, and dead-end membranes. J. Environ. Eng. 2010, 136, 475–480. [Google Scholar] [CrossRef]
- Knowles, P.; Dotro, G.; Nivala, J.; García, J. Clogging in subsurface-flow treatment wetlands: Occurrence and contributing factors. Ecol. Eng. 2011, 37, 99–112. [Google Scholar] [CrossRef]
- Ahfir, N.D.; Hammadi, A.; Alem, A.; Wang, H.Q.; Bras, G.L.; Ouahbi, T. Porous media grain size distribution and hydrodynamic forces effects on transport and deposition of suspended particles. J. Environ. Sci.-China 2017, 53, 161–172. [Google Scholar] [CrossRef]
- Zamani, A.; Maini, B. Flow of dispersed particles through porous media-Deep bed filtration. J. Pet. Sci. Eng. 2009, 69, 71–88. [Google Scholar] [CrossRef]
- Le Coustumer, S.; Fletcher, T.D.; Deletic, A.; Barraud, S. Hydraulic performance of biofilters for stormwater management: First lessons from both laboratory and field studies. Water Sci. Technol. 2007, 56, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Hatt, B.E.; Deletic, A.; Fletcher, T.D. Hydraulic and pollutant removal performance of fine media stormwater filtration systems. Environ. Sci. Technol. 2008, 42, 2535–2541. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Davis, A. Urban particle capture in bioretention media. I: Theory and model development. J. Environ. Eng. 2008, 134, 409–419. [Google Scholar] [CrossRef]
- Li, H.; Davis, A. Urban particle capture in bioretention media. II: Theory and model development. J. Environ. Eng. 2008, 134, 419–432. [Google Scholar] [CrossRef]
- Herzig, J.; Leclerc, D.; Le, G.P. Flow of suspensions through porous media-application to deep filtration. Ind. Eng. Chem. 1970, 82, 8–35. [Google Scholar] [CrossRef]
- Tong, M.; Johnson, W.P. Colloid population heterogeneity drives hyper-exponential deviation from classic filtration theory. Environ. Sci. Technol. 2007, 41, 493–499. [Google Scholar] [CrossRef]
- Johnson, W.P.; Anna, R.; Eddy, P.; Markus, H. Why variant colloid transport behaviors emerge among identical individuals in porous media when colloid-surface repulsion exists. Environ. Sci. Technol. 2018, 52, 7230–7239. [Google Scholar] [CrossRef]
- Molnar, I.L.; Johnson, W.P.; Gerhard, J.I.; Willson, C.S.; O’Carroll, D.M. Predicting colloid transport through saturated porous media: A critical review. Water Resour. Res. 2015, 51, 6804–6845. [Google Scholar] [CrossRef]
- Tufenkji, N.; Elimelech, M. Deviation from the classical colloid filtration theory in the presence of repulsive dlvo interactions. Langmuir 2004, 20, 10818–10828. [Google Scholar] [CrossRef]
- Zou, Z.; Shu, L.; Min, X.; Mabedi, E.C. Clogging of Infiltration Basin and Its Impact on Suspended Particles Transport in Unconfined Sand Aquifer: Insights from a Laboratory Study. Water 2019, 11, 1083. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Sim, Y. One-dimensional virus transport in homogeneous porous media with time-dependent distribution coefficient. J. Hydrol. 1996, 185, 199–219. [Google Scholar] [CrossRef]
- Sanya, S.; Arturo, K. Transport of colloids in saturated porous media: A pore-scale observation of the size exclusion effect and colloid acceleration. Water Resour. Res. 2003, 39, 1255–1256. [Google Scholar]
- Bradford, S.A.; Leij, F.J. Modeling the transport and retention of polydispersed colloidal suspensions in porous media. Chem. Eng. Sci. 2018, 192, 972–980. [Google Scholar] [CrossRef]
- Ma, E.; Ouahbi, T.; Wang, H.; Ahfir, N.D.; Alem, A.; Hammadi, A. Modeling of the transport and deposition of polydispersed particles: Effects of hydrodynamics and spatiotemporal evolution of the deposition rate. Environ. Pollut. 2017, 237, 1011–1022. [Google Scholar] [CrossRef] [PubMed]
- Ma, E.; Ouahbi, T.; Wang, H.; Ahfir, N.D.; Alem, A.; Hammadi, A. Modeling of retention and re-entrainment of mono- and poly-disperse particles: Effects of hydrodynamics, particle size and interplay of different-sized particles retention. Sci. Total Environ. 2017, 596–597, 222–229. [Google Scholar] [CrossRef]
- Kandra, H.S.; Asce, S.M.; Callaghan, J.; Deletic, A.; Mccarthy, D.T. Biological clogging in storm water filters. J. Environ. Eng. 2015, 141, 1–8. [Google Scholar] [CrossRef]
- Rink-Pfeiffer, S.; Ragusa, S.; Sztajnbox, P.; Vandevelde, T. Interrelationships between biological, chemical, and physical processes as an analog to clogging in aquifer storage and recovery (ASR) wells. Water Res. 2000, 34, 2110–2118. [Google Scholar] [CrossRef]
- Nogaro, G.; Datry, T.; Mermillod-Blondin, F.; Descloux, S.; Montuelle, B. Influence of streambed sediment clogging on microbial processes in the hyporheic zone. Freshw. Biol. 2010, 55, 1288–1302. [Google Scholar] [CrossRef]
- Min, X.; Shu, L.; Li, W.; Appiah-Adjei, E.K. Influence of particle distribution on filter coefficient in the initial stage of filtration. Korean J. Chem. Eng. 2013, 30, 456–464. [Google Scholar] [CrossRef]
- Bratieres, K.; Schang, C.; Deletic, A.; Mccarthy, D.T. Performance of enviss™ stormwater filters: Results of a laboratory trial. Water Sci. Technol. 2012, 66, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Duncan, H.P. Urban Stormwater Quality: A Statistical Overview; Co-operative Research Centre for Catchment Hydrology, Report 99/3; Co-Operative Research Centre for Catchment Hydrology: Melbourne, Australia, 1999. [Google Scholar]
- Alem, A.; Elkawafi, A.; Ahfir, N.D.; Wang, H.Q. Filtration of kaolinite particles in a saturated porous medium: Hydrodynamic effects. Hydrogeol. J. 2013, 21, 573–586. [Google Scholar] [CrossRef]
- Iwasaki, T. Some notes on sand filtration. J. Am. Water Works Assoc. 1937, 29, 1591–1602. [Google Scholar] [CrossRef]
- Mcdowell-Boyer, L.M.; Hunt, J.R.; Sitar, N. Particle transport through porous media. Water Resour. Res. 1986, 22, 1901–1921. [Google Scholar] [CrossRef]
- Tien, C.; Payatakes, A.C. Advances in deep bed filtration. AIChE J. 1979, 25, 737–759. [Google Scholar] [CrossRef]
- Mints, D.M.; Paskutskaya, L.N.; Chernova, Z.V. On the mechanism of the filtration process on rapid water treatment filters. Zh. Priklad. Khim. 1967, 8, 1695–1700. [Google Scholar]
- Kuhnen, F.; Barmettler, K.; Bhattacharjee, S.; Elimelech, M.; Kretzschmar, R. Transport of iron oxide colloids in packed quartz sand media: Monolayer and multilayer deposition. J. Colloid Interface Sci. 2000, 231, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Gitis, V.; Rubinstein, I.; Livshits, M.; Ziskind, G. Deep-bed filtration model with multistage deposition kinetics. Chem. Eng. J. 2010, 163, 78–85. [Google Scholar] [CrossRef]
- Altoé, F.J.; Bedrikovetsky, P.; Siqueira, A.G.; De Souza, A.L.S.; Shecaira, F.S. Correction of basic equations for deep bed filtration with dispersion. J. Pet. Sci. Eng. 2006, 51, 68–84. [Google Scholar] [CrossRef]
- Horner, R.M.W.; Jarvis, R.J.; Mackie, R.I. Deep bed filtration: A new look at the basic equations. Water Res. 1986, 20, 215–220. [Google Scholar] [CrossRef]
- Vigneswaran, S.; Prasanthi, H.; Dharmappa, H.B. Implication of particle size to transient stage of deep bed infiltration. J. Chem. Eng. 1996, 13, 565–572. [Google Scholar]
- Shapiro, A.A.; Bedrikovetsky, P.G.; Santos, A.; Medvedev, O.O. A stochastic model for filtration of particulate suspensions with incomplete pore plugging. Transp. Porous Med. 2007, 67, 135–164. [Google Scholar] [CrossRef]
- Sharma, M.M.; Yortsos, Y.C. A network model for deep bed filtration processes. AIChE J. 2016, 33, 1644–1653. [Google Scholar] [CrossRef]
- Ahfir, N.D.; Benamar, A.; Alem, A.; Wang, H.Q. Influence of internal structure and medium length on transport and deposition of suspended particles: A laboratory study. Transp. Porous Med. 2009, 76, 289–307. [Google Scholar] [CrossRef]
- Foppen, J.W.A.; Mporokoso, A.; Schijven, J.F. Determining straining of Escherichia coli from breakthrough curves. J. Contam. Hydrol. 2005, 76, 191–210. [Google Scholar] [CrossRef]
- Alem, A.; Ahfir, N.D.; Elkawafi, A.; Wang, H.Q. Hydraulic operating conditions and particle concentration effects on physical clogging of a porous medium. Transp. Porous Med. 2015, 106, 303–321. [Google Scholar] [CrossRef]
- Xu, S.; Gao, B.; Saiers, J.E. Straining of colloidal particles in saturated porous media. Water Resour. Res. 2006, 42, 1–10. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, B.; Bradford, S.A.; Wu, L.; Chen, H.; Shi, X.; Wu, J. Transport, retention, and size perturbation of graphene oxide in saturated porous media: Effects of input concentration and grain size. Water Res. 2015, 68, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Bradford, S.A.; Simunek, J.; Bettahar, M.; Van Genuchten, M.T.; Yates, S.R. Modeling colloid attachment, straining, and exclusion in saturated porous media. Environ. Sci. Technol. 2003, 37, 2242–2250. [Google Scholar] [CrossRef]
- Messina, F.; Marchisio, D.L.; Sethi, R. An extended and total flux normalized correlation equation for predicting single-collector efficiency. J. Colloid Interface Sci. 2015, 446, 185–193. [Google Scholar] [CrossRef]
- Johnson, W.P.; Pazmino, E.; Ma, H. Direct observations of colloid retention in granular media in the presence of energy barriers, and implications for inferred mechanisms from indirect observations. Water Res. 2010, 44, 1158–1169. [Google Scholar] [CrossRef] [PubMed]
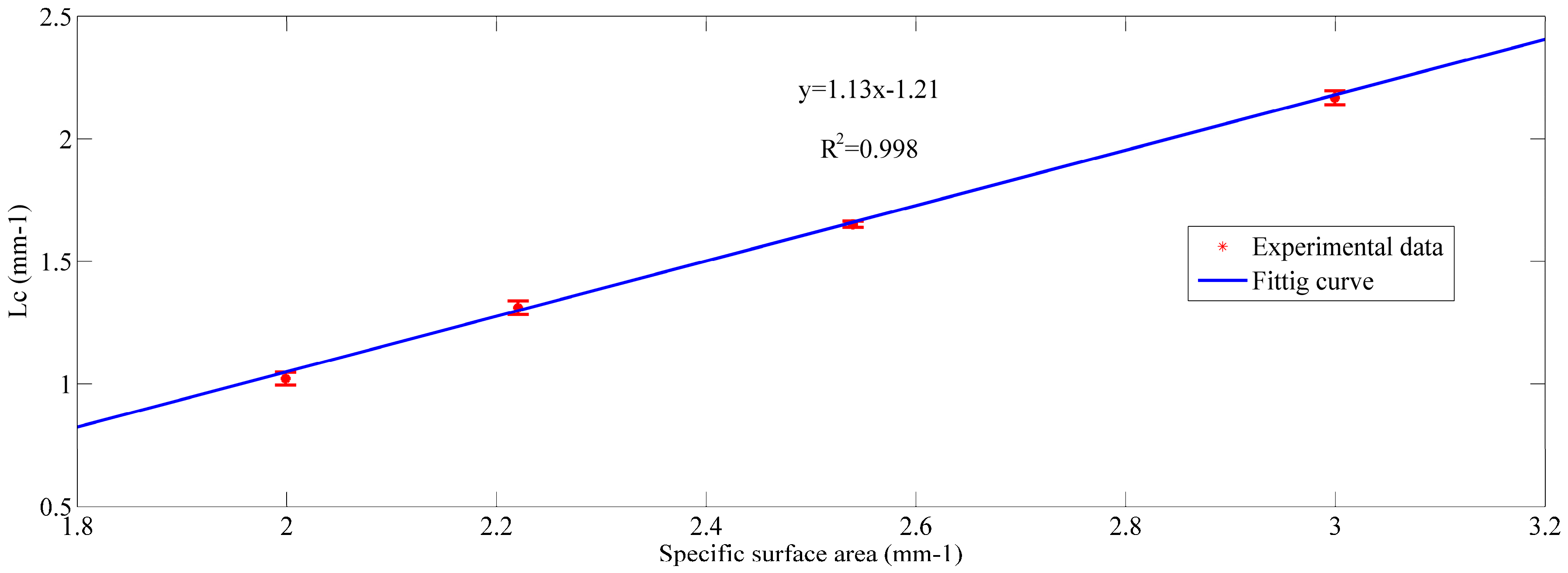
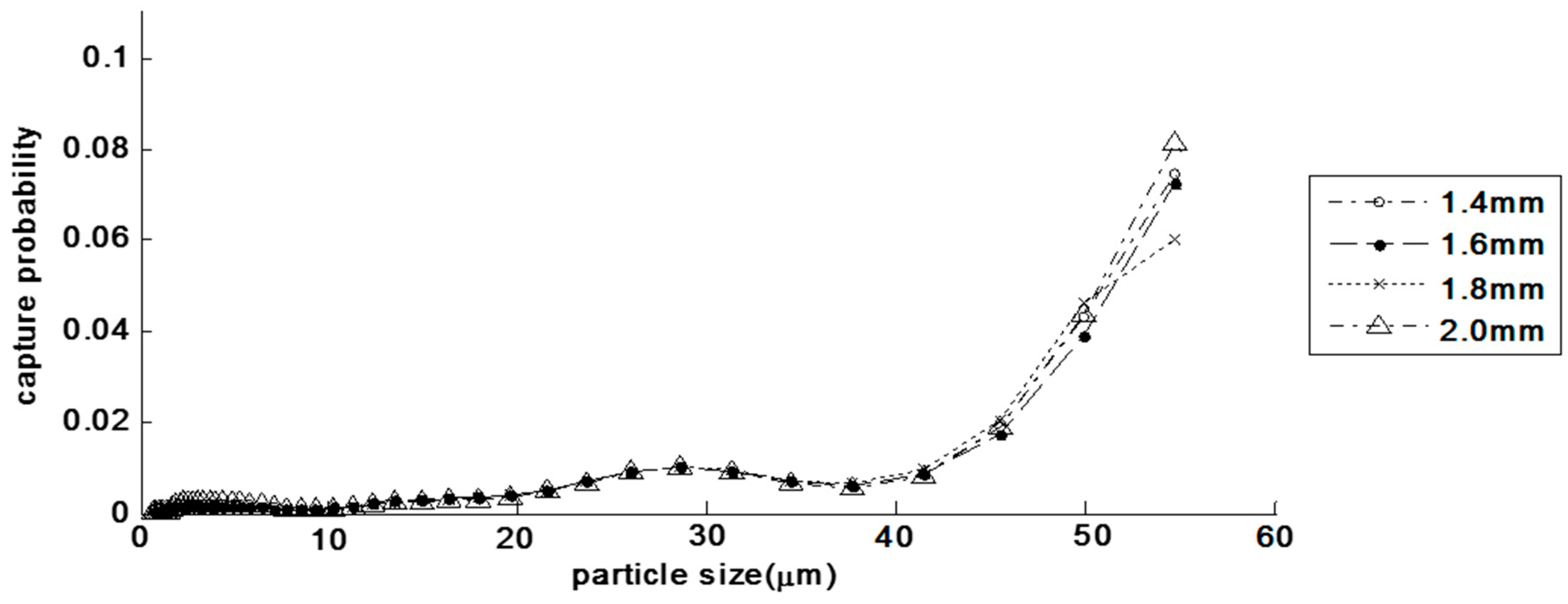
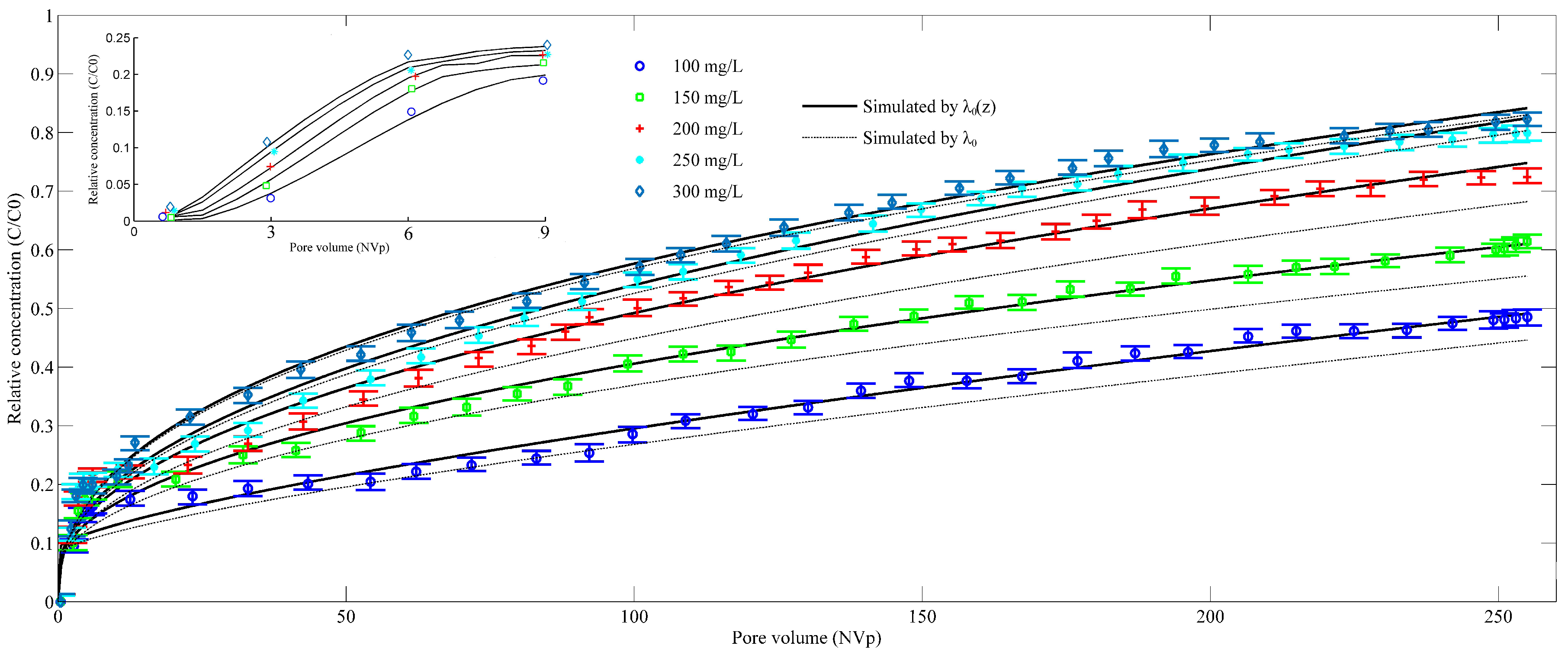
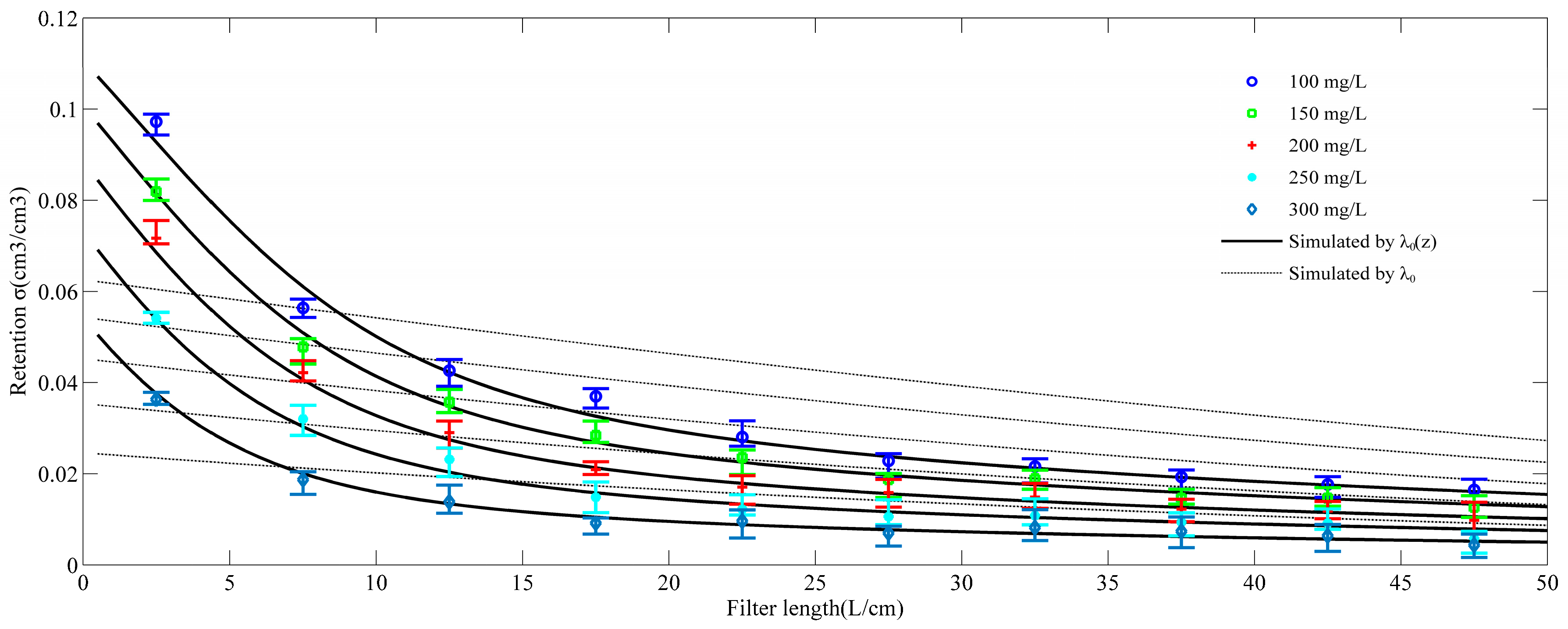


| C0 (mg/L) | Mass Deposited in Each Section (%) | Mp (%) | Meff (%) | Mtot (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
| 100 | 16.10 | 13.45 | 8.99 | 7.01 | 5.91 | 5.18 | 4.63 | 4.18 | 3.81 | 3.49 | 72.75 | 32.74 | 105.49 |
| 150 | 15.33 | 9.51 | 6.39 | 4.97 | 4.18 | 3.66 | 3.27 | 2.96 | 2.70 | 2.47 | 55.44 | 42.20 | 97.64 |
| 200 | 14.58 | 8.69 | 5.89 | 4.57 | 3.83 | 3.35 | 3.00 | 2.71 | 2.47 | 2.27 | 51.36 | 51.32 | 102.68 |
| 250 | 13.85 | 8.33 | 5.71 | 4.42 | 3.70 | 3.23 | 2.89 | 2.61 | 2.39 | 2.19 | 49.32 | 56.26 | 105.58 |
| 300 | 13.14 | 6.80 | 4.73 | 3.65 | 3.05 | 2.66 | 2.38 | 2.15 | 1.97 | 1.81 | 42.34 | 59.79 | 102.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Z.; Shu, L.; Min, X.; Chifuniro Mabedi, E. Physical Experiment and Modeling of the Transport and Deposition of Polydisperse Particles in Stormwater: Effects of a Depth-Dependent Initial Filter Coefficient. Water 2019, 11, 1885. https://doi.org/10.3390/w11091885
Zou Z, Shu L, Min X, Chifuniro Mabedi E. Physical Experiment and Modeling of the Transport and Deposition of Polydisperse Particles in Stormwater: Effects of a Depth-Dependent Initial Filter Coefficient. Water. 2019; 11(9):1885. https://doi.org/10.3390/w11091885
Chicago/Turabian StyleZou, Zhike, Longcang Shu, Xing Min, and Esther Chifuniro Mabedi. 2019. "Physical Experiment and Modeling of the Transport and Deposition of Polydisperse Particles in Stormwater: Effects of a Depth-Dependent Initial Filter Coefficient" Water 11, no. 9: 1885. https://doi.org/10.3390/w11091885
APA StyleZou, Z., Shu, L., Min, X., & Chifuniro Mabedi, E. (2019). Physical Experiment and Modeling of the Transport and Deposition of Polydisperse Particles in Stormwater: Effects of a Depth-Dependent Initial Filter Coefficient. Water, 11(9), 1885. https://doi.org/10.3390/w11091885





