On Some Properties of the Glacial Isostatic Adjustment Fingerprints
Abstract
:1. Introduction
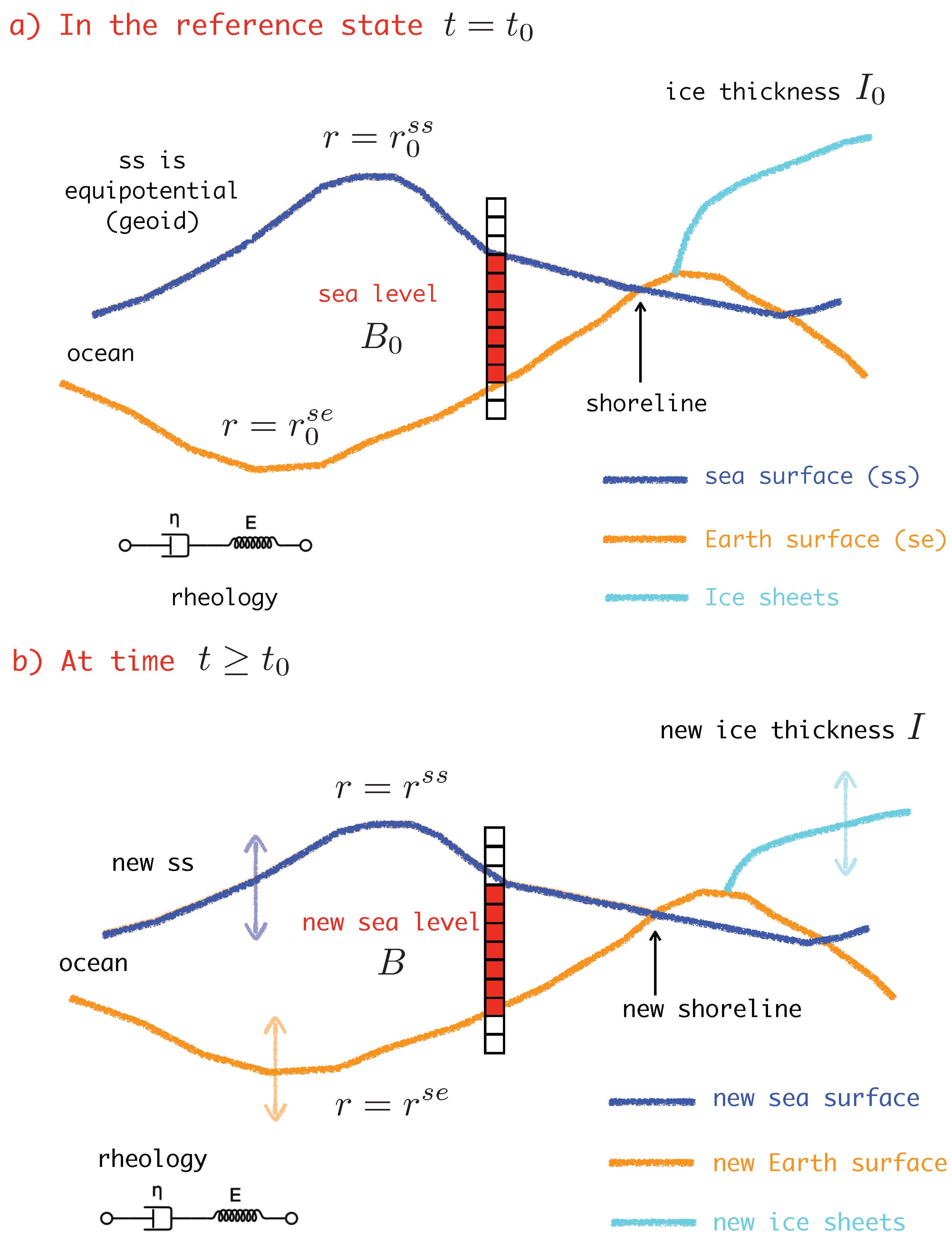
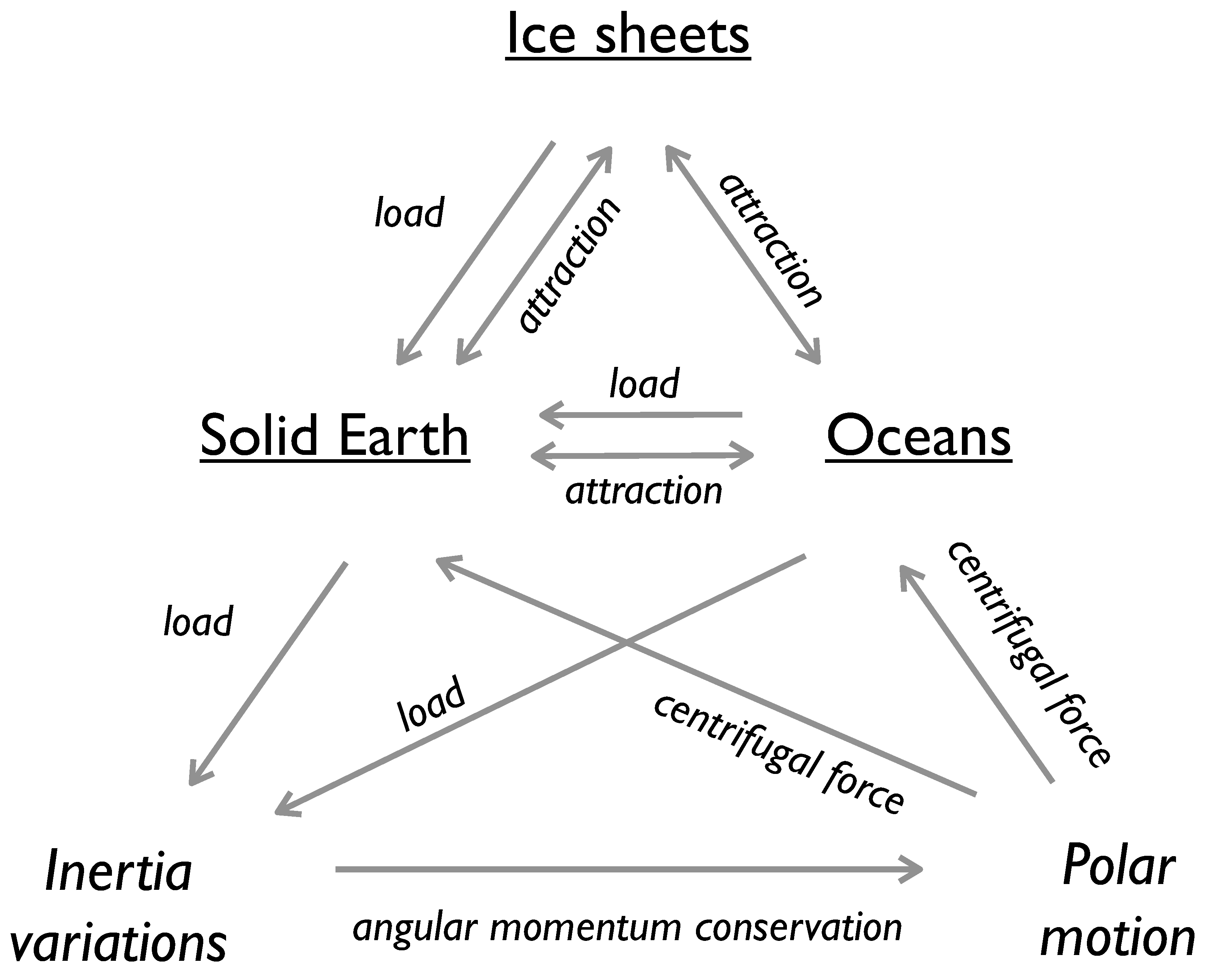
2. Theory
3. Methods
4. Some Properties of the GIA Fingerprints
4.1. Relative Sea-Level Change
4.2. Vertical Displacement
4.3. Geoid Height and Absolute Sea-Level Change
4.4. Surface Load
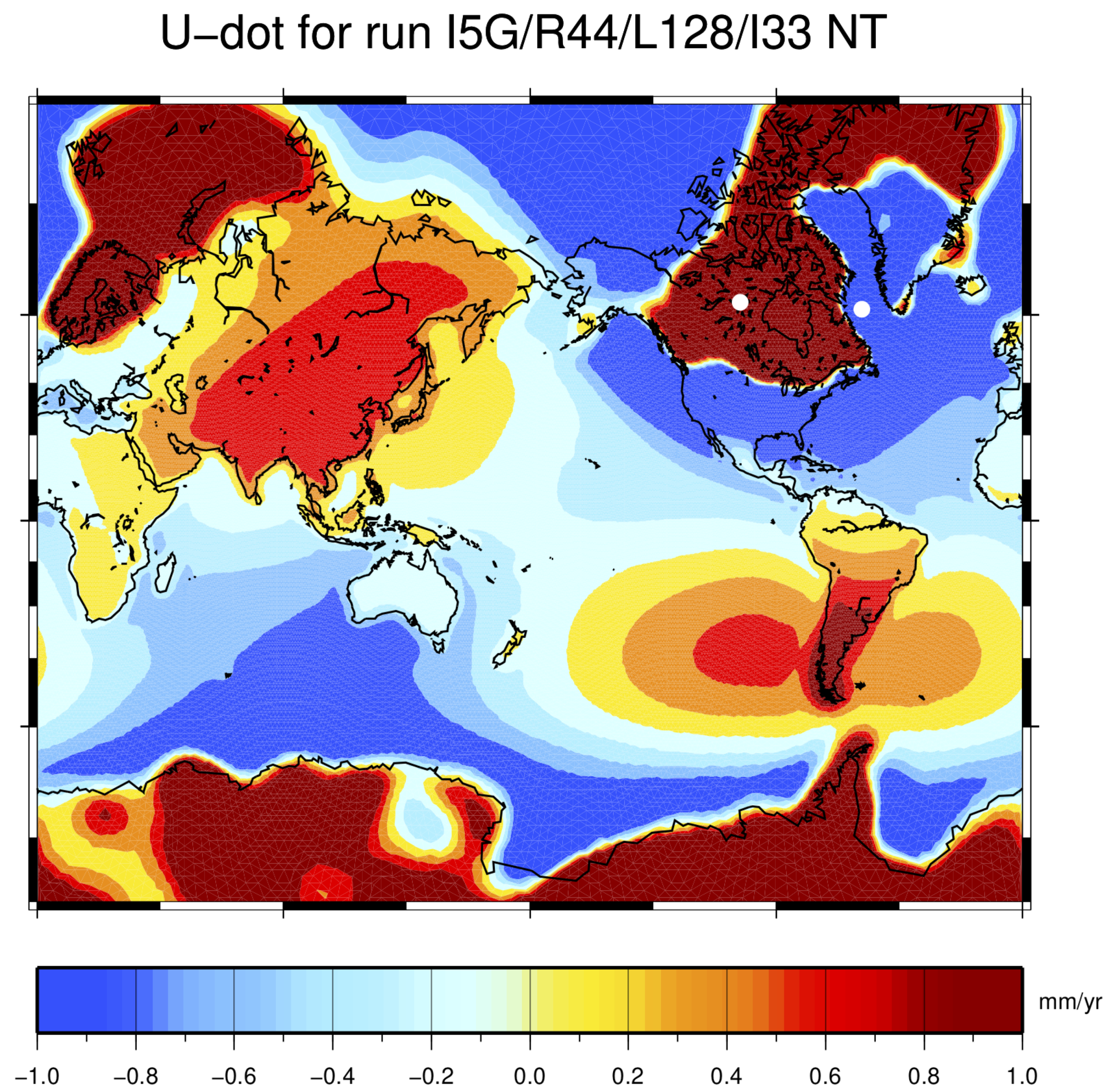
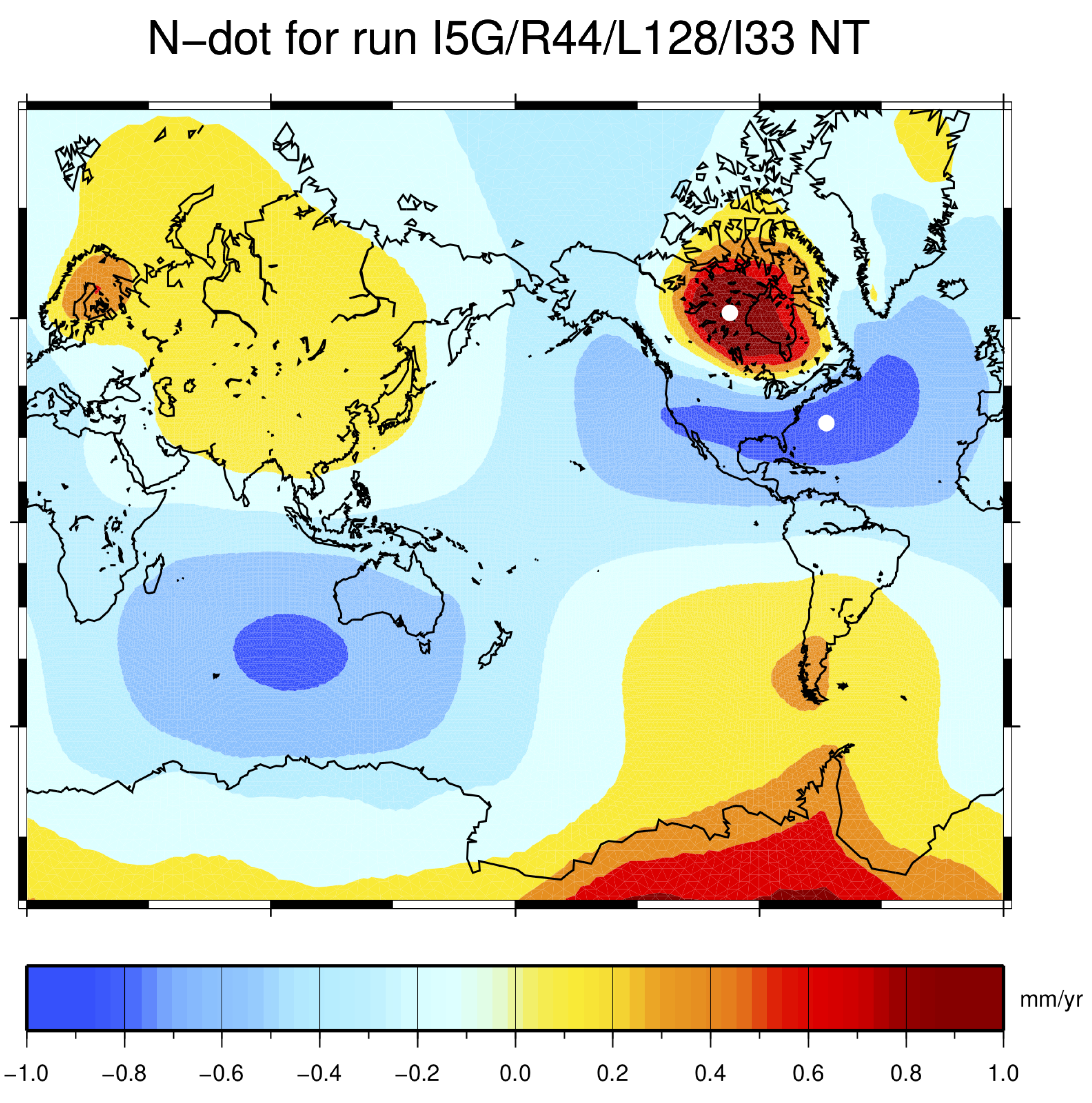
5. Observing the Global GIA Fingerprint by Vertical GPS Rates
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farrell, W.; Clark, J. On postglacial sea-level. Geophys. J. R. Astr. Soc. 1976, 46, 647–667. [Google Scholar] [CrossRef]
- Clark, J.A.; Farrell, W.E.; Peltier, W.R. Global changes in postglacial sea level: A numerical calculation. Quat. Res. 1978, 9, 265–287. [Google Scholar] [CrossRef]
- Conrad, C. The solid earth’s influence on sea level. Bull. Geol. Soc. Am. 2013, 125, 1027–1052. [Google Scholar] [CrossRef]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes And Consequences; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Peltier, W. Global sea level rise and glacial isostatic adjustment. Glob. Planet. Chang. 1999, 20, 93–123. [Google Scholar] [CrossRef]
- Woodward, R. On the form and position of mean sea level. USGS Bull. 1888, 48, 87–170. [Google Scholar]
- Daly, R.A. Pleistocene changes of level. Am. J. Sci. 1925, 10, 281–313. [Google Scholar] [CrossRef]
- Walcott, R. Past sea levels, eustasy and deformation of the earth. Quat. Res. 1972, 2, 1–14. [Google Scholar] [CrossRef]
- Suess, E. Face of the Earth; Clarendon Press: Oxford, UK, 1906. [Google Scholar]
- Milne, G.A.; Mitrovica, J.X. Searching for eustasy in deglacial sea-level histories. Quat. Sci. Rev. 2008, 27, 2292–2302. [Google Scholar] [CrossRef]
- Gregory, J.M.; Griffies, S.M.; Hughes, C.W.; Lowe, J.A.; Church, J.A.; Fukimori, I.; Gomez, N.; Kopp, R.E.; Landerer, F.; Le Cozannet, G.; et al. Concepts and terminology for sea level: Mean, variability and change, both local and global. Surv. Geophys. 2019, 1–39. [Google Scholar] [CrossRef]
- Mitrovica, J.; Milne, G. On the origin of late Holocene sea-level highstands within equatorial ocean basins. Quat. Sci. Rev. 2002, 21, 2179–2190. [Google Scholar] [CrossRef]
- Clark, P.U.; Mitrovica, J.; Milne, G.; Tamisiea, M. Sea-level fingerprinting as a direct test for the source of global meltwater pulse IA. Science 2002, 295, 2438–2441. [Google Scholar]
- Kendall, R.A.; Mitrovica, J.X.; Milne, G.A.; Törnqvist, T.E.; Li, Y. The sea-level fingerprint of the 8.2 ka climate event. Geology 2008, 36, 423–426. [Google Scholar] [CrossRef]
- Mitrovica, J.; Gomez, N.; Morrow, E.; Hay, C.; Latychev, K.; Tamisiea, M. On the robustness of predictions of sea level fingerprints. Geophys. J. Int. 2011, 187, 729–742. [Google Scholar] [CrossRef] [Green Version]
- Stocchi, P.; Spada, G. Glacio and hydro-isostasy in the Mediterranean Sea: Clark zones and role of remote ice sheets. Ann. Geophys. 2007, 50. [Google Scholar] [CrossRef]
- Mauz, B.; Ruggieri, G.; Spada, G. Terminal Antarctic melting inferred from a far-field coastal site. Quat. Sci. Rev. 2015, 116, 122–132. [Google Scholar] [CrossRef]
- Lambeck, K.; Chappell, J. Sea level change through the last glacial cycle. Science 2001, 292, 679–686. [Google Scholar] [CrossRef]
- Plag, H.P.; Jüettner, H.U. Inversion of global tide gauge data for present-day ice load changes (scientific paper). Mem. Natl. Inst. Polar Res. Spec. Issue 2001, 54, 301–317. [Google Scholar]
- Douglas, B. Concerning evidence for fingerprints of glacial melting. J. Coast. Res. 2008, 24, 218–227. [Google Scholar] [CrossRef]
- Spada, G.; Galassi, G. Spectral analysis of sea-level during the altimetry era, and evidence for GIA and glacial melting fingerprints. Glob. Planet. Chang. 2015, 143, 34–49. [Google Scholar] [CrossRef]
- Cazenave, A.; Llovel, W. Contemporary sea level rise. Annu. Rev. Mar. Sci. 2010, 2, 145–173. [Google Scholar] [CrossRef]
- Bamber, J.; Riva, R. The sea level fingerprint of recent ice mass fluxes. Cryosphere 2010, 4, 621–627. [Google Scholar] [CrossRef] [Green Version]
- Kopp, R.; Mitrovica, J.; Griffies, S.; Yin, J.; Hay, C.; Stouffer, R. The impact of Greenland melt on local sea levels: A partially coupled analysis of dynamic and static equilibrium effects in idealized water-hosing experiments. Clim. Chang. 2010, 103, 619–625. [Google Scholar] [CrossRef]
- Riva, R.E.; Bamber, J.L.; Lavallée, D.A.; Wouters, B. Sea-level fingerprint of continental water and ice mass change from GRACE. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Probabilistic reanalysis of twentieth-century sea-level rise. Nature 2015, 517, 481. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Ivins, E.R.; Frederikse, T.; Landerer, F.W.; Caron, L. Sea-level fingerprints emergent from GRACE mission data. Earth Syst. Sci. Data 2019, 11, 629–646. [Google Scholar] [CrossRef] [Green Version]
- Mitrovica, J.X.; Gomez, N.; Clark, P.U. The sea-level fingerprint of West Antarctic collapse. Science 2009, 323, 753. [Google Scholar] [CrossRef]
- Spada, G.; Bamber, J.; Hurkmans, R. The gravitationally consistent sea-level fingerprint of future terrestrial ice loss. Geophys. Res. Lett. 2013, 40, 482–486. [Google Scholar] [CrossRef] [Green Version]
- Galassi, G.; Spada, G. Sea-level rise in the Mediterranean Sea by 2050: Roles of terrestrial ice melt, steric effects and glacial isostatic adjustment. Glob. Planet. Chang. 2014, 123, 55–66. [Google Scholar] [CrossRef]
- Spada, G. Glacial Isostatic Adjustment and Contemporary Sea Level Rise: An Overview. Surv. Geophys. 2017, 38, 1–33. [Google Scholar] [CrossRef]
- Melini, D.; Spada, G. Some remarks on Glacial Isostatic Adjustment modelling uncertainties. Geophys. J. Int. 2019, 218, 401–413. [Google Scholar] [CrossRef]
- Spada, G.; Melini, D. SELEN4 (SELEN version 4.0): A Fortran program for solving the Gravitationally topographically Self-Consistent Sea Level Equ. Glacial Isostatic Adjust. Model. Geosci. Model Dev. 2019. [Google Scholar] [CrossRef]
- Tamisiea, M.E. Ongoing glacial isostatic contributions to observations of sea level change. Geophys. J. Int. 2011, 186, 1036–1044. [Google Scholar] [CrossRef]
- Farrell, W. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Milne, G.A.; Mitrovica, J.X. Postglacial sea-level change on a rotating Earth. Geophys. J. Int. 1998, 133, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Han, D.; Wahr, J. Post-glacial rebound analysis for a rotating Earth. In Slow Deformations and Transmission of Stress in the Earth; Cohen, S., Vanicek, P., Eds.; AGU Mono. Series 49; American Geophysical Union: Washington, DC, USA, 1989; pp. 1–6. [Google Scholar]
- Jerri, A. Introduction to Integral Equations with Applications; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Mitrovica, J.X.; Peltier, W. On postglacial geoid subsidence over the equatorial oceans. J. Geophys. Res. Solid Earth 1991, 96, 20053–20071. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Milne, G.A. On post-glacial sea level: I. General theory. Geophys. J. Int. 2003, 154, 253–267. [Google Scholar] [CrossRef] [Green Version]
- Spada, G.; Stocchi, P. SELEN: A Fortran 90 program for solving the “Sea Level Equation”. Comput. Geosci. 2007, 33, 538–562. [Google Scholar] [CrossRef]
- Spada, G.; Stocchi, P. The Sea Level Equation, Theory and Numerical Examples; Aracne: Roma, Italy, 2006. [Google Scholar]
- Tegmark, M. An icosahedron-based method for pixelizing the celestial sphere. Astrophys. J. 1996, 470, L81. [Google Scholar] [CrossRef]
- Peltier, W. Global glacial isostasy and the surface of the ice-age Earth: The ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Spada, G.; Barletta, V.R.; Klemann, V.; Riva, R.; Martinec, Z.; Gasperini, P.; Lund, B.; Wolf, D.; Vermeersen, L.; King, M. A benchmark study for glacial isostatic adjustment codes. Geophys. J. Int. 2011, 185, 106–132. [Google Scholar] [CrossRef] [Green Version]
- Spada, G. ALMA, a Fortran program for computing the viscoelastic Love numbers of a spherically symmetric planet. Comput. Geosci. 2008, 34, 667–687. [Google Scholar] [CrossRef]
- Peltier, W.R. Ice age paleotopography. Science 1994, 265, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Amante, C.; Eakins, B.W. ETOPO1 Arc-Minute Global Relief Model: Procedures, Data Source and Analysis; Technical Report; NOAA: Washington, DC, USA, 2009. [CrossRef]
- Eakins, B.; Sharman, G. Hypsographic curve of Earth’s surface from ETOPO1; NOAA National Geophysical Data Center: Boulder, CO, USA, 2012. [Google Scholar]
- Mitrovica, J.X.; Wahr, J.; Matsuyama, I.; Paulson, A. The rotational stability of an ice-age earth. Geophys. J. Int. 2005, 161, 491–506. [Google Scholar] [CrossRef] [Green Version]
- Mitrovica, J.X.; Wahr, J. Ice Age Earth Rotation. Annu. Rev. Earth Planet. Sci. 2011, 39, 577–616. [Google Scholar] [CrossRef]
- Spada, G.; Olivieri, M.; Galassi, G. Anomalous secular sea-level acceleration in the Baltic Sea caused by isostatic adjustment. Ann. Geophys. 2014, 57, S0432. [Google Scholar]
- Tushingham, A.; Peltier, W. ICE-3G—A new global model of late Pleistocene deglaciation based upon geophysical predictions of post-glacial relative sea level change. J. Geophys. Res. 1991, 96, 4497–4523. [Google Scholar] [CrossRef]
- Tarasov, L.; Richard Peltier, W. Greenland glacial history and local geodynamic consequences. Geophys. J. Int. 2002, 150, 198–229. [Google Scholar] [CrossRef] [Green Version]
- Tushingham, A.; Peltier, W. Validation of the ICE-3G model of Würm-Wisconsin deglaciation using a global data base of relative sea level histories. J. Geophys. Res. 1992, 97, 3285–3304. [Google Scholar] [CrossRef]
- Peltier, W.; Argus, D.; Drummond, R.; Moore, A. Postglacial rebound and current ice loss estimates from space geodesy: The new ICE-6G (VM5a) global model. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 3–7 December 2012; Volume 1, p. 2. [Google Scholar]
- Wöppelmann, G.; Miguez, B.M.; Bouin, M.N.; Altamimi, Z. Geocentric sea-level trend estimates from GPS analyses at relevant tide gauges world-wide. Glob. Planet. Chang. 2007, 57, 396–406. [Google Scholar] [CrossRef] [Green Version]
- Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef]
- Pfeffer, J.; Allemand, P. The key role of vertical land motions in coastal sea level variations: A global synthesis of multisatellite altimetry, tide gauge data and GPS measurements. Earth Planet. Sci. Lett. 2016, 439, 39–47. [Google Scholar] [CrossRef]
- Pfeffer, J.; Spada, G.; Mémin, A.; Boy, J.P.; Allemand, P. Decoding the origins of vertical land motions observed today at coasts. Geophys. J. Int. 2017, 210, 148–165. [Google Scholar] [CrossRef]
- Ivins, E.R.; James, T.S. Simple models for late Holocene and present-day Patagonian glacier fluctuations and predictions of a geodetically detectable isostatic response. Geophys. J. Int. 1999, 138, 601–624. [Google Scholar] [CrossRef] [Green Version]
- Rostami, K.; Peltier, W.; Mangini, A. Quaternary marine terraces, sea-level changes and uplift history of Patagonia, Argentina: Comparisons with predictions of the ICE-4G (VM2) model of the global process of glacial isostatic adjustment. Quat. Sci. Rev. 2000, 19, 1495–1525. [Google Scholar] [CrossRef]
- Crowley, J.W.; Katz, R.F.; Huybers, P.; Langmuir, C.H.; Park, S.H. Glacial cycles drive variations in the production of oceanic crust. Science 2015, 347, 1237–1240. [Google Scholar] [CrossRef] [Green Version]
- Conrad, C.P. How climate influences sea-floor topography. Science 2015, 347, 1204–1205. [Google Scholar] [CrossRef] [Green Version]
- Adhikari, S.; Caron, L.; Steinberger, B.; Reager, J.T.; Kjeldsen, K.K.; Marzeion, B.; Larour, E.; Ivins, E.R. What drives 20th century polar motion? Earth Planet. Sci. Lett. 2018, 502, 126–132. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Church, J.; Clark, P.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.; Nunn, P.; et al. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Sea Level Change; Stocker, T., Qin, D., Plattner, G.K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 1138–1191. [Google Scholar]
- Slangen, A.B.; Meyssignac, B.; Agosta, C.; Champollion, N.; Church, J.A.; Fettweis, X.; Ligtenberg, S.R.; Marzeion, B.; Melet, A.; Palmer, M.D.; et al. Evaluating model simulations of twentieth-century sea level rise. Part I: Global mean sea level change. J. Clim. 2017, 30, 8539–8563. [Google Scholar] [CrossRef]
- Ponte, R.M.; Quinn, K.J.; Piecuch, C.G. Accounting for gravitational attraction and loading effects from land ice on absolute sea level. J. Atmos. Ocean. Technol. 2018, 35, 405–410. [Google Scholar] [CrossRef]
- Husson, L.; Bodin, T.; Spada, G.; Choblet, G.; Kreemer, C. Bayesian surface reconstruction of geodetic uplift rates: Mapping the global fingerprint of Glacial Isostatic Adjustment. J. Geodyn. 2018, 122, 25–40. [Google Scholar] [CrossRef]
- Spada, G.; Galassi, G. New estimates of secular sea level rise from tide gauge data and GIA modelling. Geophys. J. Int. 2012, 191, 1067–1094. [Google Scholar] [CrossRef] [Green Version]
- Nakada, M.; Lambeck, K. Glacial rebound and relative sea-level variations: A new appraisal. Geophys. J. Int. 1987, 90, 171–224. [Google Scholar] [CrossRef]
- Lambeck, K.; Purcell, A.; Johnston, P.; Nakada, M.; Yokoyama, Y. Water-load definition in the glacio-hydro-isostatic sea-level equation. Quat. Sci. Rev. 2003, 22, 309–318. [Google Scholar] [CrossRef]
- Whitehouse, P.L. Glacial isostatic adjustment modelling: Historical perspectives, recent advances, and future directions. Earth Surf. Dyn. 2018, 6, 401–429. [Google Scholar] [CrossRef]
- Guo, J.; Huang, Z.; Shum, C.; van der Wal, W. Comparisons among contemporary glacial isostatic adjustment models. J. Geodyn. 2012, 61, 129–137. [Google Scholar] [CrossRef]
- Spada, G.; Ruggieri, G.; Sørensen, L.S.; Nielsen, K.; Melini, D.; Colleoni, F. Greenland uplift and regional sea level changes from ICESat observations and GIA modelling. Geophys. J. Int. 2012, 189, 1457–1474. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z. The Role of Glacial Isostatic Adjustment (GIA) Process On the Determination of Present-Day Sea-Level Rise; The Ohio State University: Columbus, OH, USA, 2013. [Google Scholar]
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Estimating the sources of global sea level rise with data assimilation techniques. Proc. Natl. Acad. Sci. USA 2013, 110, 3692–3699. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.; Grinsted, A.; Matthews, A.; Spada, G. Trends and acceleration in global and regional sea levels since 1807. Glob. Planet. Chang. 2014, 113, 11–22. [Google Scholar] [CrossRef] [Green Version]
- Caron, L.; Ivins, E.; Larour, E.; Adhikari, S.; Nilsson, J.; Blewitt, G. GIA model statistics for GRACE hydrology, cryosphere, and ocean science. Geophys. Res. Lett. 2018, 45, 2203–2212. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F. New, improved version of Generic Mapping Tools released. Eos Trans. Am. Geophys. Union 1998, 79, 579. [Google Scholar] [CrossRef]


| Radius, (km) | Radius, (km) | Density, (kg m−3) | Rigidity, (Pa × 1011) | Viscosity, (Pa·s × 1021) | Layer |
|---|---|---|---|---|---|
| 6281.000 | 6371.000 | 3192.800 | 0.596 | ∞ | LT |
| 6151.000 | 6281.000 | 3369.058 | 0.667 | 0.5 | UM1 |
| 5971.000 | 6151.000 | 3475.581 | 0.764 | 0.5 | UM2 |
| 5701.000 | 5971.000 | 3857.754 | 1.064 | 0.5 | TZ1 |
| 5401.000 | 5701.000 | 4446.251 | 1.702 | 2.7 | LM1 |
| 5072.933 | 5401.000 | 4615.829 | 1.912 | 2.7 | LM2 |
| 4716.800 | 5072.933 | 4813.845 | 2.124 | 2.7 | LM3 |
| 4332.600 | 4716.800 | 4997.859 | 2.325 | 2.7 | LM4 |
| 3920.333 | 4332.600 | 5202.004 | 2.554 | 2.7 | LM5 |
| 3480.000 | 3920.333 | 5408.573 | 2.794 | 2.7 | LM6 |
| 0 | 3480.000 | 10931.731 | 0 | 0 | Core |
| 2 | 4 | 16 | 64 | 128 | 256 | 512 | 1024 | ||
|---|---|---|---|---|---|---|---|---|---|
| Average | (a) New Theory (mm year−1) | (b) Traditional Theory (mm year−1) | (c) No Rotation (mm year−1) |
|---|---|---|---|
| −0.06 | −0.06 | −0.06 | |
| −0.27 | −0.30 | −0.24 | |
| −0.33 | −0.35 | −0.30 | |
| −0.06 | −0.09 | −0.04 | |
| +0.00 | +0.00 | +0.00 | |
| −0.27 | −0.27 | −0.26 | |
| +0.00 | +0.00 | +0.00 | |
| −0.27 | −0.27 | −0.26 | |
| +0.00 | +0.00 | +0.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spada, G.; Melini, D. On Some Properties of the Glacial Isostatic Adjustment Fingerprints. Water 2019, 11, 1844. https://doi.org/10.3390/w11091844
Spada G, Melini D. On Some Properties of the Glacial Isostatic Adjustment Fingerprints. Water. 2019; 11(9):1844. https://doi.org/10.3390/w11091844
Chicago/Turabian StyleSpada, Giorgio, and Daniele Melini. 2019. "On Some Properties of the Glacial Isostatic Adjustment Fingerprints" Water 11, no. 9: 1844. https://doi.org/10.3390/w11091844
APA StyleSpada, G., & Melini, D. (2019). On Some Properties of the Glacial Isostatic Adjustment Fingerprints. Water, 11(9), 1844. https://doi.org/10.3390/w11091844





