1. Introduction
The spatiotemporal behavior of rainfall is of great importance in the regional management of water resources and has a direct influence on human activities such as livestock management, agriculture, and commerce. One of the statistical techniques responsible for analyzing this type of behavior is spatiotemporal geostatistical analysis. The interpolation of spatiotemporal observations presents benefits compared to purely spatial predictions. One of these benefits is that interpolation can be applied to georeferencing positions over space-time [
1,
2].
In this study, a spatiotemporal geostatistical methodology was applied to monthly total rainfall data from the state of Paraíba, which is located in the northeastern region of Brazil (NEB). The NEB is characterized by an irregular, highly variable distribution of rainfall in space and time. In this region, it is common to find high rainfall rates at locations adjacent to those with no record of rain [
3]. Paraíba also experiences localized periods of drought within rainy seasons and distinct precipitation patterns among the state’s mesoregions [
4,
5]. As a consequence of this behavior, there is a need to model the rainfall distribution jointly with space and time.
In the literature, several studies have been carried out on the spatial interpolation of precipitation data using geostatistical techniques [
6,
7,
8,
9]. Martínez-Cob [
10] used three methods of geostatistical interpolation (ordinary kriging, cokriging, and modified residual kriging) to interpolate the mean total annual precipitation in a mountainous region of Aragon, located in northeastern Spain. Goovaerts [
11] constructed maps of the spatial prediction of rainfall erosivity in the Algarve region of Portugal. To calculate these predictions, the author used three geostatistical methods (simple kriging with varying local means, kriging with external drift, and collocated cokriging), in addition to linear regression, concluding that linear regression, not considering the spatial dependence among the stations, produced the greatest predictive errors. Haberlandt [
12] carried out a study on daily precipitation at 281 stations located in the southeast region of Germany using the methods of kriging with external drift and indicator kriging with external drift for spatial interpolation of precipitation. Also, an increasing number of studies in recent years have used geostatistical methods to model not only the spatial, but also the temporal, dynamics of precipitation [
13,
14].
In recent years, studies have appeared analyzing the regional spatiotemporal distribution of precipitation. Raja et al. [
15] applied the spatiotemporal kriging technique to rainfall data from Turkey. They consequently observed that Turkey is located in a region with a higher risk of possible effects from climate change, similar to the state of Paraíba, Brazil. Thus, they reported that an understanding of the temporal and spatial characteristics of rainfall is crucial for risk management, as well as for the planning, management, and utilization of water resources, which depend heavily on rainfall. Similarly, Hu et al. [
13] performed spatiotemporal regression using kriging in the Xinjiang Uygur Autonomous region, located in northwestern China, to model monthly rainfall data from 2004 to 2013. The authors identified a strong spatiotemporal correlation in the rainfall distribution in this region, thereby justifying the use of their proposed methodology. Furthermore, Martínez et al. [
14] performed a spatiotemporal analysis of rainfall data from Colombia and identified regions that exhibit irregular rainfall distributions.
The novelty of this study is the detailed presentation of a tool for spatiotemporal interpolation of precipitation in the region under study. It is worth noting that no research has applied this type of methodology to rainfall data from this region until now. The present study should help drive future research into spatiotemporal rainfall patterns across all of NEB. The purpose of this study was to provide a detailed framework to use the spatiotemporal kriging to model the space-time variability of precipitation data in Paraíba, Brazil.
2. Materials and Methods
The datasets used in this study were obtained from the Executive Agency of Water Management in the State of Paraíba (AESA), which is responsible for rainfall information in the region. The state of Paraíba spans an area of approximately 56,585 km2 in northeastern Brazil between the 6° and 8° parallels of south latitude and the 34° and 39° meridians of west longitude. The state of Paraíba is situated in a tropical region, and it is divided into the following four mesoregions: Zona da Mata, Agreste, Borborema, and Sertão.
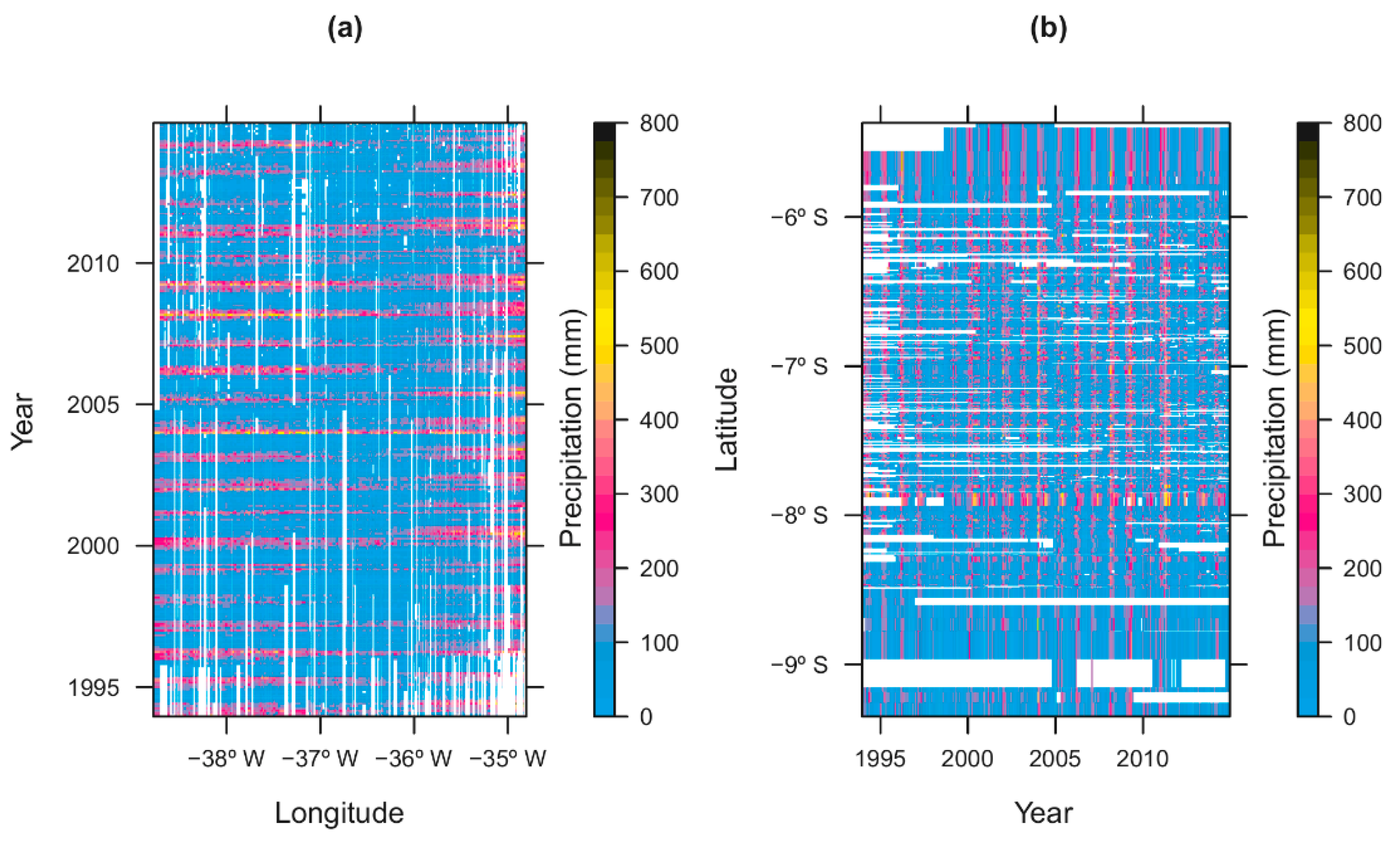
The dataset utilized in the present study includes the time series of the total monthly rainfall recorded at 269 rain gauge stations from 1994 to 2014. About 80% of the stations have missing data, represented as white tones (
Figure 1). Thus, to adjust the trend of the total monthly rainfall data and then to adjust the residual variogram, 54 stations with records for all of the months in the study period were considered because these locations adequately represent the variability in the data. The other stations excluded from the adjustment of the variogram were used to perform spatiotemporal kriging.
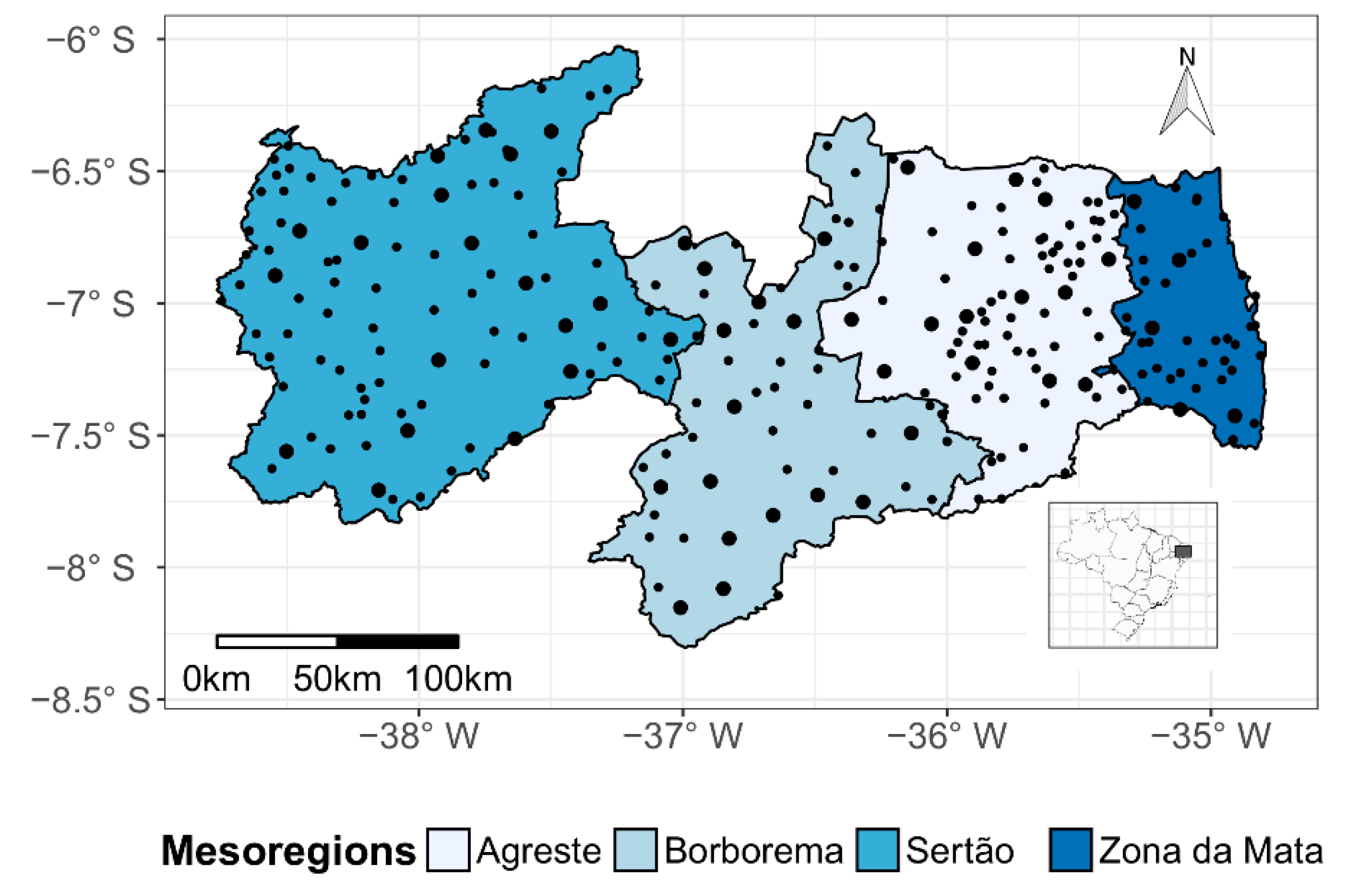
The spatial distribution of the 269 rainfall stations is shown in
Figure 2. The different color tones in the map identify the four mesoregions—namely, Zona da Mata, Agreste, Borborema, and Sertão—of Paraíba. The smaller points within the map represent rain gauge stations, whereas the larger points are the 54 rainfall stations that were used to adjust the trend and the variogram.
2.1. Spatiotemporal Model
In this study, a spatiotemporal process
was assumed, where
,
represented the two dimensions in space (latitude and longitude), and
represented only one dimension, namely, time. The spatiotemporal variation in
was established by the decomposition of the deterministic
and stochastic residual
as follows:
In Equation (1), it was assumed that
had both first- and second-order moments. The component of the tendency
is the expectation variable
. This component was determined here by an ordinary least squares (OLS) regression model. The residual
included the following three components: spatial, temporal, and interaction-based components [
1]. For modeling purposes, it was assumed that these three components were second-order stationary, mutually independent, and spatially isotropic.
The observed rainfall values were considered in the spatiotemporal random field defined in Equation (1), where the deterministic component
, which is spatiotemporally non-constant, represented a large-scale variation, while the residual
described random fluctuations at a small scale [
16].
2.2. Components of the Trend
The deterministic component
was estimated using multiple linear regression. Several studies have used this type of regression method to model the trend component in spatiotemporal geostatistics [
1,
13,
17,
18]. In this study, the geographic coordinates (latitude and longitude) and a temporal index employed to contour the effect of the annual seasonality on the precipitation were considered covariates. The adjusted trend model is given by the following:
where
and
. The
cosx and
senx functions were used as covariates in the multiple regression model to explain the seasonal variation. The variables
and
represent the latitude, longitude, and the quadratic effect of the longitude, respectively. Although the covariates exhibit spatial, temporal, and spatiotemporal variations, the regression model alone cannot account for all the variations. Therefore, the residuals of this model may exhibit spatiotemporal dependencies, indicating that a spatiotemporal variogram can be estimated and later used to interpolate the residues with kriging [
19].
2.3. Spatiotemporal Variogram
After specifying the trend component and obtaining the parameter estimates, the results were then subtracted from
, leaving the spatiotemporal stochastic residue
. The residuals produced by this regression were then used for the construction of a sample variogram. For a more detailed model, the monthly rainfall
was modeled as a sum of the trend and the spatiotemporal residue
, as defined by the following:
After analyzing and removing the spatial and temporal trends in the data, the spatiotemporal interest is shown in terms of an empirical evaluation of the covariance function [
14]. The spatiotemporal covariance was described using a spatiotemporal variogram,
, which measured the mean difference between the separated data in the spatiotemporal domain using the distance vector
. The spatiotemporal variogram was defined as follows:
In Equation (4), and for any and in the spatiotemporal domain.
An estimation of the variogram
was established as follows:
According to the sample variogram presented in Equation (5), is the cardinality for the set , that is, where and are the vectors of the spatial and temporal lags of and , respectively.
2.4. Generalized Product-Sum Model
In the next step of the analysis, a theoretical model was used to adjust the data based on the covariance functions of the spatiotemporal sample variogram. In this study, a non-separable model of a generalized product-sum [
1,
20] was used to model the spatiotemporal rainfall structure in the state of Paraíba. This model was written as follows:
In Equation (6), and are the spatial and temporal covariance functions, respectively.
The spatiotemporal variogram (
) was expressed as follows:
In Equation (7),
and
were the spatial and temporal marginal variograms, respectively. The generalized product-sum model can be seen as a surface with six parameters: two parameters for each variogram (sill and range), and a joint spatiotemporal sill and nugget [
2]. Also, the parameter
is positive and has the following identity that involves the global sill (
), together with the spatial and temporal sills, namely,
and
, respectively:
In Equation (8),
was estimated by using the information of the sill. This approach constitutes an alternative that Graler et al. [
20] described for the formulation of the product-sum model proposed in Equation (7). In this study, the authors proposed the following restructured Equation (7), which was used in this study:
To fit a spatiotemporal theoretical variogram to a sample variogram, for the weighting of squared residuals in the least-squares estimation, we used the number of pairs in the spatiotemporal bin divided by the square of the current variogram model’s value: . The marginal variograms in this study were outlined based on the sample spatiotemporal variogram . Through visual analysis, it was possible to define the theoretical models as being Gaussian, exponential, and spherical, which were components of Equation (9). In this way, it was possible to direct the structures for and .
2.5. Spatiotemporal Kriging
After establishing the trend function and the covariance for the residual, interpolation was performed using spatiotemporal regression kriging [
16,
18,
21]. According to Kilibarda et al. [
21], the variogram model is crucial in spatiotemporal kriging for calculating the best non-biased linear predictor, which was given by the following:
In Equation (10), was the linear predictor obtained using kriging for the location , was the covariance matrix of order of the residues for the points observed in space-time as derived from the spatiotemporal variogram, was a covariance vector of residues for the observed and predicted points, and was a vector of residues in the observed points.
The final predictor (
) for the rainfall variable (
) at the location
was defined as follows:
In Equation (11),
is the estimated amount for the location
obtained by Equation (2), and
is as defined in Equation (10). The error variance of the prediction in spatiotemporal kriging was defined as:
In Equation (12), is the variance for , is the matrix of order of variable predictors at the observed points, and is the vector of predictors at the prediction point.
Thus, kriging by regression was performed through the following steps:
Step 1: the values estimated using Equation (2) were extracted, followed by the extraction of the residues for all of the observations.
Step 2: After obtaining these residues, the values of the sample spatiotemporal variogram were calculated as defined in Equation (5), followed by the theoretical model fitting defined in Equation (9).
Step 3: The residues were then interpolated using Equation (10), after which, the trend component was added, resulting in the final predictor defined in Equation (11).
2.6. Selection and Performance of the Model
To determine the best theoretical variogram model that fit the sample variogram, the root mean square error (
RMSE) and Nash–Sutcliffe efficiency (
NSE) between the sampling variogram and the theoretical variogram were calculated [
22]:
where,
n is the number of observations,
is the
i-th observed value,
is the
i-th predicted value, and
is the mean observed value.
After selecting the model that best fit the cloud of points from the sample variogram, spatiotemporal kriging was conducted to measure the performance of the adjusted model. Thus, interpolation was implemented by accounting for the leave-one-out method [
14,
18,
23], as applied to all 269 rain gauge stations. This method consisted of removing an observed point from the rainfall in space-time
and then predicting its value
. This process was then repeated for all remaining points and residues of this process, after which the difference between the observed and predicted values is taken at each location
.
After the leave-one-out method was applied to measure the kriging performance, a scatter plot of the observed values versus the values predicted by spatiotemporal kriging was constructed, and the coefficient of determination was computed. It is worth noting that the application of the methodology proposed in this study allows for missing data to be entered. One of the advantages of spatiotemporal kriging relative to purely spatial kriging is that it not only interpolates to non-sampled locations but also predicts values for a time in which there was no data collection [
1,
24].
All statistical analyses were performed in software R [
25], using the packages
gstat [
20] and
sp [
26].
3. Results
3.1. Exploratory Analysis
The descriptive measures and boxplots of rainfall values in millimeters (mm) for the 1994–2014 period are shown in
Table 1 and
Figure 3.
Based on the average values and coefficient of variation, differences in rainfall distribution were observed between the analyzed months (
Table 1). Moreover, within each month, the monthly rainfall exhibited a distinct behavior in each mesoregion. Similar results were reported in References [
27,
28].
Figure 3 demonstrates that each mesoregion had a distinct rainy period and a different mechanism for the rainfall distribution. For example, in the mesoregion of Sertão, the highest rainfall volume occurred from January to April, whereas the rainfall in Zona da Mata was well distributed from January to August. For the analyzed period, September presented the greatest variability in all the mesoregions. Through these results, the spatial and temporal variability in the rainfall throughout the state is well known.
3.2. Regression Analysis for the Trend Component
The estimated parameters, standard error, statistical
,
p-value, and adjusted coefficient of determination (
R2) for the monthly total rainfall for the 1994–2014 period are presented in
Table 2.
Considering the results presented in
Table 2, the covariates
cosx,
senx, latitude, and longitude, in addition to the quadratic effect of the longitude, are associated with precipitation at the 0.01 level of significance. The
R2 estimated by the model shows that this trend model explained 29% of the variation in the total monthly precipitation. This low
R2 strongly indicates that the trend component was unable to explain the spatiotemporal variability in the precipitation. Moreover, it was challenging to provide a precise estimate for climatic variables, especially precipitation, because the spatial and temporal distributions of such variables exhibited large variations, causing the trend model to present a low
R2 [
15]. It is worth noting that the methodology proposed in this paper to estimate the precipitation accounts not only for the trend but also for the dependence of spatiotemporal data. Then, the residues produced by this trend component were modeled.
A histogram of the residues in the multiple linear regression is shown in
Figure 4. This is suitable for visual analysis of the residue behavior, which appears to have a positive asymmetry. In
Figure 4, it is also possible to perceive the large scale of the variation in the residues, which is explained by the high variability in the precipitation.
Next, the residuals from this regression were used to analyze the spatiotemporal autocorrelation using the variogram described in Equation (5).
3.3. Spatiotemporal Variogram of the Residuals
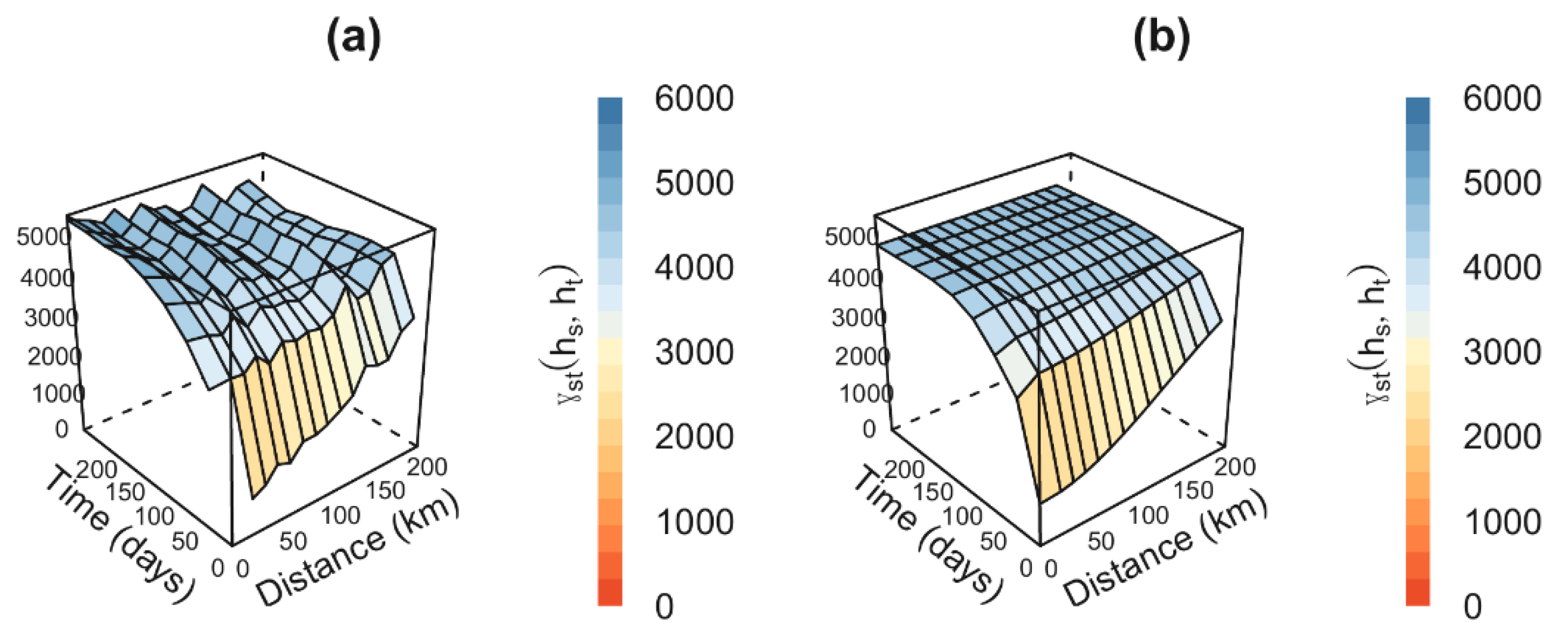
After removing the spatiotemporal rainfall trend, the variogram was calculated using the residuals. The empirical spatiotemporal variogram model (
Figure 5a) and the fitted product-sum model (
Figure 5b) are shown in
Figure 5. As shown, the residues indicated a clear correlation between both space and time, and spatial and temporal components explained the total variation in these residues. Note that the spatial structure became weaker as the time differences increased, and the temporal structure became weaker as the spatial differences increased.
The sample variogram can be visualized in terms of its marginal variograms, with one for space and another for time. The increasing trends in the spatial and temporal dimensions in the sample variogram indicated the presence of a strong spatiotemporal correlation. Hu et al. [
2] stated that the characteristics present in
Figure 5a further reinforced the need to apply spatiotemporal kriging to residues. In this sample spatiotemporal variogram, different structures were fitted for the generalized product-sum model class.
Figure 5b shows one of these results when using a Gaussian model for space and a Gaussian model for time.
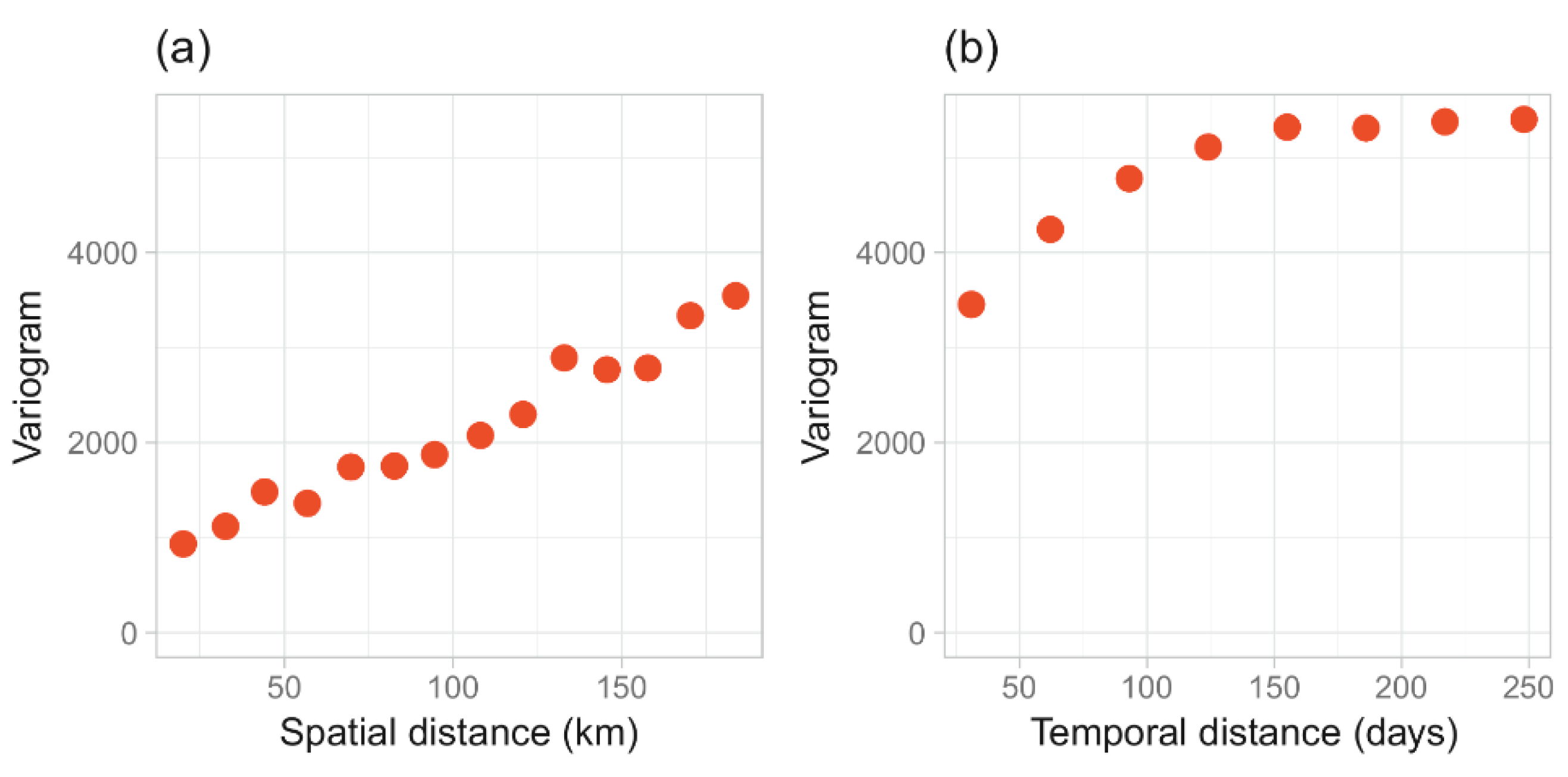
Subsequently, an exploratory analysis was performed for the empirical spatiotemporal variogram to construct the marginal variograms (
Figure 6).
For the analyzed data, the spatial variability exhibited by the spatial marginal variogram (
Figure 6a) was different from the temporal variability shown by the temporal marginal variogram (
Figure 6b) because the two variograms present different sill values. Iaco et al. [
1] observed characteristics similar to those presented in
Figure 6a,b and stated that, in this situation, the spatiotemporal correlation of the residues could be adequately fitted using the generalized product-sum variogram model defined in Equation (9). In this case, as mentioned above, the structures of the spatial and temporal correlation were noticeable. However, some studies on rainfall distribution did not present this significant correlation; for example, Muthusamy et al. [
29] developed a spatial variogram for the region of Bradford, England, but did not report a spatial correlation of the rainfall data.
Different variogram models were evaluated during the adjustment of the generalized product-sum model. For both space and time, the following models were used: Gaussian, exponential, and spherical.
3.4. Selection and Validation of the Model
The estimated parameters for the generalized product-sum model are presented in
Table 3, were obtained by considering the different structures for the spatial and temporal components. The
RMSE and
NSE were used to compare the models. Some studies, such as References [
1,
2,
21,
24], used only a single spatiotemporal correlation structure. In this study, a more comprehensive analysis was proposed by using different structures in the model formation.
For the generalized product-sum variogram model, the best structure, having the lowest RMSE and higher NSE, was found when considering the Gaussian model for both the spatial component and the temporal component. According to the selected model, the parameters related to the range showed spatial and temporal variations in the rainfall distribution over the state of Paraíba. The spatial range of 180 km suggested that the spatial correlation became insignificant after this sill, whereas the time interval of 71 days (approximately two months) indicated that the temporal correlation became insignificant after this interval.
After the best model was selected by adjusting the variogram, the cross-validation leave-one-out method was applied, and the results are presented below.
The spatiotemporal distribution of the mean
RMSE values based on the 1994–2014 period is presented for each month in
Table 4, in which high values indicate a high variability between the estimated and observed amounts in the rainfall distribution.
The highest values of the
RMSE are shown between October and December. In the mesoregion of Sertão, smaller values of
RMSE were noted between January and May, because it was during this period that the lowest variability of precipitation occurred (
Table 1). These results are similar to those found in References [
15,
27]. The rainy seasons presented high spatial variability due to the actions of different weather systems, such as the Intertropical Convergence Zone (ITCZ) and Upper-Level Cyclonic Vortex (ULCV), as described by Macedo et al. [
28].
The months from January to March provided the lowest
RMSE throughout most of the study region, indicating that the predicted values were close to the observed rainfall values. These results are consistent with Raja et al. [
15], who reported that the lowest variability in Paraíba occurred during these months. Accordingly, it was also possible to observe a substantial monthly statistical variation.
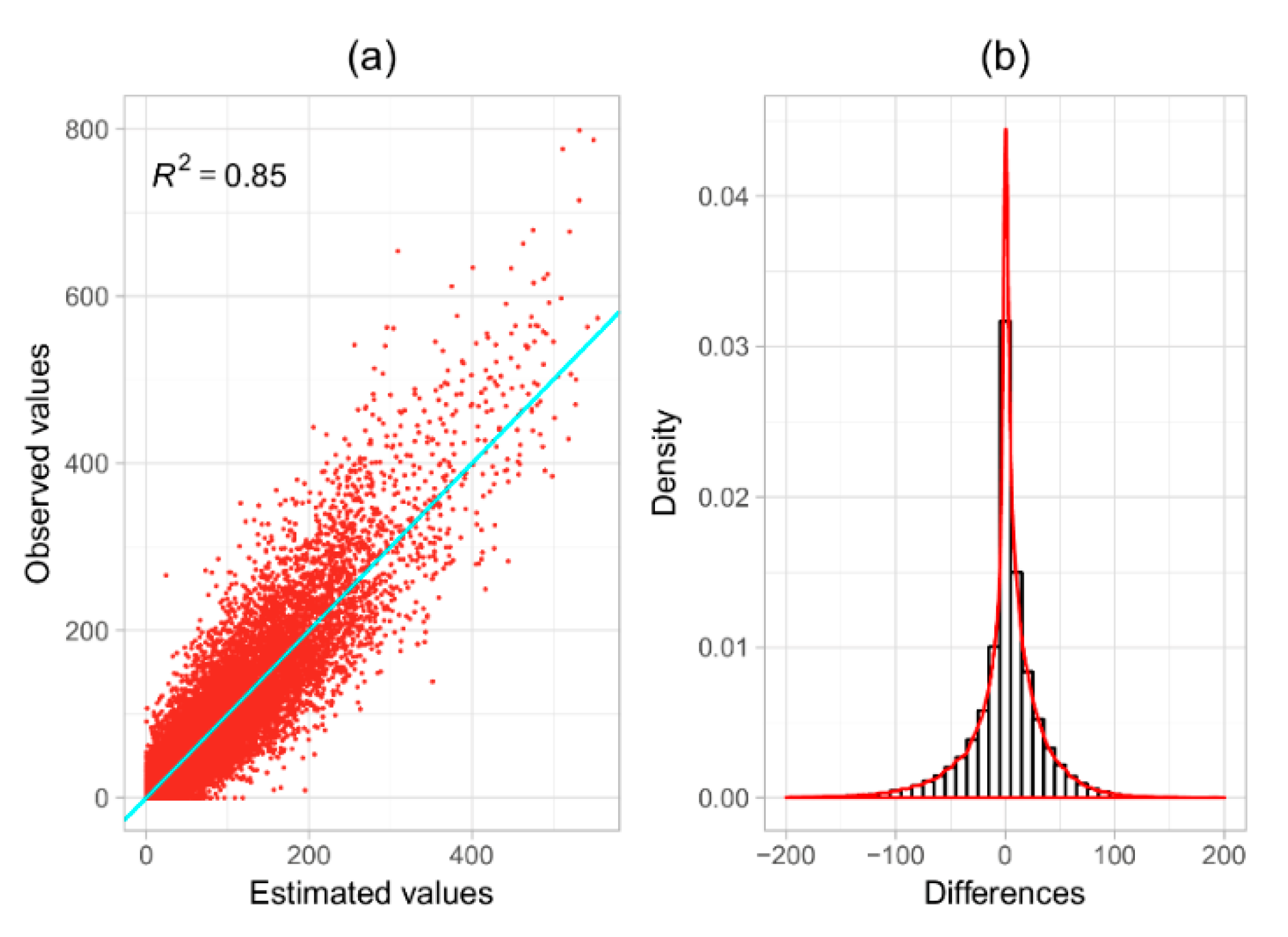
To evaluate the quality of the fit for the model that was selected earlier, graphics were created using all of the values predicted using spatiotemporal kriging according to their actual values and the histogram of the difference between these values (
Figure 7) considering all 269 rain gauge stations.
Figure 7 shows a strong linear relationship of the form
y = x between the estimated and observed values, which was supported by an
R2 value of 0.85, which indicates that 85% of the total precipitation variability could be explained using spatiotemporal kriging. Additionally, a visual analysis of the differences between these values presented in
Figure 7a shows that the differences were distributed symmetrically with a frequency near zero. In other words, the scatter plot of the observed versus the estimated values during the 1994–2014 period, as well as the histogram of the differences between these values (
Figure 7b), showed that the predictions were not significantly biased.
3.5. Spatiotemporal Kriging
Maps of the estimated rainfall for January in the years of 2015–2018 are shown in
Figure 8.
The application of the methodology proposed in this study presents a great advantage because it enables the use of spatiotemporal kriging to make predictions at any point in space-time within the chosen region. Thus, it enables an evaluation of how rainfall distribution patterns change with regard to both space and time, in addition to presenting values in places that are not monitored by weather stations. This application is illustrated in
Figure 8, which shows the predicted amount of spatiotemporal rainfall in the state of Paraíba for January in the years of 2015–2018. January was chosen because it presented the highest rainfall values throughout the entire region, and it showed high variabilities in both space and time. The predicted rainfall presented strong spatial and temporal patterns in the study region, evidencing the success achieved when applying the proposed geostatistical spatiotemporal methodology.
Regardless of the selected period, the highest rainfall level was distributed in the Zona da Mata mesoregion (
Figure 8). There was little variation in precipitation in the north–south direction. However, high variability was observed among predictions in the east–west direction. Finally, the greatest variation in rainfall was found in the Sertão mesoregion of Paraíba. In
Figure S1, which is available in the
Supplementary Material, the predicted rainfall values are shown for all months within the 2015–2020 period.
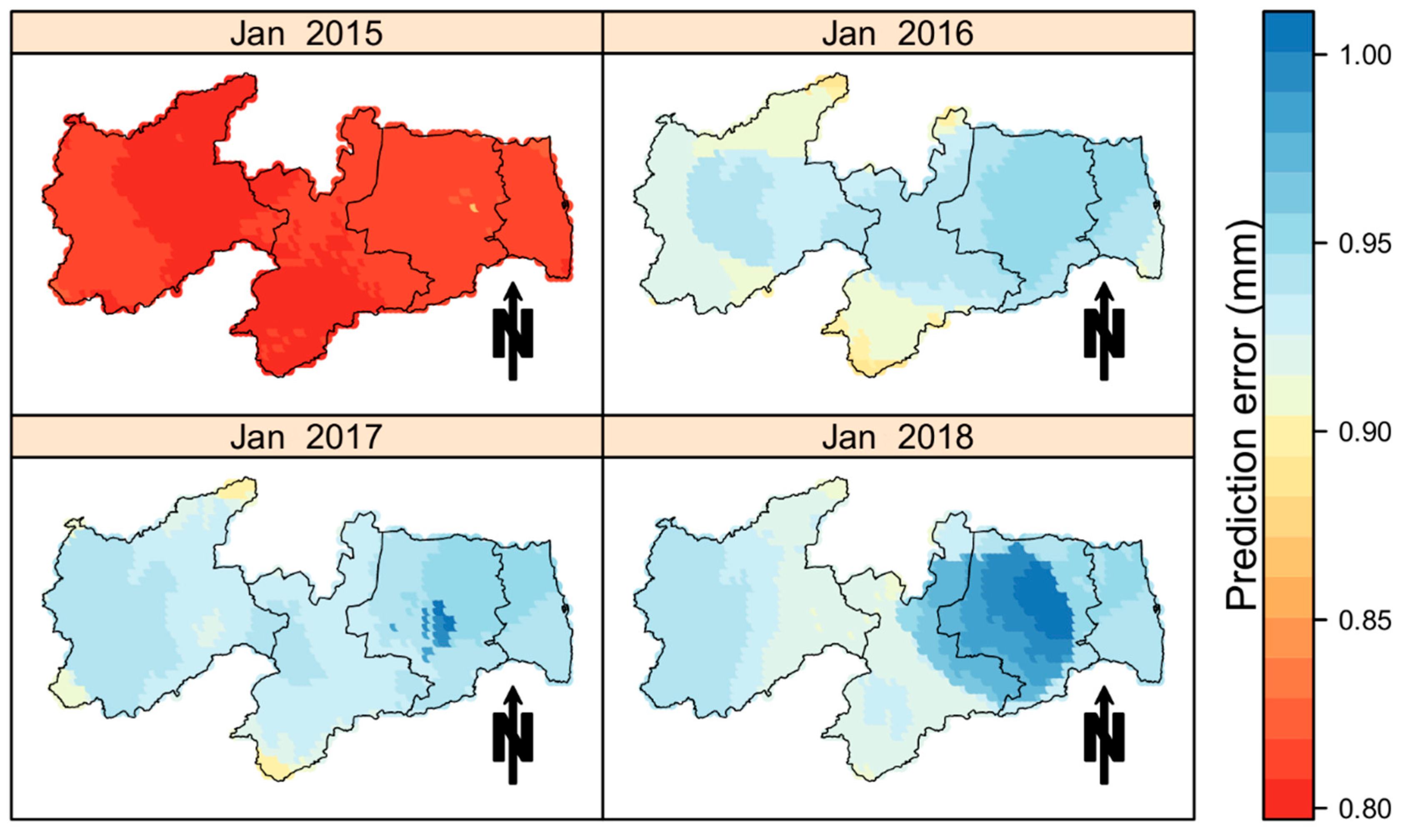
In addition to the spatiotemporal kriging-related predictions for January from 2015 to 2018,
Figure 9 shows maps of the standard error representing the uncertainty in the rainfall predictions in the chosen period. The error showed variations in the east–west direction. Moreover, within each mesoregion, there were variations in the estimates. It is also worth noting that the Borborema mesoregion presented the highest indexes for the standard error of the prediction; this behavior was attributed to the more intense rainfall in this area.
4. Discussion
In this study, rainfall in the state of Paraíba was spatiotemporally modeled using well known geostatistical techniques, such as kriging. Similar studies involving spatial [
30] or temporal [
31] analyses of rainfall distributions have already been performed for the state of Paraíba, although they did not take into account the combined spatiotemporal variability in this phenomenon. Thus, this research presents a joint spatiotemporal study of the rainfall distribution in this state.
Here, the trend component represented 29% of the temporal variability in the rainfall. Studies in References [
13,
17,
18] indicated that modeling this trend component influenced the fitting of the spatiotemporal variogram of the residues. Accordingly, this study could be improved by considering environmental factors, such as the temperature, in the adequate description of the trend component; this would likely result in an expected increase in the phenomenon variability percentage being modeled. Thus, the model for the trend only somewhat explained the variability in the data because it accounted for less than half of the variability of the spatiotemporal precipitation in the study area. Several studies have shown that the integration of climatic variables into precipitation predictions generates models with greater accuracy, thereby reducing error metrics and increasing
R2 values [
15,
32]. However, there is a lack of meteorological variables for the study region. For the state of Paraíba, only eight weather stations provided recorded data, and it was impossible to use a few of those stations in this work because their data could negatively affect the predictions in the model. For future studies, the results obtained in this study could be compared with those derived from the application of data obtained using simulations. Another important topic addressed in this research is the ability to explain the variability in the data beyond just the trend component; this analytical ability was achieved by adjusting the covariance functions for the residuals obtained by adjusting the trend because they had space-time dependence [
14,
21].
The rainfall distribution in the state of Paraíba showed a clear correlation for both space and time, thereby justifying the use of spatiotemporal kriging. When constructing the spatiotemporal variogram of the residues, several researchers found that spatial dependence became weaker with an increase in time, while the temporal dependence became insignificant over vast spatial distances [
19,
21,
27,
33]. In the studies mentioned above, the modeled phenomena did not present common characteristics in the spatiotemporal structure during the construction of the variogram. After the removal of the trend component, the rainfall data showed a clear spatial correlation structure over different temporal distances and a temporal correlation structure over different spatial distances. From a theoretical perspective, some studies fitted models to the marginal sample variograms obtained from an empirical spatiotemporal variogram and then inserted the individual fittings into the product-sum model [
1,
24]. Nevertheless, this study proposes a method to fit the spatiotemporal theoretical model because spatiotemporal interactions directly impact the parameter estimations; when theoretical models are fitted to the marginal variograms, there is no interference in the estimation from this interaction. However, this type of procedure results in problems during the optimization and determination of the parameter estimations. Examples of studies that employed this type of fitting can be found in References [
2,
34].
This research represents a breakthrough for climatological studies because it employs a technique that is more accurate than traditional statistical methods. The application of the statistical methodology proposed in this paper constitutes a significant contribution toward understanding the variability in precipitation and water resources of a region. The proposed approach considers that the spatiotemporal variability is decomposed by the trend component and the stochastic residue. However, the method presents some limitations, one of which is the difficulty in capturing the variabilities between the locations separated by great distances in the dataset. Additionally, for future work involving this type of modeling, it will be necessary to include auxiliary variables, such as the humidity and temperature, for the trend component to present better metrics.
The interpolation of climate data is widely used for research and management purposes in several disciplines, including social science [
1], hydrology [
14], and forestry [
33]. The importance of both spatial and temporal modeling of the rainfall distribution in the state of Paraíba is crucial for the management of high-priority areas that may experience a scarcity of rainfall caused by periods of drought or instances of flooding caused by excess rainfall, thereby inducing environmental and socioeconomic damages [
35]. The application of spatiotemporal kriging to obtain rainfall records from unobserved sites should provide favorable conditions for the planning and management of water resources because it will be possible to analyze regions that have a high impact on the state economy. For example, Biondi [
36] performed spatiotemporal rainfall kriging and presented results that directly addressed the planning needs for the distribution of water and natural resources once the occurrence of drought in a river basin has been diagnosed because it was possible to analyze which geographic areas were more likely to be affected by severe droughts.
5. Conclusions
The rainfall mechanisms throughout the analyzed region presented variability over both space and time. Furthermore, the spatiotemporal kriging of precipitation clarified the dramatic spatial and temporal variability of water resources among the mesoregions throughout the state, thereby providing a detailed visual analysis of sectors experiencing precipitation conditions ranging from water scarcity to an excess of rainfall.
In this study, a rainfall data analysis methodology was proposed through spatiotemporal geostatistics and was applied to irregularly spaced weather stations by considering the rainfall distribution over both space and time. Notably, the rainfall variability may be related to spatial and weather covariates, such as the temperature, humidity, and altitude, among others, suggesting the need to include such covariates for future studies to model the effect of the rainfall trend. Moreover, the monthly rainfall in the analyzed region presented a series of records with null values, which affected the application of a standard regression model to a certain extent. Exploring these issues in detail will require the development of a non-normal model that enables a better explanation regarding the variability in the rainfall distribution throughout the region. This model will constitute the next investigative step and it will be reported soon.
The results achieved in this research should motivate further research, including studies throughout the northeastern region of Brazil, to make predictions to diagnose which sites might experience droughts or floods.