Numerical Simulation of the Sound Field of a Five-Stage Centrifugal Pump with Different Turbulence Models
Abstract
:1. Introduction
2. The Laboratory Model
3. Numerical Simulation of Energy Performance
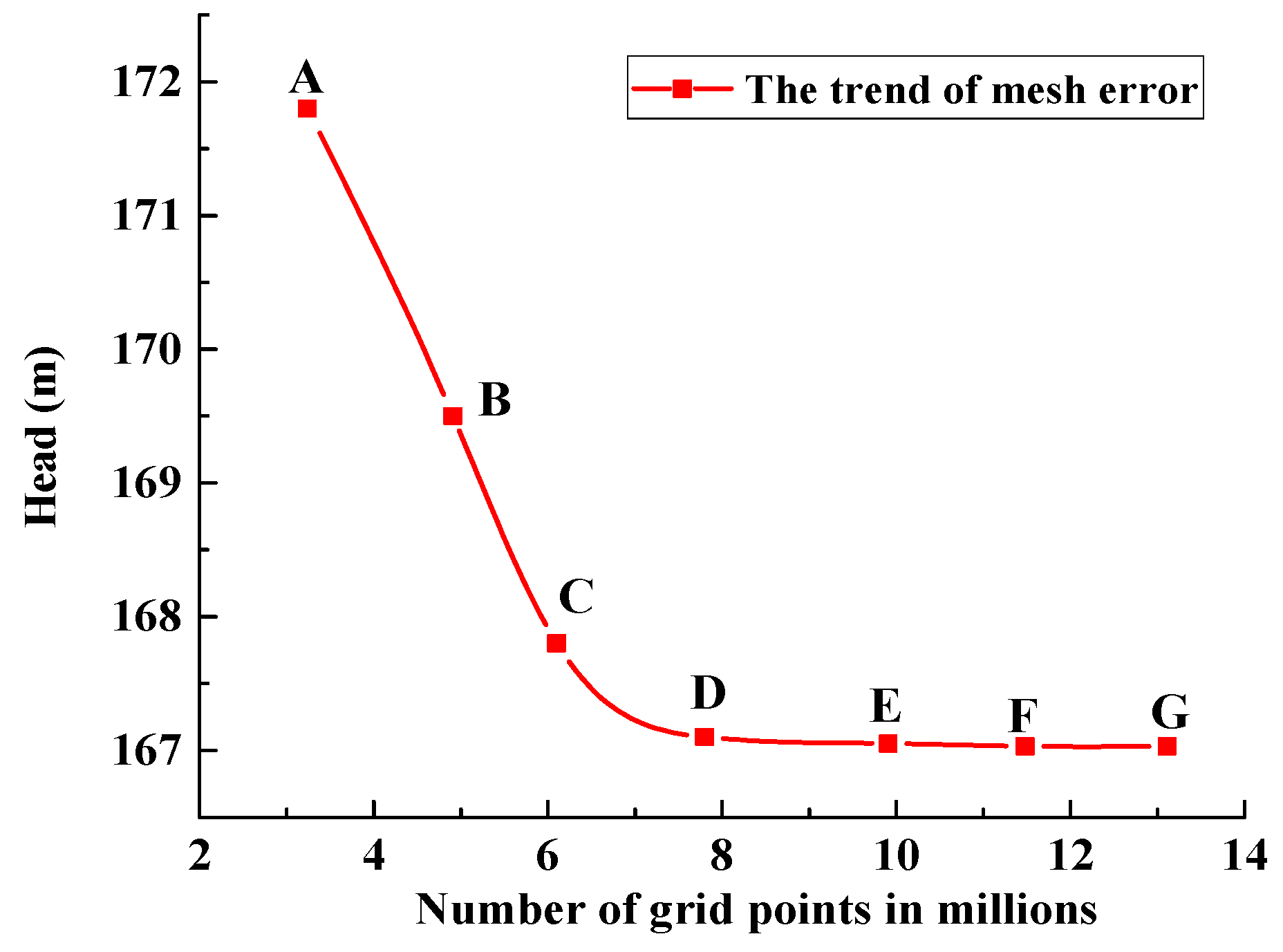
3.1. Mesh Generation and Boundary Conditions
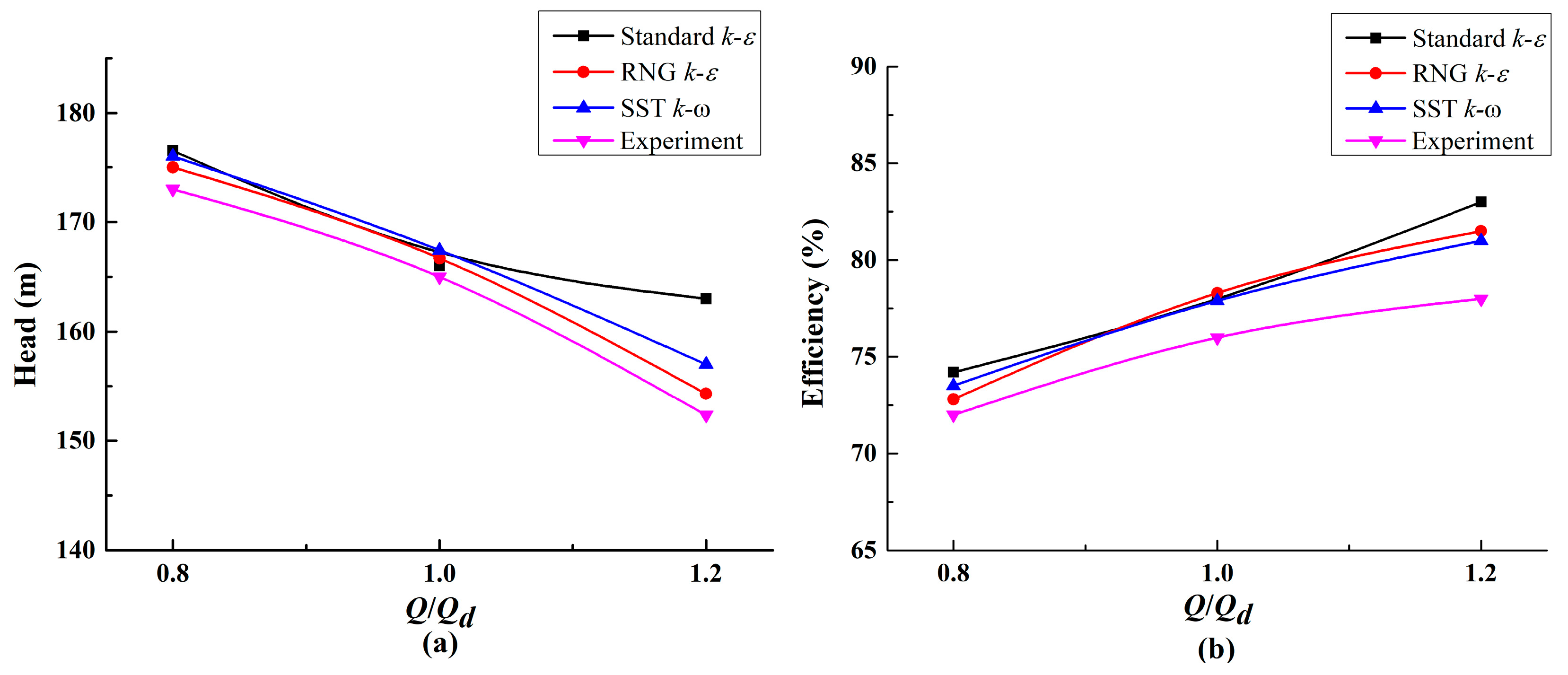
3.2. Comparison Energy Characteristic between Experiment and Numerical Simulation
3.3. Pressure Fluctuation Analysis
4. Further Methodical Details
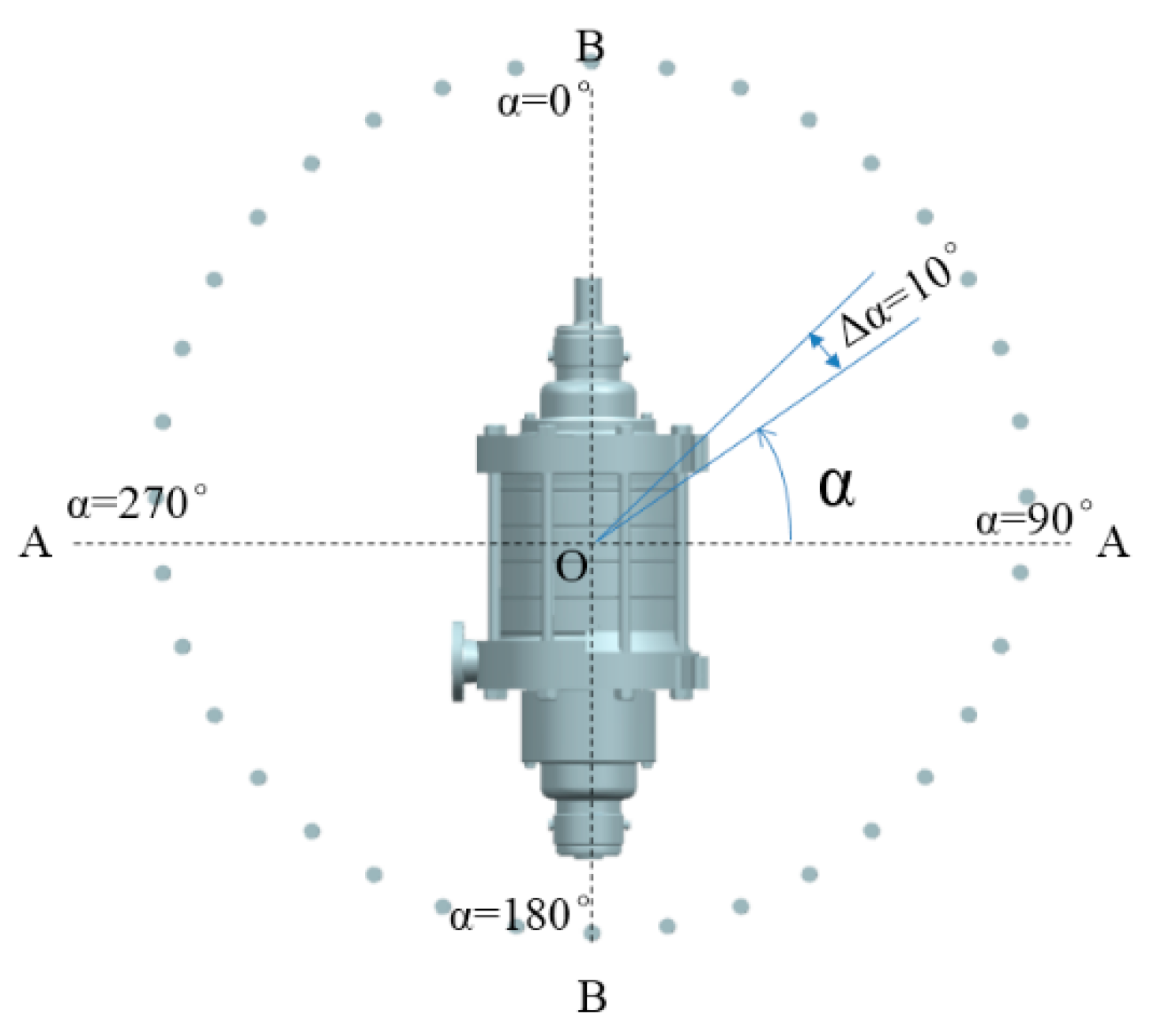
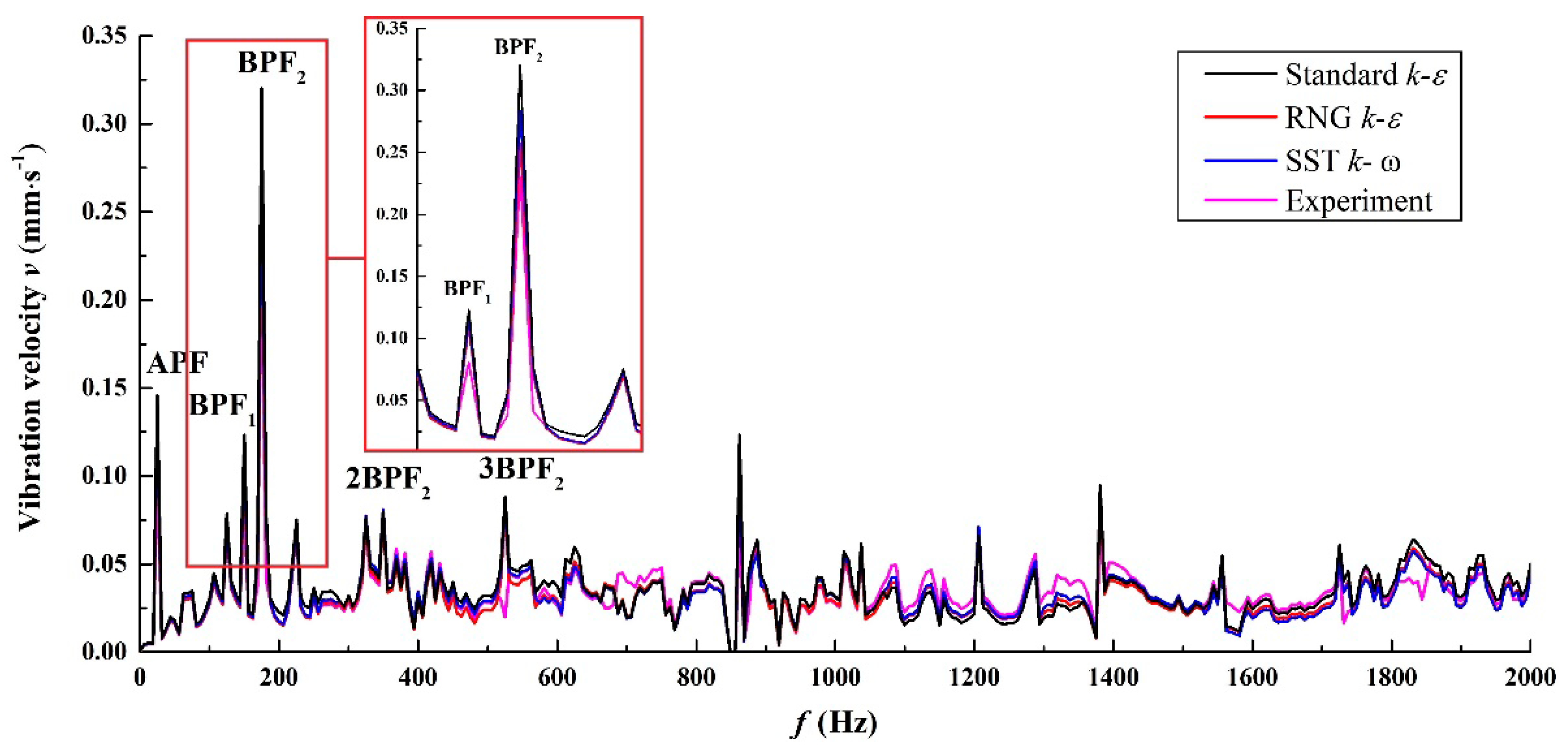
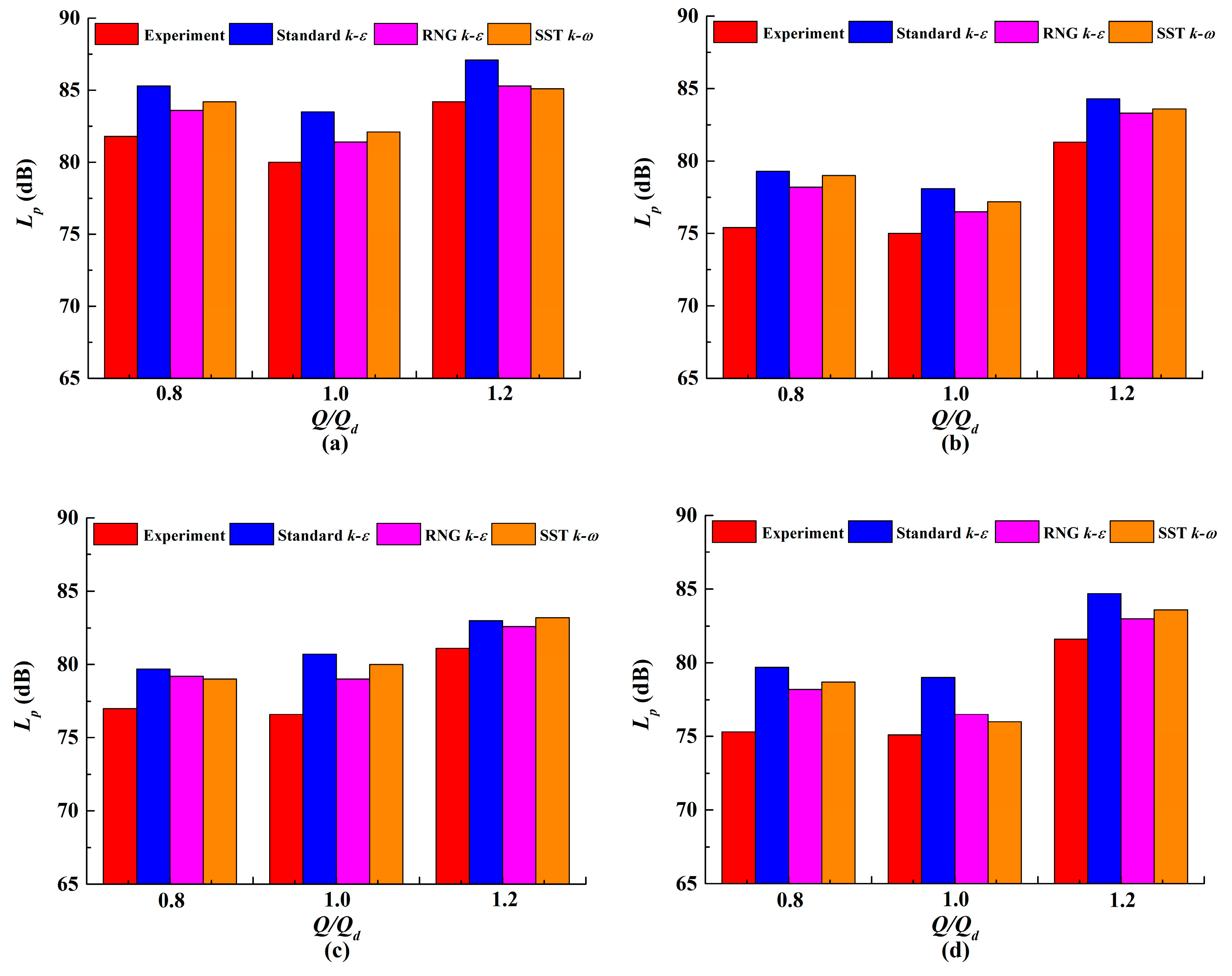
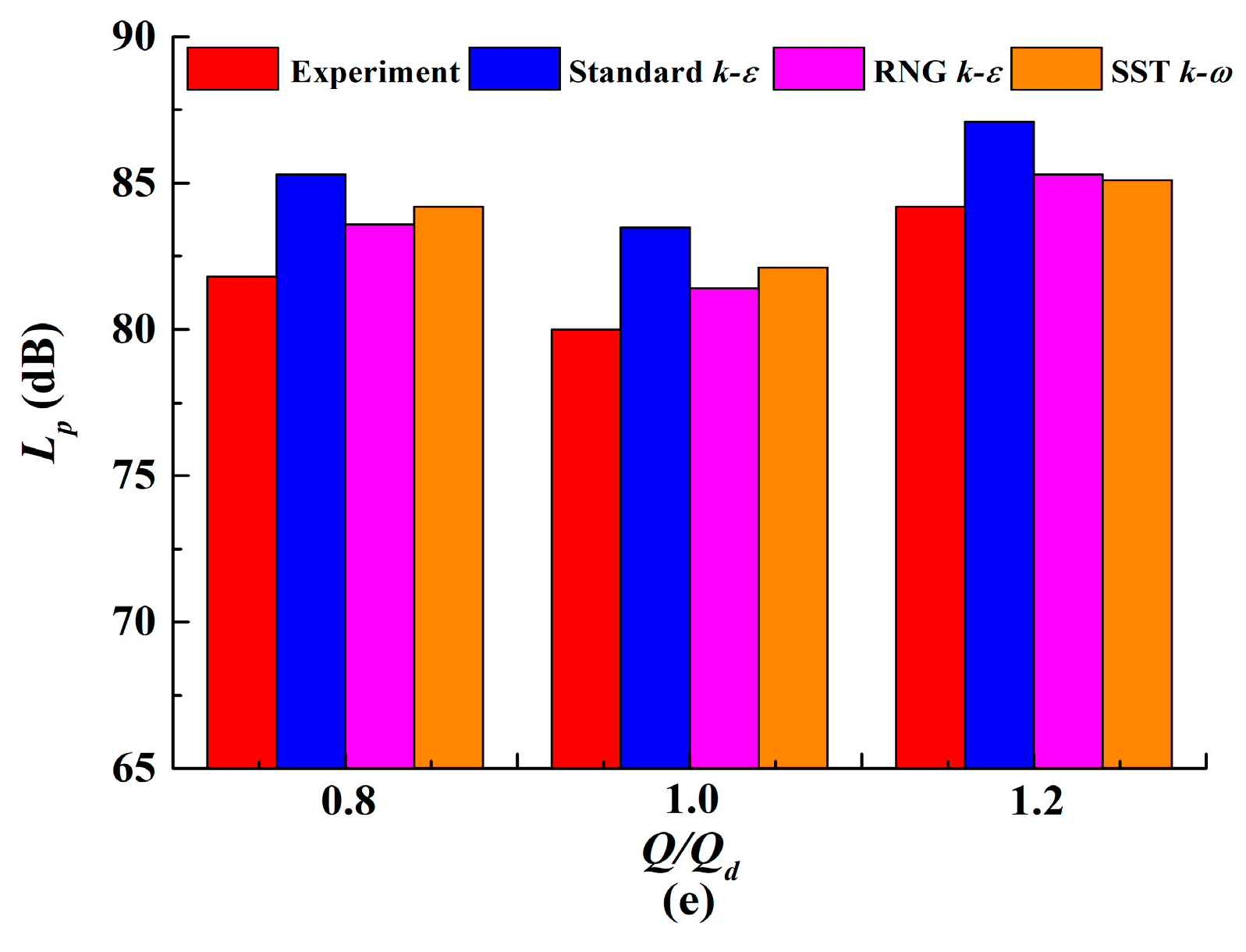
4.1. Vibration Simulation and Experimental Verification
4.2. Sound Field
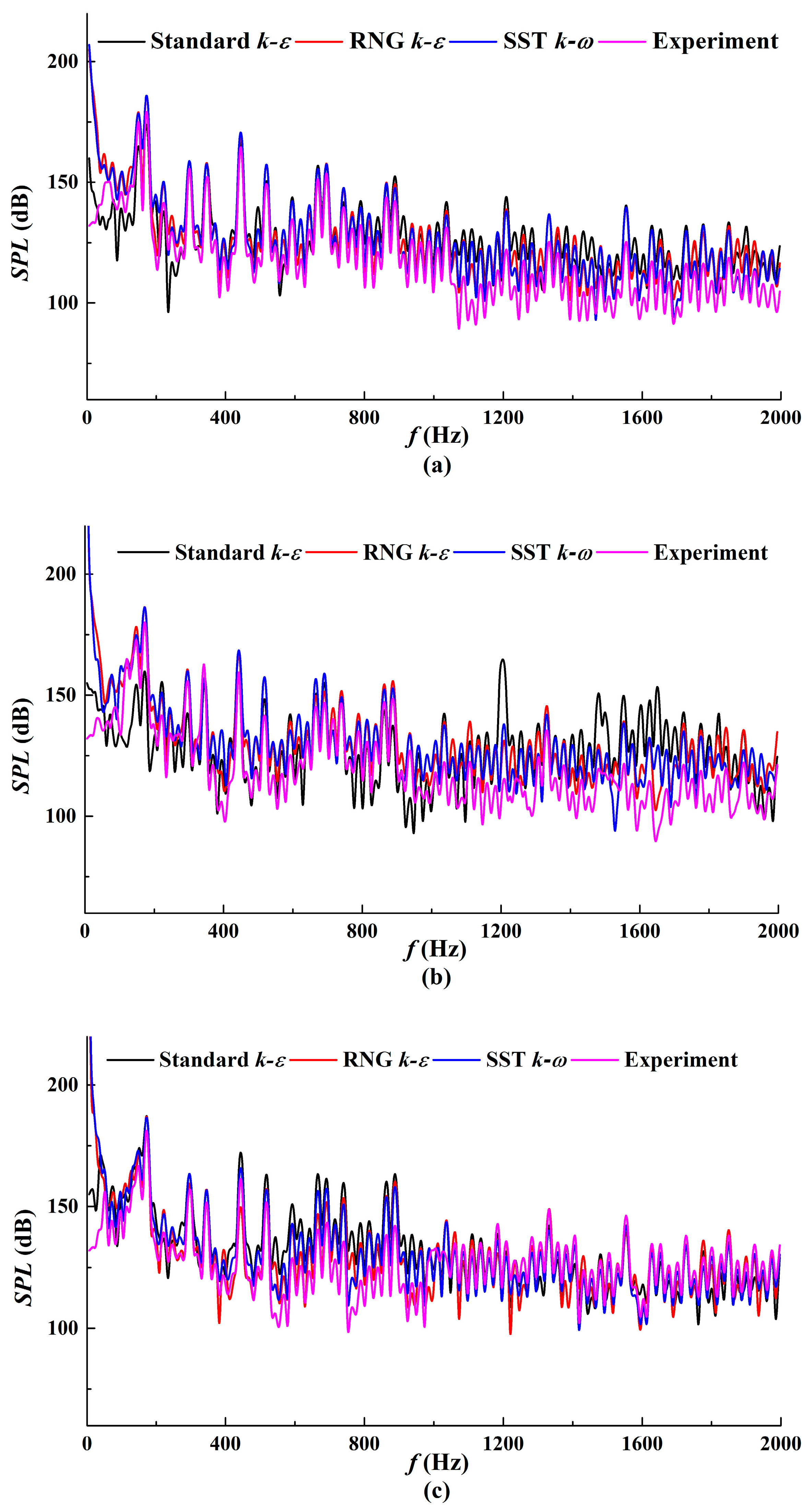
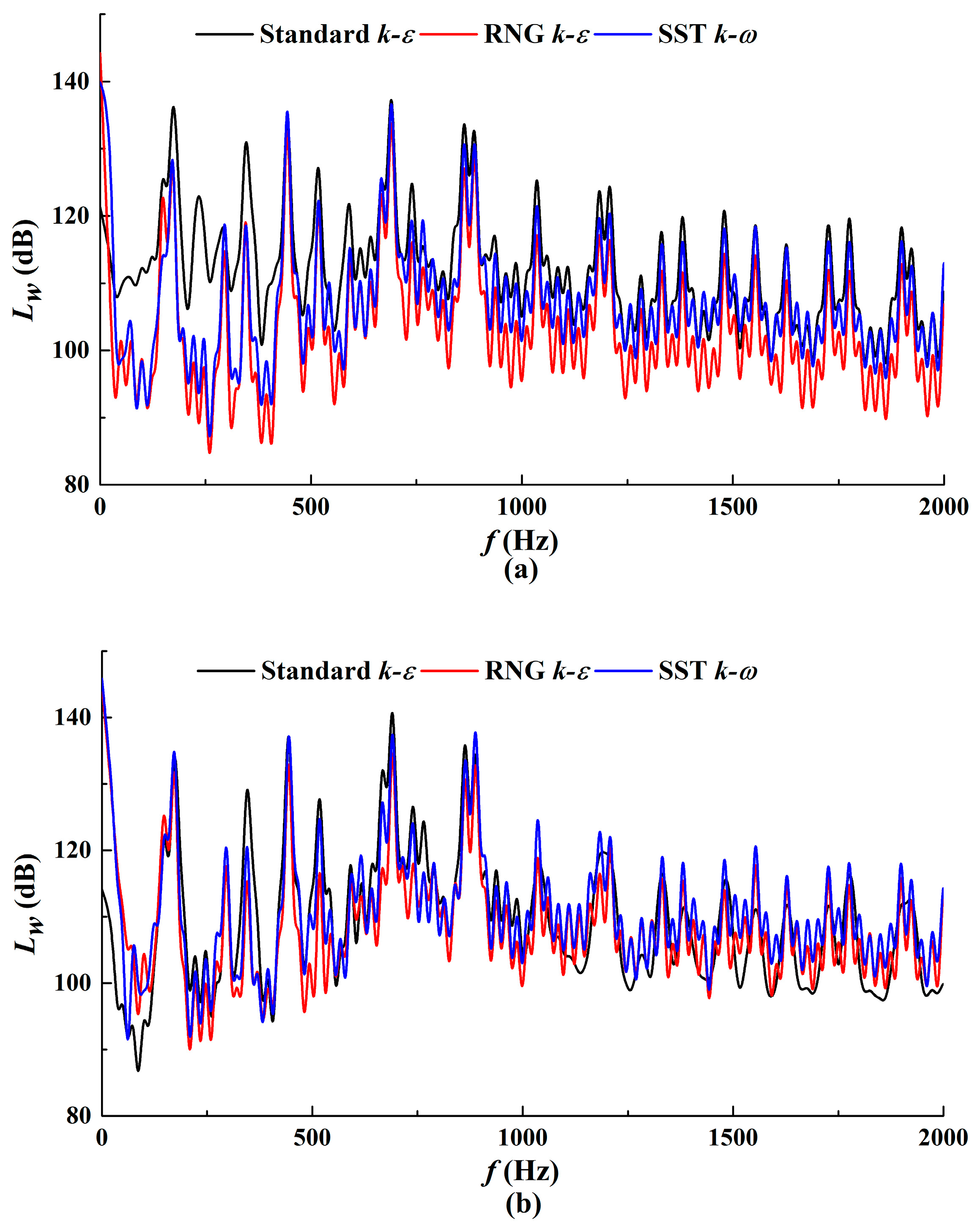
4.2.1. Internal Sound Field
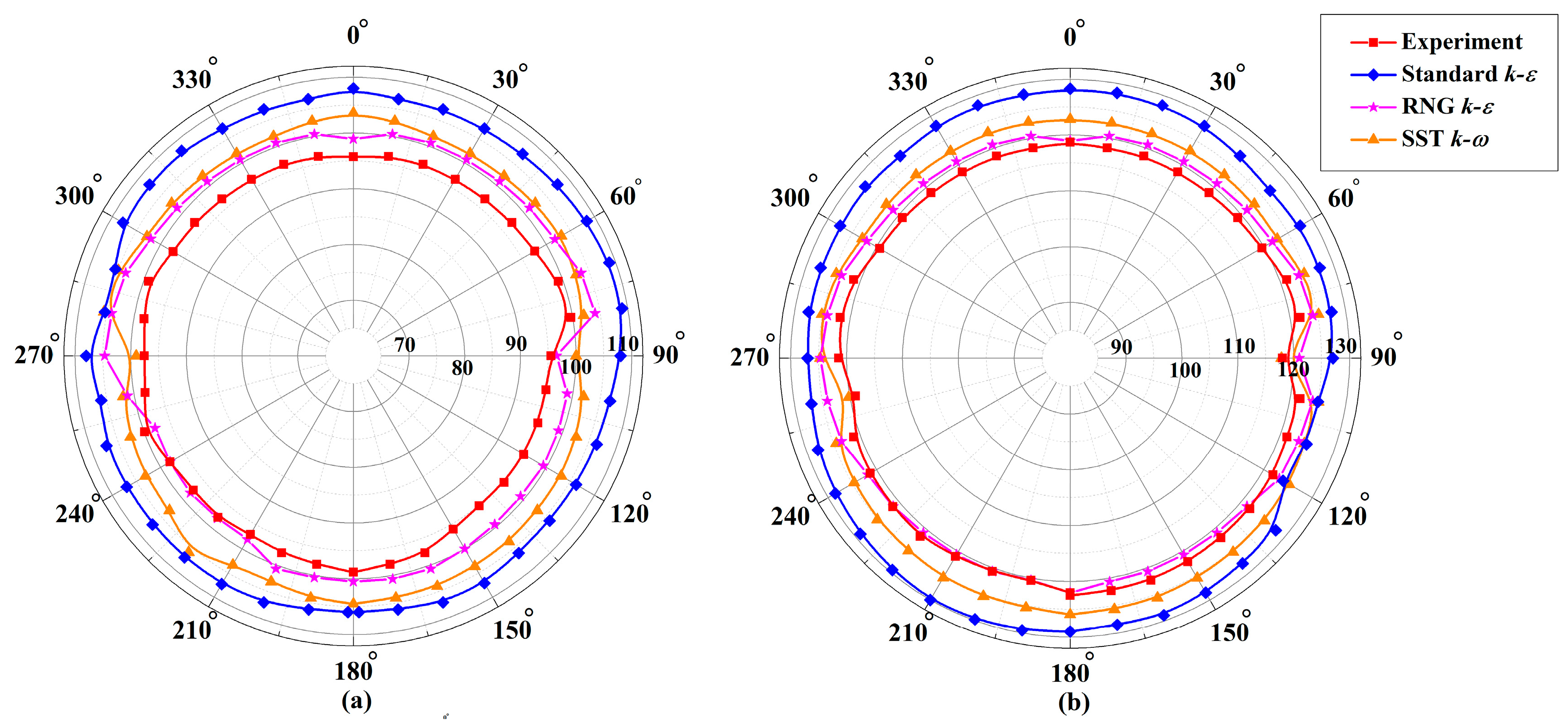
4.2.2. External Sound Field
5. Results and Discussion
5.1. Vibration Analysis
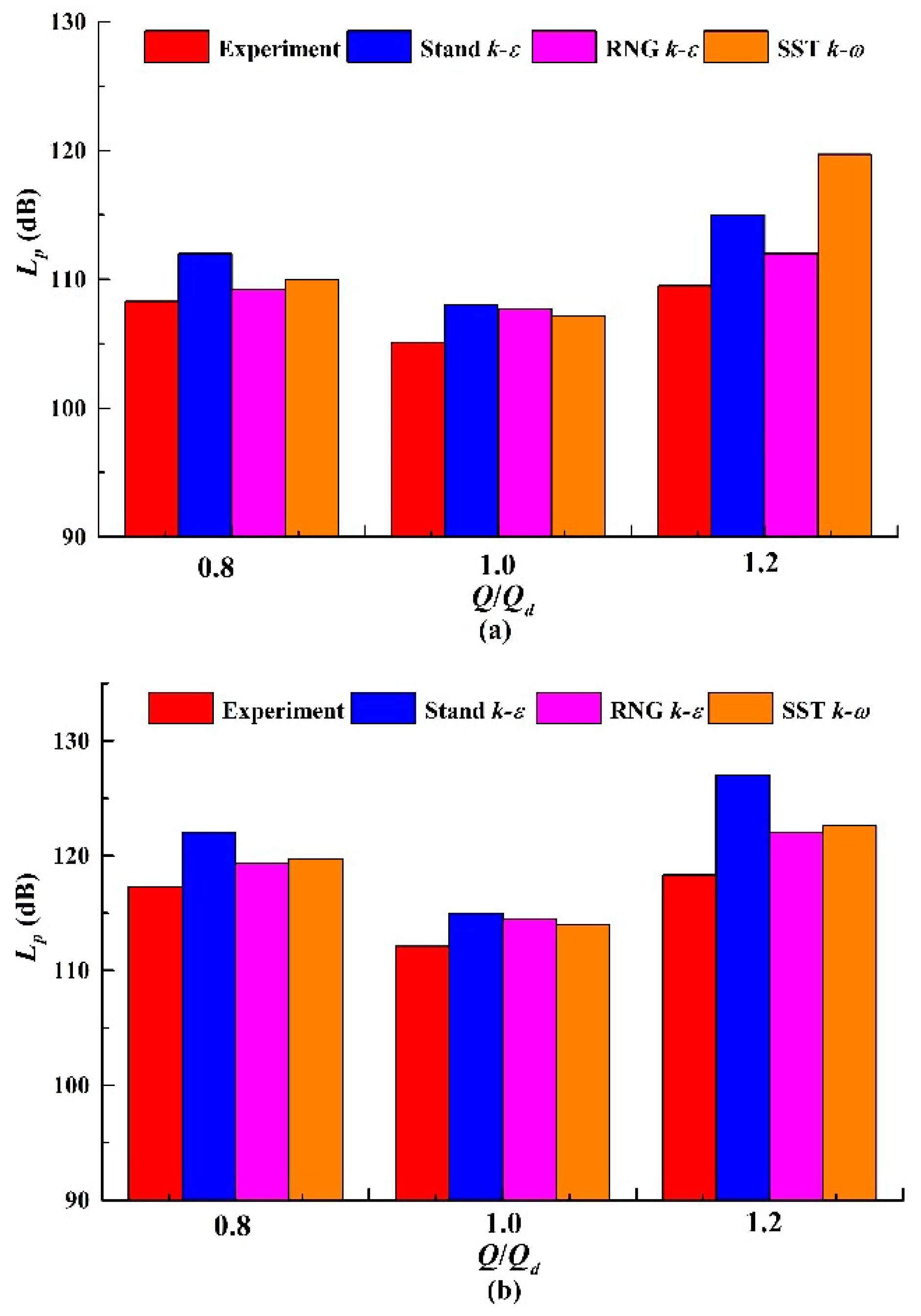
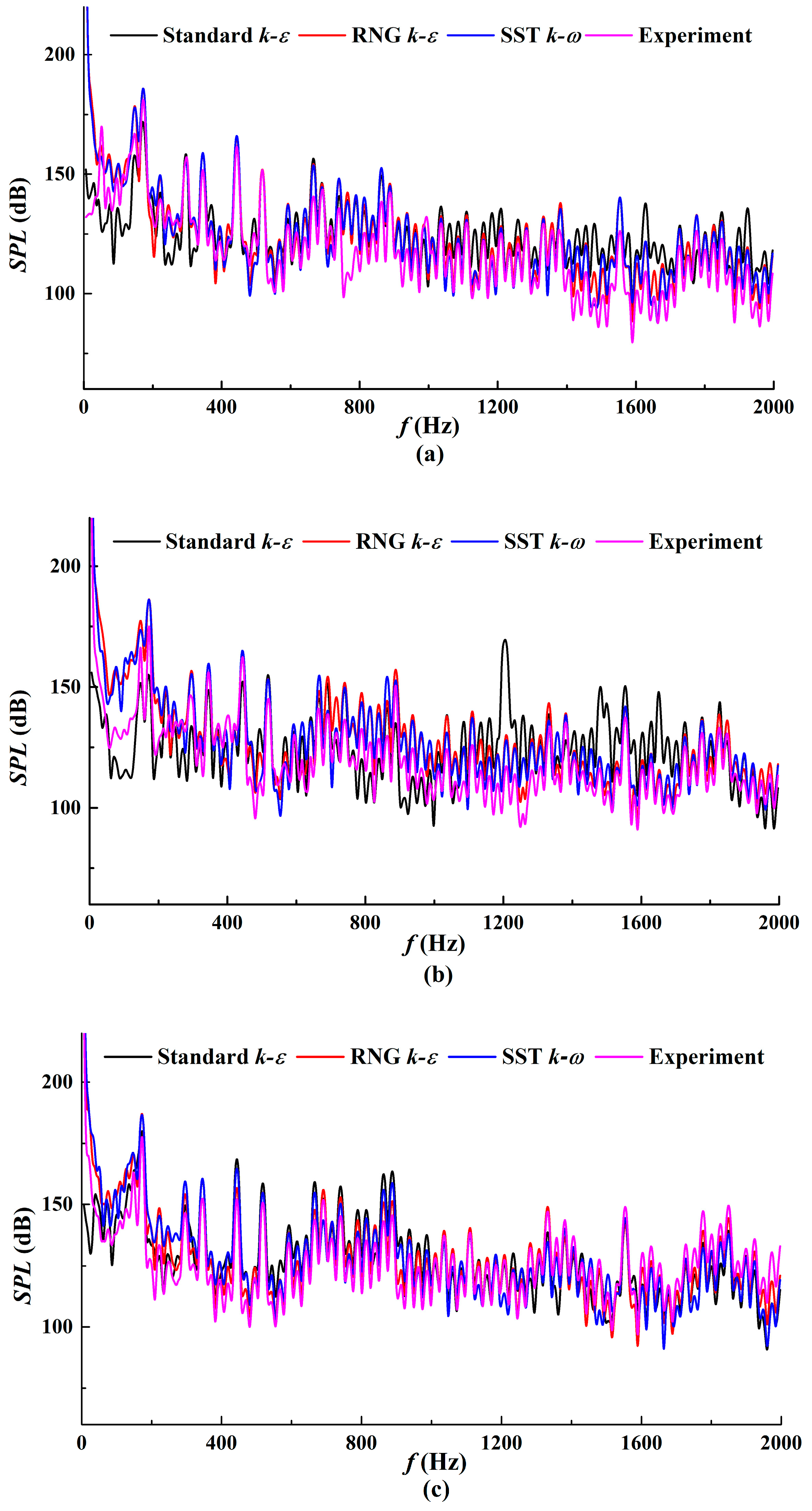
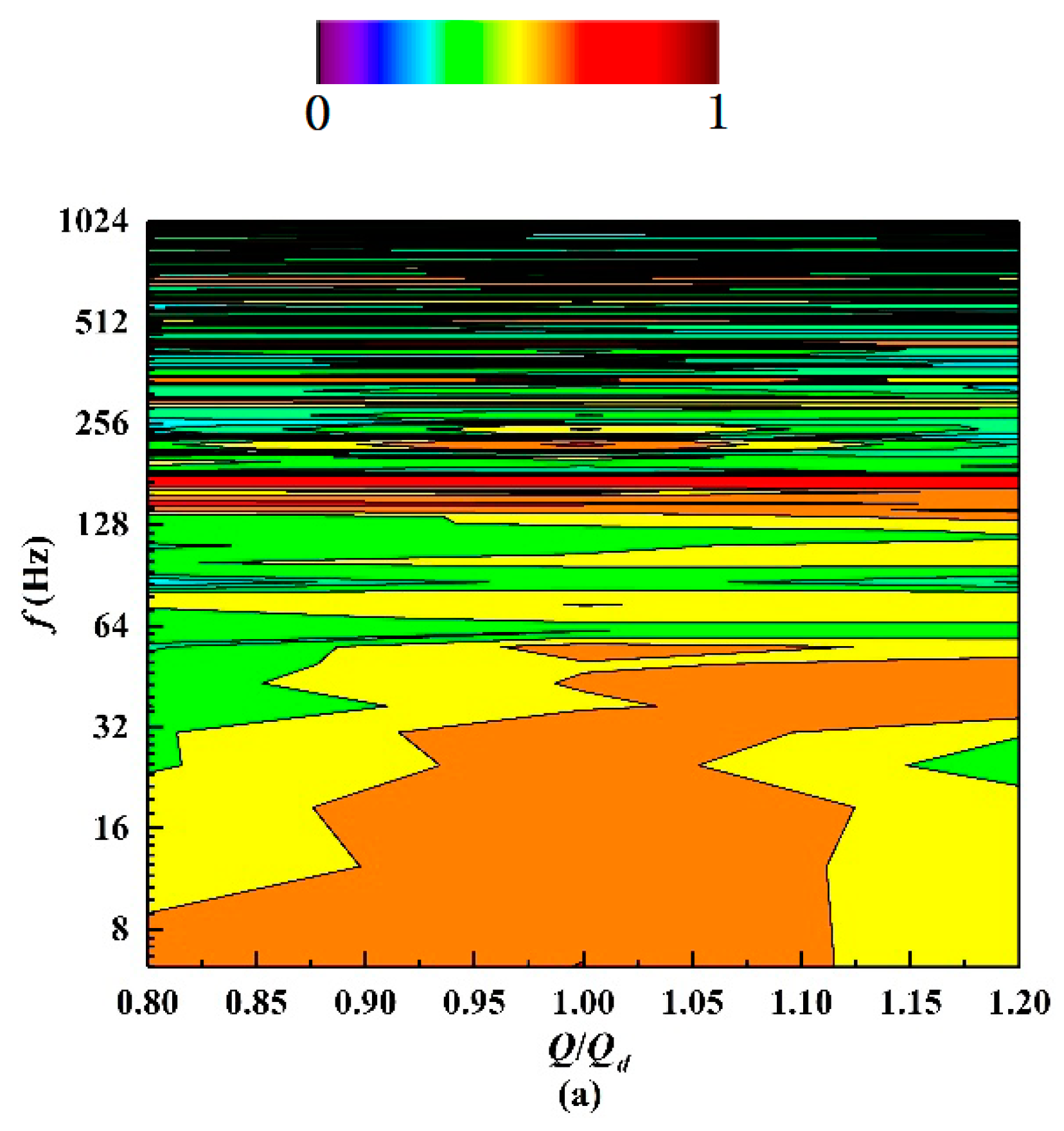
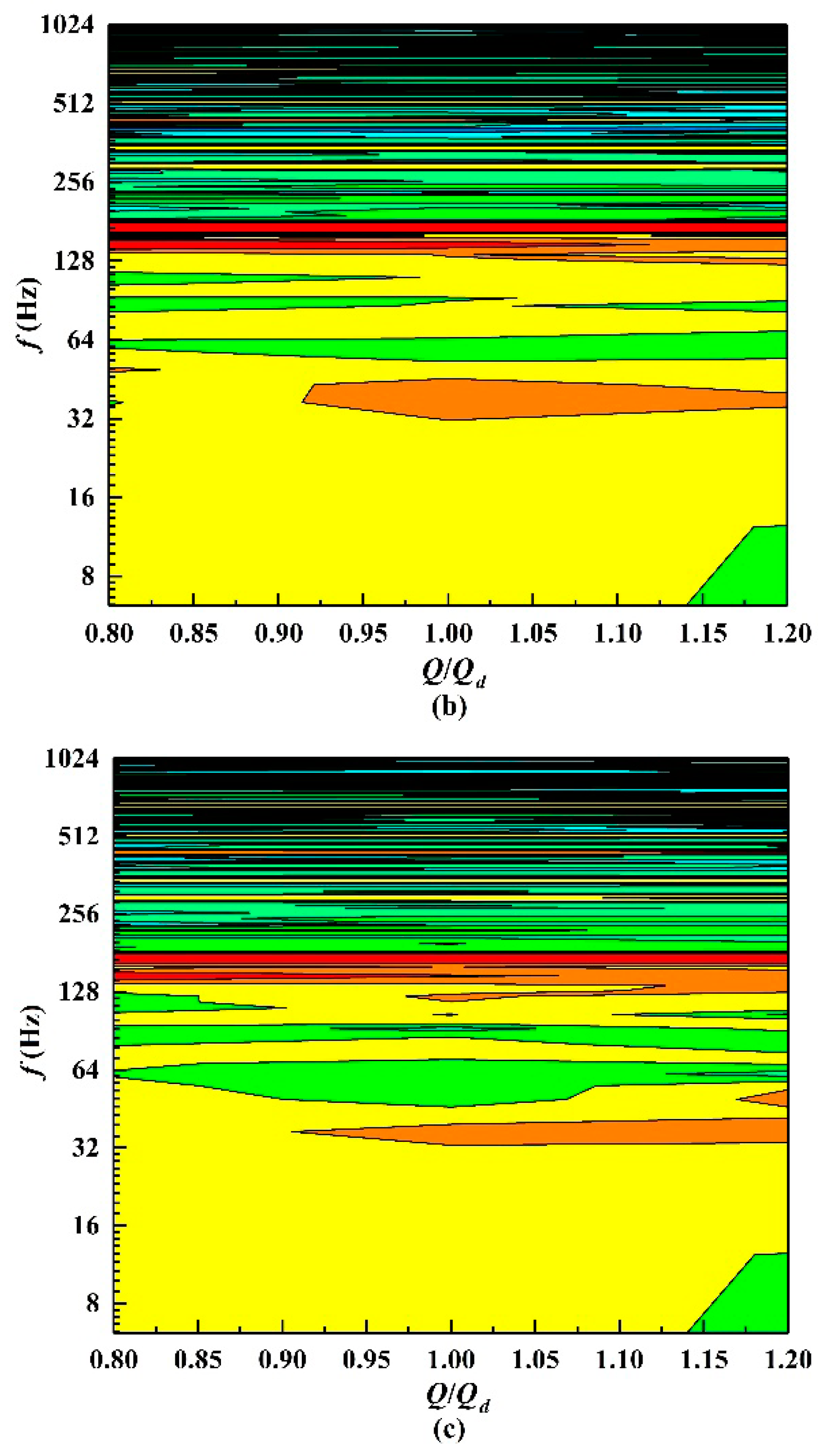
5.2. Internal Sound Field Analysis
5.3. External Sound Field
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, M.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. J. Mech. Syst. Signal Process. 2017, 460, 460–493. [Google Scholar] [CrossRef]
- Dürrer, B.; Wurm, F.H. Noise sources in centrifugal pumps. In Proceedings of the Conference on Applied and Theoretical Mechanics 2006, Venice, Italy, 20–22 November 2006. [Google Scholar]
- Khelladi, S.; Kouidri, S.; Bakir, F.; Rey, R. Predicting tonal noise from a high rotational speed centrifugal fan. J. Sound Vib. 2008, 313, 113–133. [Google Scholar] [CrossRef]
- Wolfram, D.; Carolus, T.H. Experimental and numerical investigation of the unsteady flow field and tone generation in an isolated centrifugal fan impeller. J. Sound Vib. 2010, 329, 4380–4397. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Jiang, X.; Pang, Q.; Ye, D. Vibration in a multistage centrifugal pump under varied conditions. Shock Vib. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Neise, W. Review of fan noise generation mechanisms and control methods. In Proceedings of the Fan Noise 1992 International Symposium, Senlis, France, 1–3 September 1992. [Google Scholar]
- Lu, F.A.; Qi, D.T.; Wang, X.J.; Zhou, Z.; Zhou, H.H. A numerical optimization on the vibro acoustics of a centrifugal fan volute. J. Sound Vib. 2012, 331, 2365–2385. [Google Scholar] [CrossRef]
- Parrondo, J.; Perez, J.; Barrio, R.; González, J. A simple acoustic model to characterize the internal low frequency sound field in centrifugal pumps. J. Appl. Acoust. 2011, 72, 59–64. [Google Scholar] [CrossRef]
- Trethewey, M.; Friell, J.; Chandra, M.; Lebold, M. A spectral simulation approach to evaluate probabilistic measurement precision of a reactor coolant pump torsional vibration shaft crack monitoring system. J. Sound Vib. 2008, 310, 1036–1056. [Google Scholar] [CrossRef]
- Kaiser, T.F.; Osman, R.H.; Dickau, R.O. Analysis guide for variable frequency drive operated centrifugal pumps. In Proceedings of the 24th International Pump User’s Symposium, Houston, TX, USA, 21–24 April 2008. [Google Scholar]
- Zhou, J.; Adrian, R.J.; Balachandar, S. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluids 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Chu, S.; Dong, R.; Katz, J. Relationship between unsteady flow, pressure fluctuations, and noise in a centrifugal pump—Part A: Use of PDV data to compute the pressure Field. J. Fluids Eng. 1995, 117, 24–29. [Google Scholar] [CrossRef]
- Langthjem, M.A.; Olhoff, N. A numerical study of flow-induced noise in a two-dimensional centrifugal pump—Part II. Hydroacoustics. J. Fluids Struct. 2004, 19, 369–386. [Google Scholar] [CrossRef]
- Chini, S.F.; Rahimzadeh, H.; Bahrami, M. Cavitation detection of a centrifugal pump using noise spectrum. In Proceedings of the ASME 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005. [Google Scholar]
- Srivastavm, O.P.; Pandum, K.R.; Guptam, K. Effect of radial gap between impeller and diffuser on vibration and noise in a centrifugal pump. J. Inst. Eng. 2003, 84, 36–39. [Google Scholar]
- Ji, B.; Luo, X.; Wu, Y.; Peng, X.; Xu, H. Partially averaged Navier-Stokes method with modified k-ε model for cavitating flow around a marine propeller in a non-uniform wake. Int. J. Heat Mass Transf. 2012, 55, 6582–6588. [Google Scholar] [CrossRef]
- Thai, Q.; Lee, C. The cavitation behavior with short length blades in centrifugal pump. J. Mech. Sci. Technol. 2010, 24, 2007–2016. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, L.; Zhao, R.; Shi, W.; Pan, Q.; Esch, B.P.M. Study on unsteady tip leakage vortex cavitation in an axial-flow pump using an improved filter-based model. J. Mech. Sci. Technol. 2017, 31, 659–667. [Google Scholar] [CrossRef]
- Huang, B.; Wang, G.Y.; Zhao, Y. Numerical simulation unsteady cloud cavitating flow with a filter-based density correction model. J. Hydrodyn. 2014, 26, 26–36. [Google Scholar] [CrossRef]
- Wu, J.; Wang, G.; Wei, S. Time-dependent turbulent cavitating flow computations with interfacial transport and filter-based models. Int. J. Numer. Methods Fluids 2005, 49, 739–761. [Google Scholar] [CrossRef]
- Tseng, C.C.; Wei, S. Turbulence modeling for isothermal and cryogenic cavitation. Int. J. Heat Mass Transf. 2013, 53, 513–525. [Google Scholar] [CrossRef]
- Huang, B.; Wang, G. Evaluation of a filter-based model for computations of cavitating flows. Chin. Phys. Lett. 2011, 28, 026401. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.L.; Liu, D.X.; Yuan, S.Q.; Wang, J.; Jiang, L.L. Application of the two-phase three-component computational model to predict cavitating flow in a centrifugal pump and its validation. J. Comput. Fluids 2016, 13, 142–150. [Google Scholar] [CrossRef]
- Bonet, J.; Peraire, J. An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems. Int. J. Numer. Methods Eng. 1991, 31, 1–17. [Google Scholar] [CrossRef]
- Schmitz, S. Reducing pump noise in cooling tower applications. World Pumps 2004, 456, 24–29. [Google Scholar] [CrossRef]
- Marscher, W.D. An end-user’s guide to centrifugal pump rotor dynamics. In Proceedings of the 23rd Pump Users Symposium, Houston, TX, USA, 23–26 February 2007. [Google Scholar]
- Tan, M.G.; Lian, Y.G.; Wu, X.F.; Ding, R.; Chen, K. Unsteady dynamics in double channel pump. J. Drain. Irrig. Mach. Eng. 2017, 35, 1024–1029. [Google Scholar]
- Zhou, L.; Bai, L.; Li, W.; Shi, W.; Wang, C. PIV validation of different turbulence models used for numerical simulation of a centrifugal pump diffuser. Eng. Comput. 2018, 35, 2–17. [Google Scholar] [CrossRef]
- Liu, H.L.; Ding, J.; Wang, Y.; Tan, M.G.; Xu, H. Numerical simulation of hydrodynamic noise in centrifugal pump based on LES. J. Mech. Eng. 2013, 49, 177–183. [Google Scholar] [CrossRef]
- Majidi, K. Numerical study of unsteady flow in a centrifugal pump. J. Turbomach. 2004, 127, 363–371. [Google Scholar] [CrossRef]
- Zou, C.; Liu, Z.X.; Zhang, L.Q.; Zheng, C.G. Comparison among turbulence models for impinging jet flows. J. Huazhong Univ. Sci. Technol. 2006, 34, 72–74. [Google Scholar]
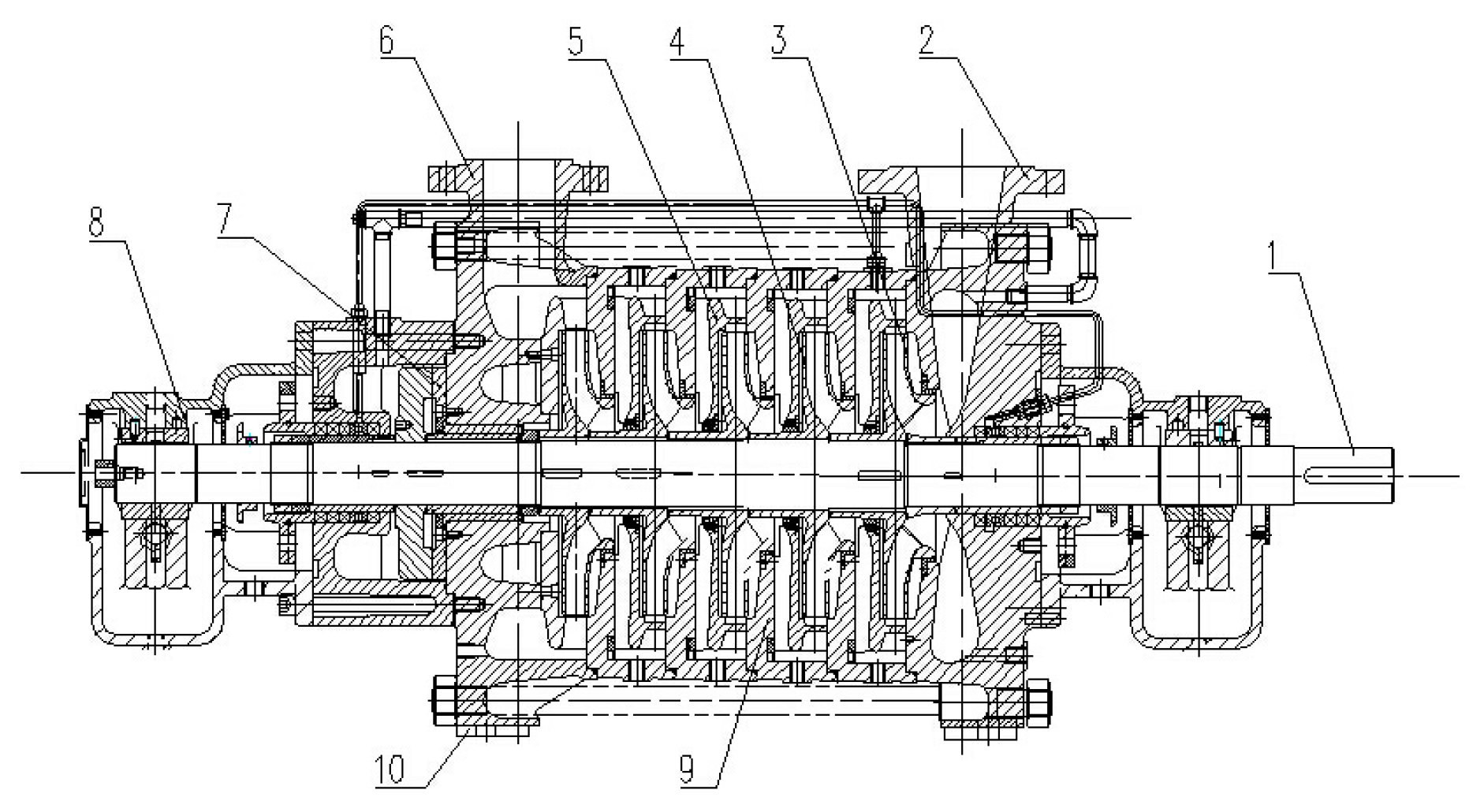

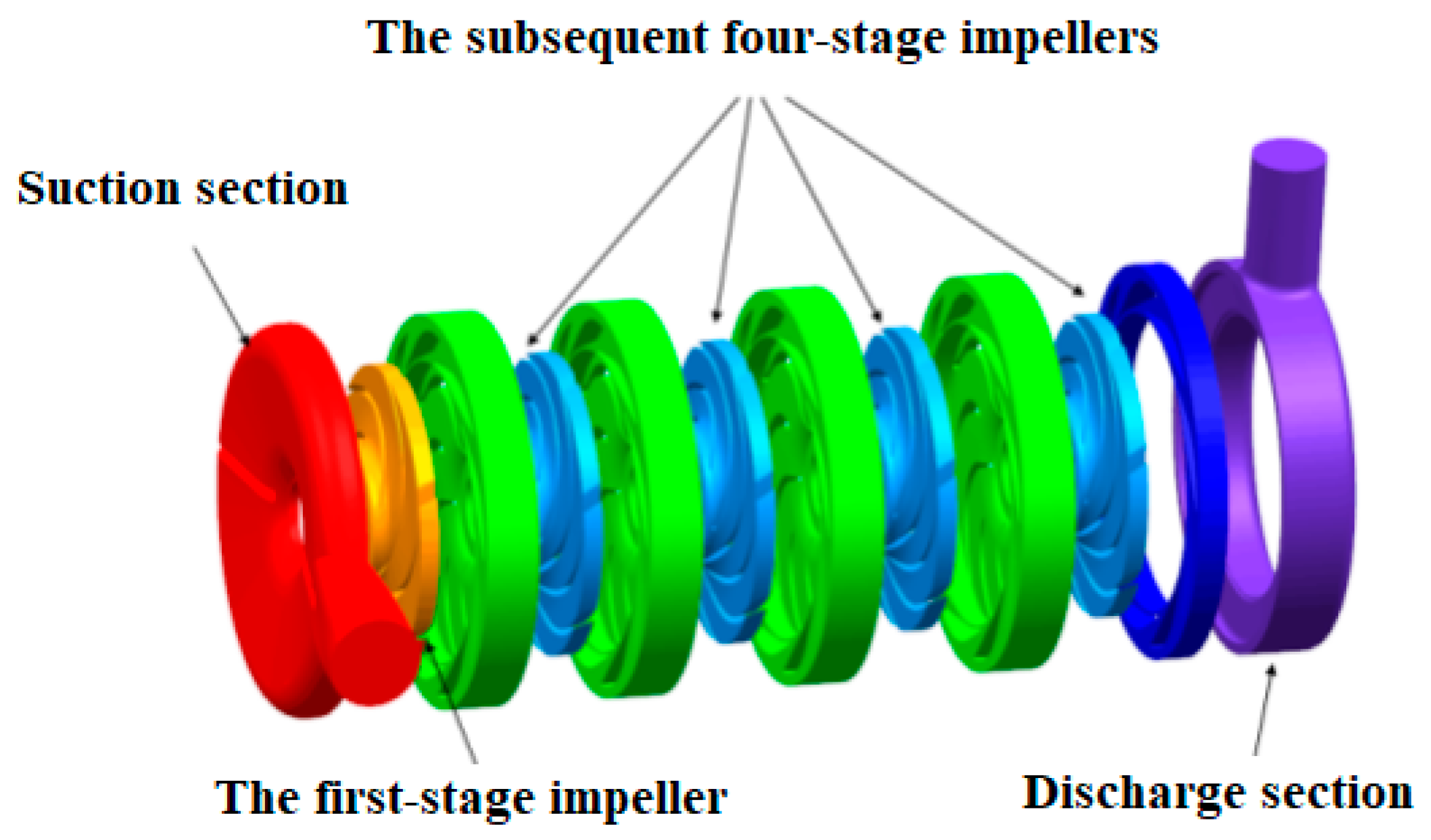






| Structure Parameters | Unit | Values |
|---|---|---|
| Inlet diameter of the first-stage impellers Dj | mm | 155 |
| Diameter of the first-stage impeller D21 | mm | 314 |
| Blade number of the first-stage impeller Z1 | 1 | 6 |
| Outlet width of the impeller b2 | mm | 20.5 |
| Diameter of the subsequent four-stage impellers D22 | mm | 314 |
| Blade number of the subsequent four-stage impellers Z2 | 1 | 7 |
| Inlet diameter of the vaned-diffuser D3 | mm | 316 |
| Outlet diameter of the vaned-diffuser D4 | mm | 409 |
| Blade numbers of the positive vaned-diffuser Z3 | 1 | 9 |
| Blade numbers of the negative vaned-diffuser Z4 | 1 | 10 |
| Inlet diameter of the pump suction section Ds | mm | 100 |
| Outlet diameter of the pump discharge section Dd | mm | 80 |
| Deviation | Standard k-ε | RNG k-ε | SST k-ω | |
|---|---|---|---|---|
| Suction | 0.8 Qd | 3.42% | 0.83% | 1.57% |
| 1.0 Qd | 2.76% | 2.47% | 2.00% | |
| 1.2 Qd | 5.02% | 2.28% | 9.31% | |
| Discharge | 0.8 Qd | 4.01% | 1.71% | 2.05% |
| 1.0 Qd | 2.59% | 2.14% | 1.69% | |
| 1.2 Qd | 7.35% | 3.13% | 3.63% | |
| Deviation | Standard k-ε | RNG k-ε | SST k-ω | |
|---|---|---|---|---|
| M3 | 0.8 Qd | 3.51% | 2.86% | 2.60% |
| 1.0 Qd | 5.35% | 3.14% | 4.44% | |
| 1.2 Qd | 2.34% | 1.85% | 2.59% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, H.; Wang, K.; Zhou, L.; Jiang, X.; Li, Y. Numerical Simulation of the Sound Field of a Five-Stage Centrifugal Pump with Different Turbulence Models. Water 2019, 11, 1777. https://doi.org/10.3390/w11091777
Wang L, Liu H, Wang K, Zhou L, Jiang X, Li Y. Numerical Simulation of the Sound Field of a Five-Stage Centrifugal Pump with Different Turbulence Models. Water. 2019; 11(9):1777. https://doi.org/10.3390/w11091777
Chicago/Turabian StyleWang, Li, Houlin Liu, Kai Wang, Ling Zhou, Xiaoping Jiang, and Yu Li. 2019. "Numerical Simulation of the Sound Field of a Five-Stage Centrifugal Pump with Different Turbulence Models" Water 11, no. 9: 1777. https://doi.org/10.3390/w11091777
APA StyleWang, L., Liu, H., Wang, K., Zhou, L., Jiang, X., & Li, Y. (2019). Numerical Simulation of the Sound Field of a Five-Stage Centrifugal Pump with Different Turbulence Models. Water, 11(9), 1777. https://doi.org/10.3390/w11091777






