Improving the Accuracy of Hydrodynamic Simulations in Data Scarce Environments Using Bayesian Model Averaging: A Case Study of the Inner Niger Delta, Mali, West Africa
Abstract
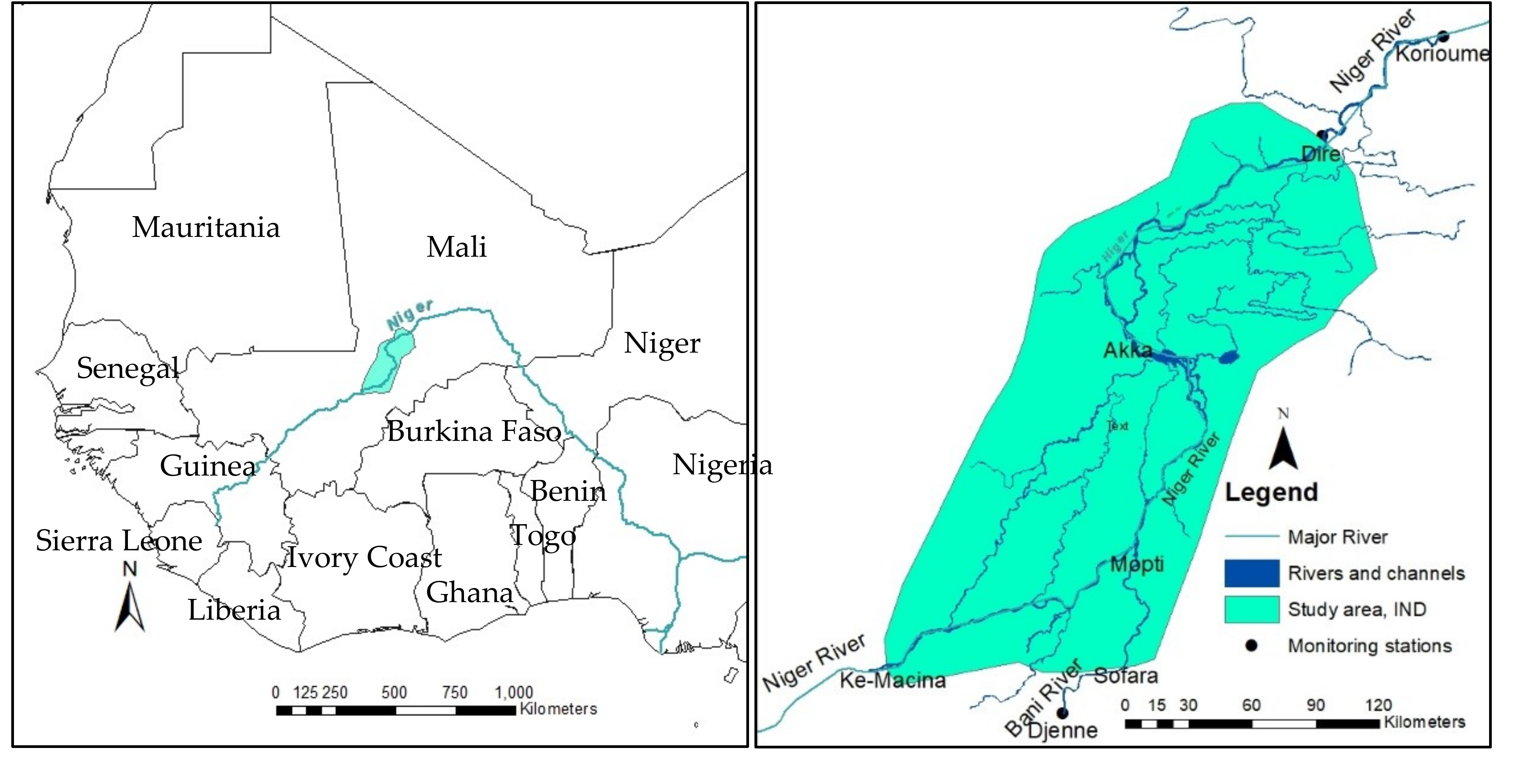
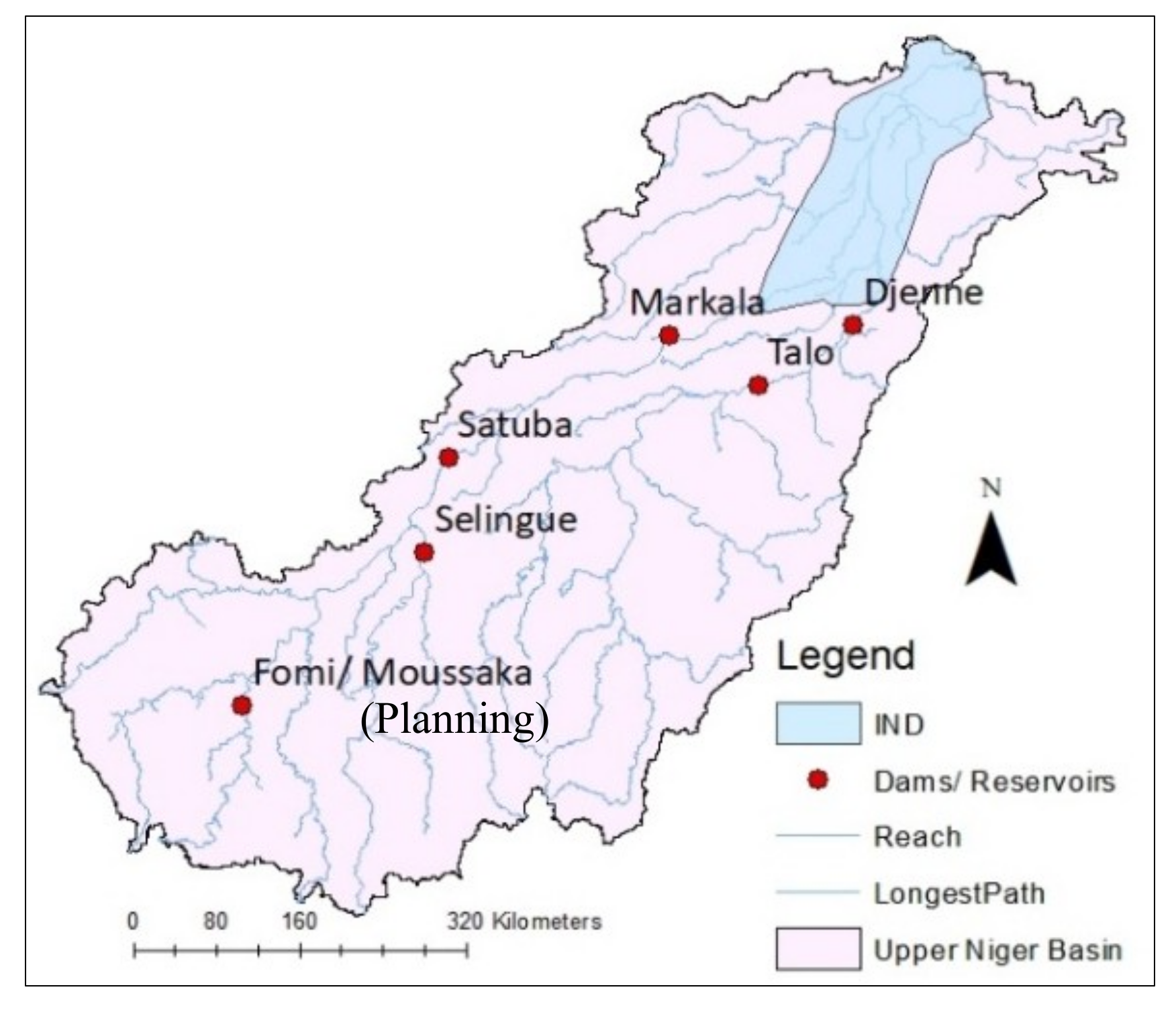
1. Introduction
2. Materials and Methods
2.1. Available Data
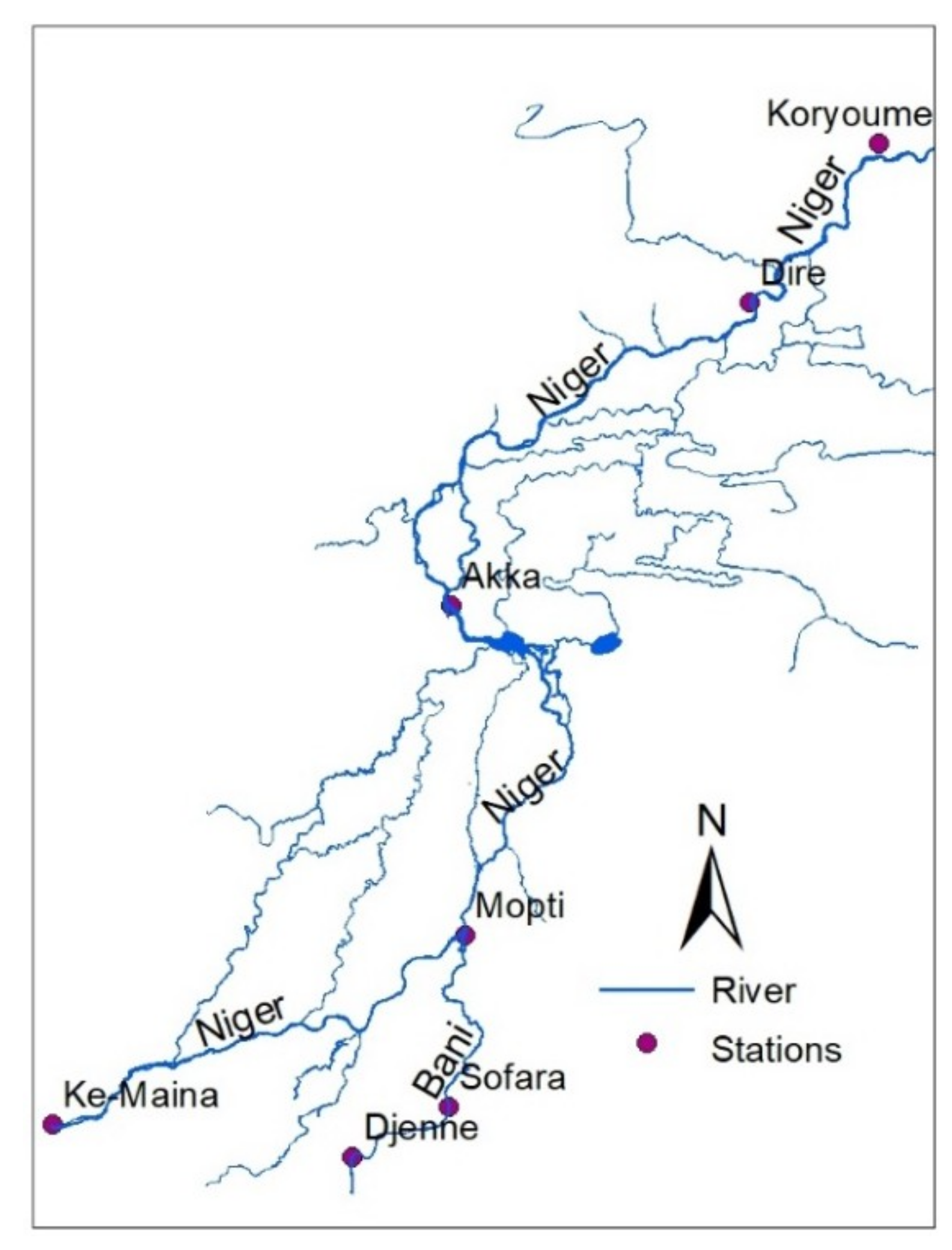
2.1.1. Discharge and Water Level
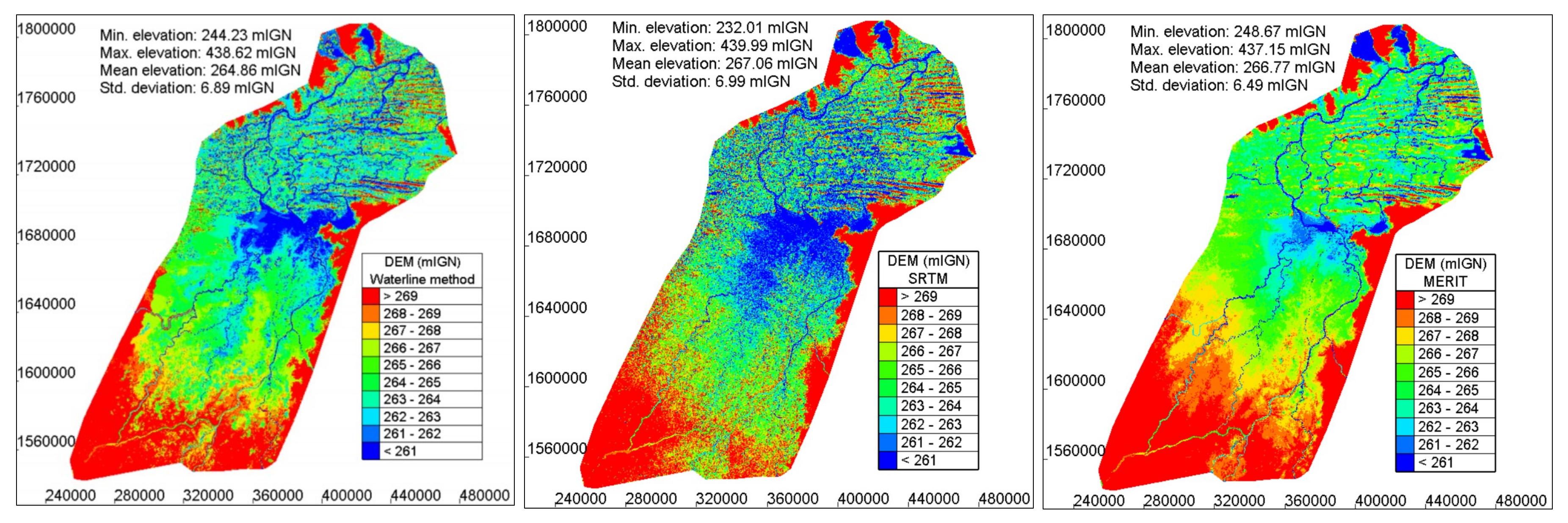
2.1.2. Topographic Data Sources
2.1.3. DEM Derivation Using the Waterline Method
- Seven inundation extent polygons derived from Landsat satellite images by Zwarts et al. [2] for dates 5 July 1985, 10 June 2001, 8 August 1984, 28 July 2001, 25 October 1984, 16 October 2001, and 28 November 1999 were selected to represent the range of possible water elevations in the Inner Delta.
- For each of the seven flood inundation maps, water levels at Ké-Macina, Mopti, Akka, and Diré were used to calculate the slope of the water surface along principal flow paths between Ké-Macina and Akka, between Mopti and Akka, and between Akka and Diré. In the absence of additional information, it was further assumed that the water level variation between any two stations is linear.
- A series of orthogonal lines were drawn at 30 m intervals along principal flow paths.
- It was assumed that water levels along these lines are constant. Therefore, an elevation value could be set at the intersection points between water extent polygon and the orthogonal lines.
- At the end of the process, an altitude was estimated for each point within the flood extent polygons.
- Areas outside the larger polygon were populated using SRTM elevation data.
- GIS was used to interpolate the elevation data inside the study area.
2.1.4. Satellite Imagery
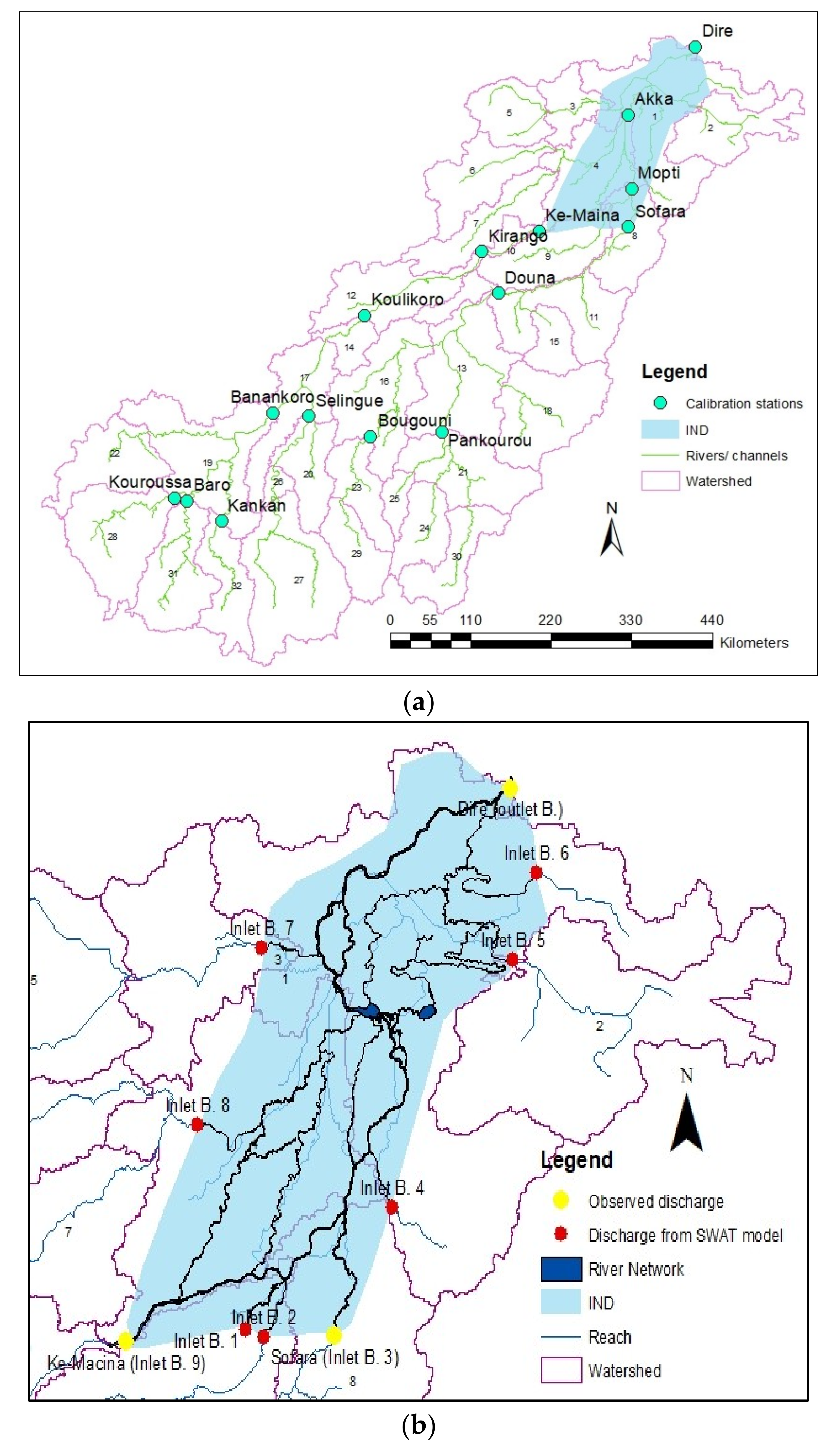
2.2. River Network
2.3. Channel Geometry
2.4. Estimation of Inflow at Ungauged Inlets
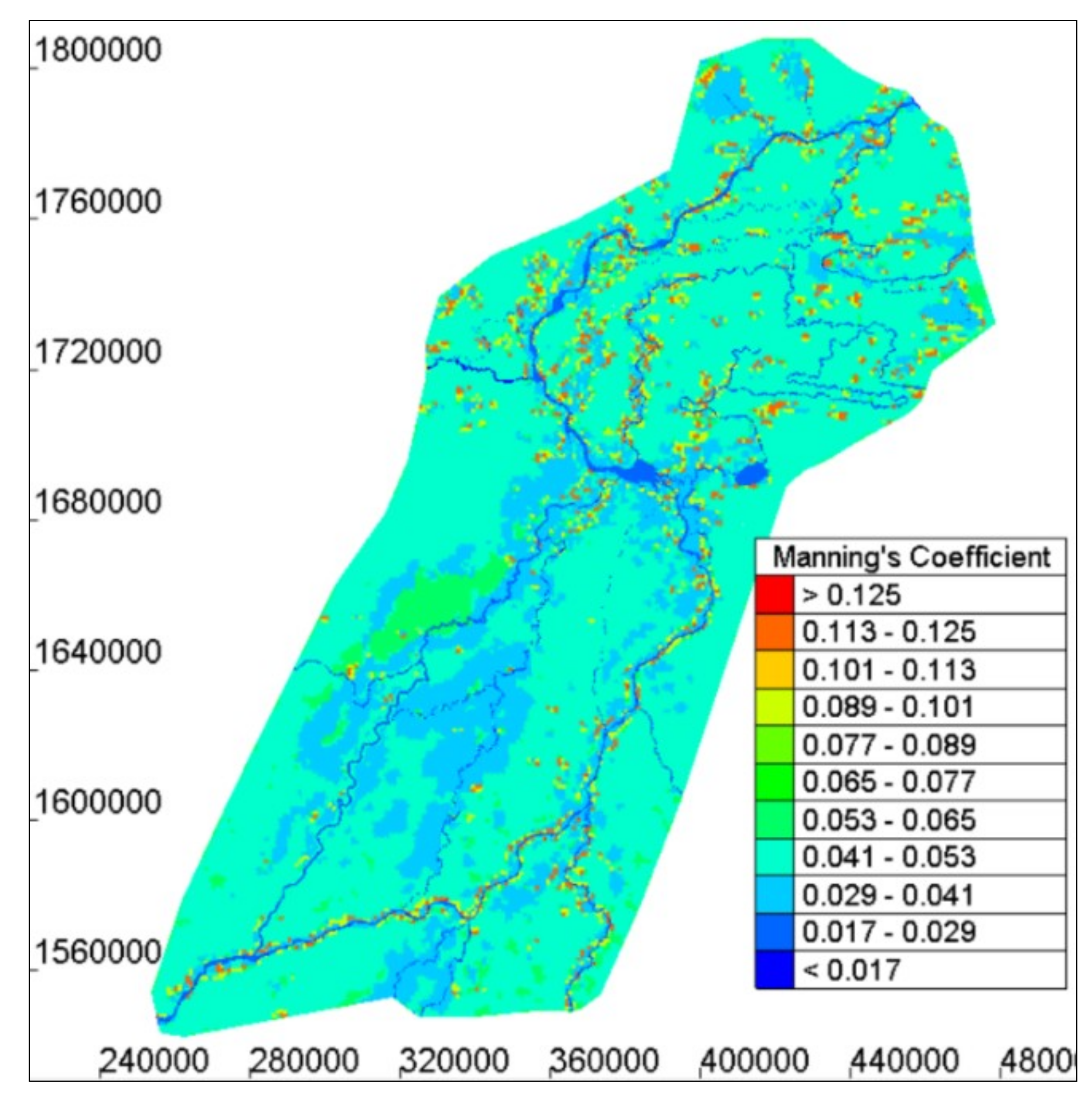
2.5. Floodplain Friction
2.6. Hydrodynamic Model Setup
2.6.1. Mesh Generation
2.6.2. Model Boundary Conditions
2.6.3. Initial Conditions
2.6.4. Model Configurations
2.7. Calibration
2.8. Bayesian Model Averaging
3. Results and Discussion
3.1. Calibration Results
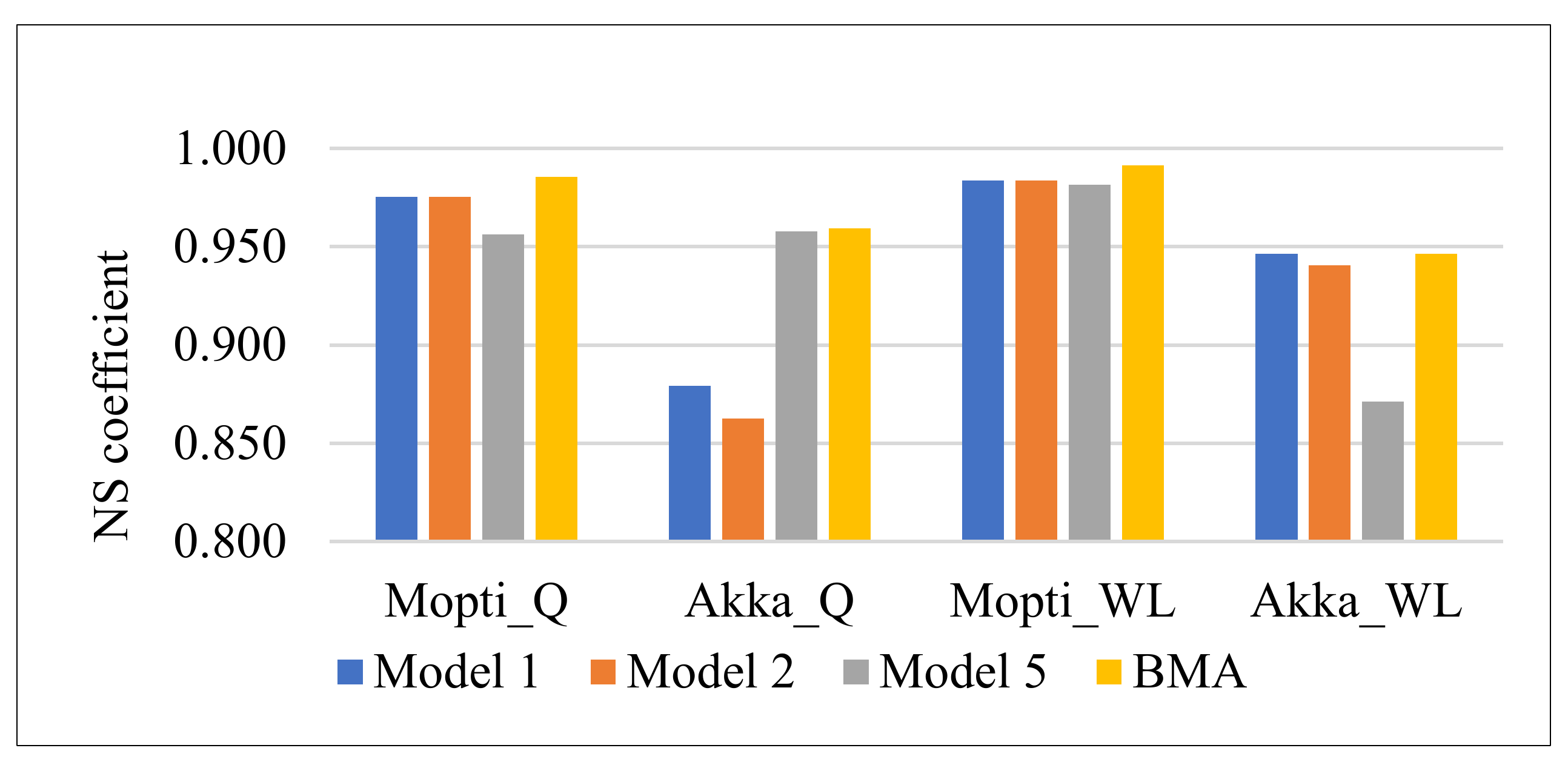
3.1.1. BMA Weights
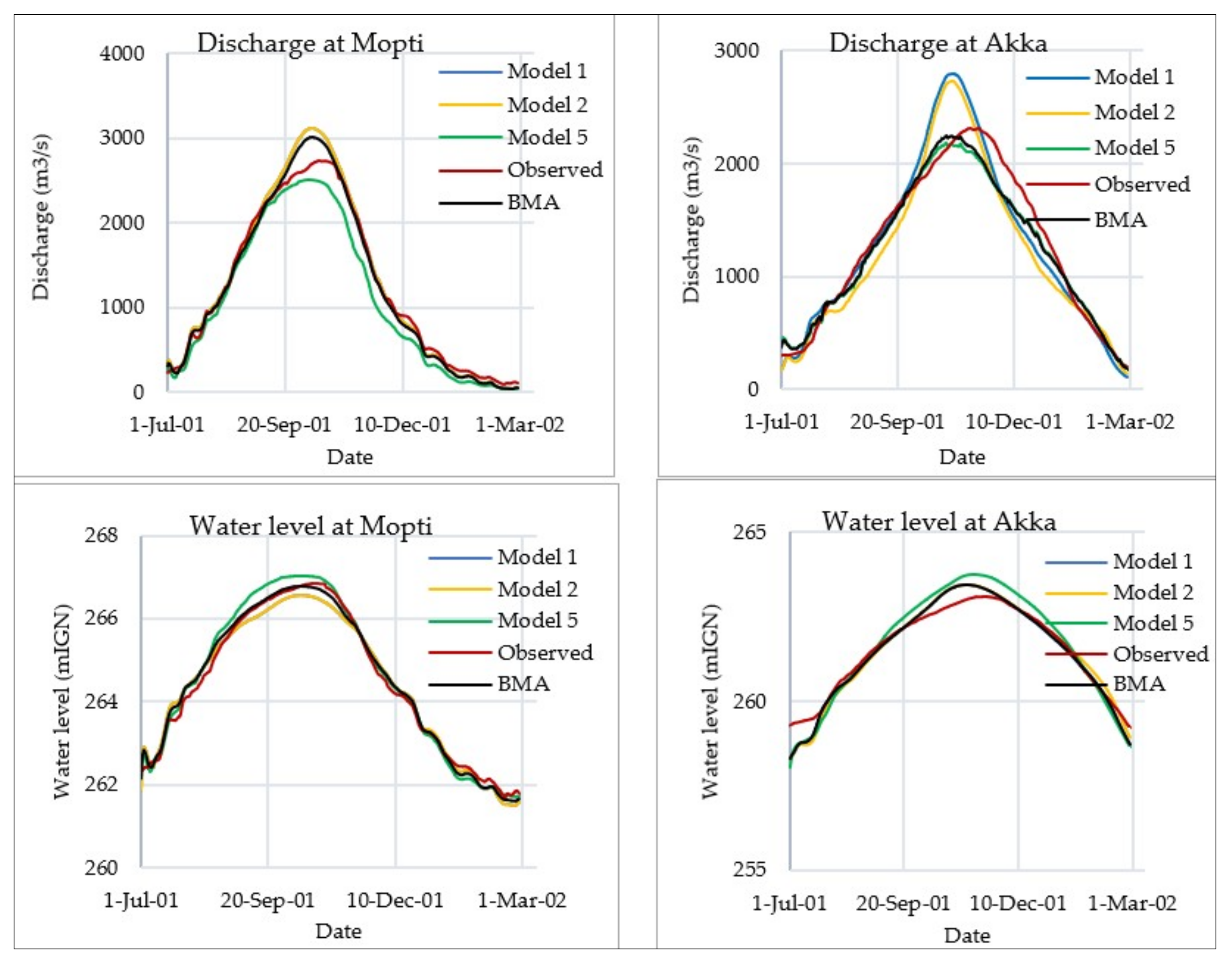
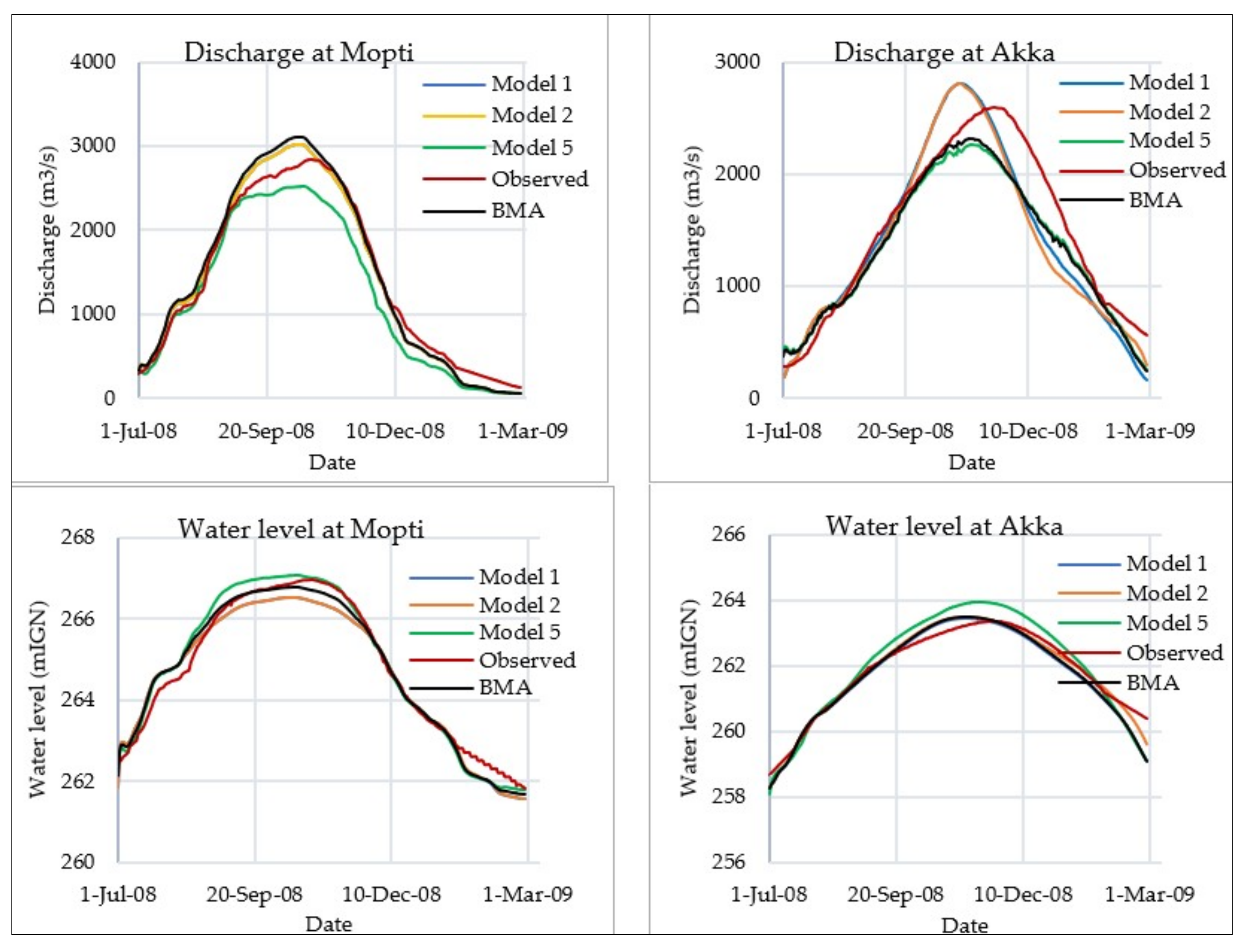
3.1.2. BMA Estimates of Water Levels and Discharge in the Calibration Period
3.2. Hydrodynamic Models Validation
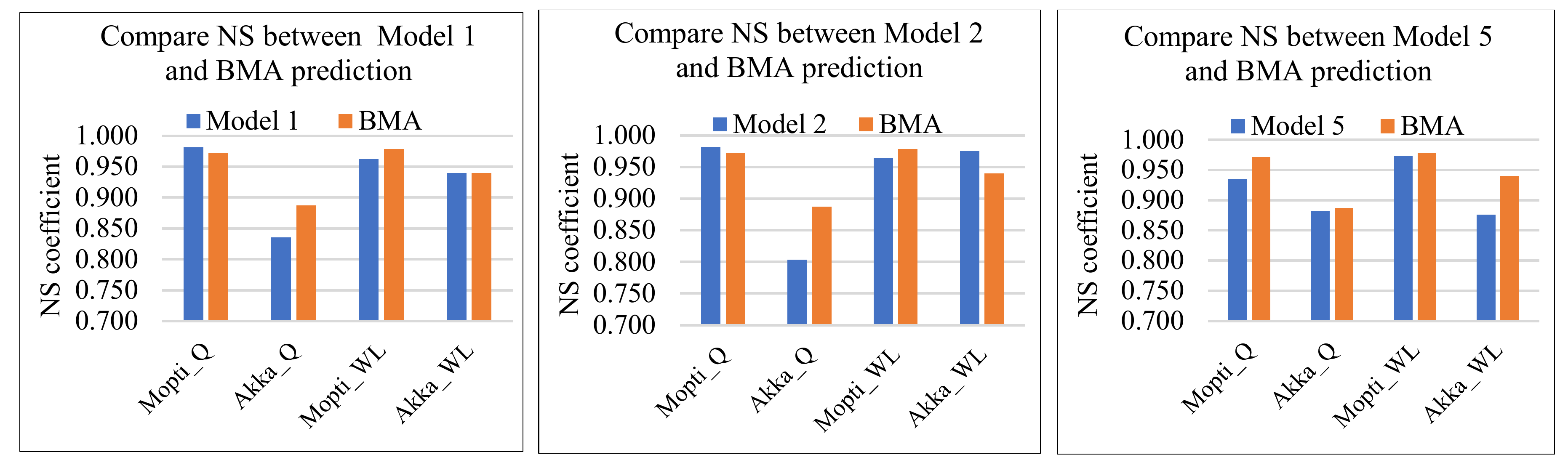
3.3. BMA Validation
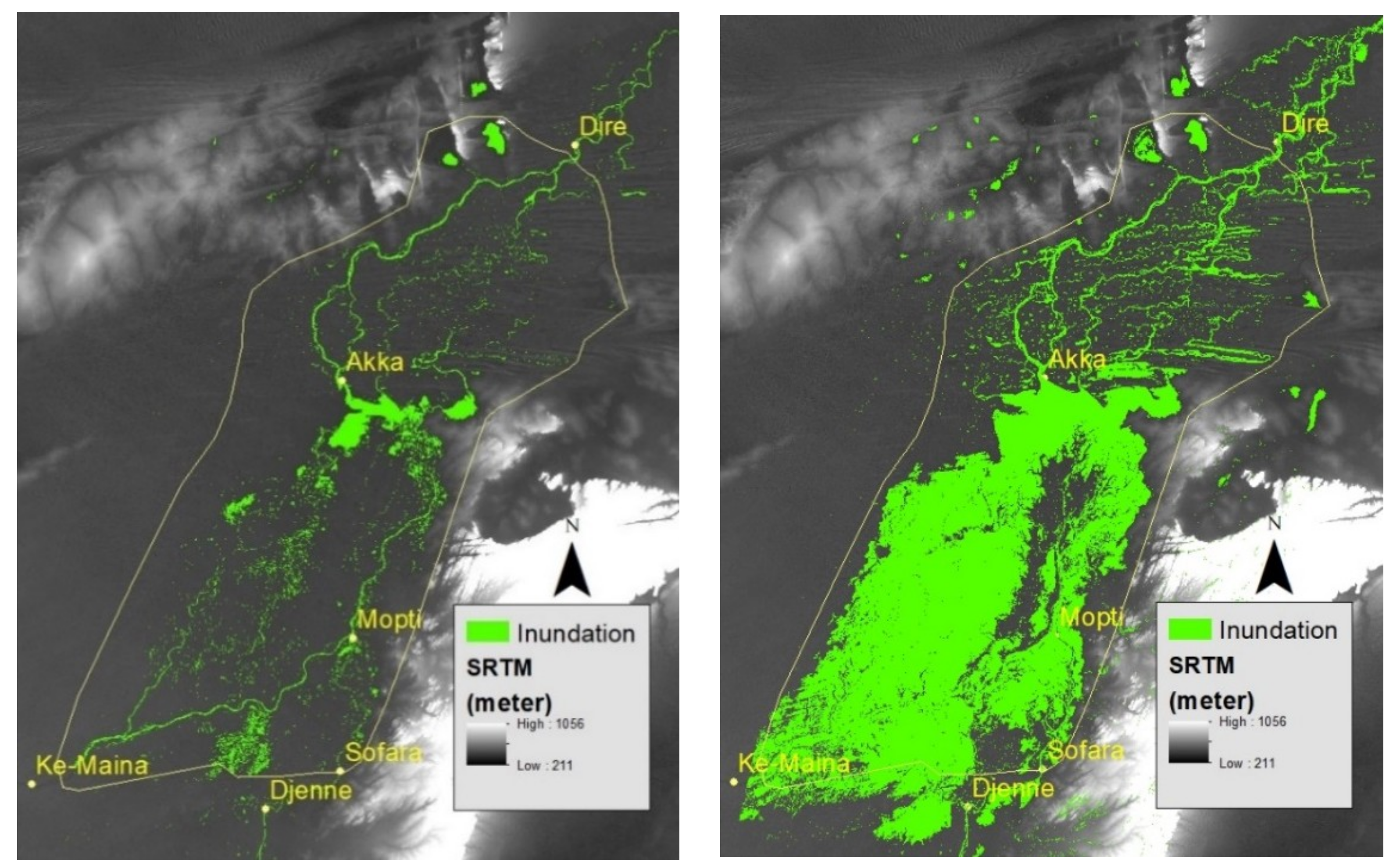
3.4. Simulated Inundation Extent from Best Individual Models
3.5. Potential Usages of the Developed Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zwarts, L.; Frerotte, J. Water Crisis in the Inner Niger Delta (Mali), Causes, Consequences, Solutions; A&W-Report 1832; Altenburg & Wymenga Ecologisch Onderzoek: Feanwâlden, The Netherlands, 2012. [Google Scholar]
- Zwarts, L.; Van Beukering, P.; Kone, B.; Wymenga, E. The Niger, a Lifeline. Effective Water Management in the Upper Niger Basin. RIZA, Lelystad/Wetlands International, Sévaré; Institute for Environmental studies (IVM): Amsterdam, The Netherlands; A&W Ecological Consultants: Veenwouden, Mali, The Netherlands, 2005. [Google Scholar]
- Liersch, S.; Fournet, S.; Koch, H. Assessment of Water Management and Climate Change Impacts on the Water Resources in the Upper Niger and Bani River Basins; BAMGIRE Programme Final Report; Potsdam Institute for Climate Impact Research: Potsdam, Germany; Wetlands International: Mali, The Netherlands, 2019. [Google Scholar]
- CDKN. The IPCC’s Fifth Assessment Report: What’s in It for Africa? Overseas Development Institute/Climate and Development Knowledge Network: London, UK, 2014; 35p, Available online: https://cdkn.org/wp-content/uploads/2014/04/AR5_IPCC_Whats_in_it_for_Africa.pdf (accessed on 14 January 2019).
- USAID. Climate Risk in Mali: Country Risk Profile. Available online: https://www.climatelinks.org/sites/default/files/asset/document/Mali_CRP_Final.pdf (accessed on 12 January 2019).
- Liersch, S.; Fournet, S.; Koch, H.; Djibo, A.G.; Reinhardt, J.; Kortlandt, J.; Van Weert, F.; Seidou, O.; Klop, E.; Baker, C.; et al. Water resources planning in the Upper Niger River basin: Are there gaps between water demand and supply? J. Hydrol. Reg. Stud. 2019, 21, 176–194. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Bates, P. A subgrid channel model for simulating river hydraulics and floodplain inundation over large and data sparse areas. Water Resour. Res. 2012, 48, W11506. [Google Scholar] [CrossRef]
- Bates, P.D.; de Roo, A. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Dadson, S.J.; Ashpole, I.; Harris, P.; Davies, H.N.; Clark, D.B.; Blyth, E.; Taylor, C.M. Wetland inundation dynamics in a model of land surface climate: Evaluation in the Niger inland delta region. J. Geophys. Res. 2010, 115, D23114. [Google Scholar] [CrossRef]
- Haag, A.V. Coupling A Large-Scale Hydrological Model to a High-Resolution Hydrodynamical Model, A Study of Floods within the Niger Inner Delta as a First Step towards a Potential Global Application. Master’s Thesis, Department of Physical Geography and Faculty of Geoscience, Utrecht University, Utrecht, The Netherlands, 2015. [Google Scholar]
- Kernkamp, H.W.J.; van Dam, A.; Stelling, G.S.; de Goede, E.D. Efficient scheme for the shallow water equations on un-structured grids with application to the Continental Shelf. Ocean Dynam. 2011, 61, 1175–1188. [Google Scholar] [CrossRef]
- Deltares. D-Flow Flexible Mesh, User Manual, draft version; Deltares: Delft, The Netherlands, 2015. [Google Scholar]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows Modelling with the Finite Element Method; Wiley: New York, NY, USA, 2007. [Google Scholar]
- NASA JPL. NASA Shuttle Radar Topography Mission Global 1 arc second, NASA EOSDIS Land Processes DAAC. 2013. Available online: https://earthexplorer.usgs.gov/ (accessed on 1 September 2016).
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Rodríguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Cracknell, A.P.; Hayes, L.W.B.; Keltie, G.F. Remote sensing of the Tay Estuary using visible and near infra-red data: mapping of the inter-tidal zone. Proc. R. Soc. Edinb. 1987, 92B, 223–236. [Google Scholar]
- Ramsey, E.W. Monitoring Flooding in coastal wetlands by using radar imagery and ground-based measurements. Int. J. Remote Sens. 1995, 16, 2495–2502. [Google Scholar] [CrossRef]
- Mason, D.C.; Davenport, I.J.; Flather, R.A.; Gurney, C. A digital elevation model of the inter-tidal areas of the Wash, England, produced by the waterline method. Int. J. Remote Sens. 1998, 9, 1455–1460. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part 1: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–417. [Google Scholar]
- Schumann, G.J.-P.; Andreadis, K.M.; Bates, P.D. Downscaling coarse grid hydrodynamic model simulations over large domains. J. Hydrol. 2014, 508, 289–298. [Google Scholar] [CrossRef]
- Biancamaria, S.; Bates, P.; Boone, A.; Mognard, N. Large-scale coupled hydrologic and hydraulic modelling of the Ob river in Siberia. J. Hydrol. Elsevier 2009, 379, 136–150. [Google Scholar] [CrossRef]
- JAXA. ALOS World 3D-30m (AW3D30), Version 2, Global Digital Surface Model, Earth Observation Research Center (EORC), Japan Aerospace Exploration Agency. 2018. Available online: https://www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm (accessed on 10 September 2017).
- Hawker, L.; Bates, P.; Neal, J.; Rougier, J. Perspectives on Digital Elevation Model (DEM) Simulation for Flood Modeling in the Absence of a High-Accuracy Open Access Global DEM. Front. Earth Sci. 2018, 6, 233. [Google Scholar] [CrossRef]
- Archer, L.; Neal, J.C.; Bates, P.C.; House, J.I. Comparing TanDEM-X data with frequently-used DEMs for Flood inundation modelling. Water Resour. Res. 2018. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalized difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Wilson, E.H.; Sader, S.A. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ. 2002, 80, 385–396. [Google Scholar] [CrossRef]
- Ogilvie, A.; Belaud, G.; Delenne, C.; Bailly, J.; Bader, J.; Oleksiak, A.; Ferry, L.; Martin, D. Decadal monitoring of the Niger Inner Delta flood dynamics using MODIS optical data. J. Hydrol. Elsevier 2015, 523, 368–383. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T.J. The hydraulic geometry of stream channels and some physiographic implications. U.S. Geol. Surv. Prof. Pap. 1953, 252, 1–57. [Google Scholar]
- Hey, R.D.; Thorne, C.R. Stable channels with mobile gravel beds. J. Hydraul. Eng. 1986, 112, 671–689. [Google Scholar] [CrossRef]
- Leopold, L.B. A View of the River: Cambridge, Mass; Harvard University Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Seidou, O. Development of Models and Tools in Support of the BAMGIRE Program; Final Report; Wetlands International and University of Ottawa: Ottawa, ON, Canada, 2019. [Google Scholar]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Jha, M.K. SWAT: Model use calibration, and validation. Trans. Asabe 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool, Theoretical Documentation: Version 2005; USDA Agricultural Research Service and Texas A&M Blackl and Research Center: Temple, TX, USA, 2005.
- USDA Soil Conservation Service. National Engineering Handbook; Section 4, Hydrology; US Government Printing Office: Washington, DC, USA, 1972.
- Monteith, J.L. Evaporation and environment. In The State and Movement of Water in Living Organisms; Fogg, G.F., Ed.; Cambridge University Press: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Abbaspour, K.C. User Manual for SWAT-CUP, SWAT Calibration and Uncertainty Analysis Programs; Swiss Federal Institute of Aquatic Science and Technology, Eawag: Dübendorf, Switzerland, 2007; Available online: https://www.eawag.ch/de/abteilung/siam/software/ (accessed on 16 June 2017).
- Maiga, F. Hydrological Impacts of Irrigation Schemes and Dams Operation in the Upper Niger Basin and Inner Niger Delta. Master’s Thesis, University of Ottawa, Ottawa, ON, Canada, 2019. [Google Scholar]
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics database and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens. 2000, 21, 1303–1330. [Google Scholar] [CrossRef]
- Asante, K.O.; Artan, G.A.; Pervez, S.; Bandaragoda, C.; Verdin, J.P. Technical Manual for the Geospatial Stream Flow Model (GeoSFM): U.S. Geological Survey Open-File Report; U.S. Geological Survey: Reston, VI, USA, 2008; 65p. Available online: https://pubs.usgs.gov/of/2007/1441/pdf/ofr2008-1441.pdf (accessed on 21 September 2018).
- Marchuk, G.I. Methods of Numerical Mathematics; Springer: New York, NY, USA, 1975; 316p. [Google Scholar]
- Brookes, A.N.; Hughes, T.J.R. Streamline Upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes Equations. Comput. Methods Appl. Mech. Eng. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Bates, P.D.; Anderson, M.G.; Hervouet, J.-M.; Hawkes, J.C. Investigating the behavior of two-dimensional finite element models of compound channel flow. Earth Surf. Process. Landf. 1997, 22, 3–17. [Google Scholar] [CrossRef]
- Zwarts, L. Will the Inner Niger Delta Shrivel up due to Climate Change and Water Use Upstream? A&W Rapport 1537; Altenburg & Wymenga Ecologisch Onderzoek: Feanwâlden, The Netherlands, 2010. [Google Scholar]
- Woodhead, S.; Asselman, N.; Zech, Y.; Soares-Frazao, S.; Bates, P.; Kortenhaus, A. Evaluation of Inundation Models; FLOODsite Report T08-07-01. 2007. Available online: https://ecapra.og/sites/default/files/documents/Flood%20Inundation%20Modelling.pdf (accessed on 6 August 2019).
- Aronica, G.; Hankin, B.; Beven, K. Uncertainty and equifinality in calibrating distributed roughness coefficients in a flood propagation model with limited data. Adv. Water Resour. 1998, 22, 349–365. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Horritt, M.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- Schöniger, A.; Wöhling, T.; Nowak, W. Model selection on solid ground: Rigorous comparison of nine ways to evaluate Bayesian model evidence. Water Resour. Res. 2014, 50, 9484–9513. [Google Scholar] [CrossRef]
- Madigan, D.; Raftery, A.E.; Volinsky, C.; Hoeting, J. Bayesian model averaging. In Proceedings of the AAAI Workshop on Integrating Multiple Learned Models, Portland, OR, USA, 4–5 August 1996; pp. 77–83. [Google Scholar]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Res. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Zhu, R.; Zheng, H.; Wang, E.; Zhao, W. Multi-Model Ensemble Simulation of Flood Events using Bayesian Model Averaging. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013. [Google Scholar]
- Beckers, J.V.L.; Sprokkereef, E.; Roscoe, K.L. Use of Bayesian Model Averaging to Determine Uncertainties in River Discharge and Water Level Forecasts. In Proceedings of the 4th International Symposium on Flood Defence: Managing Flood Risk, Reliability and Vulnerability, Toronto, ON, Canada, 6–8 May 2008. [Google Scholar]
- Raftery, A.E. Bayesian Model Selection in Structural Equation Models. In Testing Structural Equation Models; Bollen, K.A., Long, J.S., Eds.; Sage: Beverly Hills, CA, USA, 1993; pp. 163–180. [Google Scholar]
- Draper, D. Assessment and propagation of model uncertainty. J. R. Stat. Soc. Ser. B 1995, 57, 45–97. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Diks, C.G.; Clark, M.P. Ensemble bayesian model averaging using markov chain monte carlo sampling. Environ. Fluid Mech. 2008, 8, 579–595. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Krishnan, T. The EM Algorithm and Extensions; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.B.; Pfister, L.; Fraipont, P. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Guthke, A.; Höge, M.; Nowak, W. Bayesian model evidence as a model evaluation metric, Geophysical Research Abstracts, Volume 19, EGU2017-PREVIEW, EGU General Assembly. 2017. Available online: https://meetingorganizer.copernicus.org/EGU2017/EGU2017-13390-1.pdf (accessed on 8 August 2019 ).
- Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian Model Averaging. Water Resour. Res. 2007, 43, W01411. [Google Scholar] [CrossRef]
- OPIDIN. Forecast Tool to Predict the Inundations in the Inner Niger Delta. Available online: https://www.opidin.org/en/home (accessed on 9 August 2019).
| Image Source/Name | Satellite | Path/Row | Purpose | Date Captured | Resolution |
|---|---|---|---|---|---|
| Several images from Zwart et al. [2] | Landsat 5 TM | 197/49 and 197/50 | Model setup, Calibration | 1984 to 2001 | 30 m |
| MOD09A1.A2008241 MOD09A1.A2008281 MOD09A1.A2009017 | MODIS | - | Model validation | 28 August 2008 7 October 2008 17 January 2009 | 500 m |
| Monitoring Stations | Bankfull Discharge (m3/s) | Bankfull Stage (mIGN) | Bankfull Depth (m) | Bed Elevation (mIGN) |
|---|---|---|---|---|
| KeMacina | 3518.00 | 274.31 | 5.81 | 268.50 |
| Mopti | 2340.00 | 266.42 | 5.04 | 261.38 |
| Akka | 1816.00 | 262.81 | 4.61 | 258.20 |
| Dire | 1760.00 | 261.45 | 4.56 | 256.89 |
| Monitoring Station | Latitude | Longitude | NS at Calibration | NS at Validation |
|---|---|---|---|---|
| Kankan | 10.38 | −9.31 | 0.65 | 0.8 |
| Baro | 10.51 | −9.72 | 0.68 | 0.73 |
| Kouroussa | 10.64 | −9.88 | 0.68 | 0.78 |
| Banankoro | 11.68 | −8.67 | 0.86 | 0.9 |
| Sélingué | 11.64 | −8.24 | 0.45 | 0.64 |
| Koulikoro | 12.85 | −7.56 | 0.87 | 0.93 |
| Kirango | 13.69 | −6.08 | 0.86 | 0.82 |
| Ké-Macina | 13.95 | −5.36 | 0.9 | 0.91 |
| Bougouni | 11.39 | −7.45 | 0.77 | 0.78 |
| Pankourou | 11.44 | −6.58 | 0.74 | 0.6 |
| Douna | 13.21 | −5.9 | 0.79 | 0.9 |
| Mopti | 14.49 | −4.21 | 0.8 | 0.78 |
| Akka | 15.4 | −4.24 | 0.87 | 0.84 |
| Diré | 16.27 | −3.39 | 0.9 | 0.75 |
| Inlet Point Location | SWAT Model Subbasin(s) | Remarks |
|---|---|---|
| Inlet boundary 1 (Inlet B. 1) | Watershed 9 | 60% of the outflow of watershed 9 |
| Inlet boundary 2 (Inlet B. 2) | Watershed 9 | 40% of the outflow of watershed 9 |
| Inlet boundary 4 (Inlet B. 4) | Watershed 1 | 0.2126 * (Inflow of watershed 1-Outflow of watershed 1) |
| Inlet boundary 5 (Inlet B. 5) | Watershed 2 | Outflow of watershed 2 |
| Inlet boundary 6 (Inlet B. 6) | Watershed 1 | 0.125 * (Inflow of watershed 1-Outflow of watershed 1) |
| Inlet boundary 7 (Inlet B. 7) | Watershed 3 | Outflow of watershed 3 |
| Inlet boundary 8 (Inlet B. 8) | Watershed 6 and watershed 7 | Outflow of watershed 6 + Outflow of watershed 7 |
| Model Number | Elevation Data | Downstream Boundary Condition |
|---|---|---|
| Model 1 | Merit DEM | Rating curve in the form of water level as a function of discharge, R = 0.02 |
| Model 2 | Merit DEM | Rating curve in the form of discharge as a function of water level |
| Model 3 | SRTM DEM | Rating curve in the form of water level as a function of discharge, R = 0.02 |
| Model 4 | SRTM DEM | Rating curve in the form of discharge as a function of water level |
| Model 5 | Waterline DEM | Rating curve in the form of water level as a function of discharge, R = 0.02 |
| Model 6 | Waterline DEM | Rating curve in the form of discharge as a function of water level |
| Models | Discharge | Water Level | ||||||
|---|---|---|---|---|---|---|---|---|
| Mopti | Akka | Mopti | Akka | |||||
| NS | r | NS | R | NS | r | NS | r | |
| Model 1 | 0.975 | 0.996 | 0.879 | 0.944 | 0.984 | 0.992 | 0.946 | 0.988 |
| Model 2 | 0.975 | 0.995 | 0.863 | 0.983 | 0.984 | 0.999 | 0.941 | 0.992 |
| Model 3 | 0.954 | 0.995 | 0.908 | 0.983 | 0.951 | 0.999 | 0.907 | 0.992 |
| Model 4 | 0.954 | 0.995 | 0.871 | 0.974 | 0.954 | 0.999 | 0.915 | 0.986 |
| Model 5 | 0.956 | 0.994 | 0.958 | 0.986 | 0.981 | 0.997 | 0.871 | 0.998 |
| Model 6 | 0.956 | 0.994 | 0.945 | 0.983 | 0.981 | 0.997 | 0.838 | 0.994 |
| Hydrometric Station | MOPTI | AKKA | ||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Discharge | Discharge | ||||||
| d/s Boundary Condition | Type 1 a | Type 1 | Type 2 b | Type 2 | Type 1 | Type 1 | Type 2 | Type 2 |
| Performance Criteria | NS | r | NS | r | NS | r | NS | r |
| Best models/associated DEM | MERIT d (M1 c) | MERIT (M1) | MERIT (M2) | MERIT (M2) and SRTM(M4) | Waterline (M5) | Waterline (M5) | Waterline (M6) | Waterline (M6) and MERIT(M2) |
| Second model/corresponding DEM | Waterline (M5) | SRTM (M3) | Waterline (M6) | - | SRTM (M5) | SRTM (M3) | SRTM (M4) | - |
| Third model/Corresponding DEM | SRTM (M3) | Waterline (M5) | SRTM (4) | Waterline (M6) | MERIT (M1) | MERIT (M1) | MERIT (M2) | SRTM (M4) |
| Hydrometric Station | MOPTI | AKKA | ||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Water Level | Water Level | ||||||
| Boundary Condition | Type 1 a | Type 1 | Type 2 b | Type 2 | Type 1 | Type 1 | Type 2 | Type 2 |
| Performance Criteria | NS | r | NS | r | NS | r | NS | r |
| Best model/associated DEM | MERIT d (M1 c) | SRTM (M3) | MERIT (M2) | MERIT (M2) and SRTM (M4) | MERIT (M1) | Waterline (M5) | MERIT (M2) | Waterline (M6) |
| Second model/corresponding DEM | Waterline (M5) | Waterline (M5) | Waterline (M6) | Waterline (M6) | SRTM (M3) | SRTM (M3) | SRTM (M4) | MERIT (M2) |
| Third model/Corresponding DEM | SRTM (M3) | MERIT (M1) | SRTM (M4) | Waterline (M5) | MERIT (M1) | Waterline (M6) | SRTM (M4) | |
| Model | BMA Weight to Obtain Discharge | BMA Weight to Obtain Water Level | ||
|---|---|---|---|---|
| Mopti | Akka | Mopti | Akka | |
| Model 1 | 0.0002 | 0.1177 | 0.3650 | 0.9602 |
| Model 2 | 0.7931 | 0.0000 | 0.1820 | 0.0000 |
| Model 3 | 0.1417 | 0.0000 | 0.0001 | 0.0000 |
| Model 4 | 0.0000 | 0.0000 | 0.0000 | 0.0398 |
| Model 5 | 0.0614 | 0.8823 | 0.3320 | 0.0000 |
| Model 6 | 0.0017 | 0.0000 | 0.1200 | 0.0000 |
| Models | Discharge | Water Level | ||||||
|---|---|---|---|---|---|---|---|---|
| Mopti | Akka | Mopti | Akka | |||||
| NS | r | NS | R | NS | r | NS | r | |
| Model 1 | 0.982 | 0.995 | 0.836 | 0.918 | 0.962 | 0.984 | 0.940 | 0.992 |
| Model 2 | 0.982 | 0.995 | 0.803 | 0.979 | 0.964 | 0.997 | 0.975 | 0.994 |
| Model 3 | 0.939 | 0.995 | 0.830 | 0.979 | 0.933 | 0.997 | 0.917 | 0.994 |
| Model 4 | 0.939 | 0.995 | 0.800 | 0.975 | 0.939 | 0.997 | 0.953 | 0.996 |
| Model 5 | 0.935 | 0.990 | 0.882 | 0.976 | 0.973 | 0.993 | 0.876 | 0.988 |
| Model 6 | 0.935 | 0.990 | 0.857 | 0.975 | 0.974 | 0.993 | 0.881 | 0.995 |
| BMA | 0.972 | 0.995 | 0.887 | 0.972 | 0.978 | 0.990 | 0.940 | 0.983 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haque, M.M.; Seidou, O.; Mohammadian, A.; Djibo, A.G.; Liersch, S.; Fournet, S.; Karam, S.; Perera, E.D.P.; Kleynhans, M. Improving the Accuracy of Hydrodynamic Simulations in Data Scarce Environments Using Bayesian Model Averaging: A Case Study of the Inner Niger Delta, Mali, West Africa. Water 2019, 11, 1766. https://doi.org/10.3390/w11091766
Haque MM, Seidou O, Mohammadian A, Djibo AG, Liersch S, Fournet S, Karam S, Perera EDP, Kleynhans M. Improving the Accuracy of Hydrodynamic Simulations in Data Scarce Environments Using Bayesian Model Averaging: A Case Study of the Inner Niger Delta, Mali, West Africa. Water. 2019; 11(9):1766. https://doi.org/10.3390/w11091766
Chicago/Turabian StyleHaque, Md Mominul, Ousmane Seidou, Abdolmajid Mohammadian, Abdouramane Gado Djibo, Stefan Liersch, Samuel Fournet, Sara Karam, Edangodage Duminda Pradeep Perera, and Martin Kleynhans. 2019. "Improving the Accuracy of Hydrodynamic Simulations in Data Scarce Environments Using Bayesian Model Averaging: A Case Study of the Inner Niger Delta, Mali, West Africa" Water 11, no. 9: 1766. https://doi.org/10.3390/w11091766
APA StyleHaque, M. M., Seidou, O., Mohammadian, A., Djibo, A. G., Liersch, S., Fournet, S., Karam, S., Perera, E. D. P., & Kleynhans, M. (2019). Improving the Accuracy of Hydrodynamic Simulations in Data Scarce Environments Using Bayesian Model Averaging: A Case Study of the Inner Niger Delta, Mali, West Africa. Water, 11(9), 1766. https://doi.org/10.3390/w11091766






