On the Morphodynamic Alterations around Bridge Piers under the Influence of Instream Mining
Abstract
:1. Introduction
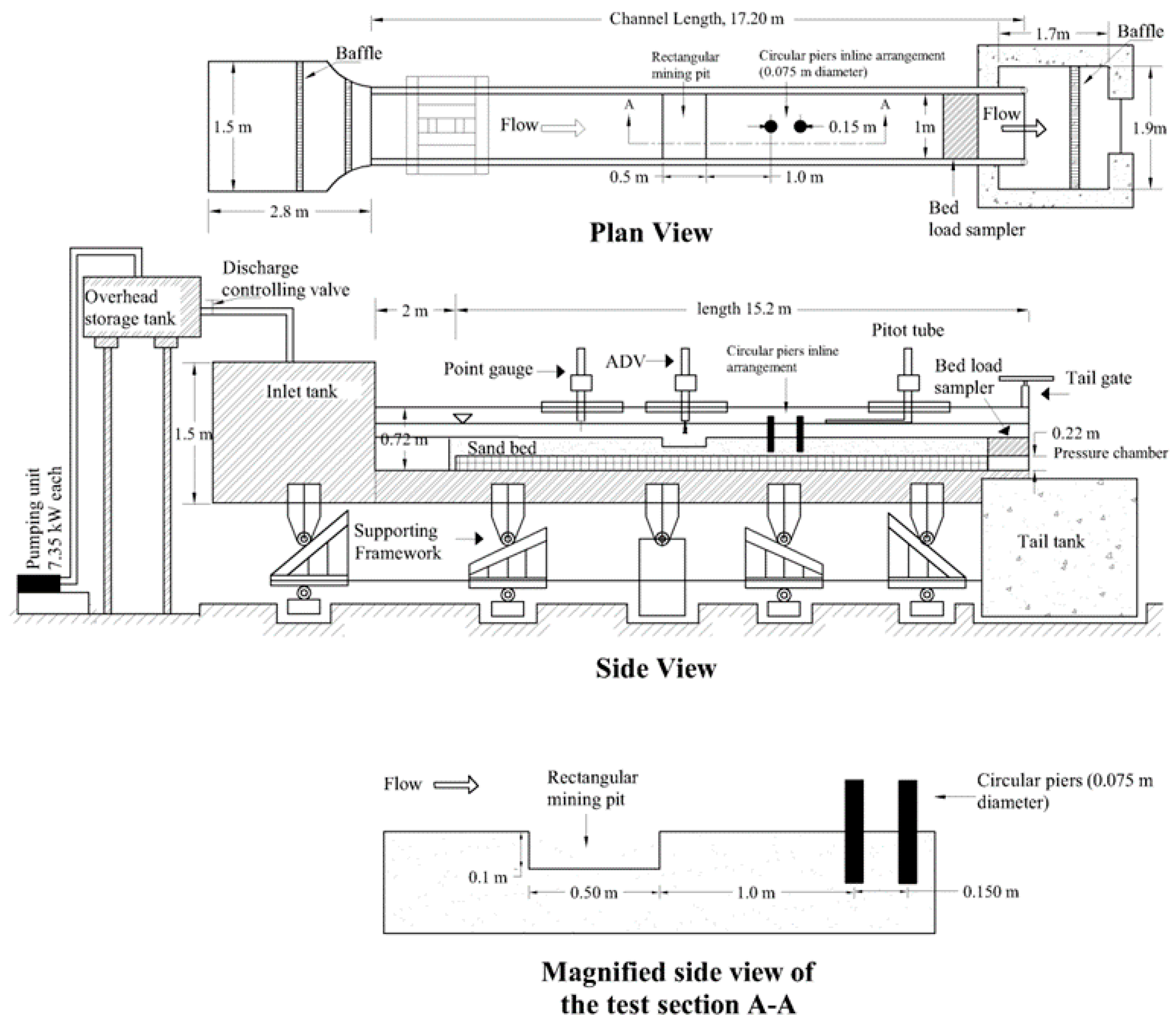
2. Materials and Methods
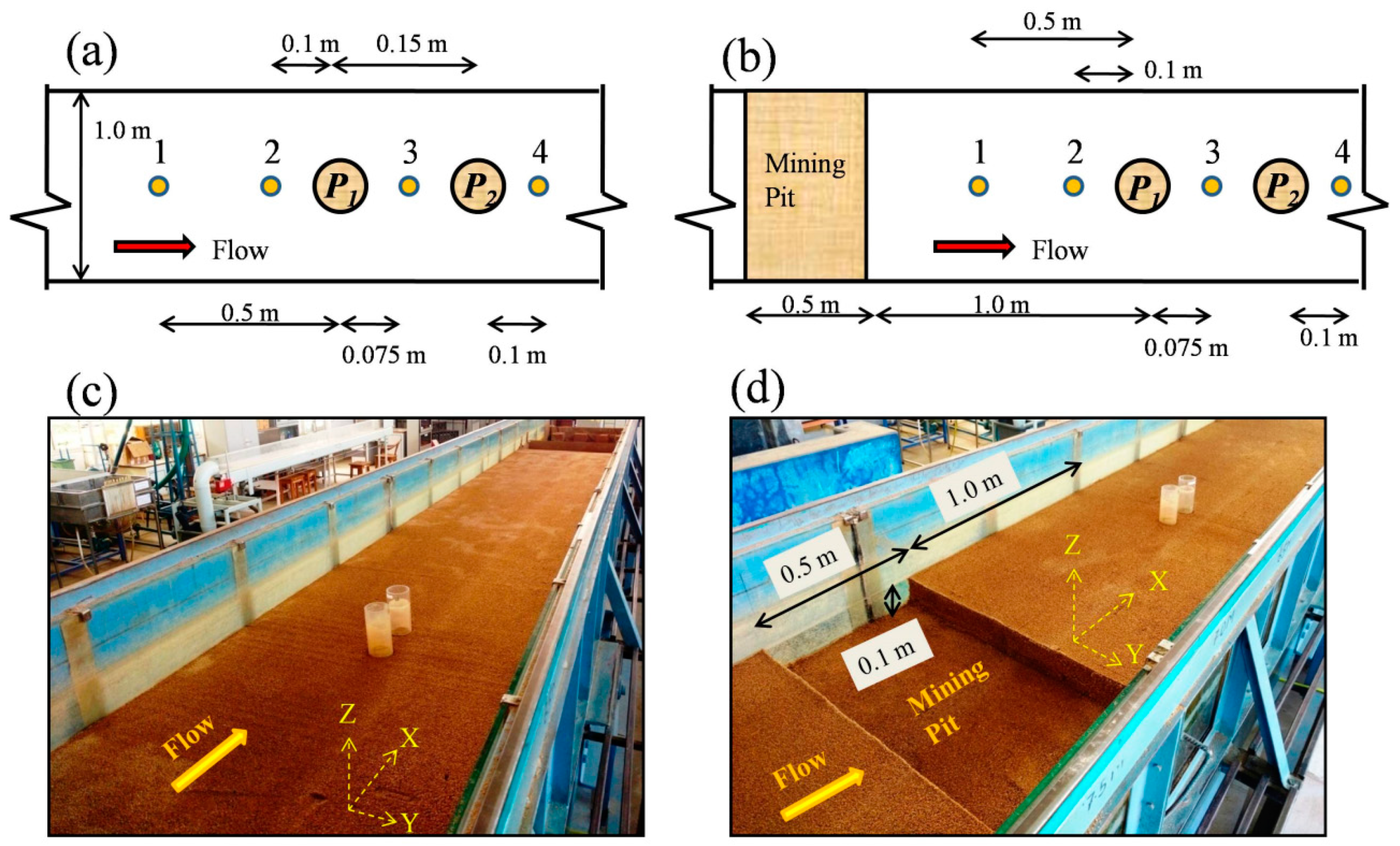
2.1. Experimental Cases
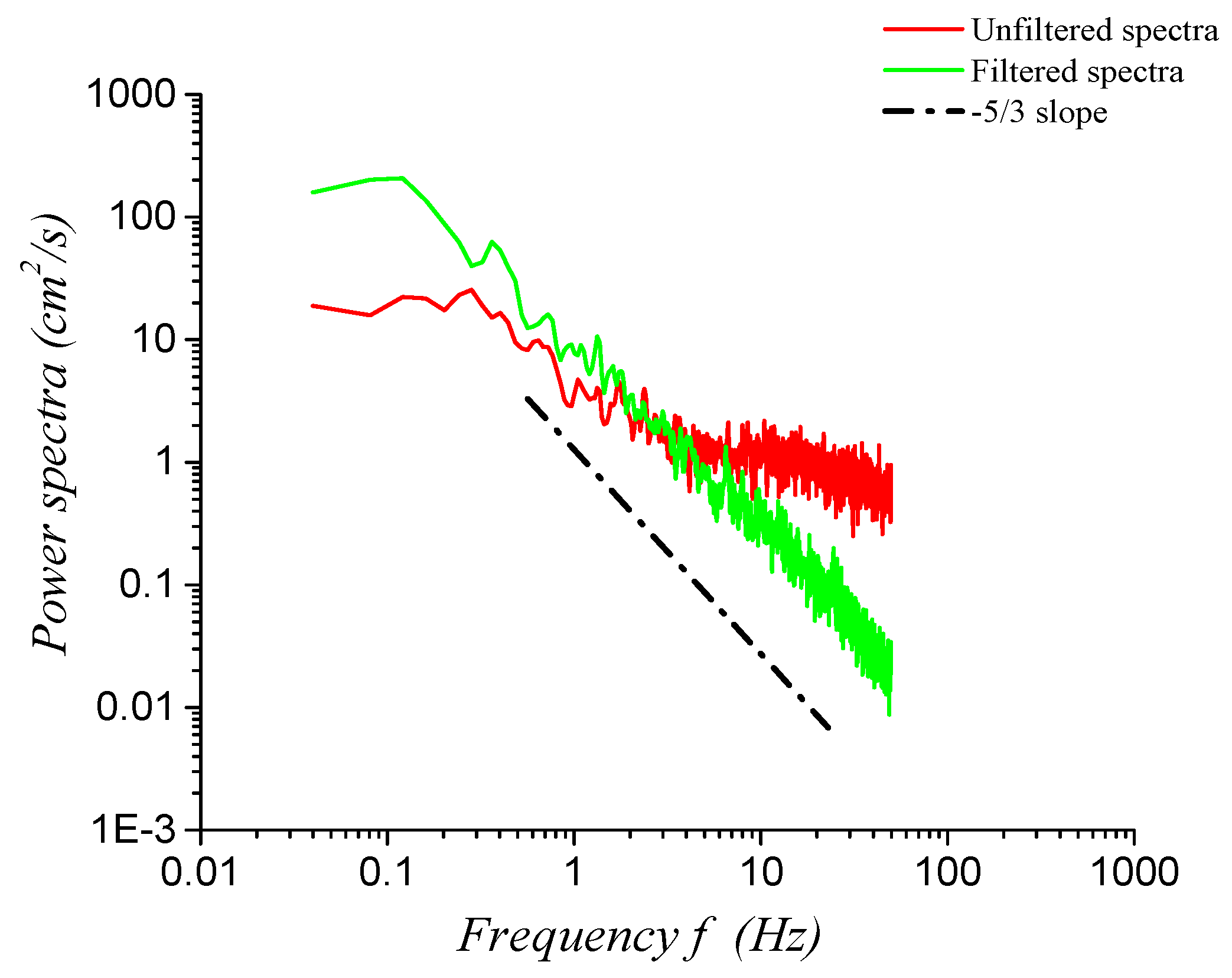
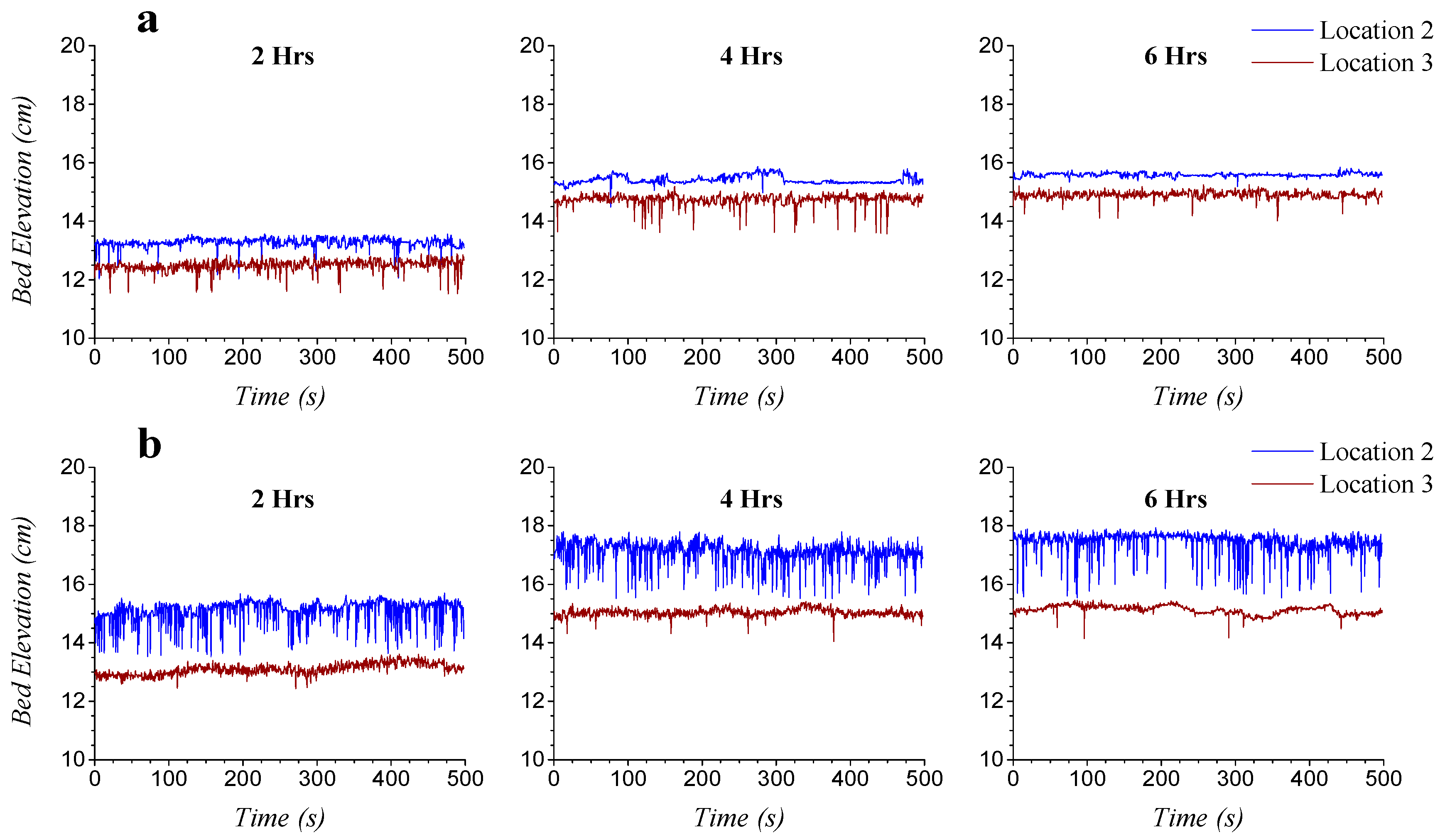
2.2. Data Collection
3. Results and Discussion
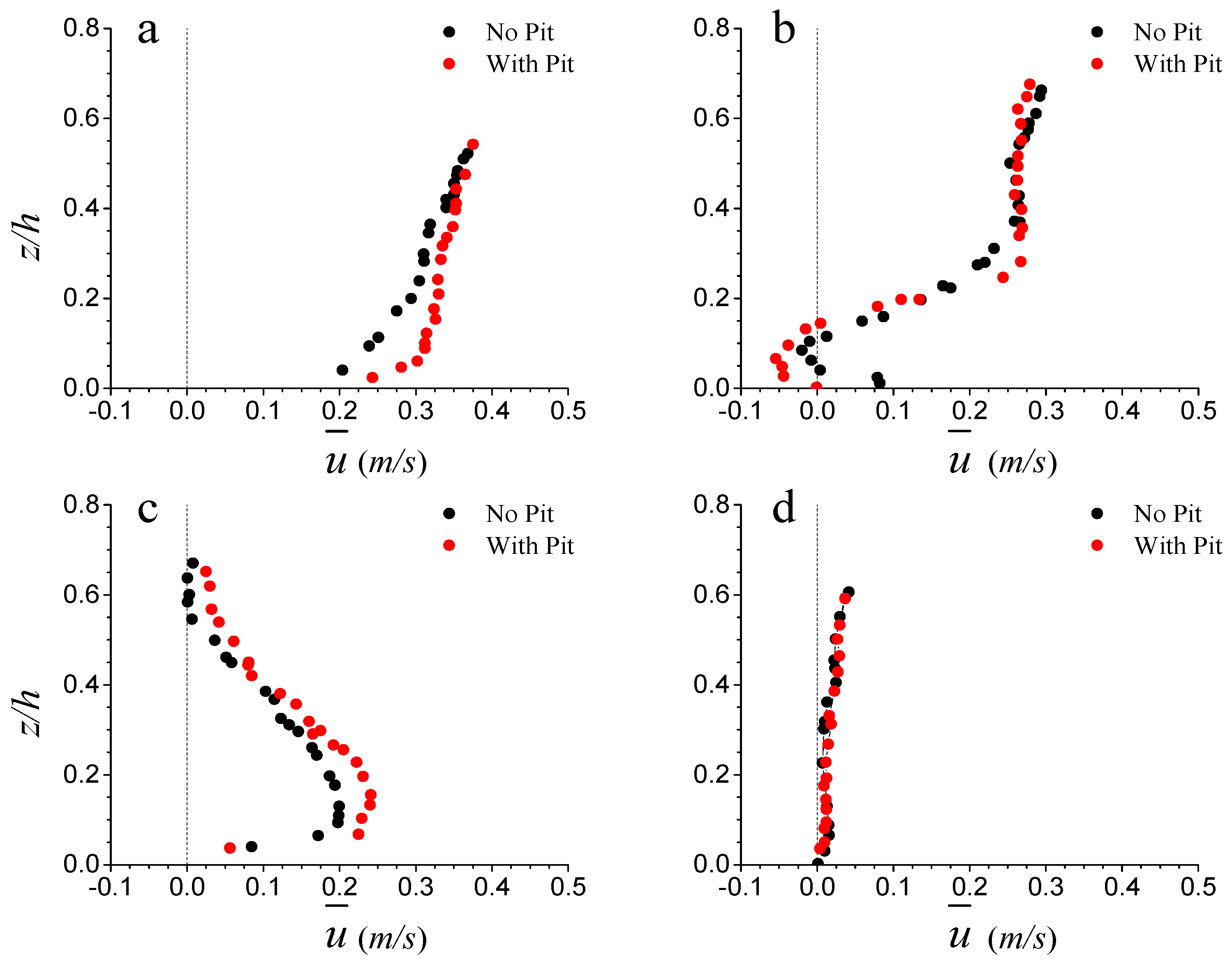
3.1. Time Averaged Flow Field
3.2. Streambed Morphology Around Tandem Piers
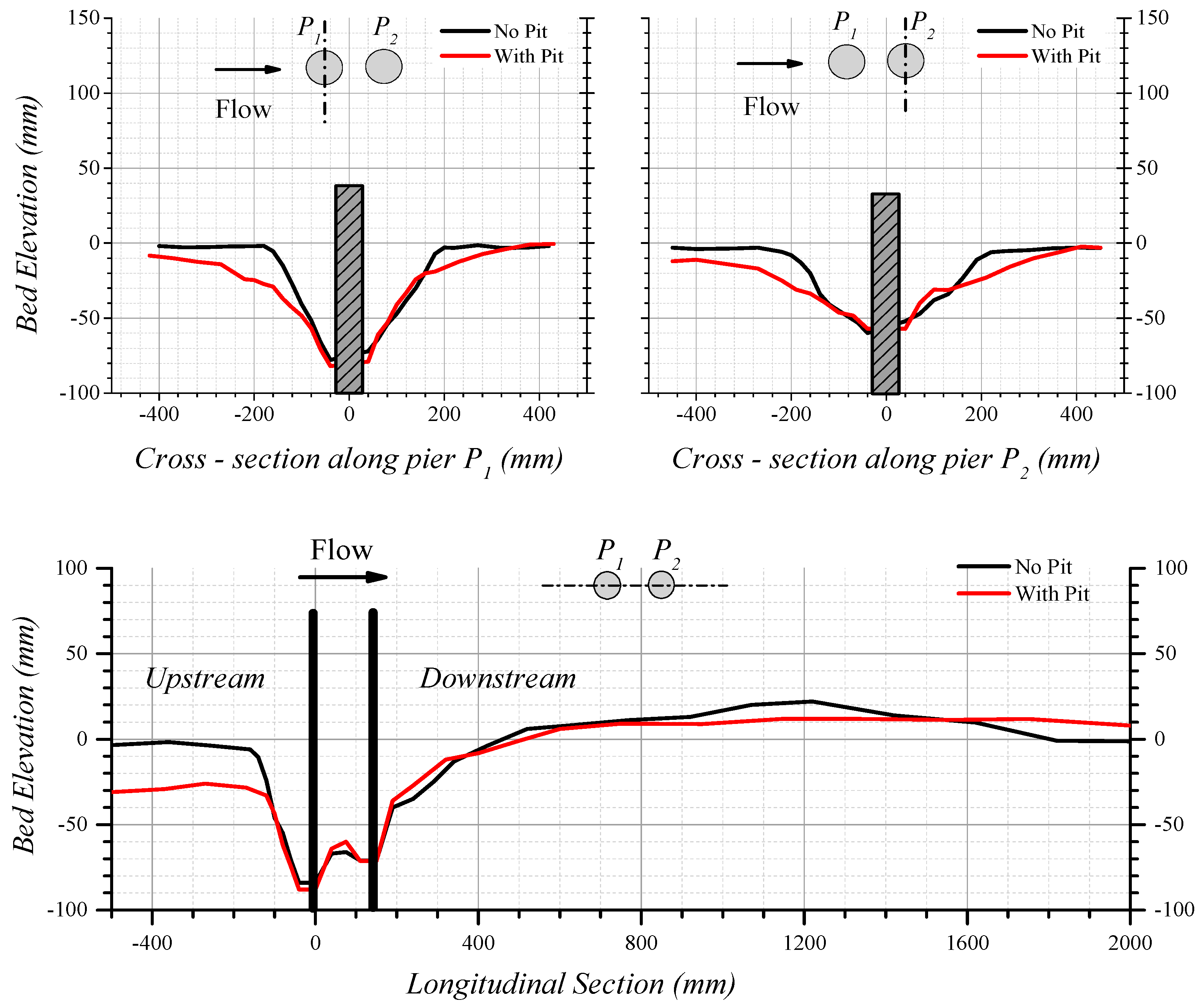
3.2.1. Morphological Features
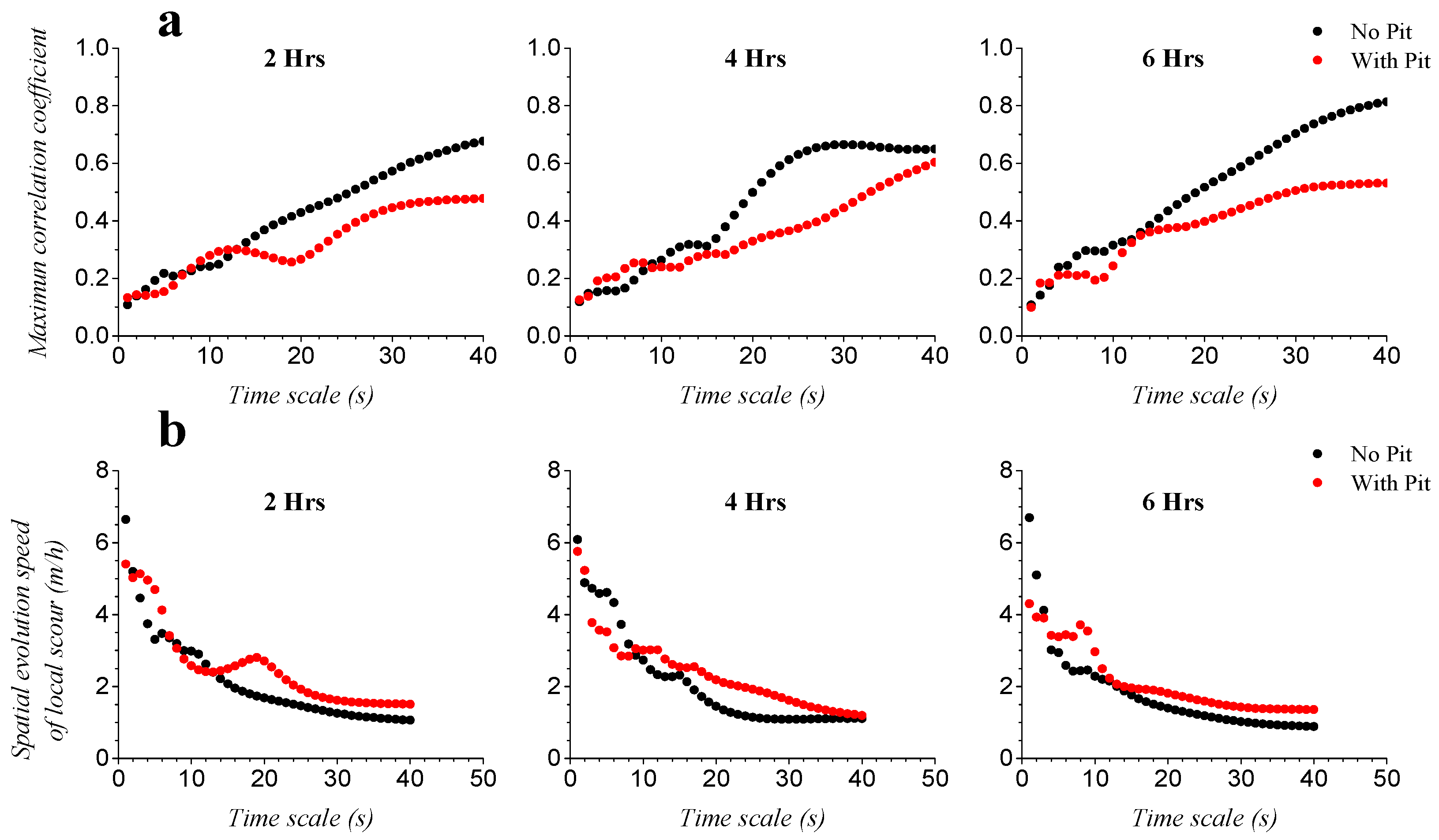
3.2.2. Wavelet-Based Statistical Evolution of Local Scour
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Kondolf, G. Geomorphic and environmental effects of instream gravel mining. Landsc. Urban Plan. 1994, 28, 225–243. [Google Scholar] [CrossRef]
- Rovira, A.; Batalla, R.J.; Sala, M. Response of a river sediment budget after historical gravel mining (The lower Tordera, NE Spain). Riv. Res. Appl. 2005, 21, 829–847. [Google Scholar] [CrossRef]
- Lee, H.Y.; Fu, D.T.; Song, M.H. Migration of rectangular mining pit composed of uniform sediment. J. Hydraul. Eng. 1993, 119, 64–80. [Google Scholar] [CrossRef]
- Gill, M.A. Hydrodynamics of mining pits in erodible bed under steady flow. J. Hydraul. Eng. 1994, 120, 1337–1348. [Google Scholar] [CrossRef]
- Cao, Z.; Pender, G. Numerical modeling of alluvial rivers subjected to interactive sediment mining and feeding. Adv. W. Resour. 2004, 27, 533–546. [Google Scholar] [CrossRef]
- Chen, D.; Acharya, K.; Stone, M. Modeling of Gravel Mining in the Rio Salado, Arizona. In Proceedings of the World Environmental and Water Resources Congress, Honolulu, HI, USA, 12–16 May 2008. [Google Scholar] [CrossRef]
- Chen, D.; Liu, M. One and two dimensional modeling of deep gravel mining in the Rio Salado. In Proceedings of the World Environmental and Water Resources Congress, Kansas City, MO, USA, 17–21 May 2009. [Google Scholar] [CrossRef]
- Barman, B.; Kumar, B.; Sarma, A.K. Turbulent flow structures and geomorphic characteristics of a mining affected alluvial channel. Earth Surf. Proces. Landf. 2018, 43, 1811–1824. [Google Scholar] [CrossRef]
- Yanmaz, A.M.; Cicekdag, O. Channel mining induced stream bed instability around bridges. In Proceedings of the Watershed Management and Operations Management, Fort Collins, CO, USA, 20–24 June 2000. [Google Scholar] [CrossRef]
- Qi, M.; Kuai, Y.R. Pier scour under influence of headcut erosion of sand pit. J. Hydraul. Eng. 2017, 48, 791–798. [Google Scholar] [CrossRef]
- Qi, M.; Yang, Y.; Kuai, Y.R. Study on Effect and Mechanism of Pier Scour Mitigation by Sill in Riverbed with Sand Excavation. China Railw. Sci. 2017, 38, 33–39. [Google Scholar] [CrossRef]
- Ahmed, F.; Rajaratnam, N. Flow around bridge piers. J. Hydraul. Eng. 1998, 124, 288–300. [Google Scholar] [CrossRef]
- Yagci, O.; Yildirim, I.; Celik, M.F.; Kitsikoudis, V.; Duran, Z.; Kirca, V.S.O. Clear water scour around a finite array of cylinders. Appl. Ocean Res. 2017, 68, 114–129. [Google Scholar] [CrossRef]
- Zdravkovich, M.M. The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Igarashi, T. Characteristics of the flow around two circular cylinders arranged in tandem: 1st report. Bull. JSME 1981, 24, 323–331. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Aslani-Kordkandi, A. Flow field around single and tandem piers. Flow Turbul. Combust. 2013, 90, 471–490. [Google Scholar] [CrossRef]
- Chavan, R.; Kumar, B. Experimental investigations on flow and scour characteristics around tandem piers in sandy channel with downward seepage. J. Marine. Sci. Appl. 2017, 16, 313–322. [Google Scholar] [CrossRef]
- Marsh, N.A.; Western, A.W.; Grayson, R.B. Comparison of methods for predicting incipient motion for sand beds. J. Hydraul. Eng. 2004, 130, 616–621. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Beheshti, A.A. Experimental investigation of clear-water local scour at pile groups. J. Hydraul. Eng. 2006, 132, 1100–1104. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S.Y. Simulation of morphological evaluation near sediment mining pits using 1-D mixed regime flow and sediment transport model. In Proceedings of the World Environmental and Water Resources Congress, Honolulu, HI, USA, 12–16 May 2008. [Google Scholar] [CrossRef]
- Muzzammil, M.; Gangadhariah, T. The mean characteristics of horseshoe vortex at a cylindrical pier. J. Hydraul. Res. 2003, 41, 285–297. [Google Scholar] [CrossRef]
- Chiew, Y.; Melville, B. Local scour around bridge piers. J. Hydraul. Res. 1987, 25, 15–26. [Google Scholar] [CrossRef]
- Kumar, V.; Ranga Raju, G.; Vittal, N. Reduction of local scour around bridge piers using slots and collars. J. Hydraul. Eng. 1999, 125, 1302–1305. [Google Scholar] [CrossRef]
- Zeng, C.; Li, C.W. Measurements and modeling of open-channel flows with finite semi-rigid vegetation patches. Environ. Fluid Mech. 2014, 14, 113–134. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Deshpande, V.; Kumar, B. Turbulent flow structures in alluvial channels with curved cross—sections under conditions of downward seepage. Earth Surf. Proces. Landf. 2016, 41, 1073–1087. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Site. Ph.D Thesis, University of Auckland, Auckland, New Zealand, 1975. Available online: https://researchspace.auckland.ac.nz/handle/2292/2537 (accessed on 7 March 2019).
- Kumar, A.; Kothyari, U.C. Three-dimensional flow characteristics within the scour hole around circular uniform and compound piers. J. Hydraul. Eng. 2012, 138, 420–429. [Google Scholar] [CrossRef]
- Soulsby, R.L.; Dyer, K.R. The form of the near-bed velocity profile in a tidally accelerating flow. J. Geophys. Res. 1981, 86, 8067–8074. [Google Scholar] [CrossRef]
- Stapleton, K.R.; Huntley, D.A. Seabed stress determinations using the inertial dissipation method and the turbulent kinetic energy method. Earth Surf. Proces. Landf. 1995, 20, 807–815. [Google Scholar] [CrossRef]
- Singh, A.; Lanzoni, S.; Wilcock, P.R.; Foufoula-Georgiou, E. Multiscale statistical characterization of migrating bed forms in gravel and sand bed rivers. W. Resour. Res. 2011, 47, W12526. [Google Scholar] [CrossRef]
- Sharma, A.; Chavan, R.; Kumar, B. Multi-scale statistical characterization of migrating pier scour depth in non-uniform sand bed channel. Int. J. River Basin Manag. 2017, 15, 265–276. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour in Signal. Processing, 3rd ed.; Academic Press: Burlington, MA, USA, 1998; pp. 409–416. [Google Scholar]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis for geophysical applications. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef] [Green Version]
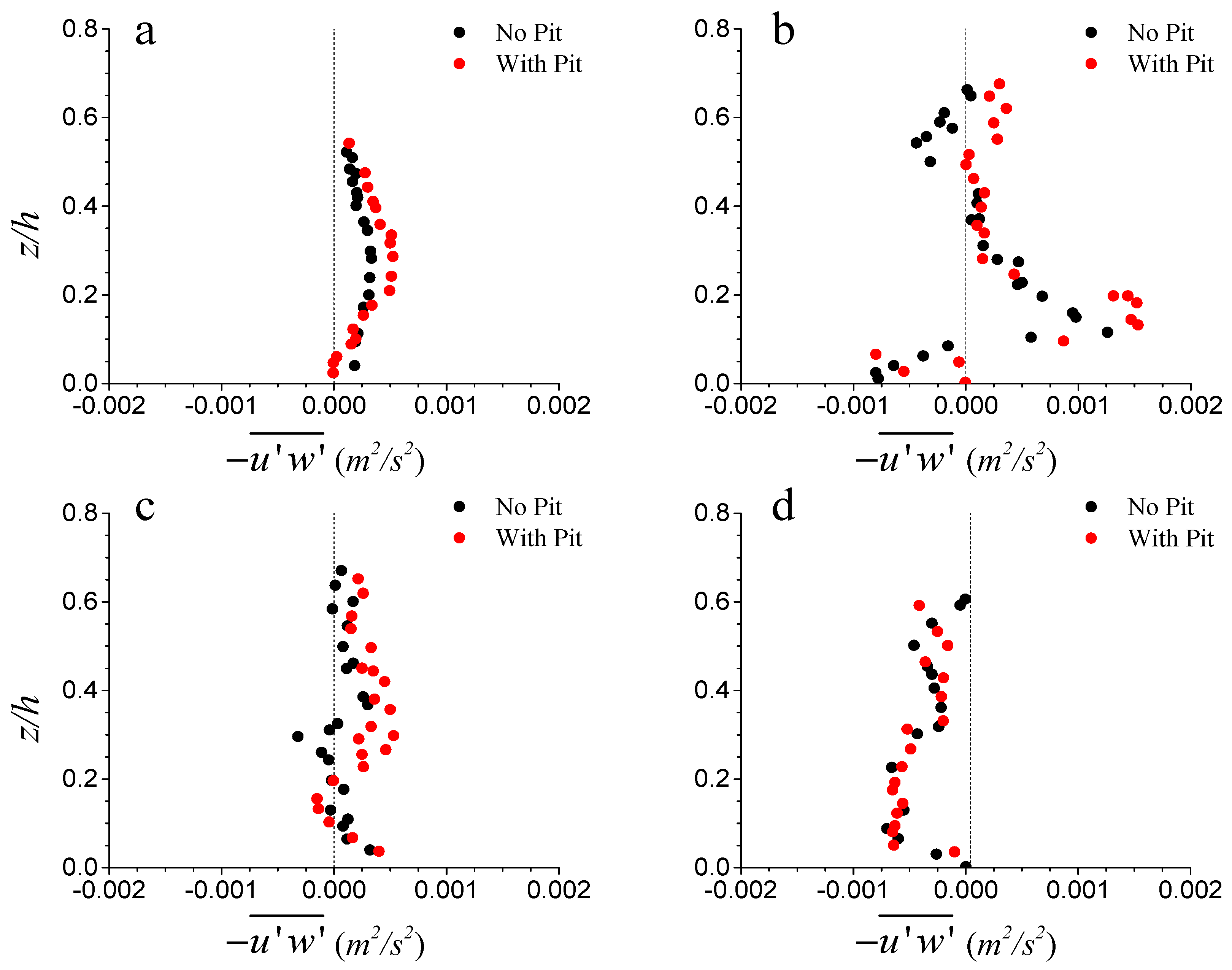
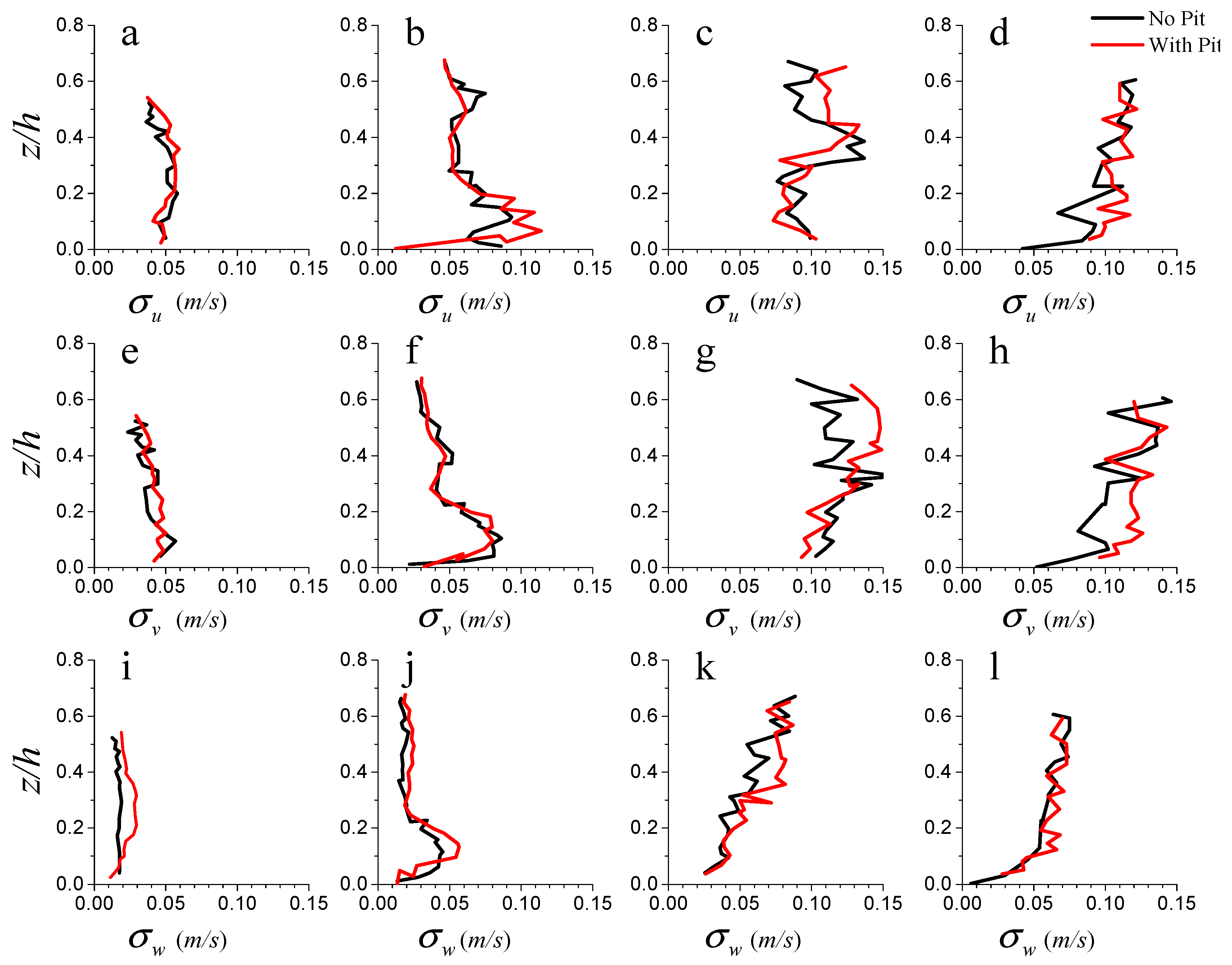
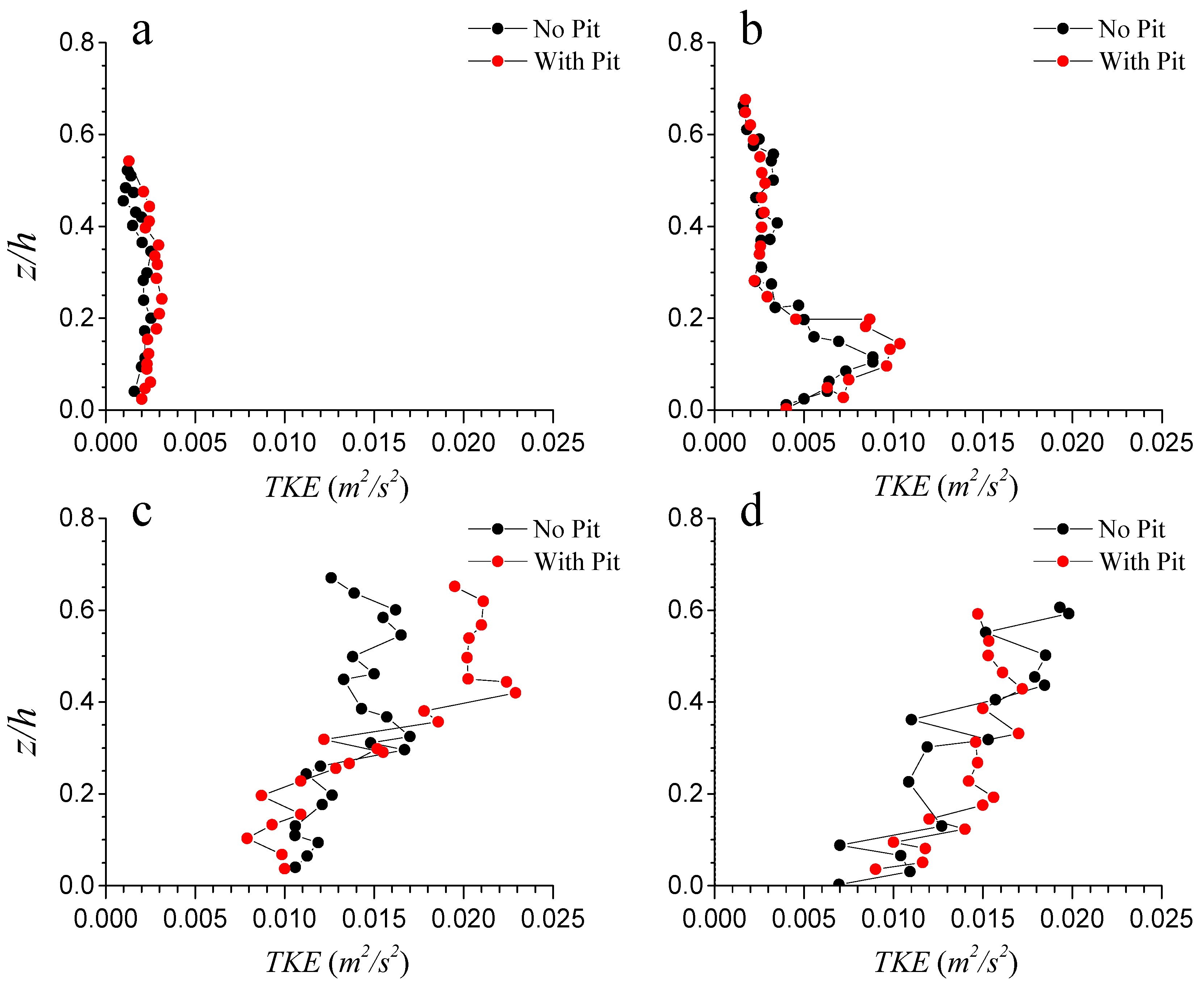
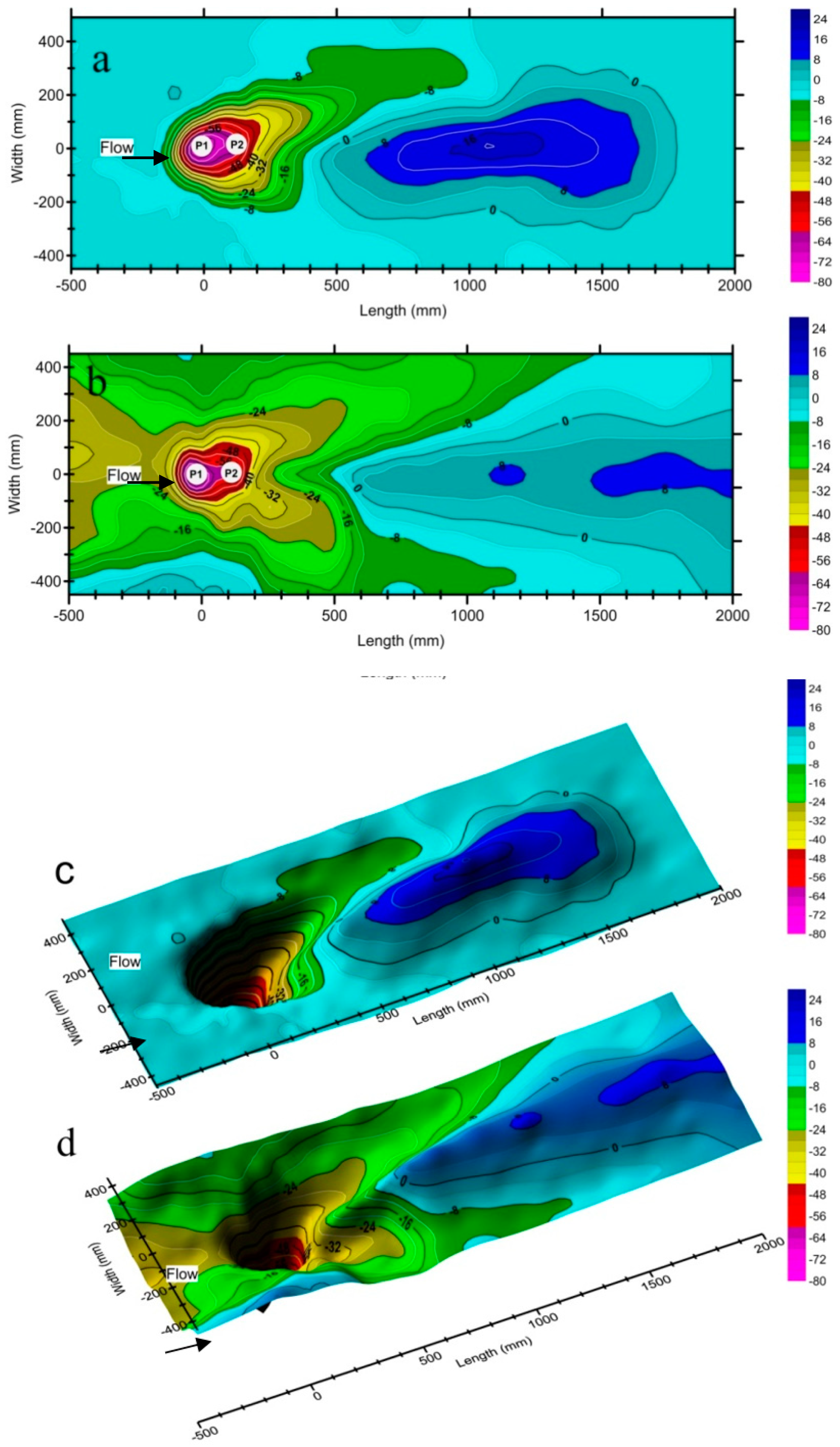

| Location | Bed Shear Stress | Shear Velocity | ||
|---|---|---|---|---|
| No Pit | With Pit | No Pit | With Pit | |
| Location-1 | 0.304 | 0.418 | 0.0174 | 0.0204 |
| Location-2 | 1.197 | 1.425 | 0.0346 | 0.0377 |
| Location-3 | 2.014 | 1.900 | 0.0449 | 0.0436 |
| Location-4 | 2.075 | 2.261 | 0.0455 | 0.0475 |
| Case | Maximum Scour Depth at P1 (mm) | Maximum Scour Depth at P2 (mm) | Scour Volume (mm3) | Average Upstream Bed Level (mm) | Distance of Dune Crest from P1 (mm) |
|---|---|---|---|---|---|
| No Pit | 77.8 | 60.0 | 12,735,436.5 | −03.0 | 1200 |
| With Pit | 82.0 | 59.5 | 19,678,061.8 | −25.0 | 1750 |
| Time Scale (s) | Spatial Evolution Speed (m/h) | |||||
|---|---|---|---|---|---|---|
| 2 h | 4 h | 6 h | ||||
| No Pit | With Pit | No Pit | With Pit | No Pit | With Pit | |
| 1 | 6.641 | 5.405 | 6.084 | 5.758 | 6.696 | 4.300 |
| 2 | 5.198 | 5.029 | 4.886 | 5.228 | 5.098 | 3.929 |
| 3 | 4.455 | 5.129 | 4.728 | 3.777 | 4.119 | 3.903 |
| 4 | 3.740 | 4.953 | 4.589 | 3.567 | 3.016 | 3.423 |
| 5 | 3.307 | 4.690 | 4.611 | 3.516 | 2.938 | 3.380 |
| 6 | 3.471 | 4.122 | 4.331 | 3.070 | 2.582 | 3.439 |
| 7 | 3.354 | 3.412 | 3.727 | 2.850 | 2.428 | 3.386 |
| 8 | 3.194 | 3.060 | 3.182 | 2.841 | 2.435 | 3.714 |
| 9 | 2.993 | 2.760 | 2.866 | 3.050 | 2.457 | 3.541 |
| 10 | 2.981 | 2.575 | 2.732 | 3.007 | 2.289 | 2.966 |
| 11 | 2.896 | 2.462 | 2.471 | 3.015 | 2.204 | 2.492 |
| 12 | 2.619 | 2.411 | 2.330 | 3.020 | 2.153 | 2.226 |
| 13 | 2.391 | 2.403 | 2.269 | 2.759 | 2.005 | 2.067 |
| 14 | 2.217 | 2.434 | 2.270 | 2.614 | 1.874 | 1.997 |
| 15 | 2.075 | 2.494 | 2.313 | 2.544 | 1.759 | 1.957 |
| 16 | 1.953 | 2.567 | 2.131 | 2.517 | 1.659 | 1.929 |
| 17 | 1.865 | 2.663 | 1.901 | 2.550 | 1.577 | 1.916 |
| 18 | 1.799 | 2.755 | 1.716 | 2.412 | 1.508 | 1.894 |
| 19 | 1.733 | 2.807 | 1.565 | 2.279 | 1.448 | 1.856 |
| 20 | 1.681 | 2.704 | 1.445 | 2.185 | 1.395 | 1.811 |
| 21 | 1.630 | 2.541 | 1.350 | 2.107 | 1.346 | 1.762 |
| 22 | 1.589 | 2.357 | 1.277 | 2.056 | 1.304 | 1.715 |
| 23 | 1.546 | 2.185 | 1.219 | 2.015 | 1.263 | 1.673 |
| 24 | 1.504 | 2.040 | 1.175 | 1.974 | 1.223 | 1.628 |
| 25 | 1.460 | 1.922 | 1.143 | 1.927 | 1.185 | 1.587 |
| 26 | 1.413 | 1.827 | 1.119 | 1.871 | 1.148 | 1.546 |
| 27 | 1.376 | 1.755 | 1.102 | 1.819 | 1.114 | 1.507 |
| 28 | 1.331 | 1.698 | 1.091 | 1.756 | 1.081 | 1.476 |
| 29 | 1.293 | 1.652 | 1.085 | 1.688 | 1.051 | 1.449 |
| 30 | 1.259 | 1.618 | 1.084 | 1.620 | 1.025 | 1.426 |
| 31 | 1.226 | 1.590 | 1.084 | 1.552 | 1.000 | 1.407 |
| 32 | 1.195 | 1.567 | 1.087 | 1.490 | 0.978 | 1.391 |
| 33 | 1.173 | 1.553 | 1.092 | 1.435 | 0.960 | 1.382 |
| 34 | 1.153 | 1.543 | 1.098 | 1.388 | 0.944 | 1.376 |
| 35 | 1.135 | 1.533 | 1.103 | 1.347 | 0.930 | 1.372 |
| 36 | 1.118 | 1.525 | 1.108 | 1.309 | 0.917 | 1.368 |
| 37 | 1.103 | 1.520 | 1.111 | 1.276 | 0.907 | 1.364 |
| 38 | 1.086 | 1.517 | 1.111 | 1.246 | 0.900 | 1.362 |
| 39 | 1.074 | 1.510 | 1.112 | 1.220 | 0.891 | 1.357 |
| 40 | 1.064 | 1.507 | 1.109 | 1.193 | 0.885 | 1.357 |
| Average speed of spatial evolution | 2.157 | 2.545 | 2.120 | 2.371 | 1.817 | 2.141 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lade, A.D.; Deshpande, V.; Kumar, B.; Oliveto, G. On the Morphodynamic Alterations around Bridge Piers under the Influence of Instream Mining. Water 2019, 11, 1676. https://doi.org/10.3390/w11081676
Lade AD, Deshpande V, Kumar B, Oliveto G. On the Morphodynamic Alterations around Bridge Piers under the Influence of Instream Mining. Water. 2019; 11(8):1676. https://doi.org/10.3390/w11081676
Chicago/Turabian StyleLade, Abhijit D., Vishal Deshpande, Bimlesh Kumar, and Giuseppe Oliveto. 2019. "On the Morphodynamic Alterations around Bridge Piers under the Influence of Instream Mining" Water 11, no. 8: 1676. https://doi.org/10.3390/w11081676
APA StyleLade, A. D., Deshpande, V., Kumar, B., & Oliveto, G. (2019). On the Morphodynamic Alterations around Bridge Piers under the Influence of Instream Mining. Water, 11(8), 1676. https://doi.org/10.3390/w11081676







