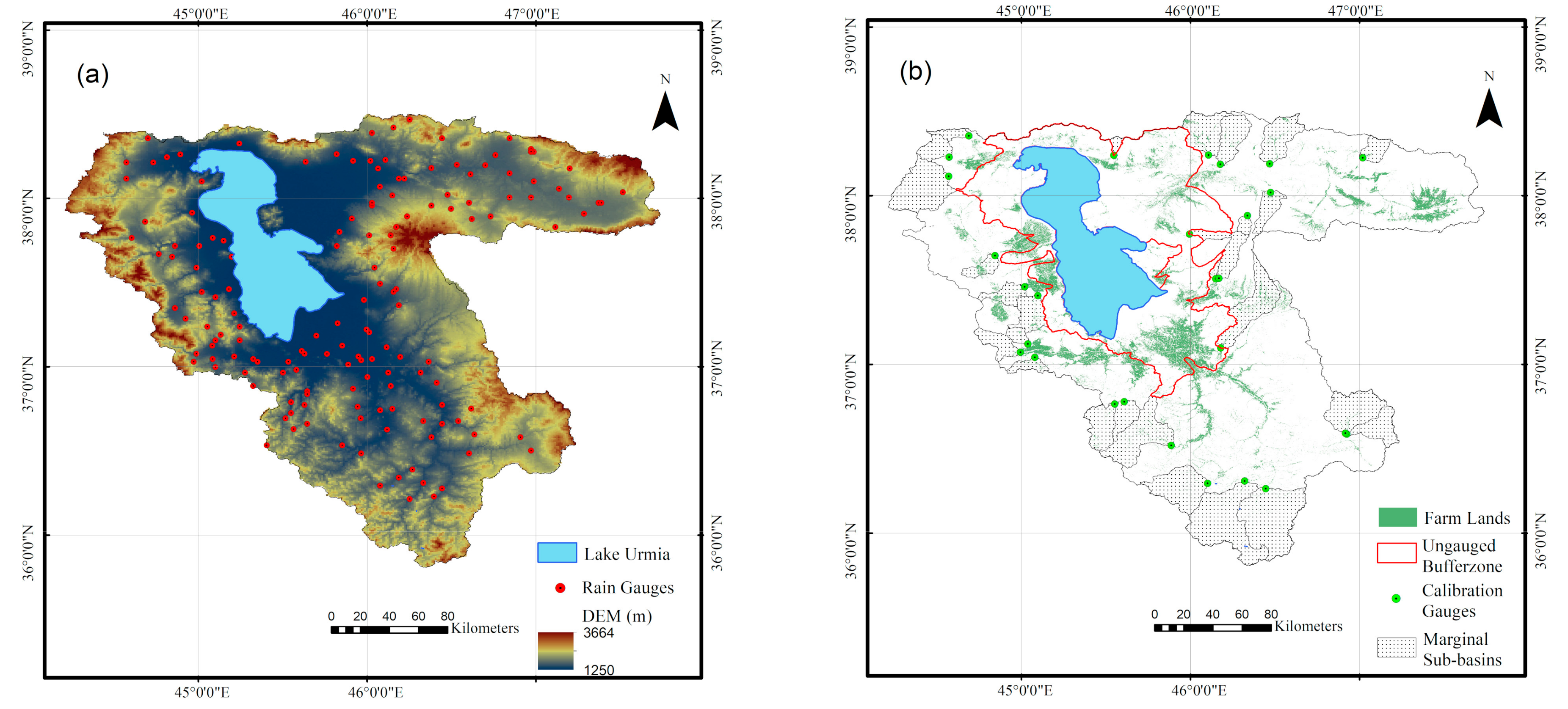
4.1. Spatiotemporal Precipitation Maps
Cokriging interpolation of rain gauge values with DEM and TRMM 3B43 V7 gave the best method accuracy, with RMSE of 81 mm for 2007 (
Table 4). This was 4 mm less than the RMSE of kriging interpolation of station data. The best method was also confirmed for 2010–2011, a normal water year in terms of rainfall, for which RMSE was reduced by 9 mm (
Table 5). The benefit of using satellite data was that RMSE was reduced by 4–9 mm across different years compared with kriging interpolation. Further, downscaled TRMM 3B43 V7 by finding an exponential relationship with DEM reduced its RMSE by 14 mm. Additionally, there was no significant relationship between NDVI and TRMM in the studied area, which can attribute to the high concentration of agricultural activities as an anthropogenic effect on NDVI.
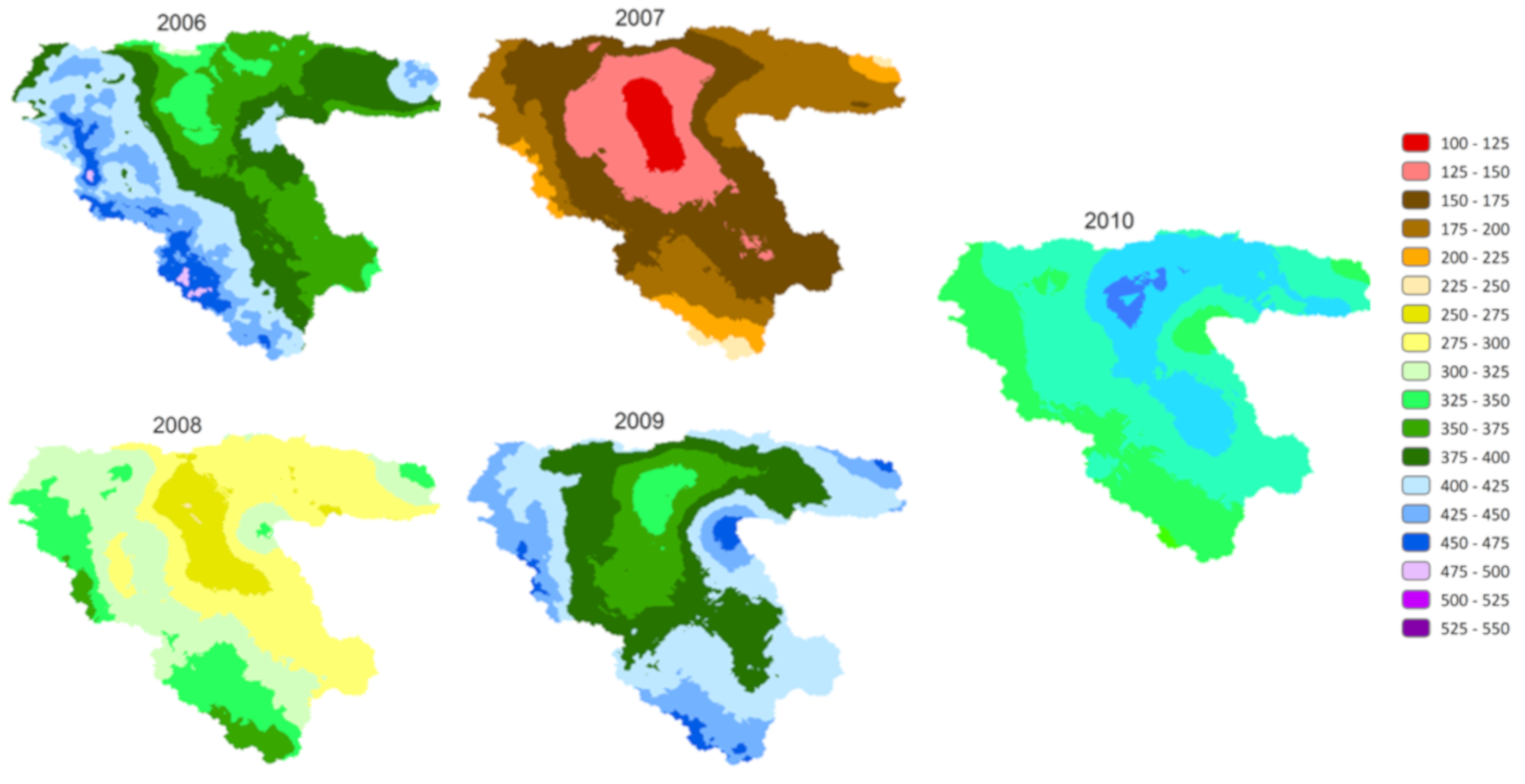
The precipitation layers for 2006–2011 obtained by cokriging interpolation of rain gauge values with DEM and TRMM 3B43 V7, as the best method, revealed high values of precipitation in marginal areas of the basin (
Figure 4). As can be seen from
Figure 1a, these marginal areas have high elevation and use of DEM in the estimation process resulted in higher values of precipitation for these mountainous regions.
4.2. Annual Direct Runoff Coefficient Map
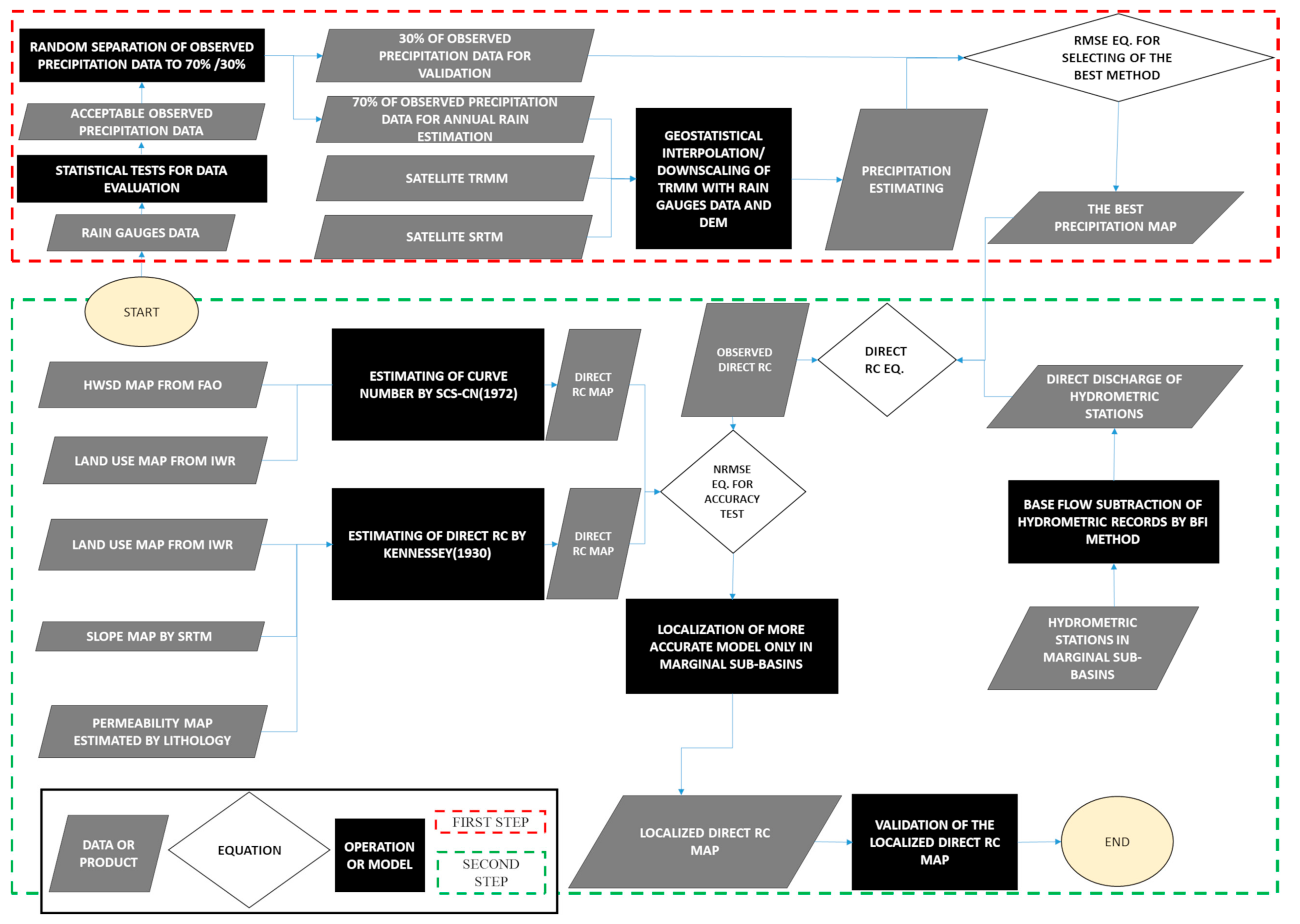
The NRMSEs obtained for the SCS-CN and Kennessey models in 2006 were 3 and 1, respectively. Therefore, Kennessey was chosen as the more accurate model for calibration. In this model,
Ia is an important parameter because, as described in
Section 3.2.3, this index as a climatic parameter is defined in Kennessey to reflect the dryness or wetness of each water year. However, applying Equation (8) from 2006 to 2011 in Lake Urmia basin gave a maximum
Ia value equal to 18. If
Ia is lower than 25, the partial coefficients lie in the same category (see
Table 2). Therefore, in the studied basin, all years from 2006 to 2011 were categorized in the same class in terms of runoff production by the default intervals of
Ia regardless of its precipitation or temperature variability. In reality, wet, dry and normal years have occurred (see
Figure 4) from 2006–2007 to 2010–2011. As novelty of this study, attempts were made to identify new intervals for
Ia to make Kennessey flexible to wetness or dryness of investigated years in Lake Urmia basin as a semi-arid region.
The values obtained indicated that in the dry year 2007–2008, Ia ranged between 3 and 6, and thus Ia < 6 can represent dryness. In normal years (2008–2009 and 2010–2011), Ia was on average 7–9 so 6 < Ia < 9 was presumed to represent the normal year. In the wet years (2006–2007 and 2009–2010), Ia was more than 9, so Ia > 9 suggested a wet year in the studied basin.
The partial coefficients of the calibrated Kennessey model are shown in
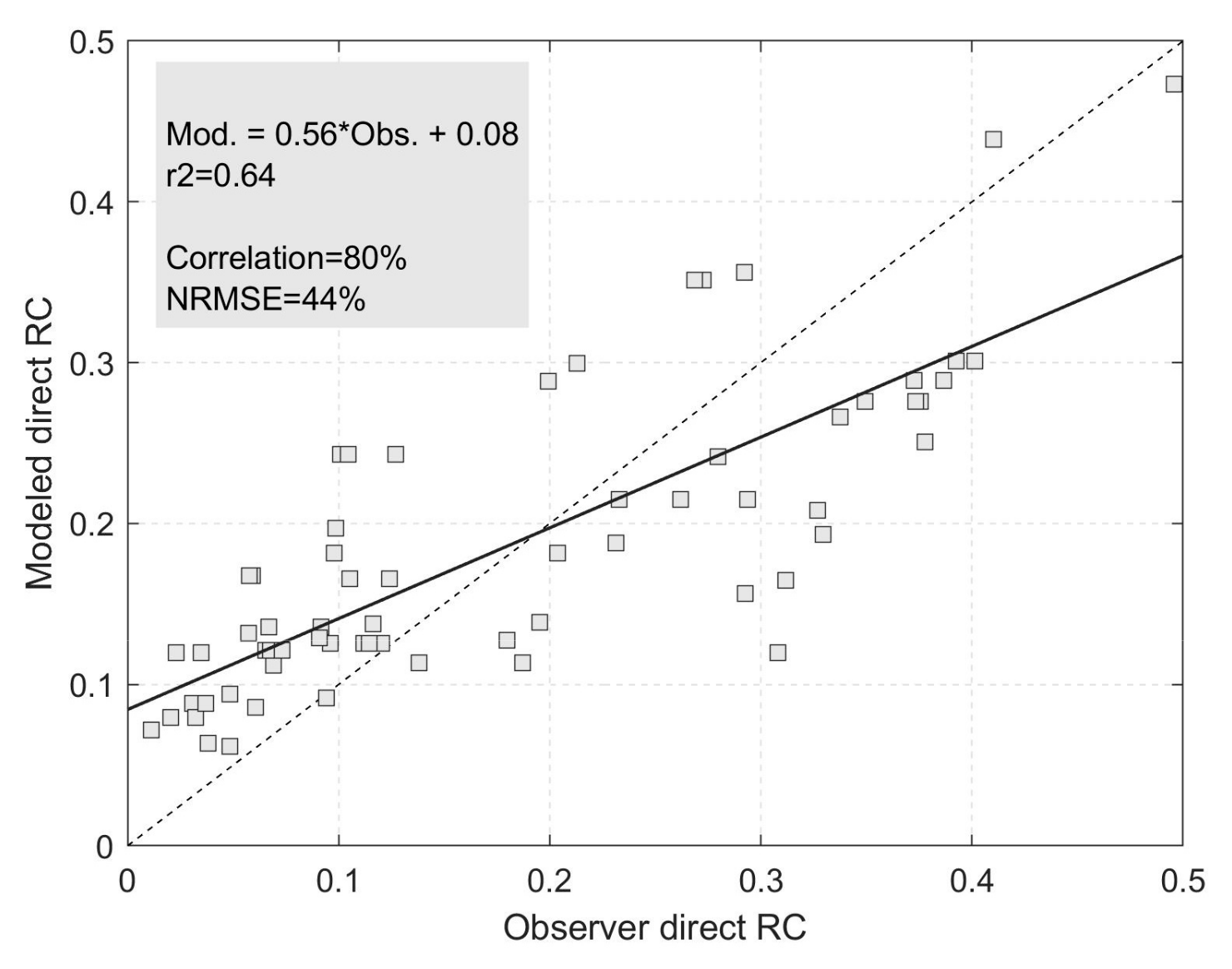
Table 6. Using the results of the calibration, a scatter plot of modeled coefficients and observed RC was created after convergence of estimated and observed values (
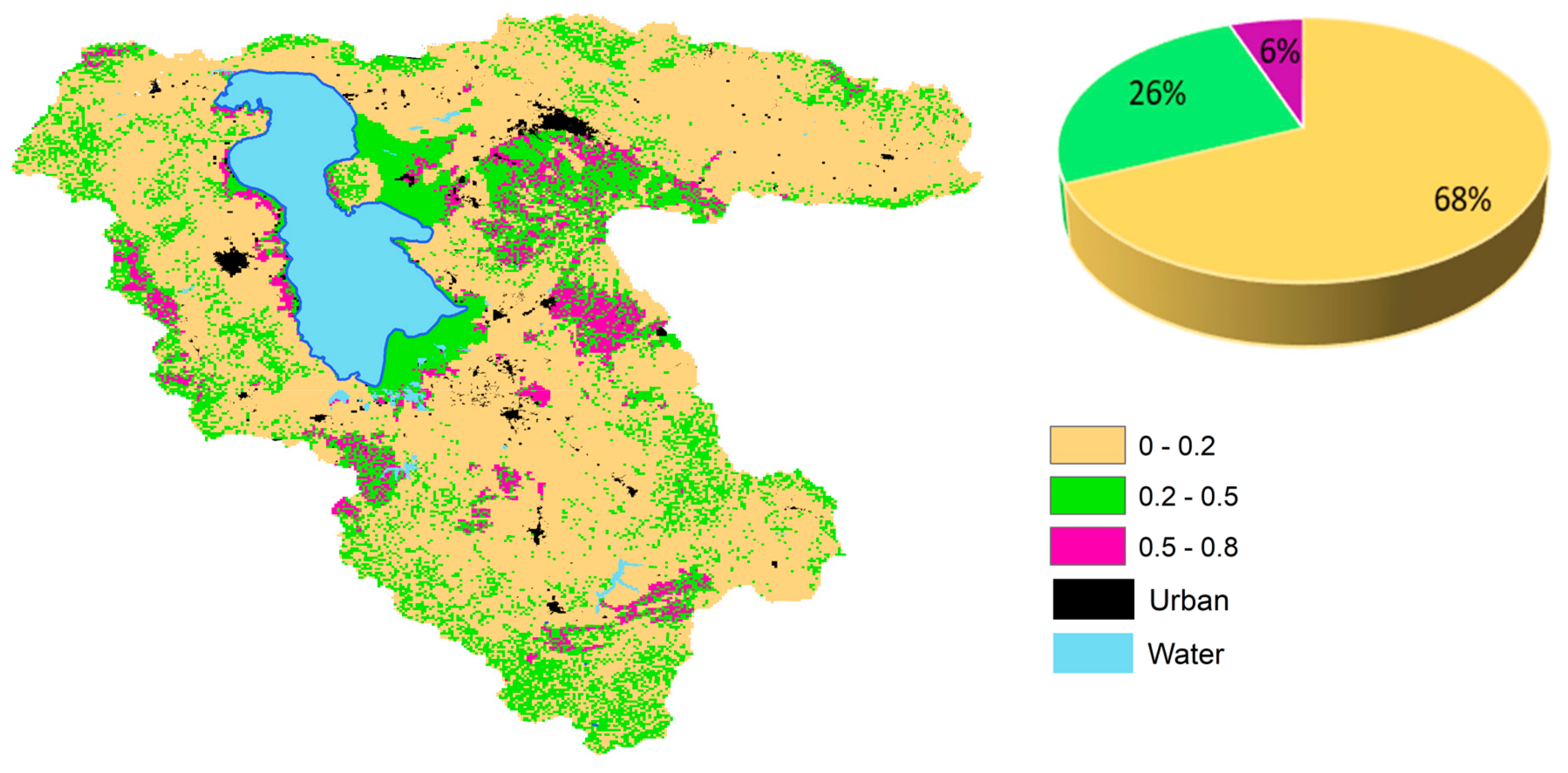
Figure 5). There was observable agreement between modeled and observed values, such that the correlation coefficient obtained 80%. The calibrated Kennessey reduced the NRMSE from 1 to 0.44. The map of the five year mean of annual direct RC for Lake Urmia basin from 2006–2007 to 2010–2011 produced by calibrated Kennessey by 1 km spatial resolution is shown in
Figure 6.
As can be seen from
Figure 5, when the observed direct RC was lower than 0.2, most of the values less than 0.2 were above the 1:1 line in the first quadrant, i.e., the model overestimated direct RC in this range. At values greater than 0.2, the model underestimated direct RC.
The direct RC map generated for Lake Urmia basin (
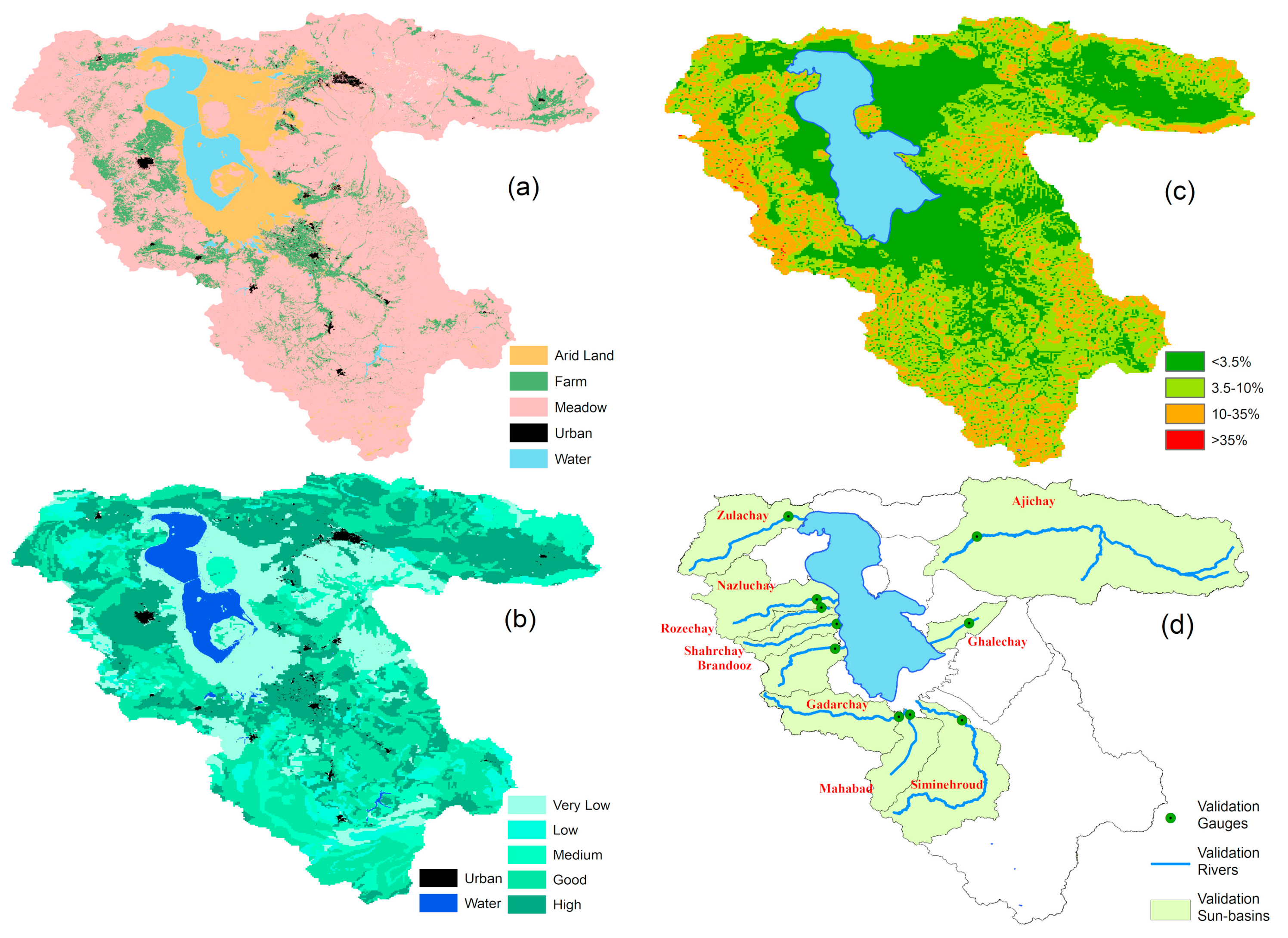
Figure 6) was validated using observed values in gauges on the main rivers of the basin. Since the water withdrawal is high in validation sub-basins by intensive farm lands (
Figure 2d), we must consider it in observation of validation gauges. The water withdrawal of the basin, published by WRM, is only available for year 2008 so we validated direct RC map of calibrated Kennessey by averaging estimated values from 2006–2007 to 2010–2011 and then compared them to the five-year mean annual observed direct runoff in validation gauges which were naturalized by considering water withdrawal in observed value of gauges (see step 2 described in
Section 3 ‘Methodology’).
By pristine validation gauges data which were not involved in the calibration process, the NRMSE of validation obtained 0.41, which is close to the calibration error, indicating success of the calibration process. In
Table 7, the main rivers in Lake Urmia basin are listed in descending order of observed runoff. The last column on the right shows the difference between the observed and modeled values divided by the observed value. As can be seen, for most of the rivers providing higher discharge to the lake, the error was less than 50%. For the major rivers, Gadarchay, Mahabad, Rozechay, and Simineroud, the accuracy is higher. The highest error was found for the Zulachay river basin, which was due to lower value of observed direct runoff (smaller fraction denominator). The mean of validation gauges for modeled values obtained 0.19 and that of the observation was 0.16 and correlation between observed and modeled values obtained 79%.
4.3. Limitations in Data, Modeling, and Assessment
The present study was based on data from 2006 to 2011. These years capture well the interannual variation in weather, including wet (e.g., 2006–2007, 2009–2010), dry (e.g., 2007–2008), and normal (e.g., 2008–2009, 2010–2011) water years. Additionally, the most recent data on water withdrawal and the land use map of the basin are for year 2008 which is in the middle of the studied time span. As described above, water withdrawal data were essential for validation of the calibrated direct runoff model. Under strategies approved by central government, the hydrological status of Lake Urmia basin has stabilized in recent years. These strategies prohibit any kind of additional withdrawal from the basin water resources or any new development, especially in the agricultural sector, prevent unpermitted withdrawal from surface waters, and stop all dam construction projects under study and under operation [
18]. Due to these measures, it can be concluded that 2006–2011 was representative of the hydrological status in Lake Urmia basin. By calibrating the model for this period, it was possible to apply the results to the whole basin in recent years.
Expanding the time span of the assessment after solving the problem of data availability would provide more observations for calibration of the direct runoff model, increasing the accuracy of the results. Considering new intervals for Ia or generating another index to replace Ia could help the Kennessey model distinguish between wet, dry, and normal years in semi-arid basins like Lake Urmia. Another limitation in the present study was that the Zarinehroud, one of the most important rivers in Lake Urmia basin, was not covered in the validation process because of its gauge data problem. Additionally, enhancing the quality of withdrawal data in terms of spatial and temporal resolution can help measure the validity of the calibrated model. Finally, it should be noted that water withdrawal data, available only for 2008, did not permit to validate the direct RC map annually and we had to compare the model and observed direct RC values by averaging them for five years from 2006–2007 to 2010–2011.