1. Introduction
Water is an indispensable natural resource for life and an increasingly limiting factor to socioeconomic developments [
1]. Water resources issues are widely discussed throughout the world. Addressing these issues requires information about the factors that drive hydrological changes and their related effects on local water resources. Evaluating water resources becomes a complex task that needs to consider many facets. Studies that detail the spatial and temporal distribution of water resources are of vital significance to inform management strategies.
Both climate variation and human actions act as stressors that contribute to putting water resources under severe pressure [
2]. Intensive human activities apart from climate change, such as land-use change, urbanization, economic development and population growth, have posed unprecedented impacts on watershed hydrological conditions. For example, these stressors can alter surface runoff, evapotranspiration, baseflow, the frequency of floods, annual mean discharge, flow routing time, peak flows and volume [
3]. Moreover, the pressures of these human activities are associated with climate variation which in turn will affect water sustainability for socioeconomic developments [
4].
The impacts of individual factors on watershed hydrology theoretically cannot be separated [
5]. This coupling effect, together with water withdrawal and retention, contributes to the uncertainties in identifying the specific impact of each factor on watershed hydrology [
6]. This creates difficulty in inferring causation on a sufficient scale, and therefore it remains unclear which of these factors dominantly contributes to watershed hydrology [
4,
5]. Indeed, several reports show conflicting conclusions when the combined hydrological responses are measured [
6,
7,
8,
9]. Climate variation exerts a control on dominant agricultural and land use practices including their spatial properties [
10,
11,
12]. The joint impact on hydrology of climate variation and land use change has been shown to be similar to that of a single climate change factor [
13,
14]. Hence, identifying the distinct impacts of changing land use from climate variability and understanding the water balance is considered a particular challenge for studies on operational management of reservoirs and river basins.
In recent years, several investigators have studied the effect of climate variation and land use change on watershed hydrology [
15,
16,
17]. Zhang et al. [
16] studied these effects on streamflow in the China Fenhe River Basin. The study found a stronger influence of land use on streamflow than climate change. Xu et al. [
17] similarly showed that land use affects streamflow variation twice as much across more than 50 watersheds throughout the Midwestern United States.
Although an increase in high streamflow and decrease in low streamflow is often associated with urbanization [
18], the impact of land use change often varies with climate [
14]. On the other hand, the changes in watershed hydrology and annual water balance can also be attributed to climate variability, especially in large scale watersheds, likely caused by compensatory effects in a complex watershed [
19]. Novotny and Stefan [
20] reported a correlation between the mean annual streamflow trend and rainfall in five major Minnesota River watersheds, while in Indiana rainfall has shown a strong relationship with low flow [
21]. In addition, Frans et al. [
22] concluded that wet climates, rather than land use change, had the most impact on streamflow in the Upper Mississippi River Basin. Comparable research was conducted by Tan et al. [
23] in the Johor River Basin in Malaysia; results indicated that climate change was the main driving force that impacted watershed hydrology. In the Yellow River Basin in China, climate fluctuation accounted for a 10 mm per year reduction in mean annual streamflow [
24]. River discharge significantly increased in the upper Syr Darya river basin due to temperature increase from 1930 to 2006 [
25]. Duan et al. [
26] evaluated the effects of projected climate change scenarios on watershed streamflow in the Upper Ishikari river basin in Japan, finding annual mean streamflow will likely increase for future climate scenarios. Therefore, it is important to distinguish between effects related to land-use changes and those due to climate variability for accurate estimation of surface and groundwater responses.
Impacts of these factors on watershed hydrology is different across watersheds. Therefore, sites must be evaluated on a local scale [
27]. Due to limited available data, it is essential to use both comprehensive and physical tools to extract as much information about hydrologic responses as possible [
28]. Hydrological models are considered an appealing approach to carry out impact assessment studies, as they provide a conceptualized framework to be used in scenario studies on the relationship between hydrological components, land-use change and climate variability [
29]. Model parameters can have physical meaning as related to measurable landscape properties and meteorological conditions [
30], and explicitly represent spatial variability [
31]. Initial model parameters describing vegetation, land use and soil types are called physically based parameter values; they can be adjusted to improve streamflow simulation through subsequent model calibration processes [
32].
Recently, water resource managers and modelers have counted on hydrological models to identify alternative strategies for water resource allocation and to obtain more information about watershed systems, hydrological processes, and their responses to both anthropogenic and natural factors [
33], including insight regarding the impacts of future climate projections [
34]. Some of these models incorporate the watershed’s heterogeneity and the spatial distribution of land use, topography, soil type, and meteorological conditions [
35]. Among these models is the Soil and Water Assessment Tool (SWAT) model. SWAT is a conceptual mathematical semi-physical, semi-distributed based model [
36]. SWAT employs parameters with time steps at a daily scale [
37]. The model is designed with basic components, for example, climate, sediment type, nutrients, and hydrology [
38]. This allows for interconnections of different physical processes that occur in the environment, making it the model able to evaluate how the hydrological components are impacted by land management methods in complex catchments with different land covers, and climate scenarios in extreme events such as droughts and floods [
39].
Streamflow and baseflow in watersheds in the US Midwest region reported upward trends with both urbanization and climate change [
16,
32]. While previous streamflow and baseflow trend investigations included urbanized watersheds in the Midwest region [
40], they lacked integration analysis, which exclusively focuses on the interactive impacts of land and climate variability on urbanized catchments. In addition, multiple factors, nonlinear relationships, and poor understanding of mechanisms limits the ability to attribute causation [
41]. Therefore, the current study focuses on this issue through a systematic investigation, taking into account the effects of both individual and coupled impacts of human and natural impacts.
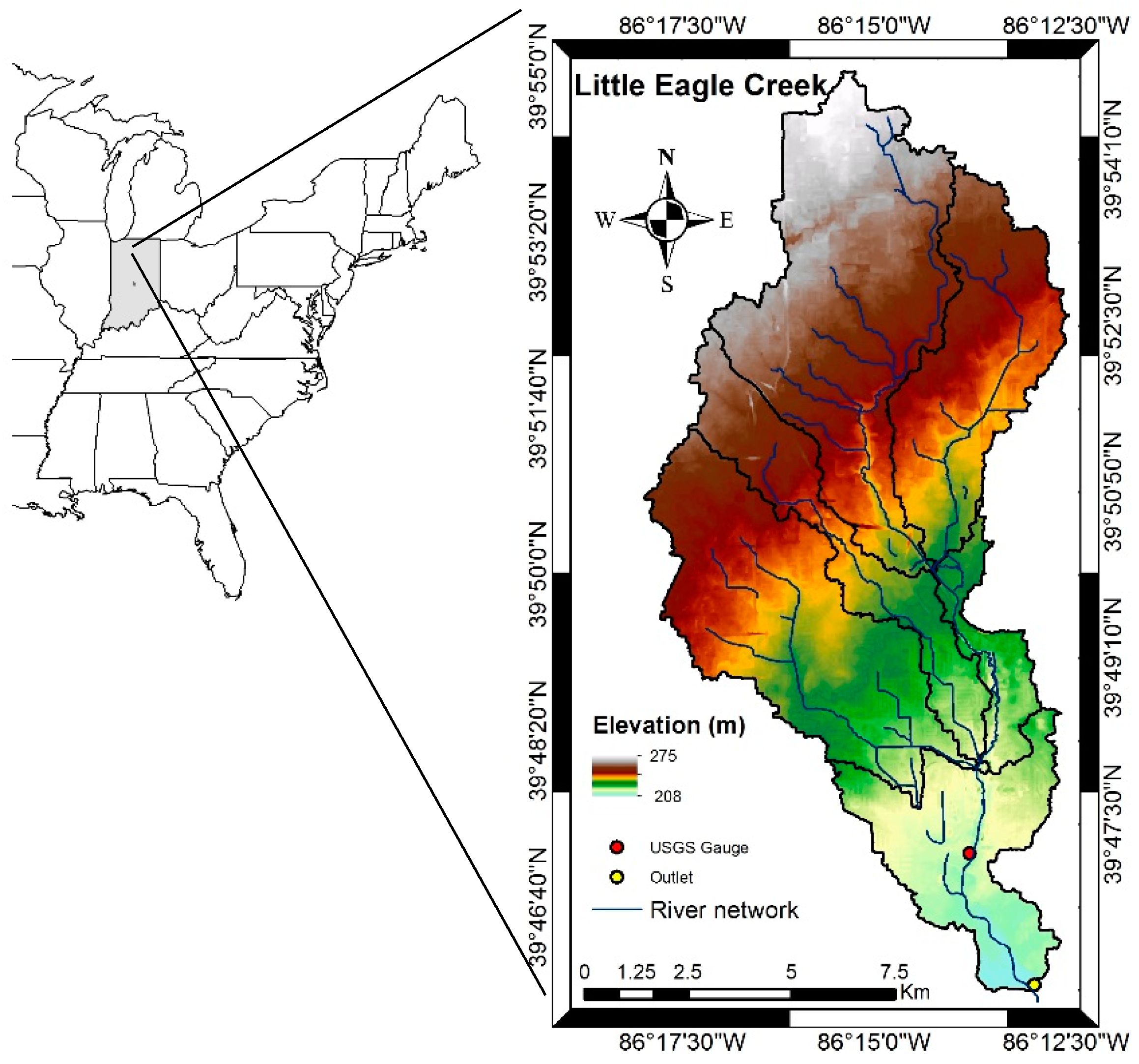
The study area, Little Eagle Creek (LEC) in central Indiana is an ideal candidate site for this type of study because it has been previously examined for many of water-related issues and has substantial data available for this study. Previously, the LEC was investigated to evaluate impacts of urbanization on water issues. Bhaduri et al. [
42] utilized the Long-Term Hydrologic Impact Assessment (L-THIA) model with different land use patterns to evaluate nonpoint source (NPS) pollution and to assess impacts on annual average runoff from the watershed. The study concluded that the 18% increase in urban areas, from 1973 to 1991, resulted in an estimated 80% and 50% increase in annual average runoff and pollutant loads, respectively. Grove et al. [
43] conducted a similar study; results were consistent with Bhaduri et al. [
42], though they reported an increase of 60% in average annual runoff depth from 1973 to 1991 due to urbanization. Doyle et al. [
44] reported that stream incision occurring in the LEC was a response to urbanization though the measures of channel stability were not directly related to levels of urbanization. Choi et al. [
45] estimated an increase in direct runoff from 49% to 63% during a 12-year time-span (1973 to 1984), suggesting that urbanization impacted direct runoff more than total runoff. In addition, they also pointed out that substantial baseflow is essential to maintain sound stream ecosystems in the LEC watershed. In their attempt to minimize the runoff impact of urbanization in the LEC, Tang et al. [
46] were able to reduce runoff increase by as much as 4.9% from 1973 to 1997.
More recently, Lim et al. [
47] estimated the effect of initial abstraction and urban growth on estimated runoff using modified curve number values in the L-THIA model. Results showed improvements in the prediction of direct runoff over the long term, resulting from using modified curve numbers and hydrologic soil groups for urbanized areas. Lim et al. [
48] reported that improved input parameters could improve L-THIA model performance.
The overall aim of this research was to evaluate the response of watershed streamflow and baseflow to climate variability and land-use change in an urban watershed in Indiana, based on simulation following a comprehensive calibration. The specific objectives are: (A) to evaluate long-term trends of historical streamflow, land use and rainfall in an urban watershed; (B) identify changes in land use from 1992 and 2011 through transition matrix analysis; (C) calibrate and validate SWAT model performance, using different land-use patterns for different periods; (D) investigate hydrological streamflow and baseflow sensitivity to land-use change and climate variability; and (E) simulate the joint effects of both climate and land-use change on hydrology in this watershed. For this goal, plausible scenarios of land-use change and climate variation were developed based on trends and information exploited from the Little Eagle Creek (LEC) watershed. The results obtained provide useful information towards the improvement of the current understanding of hydrological component variation. Additionally, the results are informative to planning and management strategies for water resources that seek to minimize the undesirable effects of land-use change and climate variation as well as water and soil preservation in urban watersheds in Midwestern USA and potentially beyond.
4. Summary and Conclusions
Recognizing the impacts of land use alteration and climate variability on hydrologic systems is the basis for pragmatic watershed sustainability and ecological restoration efforts. In this study, the impacts of climate variability and land use change from 1980 to 2017 on water streamflow and baseflow in the Little Eagle Creek watershed have been evaluated using the non-parametric Mann–Kendall statistical test, land use maps and hydrologic modeling. The novelty lies in that not only were the effects of climate variation on hydrological response investigated, but the combined impact of land use dynamics and climate variation was also evaluated in an urbanized watershed in the US Midwest.
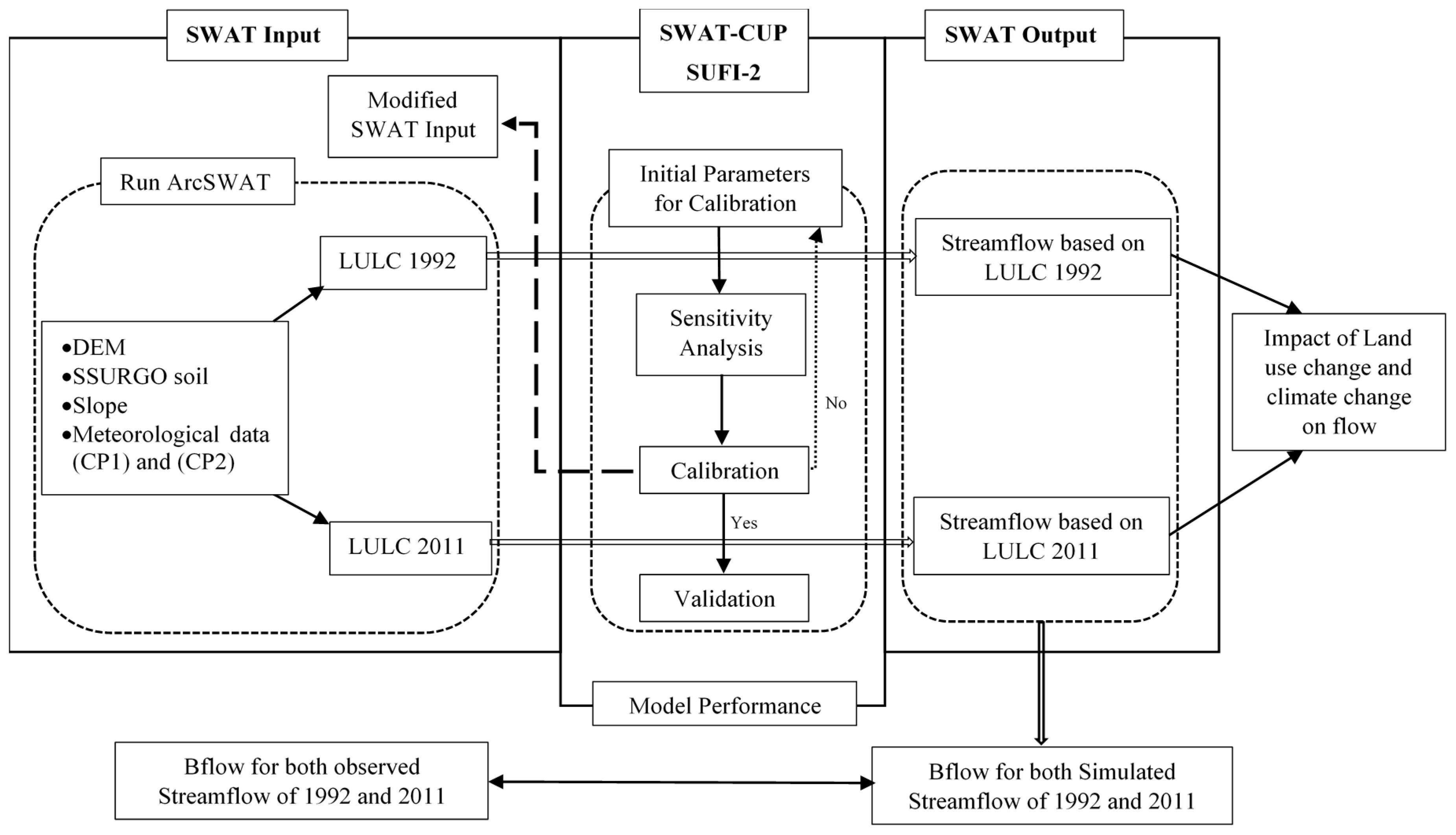
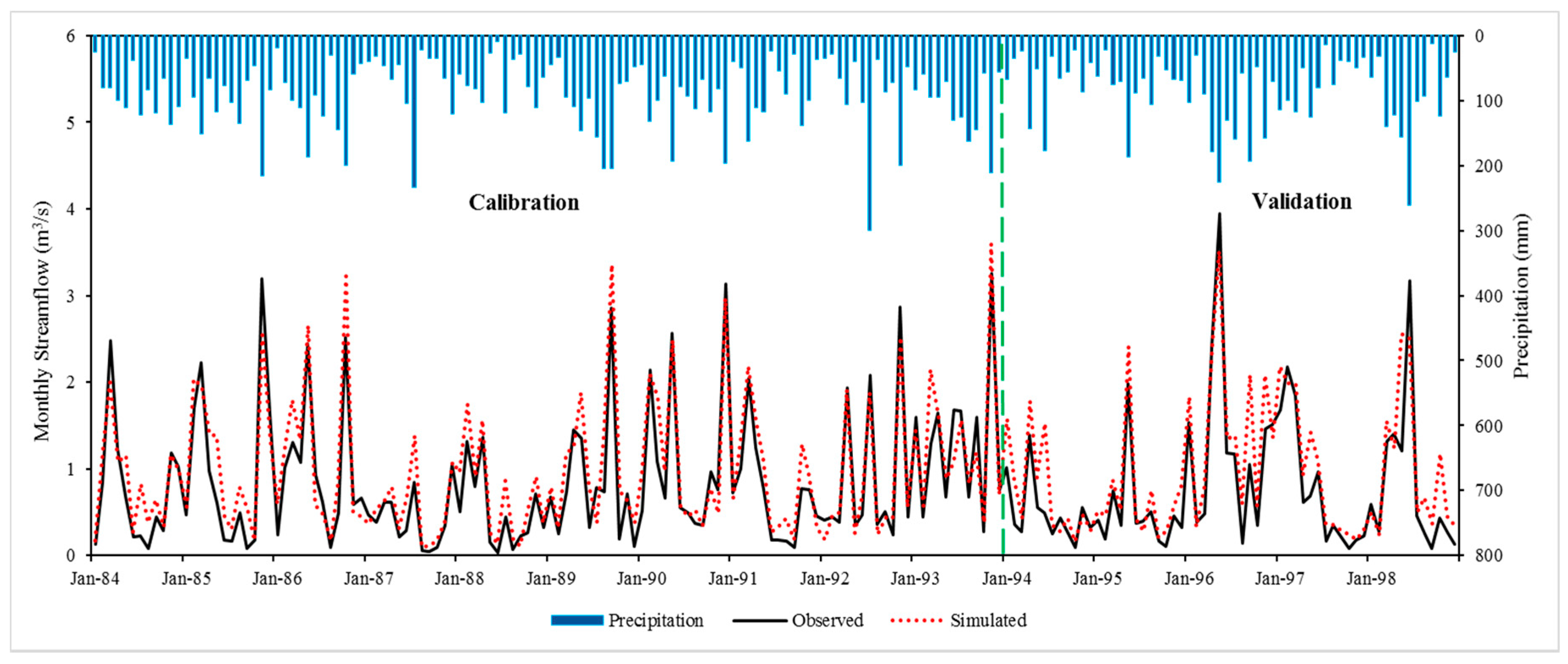
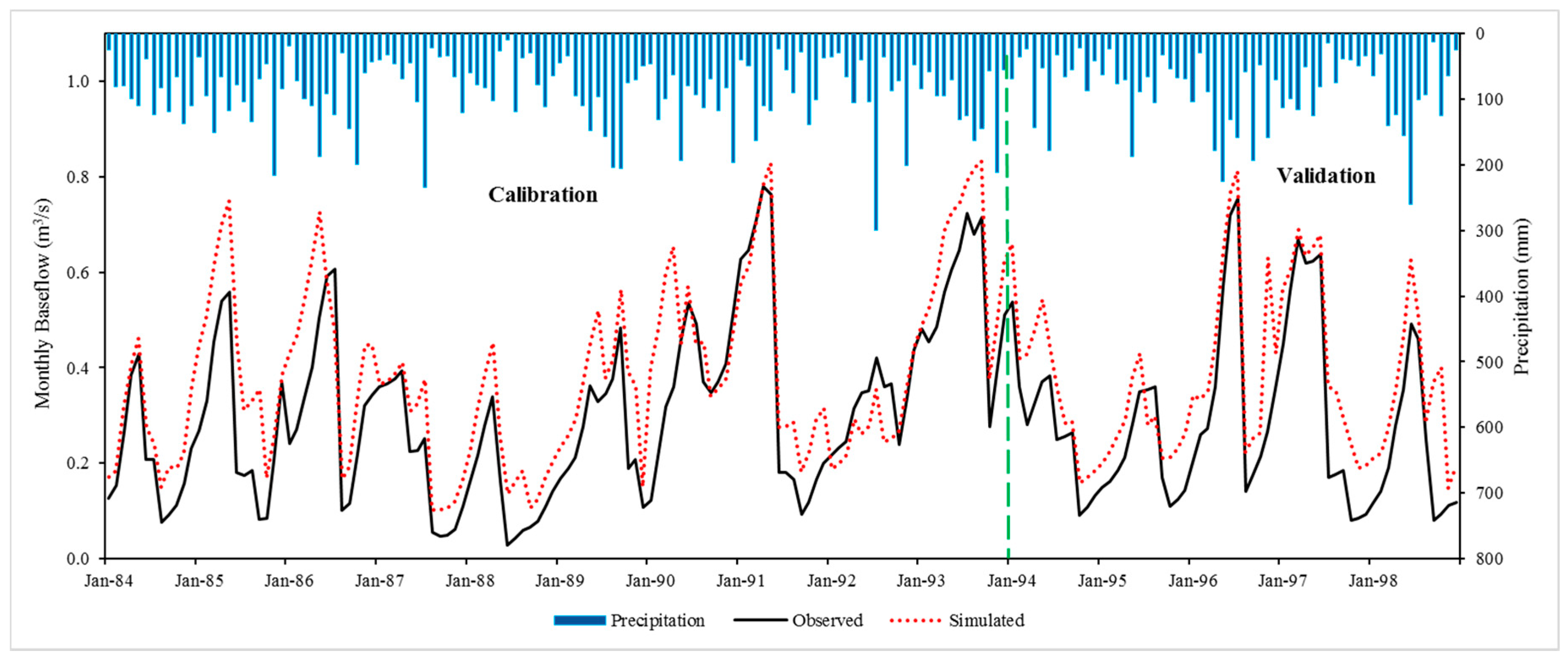
The long-term streamflow and baseflow response to land use change and climate variability were evaluated using the calibrated SWAT model. The model contained four scenarios in two periods, and applied two land use datasets (1992 and 2011) for the two climate periods (CP1 and CP2). By simulating the historical, continuous variation in streamflow, the SWAT model was calibrated and validated over the period 1980 to 1998 throughout the SUFI-2 approach within the SWAT-CUP interface. The SUFI-2 algorithm played an important role in minimizing the differences between measured and simulated streamflow in the LEC watershed. Discrepancies observed between the outputs of the model simulation and the observed data may in part occur due to the lack of meteorological input data from more than a single station. The SWAT model produced ‘very good’ and ‘good’ results for calibrating and validating observed streamflow and baseflow data. Hence, the calibrated parameters in this study can be used to carry out further future environmental and hydrological studies in similar watersheds. The hydrological balance assessment has shown that baseflow is a key component of the total discharge as it accounted for 36.5% of total flow within the LEC watershed. In general, SWAT proved versatile in modeling the effects of environmental changes in urban watersheds.
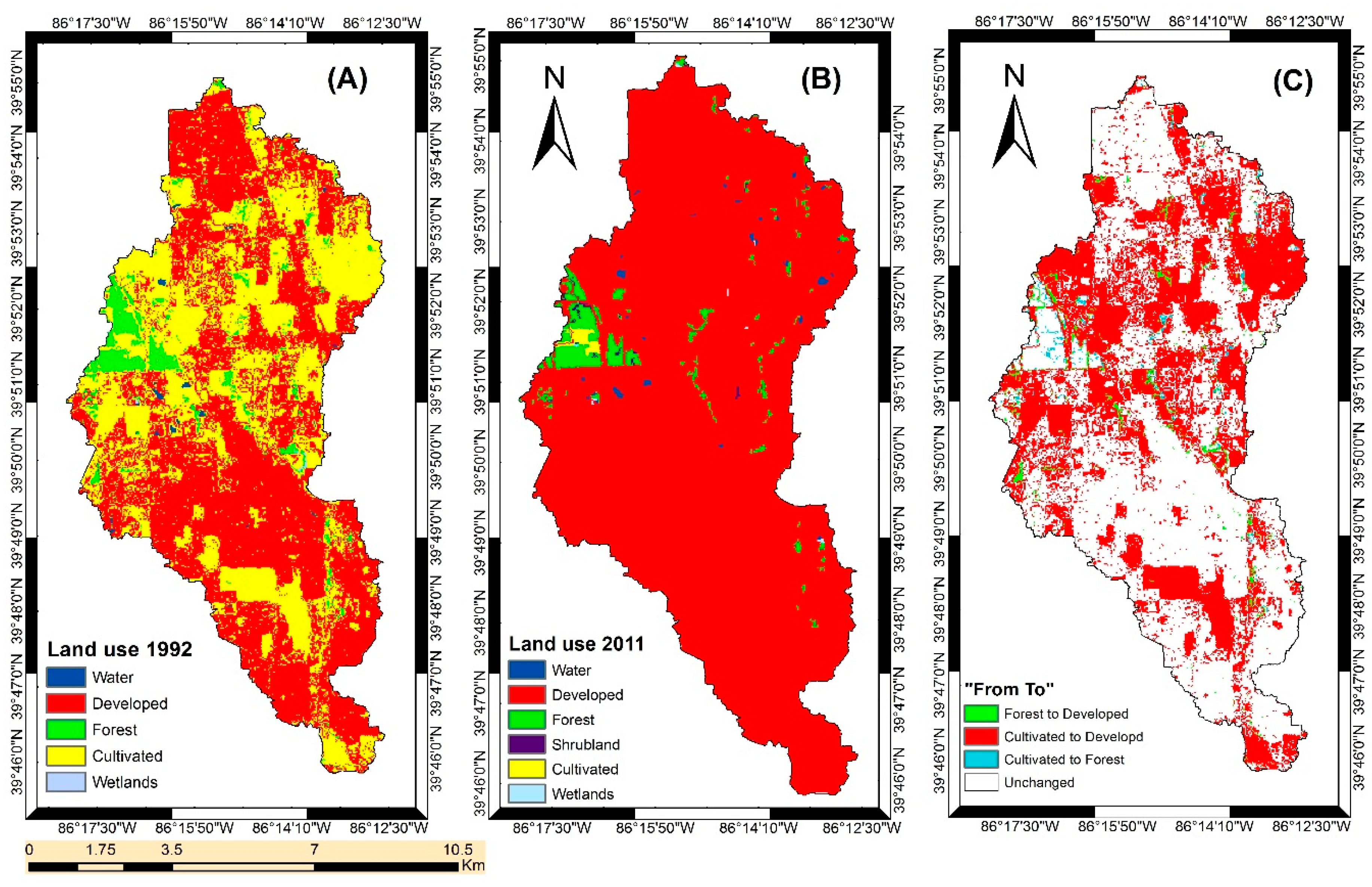
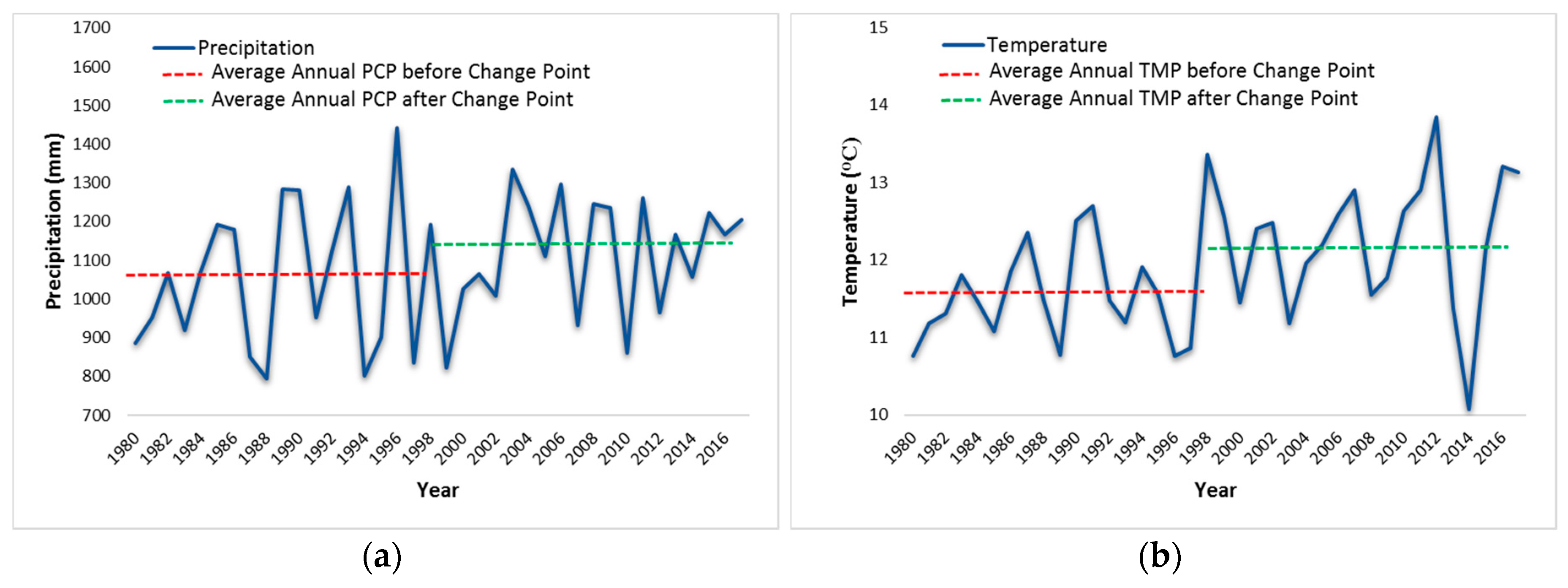
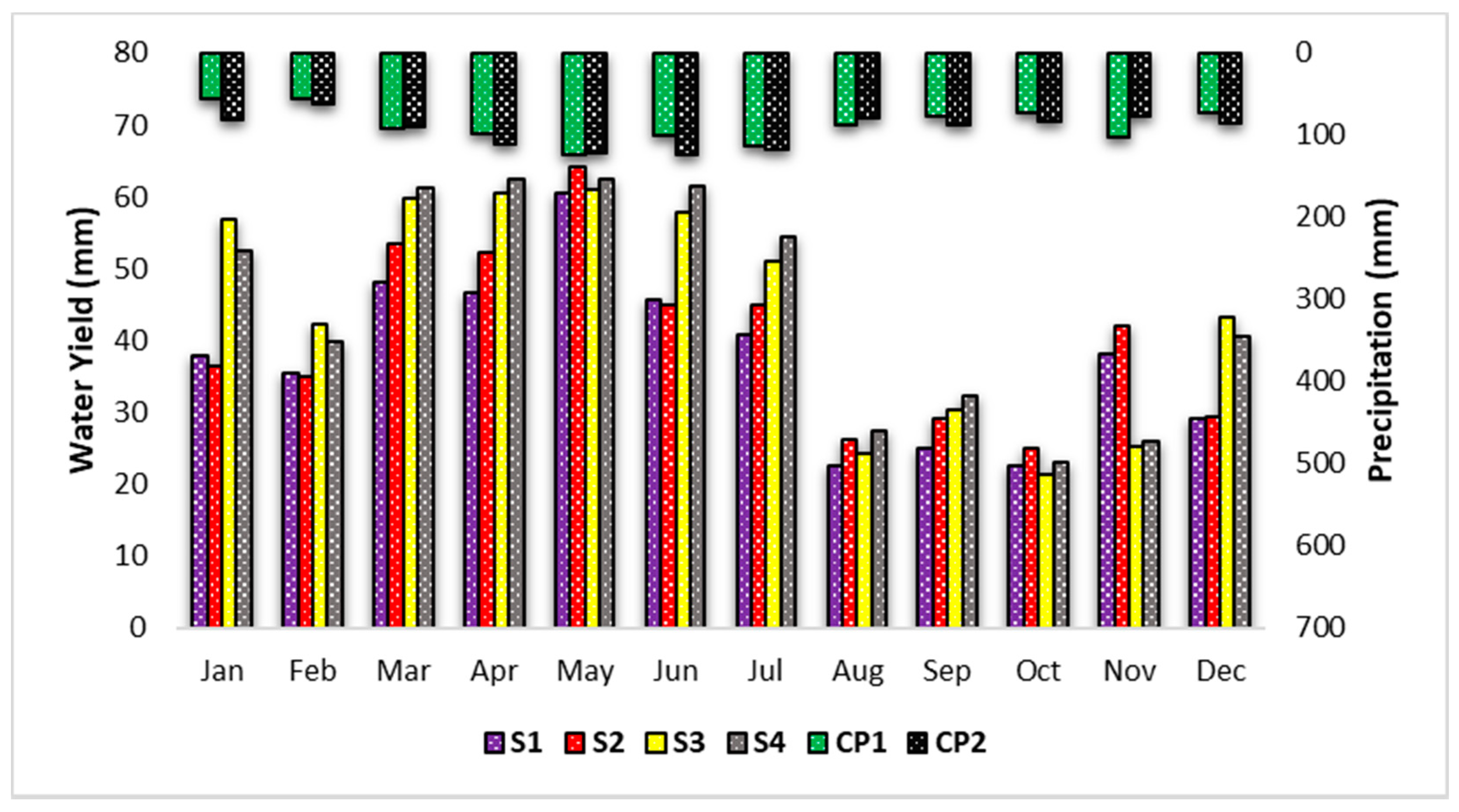
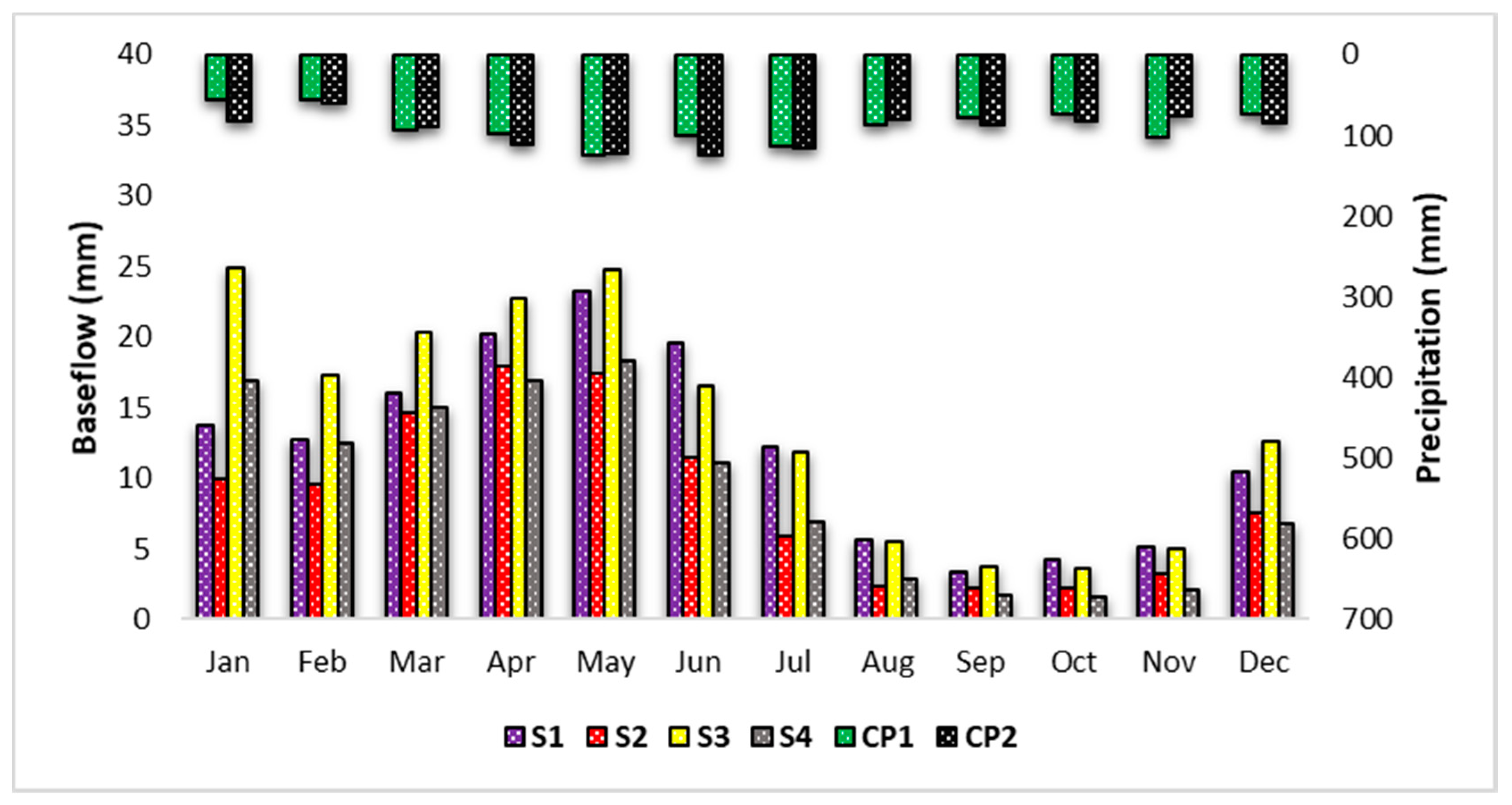
The model was used to explore likely impacts of urbanization and climate variation in an urban watershed. Much of the original cultivated and forest areas had already been converted to developed areas or urbanization. During the period of 1992–2011, about 39% of the LEC watershed area changed from cultivated to urban areas, while the climate became warmer and wetter. Overall, climate variability had the dominant impact on streamflow, while urban expansion influenced baseflow more significantly than climate change. Urbanization can be considered a major environmental stressor controlling hydrological components, including surface runoff, baseflow, and water yield in a catchment. Understanding the variation in streamflow and baseflow due to the separate and coupled effects of climate variation and land use dynamics is essential for sustainable management of water resources. The results gleaned from this study can be useful in providing information for management and planning of water resources, in addition to assessing the prospective impacts of adaptation measures to cope with climate variation, particularly in areas that are sensitive to climate variability and experiencing high urbanization.
The results obtained in this study must be interpreted carefully, with the caveat that the meteorological station records reflect data that are the result of the combined impacts of land use alteration and climate variability. Since these affects cannot be separated in this data, the predicted impact of climate variability alone on streamflow and baseflow may not be simulated accurately. Studies that focus on quantifying the effect of each land use category change on streamflow and baseflow are likely to yield useful additional insights on how climate variability and land use impact hydrological response separately. Furthermore, additional studies using catchments that exhibit different urbanization and climate regions could provide beneficial comparative results to determine the impacts of these variables on hydrological components.