Low-End Probabilistic Sea-Level Projections
Abstract
1. Introduction
2. Data
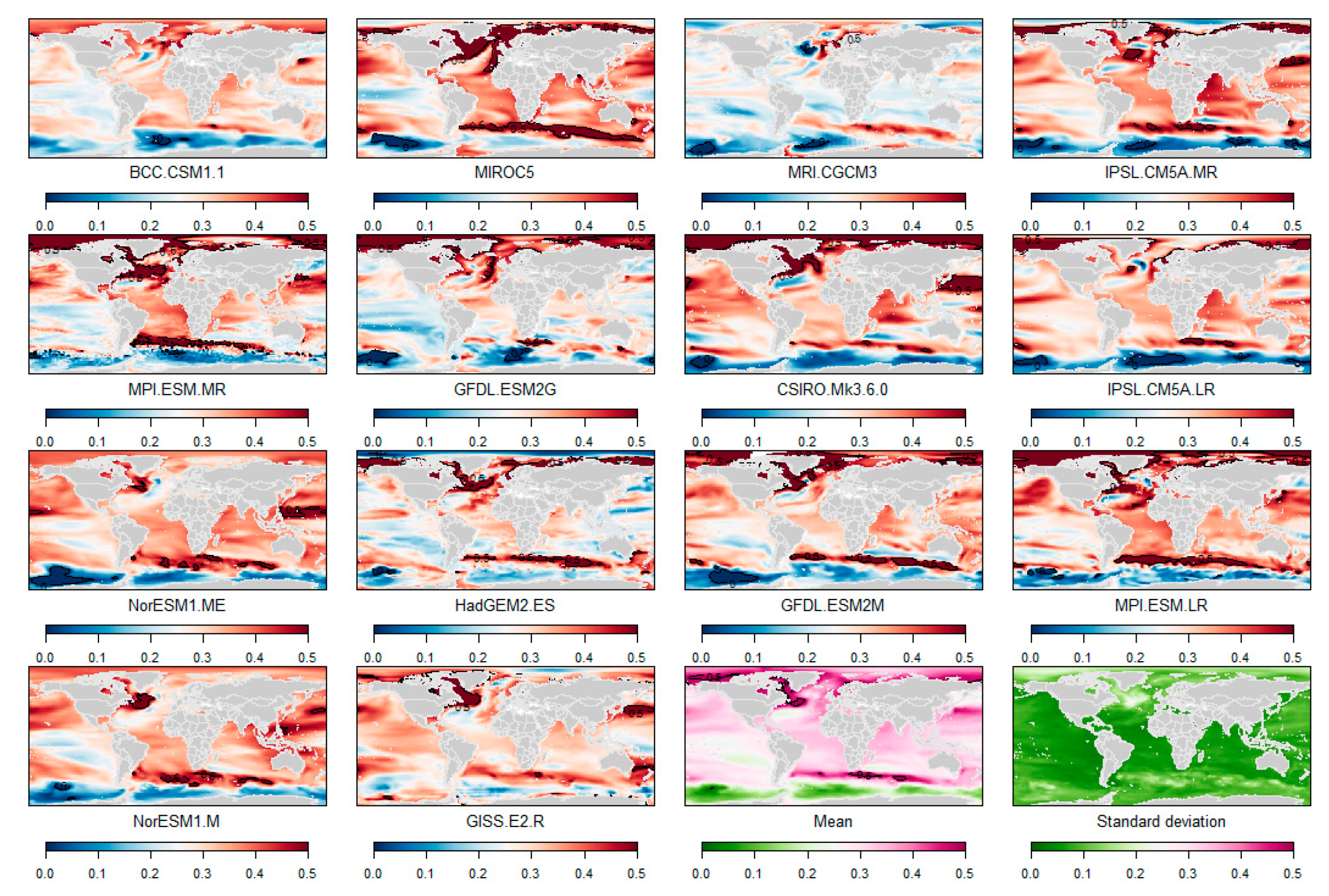
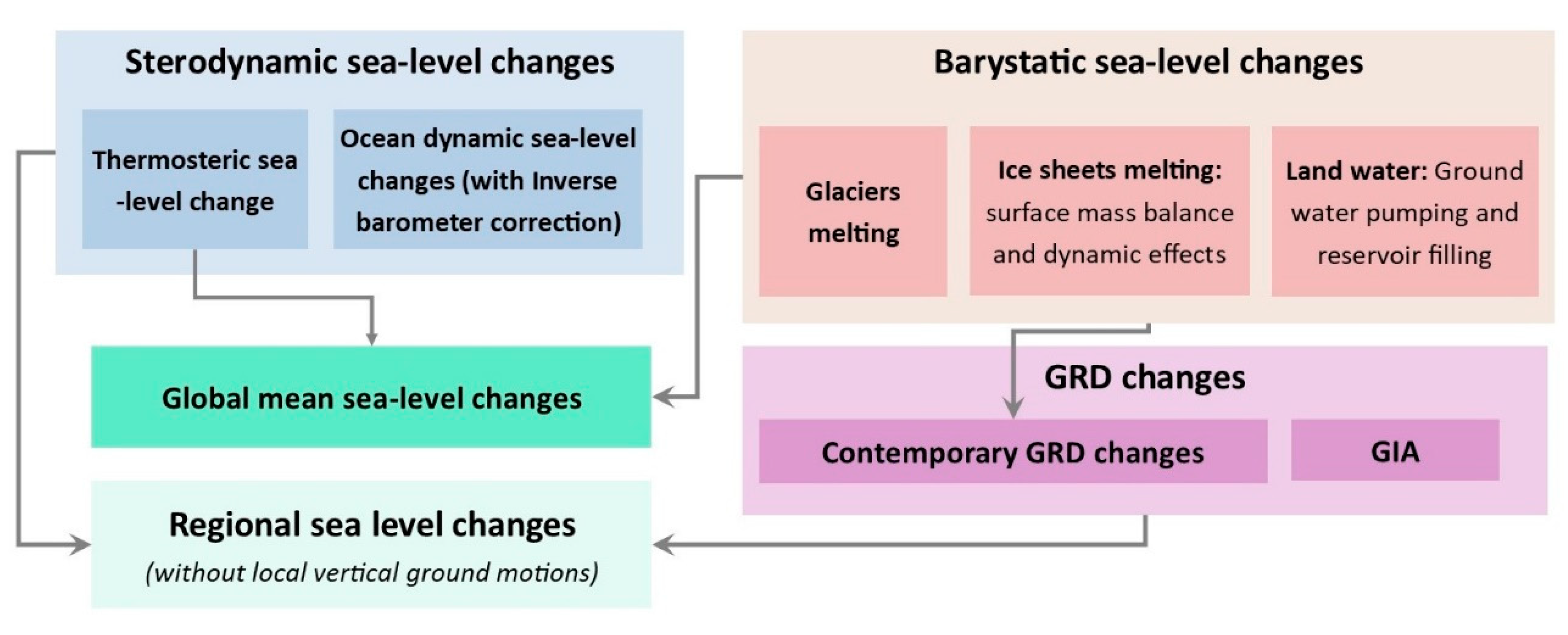
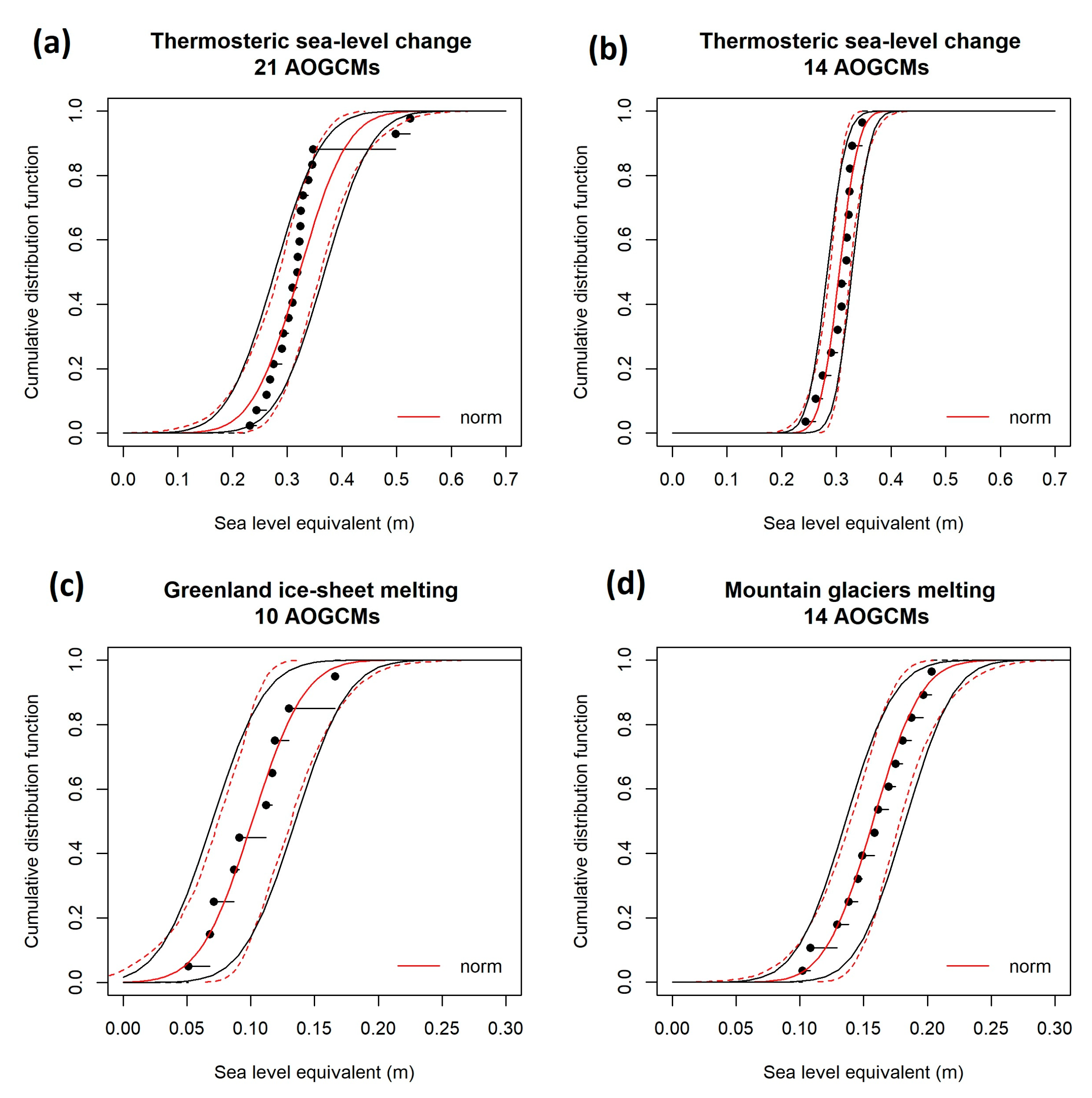
2.1. Sterodynamic Sea-Level Changes
2.2. Mountain Glaciers
2.3. Greenland
2.4. Antarctica
2.5. Land Water
2.6. Summary of Inputs
3. Methods
3.1. Integration: From Sea-Level Contributions to Global and Regional Sea-Level Scenarios
3.2. Probabilistic Distributions for Individual Components to Sea-Level Rise
3.3. Computational Approach and Statistical Dependencies
4. Results
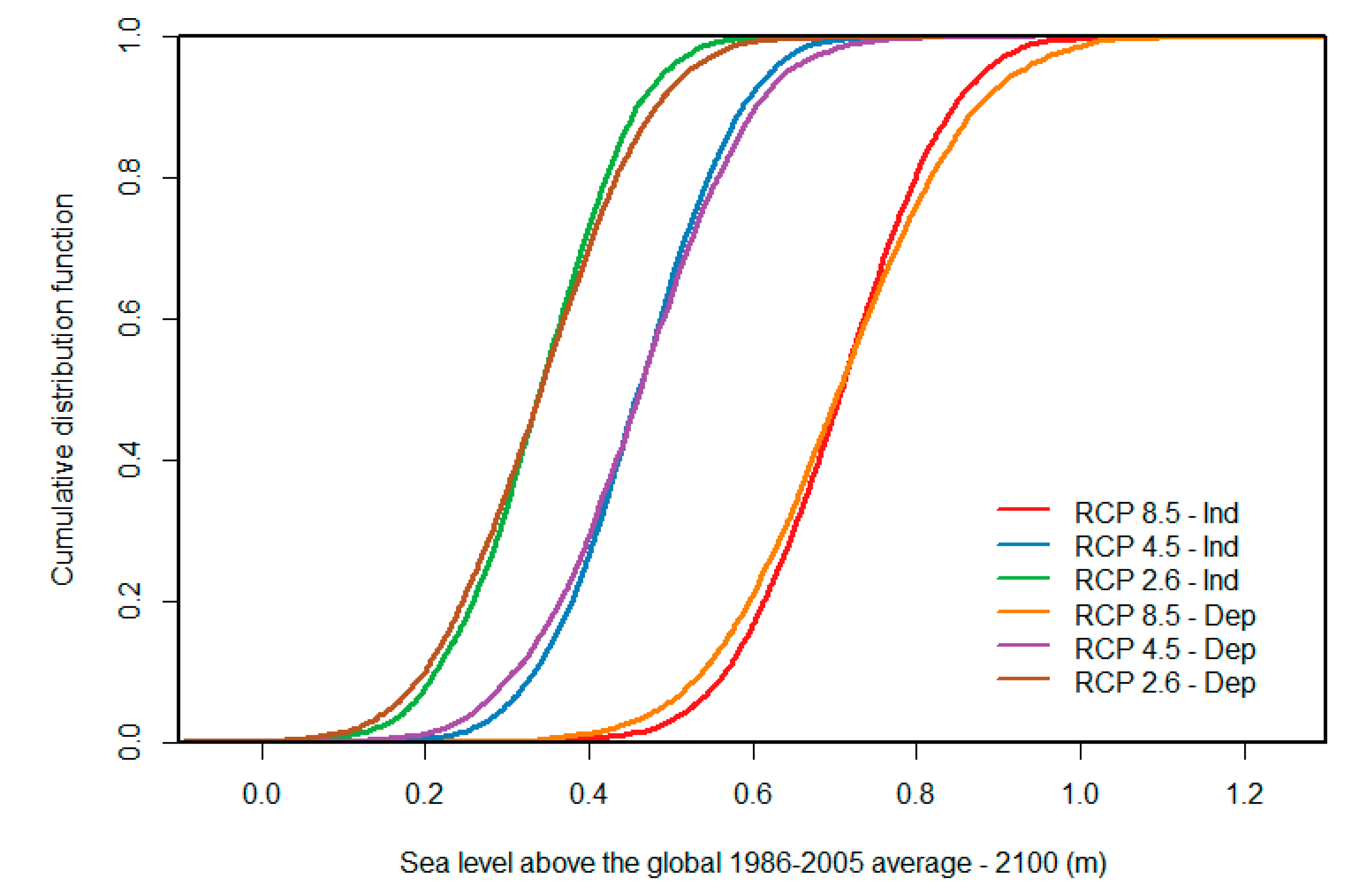
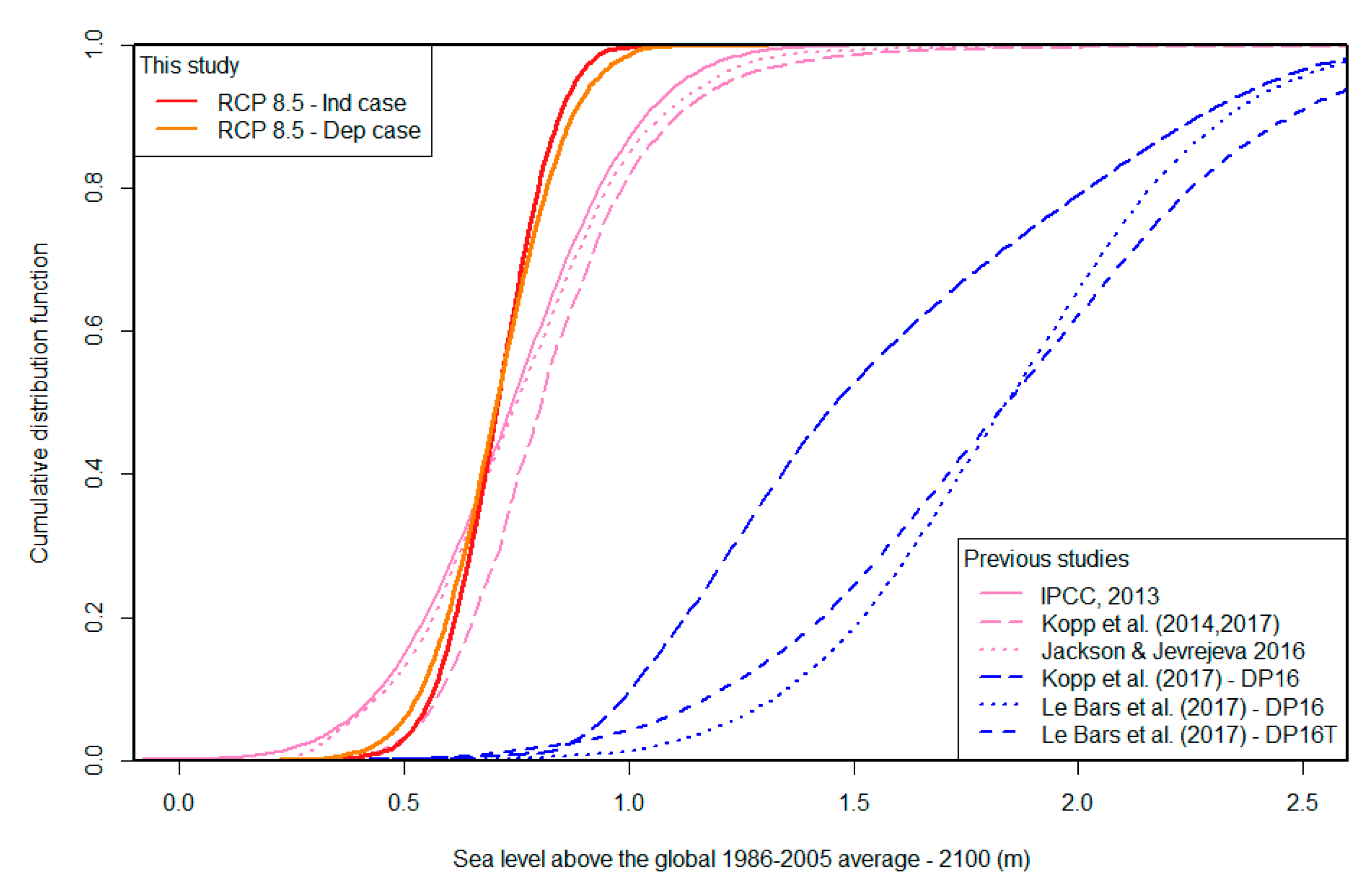
4.1. Global Probabilistic Sea-Level Projections
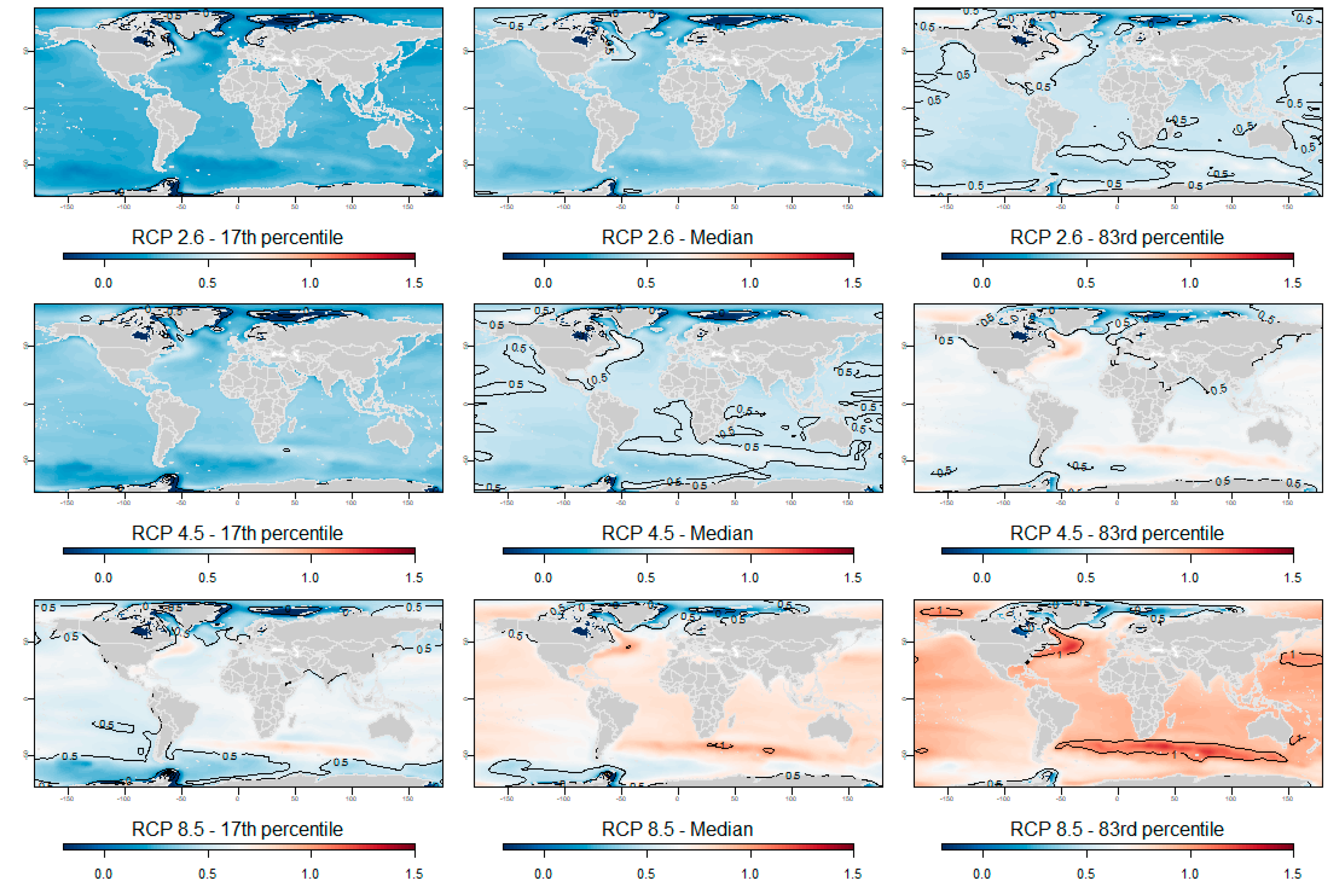
4.2. Regional Sea-Level Projections
5. Discussion and Conclusions
- (1)
- (2)
- For Antarctica, we relied on a study that probably underestimated the impact of ocean warming on the Antarctic marine ice-sheet melting, according to its own assessment [7];
- (3)
- For the sterodynamic sea-level changes, we removed AOGCMs giving high thermal expansion values; in the regional AR5 assessment, these outliers increased the mean and uncertainties of the thermal expansion.
- (4)
- We relied on modelling outcomes only, and ignored the procedure consisting of multiplying the standard deviation of model outcomes by 1.64 applied in the AR5; we argue that this procedure artificially extends the lower tail of the distribution of future sea-level rise, whereas AOGCMs have been essentially criticized so far for minimizing future sea-level changes.
- (5)
- We assumed full dependency among the sterodynamic, Mountain Glaciers, and Greenland melting components, which slightly shifts the lower tail of the probability distribution to the right compared to partial dependency schemes;
- (6)
- We did not find physical arguments supporting probabilistic projections below our projections in the published literature.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Sterodynamic Sea-Level Changes (2099, with Respect to 1986–2005)
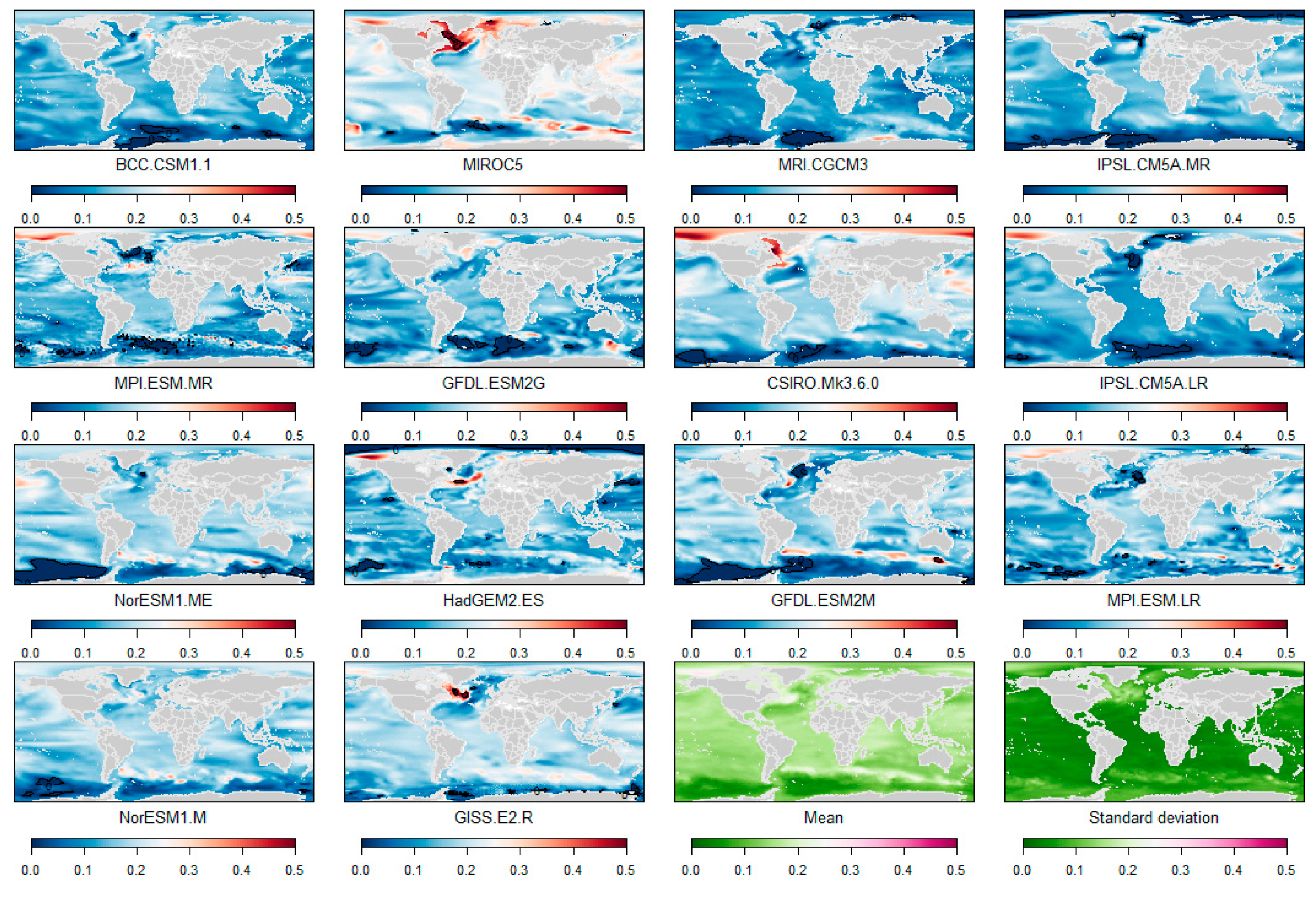
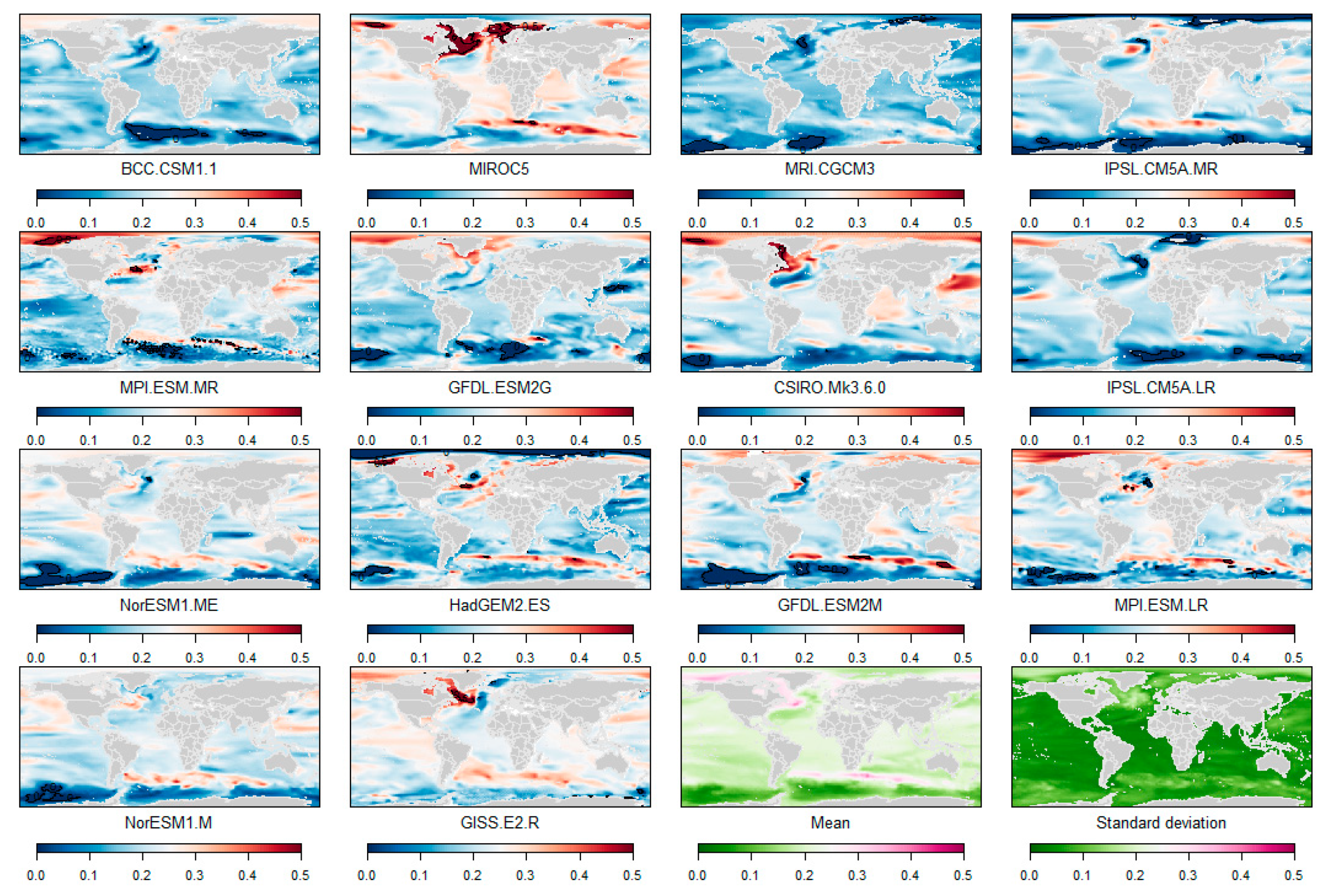
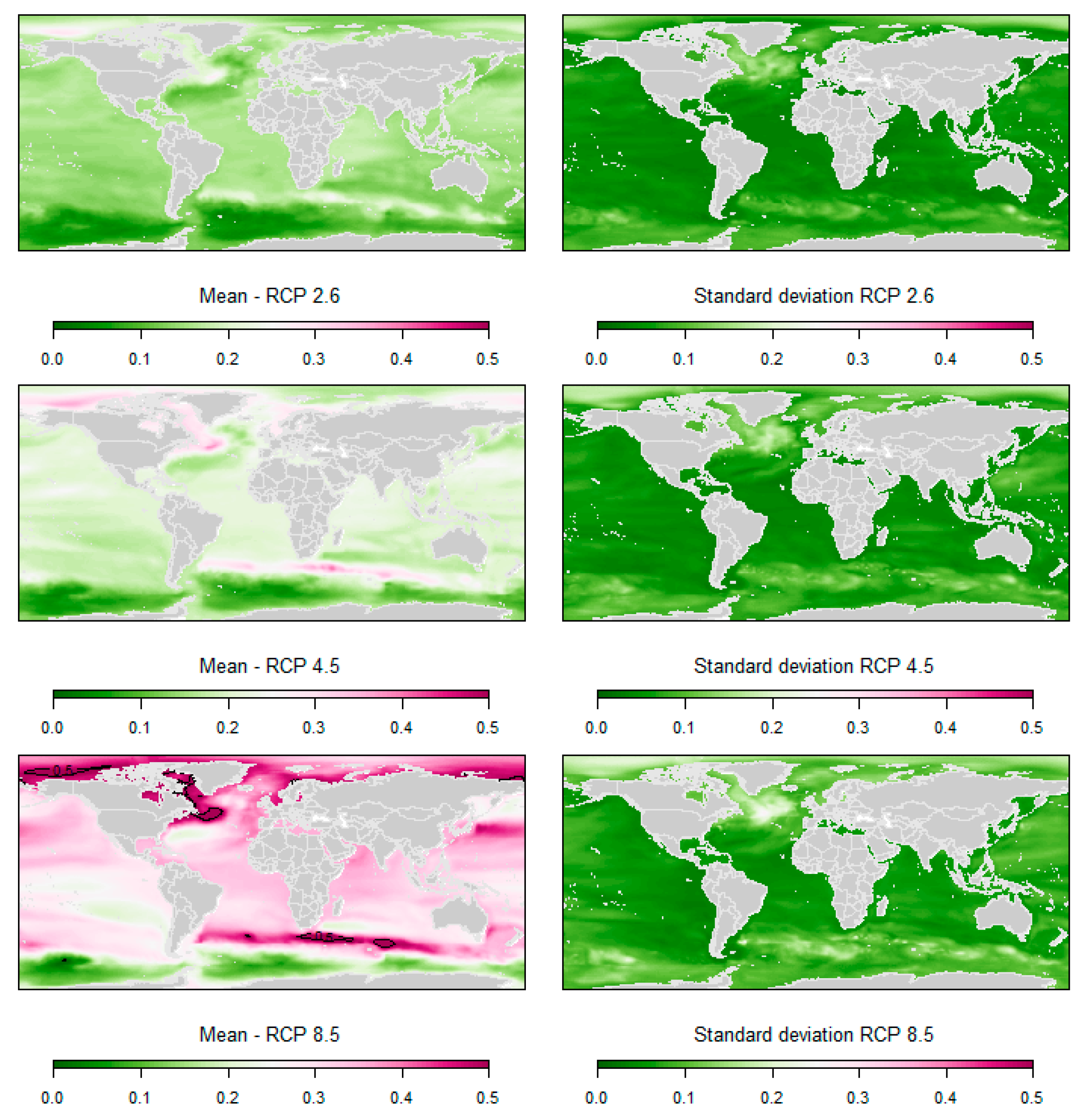
Appendix B. Regional 5th and 95th Percentiles of the Regional Low-End Sea-Level Projections
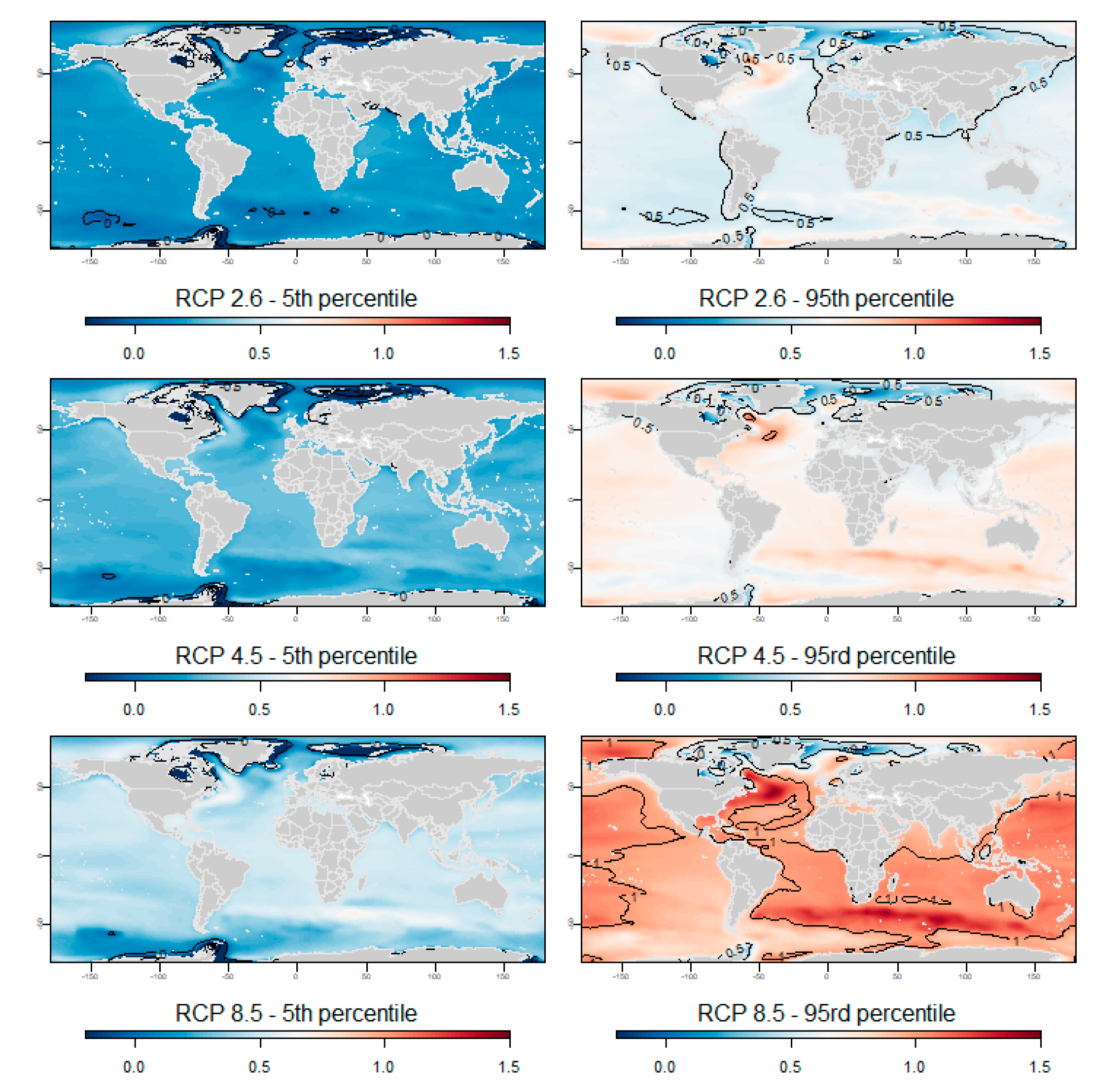
References
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Cazenave, A.; Llovel, W. Contemporary Sea Level Rise. Annu. Rev. Mar. Sci. 2010, 2, 145–173. [Google Scholar] [CrossRef] [PubMed]
- Stammer, D.; Cazenave, A.; Ponte, R.M.; Tamisiea, M.E. Causes for Contemporary Regional Sea Level Changes. Annu. Rev. Mar. Sci. 2013, 5, 21–46. [Google Scholar] [CrossRef] [PubMed]
- Little, C.M.; Horton, R.M.; Kopp, R.E.; Oppenheimer, M.; Yip, S. Uncertainty in Twenty-First-Century CMIP5 Sea Level Projections. J. Clim. 2015, 28, 838–852. [Google Scholar] [CrossRef]
- Rignot, E.; Mouginot, J.; Morlighem, M.; Seroussi, H.; Scheuchl, B. Widespread, rapid grounding line retreat of Pine Island, Thwaites, Smith, and Kohler glaciers, West Antarctica, from 1992 to 2011. Geophys. Res. Lett. 2014, 41, 3502–3509. [Google Scholar] [CrossRef]
- Ritz, C.; Edwards, T.L.; Durand, G.; Payne, A.J.; Peyaud, V.; Hindmarsh, R.C.A. Potential sea-level rise from Antarctic ice-sheet instability constrained by observations. Nature 2015, 528, 115–118. [Google Scholar] [CrossRef]
- Bulthuis, K.; Arnst, M.; Sun, S.; Pattyn, F. Uncertainty quantification of the multi-centennial response of the Antarctic ice sheet to climate change. Cryosphere 2019, 13, 1349–1380. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef]
- Marzeion, B.; Jarosch, A.H.; Hofer, M. Past and future sea-level change from the surface mass balance of glaciers. Cryosphere 2012, 6, 1295–1322. [Google Scholar] [CrossRef]
- Furst, J.J.; Goelzer, H.; Huybrechts, P. Ice-dynamic projections of the Greenland ice sheet in response to atmospheric and oceanic warming. Cryosphere 2015, 9, 1039–1062. [Google Scholar] [CrossRef]
- Palerme, C.; Genthon, C.; Claud, C.; Kay, J.E.; Wood, N.B.; L‘Ecuyer, T. Evaluation of current and projected Antarctic precipitation in CMIP5 models. Clim. Dyn. 2017, 48, 225–239. [Google Scholar] [CrossRef]
- Frieler, K.; Clark, P.U.; He, F.; Buizert, C.; Reese, R.; Ligtenberg, S.R.M.; Van den Broeke, M.R.; Winkelmann, R.; Levermann, A. Consistent evidence of increasing Antarctic accumulation with warming. Nat. Clim. Chang. 2015, 5, 348–352. [Google Scholar] [CrossRef]
- Rignot, E.; Casassa, G.; Gogineni, P.; Krabill, W.; Rivera, A.; Thomas, R. Accelerated ice discharge from the Antarctic Peninsula following the collapse of Larsen B ice shelf. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Llovel, W.; Becker, M.; Cazenave, A.; Jevrejeva, S.; Alkama, R.; Decharme, B.; Douville, H.; Ablain, M.; Beckley, B. Terrestrial waters and sea level variations on interannual time scale. Glob. Planet. Chang. 2011, 75, 76–82. [Google Scholar] [CrossRef]
- Wada, Y.; Van Beek, L.P.H.; Weiland, F.C.S.; Chao, B.F.; Wu, Y.H.; Bierkens, M.F.P. Past and future contribution of global groundwater depletion to sea-level rise. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Meyssignac, B.; Slangen, A.B.A.; Melet, A.; Church, J.A.; Fettweis, X.; Marzeion, B.; Agosta, C.; Ligtenberg, S.R.M.; Spada, G.; Richter, K.; et al. Evaluating Model Simulations of Twentieth-Century Sea-Level Rise. Part II: Regional Sea-Level Changes. J. Clim. 2017, 30, 8565–8593. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Katsman, C.A.; Van de Wal, R.S.W.; Vermeersen, L.L.A.; Riva, R.E.M. Towards regional projections of twenty-first century sea-level change based on IPCC SRES scenarios. Clim. Dyn. 2012, 38, 1191–1209. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Carson, M.; Katsman, C.A.; Van de Wal, R.S.W.; Kohl, A.; Vermeersen, L.L.A.; Stammer, D. Projecting twenty-first century regional sea-level changes. Clim. Chang. 2014, 124, 317–332. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.J.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earths Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
- Peltier, W.R. Global glacial isostasy and the surface of the ice-age earth: The ice-5G (VM2) model and grace. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Idier, D.; Paris, F.; Le Cozannet, G.; Boulahya, F.; Dumas, F. Sea-level rise impacts on the tides of the European Shelf. Cont. Shelf Res. 2017, 137, 56–71. [Google Scholar] [CrossRef]
- Melet, A.; Meyssignac, B.; Almar, R.; Le Cozannet, G. Under-estimated wave contribution to coastal sea-level rise. Nat. Clim. Chang. 2018, 8, 234–239. [Google Scholar] [CrossRef]
- Zhang, X.B.; Church, J.A.; Monselesan, D.; McInnes, K.L. Sea level projections for the Australian region in the 21st century. Geophys. Res. Lett. 2017, 44, 8481–8491. [Google Scholar] [CrossRef]
- Poitevin, C.; Woppelmann, G.; Raucoules, D.; Le Cozannet, G.; Marcos, M.; Testut, L. Vertical land motion and relative sea level changes along the coastline of Brest (France) from combined space-borne geodetic methods. Remote Sens. Environ. 2019, 222, 275–285. [Google Scholar] [CrossRef]
- Woppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef]
- De Winter, R.C.; Reerink, T.J.; Slangen, A.B.A.; De Vries, H.; Edwards, T.; Van de Wal, R.S.W. Impact of asymmetric uncertainties in ice sheet dynamics on regional sea level projections. Nat. Hazards Earth Syst. Sci. 2017, 17, 2125–2141. [Google Scholar] [CrossRef]
- Carson, M.; Kohl, A.; Stammer, D.; Slangen, A.B.A.; Katsman, C.A.; Van de Wal, R.S.W.; Church, J.; White, N. Coastal sea level changes, observed and projected during the 20th and 21st century. Clim. Chang. 2016, 134, 269–281. [Google Scholar] [CrossRef]
- Jackson, L.P.; Grinsted, A.; Jevrejeva, S. 21st Century Sea-Level Rise in Line with the Paris Accord. Earths Future 2018, 6, 213–229. [Google Scholar] [CrossRef]
- Le Bars, D.; Drijfhout, S.; De Vries, H. A high-end sea level rise probabilistic projection including rapid Antarctic ice sheet mass loss. Environ. Res. Lett. 2017, 12. [Google Scholar] [CrossRef]
- Garner, A.J.; Weiss, J.L.; Parris, A.; Kopp, R.E.; Horton, R.M.; Overpeck, J.T.; Horton, B.P. Evolution of 21st Century Sea Level Rise Projections. Earths Future 2018, 6, 1603–1615. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Adloff, F.; Jevrejeva, S.; Leclercq, P.W.; Marzeion, B.; Wada, Y.; Winkelmann, R. A Review of Recent Updates of Sea-Level Projections at Global and Regional Scales. Surv. Geophys. 2017, 38, 385–406. [Google Scholar] [CrossRef]
- Clark, P.U.; Shakun, J.D.; Marcott, S.A.; Mix, A.C.; Eby, M.; Kulp, S.; Levermann, A.; Milne, G.A.; Pfister, P.L.; Santer, B.D.; et al. Consequences of twenty-first-century policy for multi-millennial climate and sea-level change. Nat. Clim. Chang. 2016, 6, 360–369. [Google Scholar] [CrossRef]
- DeConto, R.M.; Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 2016, 531, 591–597. [Google Scholar] [CrossRef] [PubMed]
- Edwards, T.L.; Brandon, M.A.; Durand, G.; Edwards, N.R.; Golledge, N.R.; Holden, P.B.; Nias, I.J.; Payne, A.J.; Ritz, C.; Wernecke, A. Revisiting Antarctic ice loss due to marine ice-cliff instability. Nature 2019, 566, 58–64. [Google Scholar] [CrossRef] [PubMed]
- Le Bars, D. Uncertainty in Sea Level Rise Projections Due to the Dependence Between Contributors. Earths Future 2018, 6, 1275–1291. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Manceau, J.C.; Rohmer, J. Bounding probabilistic sea-level projections within the framework of the possibility theory. Environ. Res. Lett. 2017, 12. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Hanson, S.E.; Lowe, J.A.; Warrick, R.A.; Lu, X.F.; Long, A.J. Sea-level scenarios for evaluating coastal impacts. Wiley Interdiscip. Rev. Clim. Chang. 2014, 5, 129–150. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Nicholls, R.J.; Hinkel, J.; Sweet, W.V.; McInnes, K.L.; Van de Wal, R.S.W.; Slangen, A.B.A.; Lowe, J.A.; White, K.D. Sea Level Change and Coastal Climate Services: The Way Forward. J. Mar. Sci. Eng. 2017, 5, 49. [Google Scholar] [CrossRef]
- Hinkel, J.; Church, J.A.; Gregory, J.M.; Lambert, E.; Le Cozannet, G.; Lowe, J.; McInnes, K.L.; Nicholls, R.J.; Van der Pol, T.D.; Van de Wal, R. Meeting User Needs for Sea Level Rise Information: A Decision Analysis Perspective. Earths Future 2019, 7, 320–337. [Google Scholar] [CrossRef]
- Stammer, D.; Van de Wal, R.S.W.; Nicholls, R.J.; Church, J.A.; Le Cozannet, G.; Lowe, J.A.; Horton, B.P.; White, K.; Behar, D.; Hinkel, J. Framework for high-end estimates of sea-level rise for stakeholder applications. Earths Future 2019. [Google Scholar] [CrossRef]
- Huss, M.; Hock, R. A new model for global glacier change and sea-level rise. Front. Earth Sci. 2015, 3, 54. [Google Scholar] [CrossRef]
- Gregory, J.M.; Griffies, S.M.; Hughes, C.W.; Lowe, J.A.; Church, J.A.; Fukimori, I.; Gomez, N.; Kopp, R.E.; Landerer, F.; Le Cozannet, G.; et al. Concepts and Terminology for Sea Level: Mean, Variability and Change, Both Local and Global. Surv. Geophys. 2019, 1–39. [Google Scholar] [CrossRef]
- Chambers, J.M.; Cleveland, W.S.; Kleiner, B.; Tukey, P.A. Graphical Methods for Data Analysis; Chapman and Hall/CRC: London, UK, 1983; Volume 21. [Google Scholar]
- Yin, J.J.; Schlesinger, M.E.; Stouffer, R.J. Model projections of rapid sea-level rise on the northeast coast of the United States. Nat. Geosci. 2009, 2, 262–266. [Google Scholar] [CrossRef]
- Jackson, L.P.; Jevrejeva, S. A probabilistic approach to 21st century regional sea-level projections using RCP and High-end scenarios. Glob. Planet. Chang. 2016, 146, 179–189. [Google Scholar] [CrossRef]
- Kopp, R.E.; DeConto, R.M.; Bader, D.A.; Hay, C.C.; Horton, R.M.; Kulp, S.; Oppenheimer, M.; Pollard, D.; Strauss, B.H. Evolving Understanding of Antarctic Ice-Sheet Physics and Ambiguity in Probabilistic Sea-Level Projections. Earths Future 2017, 5, 1217–1233. [Google Scholar] [CrossRef]
- Radic, V.; Bliss, A.; Beedlow, A.C.; Hock, R.; Miles, E.; Cogley, J.G. Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim. Dyn. 2014, 42, 37–58. [Google Scholar] [CrossRef]
- Shannon, S.; Smith, R.; Wiltshire, A.; Payne, T.; Huss, M.; Betts, R.; Caesar, J.; Koutroulis, A.; Jones, D.; Harrison, S. Global glacier volume projections under high-end climate change scenarios. Cryosphere 2019, 13, 325–350. [Google Scholar] [CrossRef]
- Hirabayashi, Y.; Zang, Y.; Watanabe, S.; Koirala, S.; Kanae, S. Projection of glacier mass changes under a high-emission climate scenario using the global glacier model HYOGA2. Hydrol. Res. Lett. 2013, 7, 6–11. [Google Scholar] [CrossRef]
- Cazenave, A.; Meyssignac, B.; Ablain, M.; Balmaseda, M.; Bamber, J.; Barletta, V.; Beckley, B.; Benveniste, J.; Berthier, E.; Blazquez, A.; et al. Global sea-level budget 1993-present. Earth Syst. Sci. Data 2018, 10, 1551–1590. [Google Scholar] [CrossRef]
- Bamber, J.L.; Aspinall, W.P. An expert judgement assessment of future sea level rise from the ice sheets. Nat. Clim. Chang. 2013, 3, 424–427. [Google Scholar] [CrossRef]
- Calov, R.; Beyer, S.; Greve, R.; Beckmann, J.; Willeit, M.; Kleiner, T.; Ruckamp, M.; Humbert, A.; Ganopolski, A. Simulation of the future sea level contribution of Greenland with a new glacial system model. Cryosphere 2018, 12, 3097–3121. [Google Scholar] [CrossRef]
- Hanna, E.; Fettweis, X.; Hall, R.J. Brief communication: Recent changes in summer Greenland blocking captured by none of the CMIP5 models. Cryosphere 2018, 12, 3287–3292. [Google Scholar] [CrossRef]
- Shepherd, A.; Ivins, E.R.; Geruo, A.; Barletta, V.R.; Bentley, M.J.; Bettadpur, S.; Briggs, K.H.; Bromwich, D.H.; Forsberg, R.; Galin, N.; et al. A Reconciled Estimate of Ice-Sheet Mass Balance. Science 2012, 338, 1183–1189. [Google Scholar] [CrossRef]
- Dieng, H.B.; Cazenave, A.; Meyssignac, B.; Ablain, M. New estimate of the current rate of sea level rise from a sea level budget approach. Geophys. Res. Lett. 2017, 44, 3744–3751. [Google Scholar] [CrossRef]
- Pattyn, F. Sea-level response to melting of Antarctic ice shelves on multi-centennial timescales with the fast Elementary Thermomechanical Ice Sheet model (f.ETISh v1.0). Cryosphere 2017, 22, 1851–1878. [Google Scholar] [CrossRef]
- Golledge, N.R.; Kowalewski, D.E.; Naish, T.R.; Levy, R.H.; Fogwill, C.J.; Gasson, E.G.W. The multi-millennial Antarctic commitment to future sea-level rise. Nature 2015, 526, 421–425. [Google Scholar] [CrossRef]
- Schlegel, N.J.; Seroussi, H.; Schodlok, M.P.; Larour, E.Y.; Boening, C.; Limonadi, D.; Watkins, M.M.; Morlighem, M.; Van den Broeke, M.R. Exploration of Antarctic Ice Sheet 100-year contribution to sea level rise and associated model uncertainties using the ISSM framework. Cryosphere 2018, 12, 3511–3534. [Google Scholar] [CrossRef]
- Lemperiere, F.; Lafitte, R. The role of dams in the XXI Century to achieve a sustainable development target. In Proceedings of the International Symposium on Dams in the Societies of the 21st Century, Barcelona, Spain, 18–23 June 2006; pp. 1065–1072. [Google Scholar]
- Gzyl, H. The method of maximum entropy. In Series on Advances in Mathematics for Applied Sciences; Bellomo, F., Brezzi, N., Eds.; World Scientific Publishing Co.: Singapore, 1995; Volume 29, p. 160. [Google Scholar]
- Mishra, S. Assigning Probability Distributions to Input Parameters of Performance Assessment Models; INTERA Inc.: Austin, TX, USA, 2002. [Google Scholar]
- Meyssignac, B.; Fettweis, X.; Chevrier, R.; Spada, G. Regional Sea Level Changes for the Twentieth and the Twenty-First Centuries Induced by the Regional Variability in Greenland Ice Sheet Surface Mass Loss. J. Clim. 2017, 30, 2011–2028. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Foster, G.; Cazenave, A. Comparing climate projections to observations up to 2011. Environ. Res. Lett. 2012, 7. [Google Scholar] [CrossRef]
- Fettweis, X.; Franco, B.; Tedesco, M.; Van Angelen, J.H.; Lenaerts, J.T.M.; Van den Broeke, M.R.; Gallee, H. Estimating the Greenland ice sheet surface mass balance contribution to future sea level rise using the regional atmospheric climate model MAR. Cryosphere 2013, 7, 469–489. [Google Scholar] [CrossRef]
- Slater, T.; Shepherd, A. Antarctic ice losses tracking high. Nat. Clim. Chang. 2018, 8, 1025–1026. [Google Scholar] [CrossRef]
- Tietjen, G.L.; Moore, R.H. Some Grubbs-Type Statistics for the Detection of Several Outliers. Technometrics 1972, 14, 583–597. [Google Scholar] [CrossRef]
- Wilks, S.S. Determination of sample sizes for setting tolerance limits. Ann. Math. Stat. 1941, 12, 91–96. [Google Scholar] [CrossRef]
- Rohmer, J.; Manceau, J.; Guyonnet, D.; Boulahya, F. HyRisk: Hybrid Methods for Addressing Uncertainty in Risk Assessments. 2017. Available online: https://cran.r-project.org/web/packages/HYRISK/index.html (accessed on 19 July 2019).
- Bratley, P.; Fox, B. ALGORITHM 659 Implementing Sobol‘s Quasirandom Sequence Generator. ACM Trans. Math. Softw. 1988, 14, 88–100. [Google Scholar] [CrossRef]
- Hay, C.C.; Morrow, E.; Kopp, R.E.; Mitrovica, J.X. Probabilistic reanalysis of twentieth-century sea-level rise. Nature 2015, 517, 481–484. [Google Scholar] [CrossRef]
- Dangendorf, S.; Marcos, M.; Woppelmann, G.; Conrad, C.P.; Frederikse, T.; Riva, R. Reassessment of 20th century global mean sea level rise. Proc. Natl. Acad. Sci. USA 2017, 114, 5946–5951. [Google Scholar] [CrossRef]
- Chen, X.Y.; Zhang, X.B.; Church, J.A.; Watson, C.S.; King, M.A.; Monselesan, D.; Legresy, B.; Harig, C. The increasing rate of global mean sea-level rise during 1993–2014. Nat. Clim. Chang. 2017, 7, 492–495. [Google Scholar] [CrossRef]
- Riahi, K.; Van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O‘Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. Hum. Policy Dimens. 2017, 42, 153–168. [Google Scholar] [CrossRef]
- Perrette, M.; Landerer, F.; Riva, R.; Frieler, K.; Meinshausen, M. A scaling approach to project regional sea level rise and its uncertainties. Earth Syst. Dyn. 2013, 4, 11–29. [Google Scholar] [CrossRef]
- Rockström, J.; Gaffney, O.; Rogelj, J.; Meinshausen, M.; Nakicenovic, N.; Schellnhuber, H.J. A roadmap for rapid decarbonization. Science 2017, 355, 1269–1271. [Google Scholar] [CrossRef]
- Iyer, G.C.; Edmonds, J.A.; Fawcett, A.A.; Hultman, N.E.; Alsalam, J.; Asrar, G.R.; Calvin, K.V.; Clarke, L.E.; Creason, J.; Jeong, M.; et al. The contribution of Paris to limit global warming to 2 degrees C. Environ. Res. Lett. 2015, 10, 10. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea-Level Rise and Its Impact on Coastal Zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Nachmany, M.; Mangan, E. Aligning National and International Climate Targets. 2018. Available online: http://www.lse.ac.uk/GranthamInstitute/publication/targets/ (accessed on 19 July 2019).
- Idier, D.; Bertin, X.; Thompson, P.; Pickering, M.D. Interactions Between Mean Sea Level, Tide, Surge, Waves and Flooding: Mechanisms and Contributions to Sea Level Variations at the Coast. Surv. Geophys. 2019. [Google Scholar] [CrossRef]
- Haigh, I.; Green, M.; Pickering, M.; Arbic, B.; Arns, A.; Dangendorf, S.; Hill, D.; Horsburgh, K.; Howard, T.; Idier, D.; et al. The Tides They Are a-Changin. Rev. Geophys. 2019. [Google Scholar]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 2018, 9, 2360. [Google Scholar] [CrossRef]
- Han, W.Q.; Meehl, G.A.; Stammer, D.; Hu, A.X.; Hamlington, B.; Kenigson, J.; Palanisamy, H.; Thompson, P. Spatial Patterns of Sea Level Variability Associated with Natural Internal Climate Modes. Surv. Geophys. 2017, 38, 217–250. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Marinova, N.; Lowe, J.A.; Brown, S.; Vellinga, P.; De Gusmao, D.; Hinkel, J.; Tol, R.S.J. Sea-level rise and its possible impacts given a ‘beyond 4 degrees C world’ in the twenty-first century. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 161–181. [Google Scholar] [CrossRef]
| Reference | RCP2.6 | RCP4.5 | RCP8.5 |
|---|---|---|---|
| This study | 0.14 ± 0.03 m | 0.20 ± 0.03 m | 0.30 ± 0.03 m |
| IPCC AR5 (Global) [1] 1 | 0.15 ± 0.05 m | 0.20 ± 0.05 m | 0.32 ± 0.07 m |
| Kopp et al. (2014) [19] 1 | 0.19 ± 0.06 m | 0.26 ± 0.08 m | 0.37 ± 0.09 m |
| Integrated Climate Data Center at the Hamburg University 1 | 0.16 ± 0.06 m | 0.21 ± 0.07 m | 0.33 ± 0.10 m |
| Jackson et Jevrejeva (2016) [45] | N.A. | 0.21 ± 0.05 m | 0.32 ± 0.07 m |
| Component | RCP2.6 | RCP4.5 | RCP8.5 |
|---|---|---|---|
| Thermosteric | 0.14 ± 0.03 m | 0.20 ± 0.03 m | 0.30 ± 0.03 m |
| (0.15 ± 0.05 m) | (0.20 ± 0.05 m) | (0.32 ± 0.07 m) | |
| Glaciers 1 | 0.09 ± 0.02 m | 0.12 ± 0.03 m | 0.17 ± 0.03 m |
| (0.11 ± 0.06 m) | (0.13 ± 0.06 m) | (0.18 ± 0.08 m) | |
| Greenland 1 | 0.04 ± 0.02 m | 0.06 ± 0.02 m | 0.10 ± 0.03 m |
| (0.08 ± 0.04 m) | (0.09 [0.05–0.16] m) | (0.15 [0.09–0.28] m) | |
| Antarctica 1 | 0.02 ± 0.04 m | 0.04 ± 0.04 m | 0.09 ± 0.06 m |
| (0.06 ± 0.1 m) | (0.05 ± 0.1 m) | (0.04 [−0.08–0.14] m) | |
| Groundwater 2 | 0.05 ± 0.08 m | 0.05 ± 0.08 m | 0.05 ± 0.08 m |
| 0.05 [−0.01–0.11] m | 0.05 [−0.01–0.11] m | 0.05 [−0.01–0.11] m | |
| Global isostatic adjustment 3 | Based on two different GIA models, as in AR5 [1] | ||
| Correlation Scheme Name | Global Experiments | Regional Experiments |
|---|---|---|
| “Ind” | All components uncorrelated | All components uncorrelated |
| “Dep” | Fully correlated Thermosteric, Mountain Glaciers and Greenland components | Fully correlated Sterodynamic, Mountain Glaciers and Greenland components |
| RCP Scenario | 5% | 17% | 50% | 83% | 95% |
|---|---|---|---|---|---|
| RCP2.6 | 0.17 m | 0.23 m | 0.34 m | 0.45 m | 0.52 m |
| RCP4.5 | 0.27 m | 0.35 m | 0.46 m | 0.57 m | 0.63 m |
| RCP8.5 | 0.48 m | 0.58 m | 0.70 m | 0.83 m | 0.92 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Cozannet, G.; Thiéblemont, R.; Rohmer, J.; Idier, D.; Manceau, J.-C.; Quique, R. Low-End Probabilistic Sea-Level Projections. Water 2019, 11, 1507. https://doi.org/10.3390/w11071507
Le Cozannet G, Thiéblemont R, Rohmer J, Idier D, Manceau J-C, Quique R. Low-End Probabilistic Sea-Level Projections. Water. 2019; 11(7):1507. https://doi.org/10.3390/w11071507
Chicago/Turabian StyleLe Cozannet, Gonéri, Rémi Thiéblemont, Jeremy Rohmer, Déborah Idier, Jean-Charles Manceau, and Robin Quique. 2019. "Low-End Probabilistic Sea-Level Projections" Water 11, no. 7: 1507. https://doi.org/10.3390/w11071507
APA StyleLe Cozannet, G., Thiéblemont, R., Rohmer, J., Idier, D., Manceau, J.-C., & Quique, R. (2019). Low-End Probabilistic Sea-Level Projections. Water, 11(7), 1507. https://doi.org/10.3390/w11071507








