Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis
Abstract
1. Introduction
2. Methods
2.1. Study Area and Hydrometeorological Data
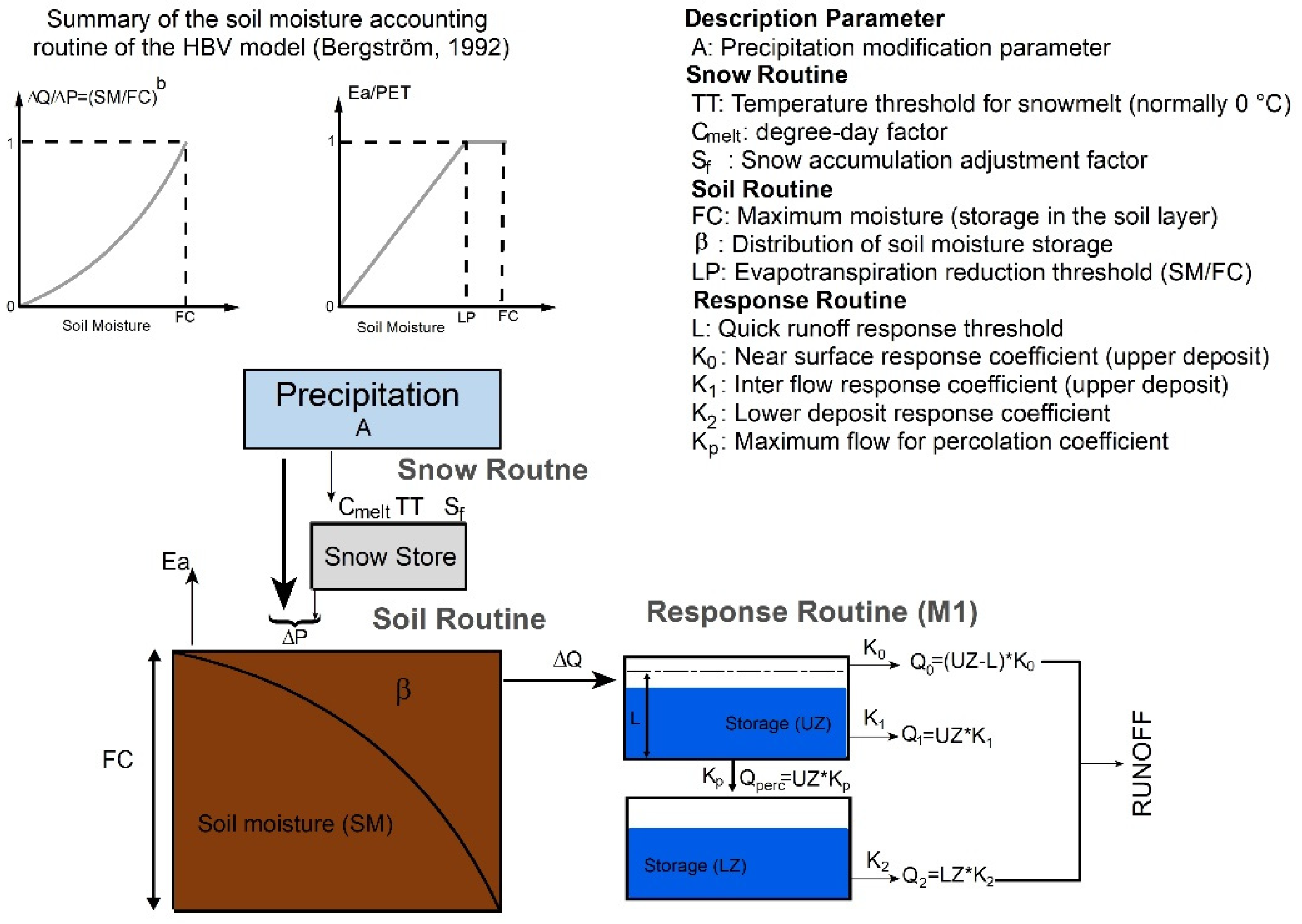
2.2. HBV Hydrological Model Description
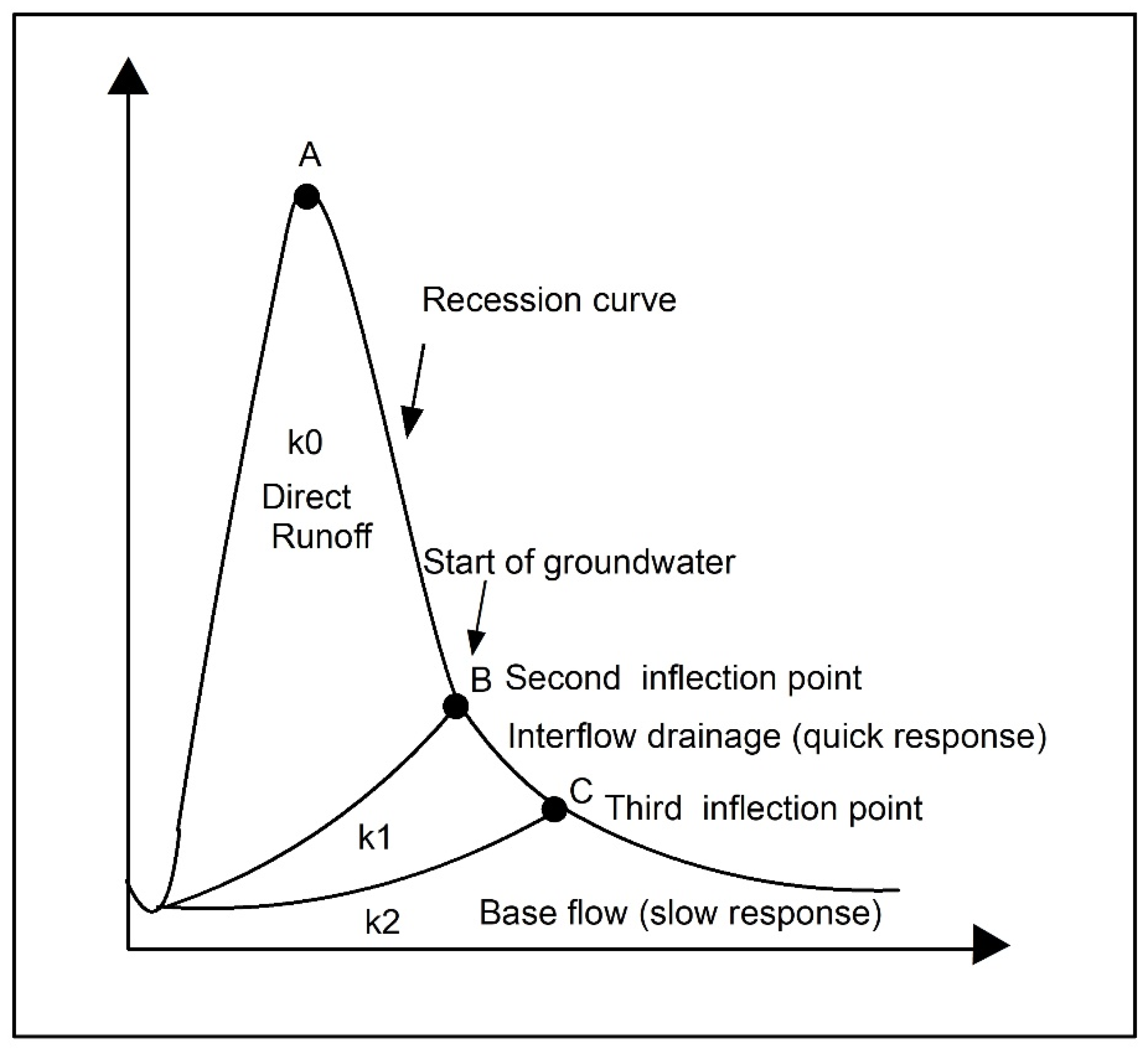
2.3. Analyzed Groundwater Storage Structures
2.4. Sensitivity Analysis and Calibration
3. Results and Discussion
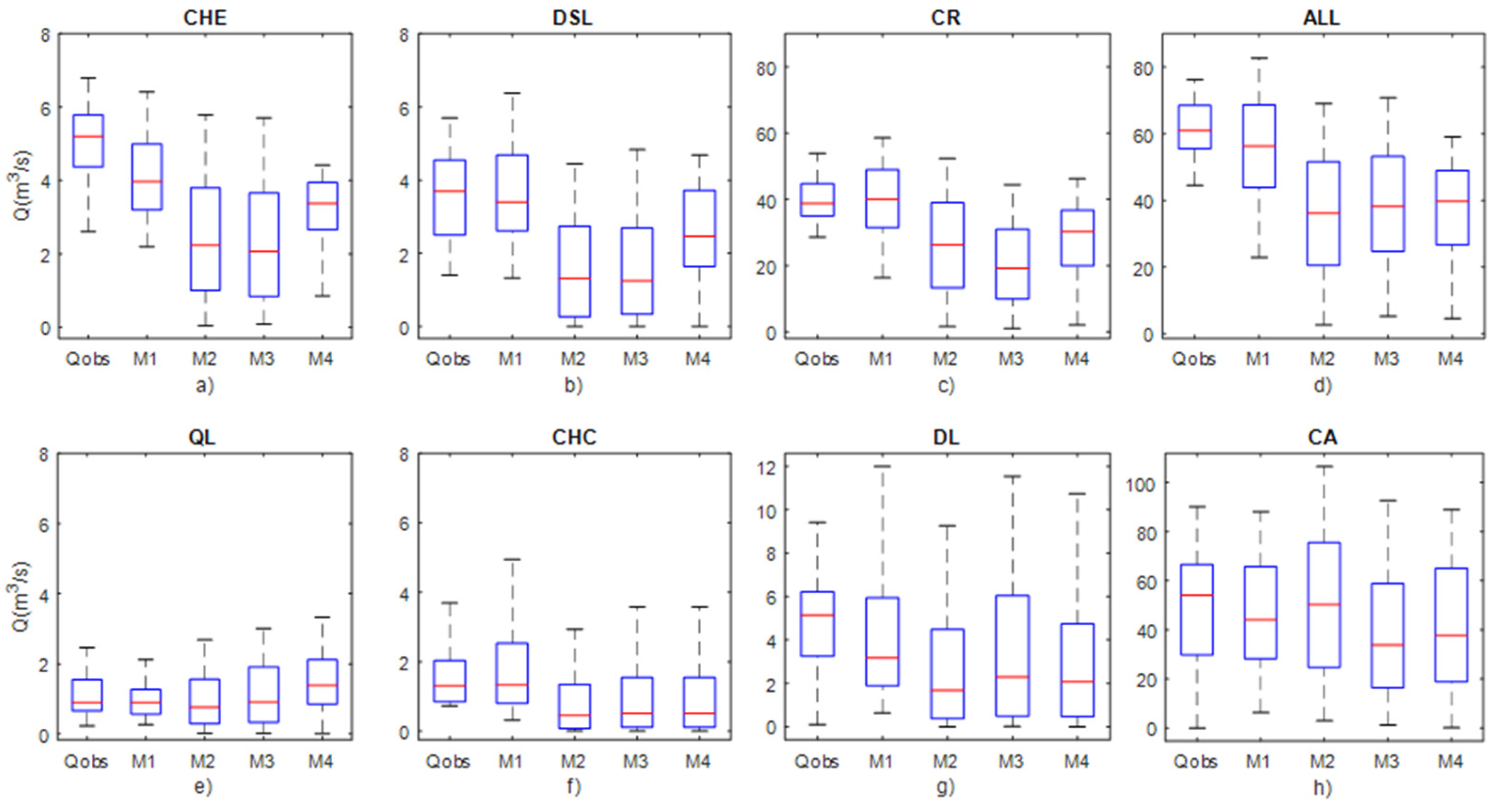
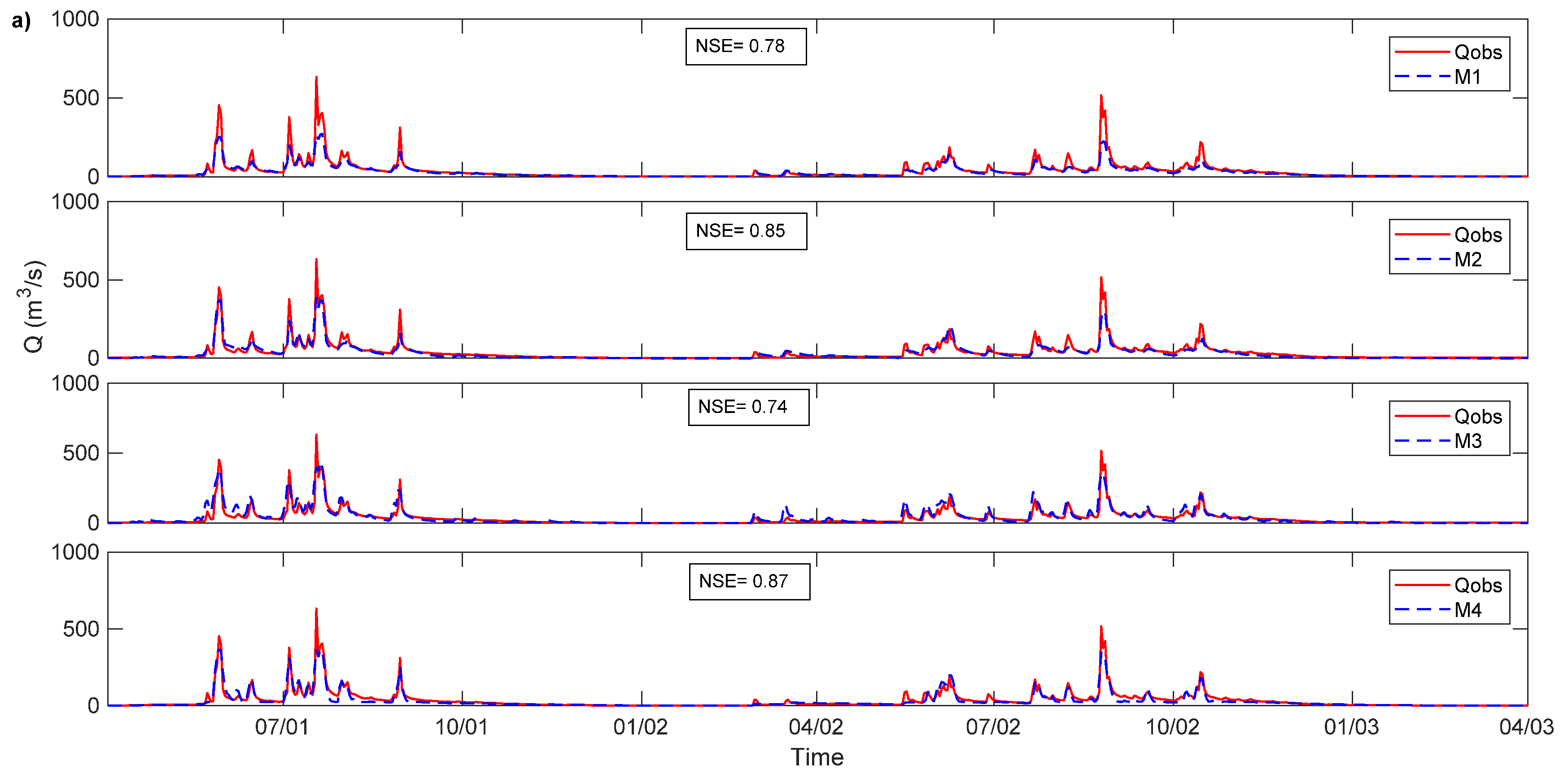
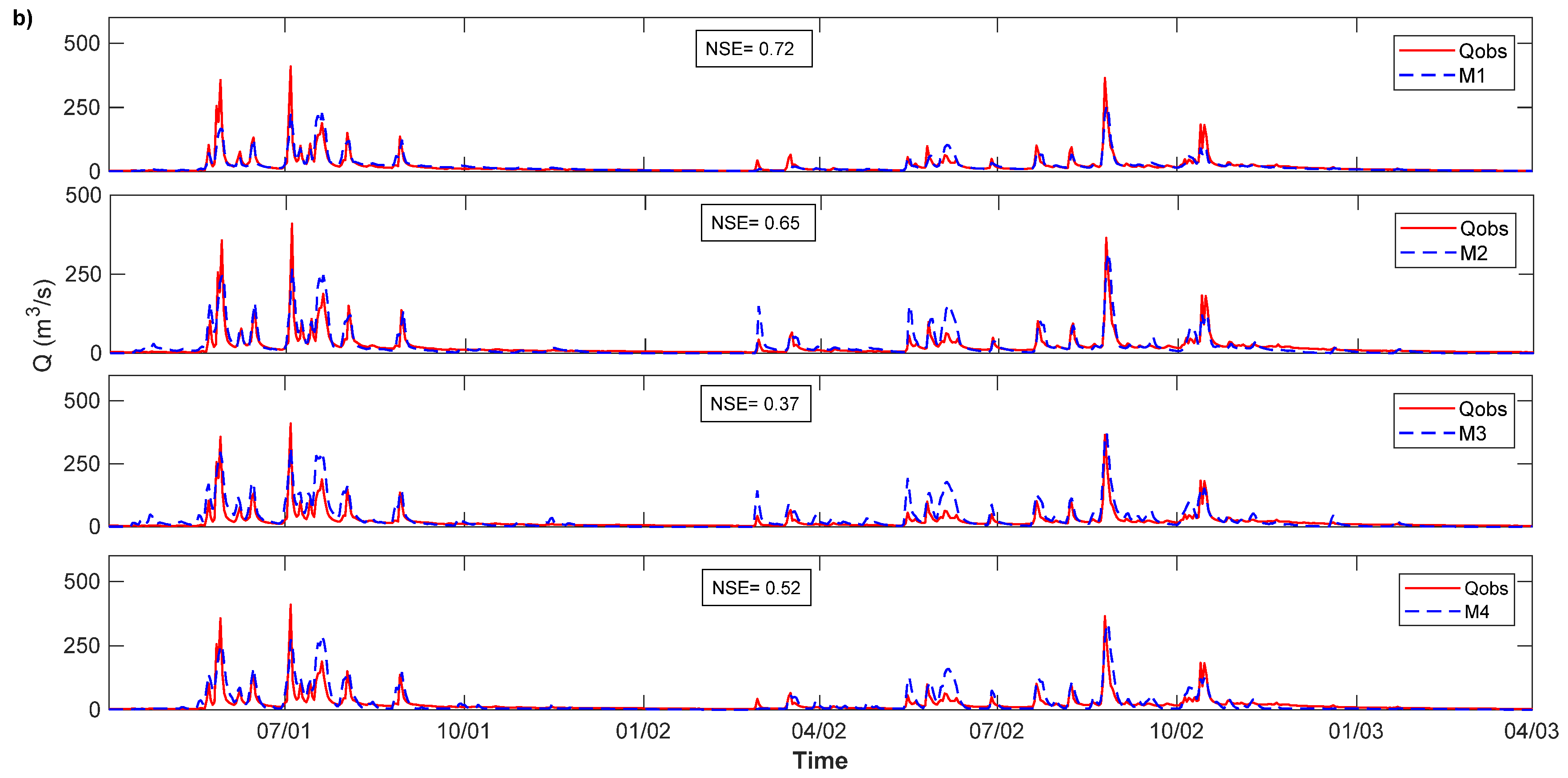
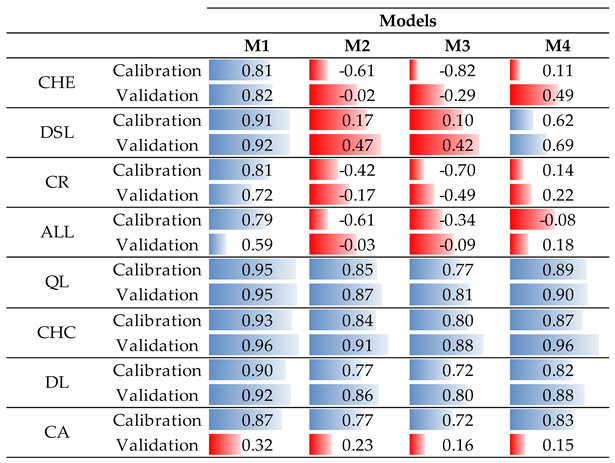
3.1. Groundwater Storage Structures Performance
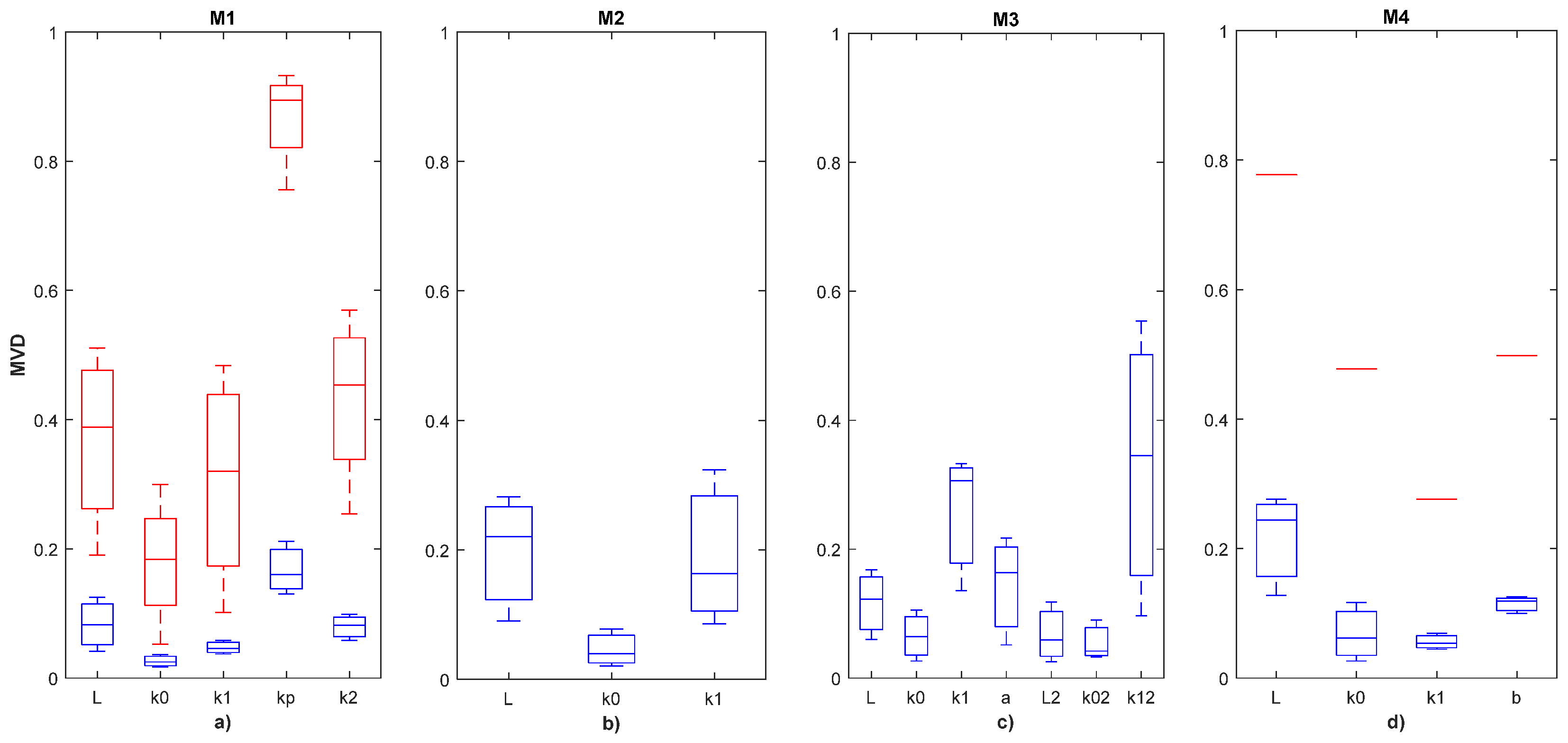
3.2. Sensitivity of the Parameters Associated to Runoff Response Sub-Models
3.3. Influence of the Hydrological Characteristics
3.4. M1 Model Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wagener, T.; Kollat, J. Numerical and visual evaluation of hydrological and environmental models using the Monte Carlo analysis toolbox. Environ. Model. Softw. 2006, 22, 1021–1033. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Singh, V.P. A Review on Monthly Water Balance Models for Water Resources Investigations. Water Resour. Manag. 1998, 12, 31–50. [Google Scholar] [CrossRef]
- Chiew, F. Lumped Conceptual Rainfall-Runoff Models and Simple Water Balance Methods: Overview and Applications in Ungauged and Data Limited Regions. Geogr. Compass. 2010, 4, 206–225. [Google Scholar] [CrossRef]
- Islam, Z. A Review on Physically Based Hydrologic Modeling; University of Alberta: Edmonton, AB, Canada, 2011; Available online: https://www.researchgate.net/publication/272169378_A_Review_on_Physically_Based_Hydrologic_Modeling (accessed on 3 May 2019).
- Kunstmann, H.; Heckl, A.; Rimmer, A. Physically based distributed hydrological modelling of the Upper Jordan catchment and investigation of effective model equations. Adv. Geosci. 2006, 9, 123–130. [Google Scholar] [CrossRef]
- Skaugen, T.; Peereborn, I.; Nilsson, A. Use of a parsimonious rainfall-run-off model for predicting hydrological response in ungauged basins. Hydrol. Process. 2014, 29, 1999–2013. [Google Scholar] [CrossRef]
- Toledo, C.; Muñoz, E.; Zambrano-Bigiarini, M. Comparison of Stationary and Dynamic Conceptual Models in a Mountainous and Data-Sparse Catchment in the South-Central Chilean Andes. Adv. Meteorol. 2015, 2015, 526158. [Google Scholar] [CrossRef]
- Muñoz, E.; Arumí, J.L.; Wagener, T.; Oyarzún, R.; Parra, V. Unraveling complex hydrogeological processes in Andean basins in south-central Chile: An integrated assessment to understand hydrological dissimilarity. Hydrol. Process. 2016, 30, 4934–4943. [Google Scholar] [CrossRef]
- Parra, V.; Fuentes-Aguilera, P.; Muñoz, E. Identifying advantages and drawbacks of two hydrological models based on a sensitivity analysis: A study in two Chilean watersheds. Hydrol. Sci. J. 2018, 63, 1831–1843. [Google Scholar] [CrossRef]
- Wittenberg, H. Baseflow recession and recharge as nonlinear storage processes. Hydrol. Process. 1999, 13, 715–726. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.; Matgen, P.; Pfister, L. Is the groundwater reservoir linear? Learning from data in hydrological modelling. Hydrol. Earth Syst. Sci. 2006, 10, 139–150. [Google Scholar] [CrossRef]
- Botter, G.; Porporato, A.; Rodriguez-Iturbe, I.; Rinaldo, A. Nonlinear storage-discharge relations and catchment streamflow regimes. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Stoelzle, M.; Weiler, M.; Stahl, K.; Morhard, A.; Schuetz, T. Is there a superior conceptual groundwater model structure for baseflow simulation? Hydrol. Process. 2015, 29, 1301–1313. [Google Scholar] [CrossRef]
- Thornthwaite, C.; Mather, J. The Water Balance; Publications in Climatology: Centerton, AR, USA, 1955. [Google Scholar]
- Thomas, H. Improved Methods for National Water Assessment, Water Resources Contract: WR15249270; Report; Harvard University: Washington, DC, USA, 1981. [Google Scholar]
- Boyle, D. Multicriteria Calibration of Hydrologic Models. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 2001. [Google Scholar]
- Mishra, A.; Takeshi, H.; Abdelhadi, W.; Tada, A.; Tanakamaru, H. Recession flow analysis of the Blue Nile River. Hydrol. Process. 2003, 17, 2825–2835. [Google Scholar] [CrossRef]
- Staudinger, M.; Stahl, K.; Seibert, J.; Clark, M.P.; Tallaksen, L.M. Comparison of hydrological model structures based on recession and low flow simulations. Hydrol. Earth Syst. Sci. 2011, 15, 3447–3459. [Google Scholar] [CrossRef]
- Nicolle, P.; Pushpalatha, R.; Perrin, C.; François, D.; Thiéry, D.; Mathevet, T.; Le Lay, M.; Besson, F.; Soubeyroux, J.-M.; Viel, C.; et al. Benchmarking hydrological models for low-flow simulation and forecasting on French catchments. Hydrol. Earth Syst. Sci. 2014, 18, 2829–2857. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N.A. multi-storage groundwater concept for the SWAT model to emphasize nonlinear groundwater dynamics in lowland catchments. Hydrol. Process. 2013, 28, 5599–5612. [Google Scholar] [CrossRef]
- Gan, R.; Lou, Y. Using the nonlinear aquifer storage–discharge relationship to simulate the base flow of glacier- and snowmelt-dominated basinsin northwest China. Hydrol. Earth Syst. Sci. 2013, 17, 3577–3586. [Google Scholar] [CrossRef]
- Voeckler, H.; Allen, D.M. Estimating regional-scale fractured bedrock hydraulic conductivity using discrete fracture network (DFN) modeling. Hydrogeol. J. 2012, 20, 1081–1100. [Google Scholar] [CrossRef]
- Tóth, J. A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 1963, 68, 4795–4812. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Evaluating the relationship between topography and groundwater using outputs from a continental-scale integrated hydrology model. Water Resour. Res. 2015, 51, 6602–6621. [Google Scholar] [CrossRef]
- Pizarro, R.; Valdés, R.; García-Chevesich, P.; Vallejos, C.; Sanguesa, C.; Morales, C.; Balocchi, F.; Abarza, A.; Fuentes, R. Latitudinal Analysis of Rainfall Intensity and Mean Annual Precipitation in Chile. Chilean J. Agric. Res. 2012, 72, 252–261. [Google Scholar] [CrossRef]
- Bozkurt, D.; Rojas, M.; Boisier, J.P.; Valdivieso, J. Climate change impacts on hydroclimatic regimes and extremes over Andean basins in central Chile. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–29. [Google Scholar] [CrossRef]
- SERNAGEOMIN. Mapa Geológico de Chile: Versión Digital. Servicio Nacional de Geología y Minería; Publicación Geológica Digital: Santiago, Chile, 2003. [Google Scholar]
- Naranjo, J.; Gilbert, J.; Sparks, R. Geología del Complejo Volcánico Nevados de Chillán, Región del Biobío; Carta Geológica de Chile, Serie Geología Básica: Santiago, Chile, 2008. [Google Scholar]
- Horton, B.K. Sedimentary record of Andean mountain building. Earth Sci. Rev. 2018, 178, 279–309. [Google Scholar] [CrossRef]
- Ruane, A.; Goldberg, R.; Chryssanthacopoulos, J. Climate forcing datasets for agricultural modeling: Merged products for gap-filling and historical climate series estimation. Agric. For. Meteorol. 2015, 200, 233–248. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Lu, G.; Wong, D. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Habib, E. Application of a conceptual hydrologic model in teaching hydrologic processes. Int. J. Eng. Educ. 2010, 26, 963–973. [Google Scholar]
- Bergström, S. The HBV Model: Its Structure and Applications; Swedish Meteorological and Hydrological Institute: Norrkoping, Sweden, 1992.
- Kollat, J.; Reed, P.; Wagener, T. When are multiobjective calibration trade-offs in hydrologic models meaningful? Water Resour. Res. 2012, 48, 48. [Google Scholar] [CrossRef]
- Muñoz, E.; Acuña, M.; Lucero, J.; Rojas, I. Correction of Precipitation Records through Inverse Modeling in Watersheds of South-Central Chile. Water 2018, 10, 1092. [Google Scholar] [CrossRef]
- Muñoz, E.; Rivera, D.; Vergara, F.; Tume, P.; Arumí, J.L. Identifiability analysis: Towards constrained equifinality and reduced uncertainty in a conceptual model. Hydrol. Sci. J. 2014, 59, 1690–1703. [Google Scholar]
- Pianosi, F.; Sarrazin, F.; Wagener, T.A. Matlab toolbox for Global Sensitivity Analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Perrin, C.; Oudin, L.; Andresassian, V.; Rojas-Serna, C.; Michel, C.; Mathevet, T. Impact of limited streamflow data on the efficiency and the parameters of rainfall-runoff models. Hydrol. Sci. J. 2007, 52, 131–151. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Brigode, P.; Oudin, L.; Perrin, C. Hydrological model parameter instability: A source of additional uncertainty in estimating the hydrological impacts of climate change? J. Hydrol. 2013, 476, 410–425. [Google Scholar] [CrossRef]
- Cui, X.; Sun, W.; Teng, J.; Song, H.; Yao, X. Effect of length of the observed dataset on the calibration of a distributed hydrological model. Proc. IAHS 2015, 368, 305–311. [Google Scholar] [CrossRef][Green Version]
- Seibert, J.; Vis, M. Teaching hydrological modeling with a user-friendly catchment-runoff-model software package. Hydrol. Earth Syst. Sci Discuss. 2012, 9, 5905–5930. [Google Scholar] [CrossRef]
- Perrin, C. Vers une Ame’Lioration D’Un Modèle Global Pluie-De´Bit au Travers D’une Approche Comparative. Ph.D. Thesis, Institut National Polytechnique de Grenoble, CEMAGREF, Grenoble, France, 2000. [Google Scholar]
- Hoffmann, L.; El Idrissi, A.; Pfister, L.; Hingray, B.; Guex, F.; Musy, A.; Humbert, J.; Drogue, G.; Leviandier, T. Development of regionalized hydrological models in an area with short hydrological observation series. River Res. Appl. 2004, 20, 243–254. [Google Scholar] [CrossRef]
- Liu, Y.B.; Batelaan, O.; De Smedt, F.; Poorova, J.; Velcicka, L. Automated calibration applied to a GIS-based flood simulation model using PEST. In Floods, from Defence to Management; van Alphen, J., van Beek, E., Taal, M., Eds.; Taylor-Francis Group: London, UK, 2005; pp. 317–326. [Google Scholar]
- Porretta-Brandyk, L.; Chormański, J.; Brandyk, A.; Okruszko, T. Automatic Calibration of the WetSpa Distributed Hydrological Model for Small Lowland Catchments. In Modelling of Hydrological Processes in the Narew Catchment; Świątek, D., Okruszko, T., Eds.; Springer: Heidelberg, Germany, 2011; pp. 43–62. [Google Scholar]
- Nobrega, M.T.; Collischonn, W.; Tucci, C.; Paz, A. Uncertainty in climate change impacts on water resources in the Rio Grande Basin, Brazil. Hydrol. Earth Syst. Sci. 2011, 15, 585–595. [Google Scholar] [CrossRef]
- Wallner, M.; Haberlandt, U.; Dietrich, J. A one-steo similarity approach for the regionalization of hydrological model parameters based on Self-Organizing Maps. J. Hydrol. 2013, 494, 59–71. [Google Scholar] [CrossRef]
- Stoelzle, M.; Stahl, K.; Morhard, A.; Weiler, M. Streamflow sensitivity to drought scenarios in catchments with different geology. Geophys. Res. Lett. 2014, 41, 6174–6183. [Google Scholar] [CrossRef]
- Van Werkhoven, K.; Wagener, T.; Reed, P.; Tang, Y. Sensitivity-guided reduction of parametric dimensionality for multi-objective calibration of watershed models. Adv. Water Resour. 2009, 32, 1154–1169. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420–421, 171–182. [Google Scholar] [CrossRef]
- Yilmaz, K.; Vrugt, J.A.; Gupta, H.V.; Sorooshian, S. Model calibration in watershed hydrology. In Advances in Databased Approaches for Hydrologic Modeling and Forecasting; Sivakumar, B., Berndtsson, R., Eds.; World Scientific: Hackensack, NJ, USA, 2010; pp. 53–105. [Google Scholar]
- Wilson, J.L.; Guan, H. Mountain-block hydrology and mountain-front recharge. In Groundwater Recharge in a Desert Environment: The Southwestern United States; Hogan, J.F., Phillips, F.M., Scanlon, B.R., Eds.; American Geophysical Union: Washington, DC, USA, 2004; pp. 113–137. [Google Scholar]
- Kao, Y.H.; Liu, C.W.; Wang, S.W.; Lee, C.H. Estimating mountain block recharge to downstream alluvial aquifers from standard methods. J. Hydrol. 2012, 426–427, 93–102. [Google Scholar] [CrossRef]
- Rusli, S.R.; Yudianto, D.; Liu, J. Effects of temporal variability on HBV model calibration. Water Sci. Eng. 2015, 8, 291–300. [Google Scholar] [CrossRef]
- Abebe, N.A.; Ogden, F.L.; Pradhan, N.R. Sensitivity and uncertainty analysis of the conceptual HBV rainfall–runoff model: Implications for parameter estimation. J. Hydrol. 2010, 389, 301–310. [Google Scholar] [CrossRef]
- Sayama, T.; McDonnell, J.J.; Dhakal, A.; Sullivan, K. How much water can a watershed store? Hydrol. Process. 2011, 25, 3899–3908. [Google Scholar] [CrossRef]
- Mohamound, Y.M. Prediction of daily flow duration curves and streamflow for ungauged catchments using regional flow duration curves. Hydrol. Sci. J. 2008, 53, 706–724. [Google Scholar] [CrossRef]
- Moore, R. Storage-outflow modelling of streamflow recessions, with application to a shallow-soil forested catchment. J. Hydrol. 1997, 198, 260–270. [Google Scholar] [CrossRef]
- Ajami, H.; Troch, P.; Maddock, T., III; Meixner, T.; Eastoe, C. Quantifying mountain block recharge by means of catchment-scale storage-discharge relationships. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Pizarro-Tapia, R.; Balocchi-Contreras, F.; Garcia-Chevesich, P.; Macaya-Perez, K.; Bro, P.; León-Gutiérrez, L.; Helwig, B.; Valdés-Pineda, R. On Redefining the Onset of Baseflow Recession on Storm Hydrographs. Open J. Mod. Hydrol. 2013, 3, 269–277. [Google Scholar] [CrossRef][Green Version]
- Balocchi, F.; Pizarro, R.; Morales, C.; Olivares, C. Modelamiento matemático de caudales recesivos en la región mediterránea andina del Maule: El caso del estero Upeo, Chile. Tecnol. Cs. Agua. 2014, 5, 179–188. [Google Scholar]
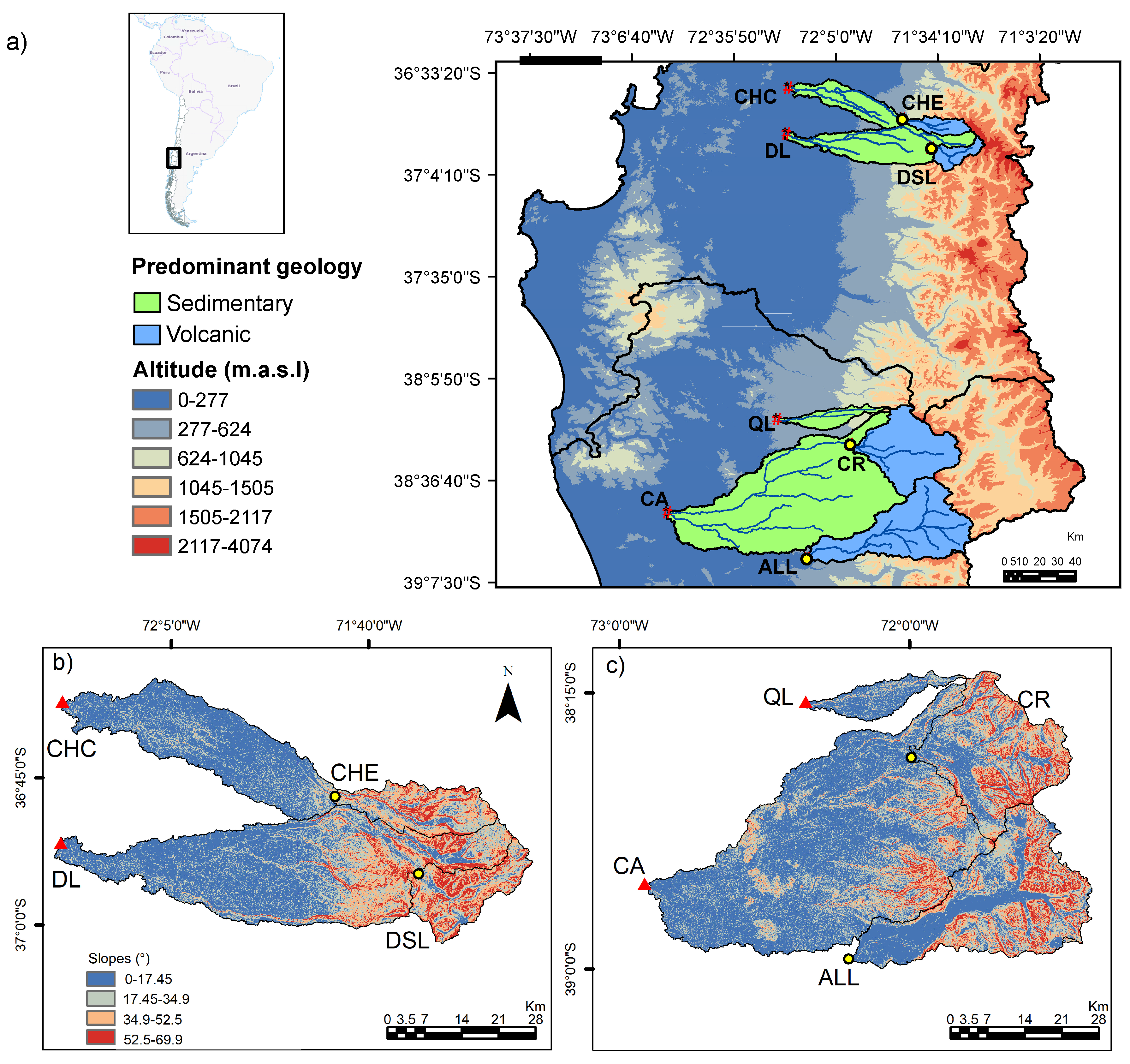

| Station (ID) | Area | Geological Formation (%) | Relief (°) | Hydro-Meteorological Information | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | Station | (km2) | V | S | O | AS | MAP | MAD | MAT | MAE |
| CHE | Chillan at Esperanza | 210 | 90.4 | 0 | 9.6 | 17.8 | 2200 | 15.6 | 9.3 | 964 |
| DSL | Diguillín at San Lorenzo | 207 | 85.1 | 0 | 14.9 | 23.6 | 2300 | 16.4 | 9.2 | 920 |
| CR | Cautin at Rari-Ruca | 1255 | 96.6 | 1.2 | 2.2 | 14.4 | 2330 | 102.7 | 8.2 | 1006 |
| ALL | Río Allipen at Laureles | 1652 | 56.3 | 21.9 | 21.8 | 13 | 2294 | 139.4 | 8.7 | 1023 |
| QL | Quino at Longitudinal | 298 | 31 | 69 | 0 | 2.4 | 1850 | 13.1 | 12.5 | 1066 |
| CHC | Chillán to Confluencia | 754 | 25.3 | 70.4 | 4.3 | 8.1 | 1500 | 29.9 | 12.1 | 1163 |
| DL | Diguillin at Longitudinal | 1239 | 26.5 | 69.7 | 3.8 | 10 | 1736 | 46.9 | 10.9 | 1103 |
| CA | Cautin at Almagro | 5470 | 58.1 | 40.1 | 1.8 | 6 | 1838 | 261 | 10.5 | 1052 |
| Parameter (Units) | M1 | M2 | M3 | M4 |
|---|---|---|---|---|
| Mass Balance | ||||
| A | 0.8–2.5 | 0.8–2.5 | 0.8–2.5 | 0.8–2.5 |
| Snow Routine | ||||
| Cmelt | 0.5–7 | 0.5–7 | 0.5–7 | 0.5–7 |
| 0.5–1.2 | 0.5–1.2 | 0.5–1.2 | 0.5–1.2 | |
| Soil Routine | ||||
| FC (mm) | 0–2000 | 1–2000 | 0–2000 | 1–2000 |
| 0–7 | 0–7 | 0–7 | 0–7 | |
| - | - | 0–0.5 | - | |
| LP | 0.3–1 | 0.3–1 | 0.3–1 | 0.3–1 |
| C () | 0.01–0.3 | 0.01–0.3 | 0.01–0.3 | 0.01–0.3 |
| Response Routine | ||||
| L (mm) | 0–100 | 0–100 | 0–100 | 0–100 |
| L2 (mm) | - | - | 0–100 | - |
| () | 0.3–0.6 | 0.3–0.6 | 0.3–0.6 | 0.3–0.6 |
| () | 0.1–0.2 | 0.1–0.2 | 0.1–0.2 | 0.1–0.2 |
| () | 0.01–0.1 | - | - | - |
| () | 0.01–0.1 | - | - | - |
| () | - | - | 0.3–0.1 | - |
| () | - | - | 0.2–0.05 | - |
| b | - | - | - | 1–0.33 |
| Watershed | Period | MAP (mm) | MAD (m3/s) | Q50 (m3/s) | Q70 (m3/s) |
|---|---|---|---|---|---|
| CHE | Calibration | 2950 | 16.3 | 10.5 | 6.6 |
| Validation | 2478 | 13.2 | 7.2 | 5.7 | |
| DSL | Calibration | 3091 | 18.3 | 10.1 | 5.6 |
| Validation | 2534 | 16.2 | 9.0 | 4.1 | |
| CR | Calibration | 2417 | 95.7 | 79.4 | 50.6 |
| Validation | 2029 | 85.5 | 66.3 | 40.0 | |
| ALL | Calibration | 2901 | 139.9 | 114.0 | 74.1 |
| Validation | 2774 | 127.9 | 105.0 | 74.8 | |
| QL | Calibration | 2652 | 13.3 | 6.1 | 2.0 |
| Validation | 2314 | 12.2 | 5.7 | 2.1 | |
| CHC | Calibration | 1681 | 26.3 | 8.7 | 2.8 |
| Validation | 1379 | 22.2 | 8.3 | 2.5 | |
| DL | Calibration | 2320 | 57.0 | 22.5 | 7.7 |
| Validation | 1891 | 46.0 | 14.5 | 5.1 | |
| CA | Calibration | 1966 | 270.0 | 167.0 | 81.1 |
| Validation | 1822 | 305.0 | 163.0 | 95.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra, V.; Arumí, J.L.; Muñoz, E. Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis. Water 2019, 11, 1506. https://doi.org/10.3390/w11071506
Parra V, Arumí JL, Muñoz E. Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis. Water. 2019; 11(7):1506. https://doi.org/10.3390/w11071506
Chicago/Turabian StyleParra, Víctor, Jose Luis Arumí, and Enrique Muñoz. 2019. "Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis" Water 11, no. 7: 1506. https://doi.org/10.3390/w11071506
APA StyleParra, V., Arumí, J. L., & Muñoz, E. (2019). Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis. Water, 11(7), 1506. https://doi.org/10.3390/w11071506





