Seepage Comprehensive Evaluation of Concrete Dam Based on Grey Cluster Analysis
Abstract
1. Introduction
2. Seepage Monitoring Model of Concrete Dams
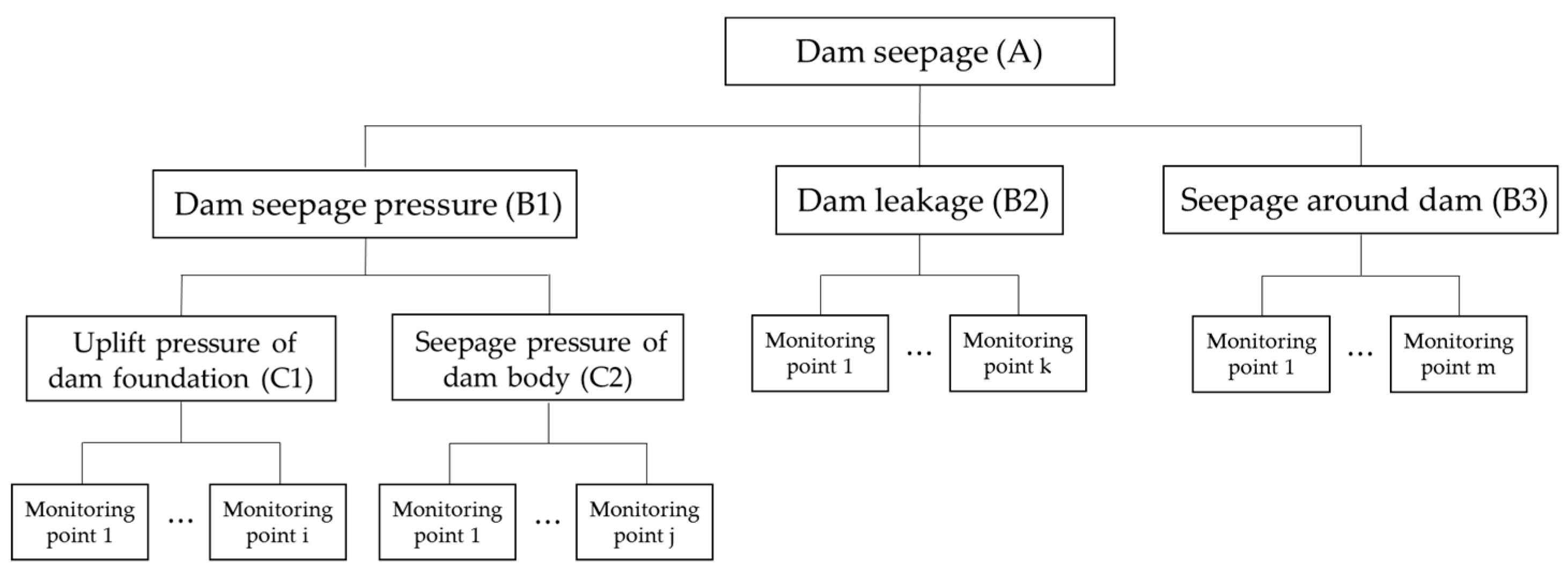
2.1. The Comprehensive Indicator System of Dam Seepage State
2.2. Seepage Monitoring Model
2.2.1. Water Level Component
2.2.2. Rainfall Component
2.2.3. Temperature Component
2.2.4. Time Effect Component
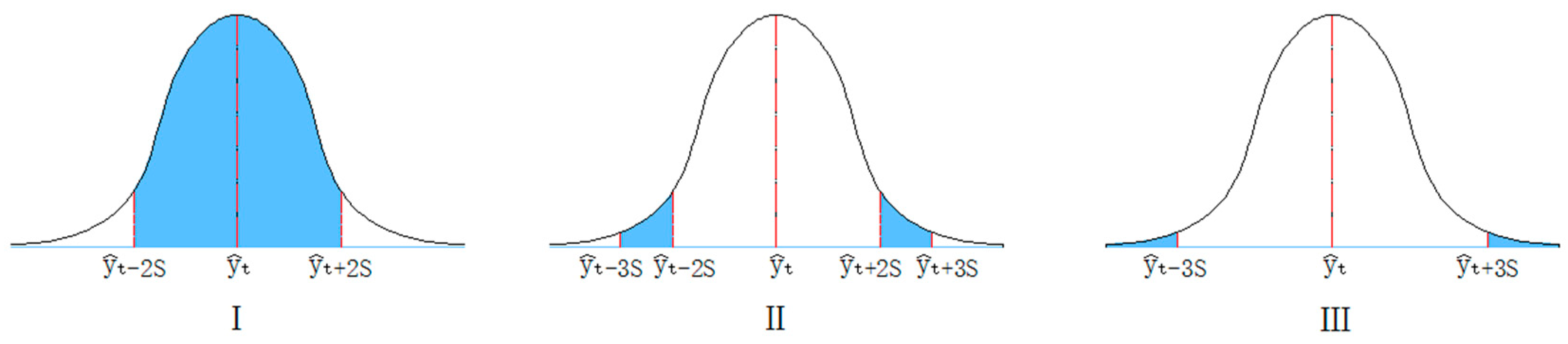
2.3. Safety Class Division Standard
3. Multi-Indicator Grey Clustering Comprehensive Analysis
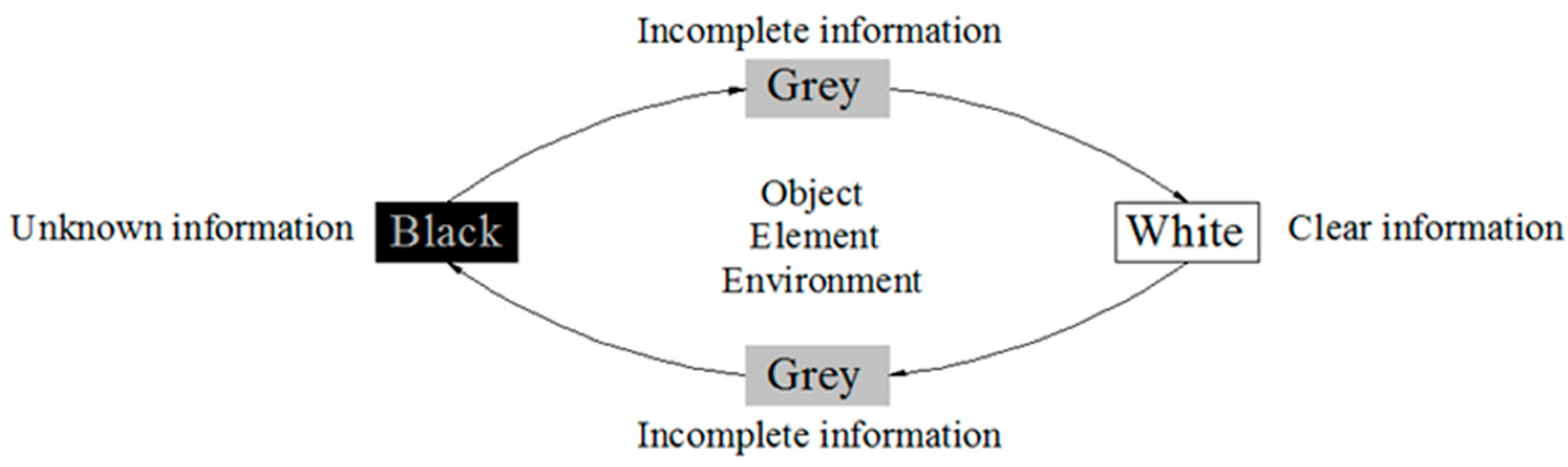
3.1. Grey Clustering Analysis Theory
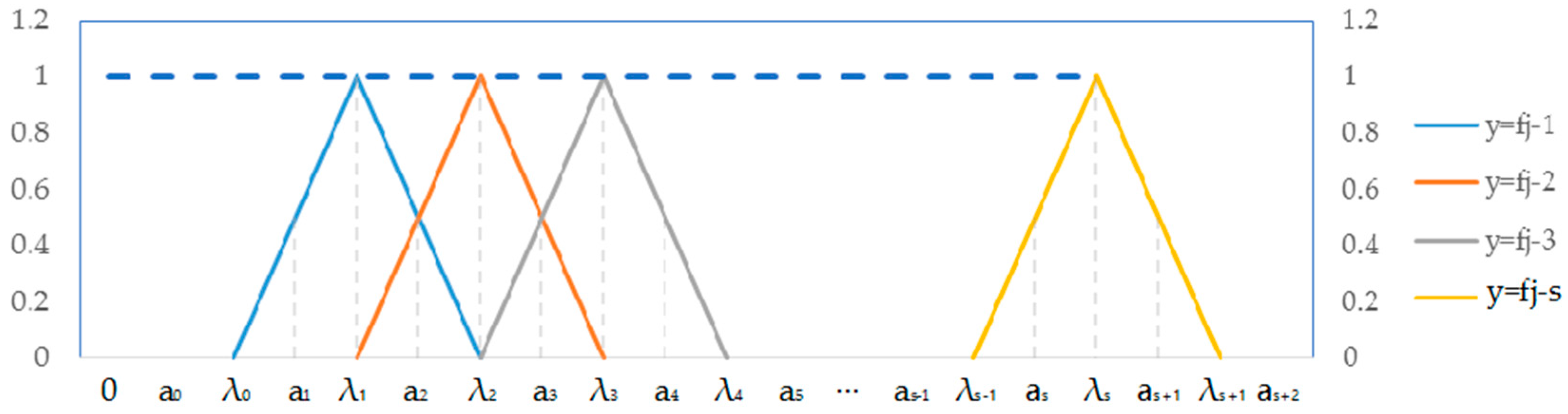
3.1.1. Basic Model
3.1.2. Modeling Steps
3.2. Multi-Indicator Grey Clustering Comprehensive Analysis of Concrete Dam Seepage
4. Case Study
4.1. Calculation of Seepage Monitoring Model
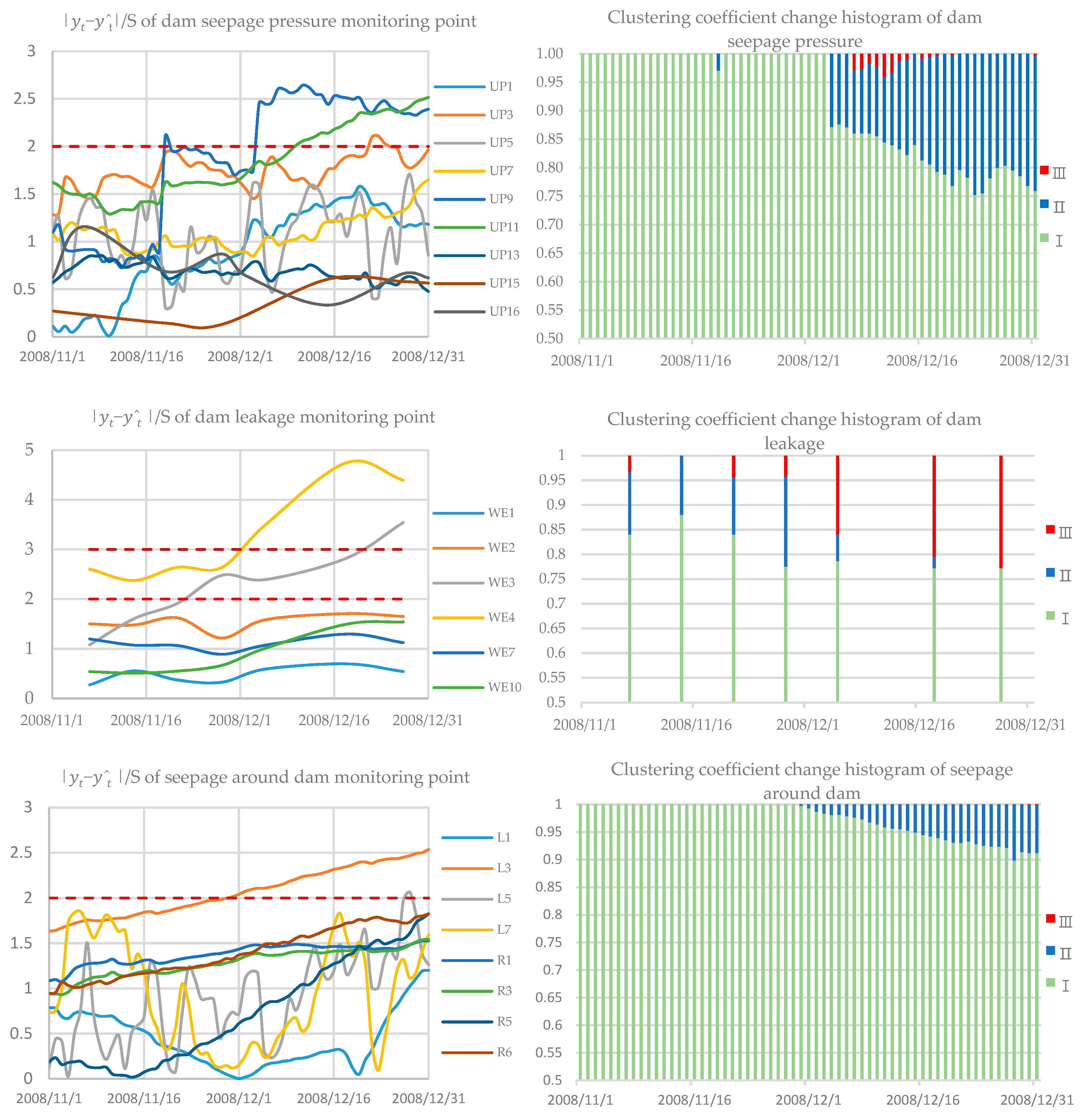
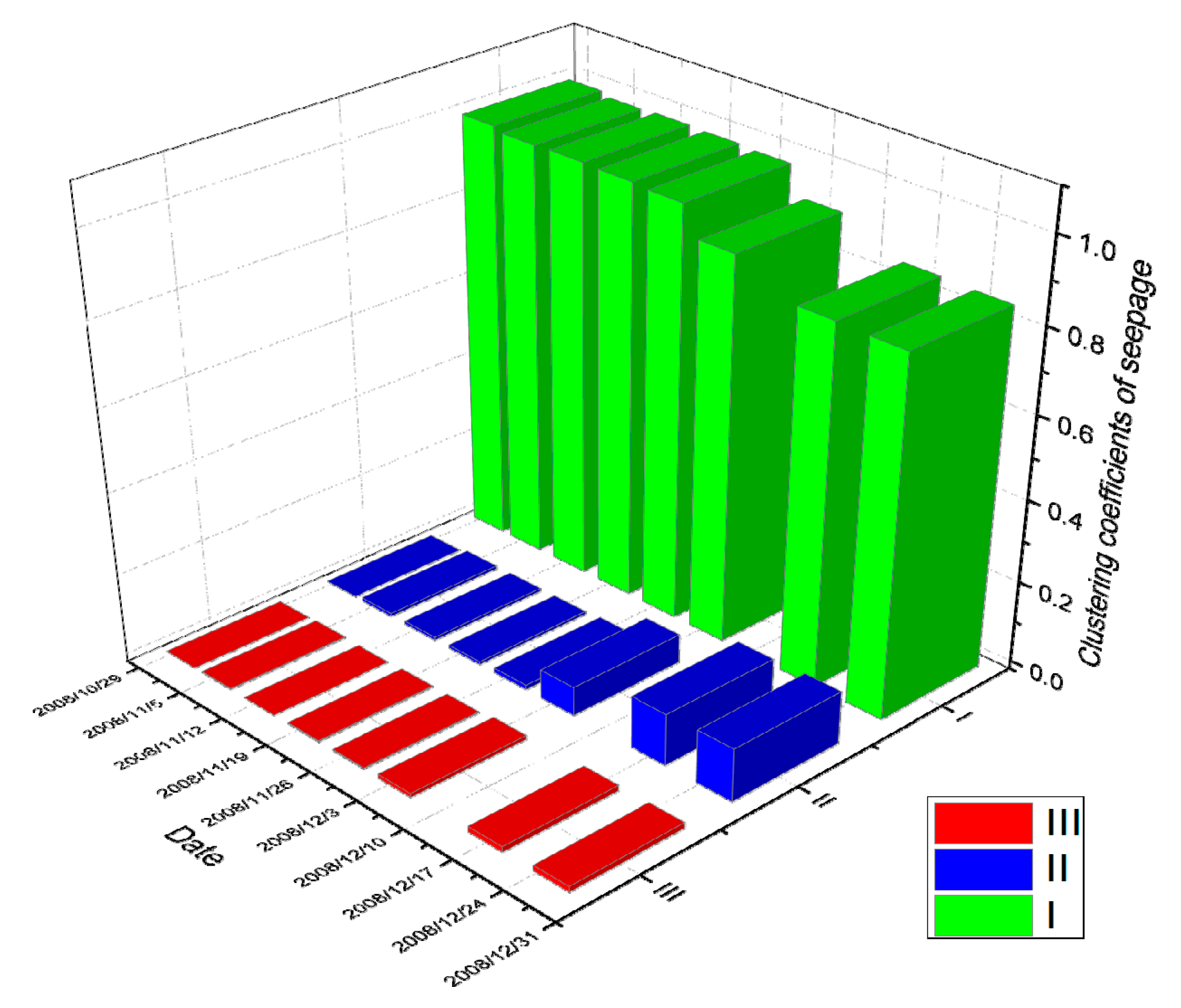
4.2. Comprehensive Clustering Calculation of Multiple Dependent Variables
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fang, C.; Duan, Y. Statistical analysis of dam-break incidents and its cautions. Yellow River 2010, 42, 96–100. [Google Scholar] [CrossRef]
- Wang, H. Dam safety and monitoring. Water Resour. Hydropower Eng. 2009, 40, 126–132. [Google Scholar] [CrossRef]
- Chen, X.; Gu, C.; Chen, H. Early warning of dam seepage with cooperation between principal component analysis and least squares wavelet support vector machine. Fresenius Environ. Bull. 2013, 22, 500–507. [Google Scholar]
- Shen, C.; Lu, Z. Factor Selection of Statistical Model for Seepage Observation of Concrete Dams. Large Dam Saf. 1992, 4, 1–10. [Google Scholar]
- Li, X.; Zhen, D.; Ju, Y. Input factor optimization study of dam seepage statistical model based on copula entropy theory. J. Hohai Univ. 2016, 44, 370–376. [Google Scholar]
- Zhang, Q.; Lin, C.; Xiang, W. Statistical regression analysis of seepage and seepage-pressure of gravity dam foundation of Shiban Hydropower Station. Rock Soil Mech. 2006, 27, 1831–1834. [Google Scholar] [CrossRef]
- Wei, B.; Gu, M.; Li, H.; Xiong, W.; Xu, Z. Modeling method for predicting seepage of RCC dams considering time-varying and lag effect. Struct. Control Health Monit. 2018, 25, 1–14. [Google Scholar] [CrossRef]
- Qiu, J.; Zhang, D.; Zhu, K. Seepage Monitoring Models Study of Earth-Rock Dams Influenced by Rainstorms. Math. Probl. Eng. 2016, 2016, 1656738. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Lv, P. Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA. Energies 2019, 12, 502. [Google Scholar] [CrossRef]
- Mei, Y.; Zhong, Y. Fuzzy extension evaluation model of dam seepage behavior based on entropy weight. Water Resour. Power 2011, 29, 58–61. [Google Scholar] [CrossRef]
- He, J.; Gao, Q.; Shi, Y. A multi-hierarchical comprehensive evaluation method of dam safety based on cloud model. Syst. Eng. Theory Pract. 2016, 36, 2977–2983. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q. Comprehensive Assessment of Dam Risk Consequences Caused by the Dam Failure Based on the Set Pair Analysis. Yellow River 2016, 38, 111–114. [Google Scholar] [CrossRef]
- Bui, K.T.T.; Bui, D.T.; Zou, J.; Van Doan, C.; Revhaug, I. A novel hybrid artificial intelligent approach based on neural fuzzy inference model and particle swarm optimization for horizontal displacement modeling of hydropower dam. Neural Comput. Appl. 2018, 29, 1495–1506. [Google Scholar] [CrossRef]
- Peyras, L.; Carvajal, C.; Felix, H.; Bacconnet, C.; Royet, P.; Becue, J.P.; Boissier, D. Probability-based assessment of dam safety using combined risk analysis and reliability methods—Application to hazards studies. Eur. J. Environ. Civ. Eng. 2012, 16, 795–817. [Google Scholar] [CrossRef]
- Fan, X.; Wu, J.; Shi, P.; Zhang, X.; Xie, Y. A novel automatic dam crack detection algorithm based on local-global clustering. Multimed. Tools Appl. 2018, 77, 26581–26599. [Google Scholar] [CrossRef]
- He, Y.; Zhao, M.; Wang, K.; Liu, P. Fuzzy Comprehensive Evaluation of Earth Rockfill Dam Seepage Security Risk Based on Cloud Model. Water Resour. Power 2018, 36, 83–86. [Google Scholar]
- Talona, A.; Curt, C. Selection of appropriate defuzzification methods: Application to the assessment of dam performance. Expert Syst. Appl. 2017, 70, 160–174. [Google Scholar] [CrossRef]
- Liu, S.; Yang, Y. Advances in grey system research (2004–2014). J. Nanjing Univ. Aeronaut. Astronaut. 2015, 47, 1–8. [Google Scholar] [CrossRef]
- Meng, W.; Liu, S.; Zeng, B.; Xie, N. Standard triangular whitenization weight function and its application in grey clustering evaluation. J. Grey Syst. 2012, 24, 39–48. [Google Scholar]
- Sun, W.; Li, L.; Zeng, H. Dam risk consequences comprehensive evaluation model based on the method of gray correlation. Yellow River 2012, 34, 102–104. [Google Scholar] [CrossRef]
- Hu, Y.; Shao, C.; Gu, C.; Meng, Z. Concrete Dam Displacement Prediction Based on an ISODATA-GMM Clustering and Random Coefficient Model. Water 2019, 11, 714. [Google Scholar] [CrossRef]
- Liu, Y. Dam Safety Evaluation Model & Its Application Based on Entropy Weight and Idea Point Method. Water Resour. Power 2016, 34, 73–76. [Google Scholar]
- Li, L.; Yang, B.; Wei, B. Cloud model of dam behavior safety diagnosis based on improved analytic hierarchy process. J. Water Resour. Water Eng. 2018, 29, 209–214. [Google Scholar] [CrossRef]
- Tao, C.; Chen, H.; Kong, S. Seepage Analysis of Clay Core Dam Based on Prototype Monitoring. J. Yangtze River Sci. Res. Inst. 2017, 34, 70–73. [Google Scholar] [CrossRef]
- Fu, X.; Zheng, D.; Su, G. Application of Improved Matter Element Extension Evaluation Method to Dam Seepage Assessment. J. China Three Gorges Univ. 2015, 37, 26–29. [Google Scholar] [CrossRef]
- Wu, Z. Safety Monitoring Theory & Its Application of Hydraulic Structures; Higher Education Press: Beijing, China, 1990; pp. 130–150. [Google Scholar]
- Zhang, X.; Xi, Q.; Liu, S. Application of GNSS monitoring data pretreatment to the prediction of deformation GNSS. Eng. Surv. Mapp. 2016, 25, 42–45. [Google Scholar] [CrossRef]
- Gu, C.S.; Wei, B.W.; Xu, Z.K.; Liu, D.W. Fluid-solid coupling model based on endochronic damage for roller compacted concrete dam. J. Cent. South Univ. 2013, 20, 3247–3255. [Google Scholar] [CrossRef]
- Zhao, B.; Ren, Y.; Gao, D.; Xu, L. Performance ratio prediction of photovoltaic pumping system basedon grey clustering and second curvelet neural network. Energy 2019, 171, 360–371. [Google Scholar] [CrossRef]
- Liu, S.; Xie, N. Grey System Theory and Application; Science Press: Beijing, China, 2013; pp. 5–18. [Google Scholar]
- Delgado, A.; Romero, I. Environmental conflict analysis using an integrated grey clustering and entropy-weight method: A case study of a mining project in Peru. Environ. Model. Softw. 2016, 77, 108–121. [Google Scholar] [CrossRef]
- Shemshadi, A.; Shirazi, H.; Toreihi, M.; Tarokh, M. A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting. Expert Syst. Appl. 2011, 38, 12160–12167. [Google Scholar] [CrossRef]
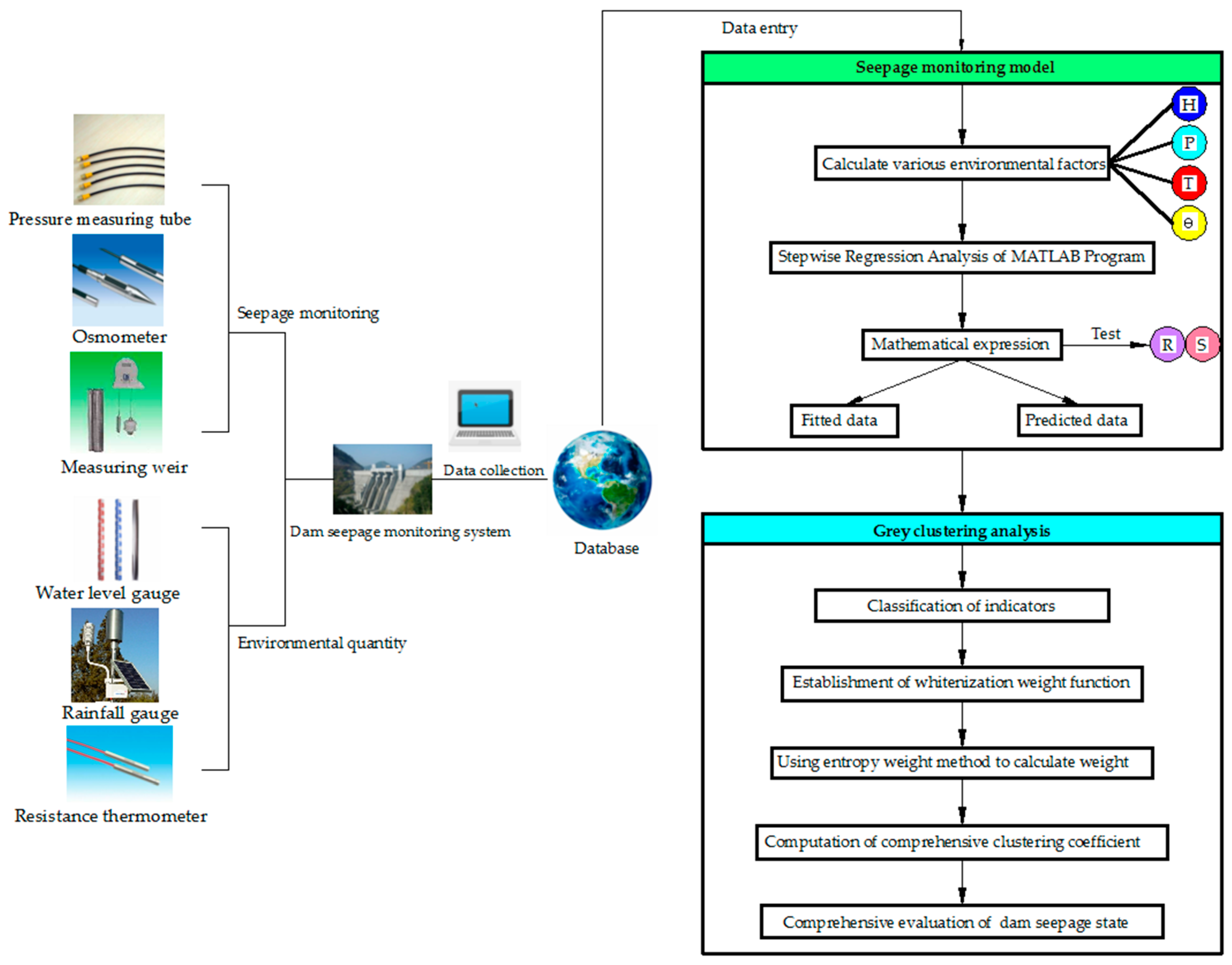



| Monitoring Object | Number of Monitoring Points | Monitoring Instrument |
|---|---|---|
| Dam seepage pressure | UP1, UP3, UP5, UP7, UP9, UP11, UP13, UP15, UP16 | Pressure measuring tube/osmometer |
| Dam leakage | WE1, WE2, WE3, WE4, WE7, WE10 | Measuring weir/osmometer |
| Seepage around dam | L1, L3, L5, L7, R1, R3, R5, R6 | Measuring weir/osmometer |
| Class | UP1 | UP3 | UP5 | UP7 | UP9 | UP11 | UP13 | UP15 | UP16 |
|---|---|---|---|---|---|---|---|---|---|
| Class Ⅰ | [0, 1.08] | [0, 0.63] | [0, 0.15] | [0, 2.76] | [0, 2.19] | [0, 3.03] | [0, 0.97] | [0, 3.54] | [0, 0.23] |
| Class Ⅱ | (1.08, 1.62] | (0.63, 0.94] | (0.15, 0.22] | (2.76, 4.14] | (2.19, 3.29] | (3.03, 4.54] | (0.97, 1.46] | (3.54, 5.32] | (0.23, 0.34] |
| Class Ⅲ | (1.62, +∞) | (0.94, +∞) | (0.22, +∞) | (4.14, +∞) | (3.29, +∞) | (4.54, +∞) | (1.46, +∞) | (5.32, +∞) | (0.34, +∞) |
| Information entropy | 61.902 | 60.892 | 66.481 | 60.338 | 57.992 | 54.404 | 36.561 | 9.097 | 9.094 |
| Weight | 0.071 | 0.069 | 0.076 | 0.069 | 0.066 | 0.062 | 0.041 | 0.009 | 0.009 |
| Class | WE1 | WE2 | WE3 | WE4 | WE7 | WE10 |
|---|---|---|---|---|---|---|
| Class Ⅰ | [0, 0.49] | [0, 0.13] | [0, 0.15] | [0, 0.75] | [0, 0.22] | [0, 0.40] |
| Class Ⅱ | (0.49, 0.74] | (0.13, 0.19] | (0.15, 0.23] | (0.75, 1.13] | (0.22, 0.33] | (0.40, 0.60] |
| Class Ⅲ | (0.74, +∞) | (0.19, +∞) | (0.23, +∞) | (1.13, +∞) | (0.33, +∞) | (0.60, +∞) |
| Information entropy | 8.464 | 12.763 | 4.495 | 9.217 | 12.511 | 10.045 |
| Weight | 0.009 | 0.014 | 0.005 | 0.010 | 0.013 | 0.010 |
| Class | L1 | L3 | L5 | L7 | R1 | R3 | R5 | R6 |
|---|---|---|---|---|---|---|---|---|
| Class Ⅰ | [0, 4.97] | [0, 4.65] | [0, 0.18] | [0, 0.91] | [0, 5.85] | [0, 5.39] | [0, 4.65] | [0, 5.80] |
| Class Ⅱ | (4.97, 7.46] | (4.65, 6.97] | (0.18, 0.26] | (0.91, 1.36] | (5.85, 8.77] | (5.39, 8.09] | (4.65, 6.98] | (5.80, 8.70] |
| Class Ⅲ | (7.46, +∞) | (6.97, +∞) | (0.26, +∞) | (1.36, +∞) | (8.77, +∞) | (8.09, +∞) | (6.98, +∞) | (8.70, +∞) |
| Information entropy | 42.261 | 36.613 | 59.311 | 66.776 | 46.283 | 45.546 | 74.592 | 39.119 |
| Weight | 0.048 | 0.041 | 0.068 | 0.076 | 0.053 | 0.052 | 0.085 | 0.044 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Chen, X.; Gu, C.; Huo, Z. Seepage Comprehensive Evaluation of Concrete Dam Based on Grey Cluster Analysis. Water 2019, 11, 1499. https://doi.org/10.3390/w11071499
Li J, Chen X, Gu C, Huo Z. Seepage Comprehensive Evaluation of Concrete Dam Based on Grey Cluster Analysis. Water. 2019; 11(7):1499. https://doi.org/10.3390/w11071499
Chicago/Turabian StyleLi, Junjie, Xudong Chen, Chongshi Gu, and Zhongyan Huo. 2019. "Seepage Comprehensive Evaluation of Concrete Dam Based on Grey Cluster Analysis" Water 11, no. 7: 1499. https://doi.org/10.3390/w11071499
APA StyleLi, J., Chen, X., Gu, C., & Huo, Z. (2019). Seepage Comprehensive Evaluation of Concrete Dam Based on Grey Cluster Analysis. Water, 11(7), 1499. https://doi.org/10.3390/w11071499







