Random Forest Ability in Regionalizing Hourly Hydrological Model Parameters
Abstract
1. Introduction
1.1. Why and How Do We Regionalize Hydrological Model Parameters?
1.2. Random Forest: A Potentially Useful Tool for Regionalization
1.3. Application of RF for Model Regionalization in Multiple Land-Use Environments
1.4. Context and Scope of the Study
2. Data
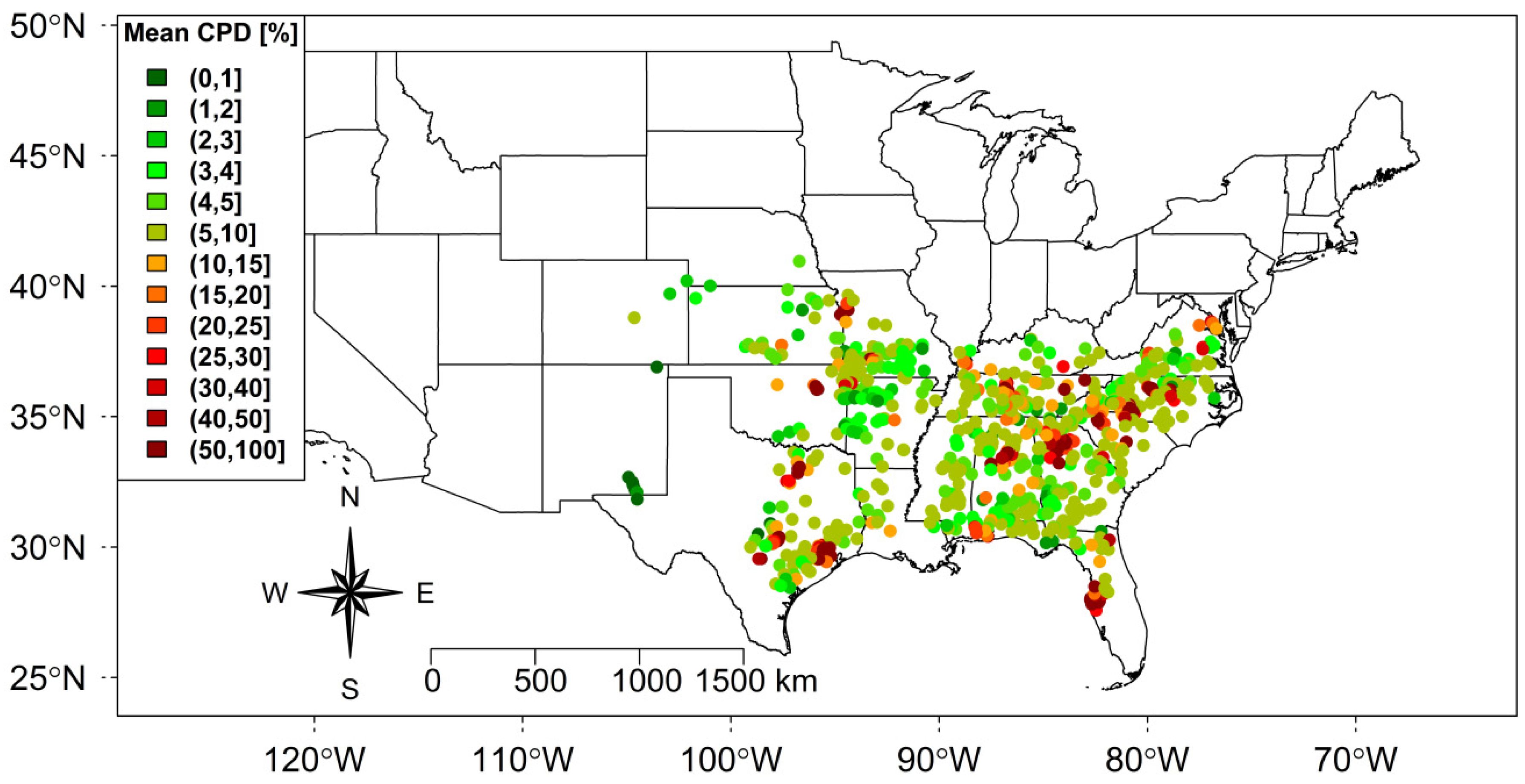
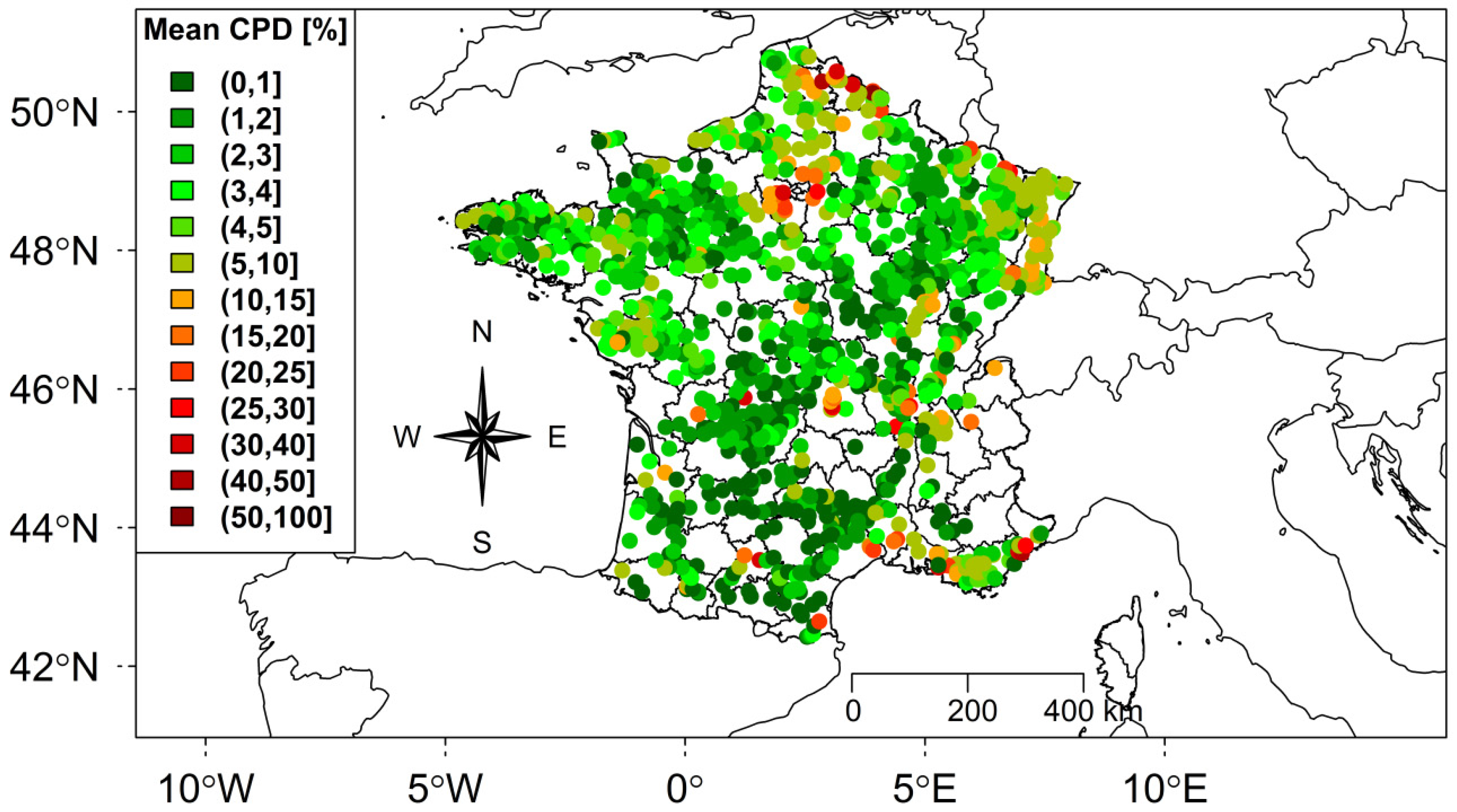
2.1. Sample Selection
2.2. Catchment Descriptors
- Climate: The catchment’s response inherits most of its variability from the catchment’s climate [66]. Many climate characteristics were computed over each catchment’s record period in order to limit their dependency on the record period. As climate descriptors, we considered mean hourly precipitations P (mm/h), mean hourly potential evapotranspiration PE (mm/h), humidity index HI (-), and flashiness of precipitations (-).
- Morphology: The catchment’s morphology is essential in predicting the catchment’s response timing and the repartition of precipitations into infiltration and runoff. For this reason, we used the catchment drained area (km2), drainage density (km/km2), and the median compound topographic index (-) as morphological descriptors.
- Land use: The catchment’s water yield and evapotranspiration losses depend on the catchment land use. Also, it is in our case of a central interest as we are dealing with the catchment’s level of urbanization. Thus, three land-use metrics were assessed: the CPD (%), the fraction of forest (%), and the fraction of open water (%).
- Geopedology: The catchment’s water transfers to and from the subjacent aquifers are modulated by the catchment’s geological and pedological characteristics. Hence, mean porosity (-), mean of log-transformed values of intrinsic permeability (m2), mean soil and subsoil content of gravel (%), silt (%), and clay (%) were considered as geopedological characteristics.
3. Methods
3.1. Model Parameters and Calibration
3.2. Estimating the Model Parameters at Ungauged Locations Using RF
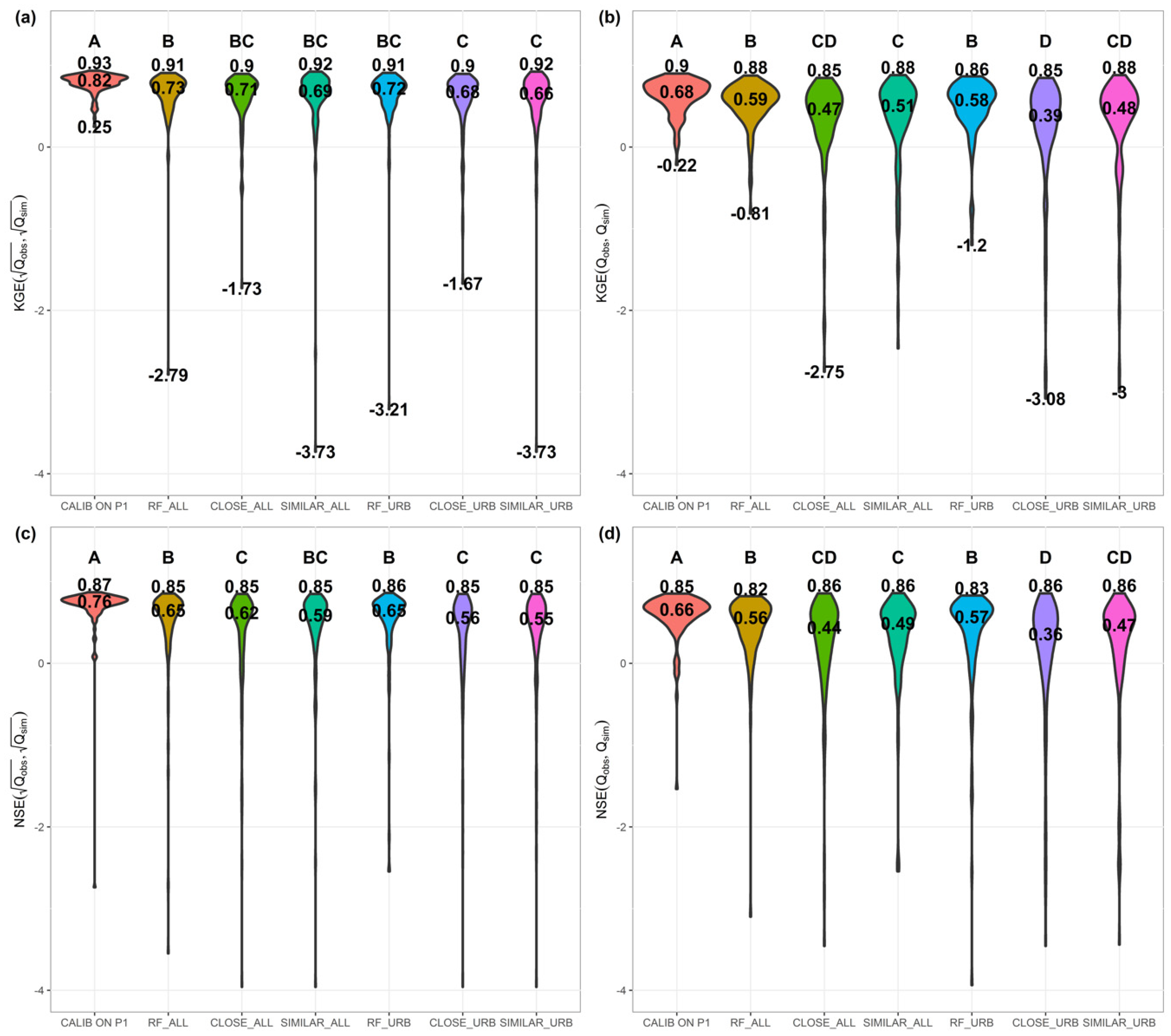
3.3. Benchmark Regionalization Techniques
- The RF-estimated parameters using the catchment descriptors.
- The transferred parameters from the closest neighbor catchment. Spatial closeness was computed by weighting the distances between the catchment centroids (80%) and outlets (20%) [97]. Close catchments were selected either from the whole 2105 catchments used to train the RF_ALL (Figure 4) or from the 119 urban catchments used to grow RF_URB.
- The transferred parameters from the most similar catchment with respect to the descriptors used to construct the RF. For each descriptor, the catchment ranks were determined. Then, the Euclidean distance between ranks was computed in the hyperspace of descriptors [15]. Similar catchments were selected either from the whole 2105 catchments used to construct the RF_ALL (Figure 4) or from the 119 urban catchments used to construct RF_URB.
4. Results
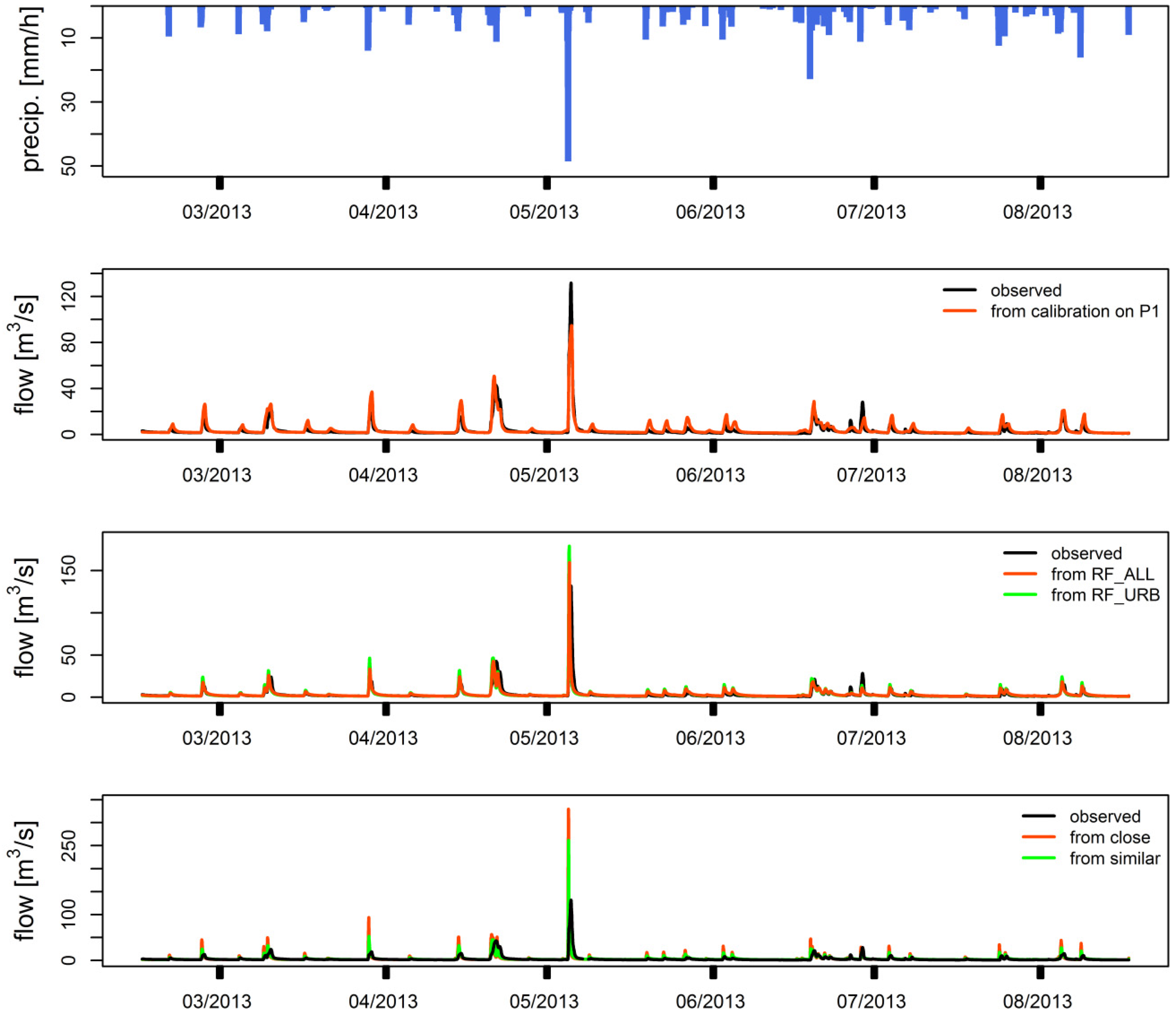
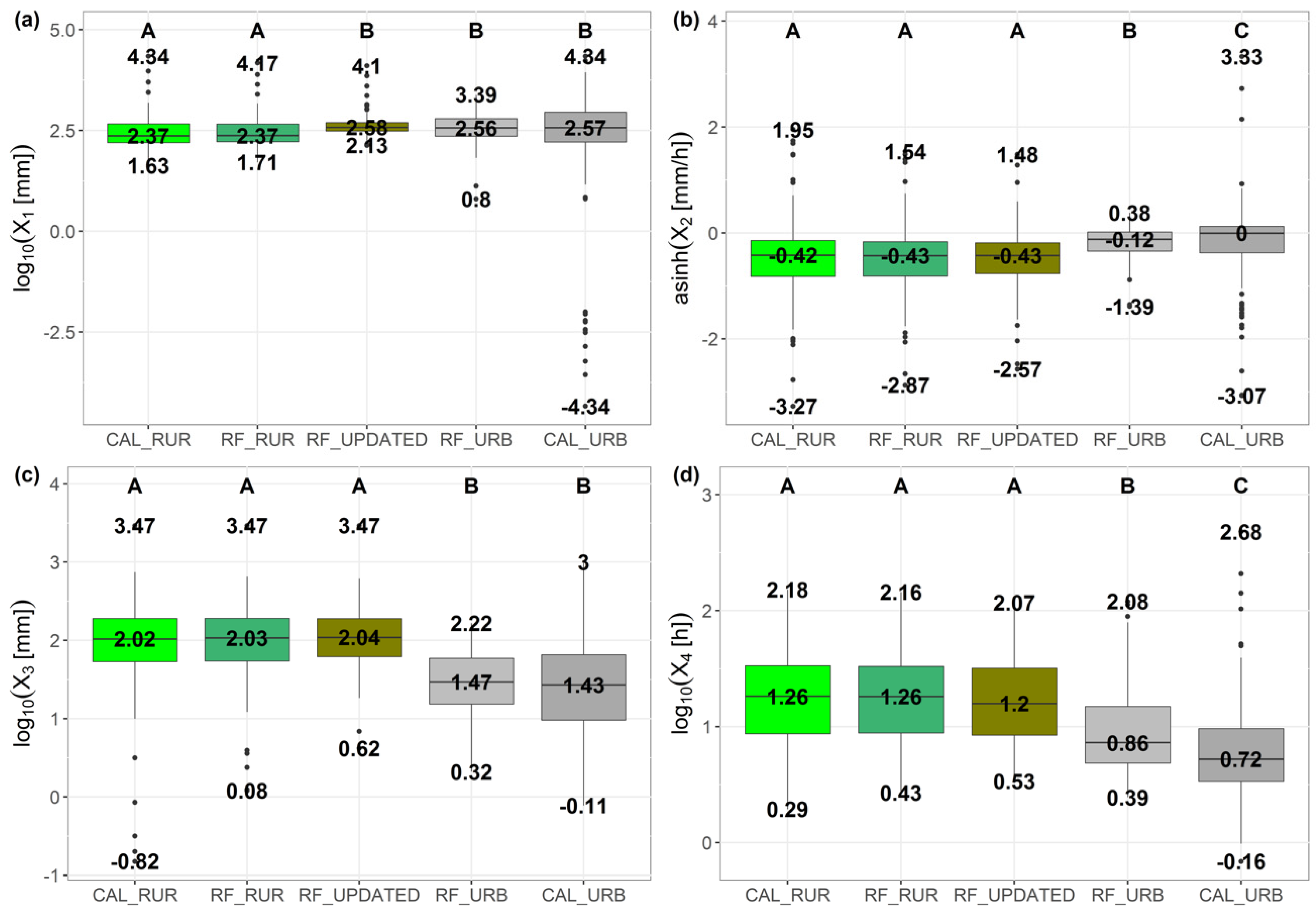
4.1. Model Performances and Estimated Parameters
4.2. Descriptor Importance
5. Discussion and Conclusions
5.1. Regionalization with RF: What Is Appreciated and What Is Depreciated?
5.2. Weak Sensitivity of the RF-Derived Relationships with the Urbanization Measure
5.3. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Beven, K. How far can we go in distributed hydrological modelling? Hydrol. Earth Syst. Sci. 2001, 5, 1–12. [Google Scholar] [CrossRef]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Beven, K. Beyond the Primer: Predictions in Ungauged Basins. In Rainfall-Runoff Modelling: The Primer; Wiley-Blackwell: Chichester, UK, 2012; pp. 329–342. ISBN 978-0-470-71459-1. [Google Scholar]
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; O’Connell, P.E.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Duan, Q.; Schaake, J.; Andréassian, V.; Franks, S.; Goteti, G.; Gupta, H.V.; Gusev, Y.M.; Habets, F.; Hall, A.; Hay, L.; et al. Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 2006, 320, 3–17. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Seibert, J. Regionalisation of parameters for a conceptual rainfall-runoff model. Agric. For. Meteorol. 1999, 98, 279–293. [Google Scholar] [CrossRef]
- Sefton, C.E.M.; Howarth, S.M. Relationships between dynamic response characteristics and physical descriptors of catchments in England and Wales. J. Hydrol. 1998, 211, 1–16. [Google Scholar] [CrossRef]
- Drogue, G.; Leviandier, T.; Pfister, L.; Idrissi, A.E.; Iffly, J.-F.; Hoffmann, L.; Guex, F.; Hingray, B.; Humbert, J. The applicability of a parsimonious model for local and regional prediction of runoff. Hydrol. Sci. J. 2002, 47, 905–920. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Regionalisation of catchment model parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Loumagne, C.; Michel, C. How informative is land-cover for the regionalization of the GR4J rainfall-runoff model? Lessons of a downward approach. IAHS Publ. 2006, 307, 246–255. [Google Scholar]
- Anderson, R.M.; Koren, V.I.; Reed, S.M. Using SSURGO data to improve Sacramento Model a priori parameter estimates. J. Hydrol. 2006, 320, 103–116. [Google Scholar] [CrossRef]
- Boughton, W.; Chiew, F. Estimating runoff in ungauged catchments from rainfall, PET and the AWBM model. Environ. Model. Softw. 2007, 22, 476–487. [Google Scholar] [CrossRef]
- Hundecha, Y.; Ouarda, T.B.M.J.; Bárdossy, A. Regional estimation of parameters of a rainfall-runoff model at ungauged watersheds using the “spatial” structures of the parameters within a canonical physiographic-climatic space. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid-based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Vandewiele, G.L.; Elias, A. Monthly water balance of ungauged catchments obtained by geographical regionalization. J. Hydrol. 1995, 170, 277–291. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalisation methods for catchment model parameters. Hydrol. Earth Syst. Sci. 2005, 9, 157–171. [Google Scholar] [CrossRef]
- Kim, U.; Kaluarachchi, J.J. Application of parameter estimation and regionalization methodologies to ungauged basins of the Upper Blue Nile River Basin, Ethiopia. J. Hydrol. 2008, 362, 39–56. [Google Scholar] [CrossRef]
- Oudin, L.; Kay, A.; Andréassian, V.; Perrin, C. Are seemingly physically similar catchments truly hydrologically similar? Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Andréassian, V.; Le Moine, N.; Perrin, C.; Ramos, M.-H.; Oudin, L.; Mathevet, T.; Lerat, J.; Berthet, L. All that glitters is not gold: the case of calibrating hydrological models: Invited Commentary. Hydrol. Process. 2012, 26, 2206–2210. [Google Scholar] [CrossRef]
- Fernandez, W.; Vogel, R.M.; Sankarasubramanian, A. Regional calibration of a watershed model. Hydrol. Sci. J. 2000, 45, 689–707. [Google Scholar] [CrossRef]
- Parajka, J.; Blöschl, G.; Merz, R. Regional calibration of catchment models: Potential for ungauged catchments. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Castiglioni, S.; Lombardi, L.; Toth, E.; Castellarin, A.; Montanari, A. Calibration of rainfall-runoff models in ungauged basins: A regional maximum likelihood approach. Adv. Water Resour. 2010, 33, 1235–1242. [Google Scholar] [CrossRef]
- Bourgin, F.; Andréassian, V.; Perrin, C.; Oudin, L. Transferring global uncertainty estimates from gauged to ungauged catchments. Hydrol. Earth Syst. Sci. 2015, 19, 2535–2546. [Google Scholar] [CrossRef]
- Olden, J.D.; Poff, N.L. Redundancy and the choice of hydrologic indices for characterizing streamflow regimes. River Res. Appl. 2003, 19, 101–121. [Google Scholar] [CrossRef]
- Yadav, M.; Wagener, T.; Gupta, H. Regionalization of constraints on expected watershed response behavior for improved predictions in ungauged basins. Adv. Water Resour. 2007, 30, 1756–1774. [Google Scholar] [CrossRef]
- Zhang, Z.; Wagener, T.; Reed, P.; Bhushan, R. Reducing uncertainty in predictions in ungauged basins by combining hydrologic indices regionalization and multiobjective optimization. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G.; Parajka, J.D. Regionalization methods in rainfall-runoff modelling using large catchment samples. IAHS Publ. 2006, 307, 117–125. [Google Scholar]
- Carbajal, J.P.; Bellos, V. An Overview of the Role of Machine Learning in Hydraulic and Hydrological Modeling. Available online: engrxiv.org/wgm72 (accessed on 25 April 2019).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Diez-Sierra, J.; del Jesus, M. Subdaily Rainfall Estimation through Daily Rainfall Downscaling Using Random Forests in Spain. Water 2019, 11, 125. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Muñoz, P.; Orellana-Alvear, J.; Willems, P.; Célleri, R. Flash-Flood Forecasting in an Andean Mountain Catchment—Development of a Step-Wise Methodology Based on the Random Forest Algorithm. Water 2018, 10, 1519. [Google Scholar] [CrossRef]
- Sultana, Z.; Sieg, T.; Kellermann, P.; Müller, M.; Kreibich, H. Assessment of Business Interruption of Flood-Affected Companies Using Random Forests. Water 2018, 10, 1049. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood hazard risk assessment model based on random forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Buchanan, B.; Auerbach, D.A.; Knighton, J.; Evensen, D.; Fuka, D.R.; Easton, Z.; Wieczorek, M.; Archibald, J.A.; McWilliams, B.; Walter, T. Estimating dominant runoff modes across the conterminous United States. Hydrol. Process. 2018, 32, 3881–3890. [Google Scholar] [CrossRef]
- Addor, N.; Nearing, G.; Prieto, C.; Newman, A.J.; Le Vine, N.; Clark, M.P. A Ranking of Hydrological Signatures Based on Their Predictability in Space. Water Resour. Res. 2018, 54, 8792–8812. [Google Scholar] [CrossRef]
- Booker, D.J.; Woods, R.A. Comparing and combining physically-based and empirically-based approaches for estimating the hydrology of ungauged catchments. J. Hydrol. 2014, 508, 227–239. [Google Scholar] [CrossRef]
- Carlisle, D.M.; Falcone, J.; Wolock, D.M.; Meador, M.R.; Norris, R.H. Predicting the natural flow regime: Models for assessing hydrological alteration in streams. River Res. Appl. 2010, 26, 118–136. [Google Scholar] [CrossRef]
- Snelder, T.H.; Lamouroux, N.; Leathwick, J.R.; Pella, H.; Sauquet, E.; Shankar, U. Predictive mapping of the natural flow regimes of France. J. Hydrol. 2009, 373, 57–67. [Google Scholar] [CrossRef]
- Brunner, M.I.; Seibert, J.; Favre, A.-C. Representative sets of design hydrographs for ungauged catchments: A regional approach using probabilistic region memberships. Adv. Water Resour. 2018, 112, 235–244. [Google Scholar] [CrossRef]
- Prieto, C.; Vine, N.L.; Kavetski, D.; Garcia, E.; Medina, R. Flow prediction in ungauged catchments using probabilistic Random Forests regionalization and new statistical adequacy tests. Water Resour. Res. 2019, 55, 4364–4392. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Li, M.; Post, D. Predicting Runoff Signatures Using Regression and Hydrological Modeling Approaches. Water Resour. Res. 2018, 54, 7859–7878. [Google Scholar] [CrossRef]
- Boulesteix, A.-L.; Janitza, S.; Kruppa, J.; König, I.R. Overview of random forest methodology and practical guidance with emphasis on computational biology and bioinformatics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2012, 2, 493–507. [Google Scholar] [CrossRef]
- Cheng, S.; Lee, C.; Lee, J. Effects of Urbanization Factors on Model Parameters. Water Resour. Manag. 2010, 24, 775–794. [Google Scholar] [CrossRef]
- Chen, R.; Chuang, W.-N.; Cheng, S. Effects of urbanization variables on model parameters for watershed divisions. Hydrol. Sci. J. 2014, 59, 1167–1183. [Google Scholar] [CrossRef]
- Kjeldsen, T.R.; Miller, J.D.; Packman, J.C. Modelling design flood hydrographs in catchments with mixed urban and rural land cover. Hydrol. Res. 2013, 44, 1040–1057. [Google Scholar] [CrossRef]
- Oudin, L.; Salavati, B.; Furusho-Percot, C.; Ribstein, P.; Saadi, M. Hydrological impacts of urbanization at the catchment scale. J. Hydrol. 2018, 559, 774–786. [Google Scholar] [CrossRef]
- Salavati, B.; Oudin, L.; Furusho-Percot, C.; Ribstein, P. Modeling approaches to detect land-use changes: Urbanization analyzed on a set of 43 US catchments. J. Hydrol. 2016, 538, 138–151. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Falcone, J.A. GAGES-II: Geospatial Attributes of Gages for Evaluating Streamflow; US Geological Survey: Reston, VA, USA, 2011.
- Hirsch, R.M.; Cicco, L.A.D. User guide to Exploration and Graphics for RivEr Trends (EGRET) and dataRetrieval: R packages for hydrologic data. In Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2015. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Homer, C.; Huang, C.; Yang, L.; Wylie, B.; Coan, M. Development of a 2001 national land-cover database for the United States. Photogramm. Eng. Remote Sens. 2004, 70, 829–840. [Google Scholar] [CrossRef]
- Homer, C.; Dewitz, J.; Fry, J.; Coan, M.; Hossain, N.; Larson, C.; Herold, N.; McKerrow, A.; VanDriel, J.N.; Wickham, J. Completion of the 2001 national land cover database for the counterminous United States. Photogramm. Eng. Remote Sens. 2007, 73, 337–341. [Google Scholar]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States–Representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Leleu, I.; Tonnelier, I.; Puechberty, R.; Gouin, P.; Viquendi, I.; Cobos, L.; Foray, A.; Baillon, M.; Ndima, P.-O. La refonte du système d’information national pour la gestion et la mise à disposition des données hydrométriques. Houille Blanche 2014, 25–32. [Google Scholar] [CrossRef]
- Büttner, G.; Kosztra, B.; Maucha, G.; Pataki, R. Implementation and Achievements of CLC2006; European Environment Agency (EEA): Barcelona, Spain, 2012. [Google Scholar]
- Poncelet, C. Du Bassin au Paramètre: Jusqu’où Peut-On Régionaliser un Modèle Hydrologique Conceptuel? Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2016. [Google Scholar]
- Budyko, M.I. Climate and Life; Internation Geophysics Series; Academic Press: New York, NY, USA, 1974; Volume 18. [Google Scholar]
- Tabary, P.; Dupuy, P.; L’henaff, G.; Gueguen, C.; Moulin, L.; Laurantin, O.; Merlier, C.; Soubeyroux, J.-M. A 10-year (1997–2006) reanalysis of Quantitative Precipitation Estimation over France: methodology and first results. IAHS Publ 2011, 351, 255–260. [Google Scholar]
- Hardegree, S.P.; Van Vactor, S.S.; Levinson, D.H.; Winstral, A.H. Evaluation of NEXRAD radar precipitation products for natural resource applications. Rangel. Ecol. Manag. 2008, 61, 346–353. [Google Scholar] [CrossRef]
- Horvat, D.J.; Horvat, C.A.; Calvert, C.; Crum, T. The Refreshed WSR-88 Level II Data Collection and Distribution Network; WSR-88D Radar Operations Center: Norman, OK, USA, 2011.
- Read, J.S.; Walker, J.I.; Appling, A.; Blodgett, D.L.; Read, E.K.; Winslow, L.A. Geoknife: Reproducible web-processing of large gridded datasets. Ecography 2015. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model? J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Vidal, J.-P.; Martin, E.; Franchistéguy, L.; Baillon, M.; Soubeyroux, J.-M. A 50-year high-resolution atmospheric reanalysis over France with the Safran system. Int. J. Climatol. 2010, 30, 1627–1644. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wei, Y.; Devarakonda, R.; Vose, R.S.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 3; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2016.
- Holko, L.; Parajka, J.; Kostka, Z.; Škoda, P.; Blöschl, G. Flashiness of mountain streams in Slovakia and Austria. J. Hydrol. 2011, 405, 392–401. [Google Scholar] [CrossRef]
- Bourgin, P.Y.; Lobligeois, F.; Peschard, J.; Andréassian, V.; Le Moine, N.; Coron, L.; Perrin, C.; Ramos, M.-H.; Khalifa, A. Description des Caractéristiques Morphologiques, Climatiques et Hydrologiques de 4436 Bassins Versants Français. Guide D’utilisation de la Base de Données Hydro-Climatique; Institut national de Recherche en Sciences et Technologies pour l’Environnement et l’Agriculture (IRSTEA): Antony, France, 2010; p. 37. [Google Scholar]
- Bocinsky, R.K.; Beaudette, D.; Chamberlain, S. FedData: Functions to Automate Downloading Geospatial Data Available from Several Federated Data Sources. Available online: https://CRAN.R-project.org/package=FedData (accessed on 14 December 2017).
- Verdin, K.L. Hydrologic Derivatives for Modeling and Analysis—A New Global High-Resolution Database; Data Series; U.S. Geological Survey: Reston, VA, USA, 2017; p. 24.
- Gleeson, T.; Moosdorf, N.; Hartmann, J.; Beek, L.P.H. A glimpse beneath earth’s surface: GLobal HYdrogeology MaPS (GLHYMPS) of permeability and porosity. Geophys. Res. Lett. 2014, 41, 3891–3898. [Google Scholar] [CrossRef]
- FAO/IIASA/ISRIC/ISS-CAS/JRC. Harmonized World Soil Database; FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2012. [Google Scholar]
- LeBauer, D. An R Package for Using the Harmonized World Soil Database (HWSD): Dlebauer/Rhwsd. Available online: https://rdrr.io/github/dlebauer/rhwsd/ (accessed on 10 November 2018).
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Le Moine, N. Le Bassin Versant de Surface vu par le Souterrain: Une Voie D’amélioration des Performances et du Réalisme des Modèles Pluie-Débit? Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2008. [Google Scholar]
- Mathevet, T. Quels Modèles Pluie-Débit Globaux Pour le pas de Temps Horaire? Développement Empirique et Comparaison de Modèles sur un Large Echantillon de Bassins Versants. Ph.D. Thesis, ENGREF (Paris), Paris, France, 2005. [Google Scholar]
- Ficchi, A. An Adaptive Hydrological Model for Multiple Time-Steps: Diagnostics and Improvements Based on Fluxes Consistency. Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2017. [Google Scholar]
- van Esse, W.R.; Perrin, C.; Booij, M.J.; Augustijn, D.C.M.; Fenicia, F.; Kavetski, D.; Lobligeois, F. The influence of conceptual model structure on model performance: A comparative study for 237 French catchments. Hydrol. Earth Syst. Sci. 2013, 17, 4227–4239. [Google Scholar] [CrossRef]
- Edijatno; De Oliveira Nascimento, N.; Yang, X.; Makhlouf, Z.; Michel, C. GR3J: A daily watershed model with three free parameters. Hydrol. Sci. J. 1999, 44, 263–277. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Breiman, L.; Cutler, A. Random Forests. Available online: https://www.stat.berkeley.edu/~breiman/RandomForests (accessed on 6 May 2019).
- Biau, G.; Scornet, E. A random forest guided tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C.; Villa-Vialaneix, N. Random Forests for Big Data. Big Data Res. 2017, 9, 28–46. [Google Scholar] [CrossRef]
- Ziegler, A.; König, I.R. Mining data with random forests: current options for real-world applications. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 55–63. [Google Scholar] [CrossRef]
- Lebecherel, L.; Andréassian, V.; Perrin, C. On regionalizing the Turc-Mezentsev water balance formula. Water Resour. Res. 2013, 49, 7508–7517. [Google Scholar] [CrossRef]
- Diem, J.E.; Hill, T.C.; Milligan, R.A. Diverse multi-decadal changes in streamflow within a rapidly urbanizing region. J. Hydrol. 2018, 556, 61–71. [Google Scholar] [CrossRef]
- Mejía, A.I.; Moglen, G.E. Impact of the spatial distribution of imperviousness on the hydrologic response of an urbanizing basin. Hydrol. Process. 2010, 24, 3359–3373. [Google Scholar] [CrossRef]
- Singh, V.P.; Woolhiser, D.A. Mathematical Modeling of Watershed Hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Wilson, B.N.; Gulliver, J.S. Improved methods to estimate the effective impervious area in urban catchments using rainfall-runoff data. J. Hydrol. 2016, 536, 109–118. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef] [PubMed]
- Besaw, L.E.; Rizzo, D.M.; Bierman, P.R.; Hackett, W.R. Advances in ungauged streamflow prediction using artificial neural networks. J. Hydrol. 2010, 386, 27–37. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Streamflow Prediction in Ungauged Basins: Review of Regionalization Methods. J. Hydrol. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Breiman, L. Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Iorgulescu, I.; Beven, K.J. Nonparametric direct mapping of rainfall-runoff relationships: An alternative approach to data analysis and modeling? Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Andréassian, V.; Bourgin, F.; Oudin, L.; Mathevet, T.; Perrin, C.; Lerat, J.; Coron, L.; Berthet, L. Seeking genericity in the selection of parameter sets: Impact on hydrological model efficiency. Water Resour. Res. 2014, 50, 8356–8366. [Google Scholar] [CrossRef]


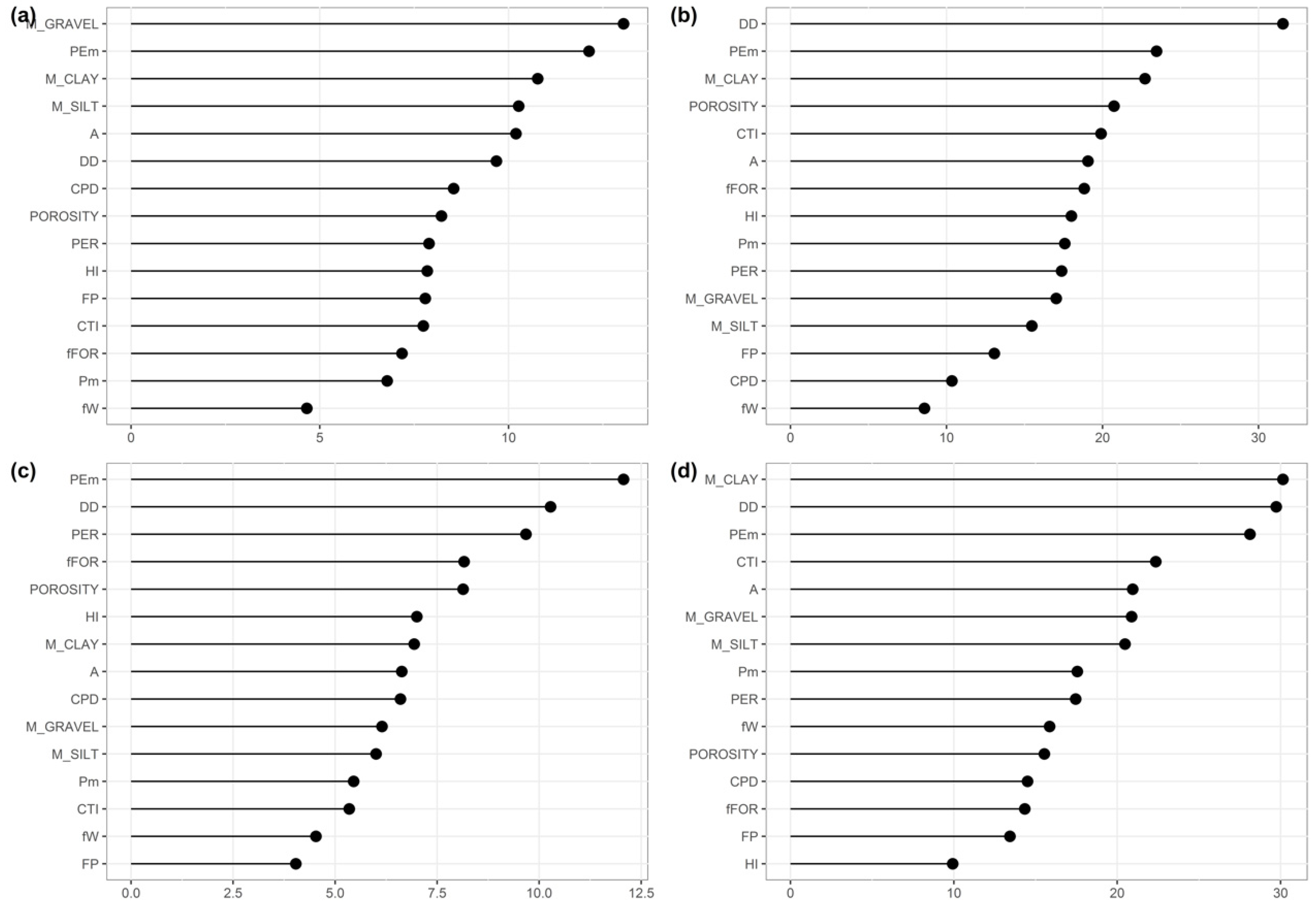
| Notation | Index Name | Computation | Unit | Data Source |
|---|---|---|---|---|
| Pm | Mean hourly precipitation | Total depth of precipitations over the recorded period (8–16 years) divided by the number of hours, aggregated spatially to the catchment scale | mm/h | COMEPHORE product of Meteo-France, 1-km resolution [67] and NEXRAD Stage IV dataset, 4-km resolution, extracted using the geoknife R Package [68,69,70] |
| PEm | Mean hourly potential evapotranspiration | Total depth of potential evapotranspiration over the recorded period (8–16 years) divided by the number of hours, aggregated spatially to the catchment scale | mm/h | Evaluated using temperature-based formula [71]. Daily temperature was extracted from SAFRAN product of Meteo-France, 8-km resolution [72] and Daymet dataset, 1-km resolution [73] |
| HI | Humidity index | — | Pm and PEm data sources | |
| FP | Flashiness of precipitation | , with Pi the precipitation depth (mm) at hour i [74] | — | Pi data source |
| A | Catchment area | — | km2 | [57,75] |
| DD | Drainage density | , with Li length of stream i (km) and A the catchment area (km2) | km/km2 | The hydrographic networks were extracted from the BD Carthage dataset (France) and the National Hydrography Dataset NHD (USA) using the FedData R Package [76] |
| CTI | Median compound topographic index | , with As,i the ith cell’s specific area and βi its slope angle | — | [77] |
| CPD | Catchment percent developed | Sum of the pixels attributed to urbanization classes divided by the total number of pixels | % | National Land Cover Database (NLCD) 2001, 2006, and 2011 (USA) and CLC 1990, 2000, 2006, and 2012 (France) |
| fW | Fraction of open water | Sum of pixels occupied by open water class divided by the total number of pixels | % | NLCD 2001, 2006, and 2011 (USA) and CLC 1990, 2000, 2006, and 2012 (France) |
| fFOR | Fraction of forest | Sum of pixels occupied by forest classes divided by the total number of pixels | % | NLCD 2001, 2006, and 2011 (USA) and CLC 1990, 2000, 2006, and 2012 (France) |
| POROSITY | Mean porosity of the catchment’s soil and subsoil geologic units | Volume of voids divided by the total volume | — | GLobal HYdrogeology MaPS (GLHYMPS) [78] |
| PER | Mean of logarithm values of soil and subsoil permeability | — | log(m2) | GLobal HYdrogeology MaPS (GLHYMPS) [78] |
| M_GRAVEL | Mean gravel content of soil and subsoil geologic units | — | % | Harmonized World Soil Database HWSD (Version 1.2) [79,80] |
| M_SILT | Mean silt content of soil and subsoil geologic units | — | % | Harmonized World Soil Database HWSD (Version 1.2) [79,80] |
| M_CLAY | Mean clay content of soil and subsoil geologic units | — | % | Harmonized World Soil Database HWSD (Version 1.2) [79,80] |
| Parameter | Objective Function | Using the 2105 Catchments | Using the 119 Urban Catchments | ||||
|---|---|---|---|---|---|---|---|
| RF | CLOSE | SIMILAR | RF | CLOSE | SIMILAR | ||
| X1 | KGESR | 0.476 *** | 0.361 *** | 0.367 *** | 0.448 *** | 0.367 *** | 0.33 *** |
| KGE | 0.144 *** | 0.077 ** | 0.066 ** | 0.08 ** | 0.047 * | 0.085 ** | |
| NSESR | 0.53 *** | 0.353 *** | 0.332 *** | 0.434 *** | 0.301 *** | 0.25 *** | |
| NSE | 0.152 *** | 0.084 ** | 0.066 ** | 0.111 *** | 0.034 * | 0.069 ** | |
| X2 | KGESR | 0.022 | 0.037 * | 0.062 ** | 0.009 | 0.014 | 0.064 ** |
| KGE | 0.054 * | 0.053 * | 0.098 *** | 0.064 ** | 0.011 | 0.045 * | |
| NSESR | 0.109 *** | 0.026 | 0.056 ** | 0.064 ** | 0.023 | 0.002 | |
| NSE | 0.11 *** | 0.085 ** | 0.047 * | 0.067 ** | 0.105 *** | 0.036 * | |
| X3 | KGESR | 0.449 *** | 0.275 *** | 0.213 *** | 0.346 *** | 0.194 *** | 0.173 *** |
| KGE | 0.222 *** | 0.147 *** | 0.094 *** | 0.245 *** | 0.094 *** | 0.069 ** | |
| NSESR | 0.408 *** | 0.444 *** | 0.333 *** | 0.442 *** | 0.374 *** | 0.202 *** | |
| NSE | 0.318 *** | 0.225 *** | 0.277 *** | 0.405 *** | 0.227 *** | 0.245 *** | |
| X4 | KGESR | 0.287 *** | 0.082 ** | 0.207 *** | 0.438 *** | 0.077 ** | 0.207 *** |
| KGE | 0.301 *** | 0.076 ** | 0.201 *** | 0.415 *** | 0.09 *** | 0.167 *** | |
| NSESR | 0.417 *** | 0.064 ** | 0.355 *** | 0.578 *** | 0.1 *** | 0.396 *** | |
| NSE | 0.613 *** | 0.121 *** | 0.284 *** | 0.604 *** | 0.096 *** | 0.262 *** | |
| Source | Parameters | Score Whole | Score Period | MaxSim/MaxObs Period | |||
|---|---|---|---|---|---|---|---|
| X1 (mm) | X2 (mm/h) | X3 (mm) | X4 (h) | ||||
| Calibration over P1 | 973.92 | 0.13 | 9.36 | 19.7 | 0.824 | 0.818 | 0.72 |
| RF_ALL | 1258.52 | 0.1 | 32.92 | 7.71 | 0.872 | 0.819 | 1.21 |
| RF_URB | 1250.69 | 0.08 | 22.87 | 7.44 | 0.876 | 0.821 | 1.36 |
| Close | 1269.62 | 0.14 | 13.27 | 3.34 | 0.719 | 0.6 | 2.5 |
| Similar | 1394.09 | 0.19 | 25.53 | 3.86 | 0.807 | 0.722 | 1.98 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saadi, M.; Oudin, L.; Ribstein, P. Random Forest Ability in Regionalizing Hourly Hydrological Model Parameters. Water 2019, 11, 1540. https://doi.org/10.3390/w11081540
Saadi M, Oudin L, Ribstein P. Random Forest Ability in Regionalizing Hourly Hydrological Model Parameters. Water. 2019; 11(8):1540. https://doi.org/10.3390/w11081540
Chicago/Turabian StyleSaadi, Mohamed, Ludovic Oudin, and Pierre Ribstein. 2019. "Random Forest Ability in Regionalizing Hourly Hydrological Model Parameters" Water 11, no. 8: 1540. https://doi.org/10.3390/w11081540
APA StyleSaadi, M., Oudin, L., & Ribstein, P. (2019). Random Forest Ability in Regionalizing Hourly Hydrological Model Parameters. Water, 11(8), 1540. https://doi.org/10.3390/w11081540





