Abstract
Flood forecasting is an essential requirement in integrated water resource management. This paper suggests a Long Short-Term Memory (LSTM) neural network model for flood forecasting, where the daily discharge and rainfall were used as input data. Moreover, characteristics of the data sets which may influence the model performance were also of interest. As a result, the Da River basin in Vietnam was chosen and two different combinations of input data sets from before 1985 (when the Hoa Binh dam was built) were used for one-day, two-day, and three-day flowrate forecasting ahead at Hoa Binh Station. The predictive ability of the model is quite impressive: The Nash–Sutcliffe efficiency (NSE) reached 99%, 95%, and 87% corresponding to three forecasting cases, respectively. The findings of this study suggest a viable option for flood forecasting on the Da River in Vietnam, where the river basin stretches between many countries and downstream flows (Vietnam) may fluctuate suddenly due to flood discharge from upstream hydroelectric reservoirs.
1. Introduction
Flooding is a significant cause of social and economic losses, as well as the loss of human life. It poses a potential danger to densely populated areas located next to and downstream of major rivers. Accurate forecasting of flood flow is an essential requirement for reducing the risk of flooding and is important for planning and managing water resources systems. However, accurate forecasting of river discharge is a difficult problem because river flood stage analysis is a complex dynamic process characterized by spatial and temporal variations. In addition, the river flow process is nonlinear and influenced by many factors such as river basin surface mantle, the rainfall process, as well as riverbed terrain and climatic characteristics. Many predictive measures, which require an enormous amount of data for forecasting, have been proposed to mitigate or prevent the effects of floods.
Currently, there are two approaches for flow prediction. The first method consists of mathematical models that simulate the hydrodynamic process of the water’s flow. This first approach is a widely used method because the mathematical models are based on concepts of hydraulics and hydrology. These models generally have a tendency to require a large amount of input data (i.e., rainfall forecasts and topography data) which may not always be available or could be difficult to obtain. In addition, the parameters of the model need to be tested and evaluated carefully as these parameters are regionally dependent, and sometimes it is difficult to estimate or calibrate the parameters that fit the model. As a result, models do not gain good performance especially in areas where available data is limited. Moreover, process-based methods have limitations regarding flood warnings because the runtime of these models is usually quite long [1]. Another drawback of conventional hydrological models is that these models do not predict the increase of the downstream flow if the upstream flow has sudden fluctuations caused by the discharge from large dams and reservoirs, especially for large river basins located in many countries.
The second approach for predicting river flow consists of data-driven methods, based on the statistical relationship between input and output data. One of the common data-driven models is the Artificial Neural Network (ANN) model. The amount of data required for the models, as well as the ability of the model to both linear and nonlinear systems without the need to make any assumptions, are implicit in most traditional statistical approaches. The data-driven approach, ANNs, may offer a promising alternative to the existing methods for the hydrological forecast of streamflow [2]. With the development of computer science in the last two decades, the ANN models have been widely used in various aspects of science and engineering because of the simplicity of its model structure. Researchers have applied various neural network model techniques such as using them alone or in combination with process-based models to reduce errors and improve the models’ prediction accuracy. Yaseen et al. [3] reviewed papers on the application of Artificial Intelligence (AI) based on models for streamflow forecasting from 2000 to 2015 and indicated that the AI had exhibited significant progress in forecasting and modeling non-linear hydrological problems. This paper also recommends the potential application of ANNs in modeling and forecasting streamflow. In addition, several studies in which the ANN model-based approaches were used for river stage forecasting are reviewed in the following paragraphs.
An ANN model was developed by Hidayat et al. [4] to forecast discharge in a tidal river for the Mahakam River, Indonesia. Input data includes information on upstream water levels, tide levels, and flow rates. The performance of the model is evaluated through three criteria: The coefficient of determination (R2), the Nash–Sutcliffe efficiency (NSE), and the root mean square error (RMSE). The study revealed that it could predict discharge for two days with reliable performance and the ANN model could be used to fill data gaps in a disrupted discharge on a time series scale. Elsafi [5] suggested an ANN model for one-day flowrate forecasting at the Dongola station in the Nile River basin (Sudan) based on upstream flow data. The author concluded that the ANN model provided a reliable means of detecting the flood hazard on the river with an accuracy (R2 value) of about 97%. This acts as a precursor to the establishment of a flood warning system for certain sections of the Nile River. Khan et al. [6] established an ANN model that exploited daily information data of discharge and water level at the stations along the river as the inputs to forecast one-day streamflow ahead for the Ramgama River in India. The results of this research demonstrated that the selected model could be useful for predicting discharge and water level for the Ramganga River with an accuracy of about 93.4% for monsoon flow pattern. Sung et al. [7] constructed an ANN model for hourly water level forecasting at Anyangcheon Stream, Korea with a lead-time of one to three hours. The model’s accuracy was validated by three statistical methods: RMSE, R2, and NSE. They concluded that the model provided good results when forecasting a one-hour to two-hour water levels.
In addition, several other techniques have also been combined with data-driven models to improve flow forecasting performance, for example, support vector regression [8], fuzzy inference systems [9], back-propagation neural network algorithms [10], genetic algorithms [11,12], and wavelet neural networks [11,13]. The review of the aforementioned studies illustrates the potential of ANN models for related hydrology fields. However, according to Govindaraju [14], the understanding of watershed processes is a limit of the ANNs model. Additionally, there is no specific reference for selecting architectures and parameters within the ANN network [5,15], as well as no really effective solution for sequential data problems such as hydrological problems [16]. Another major issue with ANNs is the lack of memory when calculating problems with sequential or time series data [17,18].
Recently, owing to the breakthrough in the field of computational science, deep learning or deep neural network (DNN) methods based on ANNs have received a growing interest both academically and practicality from scientists [18]. Moreover, the Long Short-Term Memory (LSTM) neural network, one of the state-of-the-art applications of DNN, has been successfully applied in various fields (especially for time sequence problems) such as: Speech recognition [19], machine translation [20,21], language modeling [22], tourism field [23,24], stock prediction [25], and rainfall-runoff simulation [16,26,27]. Several LSTM studies listed above suggest that LSTM-based models have been successfully used in various fields, and can be applicable to river flow forecasting.
In this research, we constructed several models of LSTM and have applied these models to forecast discharge at the Hoa Binh Station on the Da River, one of the largest river basins in Vietnam. Da River has an abundant flow, flowing through high mountain areas stretching from China to Vietnam, and yields significant hydroelectric power. The existence of large hydropower dams and reservoirs in China (upstream of Da River) causes significant difficulties in forecasting downstream flows, which flows through Vietnam. LSTM models have been developed for one-day, two-day, and three-day flowrate forecasting in advance at Hoa Binh Station. Rainfall and flowrate at meteorological and hydrological stations in the study area are input data of the model. In addition to evaluating the model’s ability in predicting flood flows as well as predicting flood peaks, the influence of the dataset characteristics on model performance is also of interest. Two scenarios of the LSTM model with different combinations of input data sets were proposed in turn for three forecasting cases.
2. Methodology
2.1. Study Area and Data
The Da River, located in the northwest area of Vietnam, is the largest tributary of the Red River system, one of the largest river systems in Vietnam. Originating from Yunnan Province in China, the Da River basin stretches out in a northwest-southeast direction. In Vietnam, the river flows through the Lai Chau, Dien Bien, Son La, and Hoa Binh provinces, before joining the Red River in Phu Tho province. The Da River basin covers an area of 52,900 km2, in which approximately 50% (26,800 km2) of the basin area is in Vietnam. It flows through the high mountain area in Vietnam and has an abundant flow, which yields substantial hydroelectric power. In addition, due to the topographical characteristics of the area, the distribution of rainfall on the basin is uneven in spatial and temporal. Rainfall concentrates mainly from May to September, accounting for 85–88% of the total annual rainfall. Information on the maximum daily precipitation and peak flood discharge in this area are summarized in Table 1. Currently, there are three large hydroelectric plants on the Da River, namely: The Hoa Binh Dam (1994), the Son La Dam (2012), and the Lai Chau Dam (2016) with the total combined power capacity of about 5520 MW.

Table 1.
Information on maximum daily precipitation and peak flood discharge on the Da River.
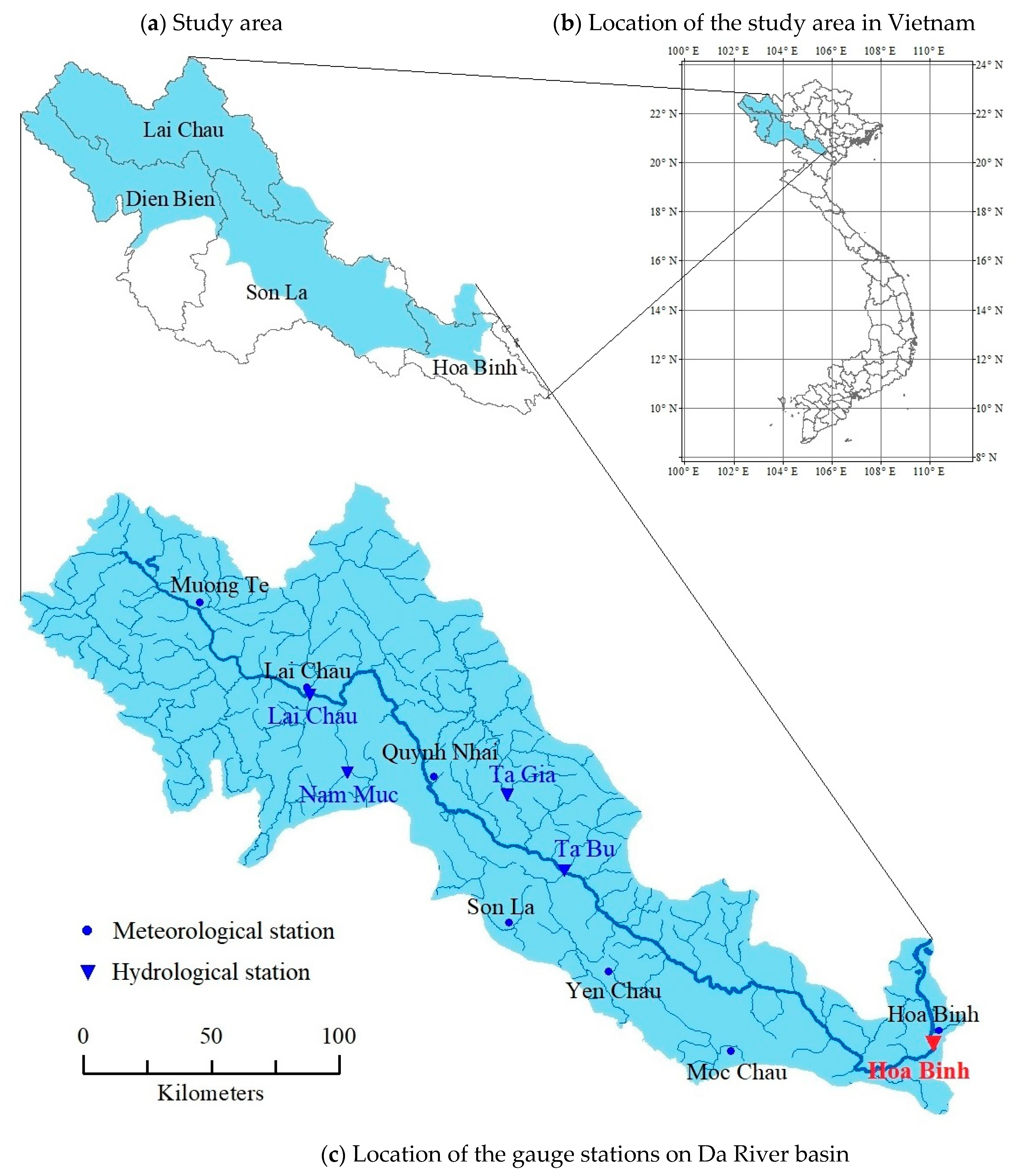
This study focuses on assessing the model’s ability in flood forecasting and the effects of input data characteristics on model performance (sequential data). Therefore, the type of input data, the amount of input data, and the correlation of the data series are considered. The daily measured data was retrieved from hydrographic data at the Vietnam National Center for Hydro-meteorological Forecasting from the period between 1961 to 1984 before the Hoa Binh Dam was built. The LSTM model was constructed to forecast the flood flowrate at the Hoa Binh Station with one day, two days, and three days of lead time. Location of gauge stations in the study area is shown in Figure 1.
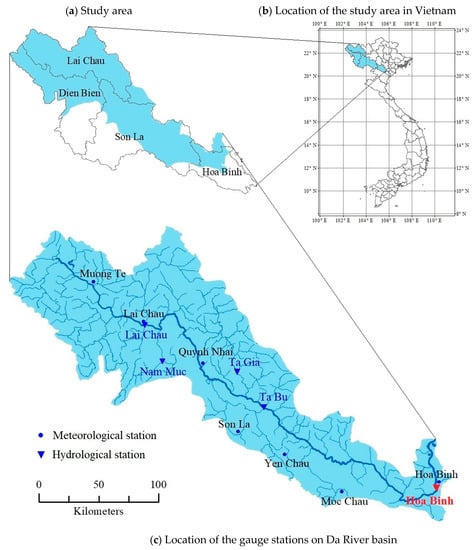
Figure 1.
Location of the study area and the gauge stations. (a) Description of Da River basin in provinces of Vietnam; (b) Description of provinces in Vietnam; (c) Description of location of gauge stations on the Da River basin.
The data collected in the study area included data on daily flowrate and precipitation. The length of the collected data series, information on hydro-meteorological stations, as well as the correlation between the flow data series at Hoa Binh station with other data series, are provided in Table 2. The rainfall was measured in millimeters (mm) and the flowrate was measured in cubic meters per second (m3/s).

Table 2.
Information about hydrological stations.
2.2. Artificial Neural Network (ANN)
An ANN is a computing system inspired by the human nervous system. It is based on theories of the massive interconnection and parallel processing architecture of the biological system. An ANN model is a data-driven mathematical model that has the ability to solve problems through machine-learning neurons. One of the advantages of ANNs is they are capable of identifying complex nonlinear relationships between inputs and outputs without inputting direct knowledge or physical processes [28]. The relationship between inputs and output has the following form [17]:
Here, Xn is the n-dimensional input vector consisting of variables X1, …, Xi, …, Xn; Y is the output vector. The functional form of f(.) in Equation (1) is not revealed explicitly by the model; rather, the network parameters will represent it.
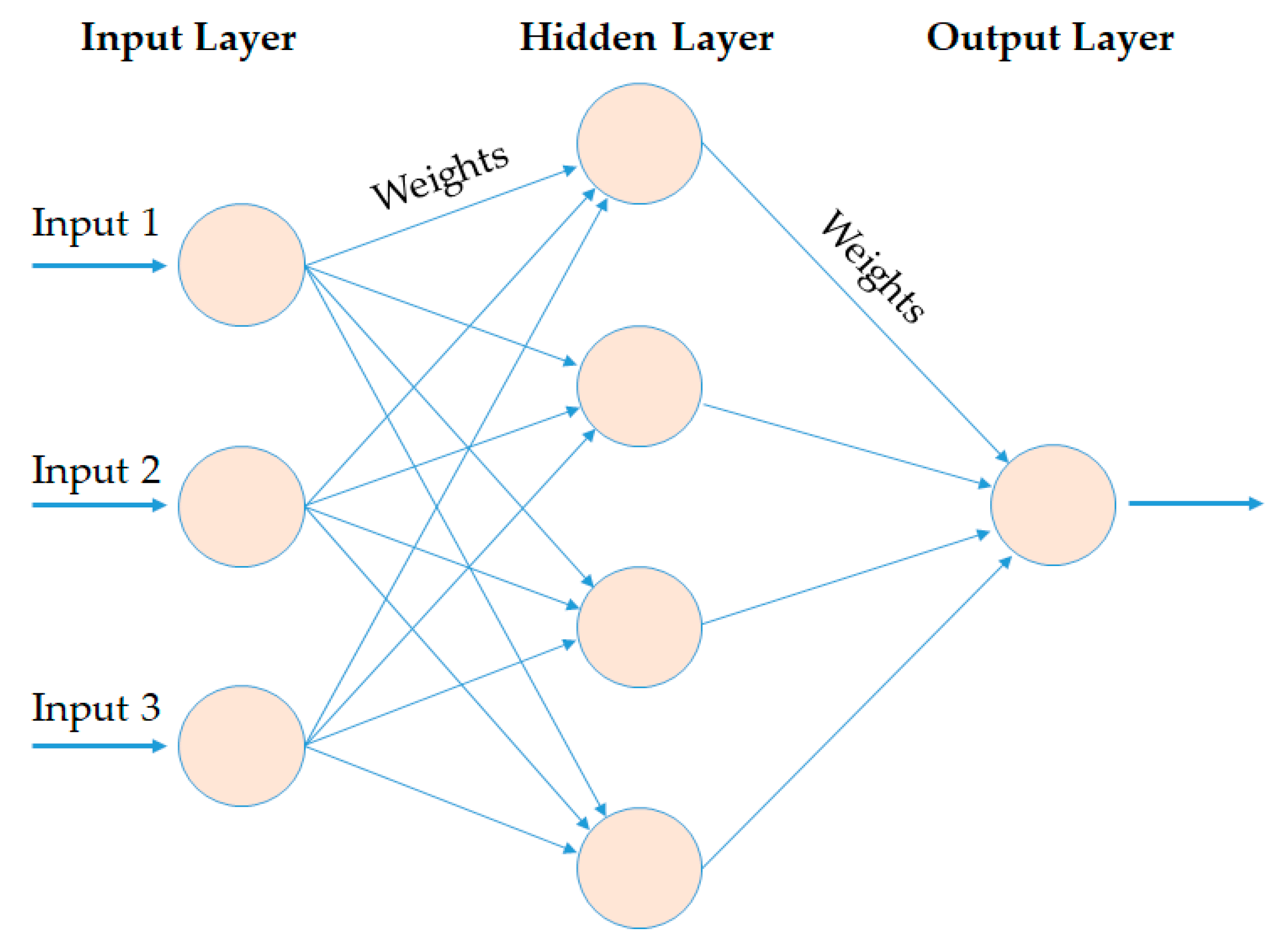
The most common type of ANNs consists of three layers, namely: An input layer, a hidden layer, and an output layer. In an ANN, the input and output data layers are independent of each other. Between the input and output layers, one or more hidden layers are often connected by weight matrices, bias, and several activation functions. Figure 2 schematically illustrates a typical ANN architecture.
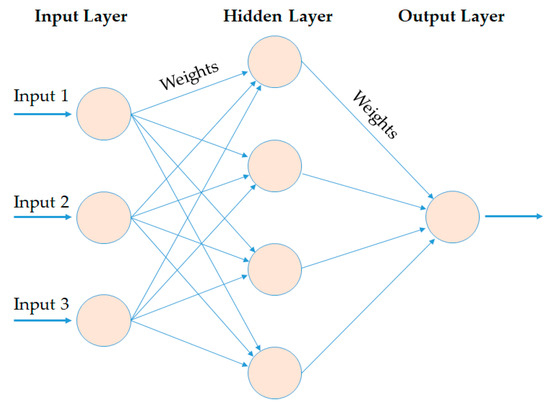
Figure 2.
Schematic of a typical Artificial Neural Network (ANN) architecture.
The main differences between the various types of ANNs involve network architecture. The architectural complexity of an ANN is closely related to the number of hidden layers as well as the number of neurons in each hidden layer. The number of hidden layers depends on the characteristics of the input data set such as data type or data size. In general, there is no specific rule for selecting these parameters. They can be determined based on the training and evaluation process through optimization of errors.
Typically, a neural network model is trained using the stochastic gradient descent optimization algorithm and weights are updated through the backpropagation algorithm based on the errors calculated from the loss function. In most neural networks, the loss function is a function that calculates the difference between the actual output and the predicted output. For different problems, such as regression or classification, different loss functions will be applied because of their direct relevance to the activation function used in the output layer of the neural networks. The backpropagation training algorithm is a supervised learning algorithm that allows the network to update the weights of neural networks to optimize the loss function. The current error is propagated backward to a previous layer by calculating gradients of the loss function. This means that the gradients have a tendency to become smaller as the calculation continues to move backwards in the network. As a result, neurons in the earlier layers learn very slowly and the training process takes a long time while the model accuracy will decrease. This is one of the main causes of the vanishing gradient problem, which is a difficulty in the training of ANN with the backpropagation algorithm [29].
Additionally, the traditional ANN model has a substantial limitation when solving sequential data problems, such as time series problems or sentence completion forms. An example of a sentence completion problem is predicting whether or not the next word is closely related to its position in the sentence as well as the words in the previous position. Additionally, understanding of watershed processes is a limitation of the ANNs model when dealing with hydrological problems [14,18]. The recurrent neural network (RNN) is a class of ANN, introduced to solve the aforementioned problems.
2.3. Recurrent Neural Network (RNN)
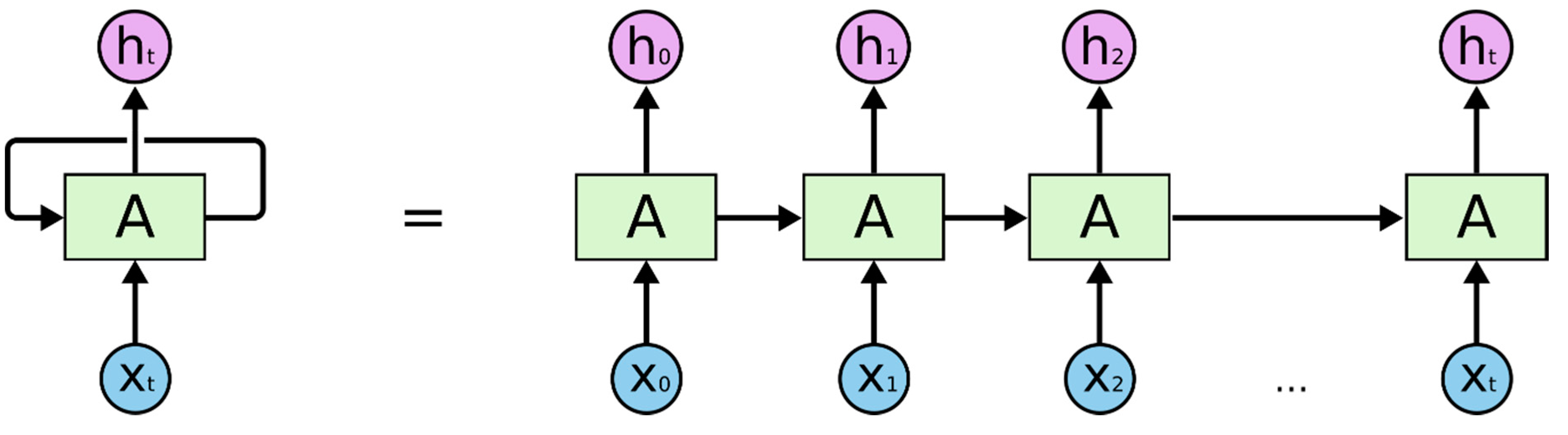
The recurrent neural network was first developed in the 1980s [30,31,32]. Its structure consists of an input layer, one or more hidden layers, and an output layer. RNNs have chain-like structures of repeating modules with the idea behind using these modules as a memory to store important information from previous processing steps. Unlike feedforward neural networks, RNNs include a feedback loop that allows the neural network to accept a sequence of inputs. This means the output from step t − 1 is fed back into the network to influence the outcome of step t, and for each subsequent step. Therefore, RNNs have been successful in learning sequences. Figure 3 shows the sequential processing in RNN.
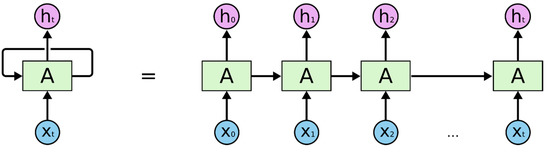
Figure 3.
Sequential processing in a Recurrent Neural Network (RNN) [33].
Figure 3 illustrates a simple RNN with one input unit, one output unit, and one recurrent hidden unit expanded into a full network, where Xt is the input at time step t and ht is the output at time step t. During the training process, RNN uses a backpropagation algorithm, a prevalent algorithm applied in calculating gradients and adjusting weight matrices in ANN. However, it will adjust and update the weights following the modification of the feedback process. Therefore, it is commonly referred to as the backpropagation through time (BPTT). The BPTT process uses a working-backward approach, layer by layer, from the network’s final output, tweaking the weights of each unit according to the unit’s calculated portion of the total output error. The information loops repeat resulting in huge updates to neural network model weights and lead to an unstable network due to the accumulation of error gradients during the updating process. Therefore, BPTT is not sufficiently efficient to learn a pattern from long-term dependency because of the gradient vanishing and the exploding gradient problems [29]. This would be one of the crucial reasons leading to difficulties in the training of recurrent neural networks [34,35,36].
2.4. Long Short-Term Memory (LSTM) Neural Network
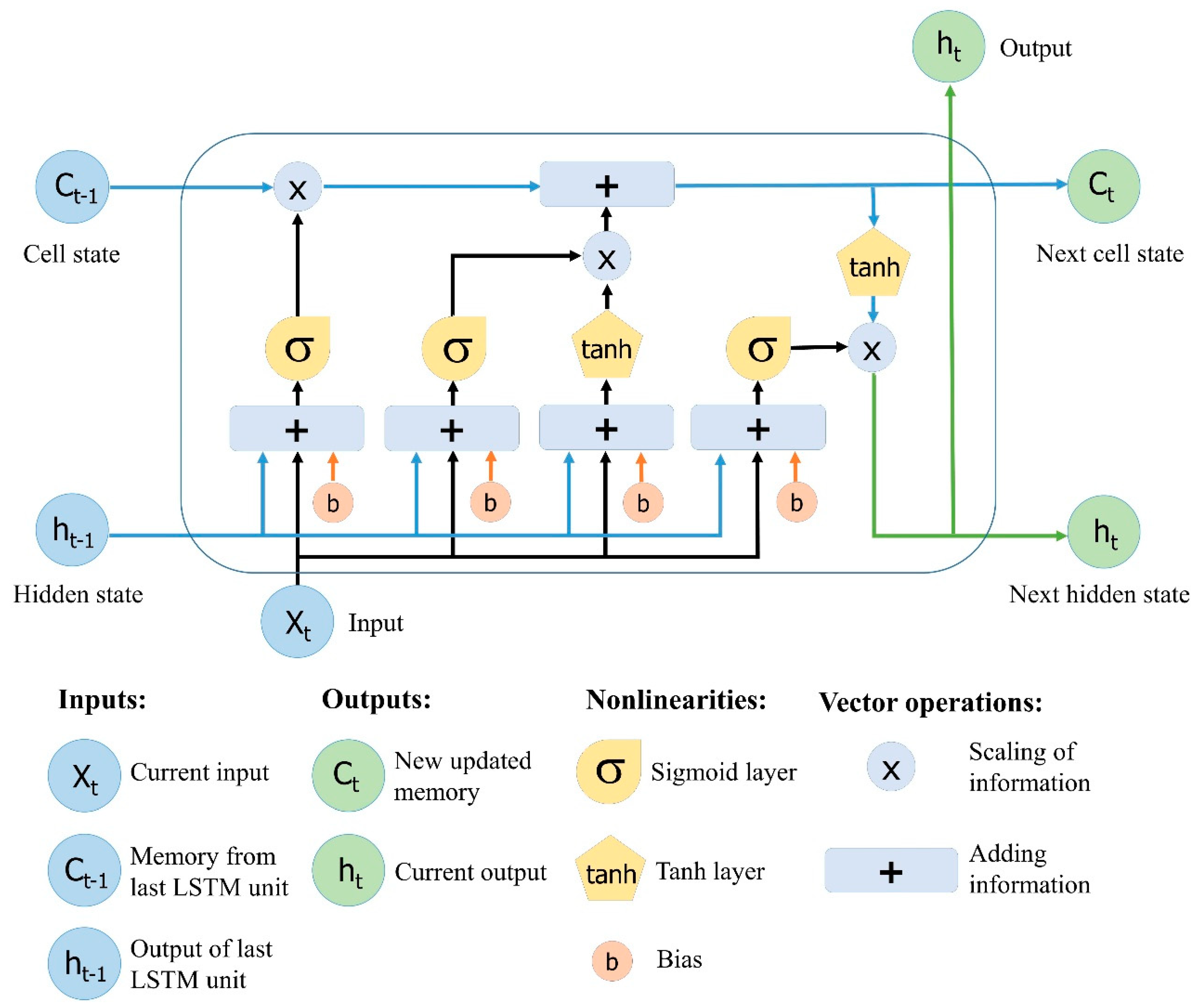
Long Short-Term Memory, an evolution of RNN, was introduced by Hochreiter and Schmidhuber [37] to address problems of the aforementioned drawbacks of the RNN by adding additional interactions per module (or cell). LSTMs are a special kind of RNN, capable of learning long-term dependencies and remembering information for prolonged periods of time as a default. According to Olah [33], the LSTM model is organized in the form of a chain structure. However, the repeating module has a different structure. Instead of a single neural network like a standard RNN, it has four interacting layers with a unique method of communication. The structure of the LSTM neural network is shown in Figure 4.
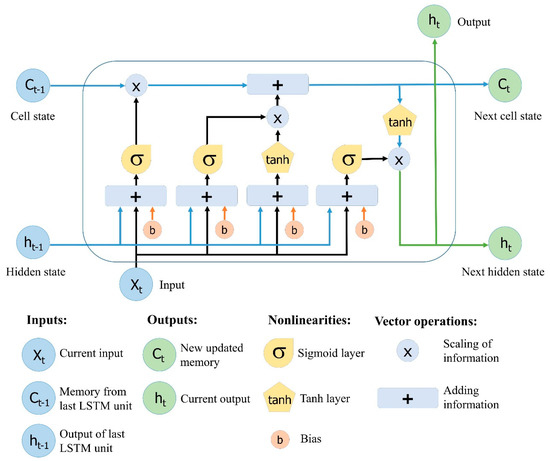
Figure 4.
The structure of the Long Short-Term Memory (LSTM) neural network. Reproduced from Yan [38].
A typical LSTM network is comprised of memory blocks called cells. Two states are being transferred to the next cell, the cell state and the hidden state. The cell state is the main chain of data flow, which allows the data to flow forward essentially unchanged. However, some linear transformations may occur. The data can be added to or removed from the cell state via sigmoid gates. A gate is similar to a layer or a series of matrix operations, which contain different individual weights. LSTMs are designed to avoid the long-term dependency problem because it uses gates to control the memorizing process.
The first step in constructing an LSTM network is to identify information that is not required and will be omitted from the cell in that step. This process of identifying and excluding data is decided by the sigmoid function, which takes the output of the last LSTM unit (ht−1) at time t − 1 and the current input (Xt) at time t. Additionally, the sigmoid function determines which part from the old output should be eliminated. This gate is called the forget gate (or ft); where ft is a vector with values ranging from 0 to 1, corresponding to each number in the cell state, Ct−1.
Herein, is the sigmoid function, and Wf and bf are the weight matrices and bias, respectively, of the forget gate.
The following step is deciding and storing information from the new input (Xt) in the cell state as well as to update the cell state. This step contains two parts, the sigmoid layer and second the tanh layer. First, the sigmoid layer decides whether the new information should be updated or ignored (0 or 1), and second, the tanh function gives weight to the values which passed by, deciding their level of importance (−1 to 1). The two values are multiplied to update the new cell state. This new memory is then added to old memory Ct−1 resulting in Ct.
Here, Ct−1 and Ct are the cell states at time t − 1 and t, while W and b are the weight matrices and bias, respectively, of the cell state.
In the final step, the output values (ht) is based on the output cell state (Ot) but is a filtered version. First, a sigmoid layer decides which parts of the cell state make it to the output. Next, the output of the sigmoid gate (Ot) is multiplied by the new values created by the tanh layer from the cell state (Ct), with a value ranging between −1 and 1.
Here, Wo and bo are the weight matrices and bias, respectively, of the output gate.
2.5. Model Evaluation Criteria
To evaluate the performance of forecasting models in fields related to hydrology, NSE and RMSE are statistical methods often used to compare predicted values with observed values. The NSE measures the ability to predict variables different from the mean and gives the proportion of the initial variance accounted for by the model [39]. The RMSE is frequently used to evaluate how closely the predicted values match the observed values, based on the relative range of the data.
In the above equations, Oi and Pi are observed discharges and simulated discharges at time t, respectively; is the mean of observed discharges; and n is the total number of observations.
The NSE values range from −∞ to 1, and an RMSE equal to zero implies a perfect fit. The LSTM model produces reliable results when the RMSE values are small, and the NSE values are approximately 1.
3. Model Structure
Our research is closely related to open source software libraries. Python [40] is the programming language of choice through the research. In addition, NumPy [41], Pandas [42], Matplotlib [43] libraries are imported for processing, management and visualization data. We developed an LSTM model depicted in Figure 4 based on TensorFlow [44], an open source software library provided by Google. TensorFlow was originally constructed to conduct research on machine learning, deep learning, and numerical computation using data flow graphs. However, this framework is sufficiently comprehensive to be applicable to a wide variety of domains.
3.1. Scenarios
In this study we propose a simple and effective model for flood forecasting, and the characteristics of the input data are also concerned because of its effects on model performance. These characteristics include the type of input data, the quantity of input data, and the correlation of the measured data series. Input data types include the daily rainfall and flow rate, collected from seven meteorological stations and five hydrological stations in the study area. The length of the measured time series is 24 years, from 1961 to 1984. As a result, two various combinations of inputs (two scenarios) were proposed for forecasting day one, day two, and day three flow rates at the Hoa Binh Station.
In the first scenario, we considered rainfall and discharge data observed as the input data for the model. Thus, the time series of the rainfall and discharge measured at the eleven upstream gauge stations, and the flow rate data at the target station were used for predicting the flow rate at the Hoa Binh Station. In the second scenario, the input data of the model consists of the observed discharge data at the five hydrological stations, the four upstream stations and the target station (Hoa Binh).
The total available data was subdivided into three non-overlapping sets for the purposes of training, validation, and testing. Depending on the scenario, the size of the training data sets varies. The first data set was used to train the LSTM model with data measured over 18 years (1961–1978). The second data set, consisting of five years of data (1979–1983), was employed for validation purpose on all scenarios to choose the best performance as well as the parameters for the proposed model. The final data set was used for testing purposes to objectively verify the performance and accuracy of the model in the flood peak forecast. We chose the flood peak in the year 1984 to test the model. The daily series of test datasets were observed in 1984 from 1 January to 19 July. The maximum discharge (10,000 m3/s) at the Hoa Binh Station occurred on 15 July 1984.
3.2. Model Design
The predicted results of the LSTM model in this paper depend only on the actual collected data at the participating gauge stations, as stated above. In comparison with the hydraulic models of the river system, the data are the boundary conditions of a hydraulic model. The LSTM models use the input data to update numerous values in the internal cell states. Contrastingly, the LSTM models do not include the principles of mass conservation or momentum conservation. Therefore, the input data does not include topography data. However, the LSTM models learn these physical principles during the training and calibration processes from the input data and observed data, and are optimized to forecast the discharges as accurately as possible.
The setup details are summarized in Table 3. Several training options and parameters of the model were changed to select the best results. The adaptable parameters of the neuron network were also updated depending on a given loss function of an iteration step.

Table 3.
Details of the LSTM model setup.
The raw data of the proposed model consists of daily measured data series of flow and rainfall from the hydro-meteorological stations within the Da River basin. This input data layer must be reformatted into three-dimensional (3D) vectors to match the architecture of the LSTM model. The input vector (3D) comprises of samples, time steps, and features with the shape num_samples, num_timesteps, and num_features, respectively. The num_samples are the data rows or the total of time steps collected. The num_timesteps are the past observation for the feature, i.e., a lag variable. The num_features are the data columns or the number of gauge stations, which are twelve and five corresponding to the 1st and 2nd scenarios, respectively.
In order for the LSTM model to learn the dependencies more effectively, there have been several modifications related to the arrangement and format of data for the input layer. Instead of using the input data vector as only the data at a specified time step, this vector has been formatted into a sequential data with a selected sequence length of ten time-steps. This may explain that the changing trend of the forecasted values can be seen from the observed values of the ten most recent time steps.
In fact, depending on the data structure, data type, and data characteristics, there will be different choices for this sequence length value. For the time series problem, the influence of sequential lengths on the predicted values depends closely on the observed frequency. For example, in the field of hydrology, the water level values observed by the hour and observed by day will have different tendencies and characteristics. Theoretically, when the value of sequential length increases, the model can capture a better trend of change. However, the selection of this high value may make the LSTM model coping with many difficulties such as consuming a large amount of time and resources of the computer during the training process because the model must train for a complex neural network. This may lead to the same limitations as the traditional RNN model mentioned above. Moreover, when the value of the sequence length varies from five to 15 or more, the model demonstrates equally excellent performance. Therefore, the sequence length value of 10 has been recommended for this study.
Another important problem in constructing the structure of a DNN model is the selection of training parameters (hyper-parameters) such as optimizer, learning rate, number of units or number of epochs. The recommended optimization algorithm for this study is Adam [45]. This is an extension of stochastic gradient descent procedure to update network weights iterative based in training data, which has been widely applied for deep learning application in computer vision and natural language processing recently. Furthermore, the chosen learning rate is 0.0001 instead of using the Adam algorithm’s default value of 0.001. The selection of small values is aimed at making the training process of the model slower and the curve showing the change of the loss function during training smoother.
In the LSTM model, the number of units is understood as the number of LSTM units per time step of the LSTM network (or the number of units in each cell). In addition, there is no specific reference structure for selecting the number of units in each cell. Therefore, different values of the number of units are suggested in Table 2 to evaluate the effect of selection on the forecast results. Another parameter of interest in establishing a model structure is the number of epochs. In deep learning, one epoch is defined as when an entire dataset is passed forward and backward through the neural network only once. In order to record the necessary information during training and validation, the maximum number of epochs recommended is 100,000.
Several other minor changes have been applied to improve the effectiveness of the model. They can be referred to as dropout and early stopping techniques to prevent overfitting problems [46]. Overfitting occurs when a model learns the detail and noise in the training data to the extent that it negatively impacts the performance of the model on new data (validation dataset). Early stopping is a widely applied technique in DNN so that the model can stop training at the point when performance on a validation dataset starts to degrade. The developed LSTM model is able to stop the training process if the performance on the validation dataset does not improve after 2000 epochs.
4. Results and Discussion
The developed forecasting models were validated and tested on independent data. The NSE and RMSE values were used to evaluate the qualitative and quantitative performance of the scenarios when comparing the observational data and forecast values made during validation and testing process. Depending on the scenario, the size of the training data sets varies. A five-year dataset (1979–1983) was used for validation purposes, and the one-year dataset (1984) was utilized for testing purposes.
4.1. Validation Results
For the validation process, the flow forecast results corresponding to the scenarios for the Hoa Binh Station are demonstrated in Table 4. The comparison results of the predicted and observed flow data for a one-day forecasting model is shown in Figure 5 and Figure 6.

Table 4.
Summary of the results and parameters of the one-day model forecast (validation phase).
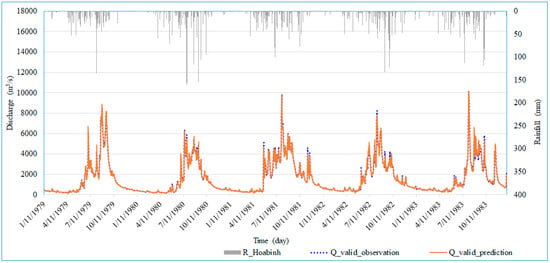
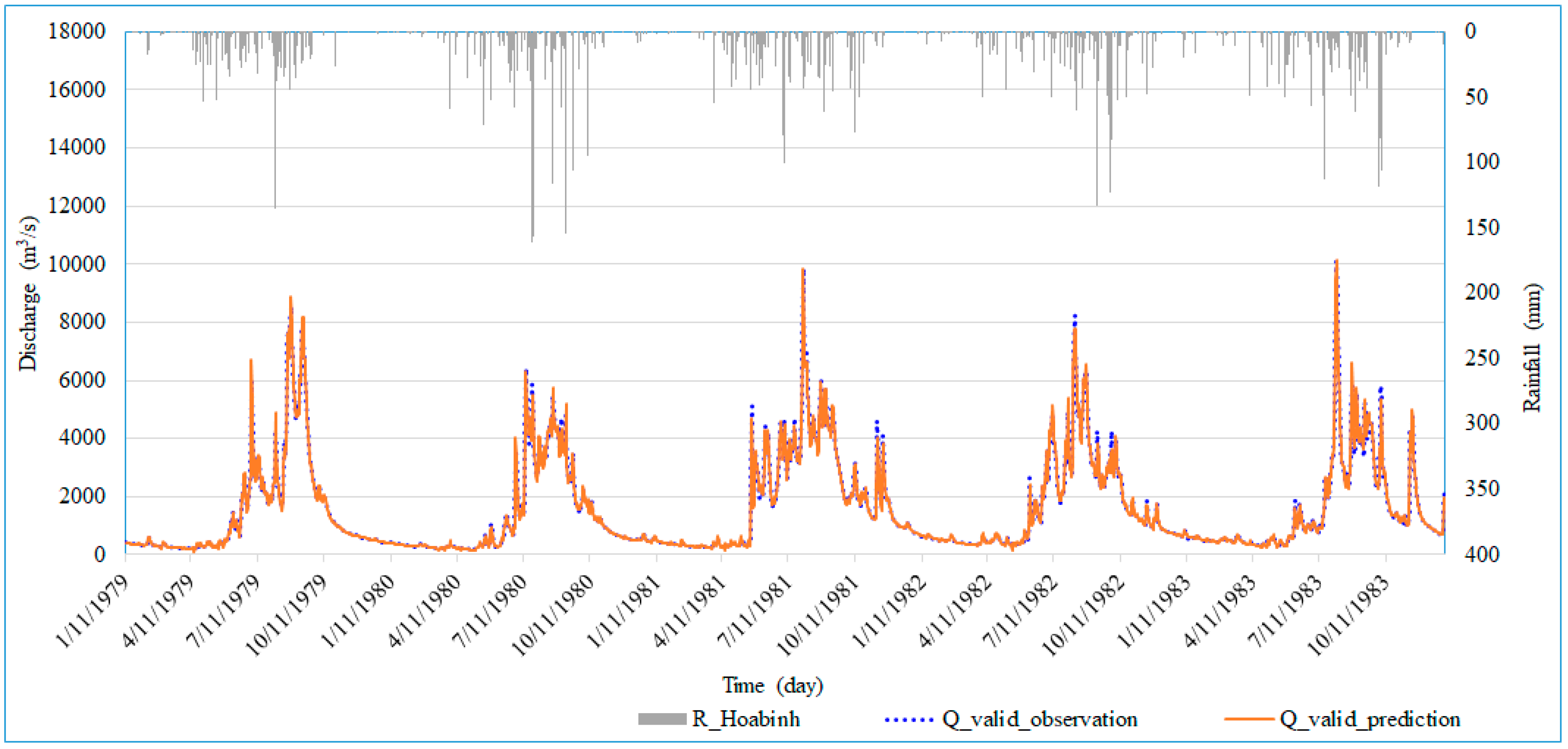
Figure 5.
Comparison between the observed and predicted one-day flow values for the first scenario (case S1_1d_2) in the validation phase.
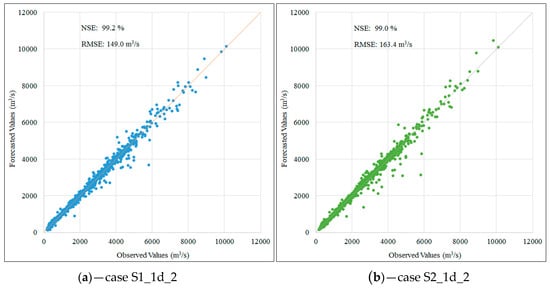
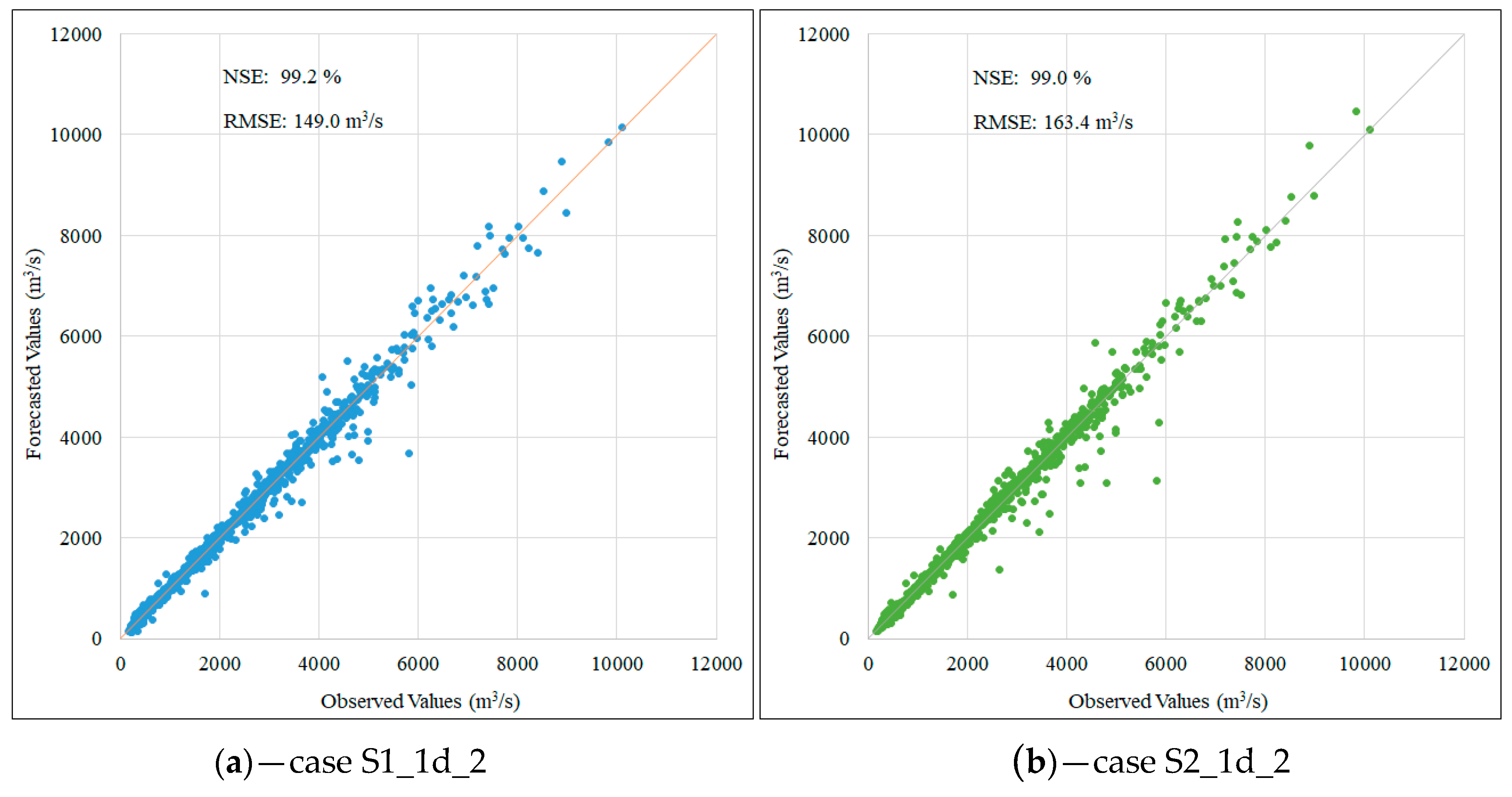
Figure 6.
Scatter plot for one-day flow forecasting in the validation phase corresponding to the first scenario (a) and the second scenario (b).
In Table 3, the input variable column is the number of data series collected from the measuring stations. Depending on the scenario, these values are not the same. The first scenario is a combination of rainfall and flow rate data, so the number of input variables is twelve. The corresponding value for the second scenario is five because the input data only consists of the flowrate data. The results in Table 3 indicates that the forecasted results of the first scenario have a slightly higher trend than the other. However, there is no significant difference in the prediction cases of flow for both scenarios (the largest difference is only about 1%). It can be said that both of these scenarios produce equally good results. In the case of forecasting the discharge one day in advance, the accuracy of the model (NSE value) reaches well above 99% and the average error of 150 m3/s (RMSE value). For the two-day and three-day flow forecast, the NSE values are approximately 95% and 87% respectively.
Figure 5 and Figure 6 demonstrate a close correlation between the observed and predicted values for forecasting one day of lead time for each scenario. There are essentially no significant differences between the predicted cases. Figure 5 illustrates how the rainfall influences the forecasted flowrate result due to the rain causing the flood flow. Rain peak usually occurs first followed by the flood peak; the lag time depends on the basin’s characteristics. Figure 6 provides information regarding the graphical performance indicator when the data pairs are close to the 45° line. Data pairs closest to the 45° line represent better prediction cases. The NSE value is almost unchanged in both scenarios (about 99%). A similar trend was witnessed in the case of a two-day and three-day forecast.
The results of the validation process also indicate that the constructed model can achieve equally impressive performance even if some parameters such as the number of units or the number of input variables have been changed. In addition to the selected values as shown in Table 2, several other cases have been considered to assess the influence of the selection of parameter values to the forecasted results. For example, the sequence length varies from five to 15 or the number of units varies from 10 to 100. However, all of these changes produce performance comparable to those represented in Table 3 and do not significantly improve the forecast results. Additionally, the results illustrate the rainfall does not significantly influence the forecasted result of the flowrate.
4.2. Test Results
Two scenarios of forecasting models were tested on data not used for training and validation with the purpose to objectively verify the performance of the model and the accuracy of the model when forecasting the flood peak. We chose the flood peak in the year 1984 to test the model with the series of the test dataset, which was observed daily in 1984 from 1 January to 31 December. During this period, the highest peak flood at the Hoa Binh Station was recorded on 15 July with a measured flowrate of 10,000 m3/s. The performance of the models was determined using the NSE and RMSE metrics when comparisons between the measured data and forecasted values were made.
4.2.1. Results for Testing Phase
The results of the testing process and prediction of flood peak for the two scenarios are summarized in the Table 5. Additionally, Figure 7, Figure 8, Figure 9 and Figure 10 illustrate the correlation between the observed and predicted values in the two scenarios for three forecast cases.

Table 5.
The results of the prediction model in the testing phase.
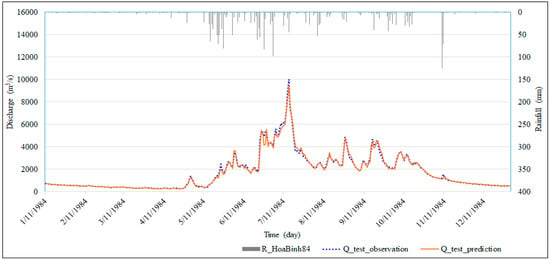
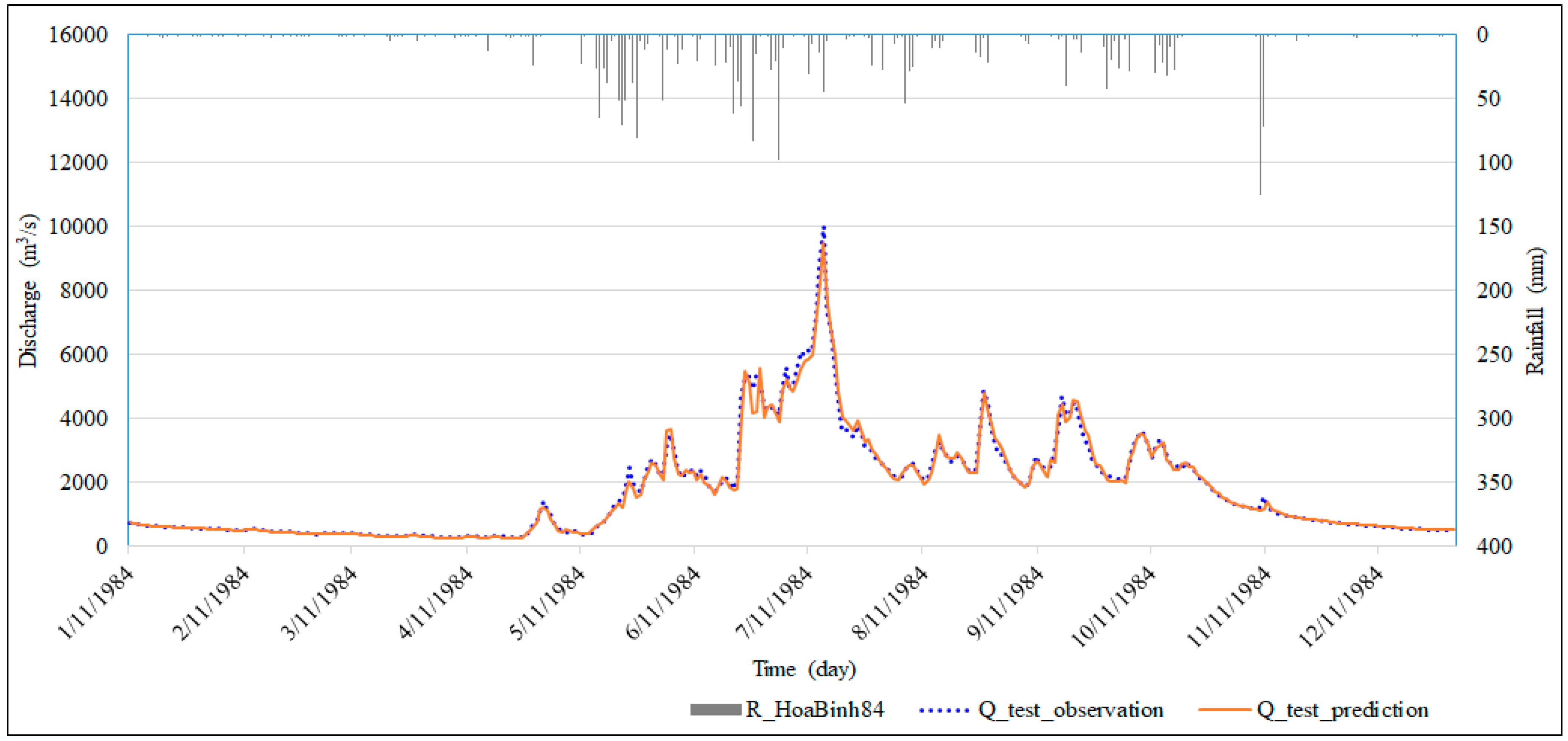
Figure 7.
Comparison between the observed and predicted one-day flow values for the second scenario (case S2_1d_2) in the testing phase.
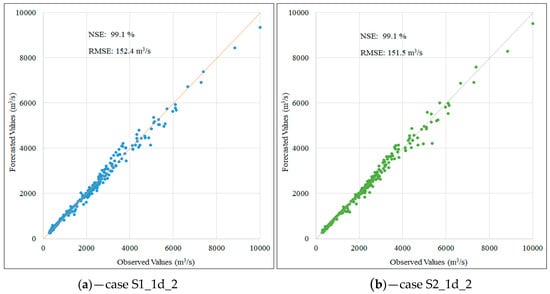
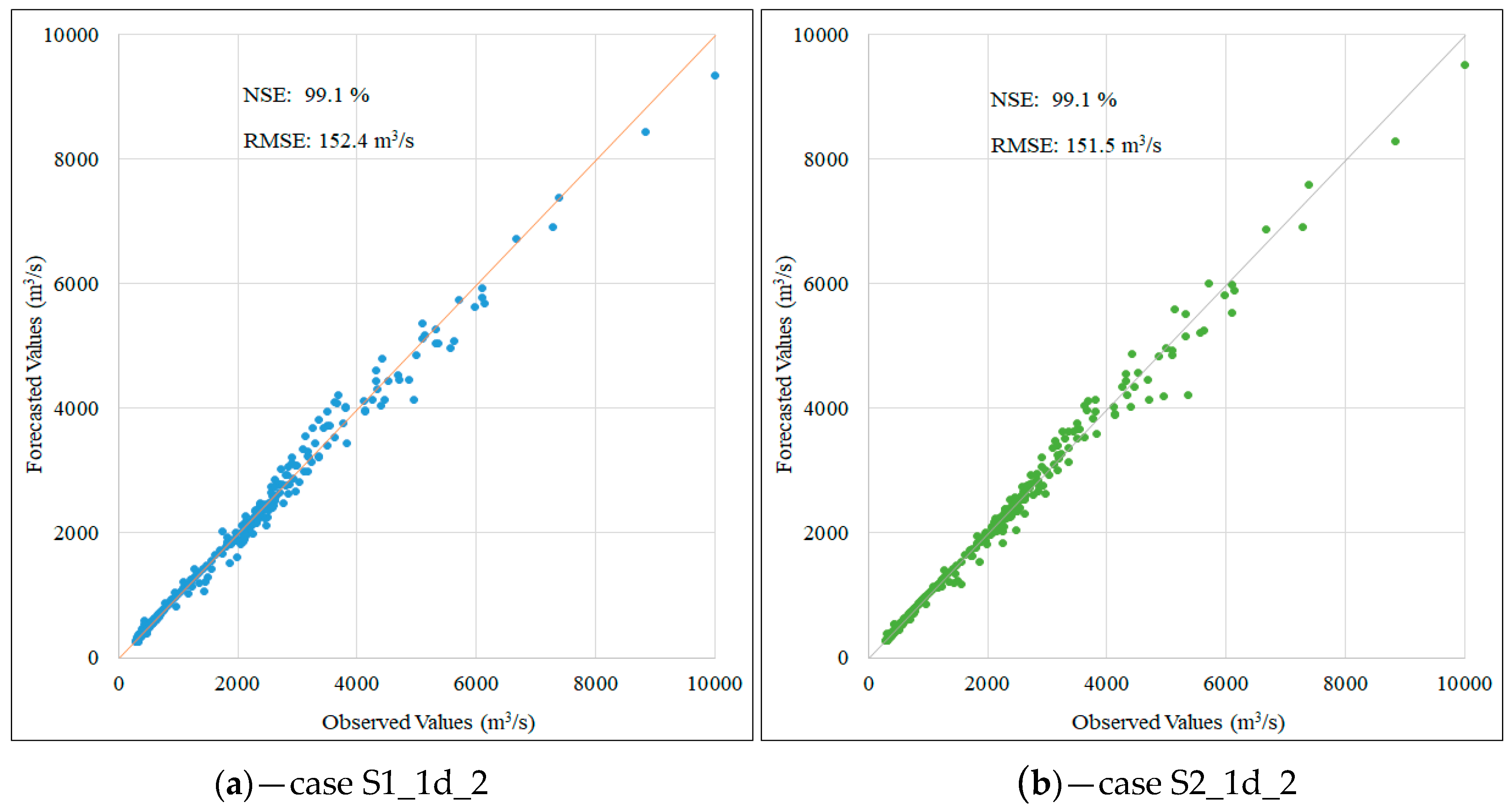
Figure 8.
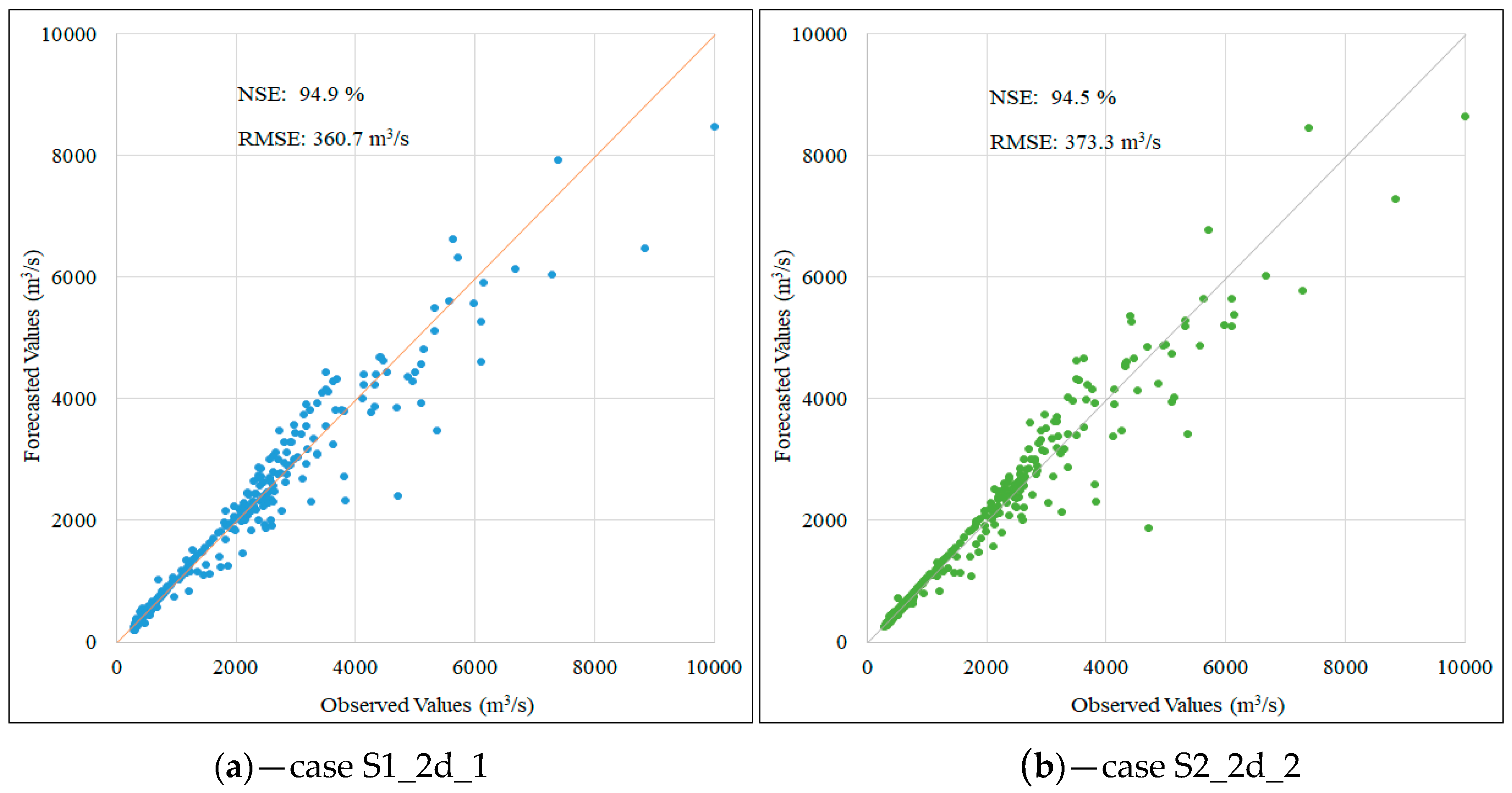
Scatter plot for one-day flow forecasting in testing phase corresponding to the first scenario (a) and the second scenario (b).
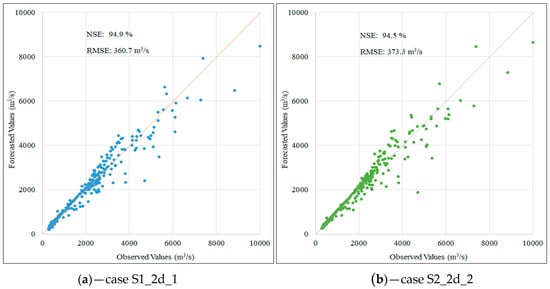
Figure 9.
Scatter plot for two-day flow forecasting in the testing phase corresponding to the first scenario (a) and the second scenario (b).
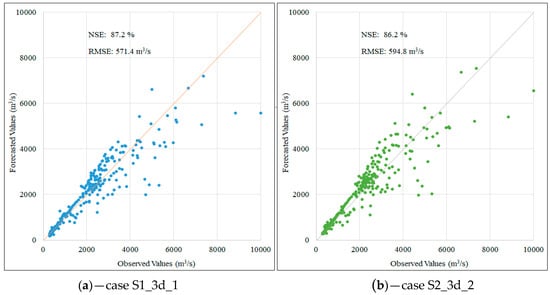
Figure 10.
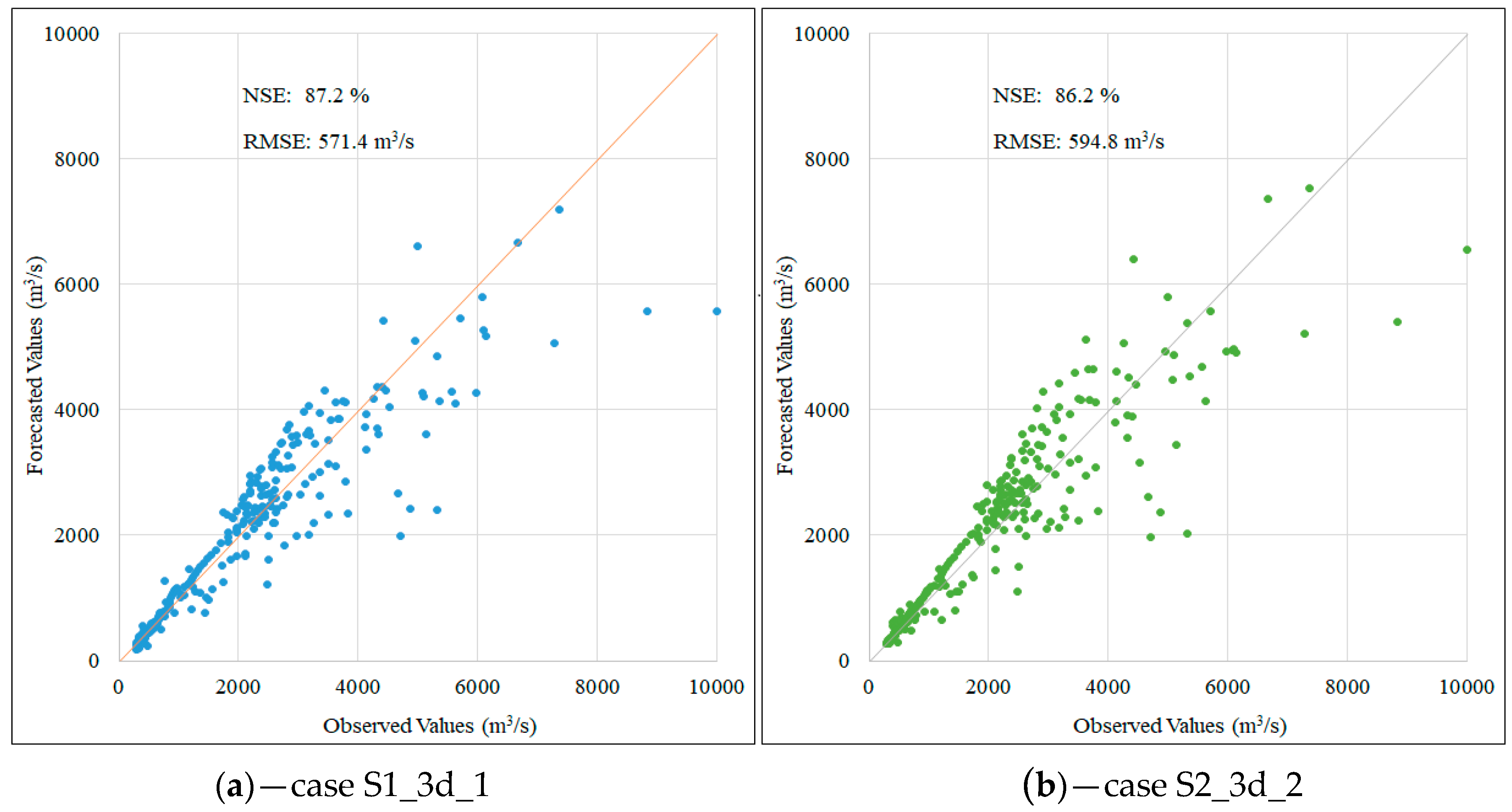
Scatter plot for three-day flow forecasting in the testing phase corresponding to the first scenario (a) and the second scenario (b).
The results in Table 4 demonstrate no significant difference in NSE and RMSE values during the test phase in comparison to the validation phase. In all three predictions, the LSTM model produced an equally high performance for both scenarios (NSE values are almost unchanged). Figure 8, Figure 9 and Figure 10 present the performance information as pairs of data represented. Data pairs closer to the 45° line indicate better prediction results. The scatter plot for one-day flow forecasting in the testing phase (Figure 7) illustrates a similarity in both scenarios with the average error in flow rate forecast of approximately 152 m3/s.
A similar trend was recorded in the two-day and three-day flow forecasting case. The comparison between the predicted and observed flow values in the testing phase demonstrates similarities between about 94.5% and 86.2% of the NSE values for two scenarios, respectively. The above-mentioned research results indicate that the LSTM model produces highly accurate and stable results in both the validation and test phases. Furthermore, the combination of input data characteristics demonstrate that flowrate data plays an important role in forecasting flood flow while the role of rainfall data is not clearly represented. It also can be seen from Table 2 that the correlation coefficients of rainfall data are less than 30% while these coefficients of flowrate range from 77% to 97%.
4.2.2. Results for Flood Peak Forecasts
The next step in evaluating the effectiveness of the LSTM model is to compare the maximum flowrate between the forecasted value and the measured value in the test dataset. Accurate flood forecasting will act as the precursor for planning, managing, and flood risk mitigation. In the 1984 test dataset, the maximum discharge value recorded at the Hoa Binh Station was 10,000 m3/s on July 15th. Base on the optimal parameters selected for the scenarios, the prediction results of the one-day, two-day, and three-day flood peaks are depicted in Table 5.
The predicted flood peaks in both scenarios appear at the same time as the observed peaks. An error value of approximately 5% and 14%, respectively, is the acceptable tolerance value in the hydrological forecast for the case of forecasting the maximum flowrate one day and two days ahead. This is because the accurate prediction of the maximum discharge value during the flood season is difficult, especially for areas with complex topography and steep slopes like the study area. Moreover, the figures in Table 5 indicate that in all forecast cases, the second scenario has a tendency to provide a slightly better predictive performance than the first scenario in flood peak value prediction. The difference between the relative error values in the forecast of the flood peaks of the two scenarios ranges from 1.5% to 3.5%, with the highly accurate predicted results belonging to the second scenario.
The LSTM model is a data-driven model based on statistical relationships between input data and output data. Therefore, the correlation between the data series at the target-forecast station and other stations is one of the vital factors determining the accuracy of the model. Meanwhile, the correlation between the series of precipitation data and the flowrate at Hoa Binh station is often significantly lower than the correlation between flowrate stations (see Table 1). This explains why the second scenario tends to forecast the largest flow value better than the first one, because occasionally the occurrence of precipitation data may result in the flow forecast becoming less accurate.
The analysis described above proves the outstanding advantage of the LSTM model in its ability to learn short dependencies effectively, and this model can completely be applied to forecast the flow two days or even three days ahead with accuracy of over 86%. Data-based methods are an effective approach with high accuracy to modeling the hydrological process owing to their simplicity, especially for developing countries such as Vietnam, where the application of remote sensing technology in constructing a real-time flood warning system is limited.
5. Conclusions
This paper has proposed an effective approach to flood forecasting based on the data-driven method. The LSTM neural network model was constructed and carefully assessed to forecast one-day, two-day, and three-day flood flow at the Hoa Binh Station on the Da River. Contrary to requiring a variety of input data such as land-use and topography for rainfall-runoff simulation, the developed model uses only the measured data information available at the target station and the upstream meteorological and hydrological stations to forecast the flowrate at the target station for multi-step output. The LSTM model has learned long-term dependencies between sequential data series and demonstrated reliable performance in flood forecasting.
Two scenarios have been considered to assess the model’s performance in flowrate forecasting and the influence of input data characteristics on the model’s flood forecasting capability. The model was validated and tested by applying criteria such as NSE value, RMSE value, as well as relative error values in forecasting the maximum flow rate using the independent data sets. For validation and testing phases, both scenarios illustrated equally good performance. Additionally, there is no substantial difference in the simulation results for all three discharge forecast cases. However, when considering the flood peak forecasting factor, the second scenario indicated slightly better-forecasted results.
The aforementioned analysis revealed that the input data type has more influence than the quantity of input data. For the data-driven model, when the correlation coefficient between the input data series and the data at the target-forecast station is higher, the model will operate more efficiently, specifically during the longer forecast period. In the case of flood forecasting, discharge data represented a more important role than rainfall data. Precipitation data does not clearly improve the accuracy of the forecast results. Occasionally, the existence of this data causes noise in accurately predicting the maximum flowrate value.
LSTM neural network (with Gated Recurrent Unit (GRU)) is one of the state-of-the-art architectures designed to address problems of sequential data or time series effectively. Streamflow prediction belongs to the class of sequential data problems because the observed data fluctuate continuously over time. The LSTM-based model provides the most viable option for actual flood forecasting, instead of traditional methods when input data is missing (not available at all sites) or difficult to obtain. The LSTM model has been successfully applied to produce for one-day, two-day, and three-day flow forecasting. In addition, the model can also be developed to provide streamflow forecasts with different periods depending on forecasting requirements and data processing. For example, producing forecasts for time steps of one-hour (one-hour, two-hour ahead) if data is observed with hourly frequencies or producing forecasts for six-hour time steps (six-hour, twelve-hour ahead) if the data is observed every six-hour. Another advantage of the data-driven model or LSTM model compared to physical-based simulation models is the ability to produce high-performance streamflow predictions in areas affected by the tide regime. These are areas where conventional hydrological models have not yet indicated their effectiveness.
Despite the fact that the LSTM model resolves sequential data problems effectively, there are several limitations that need to be considered. LSTM models, in general, are data-driven models that result in the inadequate simulation of hydrological processes like physical-based models. Specifically, LSTM (or ANN)-based models only provide highly accurate forecasts at specific locations in the study area. Therefore, these models should be combined with meteorological models such as rainfall forecasting model to obtain better performance with long-term forecasts.
The findings of this study suggest the potential of applying the LSTM model in the field of hydrology in constructing and managing real-time flood warning system. This model is a viable option for developing countries or large river basins such as the Da River basin, where the river basin stretches from China to Vietnam. The streamflow at downstream (Vietnam) may fluctuate due to flooding discharge from a large number of upstream dams and reservoirs.
Author Contributions
Conceptualization, X.H.L.; Methodology, X.H.L. and S.J.; formal analysis, X.H.L. and H.V.H.; writing—original draft, X.H.L.; supervision, G.L.
Funding
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2017R1D1A3B03033402).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thirumalaiah, K.C.; Deo, M. Hydrological forecasting using neural networks. J. Hydrol. Eng. 2000, 5, 180–189. [Google Scholar] [CrossRef]
- Kişi, Ö. A combined generalized regression neural network wavelet model for monthly streamflow prediction. KSCE J. Civ. Eng. 2011, 15, 1469–1479. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; El-shafie, A.; Jaafar, O.; Afan, H.A.; Sayl, K.N. Artificial intelligence based models for stream-flow forecasting: 2000–2015. J. Hydrol. 2015, 530, 829–844. [Google Scholar] [CrossRef]
- Hidayat, H.; Hoitink, A.J.F.; Sassi, M.G.; Torfs, P.J.J.F. Prediction of discharge in a tidal river using artificial neural networks. J. Hydrol. Eng. 2014, 19, 04014006. [Google Scholar] [CrossRef]
- Elsafi, S.H. Artificial neural networks (ANNs) for flood forecasting at Dongola station in the River Nile, Sudan. Alex. Eng. J. 2014, 53, 655–662. [Google Scholar] [CrossRef]
- Khan, M.Y.A.; Hasan, F.; Panwar, S.; Chakrapani, G.J. Neural network model for discharge and water-level prediction for Ramganga River catchment of Ganga basin, India. Hydrol. Sci. J. 2016, 61, 2084–2095. [Google Scholar] [CrossRef]
- Sung, J.; Lee, J.; Chung, I.-M.; Heo, J.-H. Hourly water level forecasting at tributary affected by main river condition. Water 2017, 9, 644. [Google Scholar] [CrossRef]
- Yu, P.-S.; Chen, S.-T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K.S. Improving real time flood forecasting using fuzzy inference system. J. Hydrol. 2014, 509, 25–41. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP neural network algorithm in traditional hydrological model for flood forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- Sahay, R.R.; Srivastava, A. Predicting monsoon floods in rivers embedding wavelet transform, genetic algorithm and neural network. Water Resour. Manag. 2014, 28, 301–317. [Google Scholar] [CrossRef]
- Londhe, S.; Charhate, S. Comparison of data-driven modelling techniques for river flow forecasting. Hydrol. Sci. J. 2010, 55, 1163–1174. [Google Scholar] [CrossRef]
- Makwana, J.J.; Tiwari, M.K. Intermittent streamflow forecasting and extreme event modelling using wavelet based artificial neural networks. Water Resour. Manag. 2014, 28, 4857–4873. [Google Scholar] [CrossRef]
- Govindaraju, R.S. Artificial neural networks in hydrology. II: Hydrologic applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Govindaraju, R.S. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems—Volume 2, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gülçehre, Ç.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Mikolov, T.; Joulin, A.; Chopra, S.; Mathieu, M.; Ranzato, M.A. Learning longer memory in recurrent neural networks. arXiv 2014, arXiv:1412.7753. [Google Scholar]
- Li, Y.; Cao, H. Prediction for tourism flow based on LSTM neural network. Procedia Comput. Sci. 2018, 129, 277–283. [Google Scholar] [CrossRef]
- Yanjie, D.; Yisheng, L.; Fei-Yue, W. Travel time prediction with LSTM neural network. In Proceedings of the IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1053–1058. [Google Scholar] [CrossRef]
- Nelson, D.M.Q.; Pereira, A.C.M.; de Oliveira, R.A. Stock market’s price movement prediction with LSTM neural networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1419–1426. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Le, X.-H.; Ho, V.H.; Lee, G.; Jung, S. A deep neural network application for forecasting the inflow into the Hoa Binh reservoir in Vietnam. In Proceedings of the 11th International Symposium on Lowland Technology (ISLT 2018), Hanoi, Vietnam, 26–28 September 2018. [Google Scholar]
- Aichouri, I.; Hani, A.; Bougherira, N.; Djabri, L.; Chaffai, H.; Lallahem, S. River flow model using artificial neural networks. Energy Procedia 2015, 74, 1007–1014. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Werbos, P.J. Generalization of backpropagation with application to a recurrent gas market model. Neural Netw. 1988, 1, 339–356. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Olah, C. Understanding LSTM Networks. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 26 June 2018).
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Hochreiter, S.; Bengio, Y.; Frasconi, P. Gradient flow in recurrent nets: The difficulty of learning long-term dependencies. In A Field Guide to Dynamical Recurrent Networks; Kolen, J., Kremer, S., Eds.; Wiley-IEEE Press: Piscataway, NJ, USA, 2001. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. III-1310–III-1318. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yan, S. Understanding LSTM and Its Diagrams. Available online: https://medium.com/mlreview/understanding-lstm-and-its-diagrams-37e2f46f1714 (accessed on 26 June 2018).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models Part I—A discussion of principles. J. Hydrol. Eng. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Rossum, G. Python Tutorial; CWI (Centre for Mathematics and Computer Science): Amsterdam, The Netherlands, 1995. [Google Scholar]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 51–56. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2015, arXiv:1603.04467. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).