Natural Variability and Vertical Land Motion Contributions in the Mediterranean Sea-Level Records over the Last Two Centuries and Projections for 2100
Abstract
1. Introduction
2. Materials and Methods: Data Set and Natural Variability
3. Results: The EMD Analysis and a Generalized Model for Long-Term Sea-Level Variations
4. Discussion: The Vertical Land Motion and Relative Sea Levels by 2050 and 2100
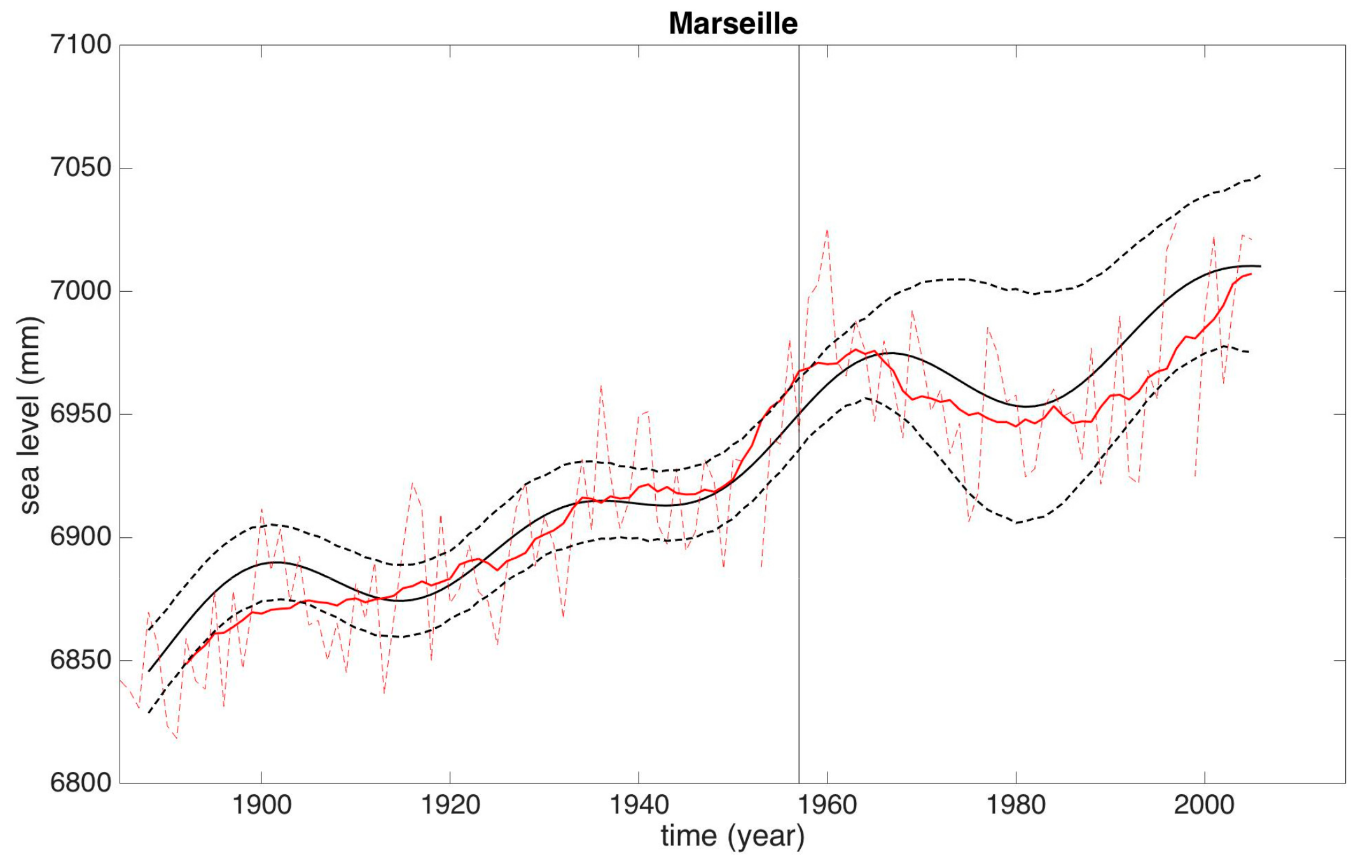
- The normalized mean squared error (NMSE) between the 15 years smoothed and the model curves, after 1957, is 4.4 × 10−6 (if a model has a very low NMSE then it reproduces the data well);
- The maximum and minimum discrepancy between the 15 years smoothed data and the model-derived sea levels are found in 1965 and 1997, respectively. Sea-level values are 6976 and 6977 mm for smoothed data, 6974 (6956, 6992) and 7000 (6968, 7032) mm for model data (values in parentheses represents the upper/lower 90% confidence interval).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vermeer, M.; Rahmstorf, S. Global sea level linked to global temperature. Proc. Natl. Acad. Sci. USA 2009, 106, 21527–21532. [Google Scholar] [CrossRef] [PubMed]
- Church, J.A.; White, N.J. Sea-Level Rise from the Late 19th to the Early 21st Century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef]
- Kemp, A.C.; Horton, B.P.; Donnelly, J.P.; Mann, M.E.; Vermeer, M.; Rahmstorf, S. Climate related sea-level variations over the past two millennia. Proc. Natl. Acad. Sci. USA 2011, 108, 11017–11022. [Google Scholar] [CrossRef] [PubMed]
- Lambeck, K.; Woodroffe, C.D.; Antonioli, F.; Anzidei, M.; Gehrels, W.R.; Laborel, J.; Wright, A.J. Paleoenvironmental Records, Geophysical Modeling, and Reconstruction of Sea-Level Trends and Variability on Centennial and Longer Timescales. In Understanding Sea-Level Rise and Variability; Blackwell: Hoboken, NJ, USA, 2010; pp. 61–121. [Google Scholar]
- Meyssignac, B.; Cazenave, A. Sea level: A review of present-day and recent-past changes and variability. J. Geodyn. 2012, 58, 96–109. [Google Scholar] [CrossRef]
- Mitchum, G.T.; Nerem, R.S.; Merrifield, M.A.; Gehrels, W.R. Modern sea level changes estimates. In Understanding Sea Level Rise and Variability; Church, J.A., Woodworth, P.L., Aarup, T., Wilson, W.S., Eds.; Wiley-Blackwell Publishing: London, UK, 2010. [Google Scholar]
- Jevrejeva, S.; Moore, J.; Grinsted, A. Sea level projections to AD2500 with a new generation of climate change scenarios. Glob. Planet. Chang. 2012, 80, 14–20. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Coastal sea level rise in southern Europe and the nonclimate contribution of vertical land motion. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Anzidei, M.; Lambeck, K.; Antonioli, F.; Furlani, S.; Mastronuzzi, G.; Serpelloni, E.; Vannucci, G. Coastal structure, sea-level changes and vertical motion of the land in the Mediterranean. Geol. Soc. Lond. Spéc. Publ. 2014, 388, 453–479. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Calafat, F.M.; Marcos, M.; Jorda, G.; Gomis, D.; Fenoglio-Marc, L.; Struglia, M.V.; Josey, S.A.; Chambers, D.; Fenoglio-Marc, L. The effect of the NAO on sea level and on mass changes in the Mediterranean Sea. J. Geophys. Res. Oceans 2013, 118, 944–952. [Google Scholar] [CrossRef]
- Fenoglio-Marc, L.; Rietbroek, R.; Grayek, S.; Becker, M.; Kusche, J.; Stanev, E. Water mass variation in the Mediterranean and Black Seas. J. Geodyn. 2012, 59, 168–182. [Google Scholar] [CrossRef]
- Fenoglio-Marc, L.; Mariotti, A.; Sannino, G.; Meyssignac, B.; Carillo, A.; Struglia, M.; Rixen, M. Decadal variability of net water flux at the Mediterranean Sea Gibraltar Strait. Glob. Planet. Chang. 2013, 100, 1–10. [Google Scholar] [CrossRef]
- Lambeck, K.; Purcell, A. Sea-level change in the Mediterranean Sea since the LGM: Model predictions for tectonically stable areas. Quat. Sci. Rev. 2005, 24, 1969–1988. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.J.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth’s Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
- Lambeck, K.; Antonioli, F.; Anzidei, M.; Ferranti, L.; Leoni, G.; Scicchitano, G.; Silenzi, S. Sea level change along the Italian coast during the Holocene and projections for the future. Quat. Int. 2011, 232, 250–257. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea rise: A redetermination. Surv. Geophys. 1997, 18, 270–292. [Google Scholar] [CrossRef]
- Knutti, R.; Stocker, T.F. Influence of the Thermohaline Circulation on Projected Sea Level Rise. J. Clim. 2000, 13, 1997–2001. [Google Scholar] [CrossRef]
- Rahmstorf, S. A Semi-Empirical Approach to Projecting Future Sea-Level Rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S.; Cazenave, A.; Church, J.A.; Hansen, J.E.; Keeling, R.F.; Parker, D.E.; Somerville, R.C.J. Recent Climate Observations Compared to Projections. Science 2007, 316, 709. [Google Scholar] [CrossRef] [PubMed]
- Milne, G.A.; Gehrels, W.R.; Hughes, C.W.; Tamisiea, M.E. Identifying the causes of sea-level change. Nat. Geosci. 2009, 2, 471–478. [Google Scholar] [CrossRef]
- Tsimplis, M.; Marcos, M.; Colin, J.; Somot, S.; Pascual, A.; Shaw, A. Sea level variability in the Mediterranean Sea during the 1990s on the basis of two 2d and one 3d model. J. Mar. Syst. 2009, 78, 109–123. [Google Scholar] [CrossRef]
- Tsimplis, M.; Spada, G.; Marcos, M.; Flemming, N. Multi-decadal sea level trends and land movements in the Mediterranean Sea with estimates of factors perturbing tide gauge data and cumulative uncertainties. Glob. Planet. Chang. 2011, 76, 63–76. [Google Scholar] [CrossRef]
- Church, J.A.; Aarup, T.; Woodworth, P.L.; Wilson, W.S.; Nicholls, R.J.; Rayner, R.; Lambeck, K.; Mitchum, G.T.; Steffen, K.; Cazenave, A.; et al. Sea-Level Rise and Variability: Synthesis and Outlook for the Future. In Understanding Sea-Level Rise and Variability, 1st ed.; Church, A.J., Woodworth, P.L., Aarup, T., Wilson, S., Eds.; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Cazenave, A.; Remy, F. Sea level and climate: Measurements and causes of changes. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 647–662. [Google Scholar] [CrossRef]
- Zhang, X.; Church, J.A. Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 2012, 39, 21701. [Google Scholar] [CrossRef]
- Galassi, G.; Spada, G. Sea-level rise in the Mediterranean Sea by 2050: Roles of terrestrial ice melt, steric effects and glacial isostatic adjustment. Glob. Planet. Chang. 2014, 123, 55–66. [Google Scholar] [CrossRef]
- Han, W.; Stammer, D.; Meehl, G.A.; Hu, A.; Sienz, F.; Zhang, L. Multi-Decadal Trend and Decadal Variability of the Regional Sea Level over the Indian Ocean since the 1960s: Roles of Climate Modes and External Forcing. Climate 2018, 6, 51. [Google Scholar] [CrossRef]
- Brambati, A.; Carbognin, L.; Quaia, T.; Teatini, P.; Tosi, L. The Lagoon of Venice: Geological setting, evolution and land subsidence. Episodes 2003, 26, 264–268. [Google Scholar]
- Carbognin, L.; Teatini, P.; Tosi, L. Eustacy and land subsidence in the Venice Lagoon at the beginning of the new millennium. J. Mar. Syst. 2004, 51, 345–353. [Google Scholar] [CrossRef]
- De Conto, R.M.; Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 2016, 531, 591–597. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Kettner, A.J.; Overeem, I.; Hutton, E.W.H.; Hannon, M.T.; Brakenridge, G.R.; Day, J.; Vörösmarty, C.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- Antonioli, F.; Anzidei, M.; Amorosi, A.; Presti, V.L.; Mastronuzzi, G.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; Lisco, S.; et al. Sea-level rise and potential drowning of the Italian coastal plains: Flooding risk scenarios for 2100. Quat. Sci. Rev. 2017, 158, 29–43. [Google Scholar] [CrossRef]
- Bosman, A.; Carluccio, R.; Casalbore, D.; Caracciolo, F.D.; Esposito, A.; Nicolosi, I.; Pietrantonio, G.; Vecchio, A.; Carmisciano, C.; Chiappini, M.; et al. Flooding scenarios due to land subsidence and sea-level rise: A case study for Lipari Island (Italy). Terra Nova 2017, 29, 44–51. [Google Scholar]
- Marsico, A.; Lisco, S.; Presti, V.L.; Antonioli, F.; Amorosi, A.; Anzidei, M.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; et al. Flooding scenario for four Italian coastal plains using three relative sea level rise models. J. Maps 2017, 13, 961–967. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea level rise. J. Geophys. Res. 1991, 96, 6981–6992. [Google Scholar] [CrossRef]
- Douglas, B.C. Global sea level rise acceleration. J. Geophys. Res. 1992, 97, 12699–12796. [Google Scholar] [CrossRef]
- Visser, H.; Dangendorf, S.; Petersen, A.C. A review of trend models applied to sea level data with reference to the “acceleration-deceleration debate”. J. Geophys. Res. Oceans 2015, 120, 3873–3895. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, E.H.; Zheng, Q.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for non-stationary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Vecchio, A.; Capparelli, V.; Carbone, V. The complex dynamics of the seasonal component of USA’s surface temperature. Atmos. Chem. Phys. 2010, 10, 9657–9665. [Google Scholar] [CrossRef]
- Vecchio, A.; Anzidei, M.; Capparelli, V.; Carbone, V.; Guerra, I. Has the Mediterranean Sea felt the March 11th, 2011, Mw 9.0 Tohoku-Oki earthquake? Europhys. Lett. 2012, 98, 59001. [Google Scholar] [CrossRef]
- Vecchio, A.; Anzidei, M.; Carbone, V. New insights on the tsunami recording of the May, 21, 2003, Mw 6.9 Boumerdès earthquake from tidal data analysis. J. Geodyn. 2014, 79, 39–49. [Google Scholar] [CrossRef]
- Breaker, L.C.; Ruzmaikin, A. The 154-year record of sea level at San Francisco: Extracting the long-term trend, recent changes, and other tidbits. Clim. Dyn. 2011, 36, 545–559. [Google Scholar] [CrossRef]
- Ezer, T.; Corlett, W.B. Is sea level rise accelerating in the Chesapeake Bay? A demonstration of a novel new approach for analyzing sea level data. Geophys. Res. Lett. 2012, 39, L19605. [Google Scholar] [CrossRef]
- Ezer, T.; Atkinson, L.P.; Corlett, W.B.; Blanco, J.L. Gulf Stream’s induced sea level rise and variability along the U.S. mid-Atlantic coast. J. Geophys. Res. Ocean 2013, 118, 685–697. [Google Scholar] [CrossRef]
- Chambers, D.P. Evaluation of empirical mode decomposition for quantifying multi-decadal variations and acceleration in sea level records. Nonlinear Proc. Geophys. 2015, 22, 157–166. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Frankcombe, L.M.; Von der Heydt, A.; Dijkstra, H.A. North Atlantic multidecadal climate variability: An Investigation of dominant time scales and processes. J. Climatol. 2010, 23, 3626–3638. [Google Scholar] [CrossRef]
- Marshall, J.; Johnson, H.; Goodman, J. A study of the interaction of the North Atlantic Oscillation with the ocean circulation. J. Clim. 2001, 14, 1399–1421. [Google Scholar] [CrossRef]
- Bellucci, A.; Gualdi, S.; Scoccimarro, E.; Navarra, A. NAO-ocean circulation interactions in a coupled general circulation model. Clim. Dyn. 2008, 31, 759–777. [Google Scholar] [CrossRef]
- Fan, M.; Schneider, E.K. Observed decadal North Atlantic tripole SST variability. Part I: Weather noise forcing and coupled response. J. Atmos. Sci. 2012, 69, 35–50. [Google Scholar]
- Knudsen, M.F.; Seidenkrantz, M.-S.; Jacobsen, B.H.; Kuijpers, A. Tracking the Atlantic Multidecadal Oscillation through the last 8,000 years. Nat. Commun. 2011, 2, 178. [Google Scholar] [CrossRef]
- Hubeny, J.B.; King, J.W.; Santos, A. Subdecadal to multidecadal cycles of Late Holocene North Atlantic climate variability preserved by estuarine fossil pigments. Geology 2006, 34, 569–572. [Google Scholar] [CrossRef]
- Calafat, F.M.; Jordà, G.; Marcos, M.; Gomis, D. Comparison of Mediterranean sea level variability as given by three baroclinic models. J. Geophys. Res. 2012, 117, c02009. [Google Scholar] [CrossRef]
- Calafat, F.M.; Chambers, D.P.; Tsimplis, M.N. Mechanisms of decadal sea level variability in the eastern North Atlantic and the Mediterranean Sea. J. Geophys. Res. 2012, 117, c09022. [Google Scholar] [CrossRef]
- Tsimplis, M.N.; Shaw, A.G.P. The forcing of mean sea level variability around Europe. Glob. Planet. Chang. 2008, 63, 196–202. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.-P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L. The roles of external forcing and natural variability in global warming hiatuses. Clim. Dyn. 2016, 47, 3157–3169. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.-P. The tropical Pacific as a key pacemaker of the variable rates of global warming. Nat. Geosci. 2016, 9, 669–673. [Google Scholar] [CrossRef]
- Marullo, S.; Artale, V.; Santoleri, R. The SST Multidecadal Variability in the Atlantic–Mediterranean Region and Its Relation to AMO. J. Clim. 2011, 24, 4385–4401. [Google Scholar] [CrossRef]
- Vigo, M.; Sánchez-Reales, J.; Trottini, M.; Chao, B. Mediterranean Sea level variations: Analysis of the satellite altimetric data, 1992–2008. J. Geodyn. 2011, 52, 271–278. [Google Scholar] [CrossRef]
- Devoti, R.; D’Agostino, N.; Serpelloni, E.; Pietrantonio, G.; Riguzzi, F.; Avallone, A.; Cavaliere, A.; Cheloni, D.; Cecere, G.; D’Ambrosio, C.; et al. The mediterranean crustal motion map compiled at INGV. Ann. Geophys. 2017, 60. [Google Scholar] [CrossRef]
- Serpelloni, E.; Faccenna, C.; Spada, G.; Dong, D.; Williams, S.D.P. Vertical GPS ground motion rates in the Euro-Mediterranean region: New evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary. J. Geophys. Res. Solid Earth 2013, 118, 6003–6024. [Google Scholar] [CrossRef]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef]
- Antonioli, F.; Anzidei, M.; Lambeck, K.; Auriemma, R.; Gaddi, D.; Furlani, S.; Orrù, P.; Solinas, E.; Gaspari, A.; Karinja, S.; et al. Sea level change during Holocene from Sardinia and northeastern Adriatic (Central Mediterranean sea) from archaeological and geomorphological data. Quat. Sci. Rev. 2007, 26, 2463–2524. [Google Scholar] [CrossRef]
- Carbognin, L.; Gatto, P.; Mozzi, G.; Gambolati, G.; Ricceri, G. New trend in the subsidence of Venice. In Proceedings of the Anaheim Symposium, Anaheim, CA, USA, 13–17 December 1976. [Google Scholar]
- Guidoboni, E.; Comastri, A. Catalogue of Earthquakes and Tsunami in the Mediterranean Area from the 11th to the 15th Century; INGV-SGA: Rome, Italy, 2007. [Google Scholar]
- Carbognin, L.; Teatini, P.; Tomasin, A.; Tosi, L. Global change and relative sea level rise at Venice: What impact in term of flooding. Clim. Dyn. 2010, 35, 1039–1047. [Google Scholar] [CrossRef]
- Lyu, K.; Zhang, X.; Church, J.A.; Slangen, A.B.A.; Hu, J. Time of emergence for regional sea-level change. Nat. Clim. Chang. 2014, 4, 1006–1010. [Google Scholar] [CrossRef]
- Bordbar, M.H.; Martin, T.; Latif, M.; Park, W. Effects of long-term variability on projections of twenty-first century dynamic sea level. Nat. Clim. Chang. 2015, 5, 343–347. [Google Scholar] [CrossRef]
- Carson, M.; Köhl, A.; Stammer, D. The Impact of Regional Multidecadal and Century-Scale Internal Climate Variability on Sea Level Trends in CMIP5 Models. J. Clim. 2015, 28, 853–861. [Google Scholar] [CrossRef]
- Kopp, R.E.; Hay, C.C.; Little, C.M.; Mitrovica, J.X. Geographic Variability of Sea-Level Change. Curr. Clim. Chang. Rep. 2015, 1, 192–204. [Google Scholar] [CrossRef]
- Little, C.M.; Horton, R.M.; Kopp, R.; Oppenheimer, M.; Yip, S. Uncertainty in Twenty-First-Century CMIP5 Sea Level Projections. J. Clim. 2015, 28, 838–852. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.S.; Nunn, P.; et al. Sea level change. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D.G.-K., Plattner, M., Tignor, S.K., Allen, J., Boschung, A., Nauels, Y., Bex, X.V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.S.; Nunn, P.; et al. Sea Level Change Supplementary Material. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D.G.-K., Plattner, M., Tignor, S.K., Allen, J., Boschung, A., Nauels, Y., Bex, X.V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Peltier, W.R. Global glacial isostasy and the surface of the ice-age earth: The ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet. Sci. 2004, 32, 111–149. [Google Scholar] [CrossRef]
- Lambeck, K.; Smither, C.; Johnston, P. Sea-level change, glacial rebound and mantle viscosity for northern Europe. Geophys. J. Int. 1998, 134, 102–144. [Google Scholar] [CrossRef]
- Aral, M.M.; Chang, B. Spatial Variation of Sea Level Rise at Atlantic and Mediterranean Coastline of Europe. Water 2017, 9, 522. [Google Scholar] [CrossRef]
- Chang, B.; Guan, J.; Aral, M.M. A Scientific Discourse: Climate Change and Sea-Level Rise. ASCE J. Hydrol. Eng. 2015, 20, A4014003. [Google Scholar] [CrossRef]
- Chang, B.; Guan, J.; Aral, M.M. Modeling Spatial Variations of Sea Level Rise and Corresponding Inundation Impacts: A Case Study for Florida, USA. Water Qual. Expo. Health 2013, 6, 39–51. [Google Scholar] [CrossRef]
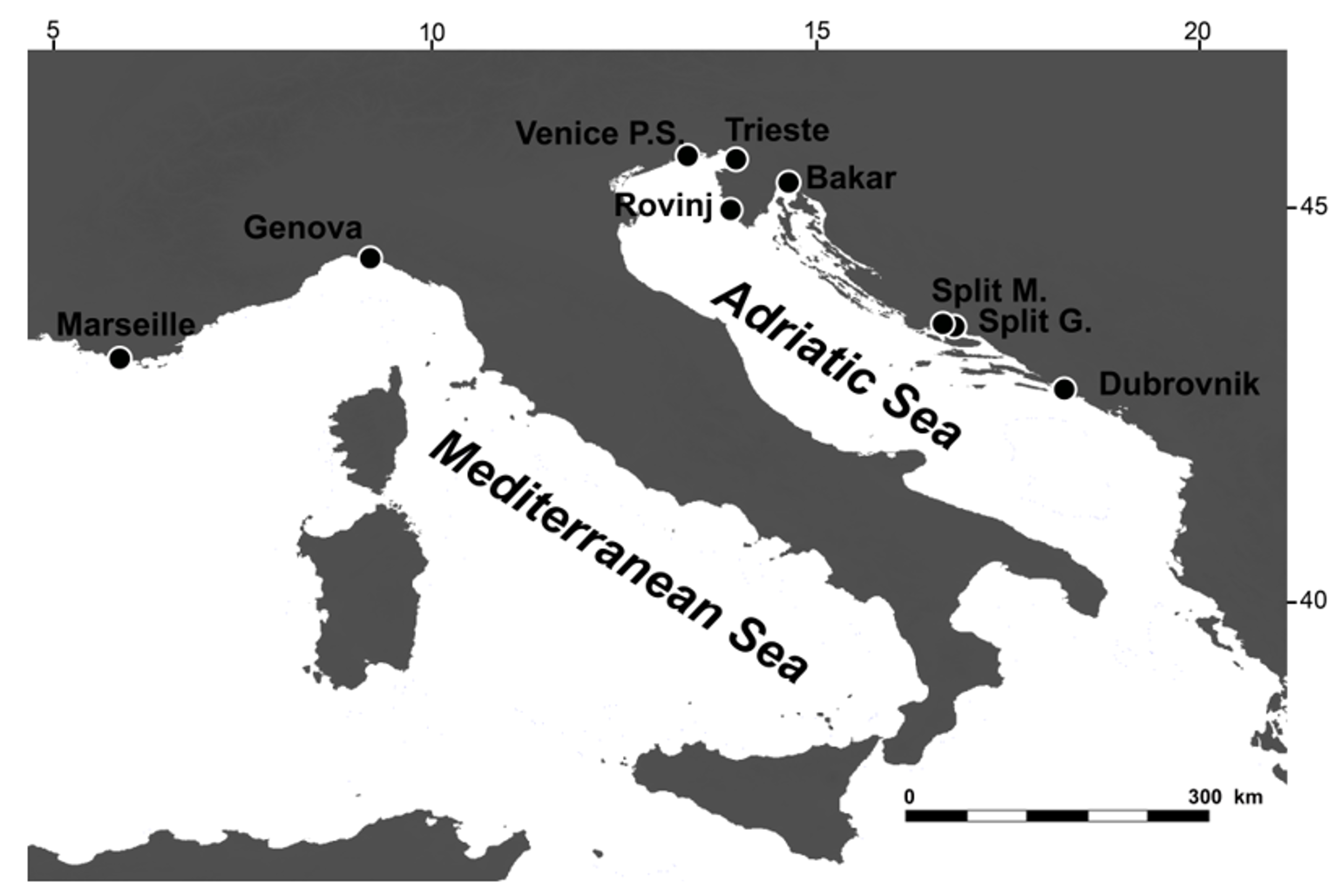
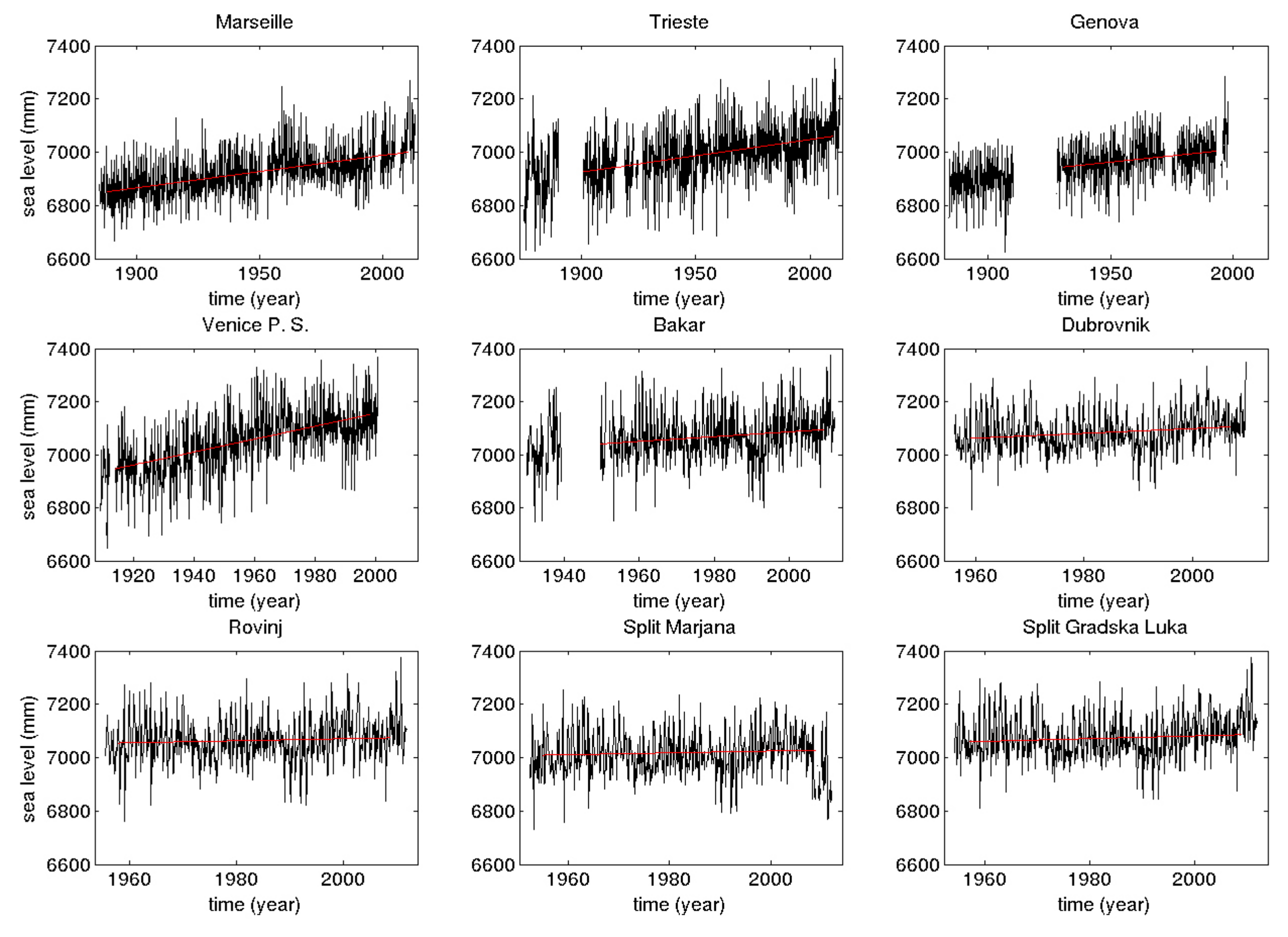
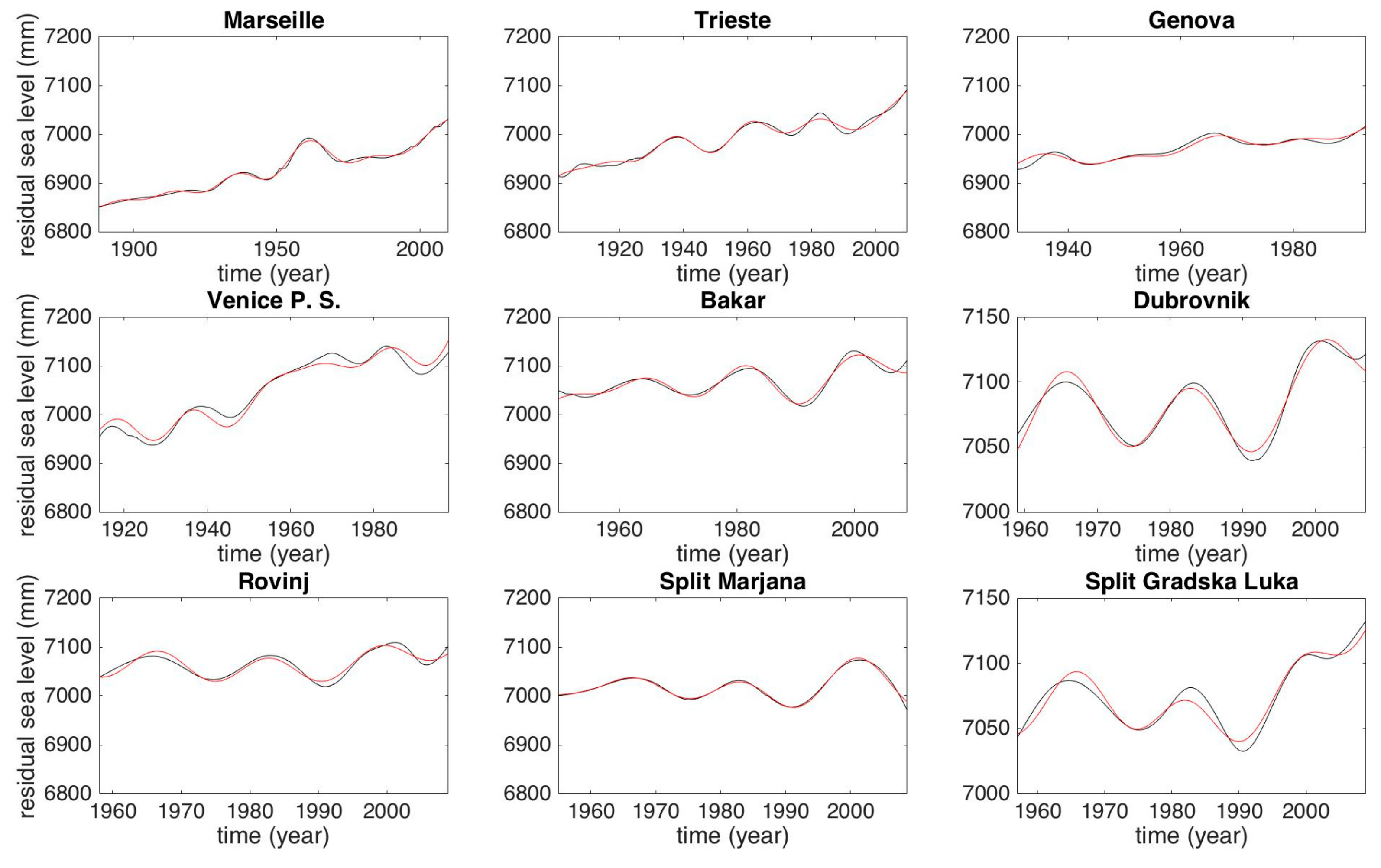
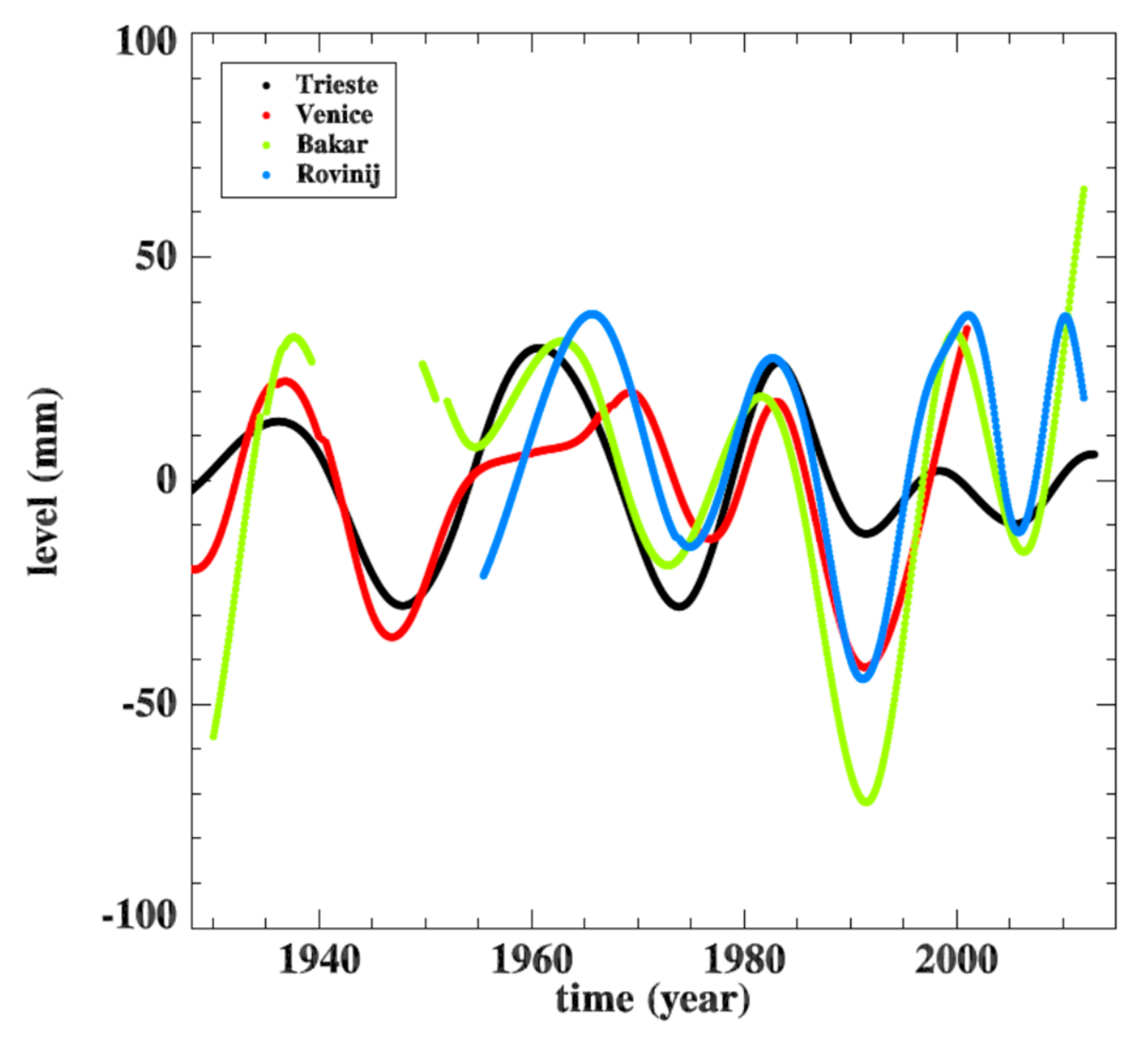
| Tide Gauge Station | n | j = 7 | j = 8 | j = 9 | j = 10 | j = 11 | j = 12 | j = 13 |
|---|---|---|---|---|---|---|---|---|
| Marseille | 15 | 29.8 ± 14.5 | 36.5 ± 7.4 | 43.1 ± 15.6 | 63.1 ± 21.2 | |||
| Trieste | 15 | 19.8 ± 4.4 | 27.0 ± 3.6 | 37.6 ± 8.8 | 52.2 ± 12.7 | 76.3 ± 45.9 | ||
| Genova | 10 | 15.3 ± 2.5 | 32.2 ± 2.1 | |||||
| Venice P.S. | 12 | 16.0 ± 2.5 | 21.0 ± 2.1 | 44.3 ± 5.0 | ||||
| Bakar | 12 | 16.9 ± 2.8 | 29.4 ± 7.7 | 58.0 ± 4.9 | ||||
| Dubrovnik | 11 | 17.0 ± 2.5 | 49.4 ± 19.2 | |||||
| Rovinj | 11 | 16.2 ± 5.6 | 36.6 ± 8.3 | |||||
| Split M. | 13 | 18.6 ± 3.4 | 21.7 ± 4.5 | 33.7 ± 25.9 | ||||
| Split G. | 11 | 17.8 ± 3.7 | 49.6 ± 16.4 |
| Tide Gauge Station | Linear Fit (mm a−1) | r (mm a−1) | c (mm) | A (mm) | Φ | R2 |
|---|---|---|---|---|---|---|
| Marseille | 1.22 ± 0.10 | 1.28 ± 0.01 | 4436 ± 12 | 10.1 ± 0.3 | 4.03 ± 0.30 | 0.9948 |
| 11.1 ± 0.3 | −0.84 ± 0.03 | |||||
| 16.1 ± 0.5 | 1.84 ± 0.04 | |||||
| 18.7 ± 0.5 | −0.42 ± 1.54 | |||||
| Trieste | 1.22 ± 0.15 | 1.59 ± 0.05 | 3874 ± 86 | 10.8 ± 0.4 | 2.54 ± 2.11 | 0.9844 |
| 13.2 ± 0.8 | 2.34 ± 0.05 | |||||
| 10.3 ± 1.7 | 4.87 ± 0.73 | |||||
| 19.1 ± 2.9 | −3.04 ± 0.13 | |||||
| 21.9 ± 2.0 | 2.52 ± 0.05 | |||||
| Genova | 1.07 ± 0.24 | 1.20 ± 0.03 | 4618 ± 54 | 7.8 ± 0.7 | −1.93 ± 0.08 | 0.9254 |
| 12.1 ± 0.6 | 2.58 ± 0.24 | |||||
| Venice P.S. | 2.43 ± 0.23 | 2.78 ± 0.04 | 1615 ± 74 | 13.1 ± 1.1 | −0.61 ± 0.09 | 0.9579 |
| 18.8 ± 1.3 | −2.03 ± 0.07 | |||||
| 23.8 ± 1.3 | 2.10 ± 0.05 | |||||
| Bakar | 0.9 ± 0.37 | 0.88 ± 0.15 | 5323 ± 306 | 21.1 ± 1.3 | 3.36 ± 0.89 | 0.9515 |
| 21.9 ± 2.2 | −1.63 ± 0.11 | |||||
| 12.1 ± 0.7 | −0.66 ± 2.36 | |||||
| Dubrovnik | 0.90 ± 0.44 | 1.24 ± 0.05 | 4520 ± 104 | 27.4 ± 0.6 | 2.41 ± 0.02 | 0.9662 |
| 20.6 ± 0.8 | −1.74 ± 0.04 | |||||
| Rovinj | 0.38 ± 0.43 | 0.97 ± 0.10 | 5144 ± 190 | 26.5 ± 0.9 | −0.45 ± 0.03 | 0.9014 |
| 20.3 ± 1.2 | 1.76 ± 0.09 | |||||
| Split M. | 0.35 ± 0.38 | 0.17 ± 0.02 | 6671 ± 29 | 18.8 ± 0.3 | 2.62 ± 0.02 | 0.9888 |
| 26.8 ± 0.4 | −1.84 ± 0.01 | |||||
| 26.4 ± 0.4 | 1.35 ± 0.01 | |||||
| Split G. L. | 0.51 ± 0.40 | 1.87 ± 0.07 | 3360 ± 137 | 17.1 ± 0.7 | 0.68 ± 0.04 | 0.9434 |
| 35.1 ± 0.1 | 1.48 ± 0.03 |
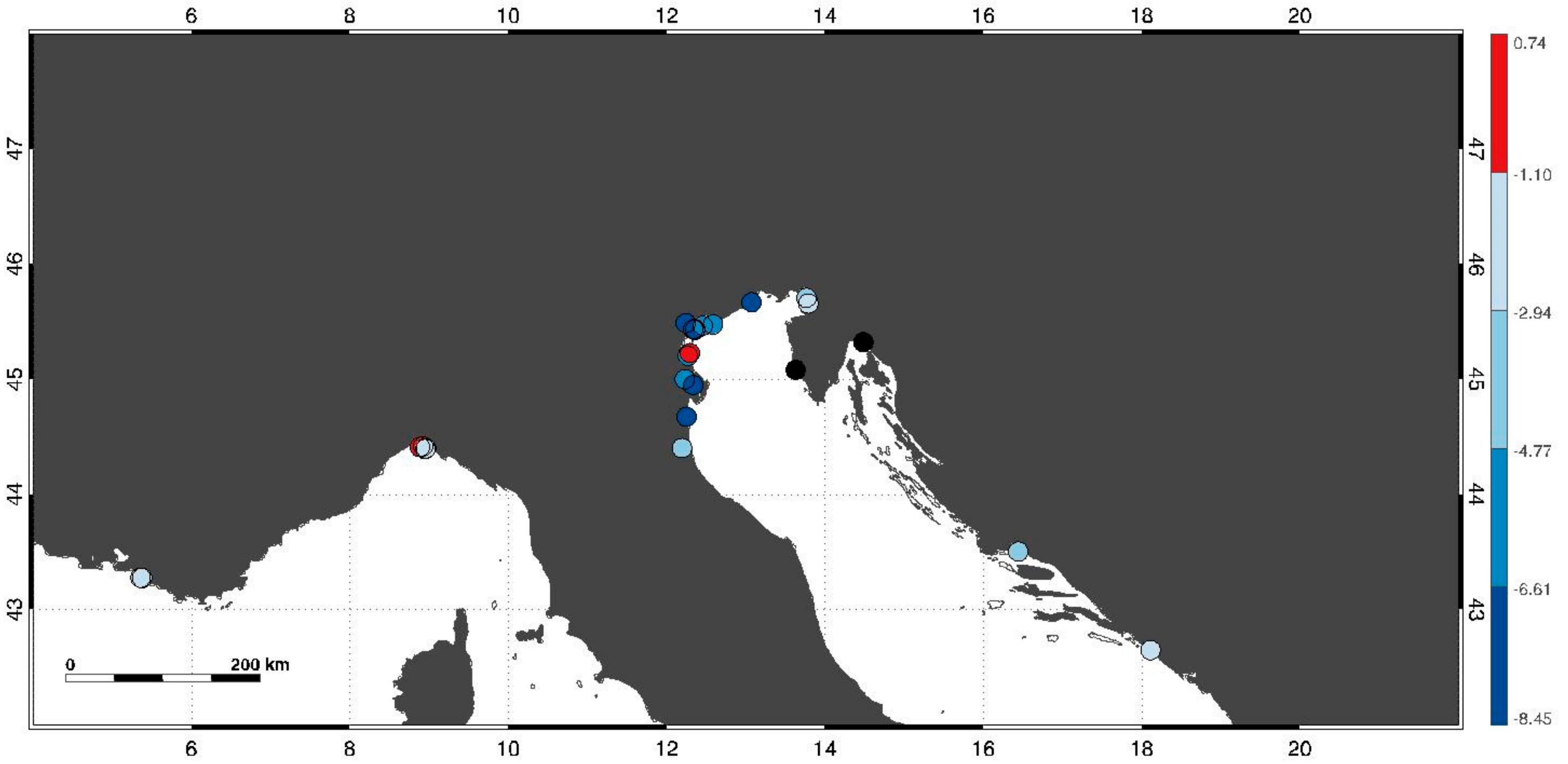
| GNSS Station | Lon | Lat | VLM (mm a−1) | Time Interval | Average VLM (mm a−1) | Tide Gauge Location |
|---|---|---|---|---|---|---|
| PRIE | 5.3727 | 43.2768 | −0.65 ± 0.55 | 2007.6397–2018.0890 | −0.61 ± 0.43 | Marseille |
| MARS | 5.3538 | 43.2788 | −0.58 ± 0.31 | 1998.5465–2018.0917 | ||
| TRIE | 13.7635 | 45.7098 | −0.20 ± 0.36 | 2003.1054–2018.0917 | −0.08 ± 0.49 | Trieste |
| TRI1 | 13.7878 | 45.6606 | 0.04 ± 0.61 | 2007.7821–2016.8948 | ||
| GENV | 8.8809 | 44.4152 | 0.74 ± 0.90 | 2008.4631–2014.7602 | −0.12 ± 1.54 | Genova |
| GENO | 8.9211 | 44.4194 | −0.25 ± 0.30 | 1998.5575–2018.0917 | ||
| GENA | 8.9482 | 44.3976 | −0.51 ± 4.30 | 2016.6270–2017.9273 | ||
| GENU | 8.9593 | 44.4027 | −0.50 ± 0.68 | 2009.9465–2017.9986 | ||
| DUB2 | 18.1103 | 42.6502 | −1.13 ± 0.96 | 2011.9739–2018.0917 | −1.56 ± 0.72 | Dubrovnik |
| DUBR | 18.1104 | 42.6500 | −1.99 ± 0.48 | 2000.7226–2012.7363 | ||
| SPLT | 16.4385 | 43.5066 | 0.56 ± 0.77 | 2005.0013–2012.2527 | 0.56 ± 0.77 | Split |
| CGIA | 12.2655 | 45.2065 | −2.91 ± 0.83 | 2010.9630–2018.0917 | −3.30 ± 0.85 | Venice |
| SFEL | 12.2913 | 45.2300 | −4.57 ± 0.67 | 2001.5465–2011.1657 | ||
| VEAR | 12.3578 | 45.4379 | −2.17 ± 1.35 | 2006.1602–2010.7164 | ||
| VEN1 | 12.3541 | 45.4306 | −1.46 ± 0.65 | 2009.8068–2018.0917 | ||
| VENE | 12.3320 | 45.4370 | −0.89 ± 0.82 | 2001.0863–2007.5630 | ||
| VE01 | 12.3339 | 45.4375 | −2.22 ± 1.56 | 2007.8506–2011.1821 | ||
| MSTR | 12.2386 | 45.4904 | −2.50 ± 0.79 | 2007.8890–2014.6315 | ||
| TREP | 12.4547 | 45.4677 | −8.45 ± 1.69 | 2004.1871–2008.0724 | ||
| CAVA | 12.5827 | 45.4794 | −2.71 ± 0.58 | 2001.5438–2011.1657 | ||
| TGPO | 12.2283 | 45.0031 | −4.89 ± 0.53 | 2007.3164–2018.0917 | ||
| PTO1 | 12.3341 | 44.9515 | −4.26 ± 0.59 | 2008.4631–2017.9301 | ||
| GARI | 12.2494 | 44.6769 | −3.25 ± 0.66 | 2009.3958–2018.0917 | ||
| RAVE | 12.1919 | 44.4053 | −4.23 ± 0.58 | 2008.0259–2017.9986 | ||
| BEVA | 13.0694 | 45.6719 | −1.69 ± 0.57 | 2008.0368–2018.0917 |
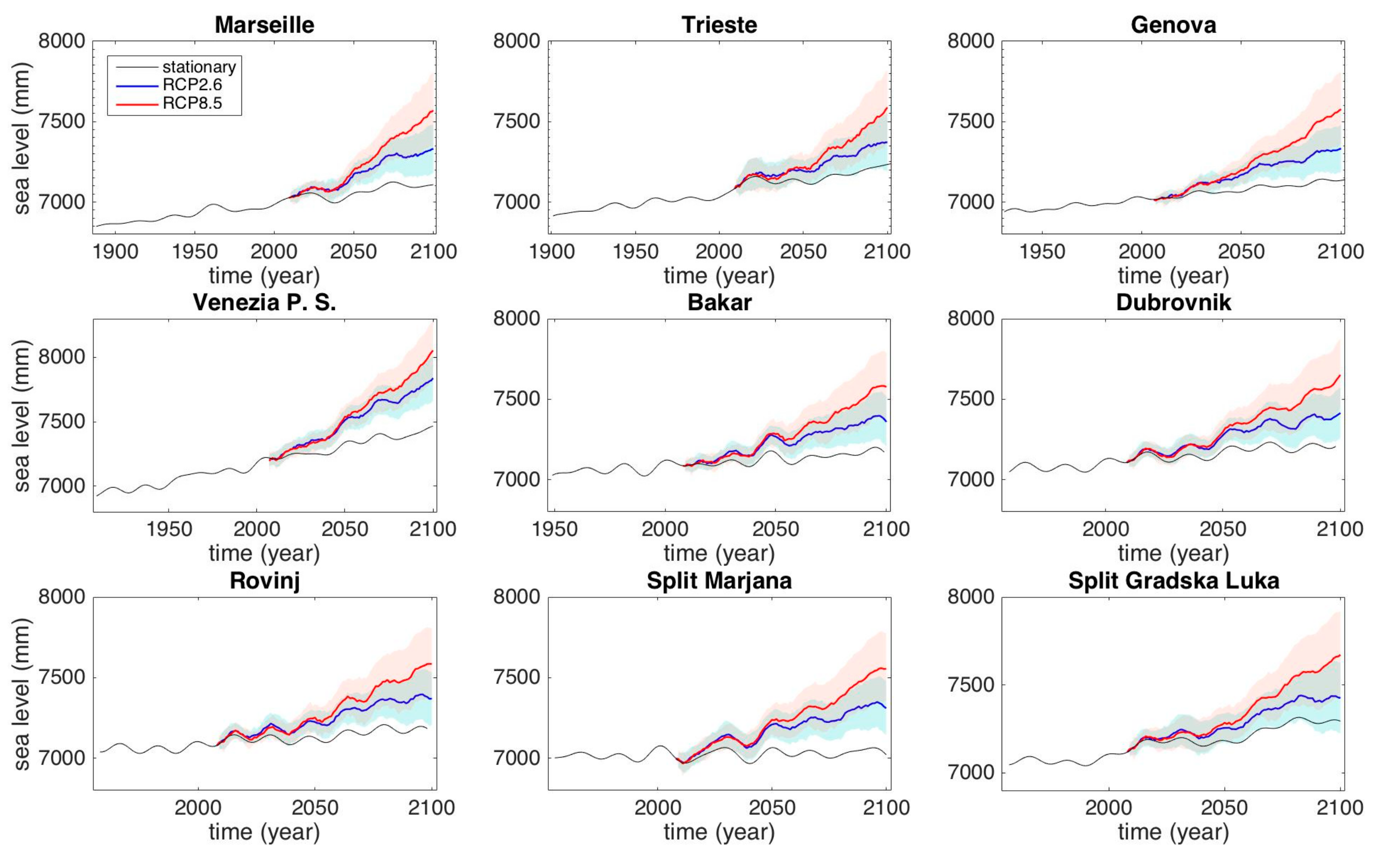
| Tide Gauge Station (Duration) | Sea Level (mm) RCP2.6 | Sea Level (mm) RCP8.5 | ||
|---|---|---|---|---|
| 2050 | 2100 | 2050 | 2100 | |
| Marseille | 182 ± 79 | 364 ± 167 | 208 ± 79 | 602 ± 240 |
| 1888–2009 | ||||
| (128 years) | ||||
| Trieste | 142 ± 82 | 336 ± 197 | 150 ± 86 | 523 ± 237 |
| 1901–2009 | ||||
| (138 years) | ||||
| Genova | 163 ± 150 | 337 ± 306 | 193 ± 156 | 581 ± 347 |
| 1931–1992 | ||||
| (92 years) | ||||
| Venice P.S. | 283 ± 103 | 603 ± 217 | 311 ± 114 | 818 ± 258 |
| 1914–1997 | ||||
| (92 years) | ||||
| Bakar | 166 ± 69 | 259 ± 165 | 182 ± 70 | 475 ± 203 |
| 1949–2008 | ||||
| (82 years) | ||||
| Dubrovnik | 225 ± 91 | 445 ± 200 | 246 ± 95 | 681 ± 246 |
| 1959–2006 | ||||
| (54 years) | ||||
| Rovinj | 149 ± 65 | 295 ± 164 | 177 ± 80 | 510 ± 216 |
| 1958–2008 | ||||
| (57 years) | ||||
| Split M. | 191 ± 106 | 322 ± 213 | 220 ± 112 | 567 ± 249 |
| 1955–2008 | ||||
| (60 years) | ||||
| Split G.L. | 174 ± 106 | 376 ± 240 | 204 ± 112 | 621 ± 273 |
| 1957–2008 | ||||
| (58 years) | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vecchio, A.; Anzidei, M.; Serpelloni, E.; Florindo, F. Natural Variability and Vertical Land Motion Contributions in the Mediterranean Sea-Level Records over the Last Two Centuries and Projections for 2100. Water 2019, 11, 1480. https://doi.org/10.3390/w11071480
Vecchio A, Anzidei M, Serpelloni E, Florindo F. Natural Variability and Vertical Land Motion Contributions in the Mediterranean Sea-Level Records over the Last Two Centuries and Projections for 2100. Water. 2019; 11(7):1480. https://doi.org/10.3390/w11071480
Chicago/Turabian StyleVecchio, Antonio, Marco Anzidei, Enrico Serpelloni, and Fabio Florindo. 2019. "Natural Variability and Vertical Land Motion Contributions in the Mediterranean Sea-Level Records over the Last Two Centuries and Projections for 2100" Water 11, no. 7: 1480. https://doi.org/10.3390/w11071480
APA StyleVecchio, A., Anzidei, M., Serpelloni, E., & Florindo, F. (2019). Natural Variability and Vertical Land Motion Contributions in the Mediterranean Sea-Level Records over the Last Two Centuries and Projections for 2100. Water, 11(7), 1480. https://doi.org/10.3390/w11071480







