Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method
Abstract
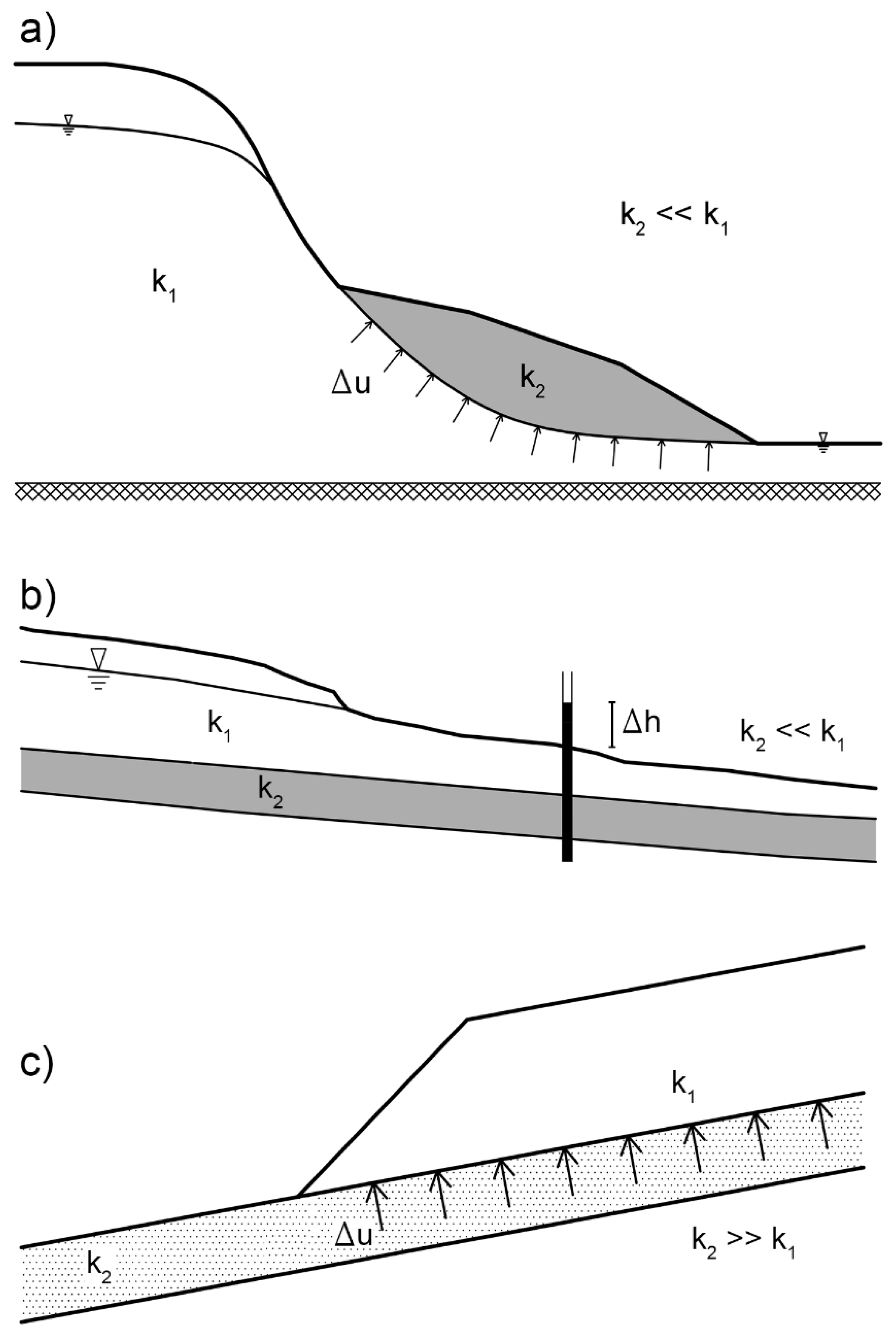
1. Introduction
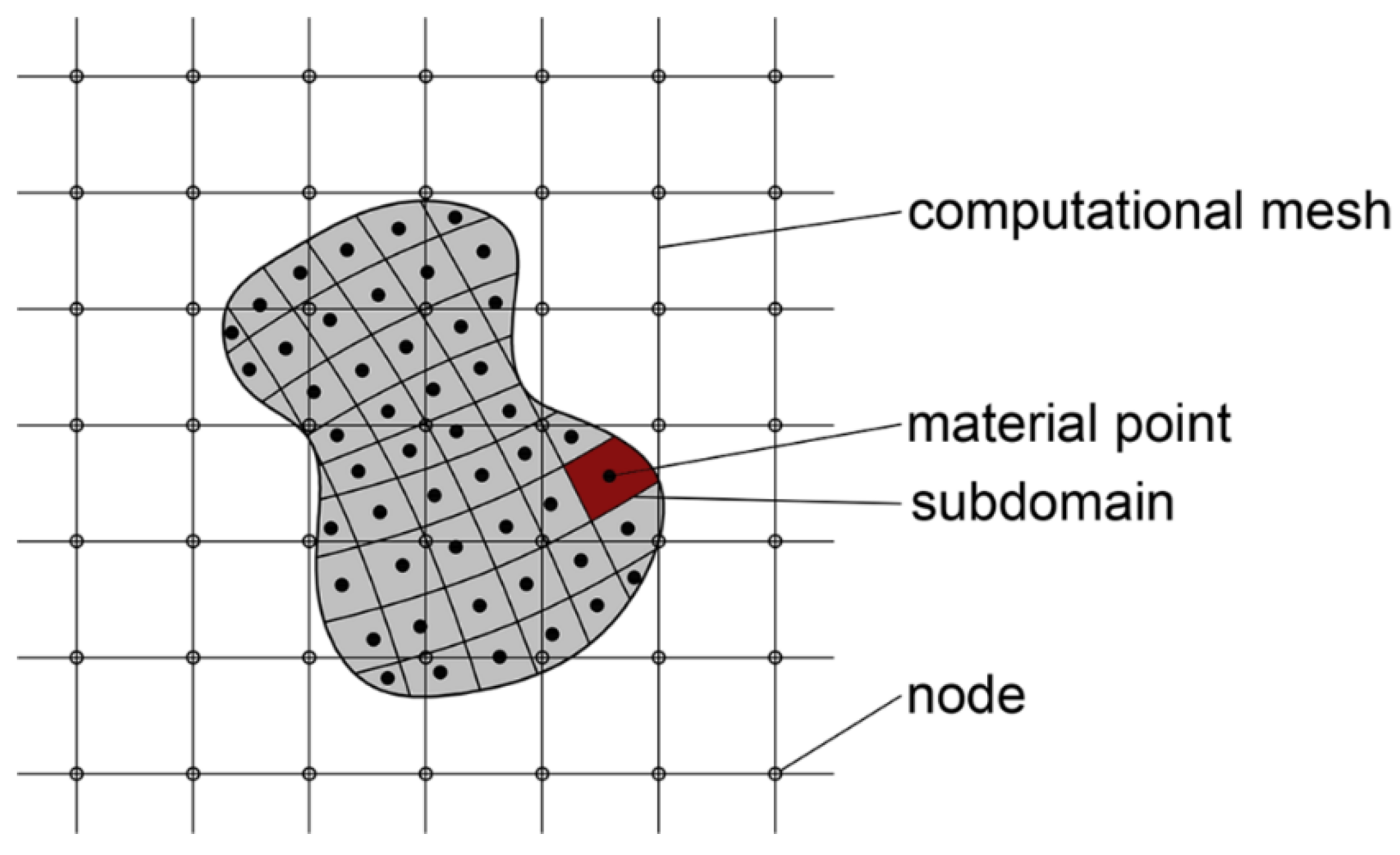
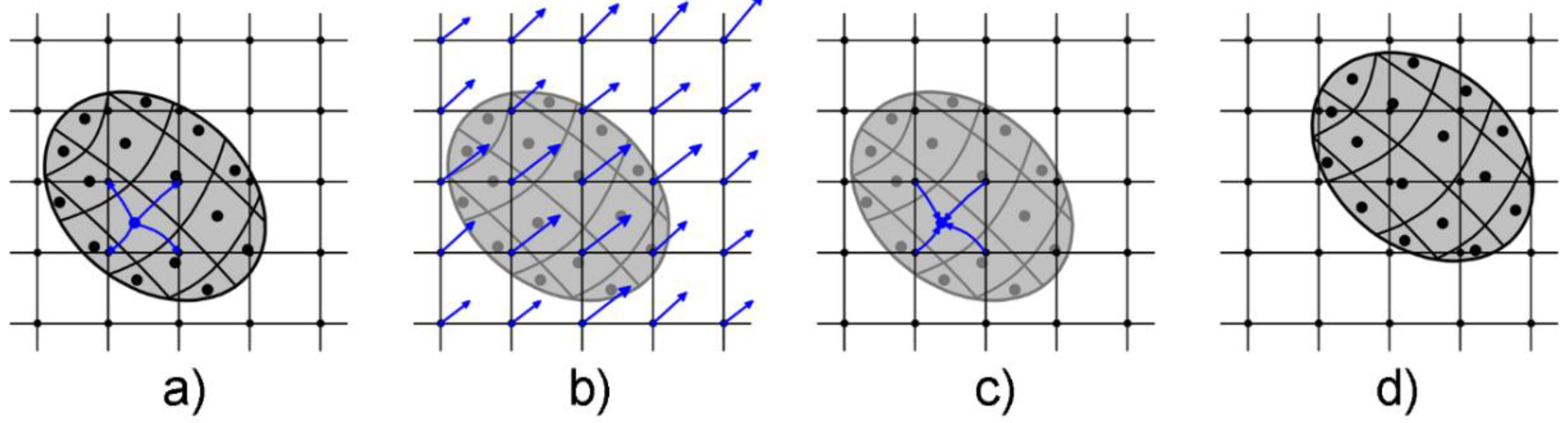
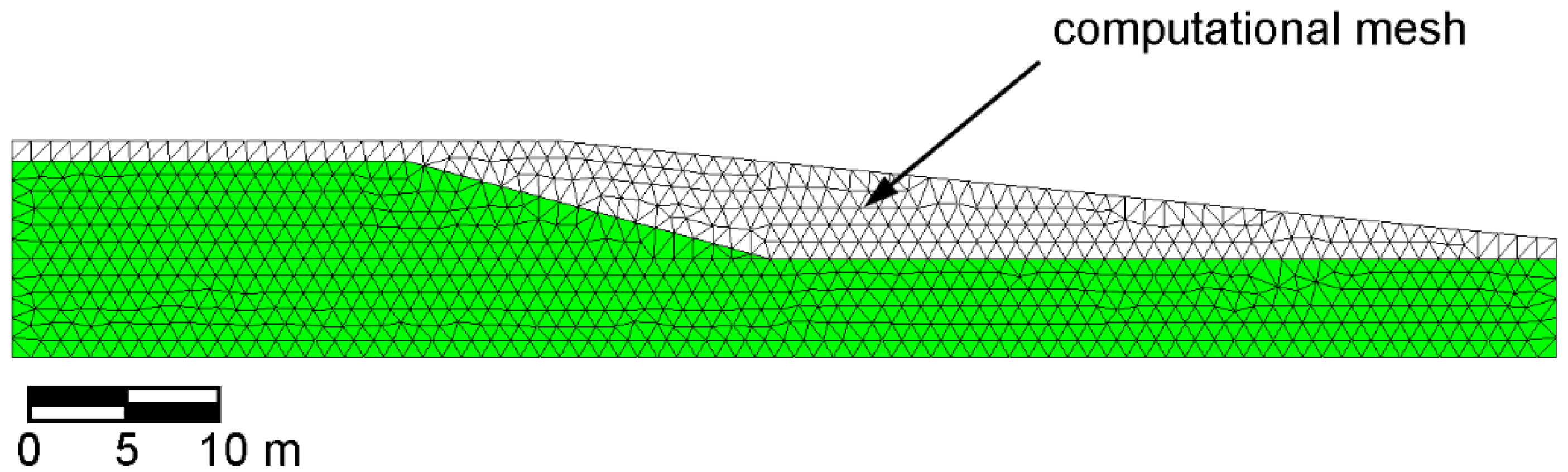
2. Material Point Method
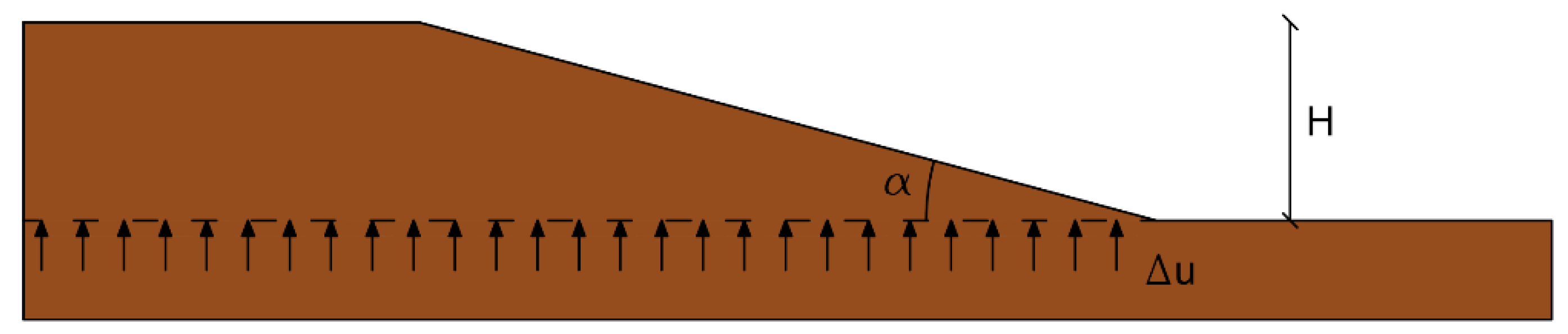
3. Parametric Study
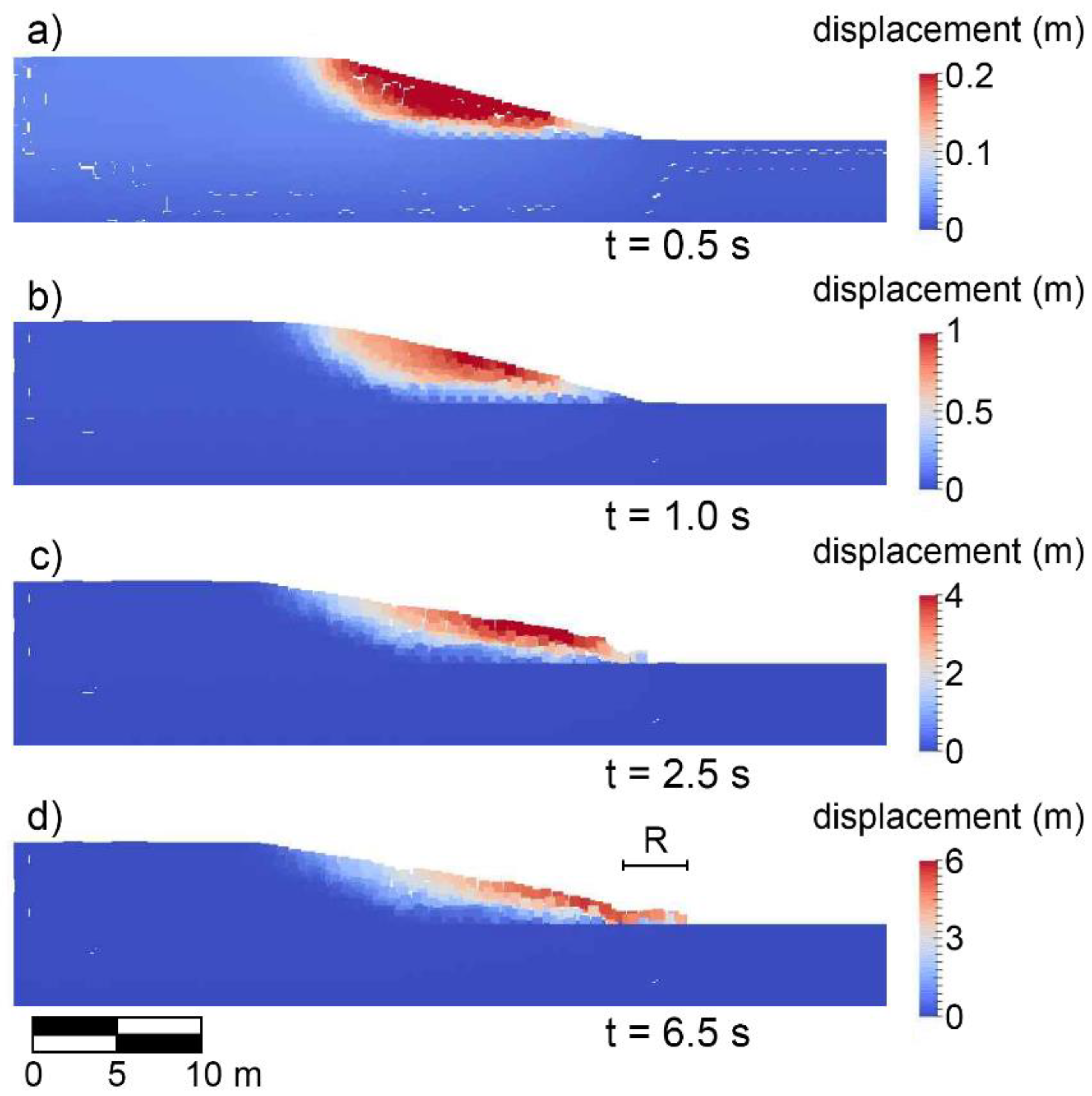
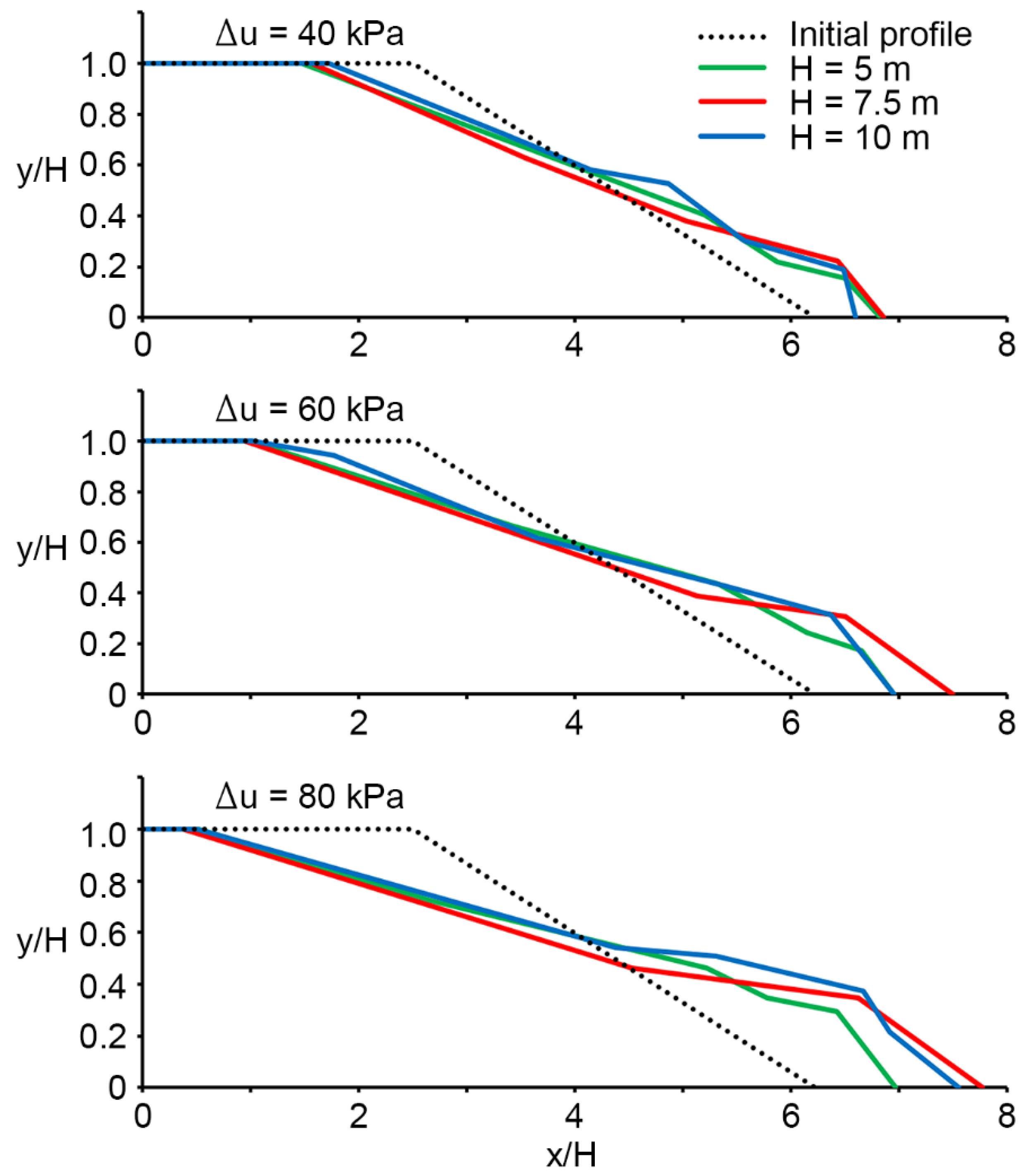
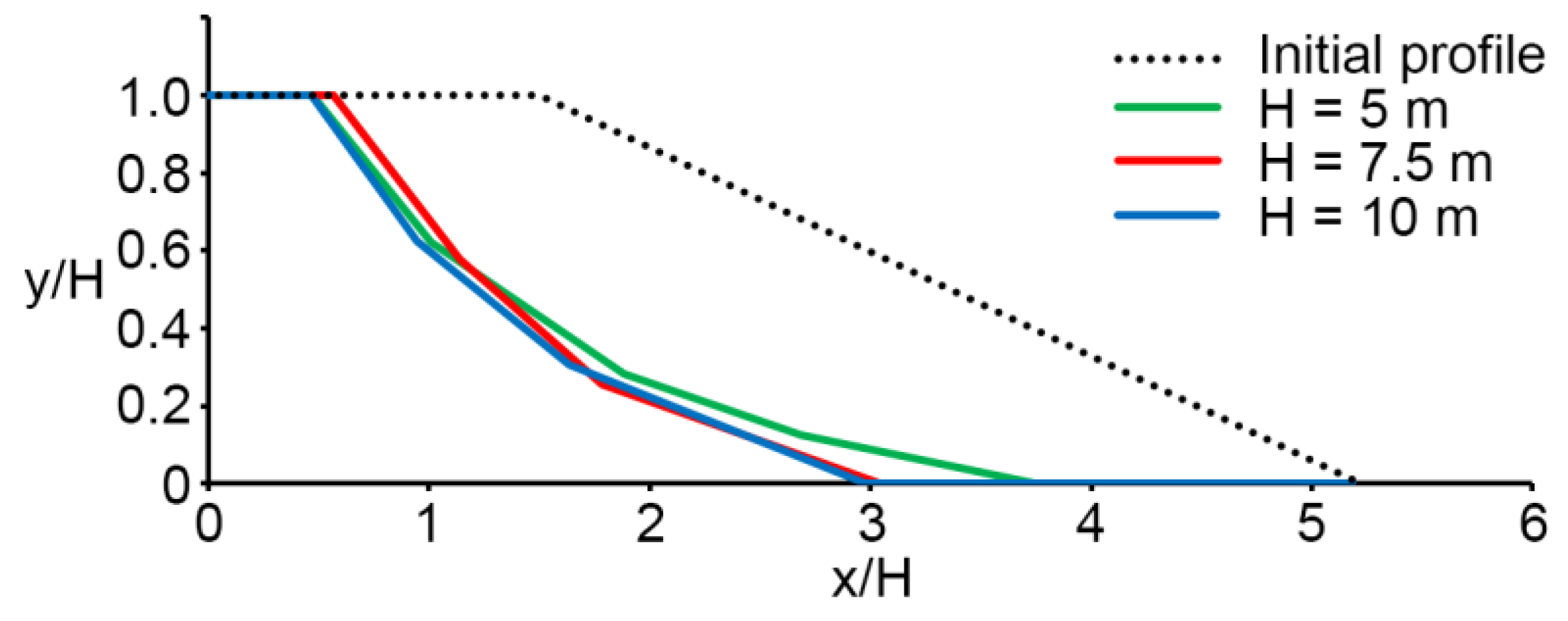
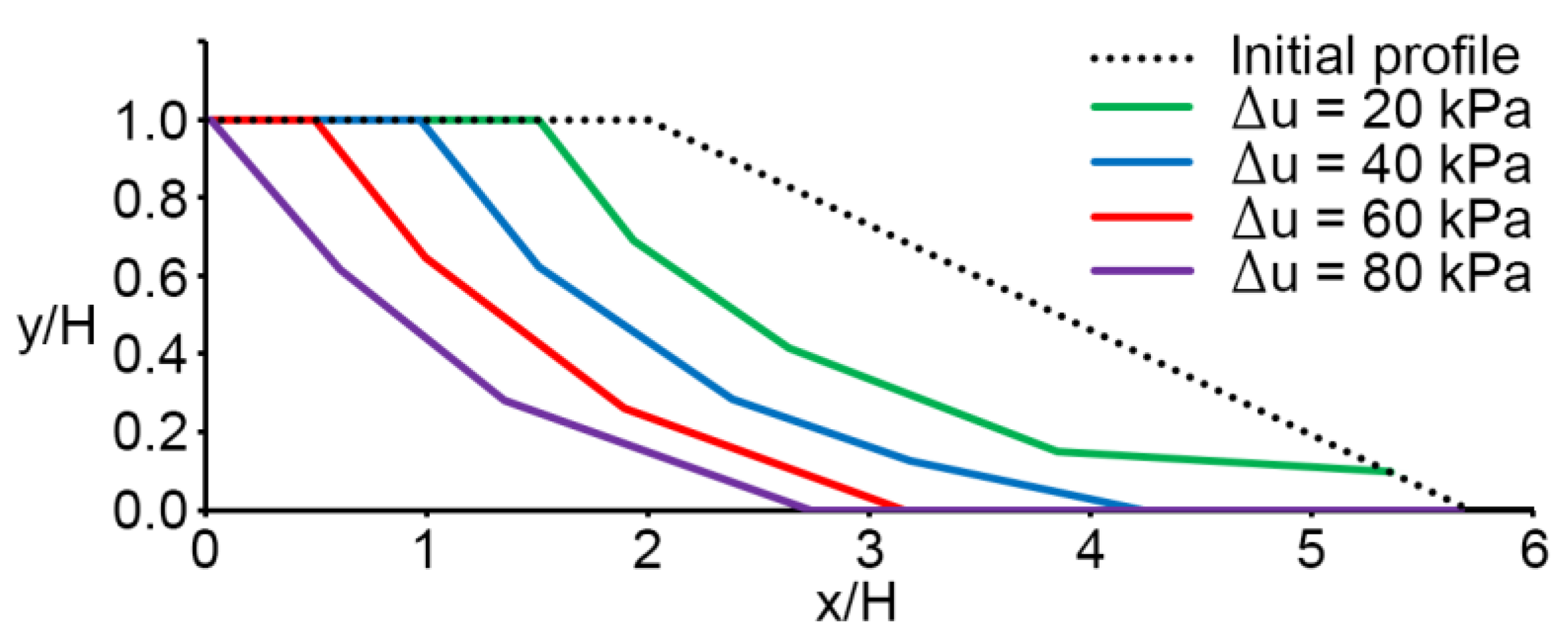
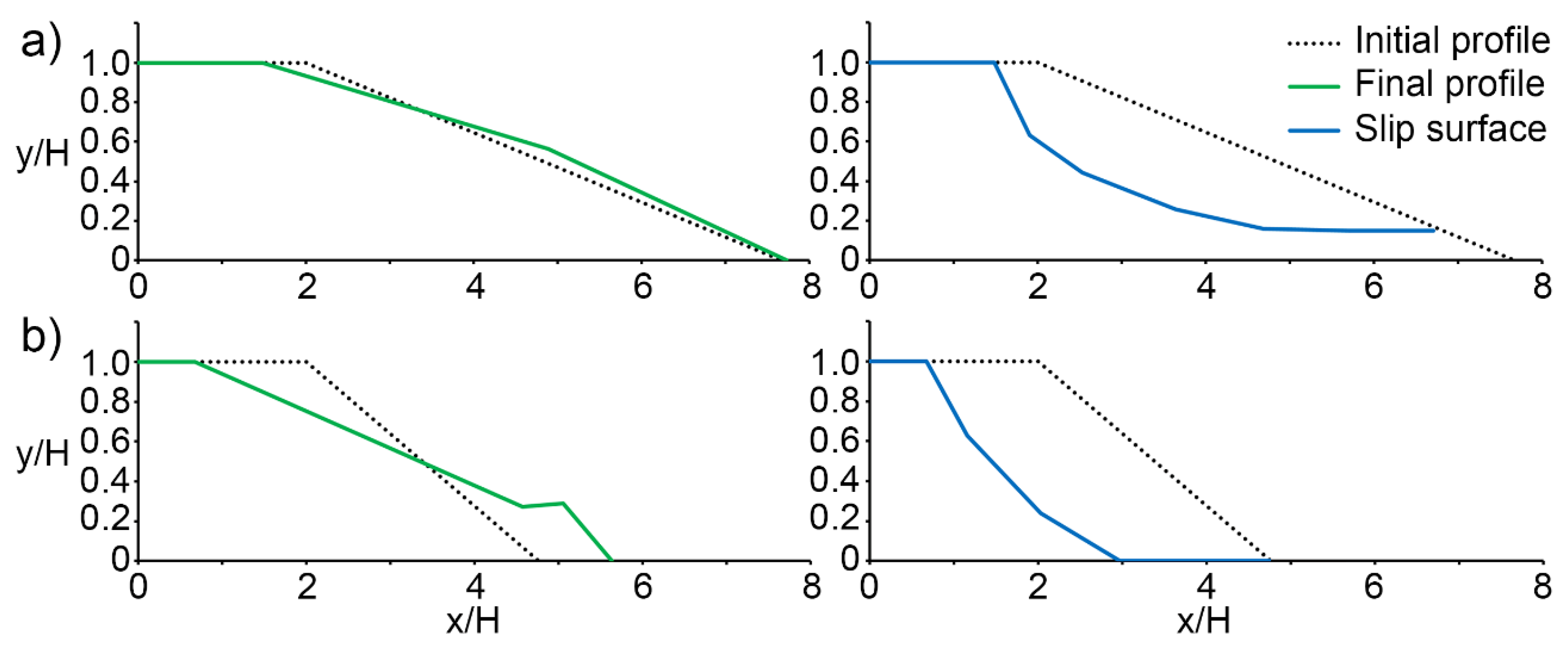
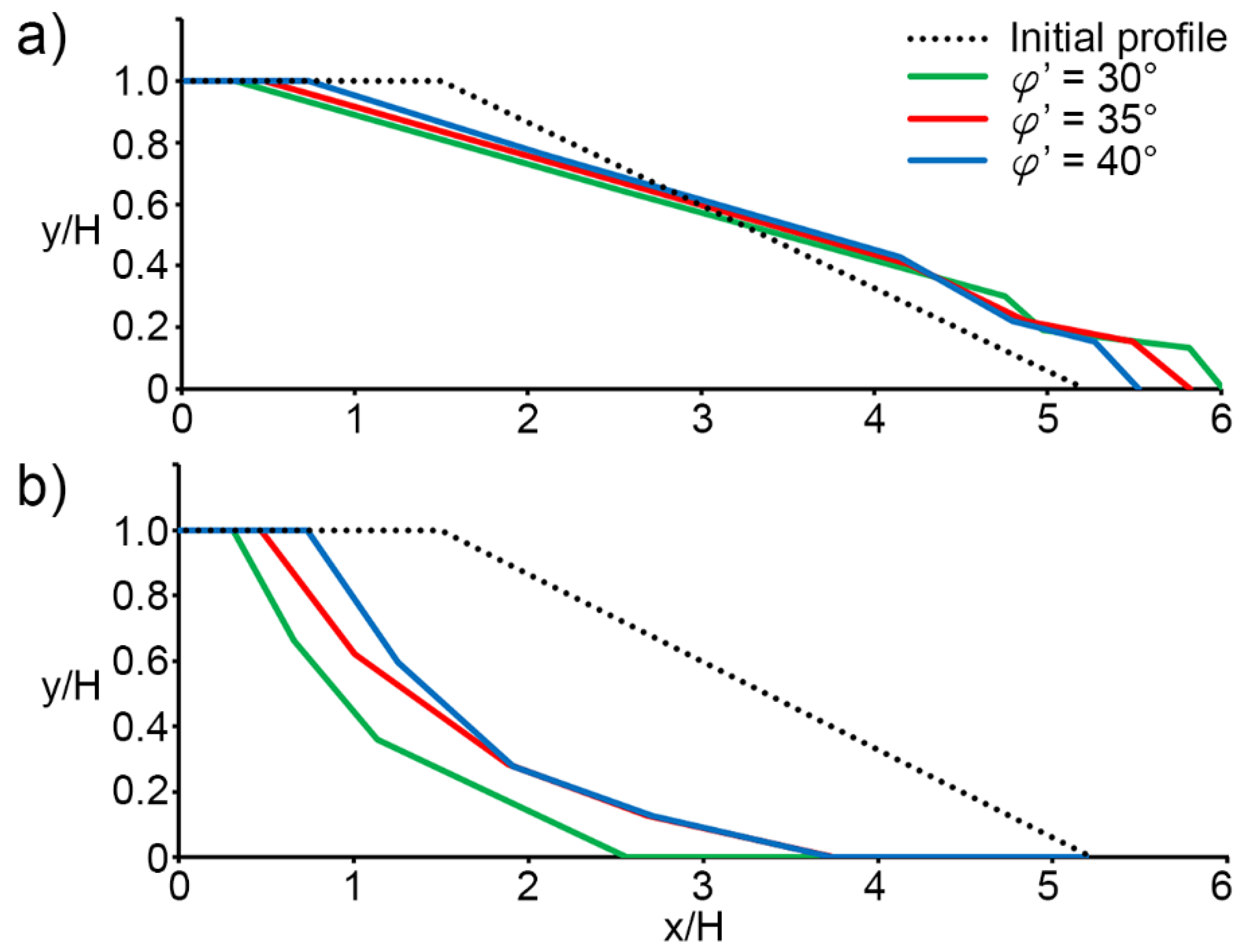
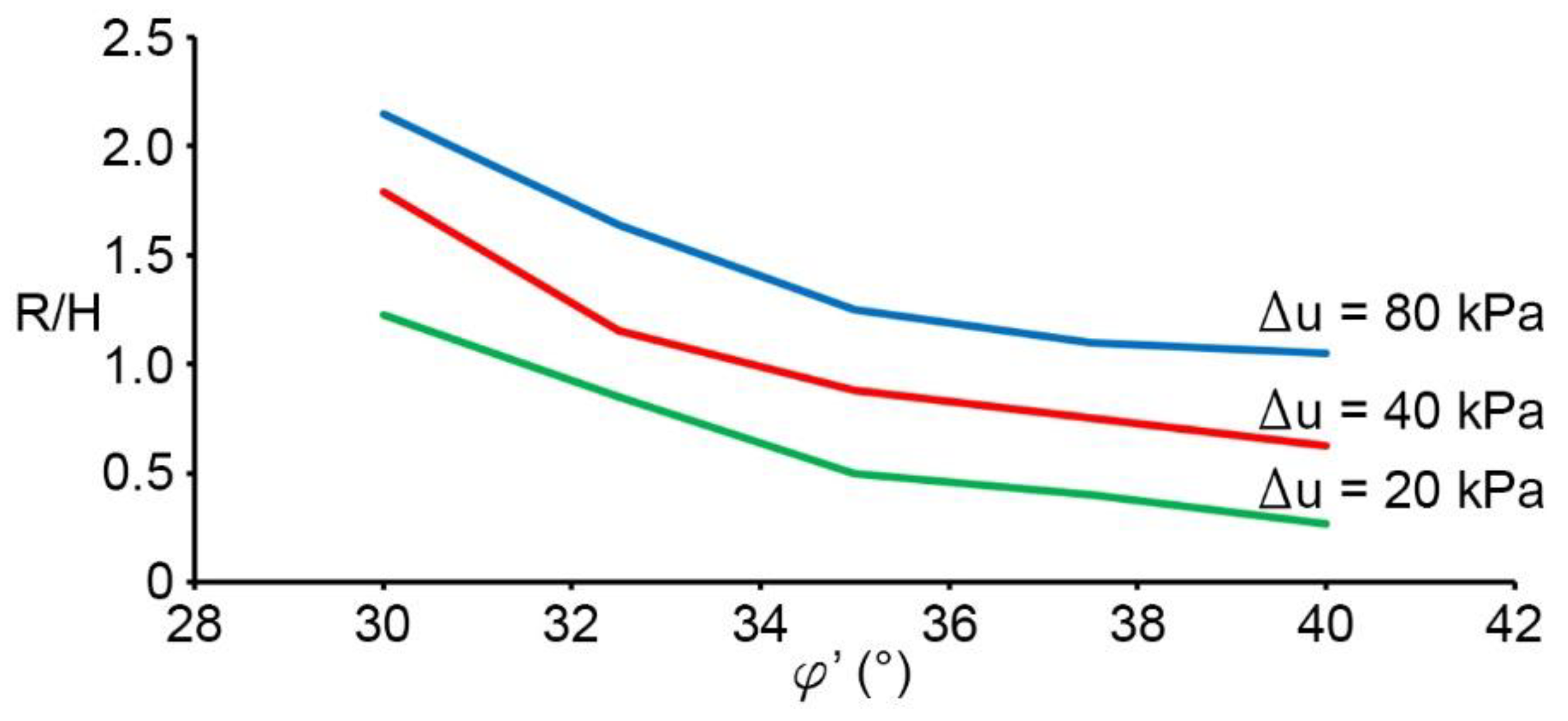
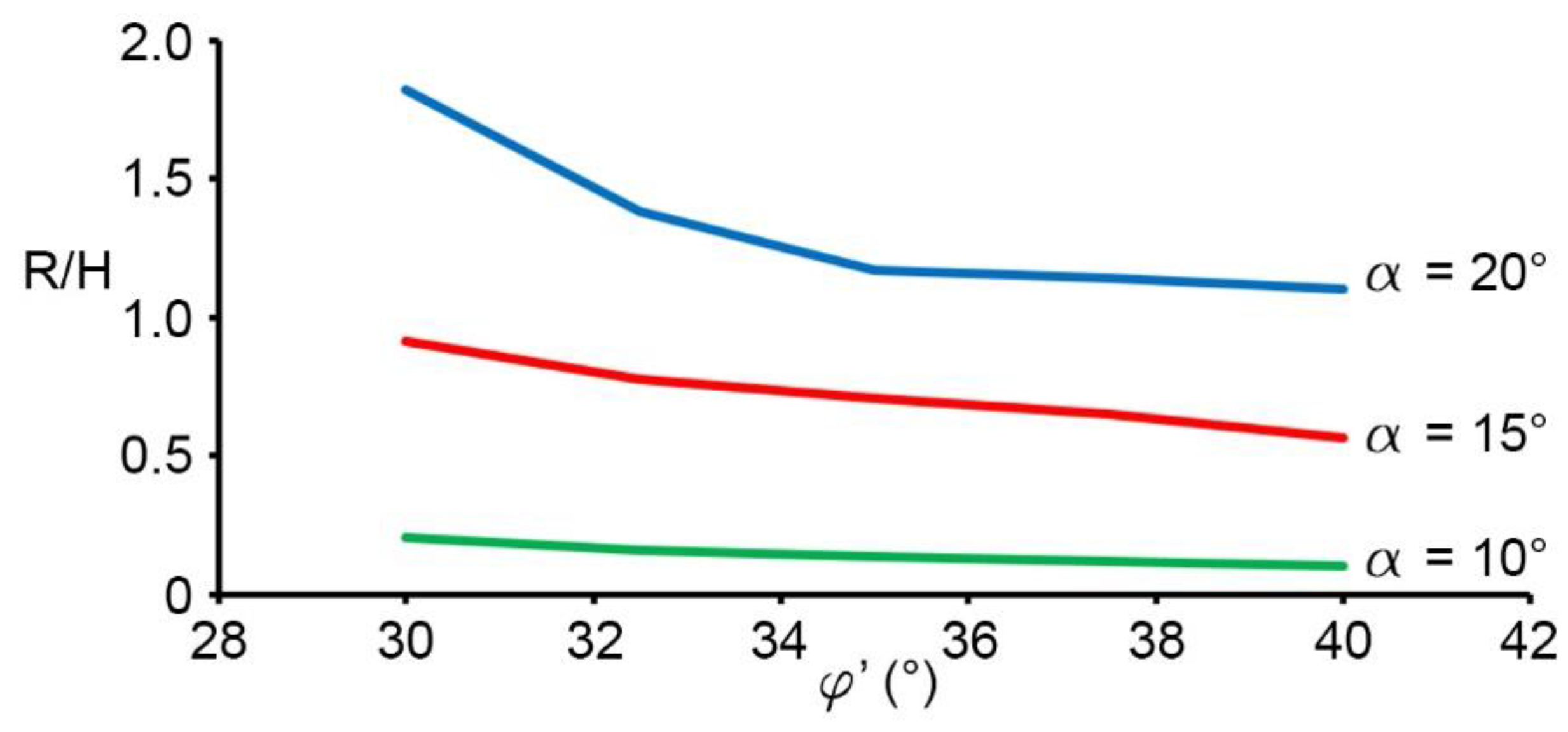
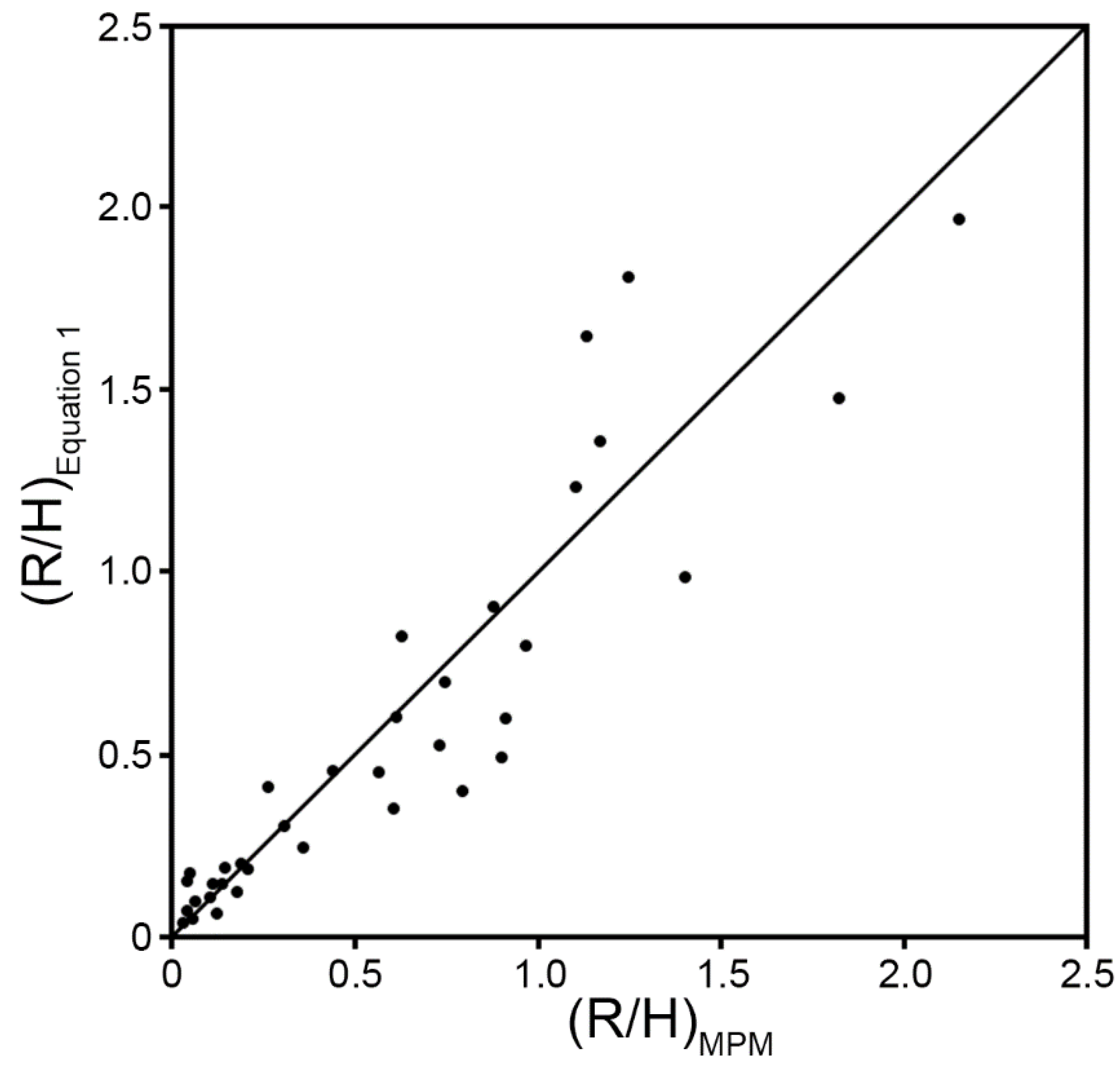
Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vaunat, J.; Leroueil, S.; Faure, R. Slope movements: a geotechnical perspective. In Proceedings of the 7th Congress International Association of Engineering Geology, Lisbon, Portugal, 5–9 September 1994; pp. 1637–1646. [Google Scholar]
- Leroueil, S.; Vaunat, J.; Picarelli, L.; Locat, J.; Faure, J.; Lee, H. A geotechnical characterization of slope movements. In Proceedings of the 7th International Symposium on Landslides, Trondheim, Norway, 17–21 June 1996; Balkema: Rotterdam, The Netherlands; pp. 53–74. [Google Scholar]
- Cascini, L.; Cuomo, S.; Sorbino, G. Flow-like mass movements in pyroclastic soils: remarks on the modelling of the triggering mechanism. Italian Geotech. J. 2005, 4, 11–31. [Google Scholar]
- Yerro, A.; Alonso, E.; Pinyol, N. Run-out of landslides in brittle soils. Comput. Geotech. 2016, 80, 427–439. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Pugliese, L.; Troncone, A. Analysis of the Maierato landslide (Calabria, Southern Italy). Landslides 2018, 15, 1935–1950. [Google Scholar] [CrossRef]
- Duncan, J.M. State of the Art: Limit Equilibrium and Finite-Element Analysis of Slopes. J. Geotech. Eng. 1996, 122, 577–596. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J.; Ledesma, A.; Lloret, A.; Gili, J.A. Prediction of ground displacements and velocities from groundwater level changes at the Vallcebre landslide (Eastern Pyrenees, Spain). Landslides 2005, 2, 83–96. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. A method for the analysis of soil slips triggered by rainfall. Géotechnique 2012, 62, 187–192. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. Stability analysis of infinite clayey slopes subjected to pore pressure changes. Géotechnique 2012, 62, 87–91. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A.; Conte, E.; Troncone, A. A performance-based method for the design of drainage trenches used to stabilize slopes. Eng. Geol. 2018, 239, 158–166. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Troncone, A. A simplified method for predicting rainfall-induced mobility of active landslides. Landslides 2017, 14, 35–45. [Google Scholar] [CrossRef]
- Dounias, G.T.; Potts, D.M.; Vaughan, P.R. Finite element analysis of progressive failure of Carsington embankment. Géotechnique 1990, 40, 79–101. [Google Scholar]
- Alonso, E.E.; Gens, A.; Delahaye, C.H. Influence of rainfall on the deformation and stability of a slope in overconsolidated clays: a case study. Hydrogeol. J. 2003, 11, 174–192. [Google Scholar] [CrossRef]
- Troncone, A. Numerical analysis of a landslide in soils with strain-softening behaviour. Géotechnique 2005, 55, 585–596. [Google Scholar] [CrossRef]
- Lollino, P.; Santaloia, F.; Amorosi, A.; Cotecchia, F. Delayed failure of quarry slopes in stiff clays: the case of the Lucera landslide. Géotechnique 2011, 61, 861–874. [Google Scholar] [CrossRef]
- Fernàndez-Merodo, J.A.; Garcìa-Davalillo, J.C.; Herrera, G.; Mira, P.; Pastor, M. 2D viscoplastic finite element modelling of slow landslides: the Portalet case study (Spain). Géotechnique 2014, 11, 29–42. [Google Scholar] [CrossRef]
- Troncone, A.; Conte, E.; Donato, A. Two and three-dimensional numerical analysis of the progressive failure that occurred in an excavation-induced landslide. Eng. Geol. 2014, 183, 265–275. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Troncone, A. A finite element approach for the analysis of active slow-moving landslides. Landslides 2014, 11, 723–731. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Géotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Potts, D.M.; Zdravkovic, L. Finite Element Analysis in Geotechnical Engineering: Application; Thomas Telford: London, UK, 2001. [Google Scholar]
- Picarelli, L.; Urciuoli, G.; Russo, C. Effect of groundwater regime on the behaviour of clayey slopes. Can. Geotech. J. 2004, 41, 467–484. [Google Scholar] [CrossRef]
- Hung, C.; Liu, C.-H.; Chang, C.-M. Numerical Investigation of Rainfall-Induced Landslide in Mudstone Using Coupled Finite and Discrete Element Analysis. Geofluids 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, L.; Chen, L.; Li, X.; Liu, D. Slope stability analysis based on the Coupled Eulerian-Lagrangian finite element method. Bull. of Eng. Geology and the Environ. 2019, 1–13. [Google Scholar] [CrossRef]
- Lin, C.-H.; Lin, M.-L. Evolution of the large landslide induced by Typhoon Morakot: A case study in the Butangbunasi River, southern Taiwan using the discrete element method. Eng. Geol. 2015, 197, 172–187. [Google Scholar] [CrossRef]
- Calvetti, F.; di Prisco, C.; Vairaktaris, E. DEM assessment of impact forces of dry granular masses on rigid barriers. Acta Geotech. 2017, 12, 129–144. [Google Scholar] [CrossRef]
- Scaringi, G.; Fan, X.; Xu, Q.; Liu, C.; Ouyang, C.; Domènech, G.; Yang, F.; Dai, L. Some considerations on the use of numerical methods to simulate past landslides and possible new failures: the case of the recent Xinmo landslide (Sichuan, China). Landslides 2018, 15, 1359–1375. [Google Scholar] [CrossRef]
- Pirulli, M.; Pastor, M. Numerical study on the entrainment of bed material into rapid landslides. Géotechnique 2012, 62, 959–972. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Zhang, L.; Choi, C.; Ng, C.W.W. Evaluation of Critical Slip Surface in Limit Equilibrium Analysis of Slope Stability by Smoothed Particle Hydrodynamics. Int. J. Geéomeéch. 2019, 19. [Google Scholar] [CrossRef]
- Alonso, E.; Zabala, F. Progressive failure of Aznalcóllar dam using the material point method. Géotechnique 2011, 61, 795–808. [Google Scholar]
- Zhang, X.; Chen, Z.; Liu, Y. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases; Elsevier: London, UK, 2017. [Google Scholar]
- Fern, J.; Rohe, A.; Soga, K.; Alonso, A. The Material Point Method for Geotechnical Engineering. A Practical Guide; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Soga, K.; Alonso, E.; Yerro, A.; Kumar, K.; Bandara, S. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method. Géotechnique 2016, 66, 1–26. [Google Scholar] [CrossRef]
- Conte, E.; Pugliese, L.; Troncone, A. Post-failure stage simulation of a landslide using the material point method. Eng. Geol. 2019, 253, 149–159. [Google Scholar] [CrossRef]
- Yerro, A.; Soga, K.; Bray, J.D. Runout evaluation of Oso landslide with the material point method. Can. Geotech. J. 2018, 1–14. [Google Scholar] [CrossRef]
- Sulsky, D.; Chen, Z.; Schreyer, H. A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
- Ceccato, F.; Beuth, L.; Simonini, P. Analysis of Piezocone Penetration under Different Drainage Conditions with the Two-Phase Material Point Method. J. Geotech. Geoenvironmental Eng. 2016, 142, 4016066. [Google Scholar] [CrossRef]
- Galavi, V.; Beuth, L.; Coelho, B.Z.; Tehrani, F.S.; Hölscher, P.; Van Tol, F. Numerical Simulation of Pile Installation in Saturated Sand Using Material Point Method. Procedia Eng. 2017, 175, 72–79. [Google Scholar] [CrossRef]
- Fern, E.J.; de Lange, D.A.; Zwanenburg, C.; Teunissen, J.A.M.; Rohe, A.; Soga, K. Experimental and numerical investigations of dyke failures involving soft materials. Eng. Geol. 2016, 219, 130–139. [Google Scholar] [CrossRef]
- Yerro, A.; Pinyol, N.M.; Alonso, E.E. Internal progressive failure in deep-seated landslides. Rock Mechanics Rock Eng. 2016, 49, 2317–2332. [Google Scholar] [CrossRef]
- Martinelli, M.; Rohe, A. Modelling fluidization and sedimentation using material point method. In Proceedings of the 1st Pan-American Congress on Computational Mechanics, Buenos-Aires, Argentina, 27–29 April 2015; pp. 1–12. [Google Scholar] [CrossRef]
- Bolognin, M.; Martinelli, M.; Bakker, K.J.; Jonkman, S.N. Validation of material point method for soil fluidisation analysis. J. Hydrodyn. 2017, 29, 431–437. [Google Scholar] [CrossRef]
- Martinelli, M.; Rohe, A.; Soga, K. Modeling Dike Failure using the Material Point Method. Procedia Eng. 2017, 175, 341–348. [Google Scholar] [CrossRef]
- Ceccato, F.; Yerro, A.; Martinelli, M. Modelling soil-water interaction with the material point method. Evaluation of single-point and double-point formulations. In Proceedings of the Numerical Methods in Geotechnical Engineering IX, Porto, Portugal, 25–27 June 2018; Informa UK Limited: Colchester, UK, 2018; Volume 1, pp. 351–357. [Google Scholar]
- Yerro, A.; Alonso, E.; Pinyol, N. The material point method for unsaturated soils. Géotechnique 2015, 65, 201–217. [Google Scholar] [CrossRef]
- Alonso, E.E.; Yerro, A.; Pinyol, N.M. Recent developments of the Material Point Method for the simulation of landslides. IOP Conf. Ser. Earth Environ. Sci. 2015, 26, 12003. [Google Scholar] [CrossRef]
- Anura3D MPM Research Community. Available online: www.anura3d.com (accessed on 10 July 2019).
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- PLAXIS 2D Reference Manual 2019. Available online: www.plaxis.com/support/manuals/plaxis-2d-manuals/ (accessed on 28 June 2019).

| Material | γ (kN/m3) | E’ (kPa) | ν’ | φ’ (°) | c’ (kPa) | ψ (°) | k (m/s) |
|---|---|---|---|---|---|---|---|
| Soil | 20 | 25,000 | 0.3 | 30–40 | 0 | 0 | 0.01 |
| α = 10° | α = 15° | α = 20° | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| φ’ (°) | Δu 20 kPa | Δu 40 kPa | Δu 60 kPa | Δu 80 kPa | Δu 20 kPa | Δu 40 kPa | Δu 60 kPa | Δu 80 kPa | Δu 20 kPa | Δu 40 kPa | Δu 60 kPa | Δu 80 kPa |
| 30 | 0.12 | 0.18 | 0.21 | 0.36 | 0.19 | 0.79 | 0.91 | 0.97 | 0.92 | 1.43 | 1.82 | 2.15 |
| 35 | 0.06 | 0.06 | 0.14 | 0.15 | 0.05 | 0.60 | 0.73 | 0.75 | 0.44 | 0.88 | 1.17 | 1.25 |
| 40 | 0.03 | 0.04 | 0.10 | 0.11 | 0.04 | 0.31 | 0.57 | 0.61 | 0.26 | 0.63 | 1.10 | 1.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Troncone, A.; Conte, E.; Pugliese, L. Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method. Water 2019, 11, 1446. https://doi.org/10.3390/w11071446
Troncone A, Conte E, Pugliese L. Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method. Water. 2019; 11(7):1446. https://doi.org/10.3390/w11071446
Chicago/Turabian StyleTroncone, Antonello, Enrico Conte, and Luigi Pugliese. 2019. "Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method" Water 11, no. 7: 1446. https://doi.org/10.3390/w11071446
APA StyleTroncone, A., Conte, E., & Pugliese, L. (2019). Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method. Water, 11(7), 1446. https://doi.org/10.3390/w11071446





