Combining TRIGRS and DEBRIS-2D Models for the Simulation of a Rainfall Infiltration Induced Shallow Landslide and Subsequent Debris Flow
Abstract
1. Introduction
2. Environment Information and TRIGRS Inputs
2.1. Description of Environment
2.2. Geological Properties
2.3. Short Term Water Table Monitoring
2.4. Model Inputs
3. Analysis of Rainfall Infiltration Induced Shallow Landslide
3.1. Rainfall Infiltration
3.2. Total Pressure Head Response
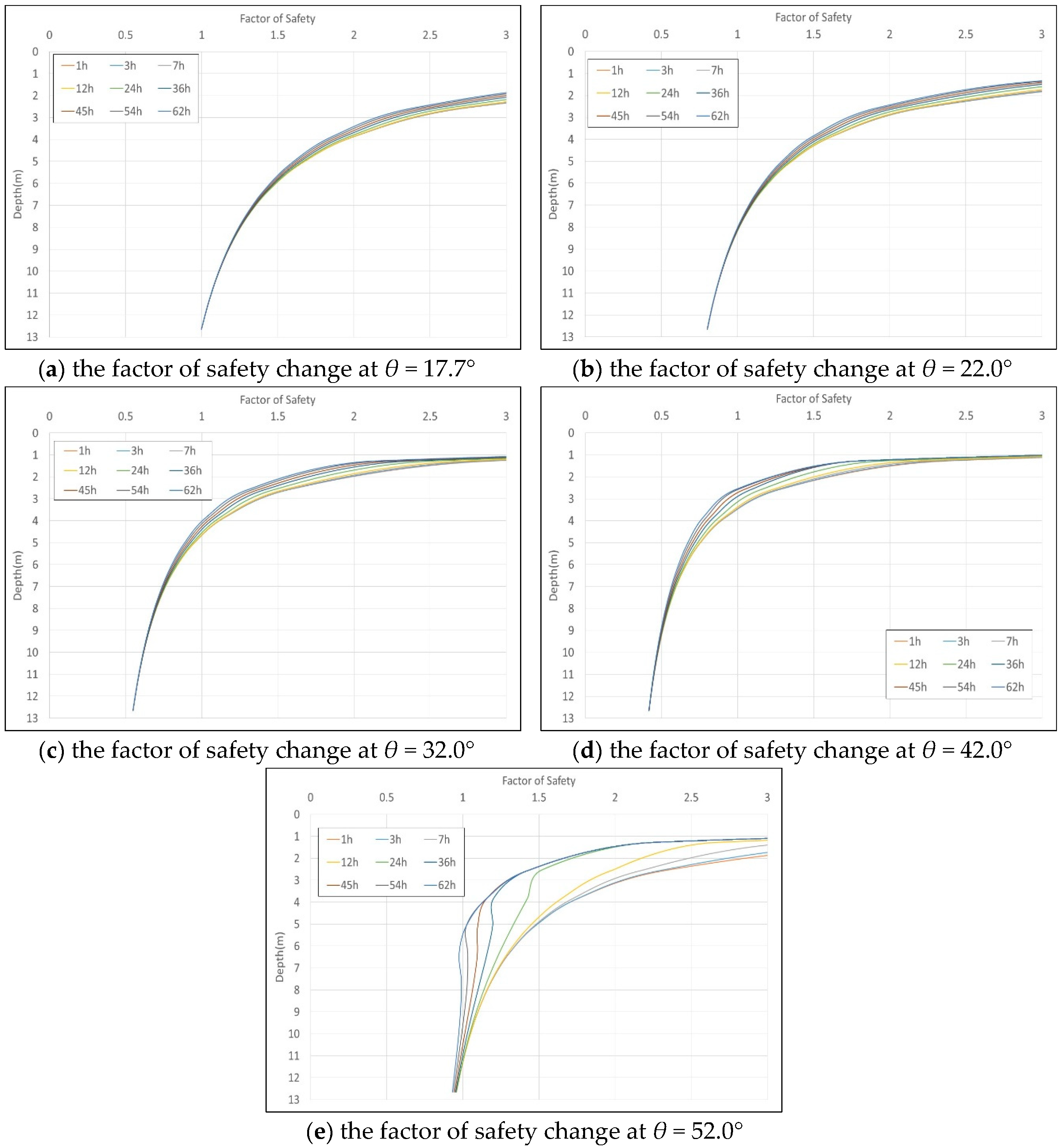
3.3. Safety Factor Response
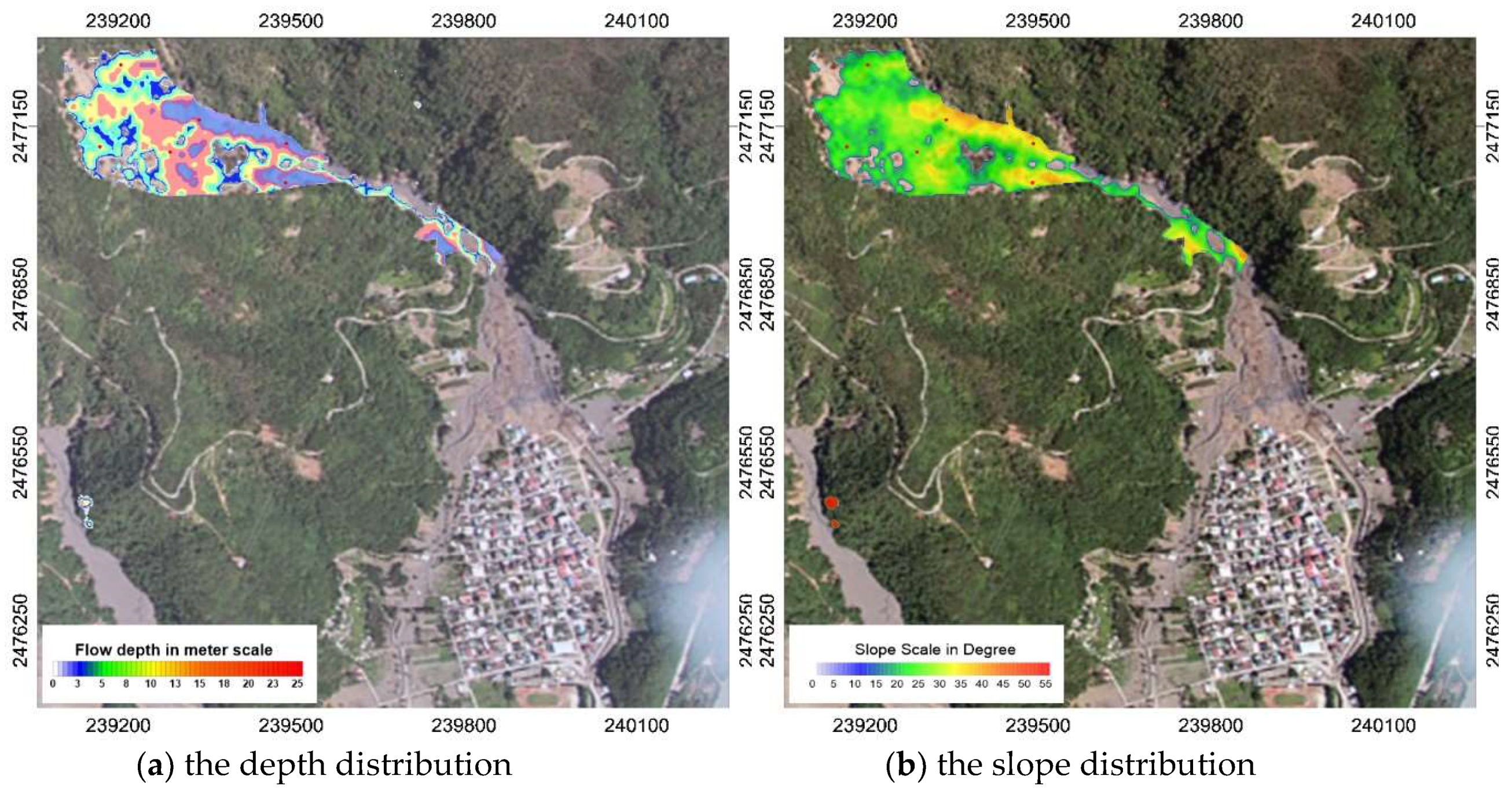
3.4. Validation of Potential Collapse Zone
4. Analysis of Subsequent Motion of Collapsed Mass
4.1. Debris Flow Spreading Model and Inputs
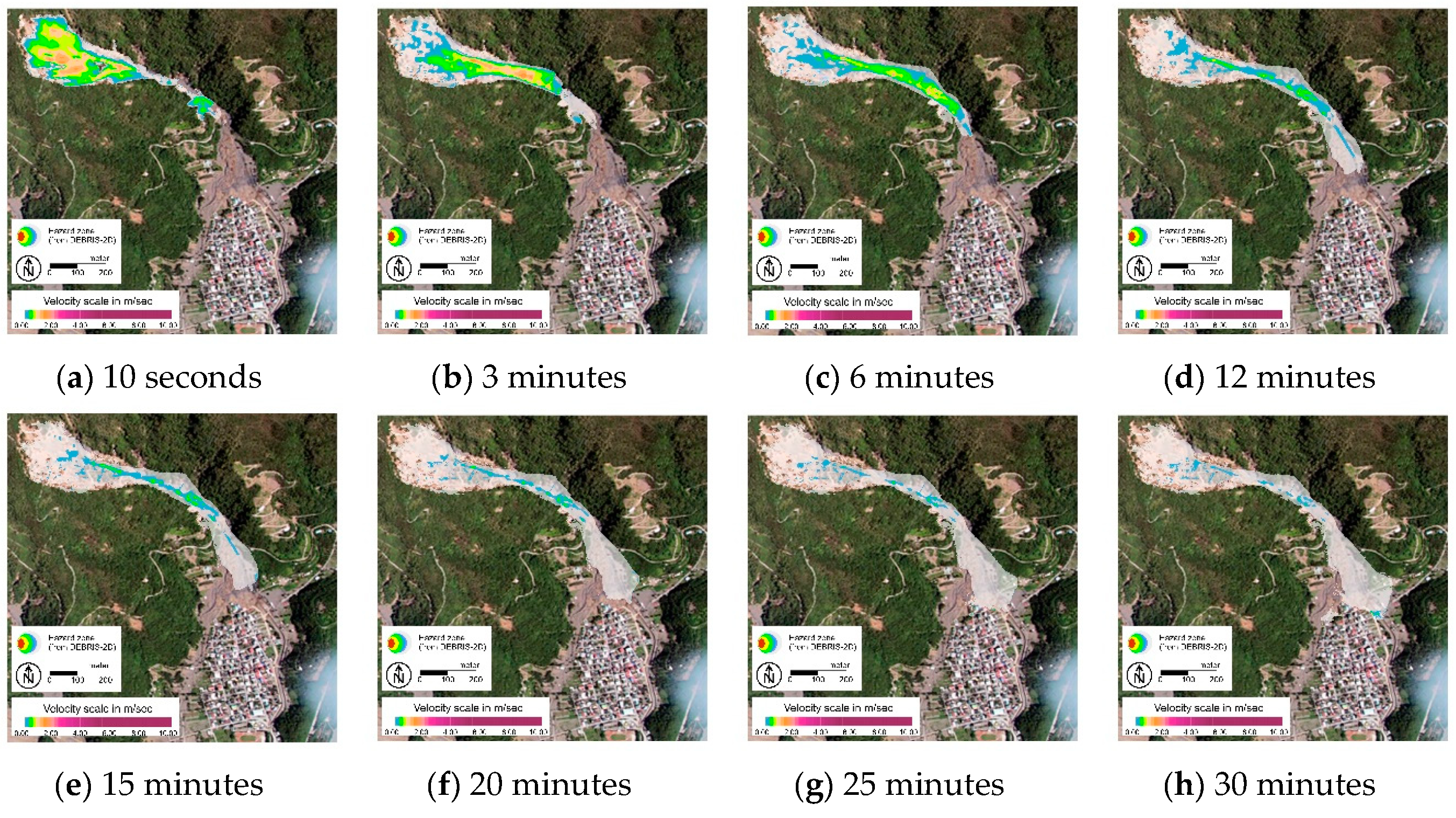
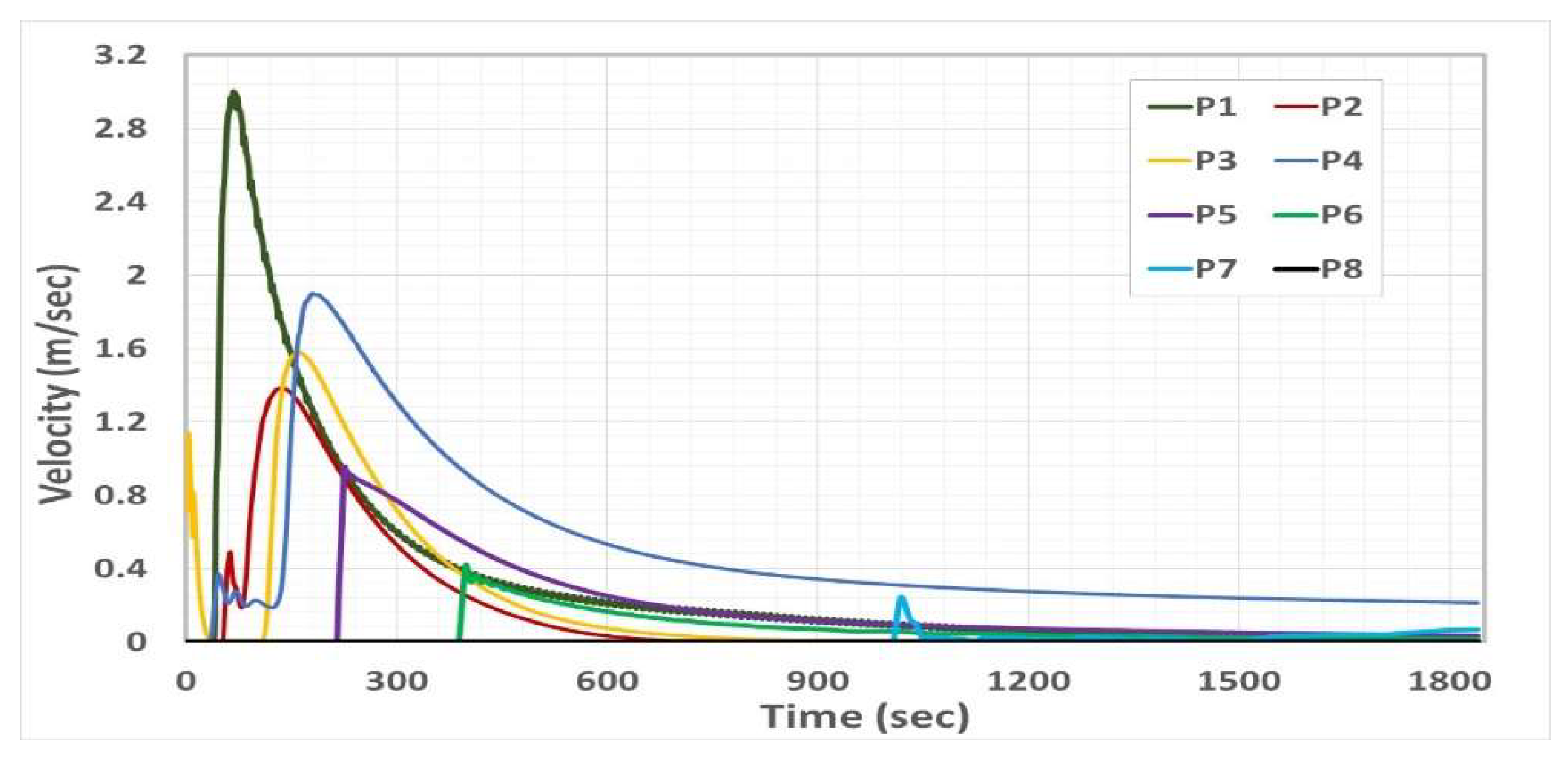
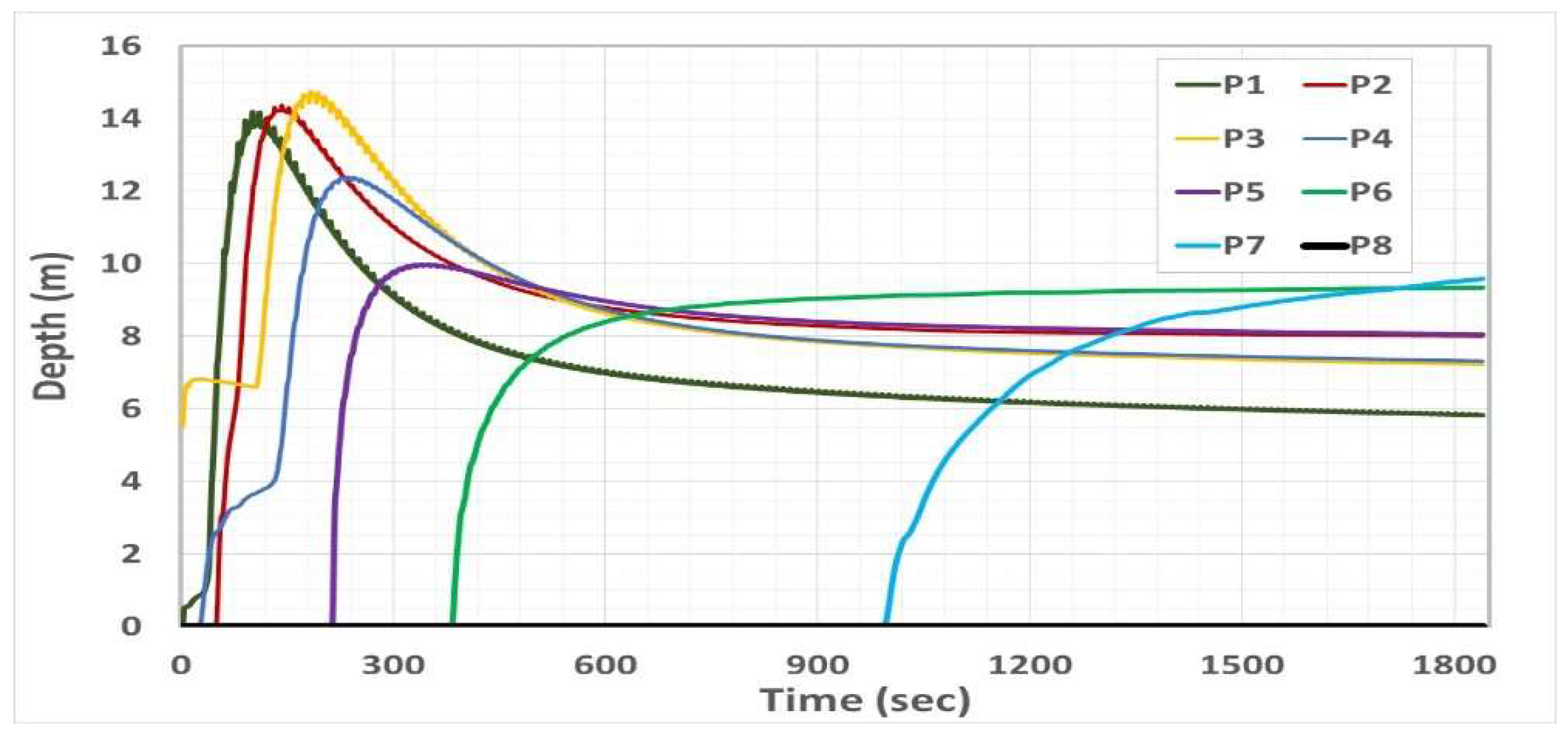
4.2. Description of Debris Flow Motion
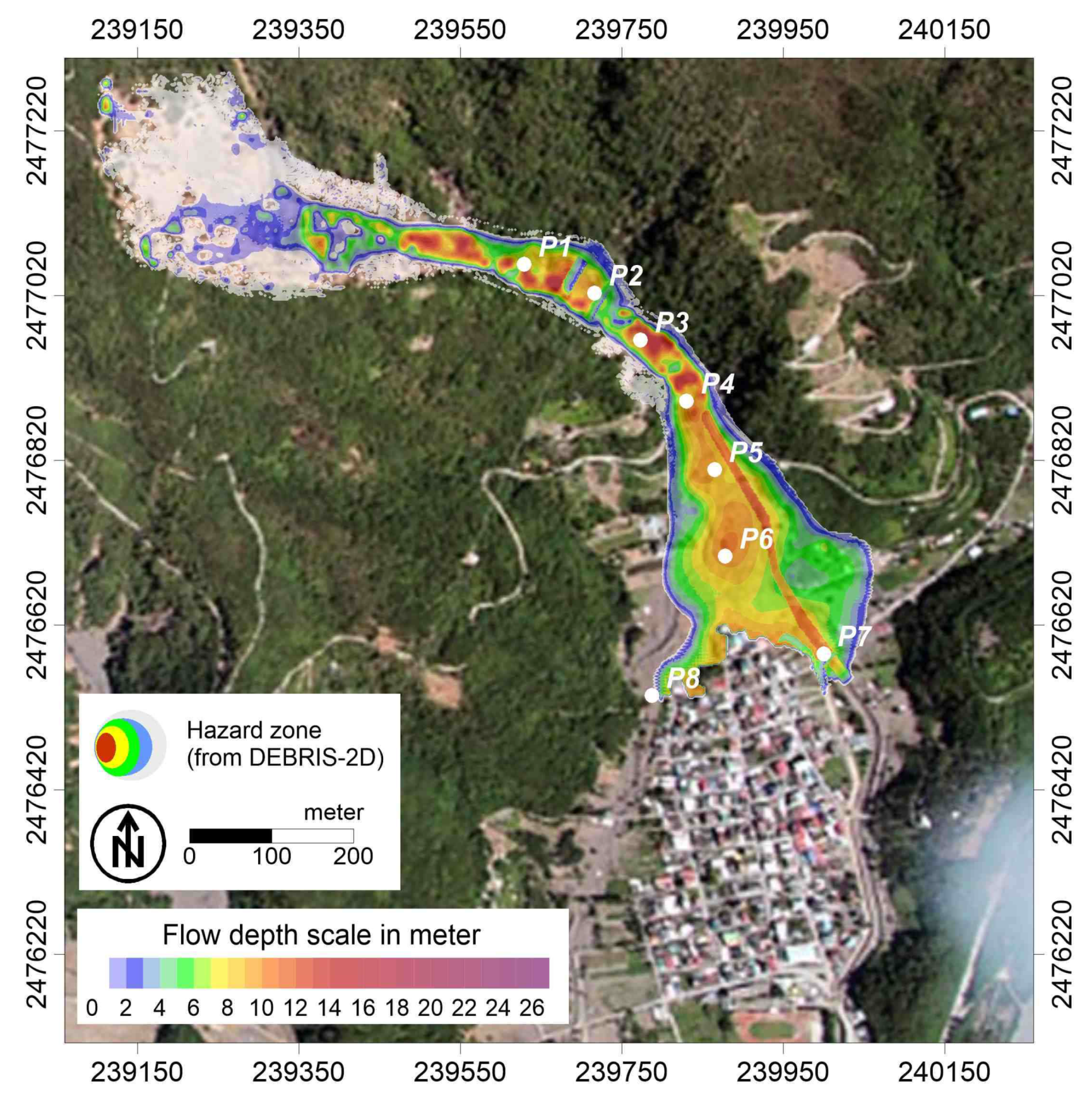
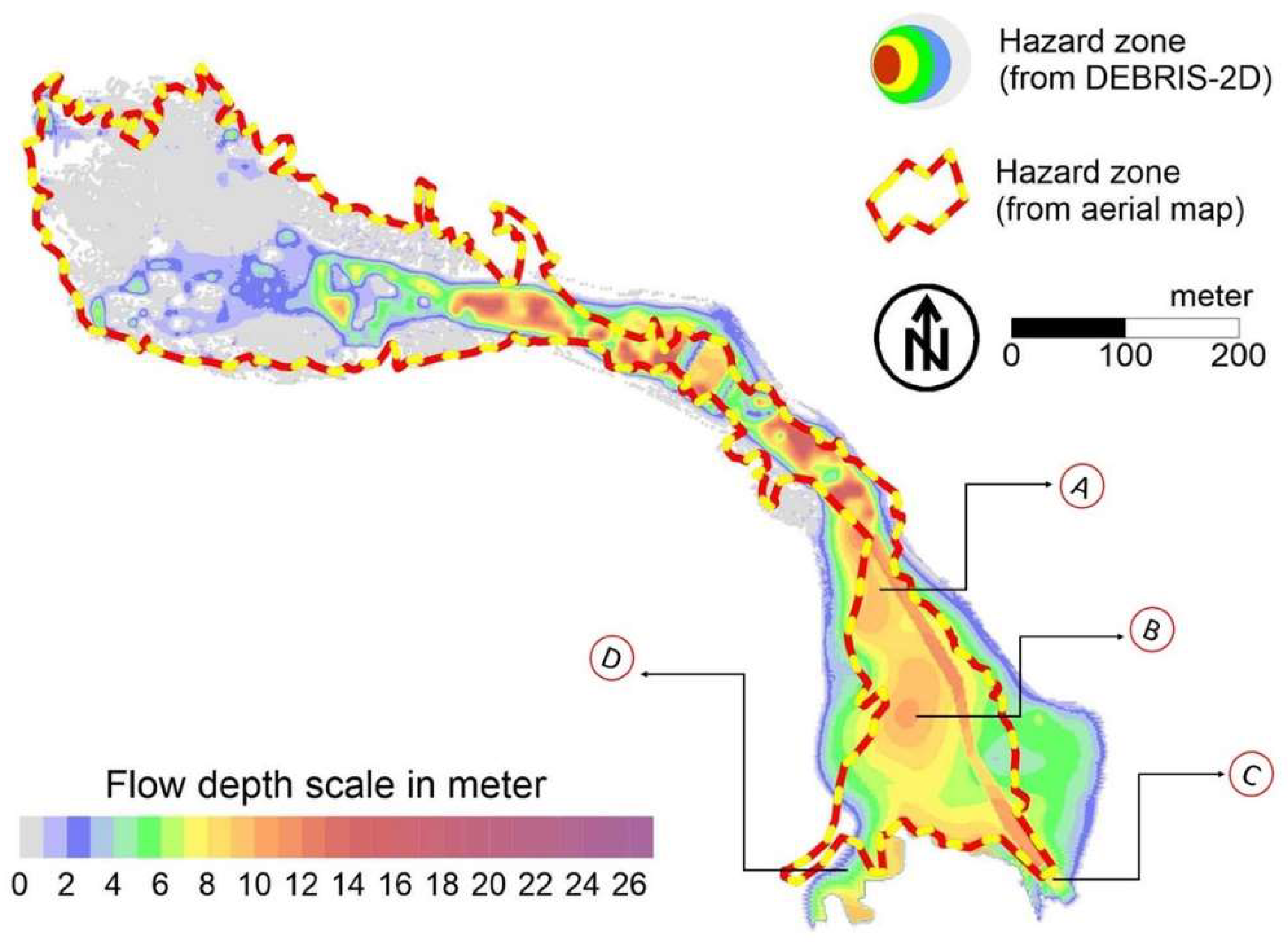
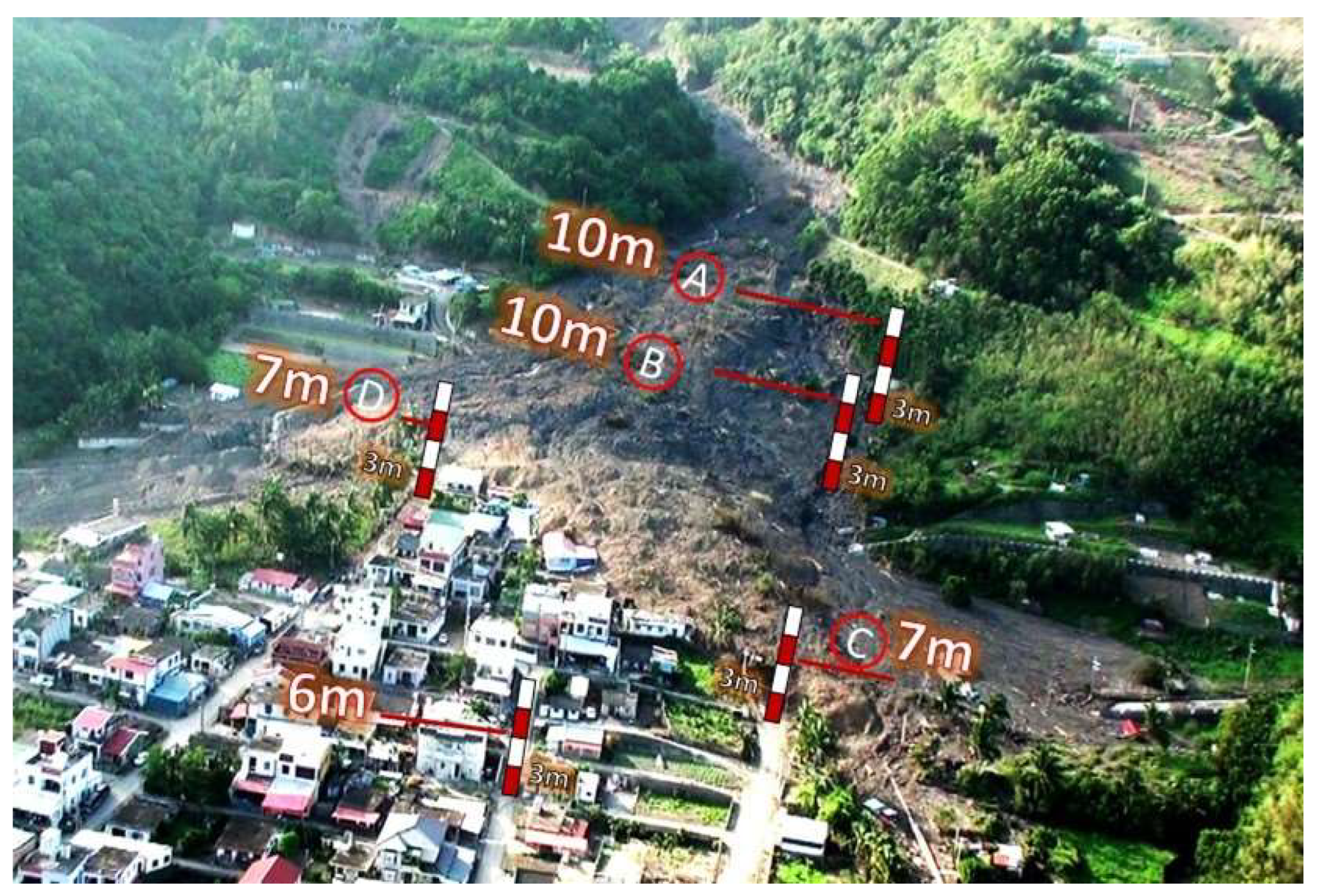
4.3. Validation of Hazard Zone
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- O’Brien, J.S.; Julien, P.Y.; Fullerton, W.T. Two-dimensional water flood and mudflow simulation. J. Hydraul. Eng. 1993, 119, 224–261. [Google Scholar] [CrossRef]
- Liu, K.F.; Huang, M.C. Numerical simulation of debris flow with application on hazard area mapping. Comput. Geosci. 2006, 10, 221–240. [Google Scholar] [CrossRef]
- Tsai, M.P.; Hsu, Y.C.; Li, H.C.; Shu, H.M.; Liu, K.F. Application of simulation technique on debris hazard zone delineation: A case study in the Daniao tribe, Eastern Taiwan. Nat. Hazards Earth Syst. Sci. 2011, 11, 3053–3062. [Google Scholar] [CrossRef]
- Piccarreta, M.; Pasini, A.; Capolongo, D.; Lazzari, M. Changes in daily precipitation extremes in the Mediterranean from 1951 to 2010: The Basilicata region, Southern Italy. Int. J. Climatol. 2013, 33, 3229–3248. [Google Scholar] [CrossRef]
- Lazzari, M.; Piccarreta, M.; Capolongo, D. Landslide triggering and local rainfall thresholds in Bradanic Foredeep, Basilicata region (Southern Italy). Landslide Sci. Pract. 2013, 2, 671–676. [Google Scholar] [CrossRef]
- Lazzari, M.; Piccarreta, M. Landslide disasters triggered by extreme rainfall events: The case of Montescaglioso (Basilicata, Southern Italy). Geosciences 2018, 2, 377. [Google Scholar] [CrossRef]
- Lazzari, M.; Piccarreta, M.; Manfreda, S. The role of antecedent soil moisture conditions on rainfall-triggered shallow landslides. Nat. Hazards Earth Syst. Sci. 2018. [Google Scholar] [CrossRef]
- Collins, B.D.; Znidarcic, D. Stability analyses of rainfall induced landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. A method for the analysis of soil slips triggered by rainfall. Geotechnique 2012, 62, 187–192. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Troncone, A. A simplified method for predicting rainfall-induced mobility of active landslides. Landslides 2017, 14, 35–45. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Delahaye, C.H. Influence of rainfall on the deformation and stability of a slope in overconsolidated clays: A case of study. Hydrogeol. J. 2003, 11, 174–192. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. Stability analysis of infinite clayey slopes subjected to pore pressure changes. Geotechnique 2012, 62, 87–91. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. A performance-based method for the design of drainage trenches used to stabilize slopes. Eng. Geol. 2018, 239, 158–166. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Ali, A.; Huang, J.; Lyamin, A.V.; Sloan, S.W.; Griffiths, D.V.; Cassidy, M.J.; Li, J. Simplified quantitative risk assessment of rainfall-induced landslides modelled by infinite slopes. Eng. Geol. 2014, 179, 102–116. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Pugliese, L.; Troncone, A. Analysis of the Maierato landslide (Calabria, Southern Italy). Landslides 2018, 15, 1935–1950. [Google Scholar] [CrossRef]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis; US Geological Survey Open-File Report; US Geological Survey: Reston, VA, USA, 2002.
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimation the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. 2010, 115, F03013. [Google Scholar] [CrossRef]
- Chiang, S.H.; Chang, K.T.; Mondini, A.C.; Tsai, B.W.; Chen, C.Y. Simulation of event-based landslides and debris flows at watershed level. Geomorphology 2012, 138, 306–618. [Google Scholar] [CrossRef]
- Hsu, S.M.; Wen, H.Y.; Chen, N.C.; Hsu, S.Y.; Chi, S.Y. Using an integrated method to estimate watershed sediment yield during heavy rain period: A case study in Hualien County, Taiwan. Nat. Hazards Earth Syst. Sci. 2012, 12, 1949–1960. [Google Scholar] [CrossRef]
- Gomes, R.A.T.; Guimaraes, R.F.; Carvalho Júnior, O.A.; Fernandes, N.F.; Amaral, E.V., Jr. Combining spatial models for shallow landslides and debris flows prediction. Remote Sens. 2013, 5, 2219–2237. [Google Scholar] [CrossRef]
- Wang, C.; Marui, H.; Furuya, G.; Watanabe, N. Two integrated models simulating dynamic process of landslide using GIS. Landslide Sci. Pract. 2013, 3, 389–395. [Google Scholar] [CrossRef]
- The Planning of Conservation and Investigation in the Watershed of Daniao Stream; Taitung Branch Office of Soil and Water Conservation Bureau in Taiwan: Taitung County, Taiwan, 2011. (In Chinese)
- Geotechdata.info: Angle of Friction. Available online: http://geotechdata.info/parameter/angele-of- friction.html (accessed on 14 September 2013).
- Geotechdata.info: Cohesion. Available online: http://geotechdata.info/parameter/cohesion (accessed on 15 December 2013).
- Rawls, W.J.; Brakensiek, D.L. A procedure to predict Green Ampt infiltration parameters. In Advances in Infiltration; ASAE Publication: St Joseph, MI, USA, 1983; pp. 102–112. [Google Scholar]
- Liu, C.N.; Wu, C.C. Mapping susceptibility of rainfall triggered shallow landslides using a probabilistic approach. Environ. Geol. 2008, 55, 907–915. [Google Scholar] [CrossRef]
- Investigate Report of Debris Flow Disaster on Daniao Tribe; Taitung Branch office of Soil and Water Conservation Bureau in Taiwan: Taitung County, Taiwan, 2009. (In Chinese)

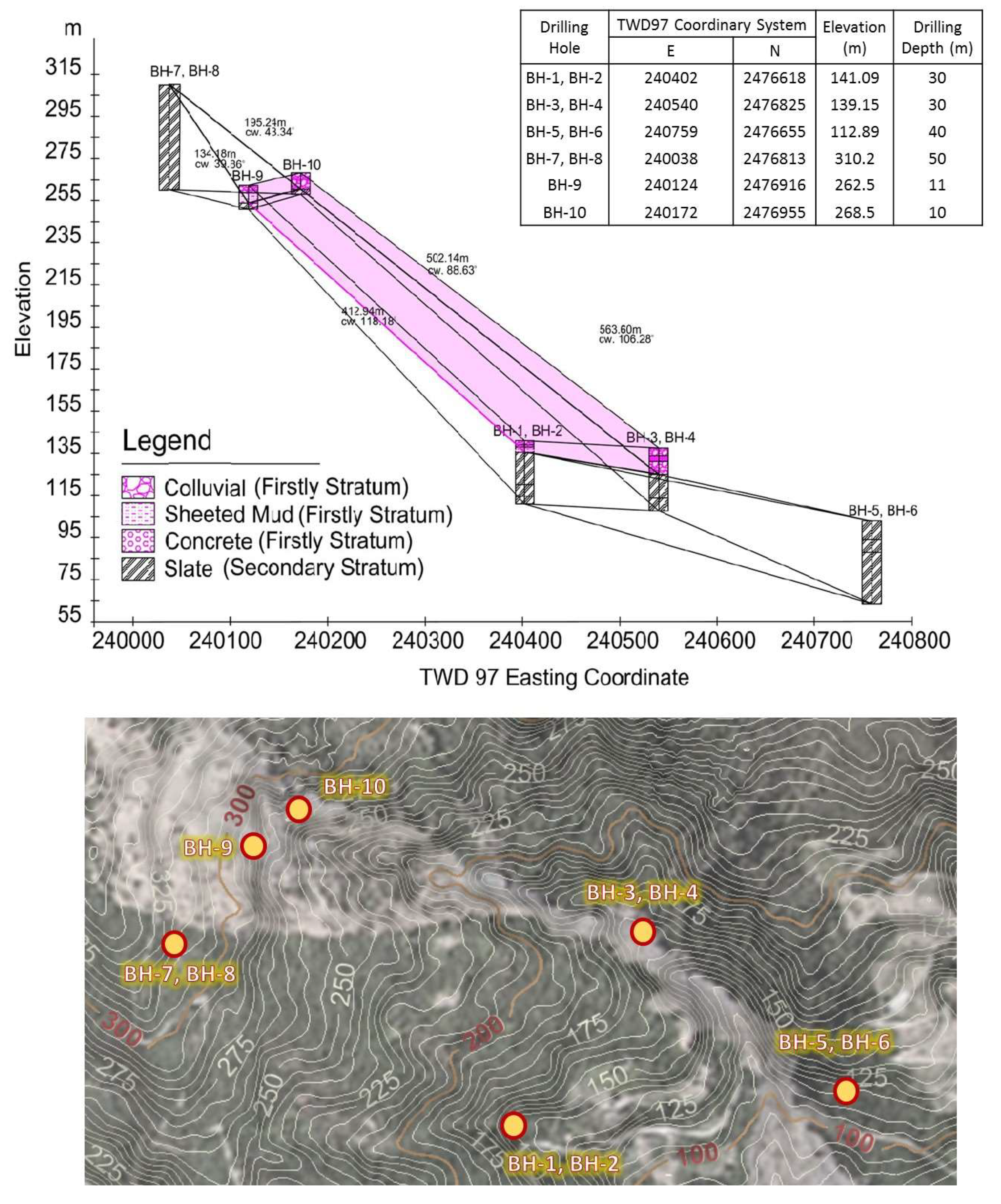
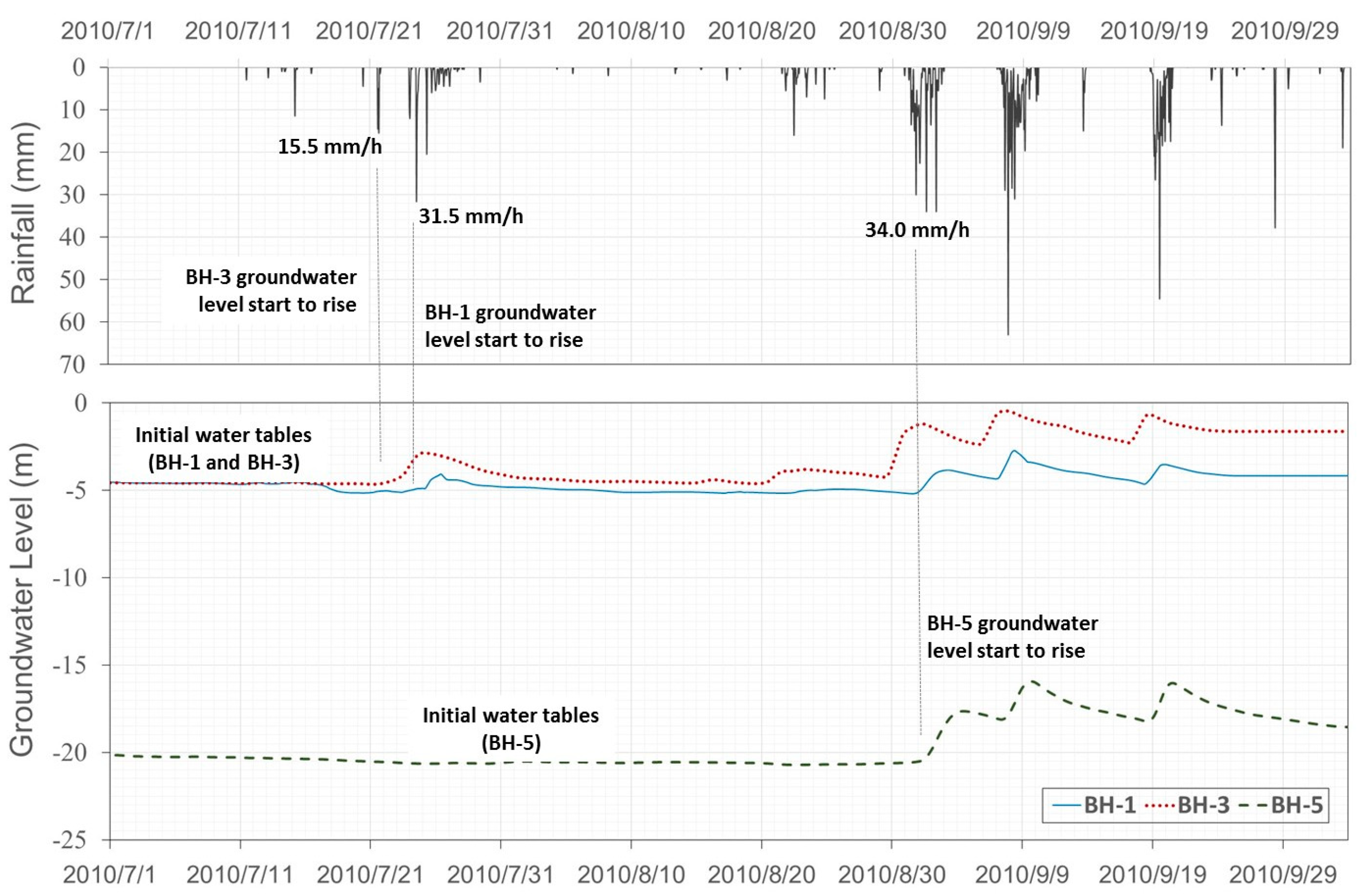
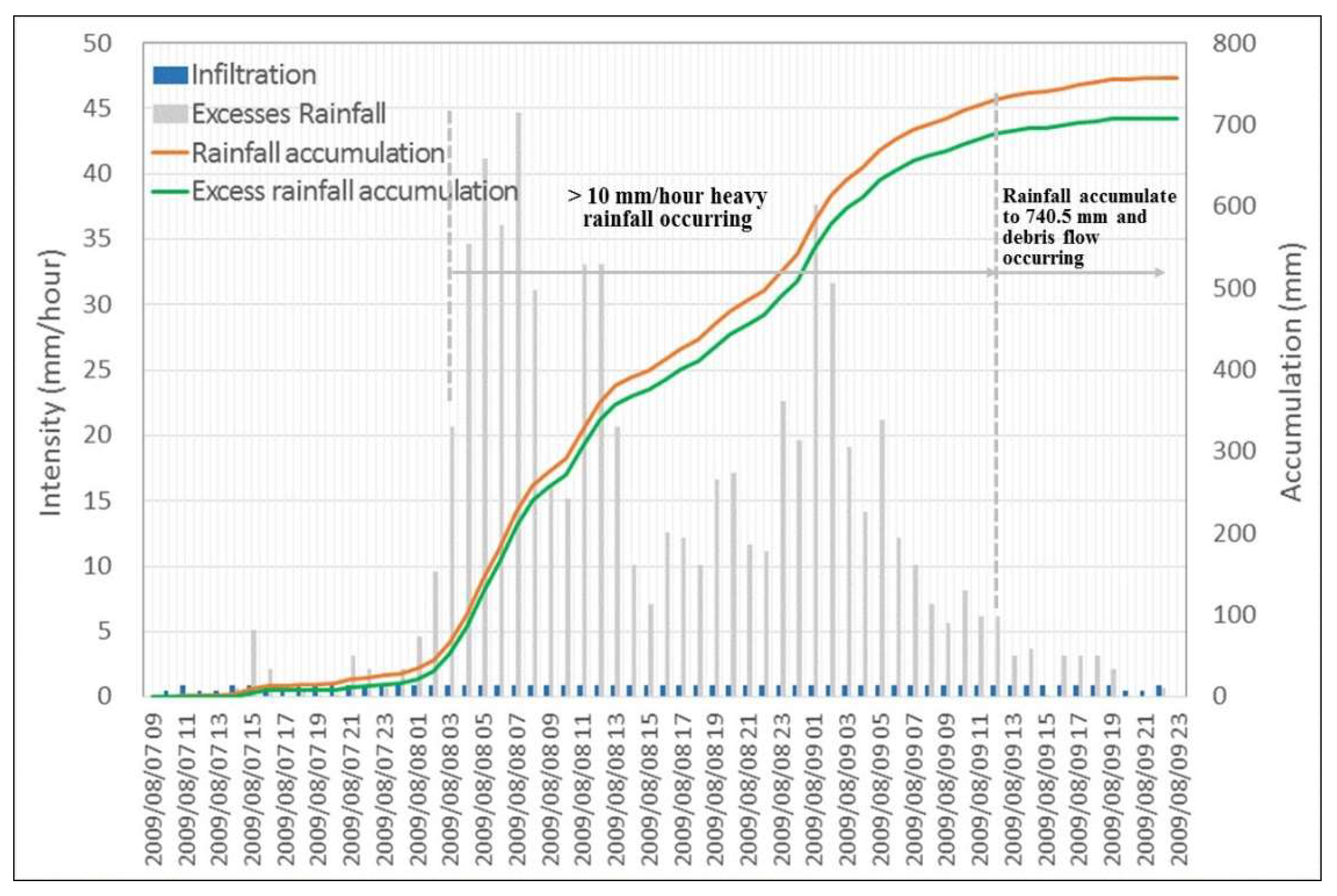
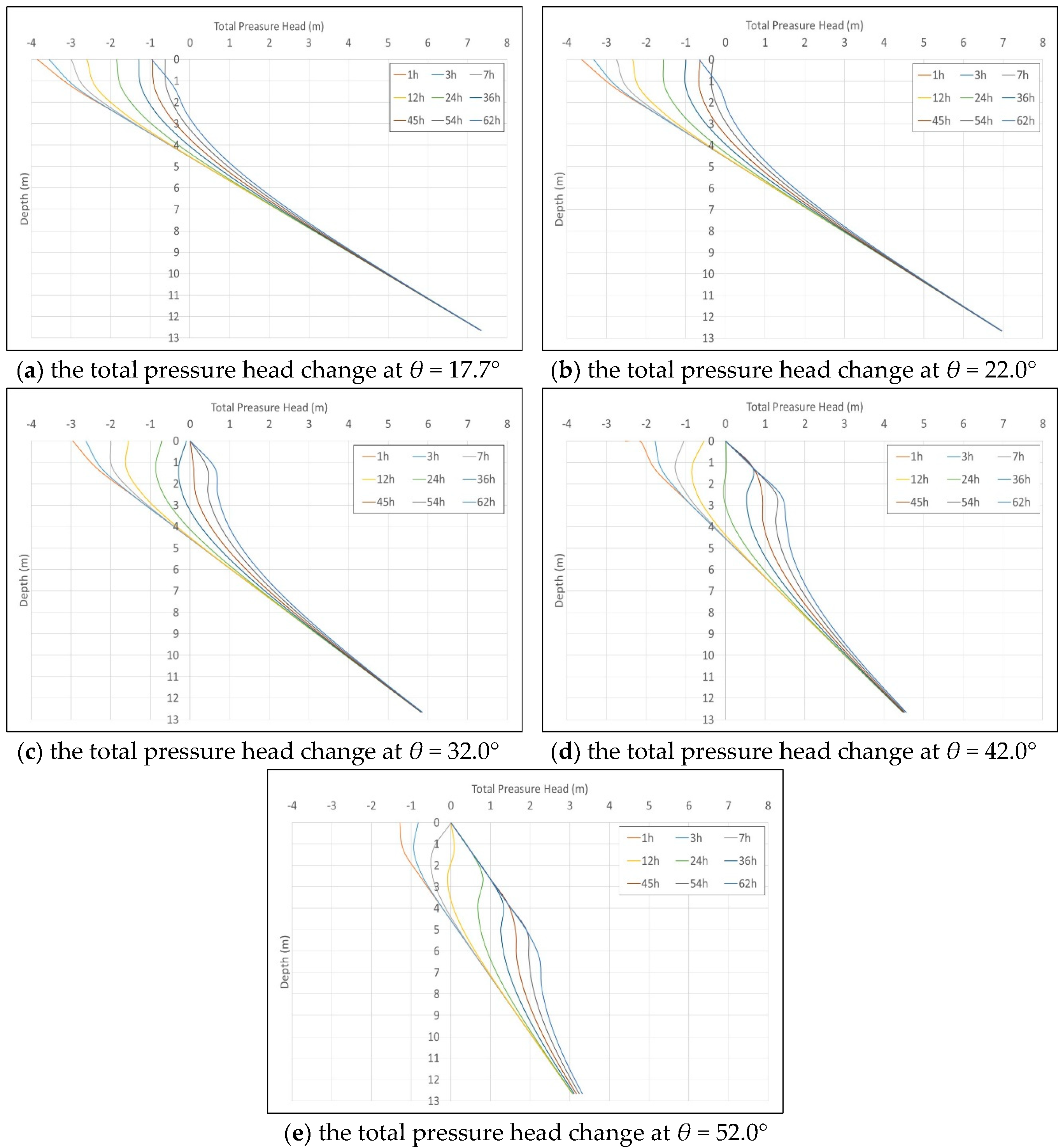


| Soil Layer | Distributed Depth (m) | Material Constituted | SPT Number (N) | Unit Weight (ton/m3) | Water Content (%) | Porosity Ratio | Liquid Limit LL (%) | Plasticity Index PI (%) |
|---|---|---|---|---|---|---|---|---|
| Brown clastic rock, concrete, gray sand backfill layer | From 0.00 m to 12.65 m underground | Collapse, Backfill layer | 8–>100 | 2.11–2.28 | 6.7–12.7 | 0.26–0.43 | 17.2–19.2 | 6.8–8.7 |
| Average 62.2 | Average 2.21 | Average 8.9 | Average 0.32 | Average 18.5 | Average 8 | |||
| Brown, gray, black and gray broken slate, shear gouge, and rust-strained quartz | From 0.75 m to 50 m underground | Broken Slate | 50–>100 | 1.86–2.20 | 8.5–9.8 | 0.31–0.57 | 17.6–19.5 | 6.8–9.5 |
| Average 69.0 | Average 2.03 | Average 9.0 | Average 0.45 | Average 18.4 | Average 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsu, Y.-C.; Liu, K.-F. Combining TRIGRS and DEBRIS-2D Models for the Simulation of a Rainfall Infiltration Induced Shallow Landslide and Subsequent Debris Flow. Water 2019, 11, 890. https://doi.org/10.3390/w11050890
Hsu Y-C, Liu K-F. Combining TRIGRS and DEBRIS-2D Models for the Simulation of a Rainfall Infiltration Induced Shallow Landslide and Subsequent Debris Flow. Water. 2019; 11(5):890. https://doi.org/10.3390/w11050890
Chicago/Turabian StyleHsu, Yu-Charn, and Ko-Fei Liu. 2019. "Combining TRIGRS and DEBRIS-2D Models for the Simulation of a Rainfall Infiltration Induced Shallow Landslide and Subsequent Debris Flow" Water 11, no. 5: 890. https://doi.org/10.3390/w11050890
APA StyleHsu, Y.-C., & Liu, K.-F. (2019). Combining TRIGRS and DEBRIS-2D Models for the Simulation of a Rainfall Infiltration Induced Shallow Landslide and Subsequent Debris Flow. Water, 11(5), 890. https://doi.org/10.3390/w11050890





