Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method
Abstract
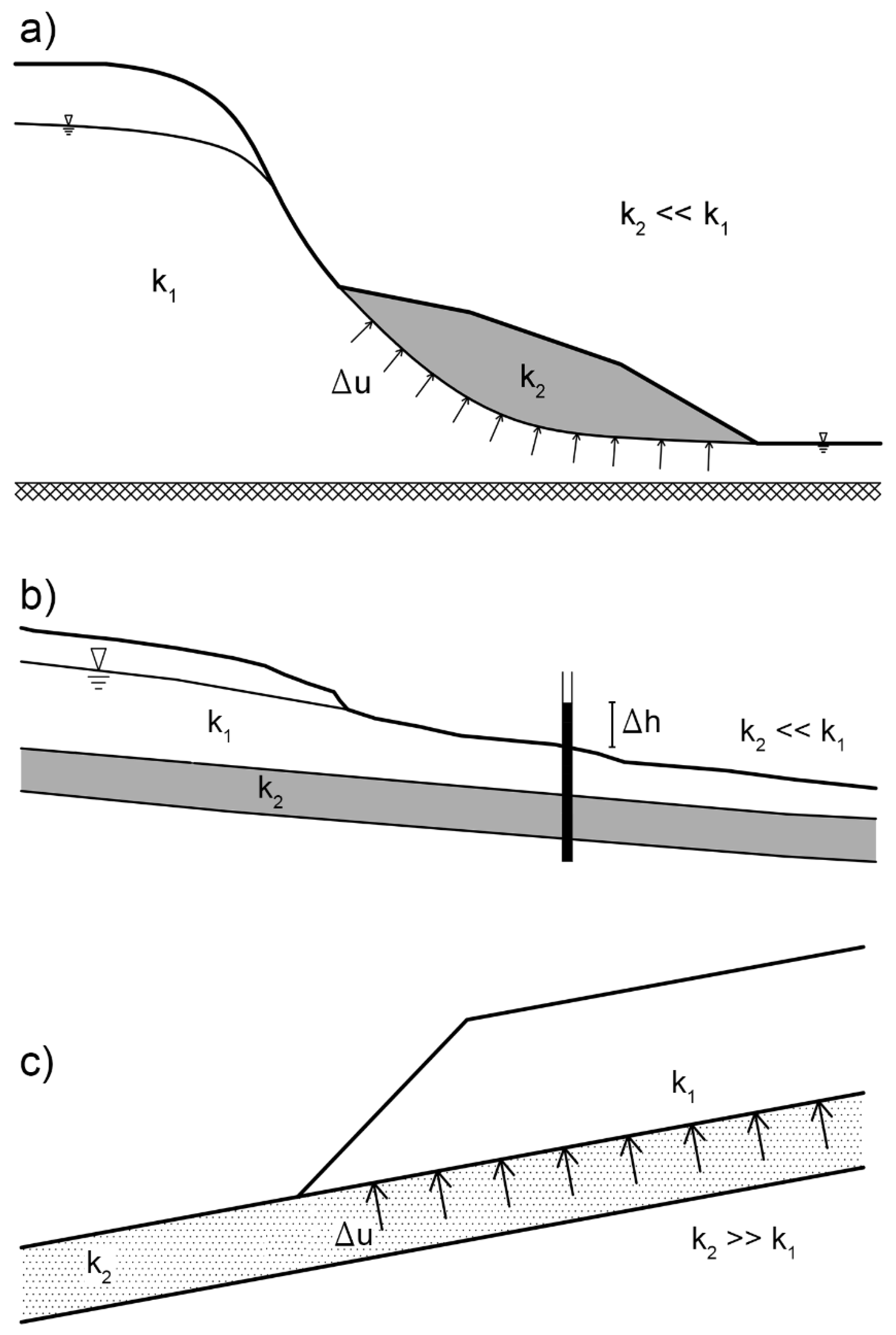
:1. Introduction
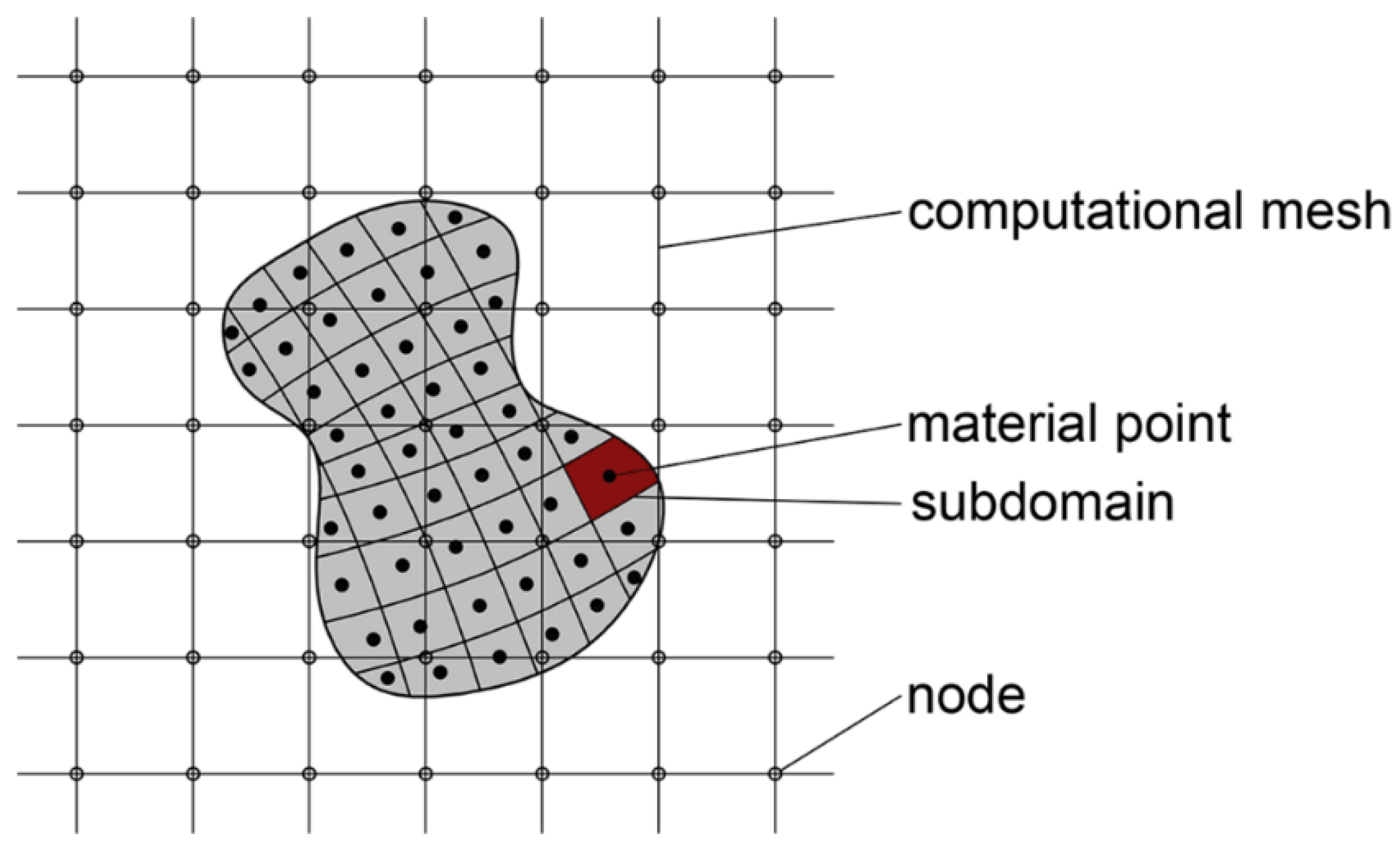
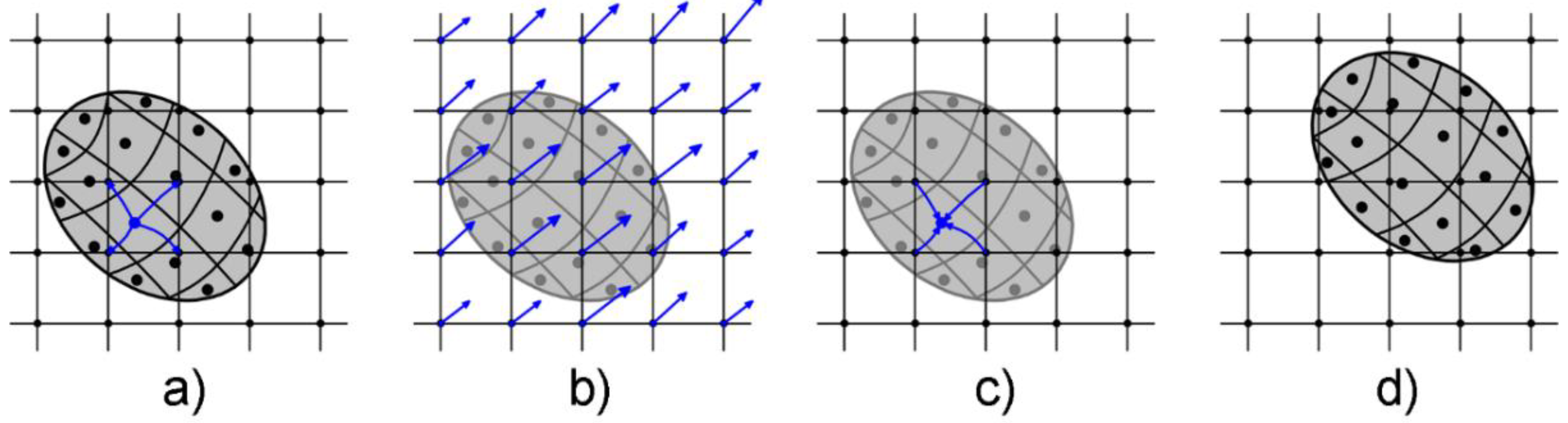
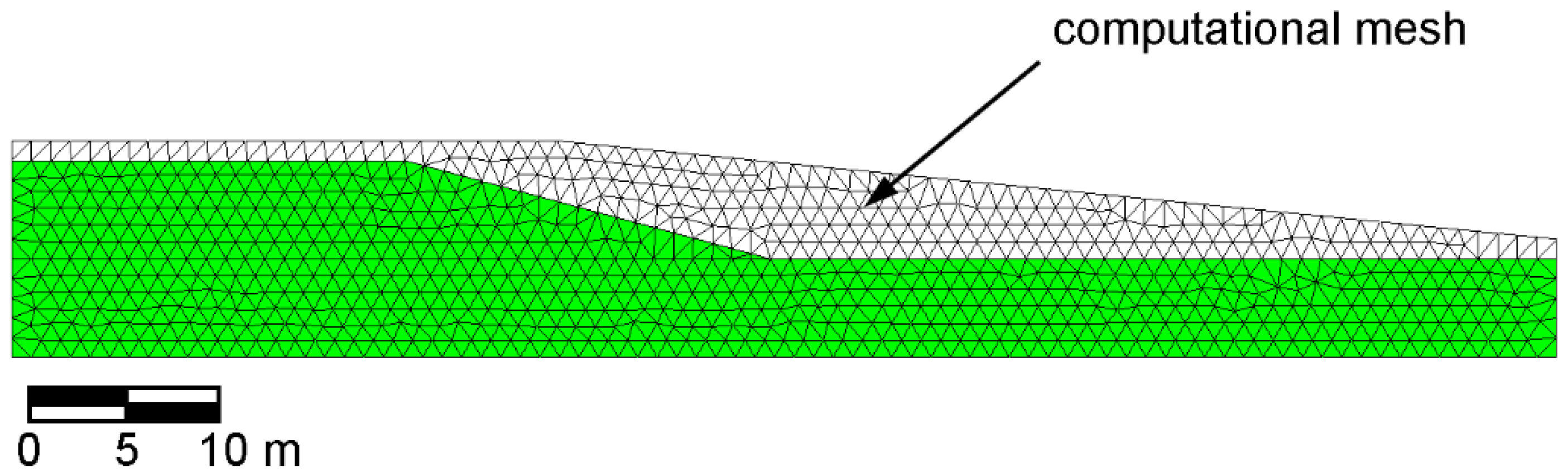
2. Material Point Method
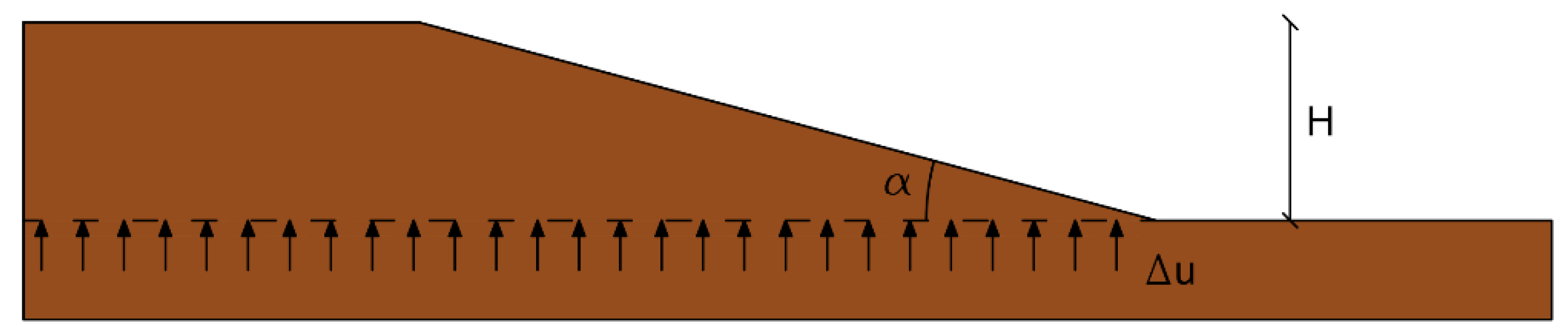
3. Parametric Study
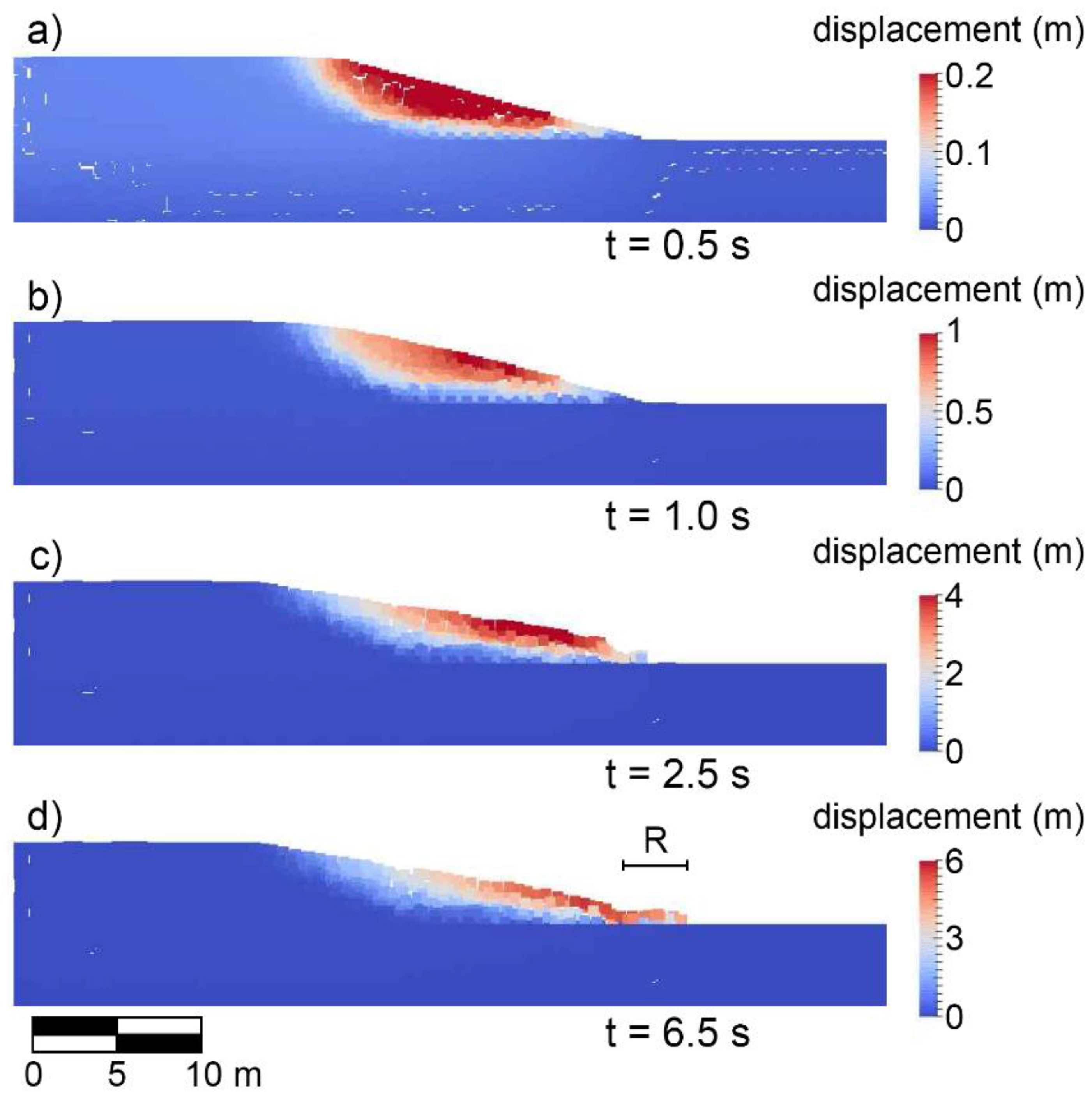
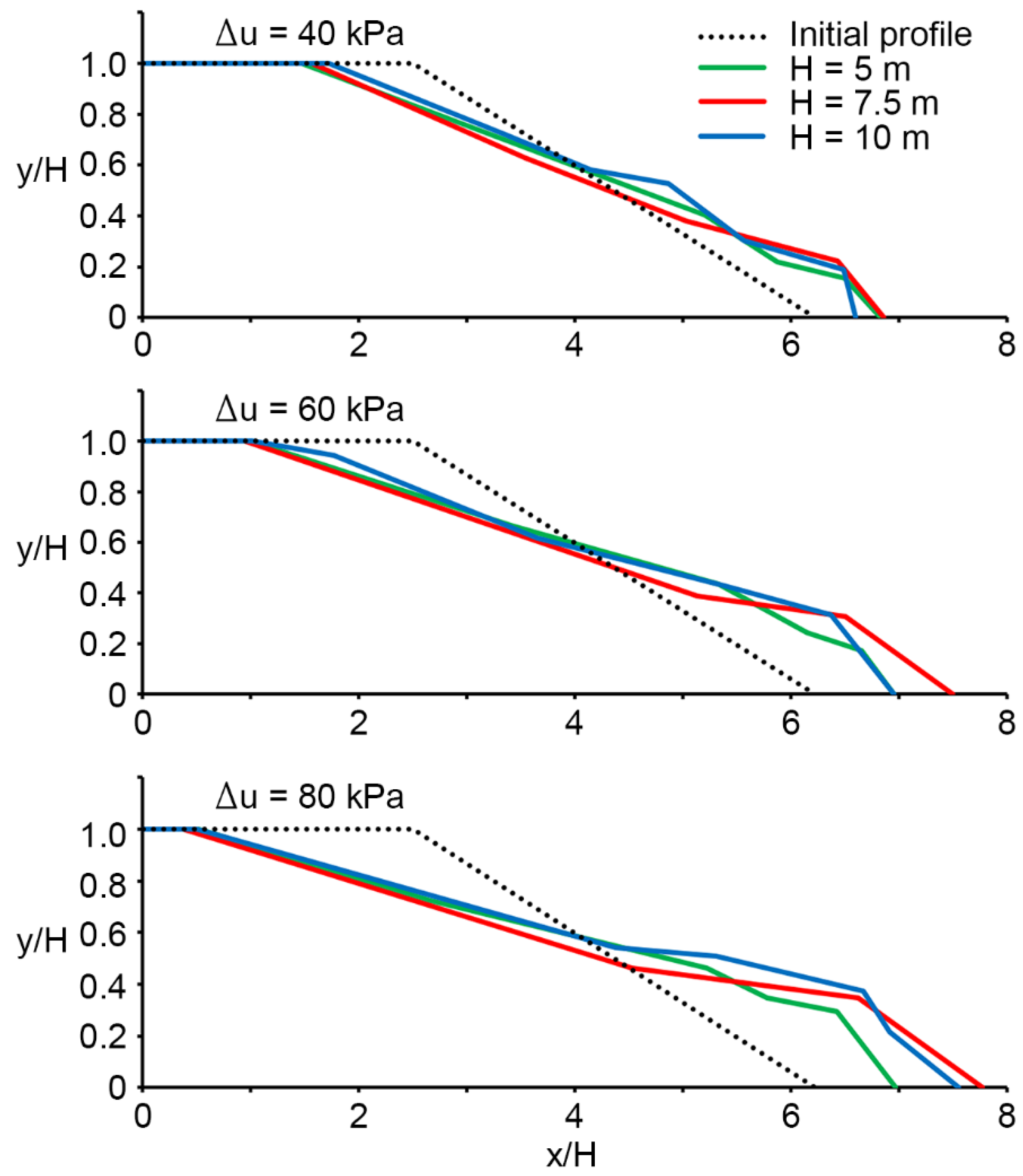
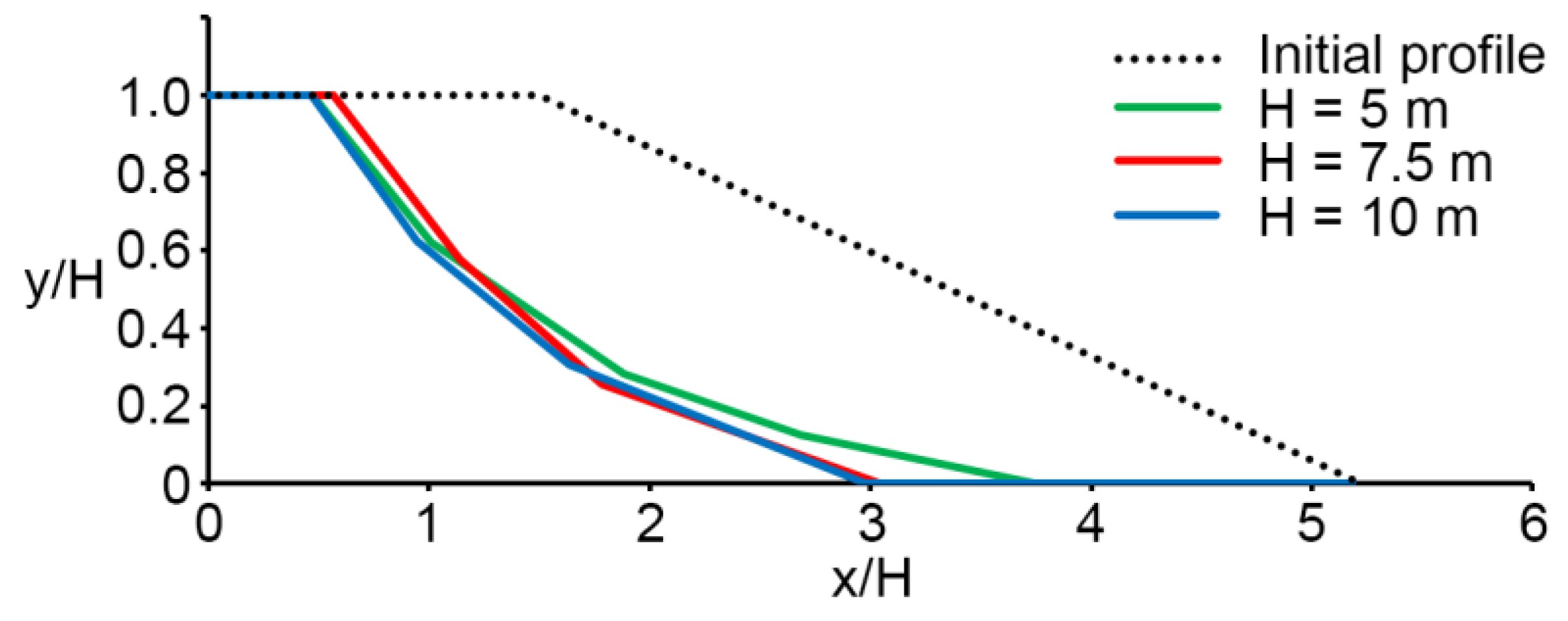
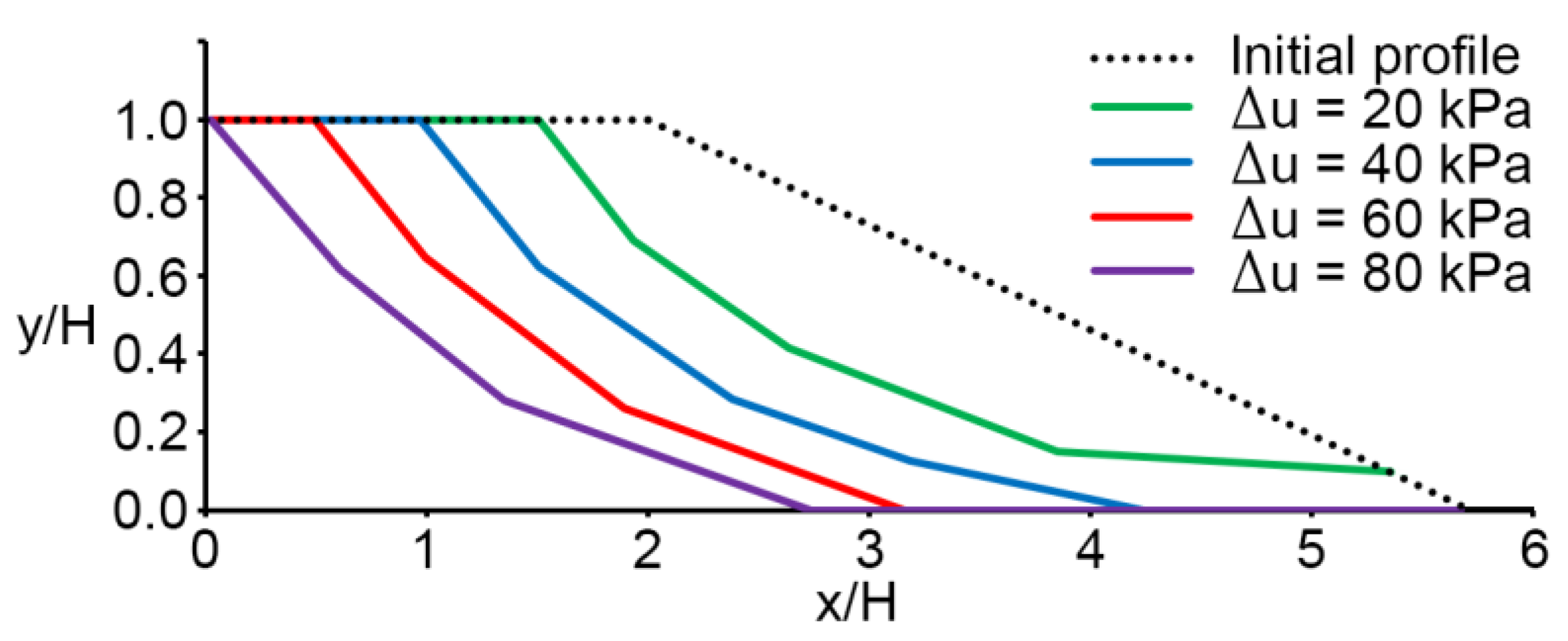
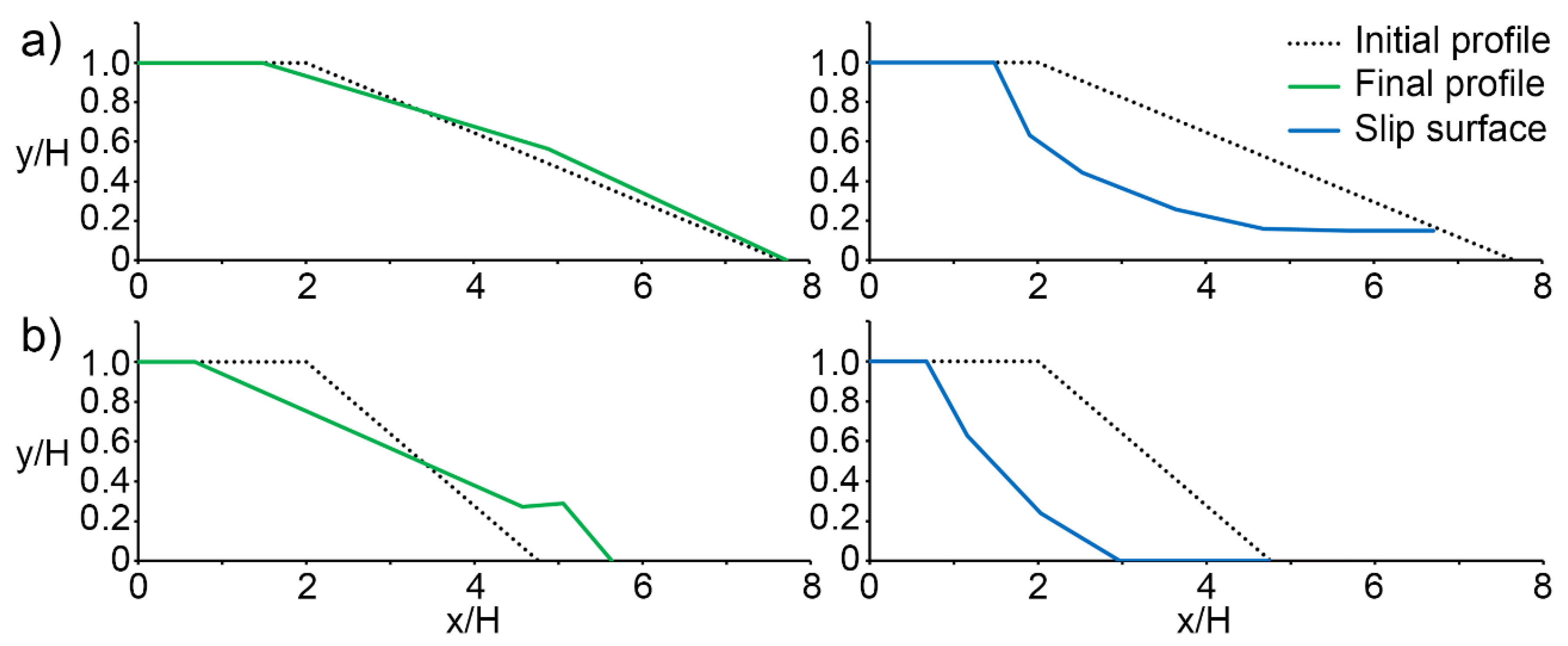
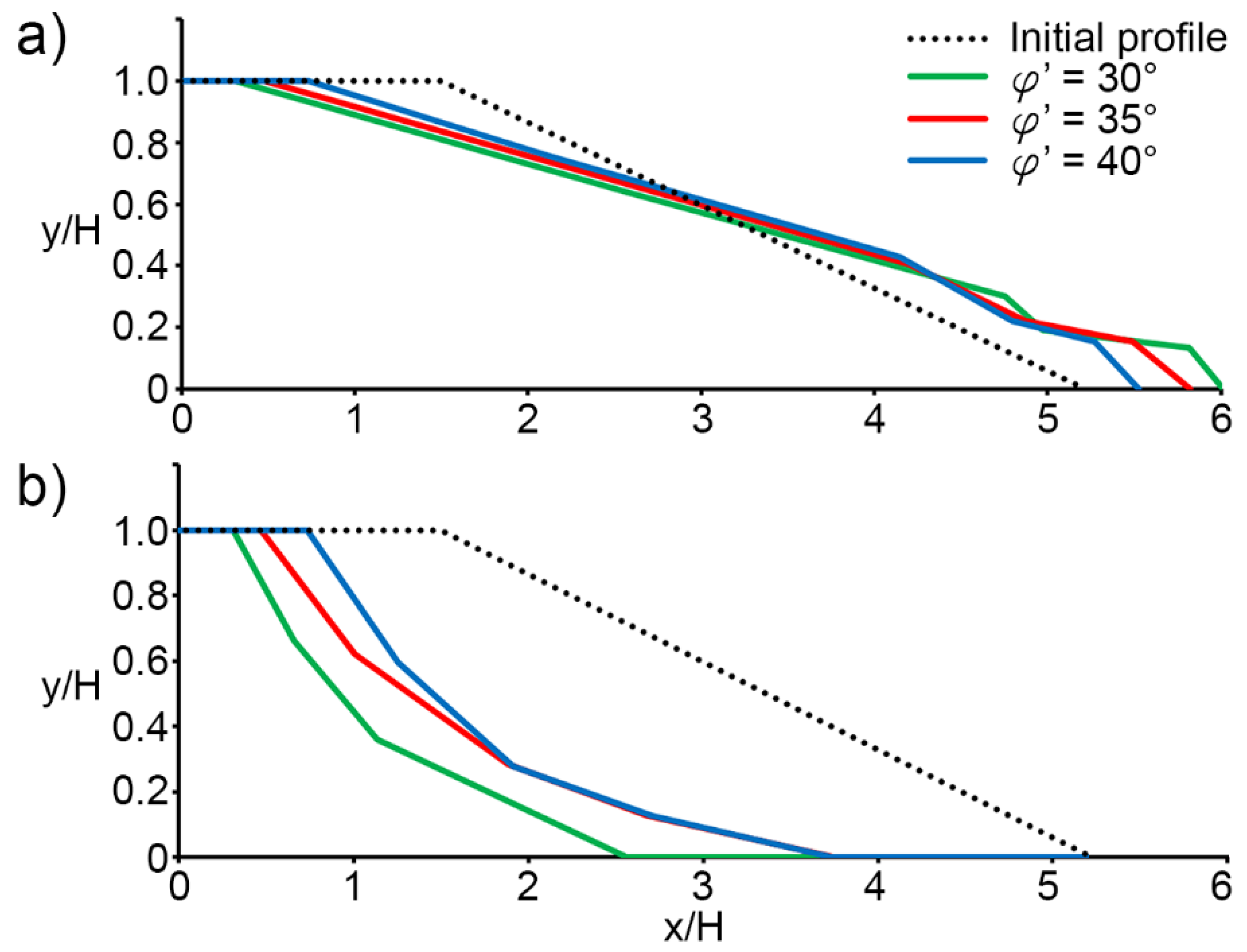
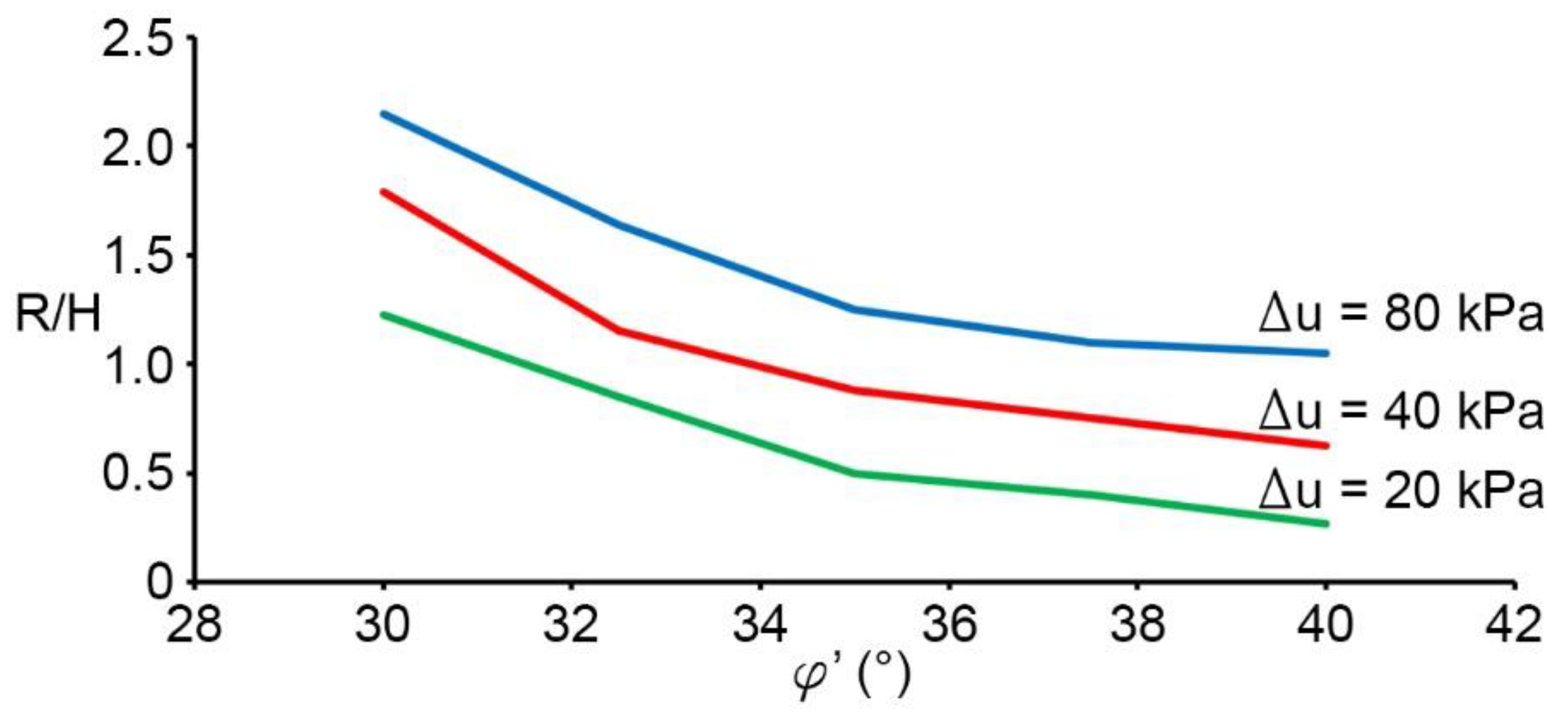
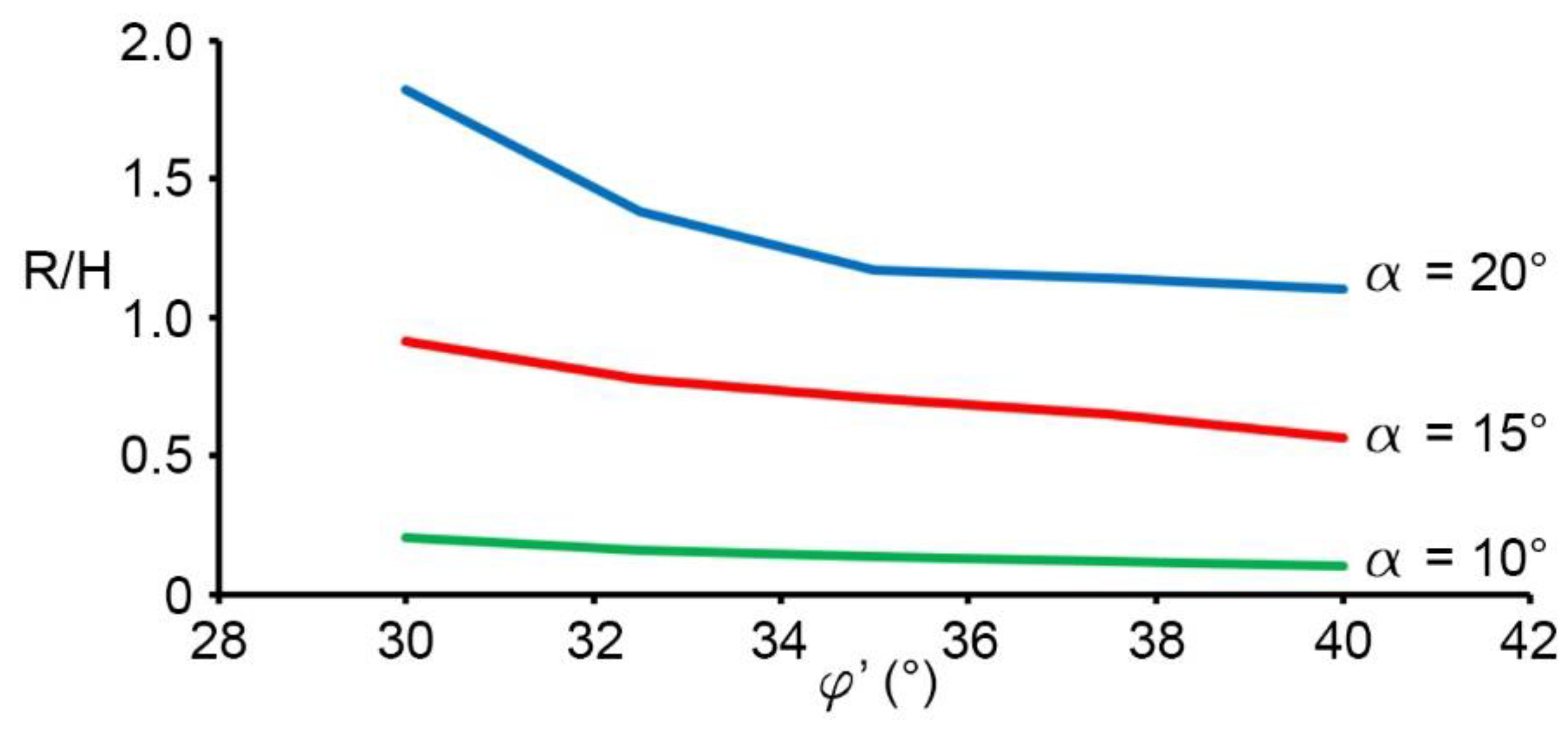
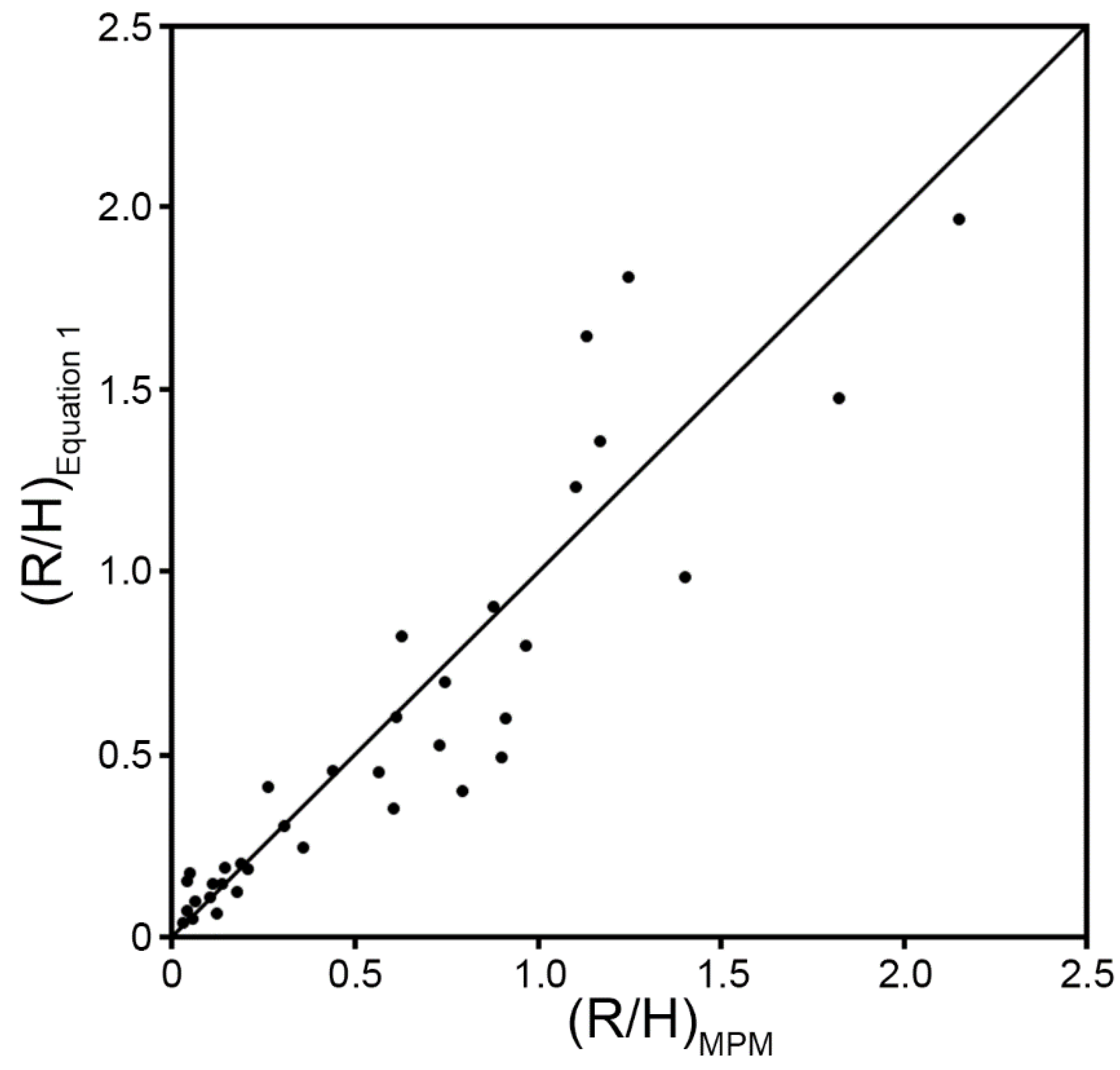
Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vaunat, J.; Leroueil, S.; Faure, R. Slope movements: a geotechnical perspective. In Proceedings of the 7th Congress International Association of Engineering Geology, Lisbon, Portugal, 5–9 September 1994; pp. 1637–1646. [Google Scholar]
- Leroueil, S.; Vaunat, J.; Picarelli, L.; Locat, J.; Faure, J.; Lee, H. A geotechnical characterization of slope movements. In Proceedings of the 7th International Symposium on Landslides, Trondheim, Norway, 17–21 June 1996; Balkema: Rotterdam, The Netherlands; pp. 53–74. [Google Scholar]
- Cascini, L.; Cuomo, S.; Sorbino, G. Flow-like mass movements in pyroclastic soils: remarks on the modelling of the triggering mechanism. Italian Geotech. J. 2005, 4, 11–31. [Google Scholar]
- Yerro, A.; Alonso, E.; Pinyol, N. Run-out of landslides in brittle soils. Comput. Geotech. 2016, 80, 427–439. [Google Scholar] [CrossRef] [Green Version]
- Conte, E.; Donato, A.; Pugliese, L.; Troncone, A. Analysis of the Maierato landslide (Calabria, Southern Italy). Landslides 2018, 15, 1935–1950. [Google Scholar] [CrossRef]
- Duncan, J.M. State of the Art: Limit Equilibrium and Finite-Element Analysis of Slopes. J. Geotech. Eng. 1996, 122, 577–596. [Google Scholar] [CrossRef]
- Corominas, J.; Moya, J.; Ledesma, A.; Lloret, A.; Gili, J.A. Prediction of ground displacements and velocities from groundwater level changes at the Vallcebre landslide (Eastern Pyrenees, Spain). Landslides 2005, 2, 83–96. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. A method for the analysis of soil slips triggered by rainfall. Géotechnique 2012, 62, 187–192. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A. Stability analysis of infinite clayey slopes subjected to pore pressure changes. Géotechnique 2012, 62, 87–91. [Google Scholar] [CrossRef]
- Conte, E.; Troncone, A.; Conte, E.; Troncone, A. A performance-based method for the design of drainage trenches used to stabilize slopes. Eng. Geol. 2018, 239, 158–166. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Troncone, A. A simplified method for predicting rainfall-induced mobility of active landslides. Landslides 2017, 14, 35–45. [Google Scholar] [CrossRef]
- Dounias, G.T.; Potts, D.M.; Vaughan, P.R. Finite element analysis of progressive failure of Carsington embankment. Géotechnique 1990, 40, 79–101. [Google Scholar]
- Alonso, E.E.; Gens, A.; Delahaye, C.H. Influence of rainfall on the deformation and stability of a slope in overconsolidated clays: a case study. Hydrogeol. J. 2003, 11, 174–192. [Google Scholar] [CrossRef] [Green Version]
- Troncone, A. Numerical analysis of a landslide in soils with strain-softening behaviour. Géotechnique 2005, 55, 585–596. [Google Scholar] [CrossRef]
- Lollino, P.; Santaloia, F.; Amorosi, A.; Cotecchia, F. Delayed failure of quarry slopes in stiff clays: the case of the Lucera landslide. Géotechnique 2011, 61, 861–874. [Google Scholar] [CrossRef]
- Fernàndez-Merodo, J.A.; Garcìa-Davalillo, J.C.; Herrera, G.; Mira, P.; Pastor, M. 2D viscoplastic finite element modelling of slow landslides: the Portalet case study (Spain). Géotechnique 2014, 11, 29–42. [Google Scholar] [CrossRef]
- Troncone, A.; Conte, E.; Donato, A. Two and three-dimensional numerical analysis of the progressive failure that occurred in an excavation-induced landslide. Eng. Geol. 2014, 183, 265–275. [Google Scholar] [CrossRef]
- Conte, E.; Donato, A.; Troncone, A. A finite element approach for the analysis of active slow-moving landslides. Landslides 2014, 11, 723–731. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Géotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Potts, D.M.; Zdravkovic, L. Finite Element Analysis in Geotechnical Engineering: Application; Thomas Telford: London, UK, 2001. [Google Scholar]
- Picarelli, L.; Urciuoli, G.; Russo, C. Effect of groundwater regime on the behaviour of clayey slopes. Can. Geotech. J. 2004, 41, 467–484. [Google Scholar] [CrossRef]
- Hung, C.; Liu, C.-H.; Chang, C.-M. Numerical Investigation of Rainfall-Induced Landslide in Mudstone Using Coupled Finite and Discrete Element Analysis. Geofluids 2018, 2018, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhang, L.; Chen, L.; Li, X.; Liu, D. Slope stability analysis based on the Coupled Eulerian-Lagrangian finite element method. Bull. of Eng. Geology and the Environ. 2019, 1–13. [Google Scholar] [CrossRef]
- Lin, C.-H.; Lin, M.-L. Evolution of the large landslide induced by Typhoon Morakot: A case study in the Butangbunasi River, southern Taiwan using the discrete element method. Eng. Geol. 2015, 197, 172–187. [Google Scholar] [CrossRef]
- Calvetti, F.; di Prisco, C.; Vairaktaris, E. DEM assessment of impact forces of dry granular masses on rigid barriers. Acta Geotech. 2017, 12, 129–144. [Google Scholar] [CrossRef]
- Scaringi, G.; Fan, X.; Xu, Q.; Liu, C.; Ouyang, C.; Domènech, G.; Yang, F.; Dai, L. Some considerations on the use of numerical methods to simulate past landslides and possible new failures: the case of the recent Xinmo landslide (Sichuan, China). Landslides 2018, 15, 1359–1375. [Google Scholar] [CrossRef]
- Pirulli, M.; Pastor, M. Numerical study on the entrainment of bed material into rapid landslides. Géotechnique 2012, 62, 959–972. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Zhang, L.; Choi, C.; Ng, C.W.W. Evaluation of Critical Slip Surface in Limit Equilibrium Analysis of Slope Stability by Smoothed Particle Hydrodynamics. Int. J. Geéomeéch. 2019, 19. [Google Scholar] [CrossRef]
- Alonso, E.; Zabala, F. Progressive failure of Aznalcóllar dam using the material point method. Géotechnique 2011, 61, 795–808. [Google Scholar]
- Zhang, X.; Chen, Z.; Liu, Y. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases; Elsevier: London, UK, 2017. [Google Scholar]
- Fern, J.; Rohe, A.; Soga, K.; Alonso, A. The Material Point Method for Geotechnical Engineering. A Practical Guide; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Soga, K.; Alonso, E.; Yerro, A.; Kumar, K.; Bandara, S. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method. Géotechnique 2016, 66, 1–26. [Google Scholar] [CrossRef]
- Conte, E.; Pugliese, L.; Troncone, A. Post-failure stage simulation of a landslide using the material point method. Eng. Geol. 2019, 253, 149–159. [Google Scholar] [CrossRef]
- Yerro, A.; Soga, K.; Bray, J.D. Runout evaluation of Oso landslide with the material point method. Can. Geotech. J. 2018, 1–14. [Google Scholar] [CrossRef]
- Sulsky, D.; Chen, Z.; Schreyer, H. A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
- Ceccato, F.; Beuth, L.; Simonini, P. Analysis of Piezocone Penetration under Different Drainage Conditions with the Two-Phase Material Point Method. J. Geotech. Geoenvironmental Eng. 2016, 142, 4016066. [Google Scholar] [CrossRef]
- Galavi, V.; Beuth, L.; Coelho, B.Z.; Tehrani, F.S.; Hölscher, P.; Van Tol, F. Numerical Simulation of Pile Installation in Saturated Sand Using Material Point Method. Procedia Eng. 2017, 175, 72–79. [Google Scholar] [CrossRef]
- Fern, E.J.; de Lange, D.A.; Zwanenburg, C.; Teunissen, J.A.M.; Rohe, A.; Soga, K. Experimental and numerical investigations of dyke failures involving soft materials. Eng. Geol. 2016, 219, 130–139. [Google Scholar] [CrossRef] [Green Version]
- Yerro, A.; Pinyol, N.M.; Alonso, E.E. Internal progressive failure in deep-seated landslides. Rock Mechanics Rock Eng. 2016, 49, 2317–2332. [Google Scholar] [CrossRef]
- Martinelli, M.; Rohe, A. Modelling fluidization and sedimentation using material point method. In Proceedings of the 1st Pan-American Congress on Computational Mechanics, Buenos-Aires, Argentina, 27–29 April 2015; pp. 1–12. [Google Scholar] [CrossRef]
- Bolognin, M.; Martinelli, M.; Bakker, K.J.; Jonkman, S.N. Validation of material point method for soil fluidisation analysis. J. Hydrodyn. 2017, 29, 431–437. [Google Scholar] [CrossRef]
- Martinelli, M.; Rohe, A.; Soga, K. Modeling Dike Failure using the Material Point Method. Procedia Eng. 2017, 175, 341–348. [Google Scholar] [CrossRef]
- Ceccato, F.; Yerro, A.; Martinelli, M. Modelling soil-water interaction with the material point method. Evaluation of single-point and double-point formulations. In Proceedings of the Numerical Methods in Geotechnical Engineering IX, Porto, Portugal, 25–27 June 2018; Informa UK Limited: Colchester, UK, 2018; Volume 1, pp. 351–357. [Google Scholar]
- Yerro, A.; Alonso, E.; Pinyol, N. The material point method for unsaturated soils. Géotechnique 2015, 65, 201–217. [Google Scholar] [CrossRef] [Green Version]
- Alonso, E.E.; Yerro, A.; Pinyol, N.M. Recent developments of the Material Point Method for the simulation of landslides. IOP Conf. Ser. Earth Environ. Sci. 2015, 26, 12003. [Google Scholar] [CrossRef]
- Anura3D MPM Research Community. Available online: www.anura3d.com (accessed on 10 July 2019).
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- PLAXIS 2D Reference Manual 2019. Available online: www.plaxis.com/support/manuals/plaxis-2d-manuals/ (accessed on 28 June 2019).

| Material | γ (kN/m3) | E’ (kPa) | ν’ | φ’ (°) | c’ (kPa) | ψ (°) | k (m/s) |
|---|---|---|---|---|---|---|---|
| Soil | 20 | 25,000 | 0.3 | 30–40 | 0 | 0 | 0.01 |
| α = 10° | α = 15° | α = 20° | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| φ’ (°) | Δu 20 kPa | Δu 40 kPa | Δu 60 kPa | Δu 80 kPa | Δu 20 kPa | Δu 40 kPa | Δu 60 kPa | Δu 80 kPa | Δu 20 kPa | Δu 40 kPa | Δu 60 kPa | Δu 80 kPa |
| 30 | 0.12 | 0.18 | 0.21 | 0.36 | 0.19 | 0.79 | 0.91 | 0.97 | 0.92 | 1.43 | 1.82 | 2.15 |
| 35 | 0.06 | 0.06 | 0.14 | 0.15 | 0.05 | 0.60 | 0.73 | 0.75 | 0.44 | 0.88 | 1.17 | 1.25 |
| 40 | 0.03 | 0.04 | 0.10 | 0.11 | 0.04 | 0.31 | 0.57 | 0.61 | 0.26 | 0.63 | 1.10 | 1.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Troncone, A.; Conte, E.; Pugliese, L. Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method. Water 2019, 11, 1446. https://doi.org/10.3390/w11071446
Troncone A, Conte E, Pugliese L. Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method. Water. 2019; 11(7):1446. https://doi.org/10.3390/w11071446
Chicago/Turabian StyleTroncone, Antonello, Enrico Conte, and Luigi Pugliese. 2019. "Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method" Water 11, no. 7: 1446. https://doi.org/10.3390/w11071446
APA StyleTroncone, A., Conte, E., & Pugliese, L. (2019). Analysis of the Slope Response to an Increase in Pore Water Pressure Using the Material Point Method. Water, 11(7), 1446. https://doi.org/10.3390/w11071446





