Abstract
Spatial variability of soil properties at the field scale can determine the extent of agricultural yields and specific research in this area is needed. The general objective of this study was to investigate the relationships between soil physical and hydraulic properties and wheat yield at the field scale and test the BEST-procedure for the spatialization of soil hydraulic properties. A simplified version of the BEST-procedure, to estimate some capacitive indicators from the soil water retention curve (air capacity, ACe, relative field capacity, RFCe, plant available water capacity, PAWCe), was applied and coupled to estimates of structure stability index (SSI), determinations of soil texture and measurements of bulk density (BD), soil organic carbon (TOC) and saturated hydraulic conductivity (Ks). Variables under study were spatialized to investigate correlations with observed medium-high levels of wheat yields. Soil physical quality assessment and correlations analysis highlighted some inconsistencies (i.e., a negative correlation between PAWCe and crop yield), and only five variables (i.e., clay + silt fraction, BD, TOC, SSI and PAWCe) were spatially structured. Therefore, for the soil–crop system studied, application of the simplified BEST-procedure did not return completely reliable results. Results highlighted that (i) BD was the only variable selected by stepwise analysis as a function of crop yield, (ii) BD showed a spatial distribution in agreement with that detected for crop yield, and (iii) the cross-correlation analysis showed a significant positive relationship between BD and wheat yield up to a distance of approximately 25 m. Such results have implications for Mediterranean agro-environments management. In any case, the reliability of simplified measurement methods for estimating soil hydraulic properties needs to be further verified by adopting denser measurements grids in order to better capture the soil spatial variability. In addition, the temporal stability of observed spatial relationships, i.e., between BD or soil texture and crop yields, needs to be investigated along a larger time interval in order to properly use this information for improving agronomic management.
1. Introduction
Soil physical and hydraulic properties can change drastically over space [1] and time [2] and their evaluation is essential for a rational soil management and, therefore, for increasing crop yields performance [3]. Moreover, they dynamically affect water balance components and crop yields by relating soil hydraulic functioning to climate patterns and crop water requirements [4,5].
Soil properties, such as saturated hydraulic conductivity, total organic carbon content, structure stability index, dry bulk density, as well as capacitive indicators obtained from the soil water retention curve (i.e., plant available water capacity, relative field capacity, air capacity) were widely and successfully applied to investigate soil management effects on soil physical and hydraulic properties [3,6,7,8]. Keller et al. [3], for example, have investigated the relationships between crop yield and soil structure in three Swedish fields, applying the simplified falling head (SFH) technique [9] to evaluate whether field-saturated hydraulic conductivity (Ks) could be used as a simple and quickly measurable indicator of crop yield. The main findings of their investigation showed that Ks may be a good indicator of low yielding zones, and degradation of soil structure has been indicated as the main reason for low yield. However, in other studies, spatial and temporal variation of soil water holding capacity was suggested to be a factor partly responsible for crop yield variation, regardless of the amount and timing of the rain contributions [10,11]. Consequently, investigations addressed at evaluating new experimental procedures for soil hydraulic characterization, and at establishing the usefulness and sensitivity of soil properties as predictors for crop yield, are needed. This is a current issue in Mediterranean agro-environments, where water resources are scarce and need to be optimally managed [12].
Soil hydraulic properties assessment, i.e., water retention curve and hydraulic conductivity function (θ(h) and K(h) relationships, respectively), is expensive and time consuming, since standard methods need specific skills and their spatialization, i.e., prediction on a distributed large scale, which can be burdensome or wholly inapplicable [13].
Several quick methods are available to obtain θ(h) and K(h) (or K(θ)) relationships. Pedotransfer functions (PTFs), for example, allow for estimating soil hydraulic properties starting with basic soil variables such as soil texture, bulk density or organic matter or hydraulic conductivity [14]. However, PTFs are not able to accurately quantify the effects of different agronomic options for soil management, unless a site-specific calibration is performed [15]. On the other hand, the most widely applied laboratory methods as hanging water column apparatus [16], pressure cells [17] or evaporation method [18], may require up to a week (or more) to obtain a single soil water retention curve [19,20]. As a consequence, although reliable and accurate, they are not easily applicable for large-scale research and simplified techniques should be chosen for these purposes [21,22].
The BEST-procedure by Lassabatère et al. [23] allows for estimating hydraulic functions repeatedly over space and time with substantially limited experimental burdens. Basically, the procedure requires three sets of experimental information: (i) cumulative infiltration by a simple infiltrometric experiment (i.e., ring infiltration test of Beerkan type), (ii) soil bulk density and volumetric soil water content at the time of experiment by sampling few (generally two) undisturbed soil cores, and (iii) soil particle-size distribution or, alternatively, clay, silt and sand percentages according to the USDA classification. Specifically, the procedure makes use of well-known analytical solutions for θ(h) and K(h) relationships and estimates (i) shape parameters, which are texture dependent, from particle-size analysis by physical-empirical PTFs, while (ii) scale parameters, which are structure dependent, by a three-dimensional field infiltration experiment at zero pressure head [23]. Therefore, BEST can be considered an adequate compromise between estimation accuracy and economic-experimental load. For example, some studies have applied BEST to establish the effects of droplet impact on soil sealing and crust formation [24,25], to carry out integrated soil physical quality assessment [26,27] or to identify the effects of tillage on some soil properties (i.e., Ks) under drip irrigation [28]. A main advantage of BEST is that it can be adopted when a large number of hydraulic measurements must be obtained at the field or at irrigation district scale, for example, for precision agriculture purposes. For instance, Mubarak et al. [29] assessed the temporal stability of both Ks and spatial structure of hydraulic properties of a loamy soil. Specifically, they compared Ks-BEST data with those estimated seventeen years earlier by applying the guelph permeameter method, under relatively comparable soil and agronomic conditions. Results showed that Ks changed significantly, but observed discrepancies were not higher than a factor of three or four. This suggests that BEST can represent an easy, robust, and inexpensive way for characterizing soil hydraulic behavior and its spatial [30] and temporal [29] variability at the field scale. The availability of a large number of georeferenced hydraulic measurements would allow delineating homogeneous sub-areas within the crop field to be submitted to uniform agronomic management [31,32]. This can lead to an increase in agricultural resources optimization [31]. In addition, dense spatial data can be used as auxiliary/covariate information in mixed effects models to improve the estimates of the target variables [33] or to improve the estimation of treatment significance reducing the risk of misleading or erroneous inferences in analysis of variance [34,35]. In other words, the potential application advantages seem attractive, but BEST has not yet been tested for soil hydraulic properties spatialization and the actual reliability for the mentioned purposes must be proven.
The general objective of this study was to test the BEST-procedure for the spatialization of soil hydraulic properties. In particular, the spatial distribution of the measured-estimated by BEST variables (soil texture, bulk density, saturated hydraulic conductivity, plant available water capacity, relative field capacity, air capacity) and ancillary soil properties (total organic carbon content, structure stability index) was investigated in a typical wheat cropping system in Southern Italy. Cross-correlation analysis was applied to establish strength and the extent of the spatial relationships between selected soil properties and crop yields.
2. Materials and Methods
2.1. Study Area
The research was carried out in the spring–summer period of 2016 at the experimental farm “Menichella” of Council for Agricultural Research and Economics, located near Foggia (41°27′02″ N, 15°30′36″ E), Southern Italy (Figure 1). The study was conducted in a field of about 5 ha (170 m × 250 m) conventionally cultivated with durum wheat (Figure 1). The field is located in a flat area characterized by Mediterranean climatic conditions and the soil was clay according to USDA classification. Additional information on the experimental site can be found in Cavallo et al. [31].

Figure 1.
Geographical location, view of “Menichella” farm, and scheme of the fifty-two sampling points.
Fifty-two geo-referenced sampling points, located at the nodes of a regular grid (175 m × 250 m) with a mesh of 20 m × 40 m, were considered in this investigation (Figure 1). The amount of observations was checked to ensure a sufficient coverage of the study area, i.e., a number of pairs for each distance class larger than the minimum required for an effective spatial analysis, as reported by Myers [36] (minimum threshold equal to 25 pairs; actual pairs observed ranging between 66 and 239). At each selected point, the wheat yield and some physical, hydraulic and chemical soil properties (e.g., soil texture, dry bulk density, saturated hydraulic conductivity, total organic carbon content) were determined to establish possible spatial structures and correlations among variables. More details on the dataset composition are given in Section 2.2.
2.2. Lab and Field Measurements
For each of the selected fifty-two sampling points, a simplified version of the BEST-procedure by Lassabatère et al. [23] was applied. The saturated hydraulic conductivity (Ks) and soil bulk density (BD) were then measured, and three capacitive indicators were estimated from soil water retention curve of BEST, namely plant available water capacity (PAWCe), air capacity (ACe) and relative field capacity (RFCe) [8]. The subscript e is used for indicating variables estimated by BEST. In detail, as required for BEST application, a falling head infiltration experiment of Beerkan type was carried out in the third decade of April at each sampling point using a metal ring (15 cm inner diameter), and the cumulative infiltration curve as function of the time (I(t)) was obtained; eighteen water volumes of 200 mL each were used in this investigation and the BEST-steady algorithm by Bagarello et al. [37] was applied to estimate the aforementioned soil properties. A relatively higher number of water volumes than usual (eighteen instead of fifteen) was chosen to be sure of sampling a representative soil volume and be more confident to reach steady-state conditions of water flow. Two undisturbed soil cores (0.05 m in height by 0.05 m in diameter) were collected at the 0 to 0.05 m and 0.05 to 0.10 m depths close to the ring to determine the soil water content at the beginning of infiltration experiments, θi, and BD. A disturbed soil sample (0–0.10 m depth) was collected at each sampling point to quantify both the soil texture, i.e., clay (Cl), silt (Si) and sand (Sa) percentages, according to the USDA classification, and the soil total organic carbon content (TOC). Soil texture was obtained with the standard pipette method [38], and TOC was quantified through dry combustion using a TOC Vario Select analyzer [39]. Soil texture fractions, BD, θi and I(t) were used to run BEST-steady and the infiltration constants, β and γ, were fixed at the reference values of literature [23,40]. More detail concerning the BEST-procedure application can be found in Castellini et al. [8]. At harvesting (end of June 2016), wheat grain yield data were collected on the fifty-two geo-referenced locations (i.e., nodes of a 20 m × 40 m grid). Yield data were recorded on sampling areas of 1 m2 and normalized to 13% moisture content of grain.
2.3. Physical and Hydraulic Soil Properties
The saturated hydraulic conductivity (Ks) is the soil’s ability to absorb and transmit soil water to the root zone, as well as drain excess water out of the root zone [41]. Since Ks is mainly controlled by soil structure and texture, e.g., [42], in the same soil or soil class it may be used as a measure of structural status of agricultural soils [3]. References of literature suggest optimal Ks values for agriculture soils within the range 0.005–0.05 mm s−1 to promote a rapid infiltration and redistribution of plant available water [41]. However, in order to select soil properties that directly (or indirectly) account for soil structure, we also considered (i) dry bulk density (BD), (ii) total organic carbon content (TOC) and (iii) structural stability index (SSI) by Pieri [43]. SSI is calculated from TOC and fine soil texture (SSI = 1.724·TOC%/(silt% + clay%)·100) components [27]. For these soil indicators the following critical limits were considered: optimal BD values within the range 0.9–1.2 g cm−3; optimal or poor TOC values, general for plant husbandry, were equal to 30–50 or <23 g kg−1, respectively, although good values for agricultural fine-textured soils were reported in the range of 15–22 g kg−1 by Sequi and Nobili [44]. Therefore, a comparison between these two references has been made. SSI values >7% or ≤7% are representative of low or high risk of structural degradation, respectively [6].
Conversely, a second set of indicators that gives an account of the proportion between water and air into the soil was considered. Plant available water capacity (PAWCe) (cm3 cm−3), in fact, is the amount of water held in the soil and available for crop growth and obtained as the difference between the water contents at field capacity (at h = −100 cm) and at permanent wilting point (at h = −15,300 cm) [45]; according to the literature [6], the following PAWCe limits were considered in this investigation: PAWCe ≥ 0.20 ideal; 0.15 < PAWCe < 0.20 good; 0.10 < PAWCe < 0.15 limited; PAWCe < 0.10 poor. Air capacity (ACe) (cm3 cm−3) provided information on the soil ability to store and transmit air (Reynolds et al. [6]). According to Castellini et al. [7], an optimal ACe value falls in the range 0.10–0.26 cm3 cm−3, while higher or lower values represent inadequate soil aeration conditions; this interval was optimal for a clay soil bordering with that studied [7]. Finally, the relative field capacity (RFCe), obtained as the ratio between the water contents at field capacity and at water saturation, was considered, since it partially combines ACe and PAWCe, thus expressing the soil capacity to store air and water relative to the soil’s total pore volume [46]. Optimal values for RFCe were suggested within the range 0.6–0.7; consequently, lower or higher values are representative respectively of “water limited” or “aeration limited” (i.e., for a given soil texture, too porous or too compact) soil conditions [6].
2.4. Data Analysis
2.4.1. Preliminary Statistical Analysis
Descriptive statistics were computed in order to summarize the main features of data distribution for yield and the soil variables under study: bulk density (BD), capacitive indicators from the estimated soil water retention curve (ACe, PAWCe, RFCe), saturated soil hydraulic conductivity (Ks), soil total organic carbon content (TOC), fine soil texture components (Cl + Si) and soil structural stability index (SSI). In addition, hypothesis of normality was tested using the Kolmogorov–Smirnov test [47].
2.4.2. Correlation and Spatial Analysis
Relationships among studied variables were investigated using parametric correlation analysis, computing Pearson correlation coefficients.
The predisposition of the considered variables to be spatialized was investigated using Moran statistics. Moran’s autocorrelation coefficient (often denoted as I) is an extension of the Pearson product–moment correlation coefficient to a univariate series [48]. Specifically, Moran statistics computes a weighted Pearson product–moment correlation of a variable against itself, where the weighting relates to the variable’s spatial arrangement [49]. Moran’s I allows for the investigation of correlation within a single variable due to the spatial relationship amongst its observations. The weights (wij) are a function of the distance between each pair of observations of the variable under study (xi; xj). In its simplest form, weights will take values 1 for close neighbours, and 0 otherwise; we also set wii = 0. These weights are sometimes referred to as a neighbouring function.
Moran’s I statistics is represented by the following equations:
where zi is the deviation of an attribute from its mean and S0 is the aggregate of all the spatial weights (wij).
2.4.3. Geostatistical Analysis
The geostatistical analysis is aimed at evaluating spatial heterogeneity of the studied variables by means of structural analysis (variography) and at producing maps of the collected data by means of spatial prediction approaches (kriging).
Variography
Under the name of (semi)variogram, two different types of functions related to geographically referenced data are usually denoted, namely the experimental variogram and the variogram model. The former is discrete and represents the half of the average squared difference between points separated by the distance h (the red-dotted line in Figure 2). The latter is parametric, continuous and a conditionally negative definite [50] (the solid line in Figure 2). The most important parameters for the model are the partial sill (σ2) indicating the structured component of the variance, the nugget (), indicating the random uncorrelated component, and the range (α); this latter can be interpreted as the distance beyond which the spatial correlation becomes negligible (Figure 2). A list of the main variogram models is summarized in Figure 2.

Figure 2.
Examples of parametric families of theoretical variograms and experimental and model variograms (red squares and black line, respectively) with corresponding parameters, on the left and right respectively. The parameter (the partial sill) identifies the variance of the process and is always positive; the parameter (the range) identifies the length of the spatial process and is also positive. Other parameter restrictions are reported in the last column.
Variogram models were fitted to the experimental variograms of the variables under study. By virtue of the parsimony principle, the preferred spatial model should be isotropic. Regardless, a test has been applied to test for anisotropy. In detail, isotropic and anisotropic models were compared by means of a Likelihood Based Parameter Estimation for Gaussian Random Fields test, using REML, in order to estimate the two parameters characterizing anisotropy, namely the anisotropy angle and the ratio between the two ellipse axes [51].
Leave-one-out cross-validation was carried out and Pearson correlation coefficients (r) between predicted and observed data were used to quantify the goodness of model adaptation to the experimental variogram.
Spatial Interpolation
All the variables were interpolated using a univariate approach, the ordinary kriging (OK). Such a predictor is one of the most basic forms of kriging in which the unknown value z(x0) of a given realization of Z(x0) is predicted from the known values z(xi) i = 1, 2, …, N, at the support points xi. The ordinary kriging predictor can be written as:
where λi are weights associated with the N sampling points. The weights are chosen in such a way that the predictor is unbiased, the values are continuous and the estimation error is minimized:
This ensures that kriging is an exact interpolator because the estimated values are identical to the observed values when a kriged location coincides with a sample location [33,52,53].
2.4.4. Cross-Correlogram
In order to compare prediction maps of different variables, cross-correlograms were computed. In detail, given the prediction maps of two different variables, MA and MB, there are several methods with which to compare them [33,54,55]. To account for the inherently spatial characteristics of map representation, the cross-correlogram, which measures the correlation as a function of the distance between observations, is particularly well-suited. The analytical formulation of the cross-correlogram is the following:
where and represent the values at locations and of the two maps separated by the h distance, respectively; represents the distance between the two locations, E denotes the mathematical expectation, mA and mB represent the populations means and sA and sB represent the populations standard deviations. If patterns are completely similar, apart from a constant, should be equal to 1. To estimate from the available data the following equation can be used:
To compute , the procedure is as follows: from both the maps, all the couples whose locations are separated by the distance h are collected. Indices and represent the mean and the standard deviation of mapped and , respectively. N(h) is the total number of these pairs. If the methods being compared produce similar results, a decreasing cross-correlogram for increasing values of h is expected.
For summarizing the results and comparing different outcomes, results of cross-correlation analysis were reported in form of tables containing correlations at specified lag distances (0 m, 25 m, 50 m, 75 m, 100 m); in this way, practical information on the strength and extent of the spatial relationships between soil properties and crop yields was provided.
3. Results
3.1. Preliminary Statistical Analysis
The preliminary statistical analysis on the studied variables highlighted some slight departures from normal distribution (Table 1). In particular, Ks and TOC showed positive and negative longer tails due to a few larger and smaller observations. The Kolmogorov–Smirnov test results indicated a significant departure from normality only for ACe and Ks, although not extremely significant (P = 0.0291; P = 0.0209; Table 2). For this reason, it was not deemed necessary to transform the original data.

Table 1.
Summary statistics for the studied variables.

Table 2.
Outcomes of the Kolmogorov-Smirnov test (D).
3.2. Physical and Hydraulic Soil Properties
Physical and hydraulic properties of the investigated clay soil were summarized in Figure 3. Overall, according to the suggested criteria to detect relatively good or poor soil conditions of BD, TOC, SSI, Ks, PAWCe, ACe, RFCe and to obtain acceptable crop yields, results showed relatively good findings as only three of the seven soil properties indicated non optimal conditions. In further detail, the following was observed: (i) relatively low levels of organic carbon content (TOC) for threshold values reported by Reynolds [6], but good levels for ranges defined by Sequi and Nobili [44], (ii) risks of structural instability (SSI) and (iii) potential conditions of soil compaction (RFCe). In agreement with these findings, although ACe was within the suggested optimal range, it showed relatively low air capacity (Figure 3). Optimal hydrodynamic soil properties were also recognized for Ks, as the entire range of variation of the measurements fell within the limits defined by Reynolds et al. [41]. However, two clarifications should be provided because: (i) observed low TOC values are not entirely unexpected as they are quite common for a monoculture of wheat, in a typical Mediterranean environment, and (ii) BD evaluation showed optimal conditions, i.e., a soil compaction was not recognized, indicating a different assessment when compared with RFCe or ACe (Figure 3). In other words, soil physical and hydraulic assessment carried out using available references of literature has suggested optimal, or near optimal, conditions of investigated soil. This finding was in agreement with results of wheat yields, as obtained mean values equal to 3.86 t ha−1 may be considered as medium-high production levels for the investigated agro-environment. However, as TOC limits used do not appear to be entirely in line with the case under study, a specific discussion has been made in Section 4.

Figure 3.
Box plots of dry bulk density (BD), total organic carbon content (TOC), structure stability index (SSI), saturated hydraulic conductivity (Ks), plant available water content (PAWC), air capacity (AC) and relative field capacity (RFC). The thick-black line within each box represents the mean value (the fine-black line, the median). Open circles represent outliers (closed circle, extreme outlier for TOC). Dot green-line or dashed red-line represents optimal or critical values, respectively, according to Section 2.3. For TOC, a further classification by Sequi and Nobili [43] was specifically reported (solid lines, which identify four areas, from poor to very good) for fine textured soils (clay, clay-loam, silty-clay and silty-clay-loam, according to USDA).
3.3. Correlation and Spatial Analysis
Results of correlation analysis are reported in Figure 4. Significant correlations were observed between crop yield and BD and PAWCe, with a positive and negative relationship respectively (r = 0.381, P = 0.005 and r = −0.400, P = 0.003); in addition, a positive correlation, although not significant (P = 0.063), was found with Ks. Overall, soil variables showed interesting relationships. As concerns capacitive indicators derived from the soil water retention curve of BEST, a strong negative correlation was found between RFCe and ACe (r = −0.922, P < 0.0001) as observed also in previous studies [7]. PAWCe was strongly negatively related to BD (r = −0.780, P < 0.0001). An interesting relationship was observed between Ks and the three capacitive indicators (P = < 0.0001, 0.001 and 0.009, respectively for RFCe, ACe and PAWCe). TOC was negatively correlated to BD (P < 0.006) and showed a weak relation with PAWCe (P < 0.065). Finally, SSI, synthetizing the information deriving from TOC and fine texture components (Cl + Si), showed to be an effective summary indicator highlighting good correlations also with BD (P = 0.005), PAWCe (P = 0.006) and Ks (P = 0.059). A more in-depth discussion on the correlations obtained is reported in the Discussion section.

Figure 4.
Bivariate scatterplots for the variables under study. Red dots highlight significant correlations at P < 0.05. BD is the bulk density (g cm−3), Cl + Si is the sum of clay and silt content (%), Ks is the saturated soil hydraulic conductivity (mm s−1), TOC is the soil total organic carbon (g kg−1), SSI is the structure stability index (%), PAWCe is the plant available water capacity (cm3 cm−3), ACe is the air capacity (cm3 cm−3) and RFCe is the relative field capacity (dimensionless).
Moran’s I spatial autocorrelation statistics gave a hint about the predisposition of the single variables to be spatialized (Table 3). For the case at hand, Moran values ranged from −0.2232 for RFCe, indicating a non-significant spatial correlation, to 0.3920, 0.4474, 0.4564 and 0.5889, for BD, SSI, PAWCe and Cl + Si respectively, indicating highly significant overall spatial dependence. Yield and TOC showed also a significant spatial correlation (Table 3). It is noteworthy that the variables correlated each other, showing also a similar overall spatial structure.

Table 3.
Moran’s I spatial autocorrelation statistics.
Theoretical models were fitted to the experimental variograms of the variables under study, consisting generally of these nested models: a nugget effect and a spatial covariance function. Since the anisotropy ratio and the anisotropy angle parameters were not significant according to the Likelihood Based Parameter Estimation test, isotropic models were selected. In Table 4, the fitted variogram models are reported and described by the model name and the following parameters, namely nugget, partial sill and range. Actually, the Matérn model demonstrated to be the best suited theoretical function to describe spatial structure of the considered variables except for BD and PAWCe, since it was more flexible with respect to the classical models, having an additional shape parameter (k) (Figure 2). Following Cambardella et al. [56], the nugget-to-sill ratio can be a useful means to describe the spatial structure of the studied variables. In particular, the nugget semivariance expressed as a percentage of the total semivariance enables comparison of the relative size of the nugget effect among studied variables, with ratios <25% indicating strong spatial dependence, ratios between 25 and 75% moderate spatial dependence, ratios >75% weak spatial dependence. The analysis of the nugget-to-sill ratios (Table 4) indicated almost strong spatial dependence for TOC, Cl + Si and SSI (with values of 0.264, 0.272 and 0.263, respectively); these results were confirmed by the high predicted vs. observed correlations (r = 0.42, 0.63 and 0.74). RFCe, together with Ks, showed a weak spatial dependence, with nugget to sill ratios of 0.847 and 0.910, results confirmed also by not significant cross-validation outcomes (predicted vs. observed correlations) and by the findings of overall spatial correlation analysis (Moran statistics, Table 3). Yield fell between the moderate to weak classes, with a nugget to sill ratio of 0.761. PAWCe and BD presented a moderate adaptation as showed by the predicted vs. observed correlation (r = 0.49 and 0.46); the nugget-to-sill ratio was not computed because the nugget was not significant different from zero. The variogram estimated parameters for ACe appeared to be not physically based (an estimated value of 773 m was observed for the range). All the remaining range parameters values were consistent and below the maximum distance between observations (Table 4).

Table 4.
Parameters of the theoretical variograms fitted to the studied variables.
Spatial estimates of yield and spatially structured soil variables are reported in Figure 5. By visually inspecting the maps, a similar spatial behavior emerged for yield and BD with lower values in the left part of the experimental area and larger values in the lower right part. An inverse relationship was instead observed between yield and PAWCe. These results confirm the significant overall correlations already reported between yield and BD and PAWCe (Figure 4). TOC varied in a quite narrow range, apart from a few outliers, and the highest values were observed in the upper central part of the area. As expected, SSI map resembled TOC spatial behavior; at the same time, SSI brought the information related to the fine texture component (Cl + Si), showing as a consequence spatial similarity with the mentioned physical indicators maps.
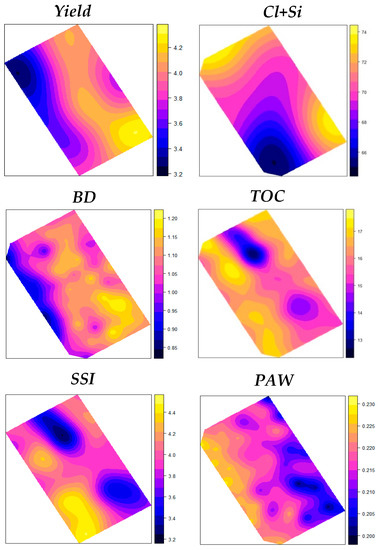
Figure 5.
Spatial estimates of wheat yield (t ha−1), clay and silt content Cl + Si (%), dry bulk density, BD (g cm−3), soil total organic carbon, TOC (g kg−1), structure stability index, SSI (%) and plant available water capacity, PAWCe (cm3 cm−3).
To further deepen the SSI behavior observed, cross-correlograms were computed and cross-correlation coefficients at specific lags (0 m, 25 m, 50 m, 75 m, 100 m) were extracted (Table 5). SSI was strongly correlated with TOC and fine texture components, positively and negatively respectively, up to about 25 m distance for TOC and up to 50 m for Cl + Si. In addition, a moderate correlation was observed with PAWCe (positive) and BD (negative) up to 25 m, indicating the contribution of texture in driving this relationship. A weak correlation was observed between SSI and yield at lag 0, confirming that the behavior arose by the Pearson’s overall correlation analysis (Figure 4). Finally, the cross-correlation between SSI and RFCe was negligible, as expected.

Table 5.
Cross-correlation coefficients computed at different lags between SSI and other indicators maps.
By considering the role of BD as key soil indicator, cross-correlograms between the maps of BD and the other indicators were also computed (Table 6). Strong negative correlations were observed with PAWCe up to about a 50 m distance. Moderate positive correlations were found with RFCe (up to 50 m) and yield (up to 25 m), whereas negative with TOC and SSI, as already observed, up to 25 m distance.

Table 6.
Cross-correlation coefficients computed at different lags between BD and other indicators maps.
4. Discussion
Overall, the observed correlations showed physically plausible relationships among soil properties (Figure 4). In particular, inverse relationships between ACe, TOC, SSI and BD were detected, as well as between ACe, Ks and RFCe. As expected, Ks was positively correlated with ACe, as increasing values of soil aeration should match with increasing saturated hydraulic conductivity (Ks); a reasonable positive relationship between Cl + Si fraction and Ks was also detected. Expected correlations have been verified between SSI and TOC (positive) or between SSI and Cl + Si (negative), since TOC and Cl + Si terms appear, respectively, in the numerator and in the denominator of Pieri’s equation [6]. However, uncertain results were obtained for the significant correlations of PAWCe, because indirect relationships between PAWCe and Cl + Si, as well as BD, were detected. In fact, although the latter was quite verified in the literature for medium-high BD values [6,57,58], the former relationship does not seem entirely plausible because higher PAWCe values should correspond to higher contents of fine particles of the soil. A similar explanation can also be given for the relationship (both general and spatial) between PAWCe and crop yield.
Agronomic results of this investigation showed medium-high wheat yields on average (Table 1). However, according with the hypothesis that good conditions of soil physical quality should correspond to good yields [3,59], findings showed non optimal soil conditions in terms of TOC, SSI, and RFCe (Figure 3), i.e., in 43% of cases, and some considerations are due, particularly for optimal TOC ranges. For instance, the suggested lower critical TOC limits for agricultural soils (i.e., about 20 g kg−1) by Reynolds et al. [6] were obtained for urban soils, namely for sustainable establishment of plants in constructed landscaping soils used in urban parks, playing fields, curbside plantings, etc. [6,60]. Despite this critical threshold being applied in the literature e.g., [46,61,62], different limits should be considered for agricultural soils, and specifically for crops grown in Mediterranean environments. For example, TOC mean values observed in this investigation (i.e., about 16 g kg−1) were relatively high as compared to those reported in Table 1 by Ventrella et al. [63], for eight experimental farms and soils with different texture, located from north to south of Italy (5.2 ≤ TOC ≤ 15.3 g kg−1). In addition, in other investigations where a variety of plant species was considered, optimal TOC levels, as suggested in the literature (i.e., 30 < TOC < 50 g kg−1), were seldom reached. For instance, for approximately two-hundred soil cores collected in three areas and 18 spot sites of agricultural and forest Sicilian environments, Castellini and Iovino ([14]; Table 2) reported TOC values equal to 10.8 g kg−1 on average (0.9–37 g kg−1 as a measured interval). To provide more concrete examples, Table 7 summarizes other results of some investigations carried out in the Mediterranean environments of Apulia, Sicily and Sardinia (south-central Italy). With reference to such investigations, listed TOC values were equal, at most, to 16.7 g kg−1 for conservation soil management of durum wheat, equal to 22.6 g kg−1 for a citrus groove or slightly higher for a grassland, suggesting that it is not common to find considerably higher TOC levels in Mediterranean agricultural environments. On the other hand, TOC values close to the upper limit suggested by Reynolds et al. [6], 50 g kg−1, were only detected for a sandy loam soil under high maquis (holm oak), i.e., when organic matter accumulation and probably slow organic matter mineralization rate can lead to such high levels (Table 7). As an example, Figure 3 shows how the TOC classification by Sequi and Nobili [44], specifically referred to fine textured soils (clay, clay–loam, silty–clay and silty–clay–loam), is more suitable for the specific characteristics of Mediterranean agricultural soils. As a consequence, more accurate optimal or critical values should be provided for specific agro-environments, for example performing ad-hoc new research or by reviewing the available literature (e.g., through meta-analysis). Similar considerations can be made for SSI, as it is obtained from TOC and texture, and is not related directly to the soil structure, but is rather related to the soil resilience [6]. On the contrary, RFCe limits may be considered relatively more reliable as they were successfully verified in reference to other soil physical properties (i.e., BD, TOC, ACe, macroporosity) by Reynolds et al. [64] for a clay loam soil, as well as in comparison with literature guidelines.

Table 7.
Mean values of soil total organic carbon contents (TOC) measured for different types of vegetation, Mediterranean agro-environments and management, and soils textural classes (USDA classification).
Among those investigated, only five soil physical properties were found spatially structured, i.e., Cl + Si, BD, TOC, SSI and PAWCe, but their relationships with grain yield did not appear to be always convincing (Figure 5). In detail, in comparison to the yield map (i.e., lower or higher yielding zones), relatively coherent spatial distributions were identified in terms of fine soil texture components (Cl + Si) and BD; this suggests that, especially bulk density, can represent a reliable physical indicator to manage within-field sub-areas with different productivity. For this soil indicator, the map also shows that the sub-areas with relatively lower productivity correspond to those with very low BD values (as specified by the critical lower value of 0.9 g cm−3 of Figure 3), suggesting that this limit seems quite realistic for the case under study. On the contrary, conflicting information between yield and PAWCe maps were obtained (i.e., an inverse spatial structure), as already shown by the overall correlation. These results can be attributed to uncertainties of the PAWCe estimates obtained by BEST which would require further deepening. As expected, a relatively similar spatial distribution was observed for TOC and SSI, but not consistent with that of crop yield. In other words, findings provided by variables directly measured, both for overall correlation and for spatial analysis, were more convincing than those derived by variables estimated by BEST, for which further investigations are probably needed to quantify the accuracy degree of estimated soil water retention curve.
To deepen the aforementioned results and corroborate the relationships between yield and considered soil properties, a stepwise analysis was carried out to identify the variables most affecting wheat yield among those directly quantified (TOC, BD, fine textural components) or derived from laboratory measurements (SSI). Results of stepwise analysis showed that BD was the only variable selected (P = 0.0054), thus confirming the key role of soil porosity and compaction in affecting crop yield. Consequently, for investigated soil variables, only the BD map seems utilisable for agronomic management, i.e., for precision agriculture applications, because several factors may have contributed to produce unexpected or uncertain results for the other variables. Among these factors, particular relevance can be attributed to: (i) the uncertainties of the PAWCe estimates obtained by BEST; (ii) the relatively poor correspondence between observed physical–chemical fertility of the soil and agricultural yields in the specific conditions investigated; (iii) a possible spatial variability at a scale smaller than that experimentally measured (i.e., lower than about the mesh side). About the last statement, as Ks showed no significant spatial structure, we could make a plausible conjecture suggesting that spatial variability of Ks occurred at a smaller scale than that investigated [67]. However, no significant relationship between Ks and crop yield (or BD) was detected. Overall, Ks is reported to be a better soil structure indicator [68] than BD, as the latter does not provide any information on soil pore distribution, i.e., architecture, connectivity and tortuosity of soil porosity [3]. In our case study, a very good spatial correspondence between crop yield and soil bulk density was detected, and the cross-correlation analysis also showed a significant positive relationship with the crop yield for the lower distance, of about 25 m. Although this result could be considered questionable from the perspective of precision agriculture application (i.e., for implementation on platforms with on-the-go soil sensors), it is quite significant as BD measurements can be obtained more easily if compared to Ks, and it can be easily related to penetrometric soil measurements.
As a final remark, it should be noticed that SSI showed promising characteristics to be used as a representative indicator to identify homogeneous within-field areas, because of its tight relationships with chemical (TOC) and hydrological (fine texture components, and in turn PAWCe and BD) indicators and its predisposition to spatialization, thus suggesting a possible significant correlation with yield under a denser spatial sampling scheme. If this were the case, SSI would candidate itself as a key indicator for precision agriculture applications.
5. Conclusions
In this investigation a set of eight physical and hydraulic soil properties directly measured or estimated by BEST was obtained and spatialized to investigate correlations and identify intervals corresponding to medium-high levels of wheat yields, in order to provide useful information for site-specific agronomic management.
According to the guidelines of literature, a soil physical quality evaluation highlighted that soil under study had optimal bulk density, plant available water capacity, air capacity and saturated hydraulic conductivity values, but that the total organic carbon content, structure stability index and relative field capacity suggested too low levels of organic carbon or excessive soil compaction. However, both a literature analysis for different types of Mediterranean vegetation cover and the correlation analysis (overall and spatial correlation) suggested that a review of the optimal or critical TOC values for typical crops of Mediterranean environments should be made, as TOC value around 20 g kg−1 is hardly achievable even under conservation agriculture systems, and literature values are probably not entirely realistic for Southern Italy’s cereal crops. In addition, capacitive indicators estimated from the soil water retention curve of BEST provided both expected and uncertain correlations, especially with regard to the inverse relationship between plant available water capacity and wheat yield. Therefore, for the soil–crop system studied, application of the simplified BEST-procedure did not return completely reliable results and further investigations are needed to quantify the accuracy and reliability of estimated soil water retention curve. These main results open up new research perspectives to improve our knowledge on this topic.
Among measured soil properties, BD showed a spatial distribution in agreement with that detected for crop yield, and the cross-correlation analysis also showed a significant positive relationship only for short lags. Finally, SSI showed promising characteristics suggesting a possible significant correlation with yield under a denser spatial sampling scheme, and a potentiality as a key indicator for precision agriculture applications.
Further research on this topic is needed for Mediterranean agro-environments, by deepening: (i) the reliability of available measurement methods for accurately estimating representative physical and hydraulic soil properties, and (ii) the temporal stability of observed spatial relationships between soil properties (soil bulk density or soil texture) and crop yields along a larger time interval.
Author Contributions
M.C. outlined the investigation. M.T., A.M.S. and E.B. have carried out data analysis. All authors contributed to critically discuss the results, to write and review the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Alessandro Vittorio Vonella for his valuable support in the field measurements.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bagarello, V.; Baiamonte, G.; Castellini, M.; Di Prima, S.; Iovino, M. A comparison between the single ring pressure infiltrometer and simplified falling head techniques. Hydrol. Process. 2014, 28, 4843–4853. [Google Scholar] [CrossRef]
- Alletto, L.; Coquet, Y. Temporal and spatial variability of soil bulk density and near-saturated hydraulic conductivity under two contrasted tillage management systems. Geoderma 2009, 152, 85–94. [Google Scholar] [CrossRef]
- Keller, T.; Stutter, J.A.; Nissen, K.; Rydberg, T. Using field measurement of saturated soil hydraulic conductivity to detect low-yielding zones in three Swedish fields. Soil Tillage Res. 2012, 124, 68–77. [Google Scholar] [CrossRef]
- Pinheiro, E.A.R.; de Jong van Lier, Q.; Šimůnek, J. The role of soil hydraulic properties in crop water use efficiency: A process-based analysis for some Brazilian scenarios. Agric. Syst. 2019, 173, 364–377. [Google Scholar] [CrossRef]
- Ventrella, D.; Charfeddine, M.; Giglio, L.; Castellini, M. Application of DSSAT models for an agronomic adaptation strategy under climate change in Southern Italy: Optimum sowing and transplanting time for winter durum wheat and tomato. Ital. J. Agron. 2012, 7, 109–115. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Drury, C.F.; Tan, C.S.; Fox, C.A.; Yang, X.M. Use of indicators and pore volume-function characteristics to quantify soil physical quality. Geoderma 2009, 152, 252–263. [Google Scholar] [CrossRef]
- Castellini, M.; Stellacci, A.M.; Barca, E.; Iovino, M. Application of multivariate analysis techniques for selecting soil physical quality indicators: A case study in long-term field experiments in Apulia (southern Italy). Soil Sci. Soc. Am. J. 2019, 83, 707–720. [Google Scholar] [CrossRef]
- Castellini, M.; Fornaro, F.; Garofalo, P.; Giglio, L.; Rinaldi, M.; Ventrella, D.; Vitti, C.; Vonella, A.V. Effects of No-Tillage and Conventional Tillage on Physical and Hydraulic Properties of Fine Textured Soils under Winter Wheat. Water 2019, 11, 484. [Google Scholar] [CrossRef]
- Bagarello, V.; Iovino, M.; Elrick, D. A simplified falling-head technique for rapid determination of field-saturated hydraulic conductivity. Soil Sci. Soc. Am. J. 2004, 68, 66–73. [Google Scholar] [CrossRef]
- Blackmore, S.; Godwin, R.J.; Fountas, S. The analysis of spatial and temporal trends in yield map data over six years. Biosyst. Eng. 2003, 84, 455–466. [Google Scholar] [CrossRef]
- Hakojärvi, M.; Hautala, M.; Ristolainen, A.; Alakukku, L. Yield variation of spring cereals in relation to selected soil physical properties in three clay soil fields. Eur. J. Argon. 2013, 49, 1–11. [Google Scholar] [CrossRef]
- Garofalo, P.; Ventrella, D.; Kersebaum, K.C.; Gobin, A.; Trnka, M.; Giglio, L.; Dubrovský, M.; Castellini, M. Water footprint of winter wheat under climate change: Trends and uncertainties associated to the ensemble of crop models. Sci. Total Environ. 2019, 658, 1186–1208. [Google Scholar] [CrossRef]
- Fernández-Gálvez, J.; Pollacco, J.A.P.; Lassabatere, L.; Angulo-Jaramillo, R.; Carrick, S. A general Beerkan Estimation of Soil Transfer parameters method predicting hydraulic parameters of any unimodal water retention and hydraulic conductivity curves: Application to the Kosugi soil hydraulic model without using particle size distribution data. Adv. Water Resour. 2019, 129, 118–130. [Google Scholar] [CrossRef]
- Castellini, M.; Iovino, M. Pedotransfer functions for estimating soil water retention curve of Sicilian soils. Arch. Agron. Soil Sci. 2019, 65, 1401–1416. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, J.; Wendroth, O.; Matocha, C.; Edwards, D. Effect of Macroporosity on Pedotransfer Function Estimates at the Field Scale. Vadose Zone J. 2019, 18, 180151. [Google Scholar] [CrossRef]
- Burke, W.; Gabriels, D.; Bouma, J. Soil Structure Assessment; Balkema: Rotterdam, The Netherlands, 1986. [Google Scholar]
- Dane, J.H.; Hopmans, J.W. Water retention and storage: Laboratory. In Methods of Soil Analysis, Part 4, Physical Methods; Dane, J.H., Topp, G.C., Eds.; SSSA: Madison, WI, USA, 2002; pp. 688–692. [Google Scholar]
- Wind, G.P. Capillary conductivity data estimated by a simple method. In Water in the Unsaturated Zone: Proceedings of Wageningen Syposium, June 1966; Rijtema, P.E., Wassink, H., Eds.; IASAH: Gentbrugge, Belgium, 1968; Volume 1, pp. 181–191. [Google Scholar]
- Hosseini, S.M.M.M.; Ganjian, N.; Pisheh, Y.P. Estimation of the water retention curve for unsaturated clay. Can. J. Soil Sci. 2011, 91, 543–549. [Google Scholar] [CrossRef]
- Rustanto, A.; Booij, M.J.; Wösten, H.; Hoekstra, A.Y. Application and recalibration of soil water retention pedotransfer functions in a tropical upstream catchment: Case study in Bengawan Solo, Indonesia. J. Hydrol. Hydromech. 2017, 65, 307–320. [Google Scholar] [CrossRef]
- Lozano-Baez, S.E.; Cooper, M.; Ferraz, S.F.B.; Ribeiro Rodrigues, R.; Pirastru, M.; Di Prima, S. Previous land use affects the recovery of soil hydraulic properties after forest restoration. Water 2018, 10, 453. [Google Scholar] [CrossRef]
- Di Prima, S.; Castellini, M.; Abou Najm, M.R.; Stewart, R.D.; Angulo-Jaramillo, R.; Winiarski, T.; Lassabatere, L. Experimental Assessment of a New Comprehensive Model for Single Ring Infiltration Data. J. Hydrol. 2019, 573, 937–951. [Google Scholar] [CrossRef]
- Lassabatère, L.; Angulo-Jaramillo, R.; Ugalde, J.M.S.; Cuenca, R.; Braud, I.; Haverkamp, R. Beerkan estimation of soil transfer parameters through infiltration experiments: BEST. Soil Sci. Soc. Am. J. 2006, 70, 521–532. [Google Scholar] [CrossRef]
- Bagarello, V.; Castellini, M.; Di Prima, S.; Iovino, M. Soil hydraulic properties determined by infiltration experiments and different heights of water pouring. Geoderma 2014, 213, 492–501. [Google Scholar] [CrossRef]
- Alagna, V.; Bagarello, V.; Di Prima, S.; Guaitoli, F.; Iovino, M.; Keesstra, S.; Cerdà, A. Using Beerkan experiments to estimate hydraulic conductivity of a crusted loamy soil in a Mediterranean vineyard. J. Hydrol. Hydromech. 2019, 67, 191–200. [Google Scholar] [CrossRef]
- Di Prima, S.; Rodrigo-Comino, J.; Novara, A.; Iovino, M.; Pirastru, M.; Keesstra, S.; Cerda, A. Assessing soil physical quality of citrus orchards under tillage, herbicide and organic managements. Pedosphere 2018, 28, 463–477. [Google Scholar] [CrossRef]
- Castellini, M.; Iovino, M.; Pirastru, M.; Niedda, M.; Bagarello, V. Use of BEST procedure to assess soil physical quality in the Baratz Lake catchment (Sardinia, Italy). Soil Sci. Soc. Am. J. 2016, 80, 742–755. [Google Scholar] [CrossRef]
- Khaledian, M.R.; Shabanpour, M.; Alinia, H. Saturated hydraulic conductivity variation in a small garden under drip irrigation. Geosyst. Eng. 2016, 19, 266–274. [Google Scholar] [CrossRef]
- Mubarak, I.; Angulo-Jaramillo, R.; Mailhol, J.C.; Ruelle, P.; Khaledian, M.; Vauclin, M. Spatial analysis of soil surface hydraulic properties: Is infiltration method dependent? Agric. Water Manag. 2010, 97, 1517–1526. [Google Scholar] [CrossRef]
- Lassabatère, L.; Di Prima, S.; Angulo-Jaramillo, R.; Keesstra, S.; Salesa, D. Beerkan multi-runs for characterizing water infiltration and spatial variability of soil hydraulic properties across scales. Hydrol. Sci. J. 2019. [Google Scholar] [CrossRef]
- Cavallo, G.; De Benedetto, D.; Castrignanò, A.; Quarto, R.; Vonella, A.V.; Buttafuoco, G. Use of geophysical data for assessing 3D soil variation in a durum wheat field and their association with crop yield. Biosyst. Eng. 2016, 152, 28–40. [Google Scholar] [CrossRef]
- De Benedetto, D.; Castrignanò, A.; Rinaldi, M.; Ruggieri, S.; Santoro, F.; Figorito, B.; Gualano, S.; Diacono, M.; Tamborrino, R. An approach for delineating homogeneous zones by using multi-sensor data. Geoderma 2013, 199, 117–127. [Google Scholar] [CrossRef]
- Barca, E.; De Benedetto, D.; Stellacci, A.M. Contribution of EMI and GPR proximal sensing data in soil water content assessment by using linear mixed effects models and geostatistical approaches. Geoderma 2019, 343, 280–293. [Google Scholar] [CrossRef]
- Ventrella, D.; Stellacci, A.M.; Castrignanò, A.; Charfeddine, M.; Castellini, M. Effects of crop residue management on winter durum wheat productivity in a long term experiment in Southern Italy. Eur. J. Agron. 2016, 77, 188–198. [Google Scholar] [CrossRef]
- Campi, P.; Mastrorilli, M.; Stellacci, A.M.; Modugno, F.; Palumbo, A.D. Increasing the effective use of water in green asparagus through deficit irrigation strategies. Agric. Water Manag. 2019, 217, 119–130. [Google Scholar] [CrossRef]
- Myers, D.E. Interpolation and estimation with spatially located data. Chemom. Intell. Lab. Syst. 1991, 11, 209–228. [Google Scholar] [CrossRef]
- Bagarello, V.; Di Prima, S.; Iovino, M. Comparing alternative algorithms to analyze the Beerkan infiltration experiment. Soil Sci. Soc. Am. J. 2014, 78, 724–736. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J. Particle-size Analysis, In Methods of Soil Analysis, Part 1, 2nd ed.; American Society of Agronomy/Soil Science Society of America: Madison, WI, USA, 1986. [Google Scholar]
- Vitti, C.; Stellacci, A.M.; Leogrande, R.; Mastrangelo, M.; Cazzato, E.; Ventrella, D. Assessment of organic carbon in soils: A comparison between the Springer–Klee wet digestion and the dry combustion methods in Mediterranean soils (Southern Italy). Catena 2016, 137, 113–119. [Google Scholar] [CrossRef]
- Castellini, M.; Di Prima, S.; Iovino, M. An assessment of the BEST procedure to estimate the soil water retention curve: A comparison with the evaporation method. Geoderma 2018, 320, 82–94. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Drury, C.F.; Yang, X.M.; Fox, C.A.; Tan, C.S.; Zhang, T.Q. Land management effects on the near-surface physical quality of a clay loam soil. Soil Tillage Res. 2007, 96, 316–330. [Google Scholar] [CrossRef]
- Dexter, A.R. Soil physical quality. Part I. Theory, effects of soil texture, density, and organic matter, and effects on root growth. Geoderma 2004, 120, 201–214. [Google Scholar] [CrossRef]
- Pieri, C.J.M.G. Fertility of soils: A Future for Farming in the West African Savannah. In Fertility of Soils: A Future for Farming in the West African Savannah; Springer: Berlin, Germany, 1992; p. 558. [Google Scholar]
- Sequi, P.; De Nobili, M., VII. Carbonio organico. In Metodi di Analisi Chimica del Suolo. Ministero per le Politiche Agricole e Forestali, Osservatorio Nazionale Pedologico e per la Qualità del Suolo; Violante, P., Ed.; Franco Angeli Editore: Milano, Italy, 2000. [Google Scholar]
- Castellini, M.; Pirastru, M.; Niedda, M.; Ventrella, D. Comparing physical quality of tilled and no-tilled soils in an almond orchard in southern Italy. Ital. J. Agron. 2013, 8, 149–157. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Drury, C.F.; Yang, X.M.; Tan, C.S.; Yang, J.Y. Impacts of 48 years of consistent cropping, fertilization and land management on the physical quality of a clay loam soil. Can. J. Soil Sci. 2014, 94, 403–419. [Google Scholar] [CrossRef]
- Barca, E.; Bruno, E.; Bruno, D.E.; Passarella, G. GTest: A software tool for graphical assessment of empirical distributions’ Gaussianity. Environ. Monit. Assess. 2016, 188, 138. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Rura, M.J.; Griffith, D.A. Spatial Statistics in SAS. In Handbook of Applied Spatial Analysis; Fischer, M., Getis, A., Eds.; Springer: Berlin/Heidelberg, 2010. [Google Scholar]
- Barca, E.; Porcu, E.; Bruno, D.; Passarella, G. An automated decision support system for aided assessment of variogram models. Environ. Model. Softw. 2017, 87, 72–83. [Google Scholar] [CrossRef]
- Ribeiro, P.J., Jr.; Diggle, P.J. geoR: A package for geostatistical analysis. R News 2001, 1/2, 14–18. [Google Scholar]
- Vieira, S.R.; Hatfield, T.L.; Nielsen, D.R.; Biggar, J.W. Geostatistical theory and application to variability of some agronomical properties. Hilgardia Berkeley. 1983, 51, 1–75. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University press: New York, NY, USA, 1989. [Google Scholar]
- Stein, A.; Brouwer, J.; Bouma, J. Methods for comparing spatial variability patterns of millet yield and soil data. Soil Sci. Soc. Am. J. 1997, 61, 861–870. [Google Scholar] [CrossRef]
- Barca, E.; Passarella, G. Spatial evaluation of the risk of groundwater quality degradation. A comparison between disjunctive kriging and geostatistical simulation. Environ. Monit. Assess. 2008, 137, 261–273. [Google Scholar] [CrossRef]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iova soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Hoshino, A.; Tamura, K.; Fujimaki, H.; Asano, M.; Ose, K.; Higashi, T. Effects of crop abandonment and grazing exclusion on available soil water and other soil properties in a semi-arid Mongolian grassland. Soil Tillage Res. 2009, 105, 228–235. [Google Scholar] [CrossRef]
- Iovino, M.; Castellini, M.; Bagarello, V.; Giordano, G. Using static and dynamic indicators to evaluate soil physical quality in a Sicilian area. Land Degrad. Dev. 2016, 27, 200–210. [Google Scholar] [CrossRef]
- Topp, G.C.; Reynolds, W.D.; Cook, F.J.; Kirby, J.M.; Carter, M.R. Physical attributes of soil quality. In Soil Quality for Crop Production and EcosystemHealth; Developments in Soil Science, volume 25; Gregorich, E.G., Carter, M.R., Eds.; Elsevier: New York, NY, USA, 1997; pp. 21–58. [Google Scholar]
- Reynolds, W.D.; Yang, X.M.; Drury, C.F.; Zhang, T.Q.; Tan, C.S. Effects of selected conditioners and tillage on the physical quality of a clay loam soil. Can. J. Soil Sci. 2003, 83, 318–393. [Google Scholar] [CrossRef]
- Agnese, C.; Bagarello, V.; Baiamonte, G.; Iovino, M. Comparing physical quality of forest and pasture soils in a Sicilian Watershed. Soil Sci. Soc. Am. J. 2011, 75, 1958. [Google Scholar] [CrossRef]
- Cullotta, S.; Bagarello, V.; Baiamonte, G.; Gugliuzza, G.; Iovino, M.; La Mela Veca, D.S.; Maetzke, F.; Palmeri, V.; Sferlazza, S. Comparing Different Methods to Determine Soil Physical Quality in a Mediterranean Forest and Pasture Land. Soil Sci. Soc. Am. J. 2016, 80, 1038–1056. [Google Scholar] [CrossRef]
- Ventrella, D.; Virzì, N.; Intrigliolo, F.; Palumbo, M.; Cambrea, M.; Platania, A.; Sciacca, F.; Licciardello, S.; Troccoli, A.; Russo, M.; et al. Environmental effectiveness of GAECcross-compliance standard 2.1 ‘Maintaining the level of soil organic matter through management of stubble and crop residues’ and economic evaluation of the competitiveness gap for farmers. Ital. J. Agron. 2015, 10, 697. [Google Scholar]
- Reynolds, W.D.; Drury, C.F.; Yang, X.M.; Tan, C.S. Optimal soil physical quality inferred through structural regression and parameter interactions. Geoderma 2008, 146, 466–474. [Google Scholar] [CrossRef]
- Castellini, M.; Niedda, M.; Pirastru, M.; Ventrella, D. Temporal changes of soil physical quality under two residue management systems. Soil Use Manag. 2014, 30, 423–434. [Google Scholar] [CrossRef]
- Ferrara, R.M.; Mazza, G.; Muschitiello, C.; Castellini, M.; Stellacci, A.M.; Navarro, A.; Lagomarsino, A.; Vitti, C.; Rossi, R.; Rana, G. Short-term effects of conversion to no-tillage on respiration and chemical-physical properties of the soil: A case study in a wheat cropping system in semi-dry environment. Ital. J. Agrometeorol. 2017, 1, 47–58. [Google Scholar]
- Bagarello, V.; Di Stefano, C.; Ferro, V.; Iovino, M.; Sgroi, A. Physical and hydraulic characterization of a clay soil at the plot scale. J. Hydrol. 2010, 387, 54–64. [Google Scholar] [CrossRef]
- Dexter, A.R. Advances in characterization of soil structure. Soil Tillage Res. 1988, 11, 199–238. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).