Identifying Climate and Human Impact Trends in Streamflow: A Case Study in Uruguay
Abstract
1. Introduction
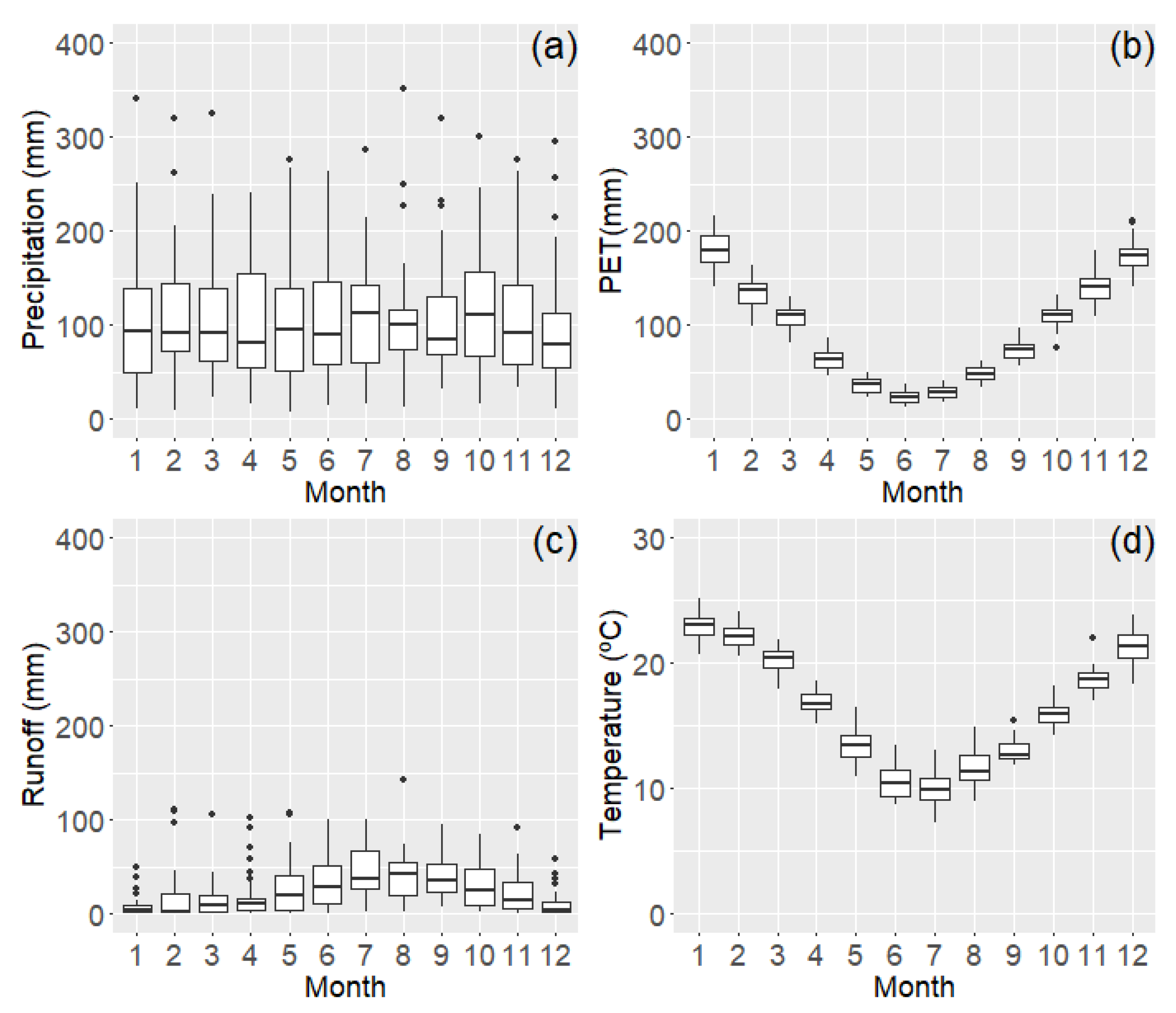
2. Study Area and Dataset
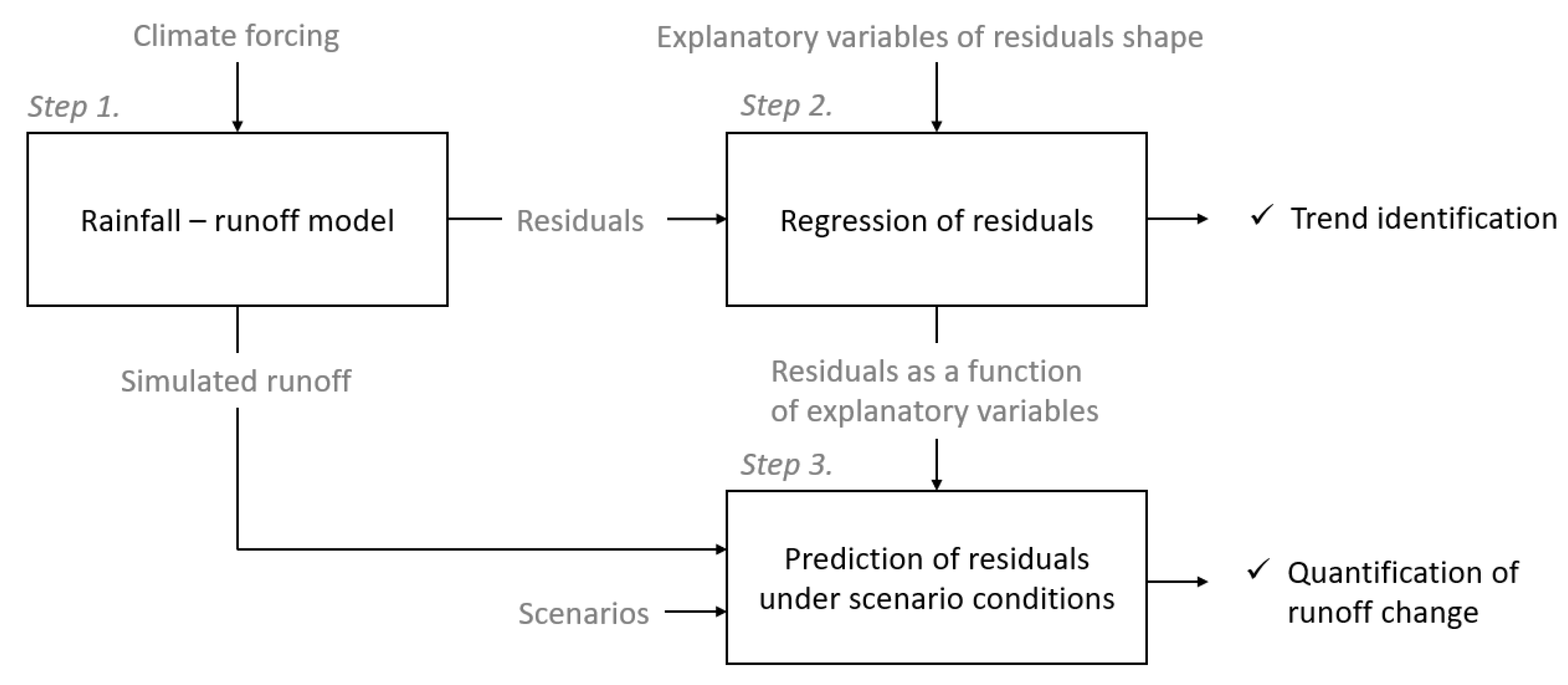
3. Methodology
3.1. Rainfall-Runoff Simulation
3.2. Trend Simulation of Runoff Residuals
3.3. Quantifying the Effect of Land Use Change and Water Licenses on Streamflow
4. Results
4.1. Rainfall-Runoff Model Performance
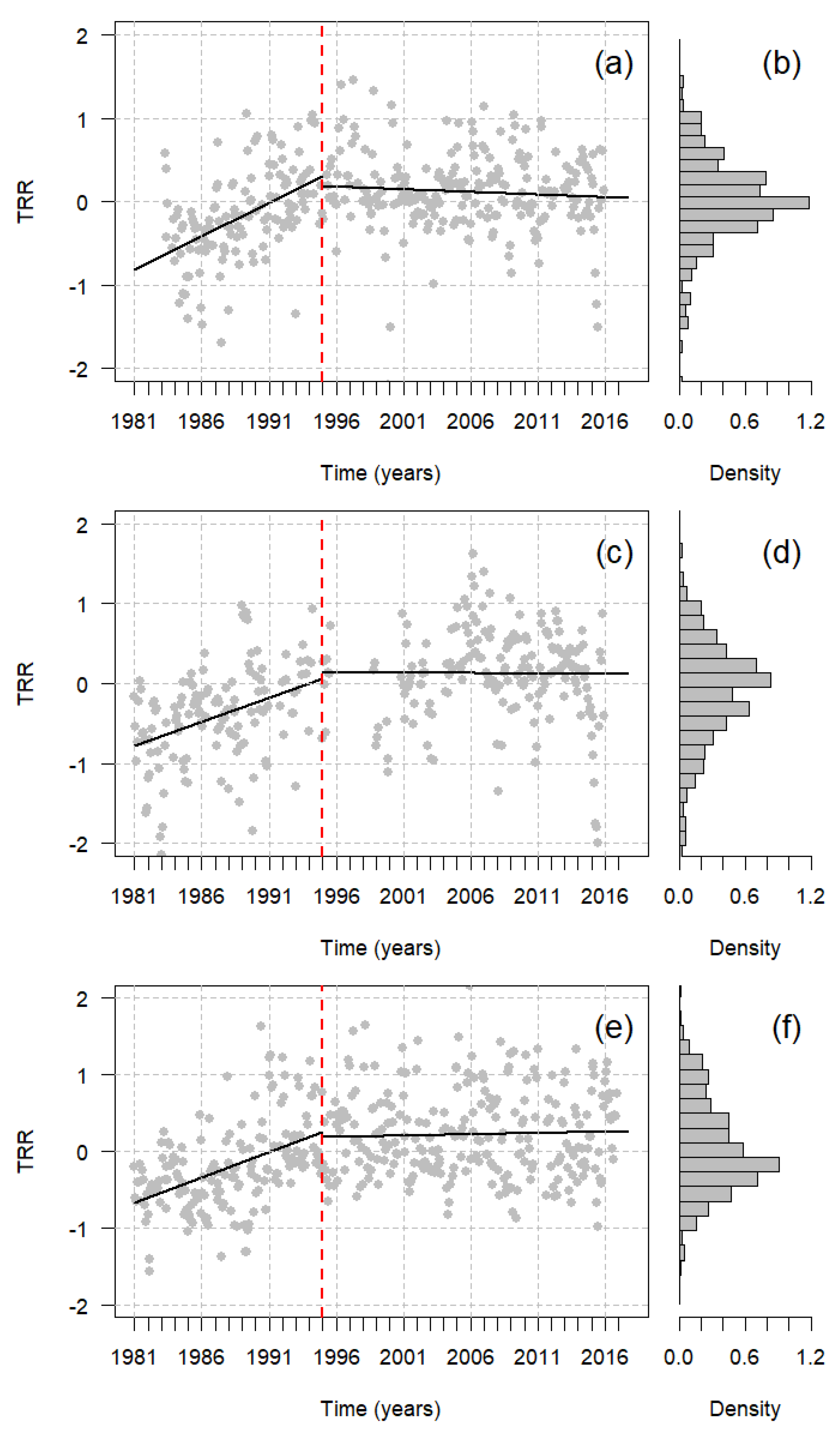
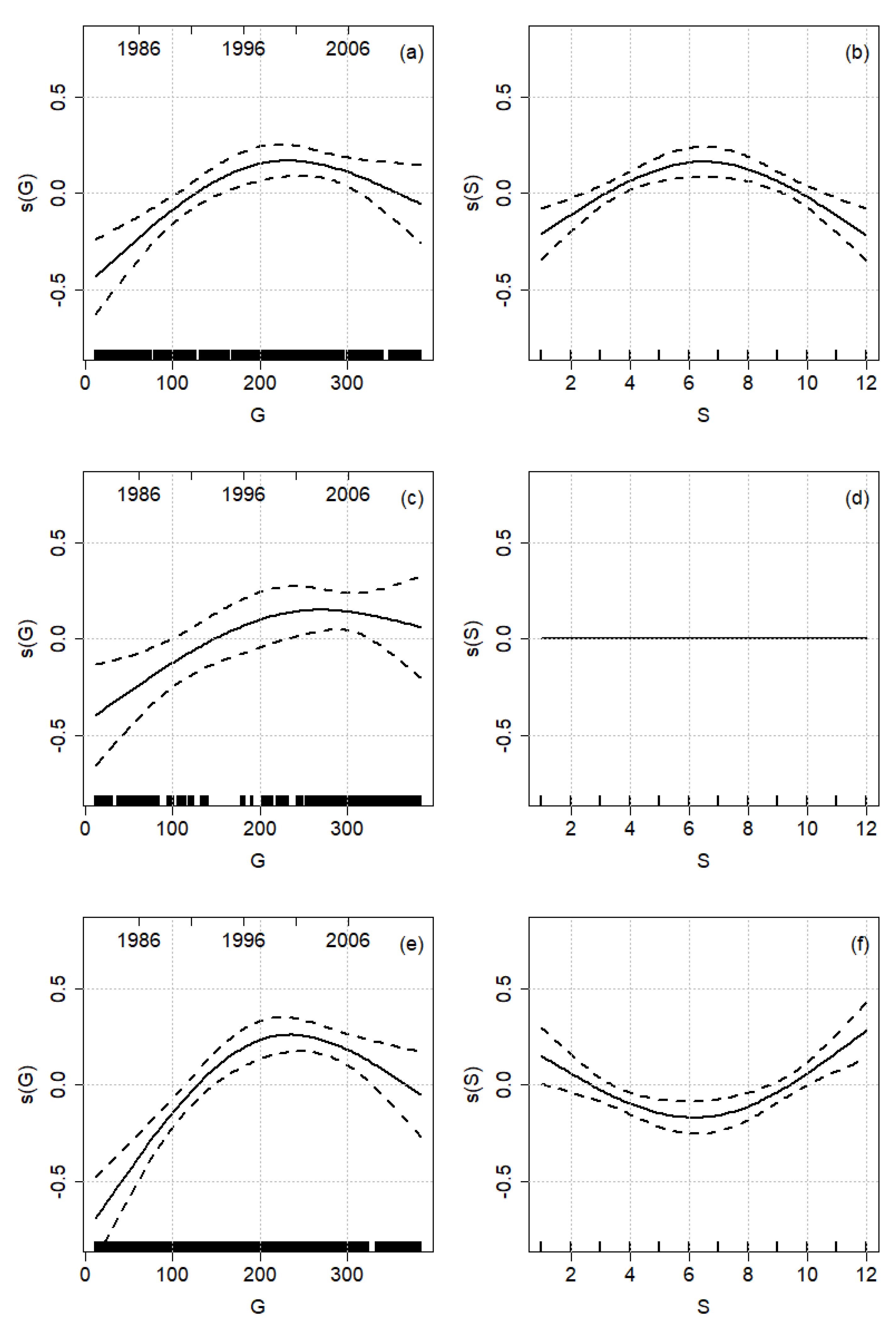
4.2. GAMM Analysis of Runoff Residuals
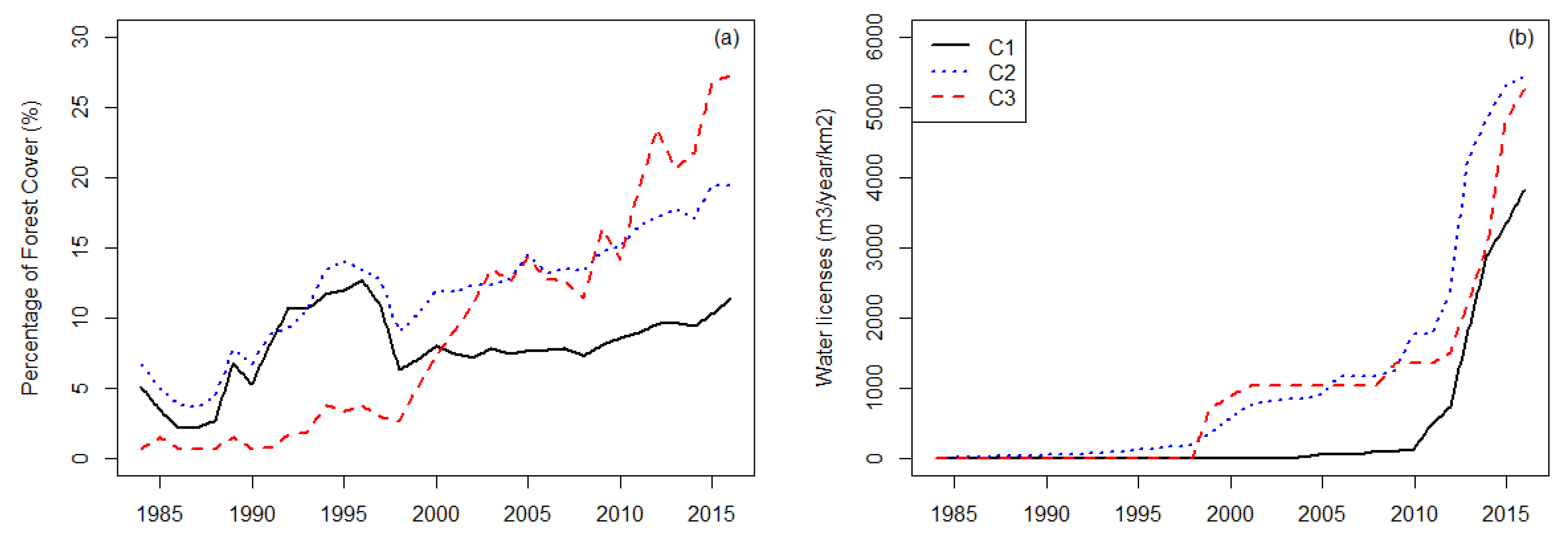
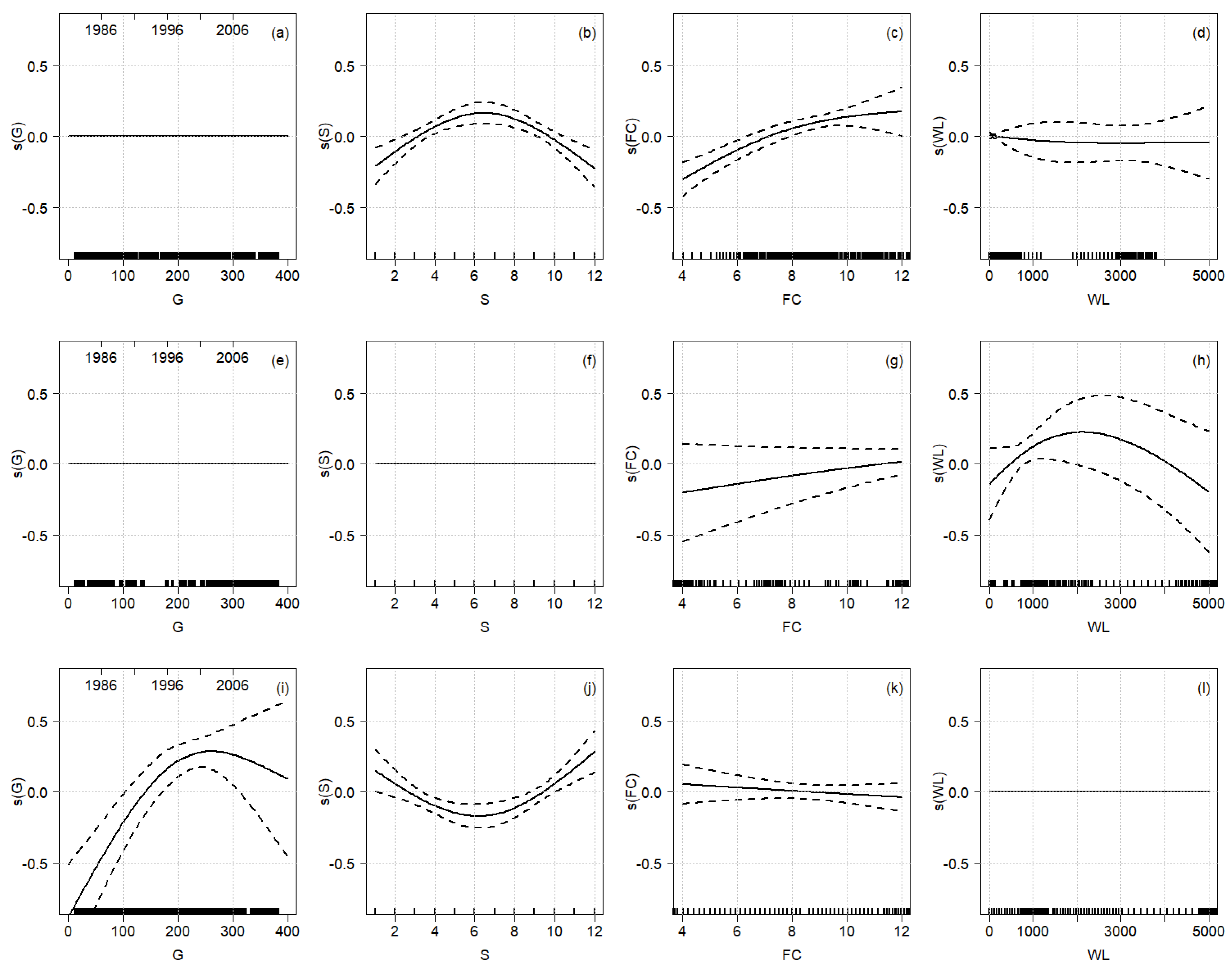
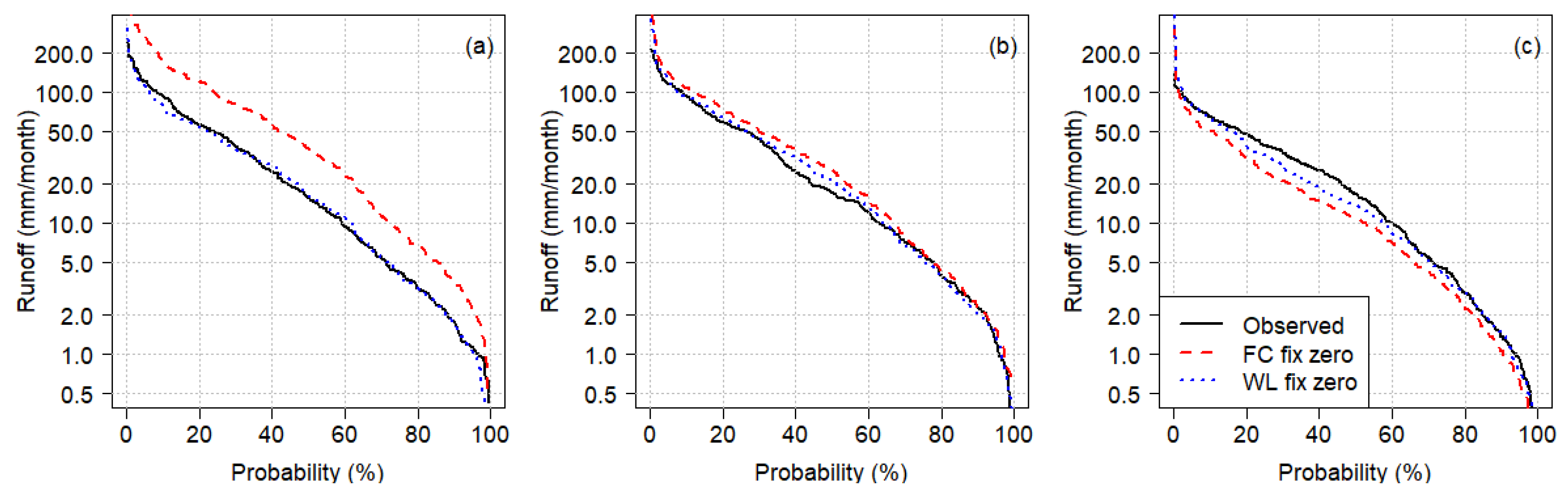
4.3. Effect of Land Use Change and Water Licenses on Streamflow
5. Discussion
5.1. Seasonal and Global Trends in the Observed Runoff (Aim 1)
5.2. Identifying the Effect of Exogenous Trends (Forest Cover and Water License, Aim 2)
5.3. Further Considerations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gleick, P.H. Global Freshwater Resources: Soft-Path Solutions for the 21st Century. Science 2003, 302, 1524–1528. [Google Scholar] [CrossRef] [PubMed]
- Aparicio, J.; Lafragua, J.; Lopez, A.; Mejia, R.; Aguilar, E.; Mejía, M. Water Resources Assessment: Integral Water Balance in Basins, phi-vii ed.; Number 14 in Technical Document; UNESCO Office Montevideo and Regional Bureau for Science in Latin America and the Caribbean: Montevideo, Uruguay, 2008. [Google Scholar]
- Hölzel, H.; Diekkrüger, B. Predicting the impact of linear landscape elements on surface runoff, soil erosion, and sedimentation in the Wahnbach catchment, Germany. Hydrol. Process. 2012, 26, 1642–1654. [Google Scholar] [CrossRef]
- Ren, L.; Wang, M.; Li, C.; Zhang, W. Impacts of human activity on river runoff in the northern area of China. J. Hydrol. 2002, 261, 204–217. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, L.; Zhang, X.; Cheng, L.; Potter, N.; Cowan, T.; Cai, W. Long-term streamflow trends in the middle reaches of the Yellow River Basin: Detecting drivers of change: Streamflow Trends in the Middle Reach of the Yellow River Basin. Hydrol. Process. 2016, 30, 1315–1329. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, N.; Harper, R.; Li, Q.; Liu, K.; Wei, X.; Ning, D.; Hou, Y.; Liu, S. A global review on hydrological responses to forest change across multiple spatial scales: Importance of scale, climate, forest type and hydrological regime. J. Hydrol. 2017, 546, 44–59. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Si, J.; Li, C.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1112. [Google Scholar] [CrossRef]
- Mekonnen, D.F.; Duan, Z.; Rientjes, T.; Disse, M. Analysis of combined and isolated effects of land-use and land-cover changes and climate change on the upper Blue Nile River basin’s streamflow. Hydrol. Earth Syst. Sci. 2018, 22, 6187–6207. [Google Scholar] [CrossRef]
- Silveira, L.; Gamazo, P.; Alonso, J.; Martínez, L. Effects of afforestation on groundwater recharge and water budgets in the western region of Uruguay. Hydrol. Process. 2016, 30, 3596–3608. [Google Scholar] [CrossRef]
- Silveira, L.; Alonso, J. Runoff modifications due to the conversion of natural grasslands to forests in a large basin in Uruguay. Hydrol. Process. 2009, 23, 320–329. [Google Scholar] [CrossRef]
- Berri, G.J.; Ghietto, M.A.; García, N.O. The Influence of ENSO in the Flows of the Upper Paraná River of South America over the Past 100 Years. J. Hydrometeorol. 2002, 3, 57–65. [Google Scholar] [CrossRef]
- Camilloni, I.A.; Barros, V.R. Extreme discharge events in the Paraná River and their climate forcing. J. Hydrol. 2003, 278, 94–106. [Google Scholar] [CrossRef]
- Krepper, C.M.; García, N.O.; Jones, P.D. Interannual variability in the Uruguay river basin. Int. J. Climatol. 2003, 23, 103–115. [Google Scholar] [CrossRef]
- Kendall, M.G.; Gibbons, J.D. Rank Correlation Methods, 5th ed.; Arnold, E., Ed.; Oxford University Press: London, UK; New York, NY, USA, 1990. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. Appl. Stat. 1979, 28, 126. [Google Scholar] [CrossRef]
- Burn, D.H.; Hag Elnur, M.A. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Tramblay, Y.; El Adlouni, S.; Servat, E. Trends and variability in extreme precipitation indices over Maghreb countries. Nat. Hazards Earth Syst. Sci. 2013, 13, 3235–3248. [Google Scholar] [CrossRef]
- Villarini, G.; Smith, J.A.; Serinaldi, F.; Ntelekos, A.A. Analyses of seasonal and annual maximum daily discharge records for central Europe. J. Hydrol. 2011, 399, 299–312. [Google Scholar] [CrossRef]
- Zeng, S.; Xia, J.; Du, H. Separating the effects of climate change and human activities on runoff over different time scales in the Zhang River basin. Stoch. Environ. Res. Risk Assess. 2014, 28, 401–413. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Nonstationarity versus scaling in hydrology. J. Hydrol. 2006, 324, 239–254. [Google Scholar] [CrossRef]
- Simpson, G.L. Modelling palaeoecological time series using generalized additive models. bioRxiv 2018. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman & Hall/CRC Texts in Statistical Science; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wang, Q.; Liu, R.; Men, C.; Guo, L.; Miao, Y. Effects of dynamic land use inputs on improvement of SWAT model performance and uncertainty analysis of outputs. J. Hydrol. 2018, 563, 874–886. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Amoussou, E.; Tramblay, Y.; Totin, H.S.; Mahé, G.; Camberlin, P. Dynamique et modélisation des crues dans le bassin du Mono à Nangbéto (Togo/Bénin). Hydrolog. Sci. J. 2014, 59, 2060–2071. [Google Scholar] [CrossRef]
- Arnaud, P.; Lavabre, J.; Fouchier, C.; Diss, S.; Javelle, P. Sensitivity of hydrological models to uncertainty in rainfall input. Hydrolog. Sci. J. 2011, 56, 397–410. [Google Scholar] [CrossRef]
- Santos, L.; Thirel, G.; Perrin, C. Continuous state-space representation of a bucket-type rainfall-runoff model: A case study with the GR4 model using state-space GR4 (version 1.0). Geosci. Model. Dev. 2018, 11, 1591–1605. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation using gstat. RFID J. 2016, 8, 204–218. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Andrews, F.; Croke, B.; Jakeman, A. An open software environment for hydrological model assessment and development. Environ. Model. Softw. 2011, 26, 1171–1185. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Bos, M.G.; Kselik, R.; Allen, R.; Molden, D. Water Requirements for Irrigation and the Environment; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Schilling, K.E.; Jha, M.K.; Zhang, Y.K.; Gassman, P.W.; Wolter, C.F. Impact of land use and land cover change on the water balance of a large agricultural watershed: Historical effects and future directions. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Lerat, J.; Michel, C. Has land cover a significant impact on mean annual streamflow? An international assessment using 1508 catchments. J. Hydrol. 2008, 357, 303–316. [Google Scholar] [CrossRef]
- King, R.S.; Baker, M.E.; Whigham, D.F.; Weller, D.E.; Jordan, T.E.; Kazyak, P.F.; Hurd, M.K. Spatial considerations for linking watershed land cover to ecological indicators in streams. Ecol. Appl. 2005, 15, 137–153. [Google Scholar] [CrossRef]
- Guzha, A.; Rufino, M.; Okoth, S.; Jacobs, S.; Nóbrega, R. Impacts of land use and land cover change on surface runoff, discharge and low flows: Evidence from East Africa. J. Hydrol. Reg. Stud. 2018, 15, 49–67. [Google Scholar] [CrossRef]
- MGAP. Cartografía Forestal 2018; Dirección General Forestal: Montevideo, Uruguay, 2018. [Google Scholar]

| Model Id. | Equation (TRR Equal to) |
|---|---|
| L1 | |
| S1 | |
| L2 | |
| S2 | |
| L3 | |
| S3 | |
| L4 | |
| S4 |
| Daily Scale | Monthly Scale | |||||
|---|---|---|---|---|---|---|
| Catchment | NSE | BIAS | NSE | BIAS | ||
| C1 | 0.82 | −0.04 | 0.85 | 0.91 | −0.04 | 0.91 |
| C2 | 0.81 | −0.05 | 0.84 | 0.85 | −0.03 | 0.86 |
| C3 | 0.57 | −0.07 | 0.79 | 0.78 | −0.10 | 0.80 |
| Catchment | Model Id. | Intercept | G | S | FC | W | Adjusted |
|---|---|---|---|---|---|---|---|
| C1 | L1 | ** | ** | *** | ⊗ | ⊗ | 0.115 |
| S1 | *** | *** | ⊗ | ⊗ | 0.188 | ||
| L2 | *** | *** | ⊗ | 0.208 | |||
| S2 | *** | *** | ⊗ | 0.211 | |||
| L3 | *** | ** | *** | ⊗ | * | 0.144 | |
| S3 | *** | *** | ⊗ | 0.188 | |||
| L4 | *** | *** | * | 0.222 | |||
| S4 | *** | *** | 0.214 | ||||
| C2 | L1 | ** | * | ⊗ | ⊗ | 0.096 | |
| S1 | * | * | * | ⊗ | ⊗ | 0.072 | |
| L2 | * | * | ⊗ | 0.125 | |||
| S2 | * | ** | ⊗ | 0.117 | |||
| L3 | . | * | ⊗ | ** | 0.134 | ||
| S3 | * | ⊗ | *** | 0.139 | |||
| L4 | . | * | ** | 0.134 | |||
| S4 | * | . | ** | 0.149 | |||
| C3 | L1 | *** | *** | *** | ⊗ | ⊗ | 0.17 |
| S1 | *** | *** | ⊗ | ⊗ | 0.285 | ||
| L2 | *** | *** | *** | *** | ⊗ | 0.269 | |
| S2 | *** | *** | . | ⊗ | 0.295 | ||
| L3 | *** | *** | *** | ⊗ | ** | 0.229 | |
| S3 | *** | *** | ⊗ | 0.285 | |||
| L4 | *** | *** | *** | *** | 0.269 | ||
| S4 | *** | *** | . | 0.295 |
| Catchment | Slope (G) | p-Value |
|---|---|---|
| C1 | ||
| C2 | ||
| C3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navas, R.; Alonso, J.; Gorgoglione, A.; Vervoort, R.W. Identifying Climate and Human Impact Trends in Streamflow: A Case Study in Uruguay. Water 2019, 11, 1433. https://doi.org/10.3390/w11071433
Navas R, Alonso J, Gorgoglione A, Vervoort RW. Identifying Climate and Human Impact Trends in Streamflow: A Case Study in Uruguay. Water. 2019; 11(7):1433. https://doi.org/10.3390/w11071433
Chicago/Turabian StyleNavas, Rafael, Jimena Alonso, Angela Gorgoglione, and R. Willem Vervoort. 2019. "Identifying Climate and Human Impact Trends in Streamflow: A Case Study in Uruguay" Water 11, no. 7: 1433. https://doi.org/10.3390/w11071433
APA StyleNavas, R., Alonso, J., Gorgoglione, A., & Vervoort, R. W. (2019). Identifying Climate and Human Impact Trends in Streamflow: A Case Study in Uruguay. Water, 11(7), 1433. https://doi.org/10.3390/w11071433






