1. Introduction
Scour around bridge elements like abutments and piers have been recognized as the main cause of bridge collapse [
1]. Hence, for the economical and safe design of bridge elements, it is necessary to estimate precise calculations of scour depths. Several studies are available on this subject, mostly dealing with uniform non-cohesive sediment beds [
2,
3,
4,
5,
6,
7,
8,
9]. For refraining bridges with pier hazards, it is necessary to propose a pier scour study based on many factors, classified as structural parameters of pier, bed sediment characteristics and hydraulic conditions prevailing at the site. So far, those objectives have not been met.
Characteristically, riverbeds in upper reaches deal with non-uniform coarser sediments such as non-uniform gravels, sand-gravel mixtures, sand-boulder-gravel mixtures etc. However, present study only focuses on non-uniform gravels. It is hard to accurately predict scour depths using uniform sediment bed approaches [
10]. Sediment transport difficulties involving non-uniform gravel beds could not be simply explained critically. This is because the physical process of sediment transport phenomenon has not yet been ideally defined. Jueyi et al. [
11] stated that a protecting layer of coarser particles formed around the pier is identified as the armor layer. In other words, the formation of an armor layer in a streambed stops the scouring process; however, some finer particles from the stream can be transported downstream through the armored bed [
12]. An armor layer plays a significant role in river evolution.
When the incipient condition of uniform sediment in a streambed exceeds, the particles start to move. However, the entrainment development of a single particle in a non-uniform sediment bed is complex. The resistance to single particle motion is a function of shape, size and relative density of the particle. Schmidt and Gintz [
13] stated that Platy shaped particles have a lesser possibility to be entrained than more compacted sediments. In addition, resistance to particle movement is also affected by the exposure and hiding effects in non-uniform sediments [
13].
The development of scour processes in non-uniform streambeds stops because of the development of a steady armor coating, due to the removal of fine sediment particles by the flowing water from the channel bed material (parent bed material) near the pier. Usually, the value of geometric standard deviation of the stratified layer particles is less than parent bed material and these particles are larger in median diameter than parent bed particles [
14]. It was observed experimentally by Jueyi et al. [
11] that the removal of finer sediment tends to occur earlier because it entails less energy to move. The development of armor layer by flushing fine particles from the scoured hole, and gradual exposure of coarser particles does not allow the further removal of sediment from the scoured hole. This phenomenon is also known as the end condition for scour in non-uniform sediments, and the scoured zone does not undergo further changes with time. The condition of end scour and the formation of the armor layer is dependent on the approach flow parameters, sediment properties, channel bed geometry and pier shape.
The armor layer at equilibrium scour condition on streambed plays a significant role in pier scour. In the literature, only a few studies are available related to scour processes and the behavior of different parameters around bridge piers in armored streambeds [
11,
15,
16,
17]. Most recently, Jueyi et al. [
11] derived a maximum dimensionless scour depth equation in the presence of the armoring layer. Guo [
15] and Kim et al. [
16] conducted pier scour study in non-uniform sediment and proposed maximum scour depth relationships. However, they did not consider the armor layer in their study. Jueyi et al. [
11] conducted an experimental study for abutment scour in non-uniform gravel bed and proposed an empirical relationship to describe the maximum depth of scour at equilibrium state.
Presently, only a few studies are available to describe the scour processes around bridge piers in non-uniform streambeds [
10,
14,
15,
16]. In this study, we investigated the scour processes and behavior of different parameters on maximum scour depth in armored streambed. All experiments have been carried out in a laboratory flume under the clear water scour condition using different sizes of non-uniform gravels and flow conditions.
2. Experimental Setup and Procedure
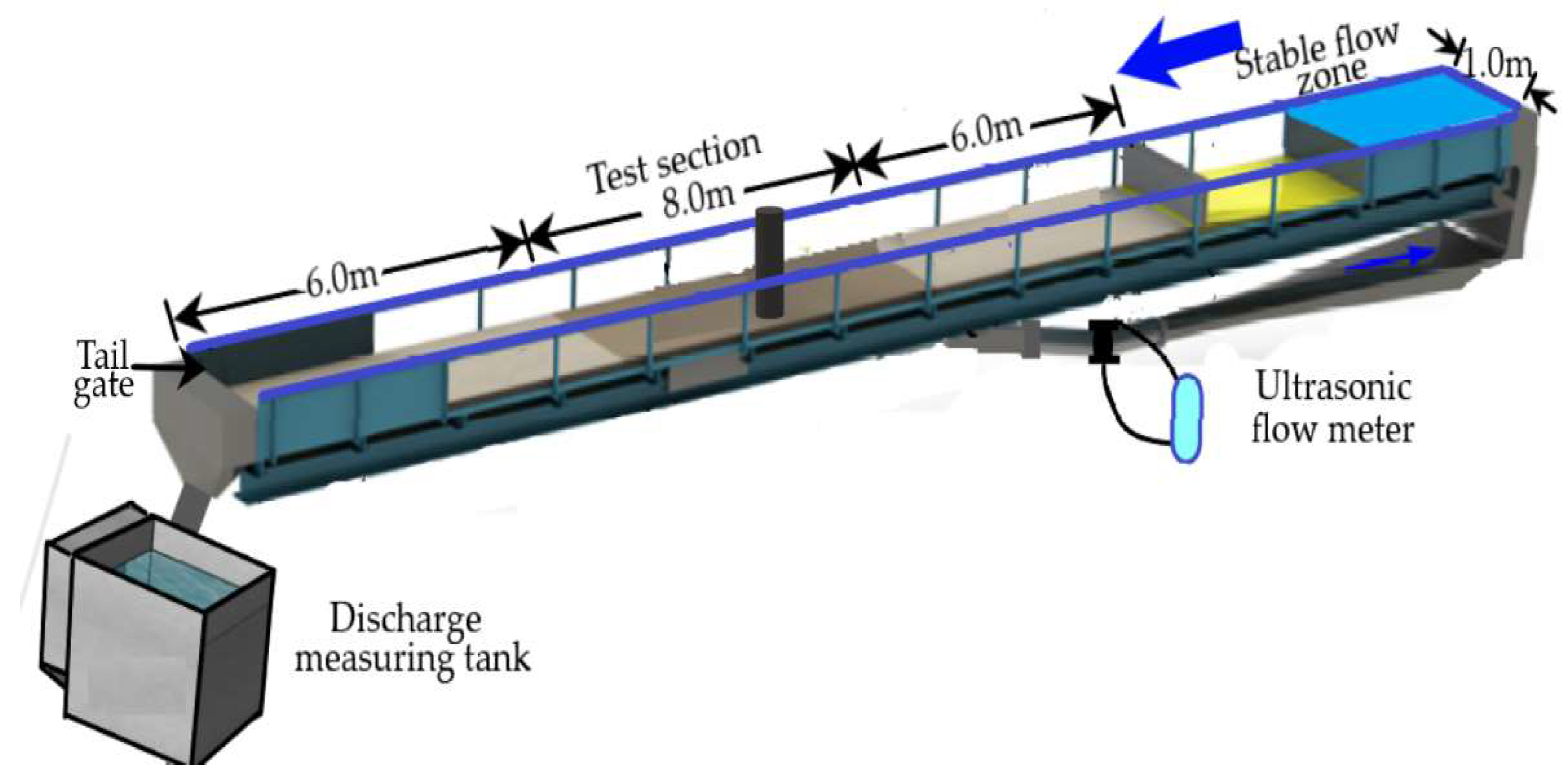
In this study, a total of 85 tests were carried out in a 20.0 m long and 1.0 m wide rectangular flume, as shown in
Figure 1. Four different diameters (
b) of circular bridge piers, i.e., 6.6 cm, 8.4 cm, 11.5 cm and 13.5 cm were used for present experiments. All piers were made of hollow cast iron pipes.
All experiments have been completed under different flow conditions and sediment properties like time-averaged velocities (
U), approach flow depths (
y), pier diameters (
b), median diameter of parent streambed particles (
d50) and geometric standard deviation (
σ). Test limits are mentioned in
Table 1 for cases (a–h).
The working section starts from 6.0 m of the flume entrance, as shown in
Figure 1. The working section (8.0 m long and 0.35 m deep) was completely filled with eight different sizes of non-uniform gravels (
σ > 1.4) having 3.26, 3.82, 4.38, 4.94, 7.5, 8.6, 9.1 and 10.7 mm median diameter (
d50) and 1.57, 1.66, 1.88, 1.56, 1.59, 1.63, 1.71 and 1.51 geometric standard deviation of parent particle size distribution, respectively. The discharge was measured with an ultrasonic flow meter, which was provided at inlet pier of the flume. Approach flow depth was adjusted using a tailgate, which was located at the downstream end of the flume. A wave regulator or straighter was facilitated at the flume entrance to produce a uniform or near uniform flow condition in the experimental flume. In the present study, the maximum scour depth (
hs) was measured with a Vernier point gauge. All tests were prepared for 24 hours. However, experimentally it was observed that the equilibrium scour stage was reached within 14 hours. After the equilibrium time of scour,, i.e., 14 hours, the scour depth at different points near the pier was the same at every 30 minutes’ interval. Before the start of each experiment, the working section of the flume was made perfectly level with respect to flume bed and covered with a thin Perspex sheet. Once preset flow conditions were achieved, the Perspex sheet was separated very carefully to avoid undesirable scour around the pier.
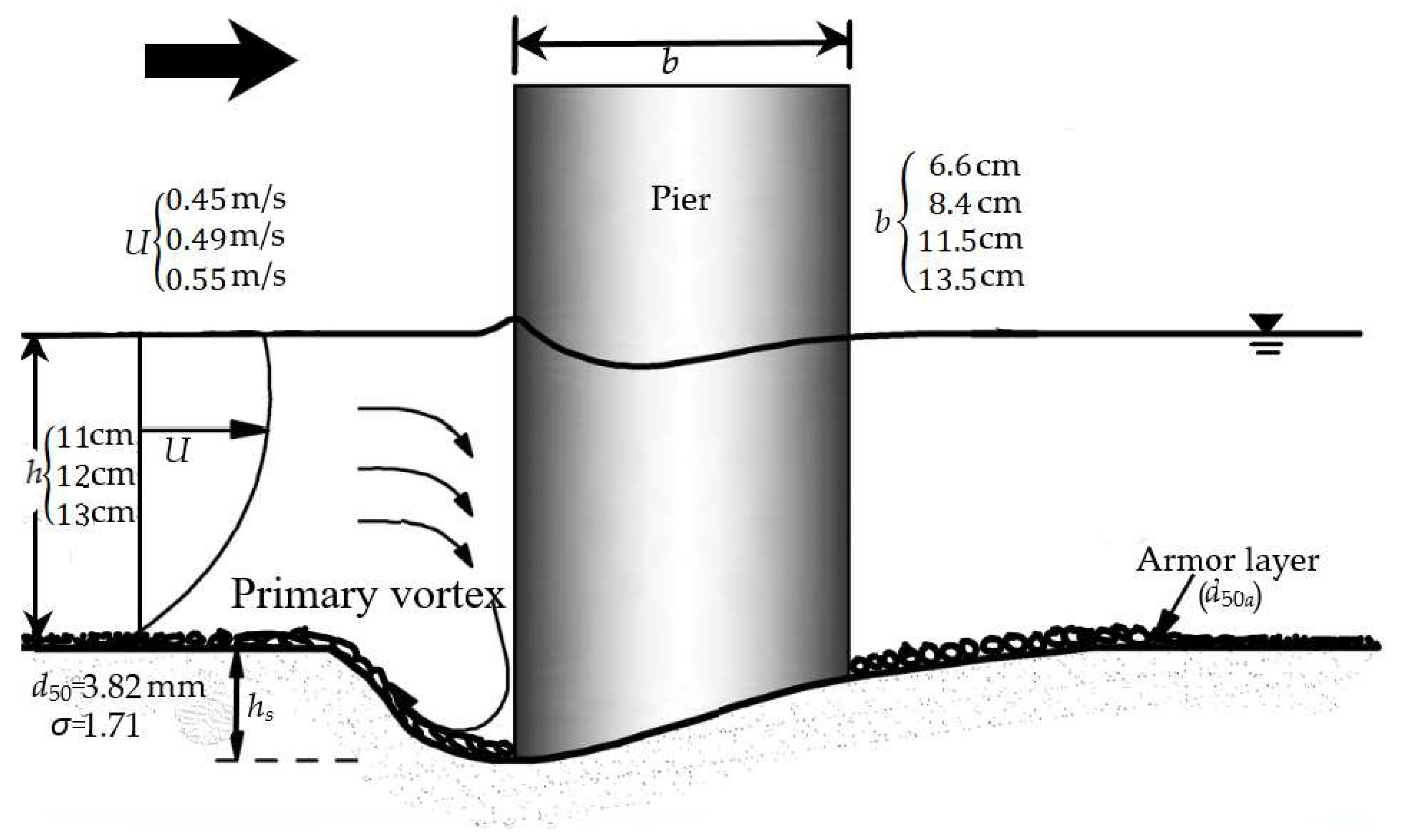
Figure 2 shows a definition sketch of pier scour in armored bed for case (b), followed by
Table 1.
After equilibrium scour state, the maximum scour depth (hs) was measured with a Vernier point gauge at upstream nose of the pier. We also collected the armor layer sediment for further particle size distribution and used the median diameter of armor layer (d50a) for scour depth analysis.
Critical velocity
Uc, was computed by Melville and Sutherland [
18] and varied with present flume experiments. Shield’s approach was obtained for calculating the critical shear velocity (
u*c).
3. Scour Processes and Armor Layer Formation
The interaction between gravel particles and the flow is complex, and this a significant information for designing a pier in gravel-bed streams. Armoring is a common phenomenon in rivers and occurs when selective entrainment of finer particles leave the stream-bed with a coarser gravel size than that of the underlying bed. Experimentally, it was stated by various researchers that when shear velocity (
u*) exceeds the critical shear velocity (
u*c) of streambed particles then incipient motion condition develops in the stream, and then further increment in shear velocity develops scour processes near the bridge elements [
6,
14]. Melville and Sutherland [
18] stated that the scour near the bridge elements occurs when approach shear velocity is almost 0.5 times of
u*c of armor bed particles. At the critical condition, the selective entrainment of gravels leaves the higher, more stable gravels on the stream-bed. Further increase in flow, the entrainment frequency increases and an armor layer of coarser gravel particles starts to form. The scour hole starts forming due to the formation of primary-vortex and drops into the scour hole as the scour hole volume increases with time [
16]. Hydrodynamic forces are induced on particles and eliminate the particles around the pier. The drag and lift forces decrease with a rise in scour depth. In actuality, the depletion of the particles near the bridge elements (pier and abutments) occur layer-by-layer [
14]. The scour processes end in non-uniform sediment beds with the development of a stable armor layer [
16]. At equilibrium scour condition, this armor layer does not permit the further removal sediment from the scoured hole. An armor layer holds partially of cluster creations, which are more constant than specific particles. The cluster creations have a noteworthy influence on pier scour, they can offer more stable bed after equilibrium scour state. After flume experimental study, it has been found that the stable armor layer usually has uniform sediment, with lesser geometric standard deviation in comparison to parent streambed material and depends on the strength and quantity of coarser particles [
14].
The strength of the scour hole depends on movement of coarser particles [
11]. In this study, it has been noted by us that coarser particles are more stable inside the scour hole because of their larger mass (more energy is required to remove from scour hole). At the same phase, finer gravels are protected by coarser gravels. Slowly, this process results in the development of clusters of different sizes of gravels. For a definite expanse, these clusters show the same characteristics [
11]. Kothyari et al. [
14] stated that the formation of armor layer may be noticed as a nonstop process of developments and collapses of clusters.
4. Results and Discussion
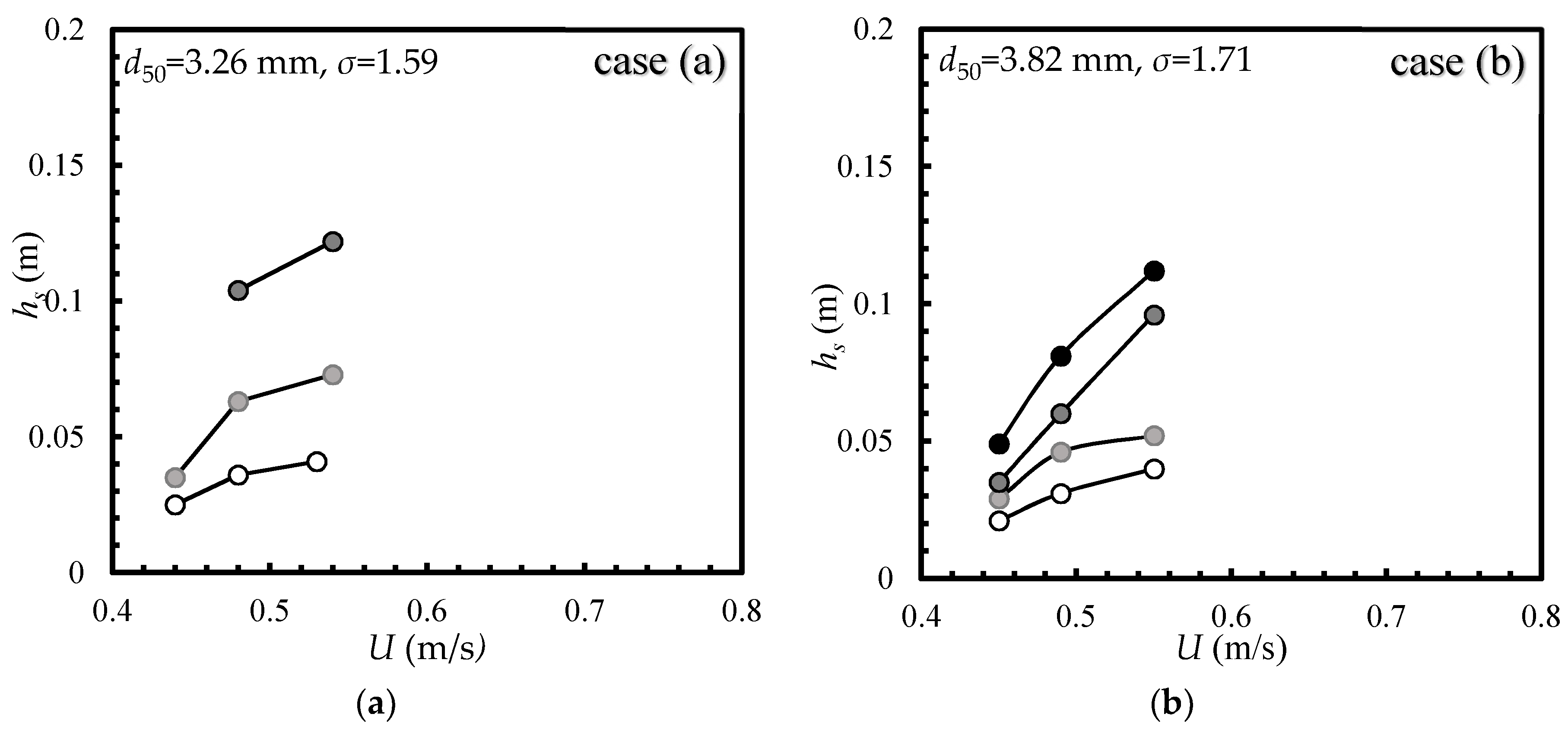
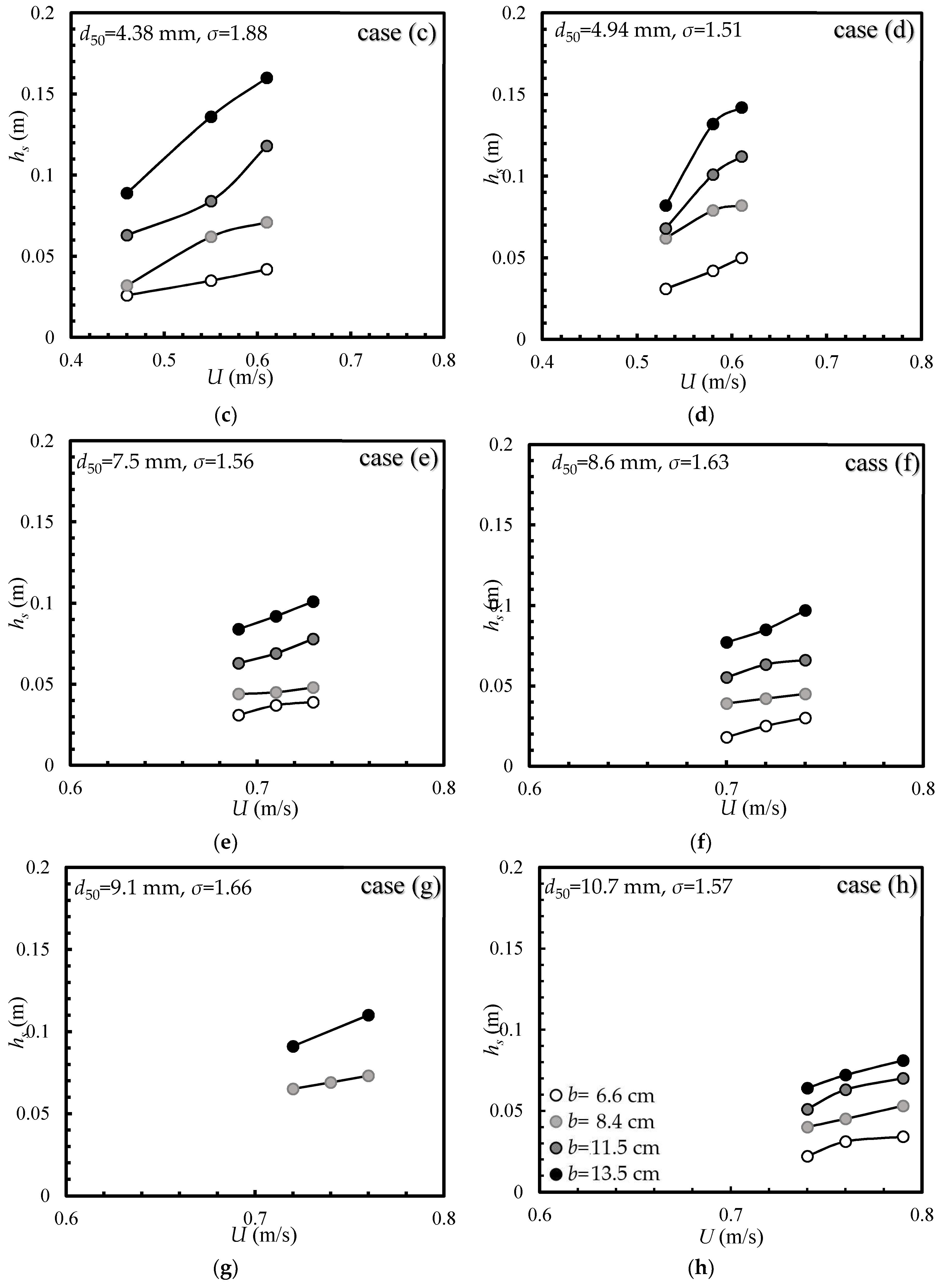
The stability of armor layer around the pier is influenced by parent particle size, median diameter of armor particles and approach flow properties. The maximum scour depth (
hs) variations at equilibrium condition with time-averaged flow velocity (
U) for different diameters of piers along with different sizes of gravels is shown in
Figure 3a–h. It can be noted that coarser gravels show less variation of maximum scour depth with approach flow velocity, while medium gravels show higher variation. It can also be noted from
Figure 3, the maximum scour depth in armored streambeds increases with approach flow velocity and that for any sizes of streambed particles, different sizes of particles of armored streambeds illustrate a different maximum scour depth. It has been found that the maximum scour depth variation is higher for fine gravel beds (
d50 = 3.26 − 4.94 mm) and lower for coarser gravel bed (
d50 = 7.5 − 10.7 mm). For particular streambed sediment, the maximum scour depth increases with increase in pier diameter and approach velocity.
We observed that the median diameter of armoring layer (
d50a) at equilibrium scour condition depends on
σ and increases with
σ, as shown in
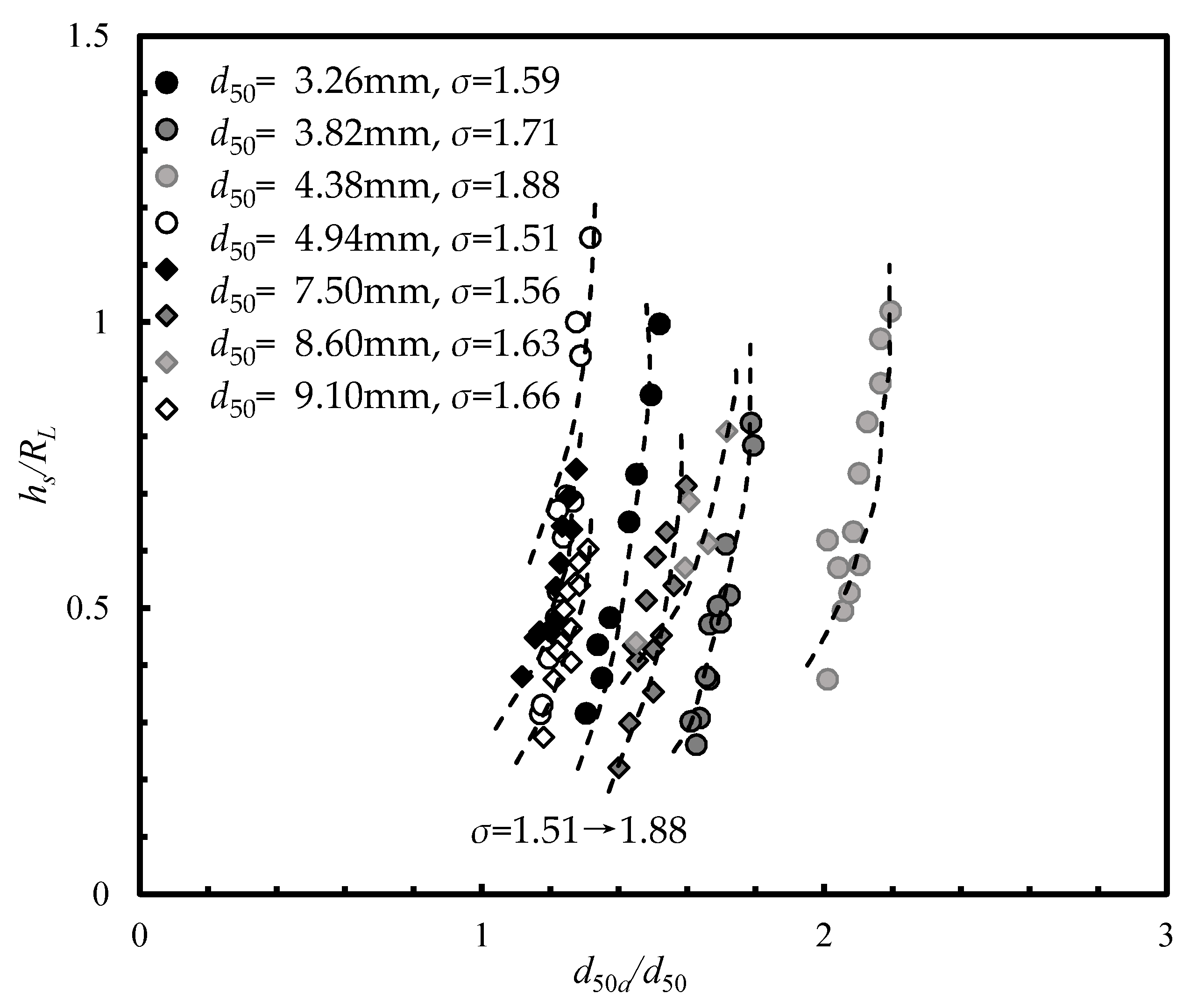
Figure 4. Armoring ratio (
d50a/
d50) defines the degree of armoring and mainly depends on the flow properties [
19]. For
σ = 1.63 − 1.88, the armoring ratio varied from 1.7–2.5, while for the lesser values of
σ, i.e.,
σ = 1.5 − 1.6, the armoring ratio varied from 1.25–1.7, as can be seen in
Figure 4. Wu et al. [
17] stated that the size of equilibrium scour-hole illustrates a strong dependency with parent particle size distribution. Kothyari et al. [
14] concluded that the maximum scour depth variation in non-uniform and non-cohesive sediment mixture is a function of geometric standard deviation of parent particle size distribution. Similar results were noted by us in the present study and the value of armoring ratio increases with
σ. However, the increment in dimensionless scour depth with armor ratio is very gradual up to
hs/
RL = 0.5, where
RL is the reference length and defined as (
b2y)
1/3 by Oliveto and Hager [
20,
21] and Kothyari et al. [
14]. After
hs/
RL = 0.5, there is no change in dimensionless scour depth with armor ratio, as can be seen in
Figure 4. It indicates that the dimensionless scour depths have -less dependency on degree of armoring ratio, but maximum scour depths have shown noteworthy changes with pier diameter and time-averaged velocity, as can be seen in
Figure 3.
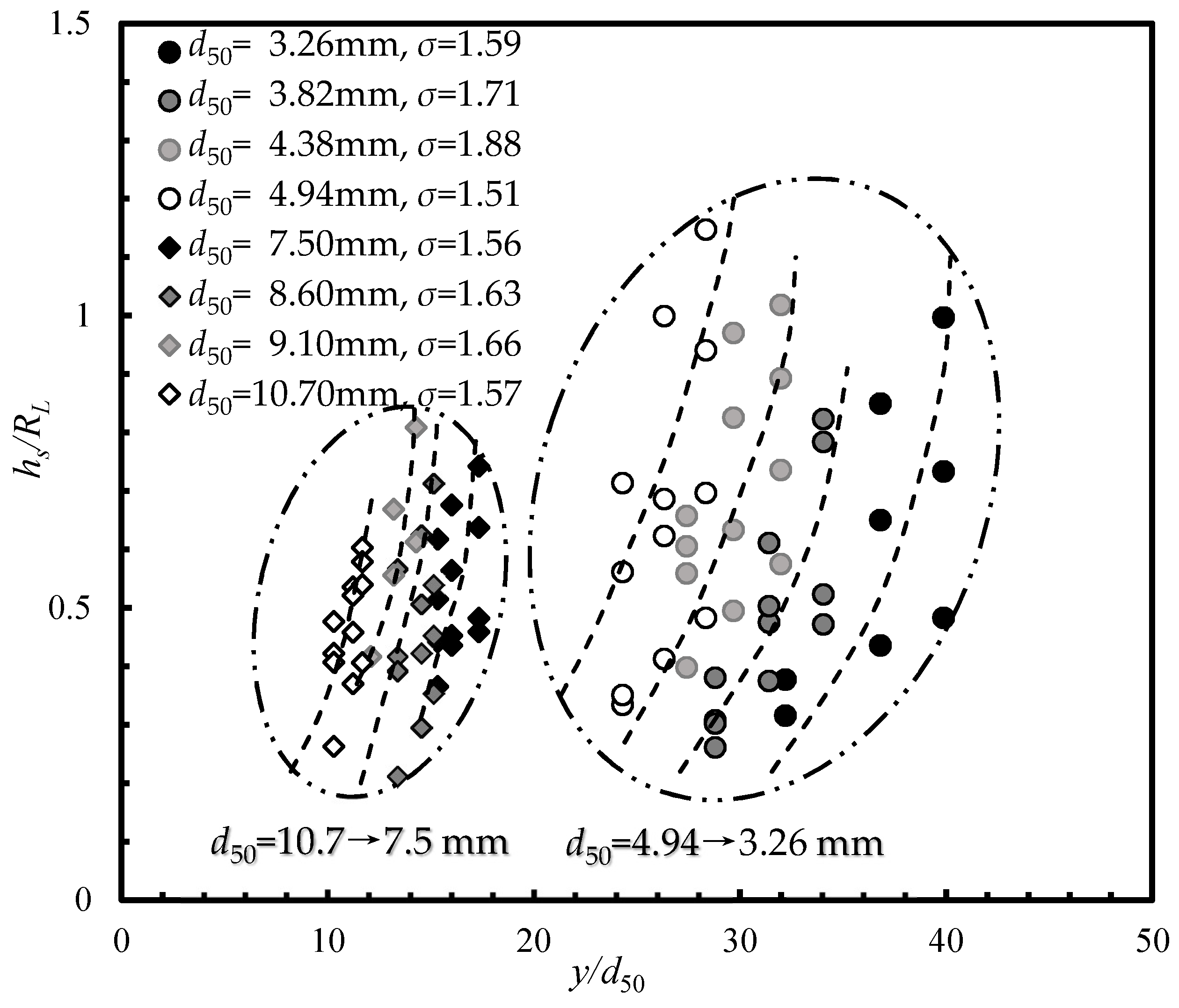
Figure 5 shows the dimensionless scour depth (
hs/RL) variation with
y/d50 ratio, where
y is approach flow depth. For a particular sediment property, the maximum scour depth increases with approach flow depth (
y).
Figure 5 clearly shows that the maximum scour depth variation with approach flow depth is higher for
d50 = 3.26 − 4.94 mm (fine gravel) and lowest for
d50 = 7.5 − 10.7 mm (coarse gravel). Moreover, the finer streambed particles (
d50 = 3.26 − 4.94 mm) result in a higher dimensionless scour depth variation than that of coarser streambed particles (
d50 = 7.5 − 10.7 mm).
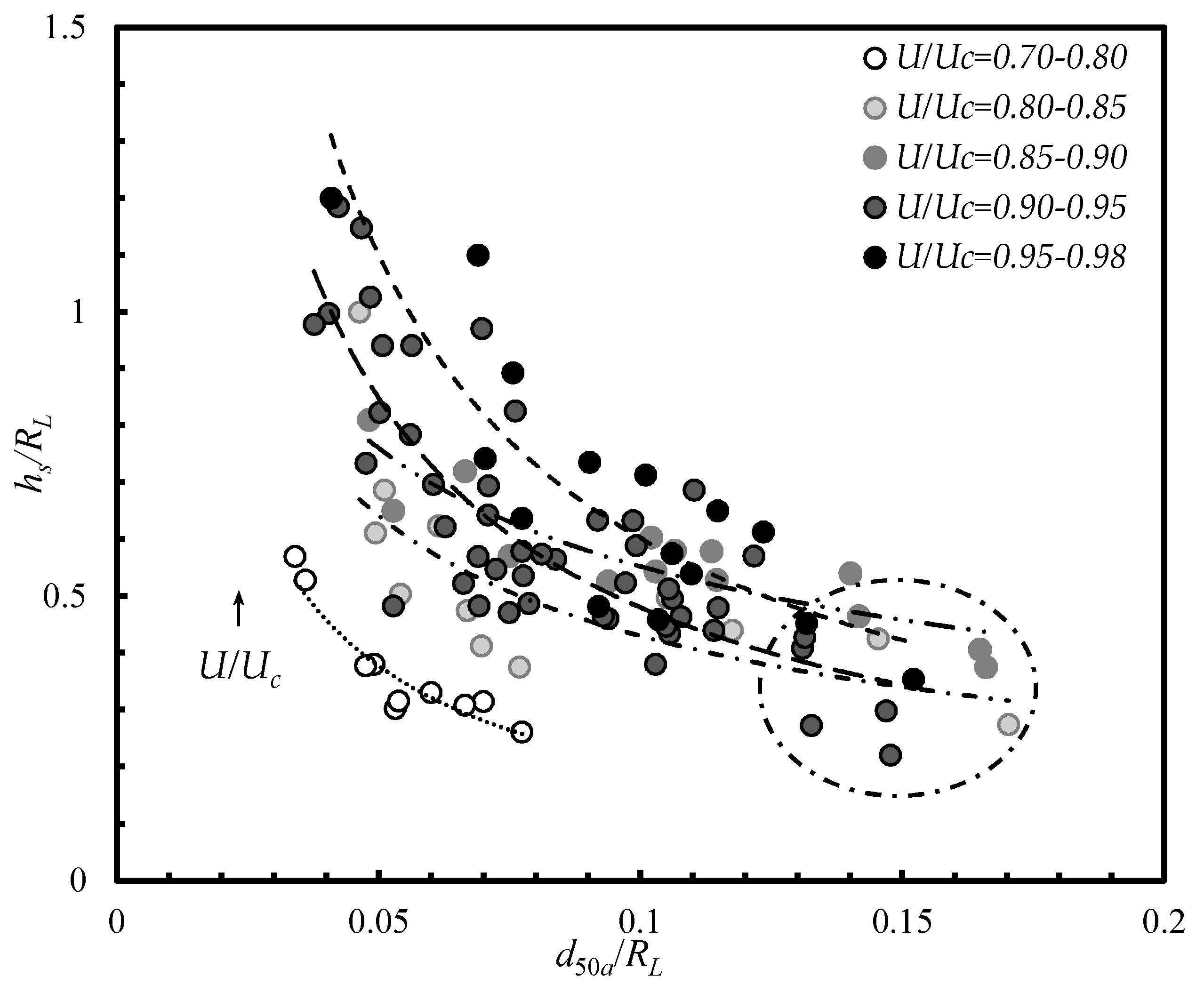
Figure 6 shows the dimensionless scour depth (
hs/RL) variation with
d50a/RL, for different ranges of critical velocity ratio (
U/Uc), and critical velocity ratio is known as the ratio of the approach mean velocity to the critical velocity of sediment. The range of critical velocity ratio is from 0.70 to 0.98. It can be identified that the dimensionless scour depth variation with
d50a/RL is highest for maximum range of critical velocity ratio, i.e.,
U/Uc ≈ 0.95 − 0.98. Hence, maximum number of experiments were carried out for
U/Uc ≈ 0.90 − 0.95 and it was noted that for all ranges of critical velocities,
hs increases with decrease of
d50a. It has been observed that the lowest variation of dimensionless scour depth with
d50a/RL for
U/Uc ≈ 0.70 − 0.80, as can be seen in
Figure 6.
Figure 6 clearly illustrates that the dimensionless scour depth variation increases with
U/Uc. It can also be noted that the time to reach near equilibrium depths for low values of
U/Uc is larger than the higher values of
U/Uc.
Implications for Design
In the past studies, several investigators have derived numerous dimensionless scour depth relationships [
2,
14,
22,
23,
24,
25,
26,
27,
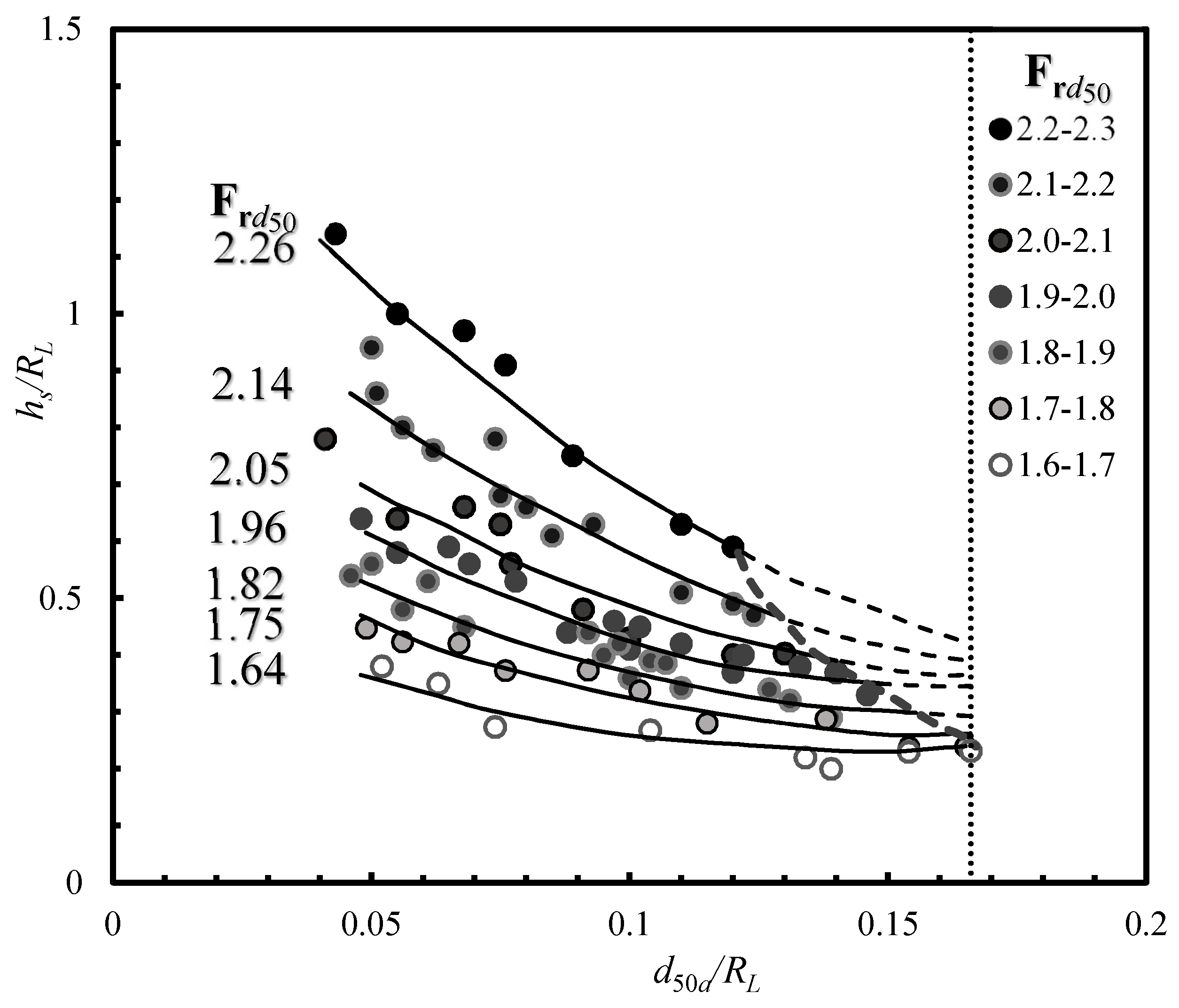
28]. Present experimental results show that scour depth is not only a function of flow parameters, but also depends on particle size and geometric standard deviation of parent bed material and armor layer particle size. Pier scour experimental data collected under armor streambeds are shown in
Table 1, and were used to illustrate the dimensionless scour depth variation with parent densimetric particle Froude number, F
rd50 =
U/[(
S − 1)
gd50]
0.5 and ratio of armor layer particle size − reference length (
d50a/RL), as shown in
Figure 7. Where
S is specific gravity of gravel equal to 2.65. It can be noted that for a particular range of F
rd50, the dimensionless scour depth decreases with an increase in
d50a/RL. The reducing frequency of dimensionless scour depth was very rapid for the higher value of densimetric Froude number, as can be seen in
Figure 7. It can be noted that the decreasing rate of dimensionless scour depth variation with
d50a/RL is lowest for F
rd50 = 1.6–1.7. Meanwhile,
Figure 5 shows the dimensionless scour depth gradually increasing with increase in armor ratio, for a particular sediment property.
Figure 6 and
Figure 7clearly illustrate that the dimensionless scour depth variation with
d50a/RL depends on
U/Uc and F
rd50, respectively. During the experiments, it was observed that the armor layer around the pier is washed out for higher value of
U/Uc due to the higher critical velocity of armor particles than the parent particles. For an armor-layered streambed, maximum scour depth increases with the decrease of parent streambed particle size and the increase of pier diameter and approach velocity, as shown in
Figure 3 and
Figure 5. Therefore, under fixed flow conditions and parent streambed properties, the maximum scour depth in equilibrium condition is larger in finer parent particle streambeds.
5. Conclusions
To date, very few studies are available for local scour around pier founded in armored gravel-bed streams. In the present study, a total of 85 experiments were carried out under different armor streambeds, along with different pier diameters and flow conditions. Using these different parameters, the maximum scour depth in armor streambeds was analyzed. A new graphical approach was proposed for the maximum scour depth computation.
It was observed that the scour hole around the pier occurs through the formation of an armor layer and scour hole has been reached within equilibrium scour state, when the armor layer particles cover the scour hole and no further movement allows from parent bed material. We found that the maximum scour depth is not only a function of flow parameters, but also depends on particle size and geometric standard deviation of parent bed material and armor layer particle size. The dimensionless scour depth variation with d50a/RL depends on the parent densimetric particle Froude number, and the decreasing rate of dimensionless scour depth decreases with Frd50. We found that the influence of armor ratio on dimensionless scour depth is less, up to hs/RL = 0.5, however, after hs/RL = 0.5, change in dimensionless scour depth was negligible. The maximum scour depth around the pier increases with increase in pier diameter, approach velocity, critical velocity ratio and decreases with the size of parent streambed particles. The maximum scour depth decreases with an increase of armor layer particle size for a particular bed material having the same parent bed material. This research indicates the necessity for additional non-uniform coarser bed scour study as it relates to fluvial hydraulics.