Numerical and Physical Modeling to Improve Discharge Rates in Open Channel Infrastructures
Abstract
:1. Introduction
2. Methods
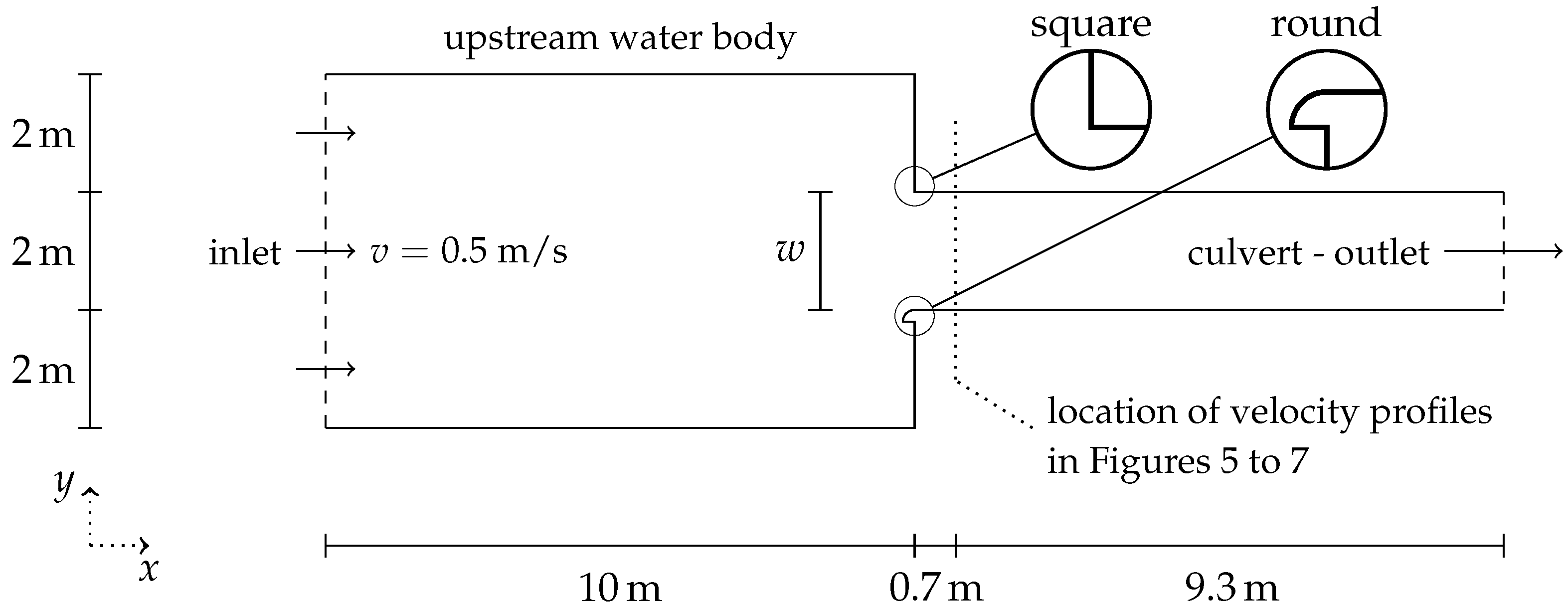
2.1. Simulation Setup
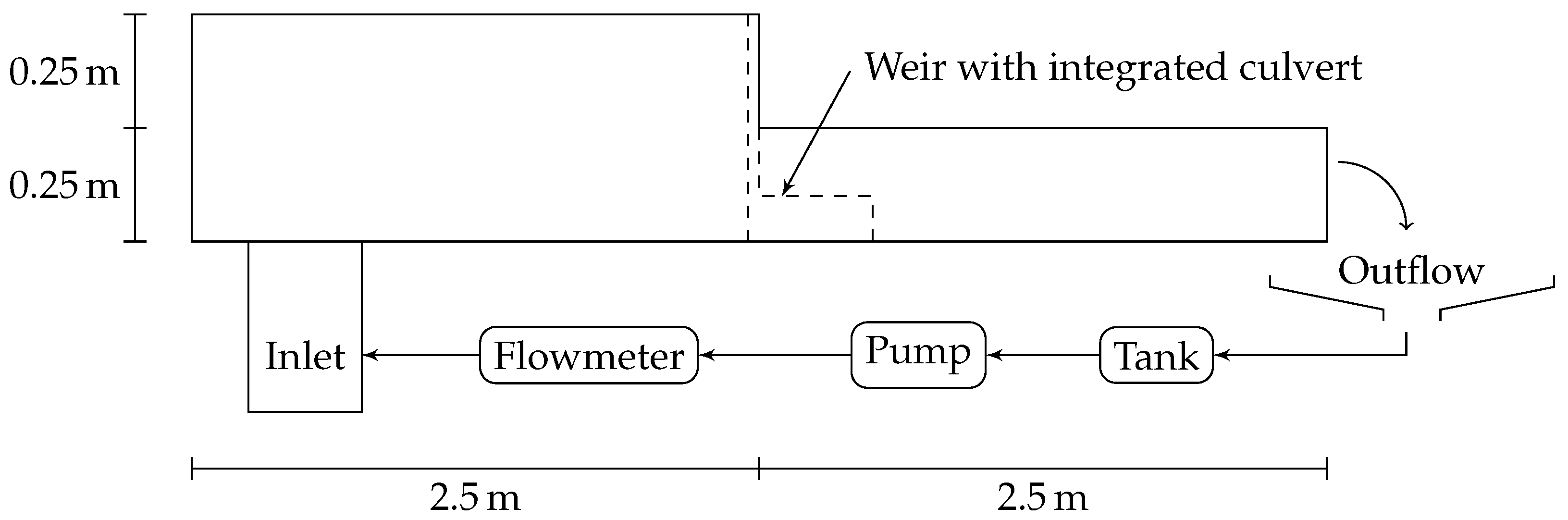
2.2. Experimental Setup
3. Results
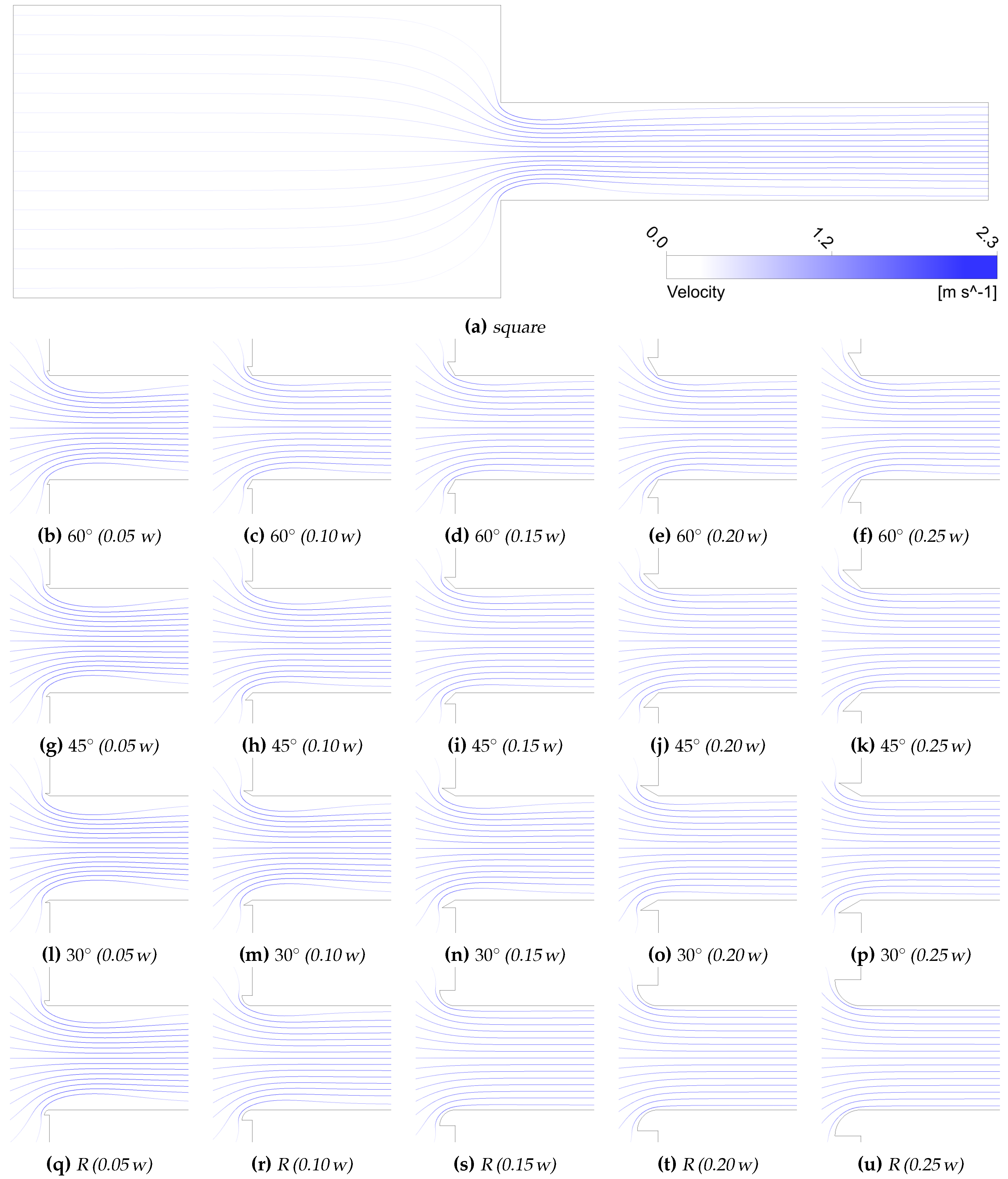
3.1. Numerical Simulation Results
3.2. Experimental Flume Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | computational fluid dynamics |
| MEL | minimum energy loss (culverts) |
| RANS | Reynolds averaged Navier–Stokes |
| TKE | turbulent kinetic energy |
| angle | |
| discharge coefficient | |
| D | diameter |
| h | height |
| l | length |
| non-dimensional flow rate | |
| r | radius |
| v | velocity |
| w | width (culvert) |
Appendix A
Appendix A.1. Methods
| Defaults | |
| Physics preference | CFD |
| Solver preference | Fluent |
| Sizing | |
| Use advanced size function | On: proximity and curvature |
| Relevance centre | Fine |
| Initial size seed | Active assembly |
| Smoothing | High |
| Span angle centre | Fine |
| Max face size | |
| Max size | |
| Inflation | |
| Scoping method | Geometry selection (- -) |
 | |
| Type | Element size |
| Element size | |
| Behaviour | Soft |
Appendix A.2. Results
References
- French, J.L. First Progress Report on Hydraulics of Short Pipes: Hydraulic Characteristics of Commonly Used Pipe Entrances; NBS Report; U.S. Dept. of Commerce, National Bureau of Standards: Washington, DC, USA, 1955; Volume 4444.
- French, J.L. Second Progress Report on Hydraulics of Culverts: Pressure and Resistance Characteristics of a Model Pipe Culvert; NBS Report; U.S. Dept. of Commerce, National Bureau of Standards: Washington, DC, USA, 1956; Volume 4911.
- French, J.L. Third Progress Report on Hydraulics of Culverts: Effect of Approach Channel Characteristics on Model Pipe Culvert Operation; NBS Report; U.S. Dept. of Commerce, National Bureau of Standards: Washington, DC, USA, 1957; Volume 5306.
- French, J.L. Fourth Progress Report on Hydraulics of Culverts: Hydraulics of Improved Inlet Structures for Pipe Culverts; NBS Report; U.S. Dept. of Commerce, National Bureau of Standards: Washington, DC, USA, 1961; Volume 7178.
- French, J.L. Fifth Progress Report on Hydraulics of Culverts Nonenlarged Box Culvert Inlets; NBS Report; NBS: Washington, DC, USA, 1966; Volume 9327.
- French, J.L. Sixth Progress Report on Hydraulics of Culverts: Tapered Box Culvert Inlets; NBS Report; U.S. Dept. of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1966; Volume 9355.
- French, J.L.; Bossy, H.G. Seventh Progress Report on Hydraulics of Culverts: Tapered Box Culvert Inlets with Fall Concentration in the Inlet Structure; National Bureau of Standards: Washington, DC, USA, 1967.
- Bodhaine, G.L. Measurement of Peak Discharge at Culverts by Indirect Methods. In Techniques of Water-Resources Investigations of the United States Geological Survey; U.S. G.P.O: Washington, DC, USA, 1968; Volume 3, Chapter A3. [Google Scholar]
- Apelt, C.J. Hydraulics of Minimum Energy Culverts and Bridge Waterways. Aust. Civ. Eng. Trans. I. E. Aust. 1983, CE25, 89–95. [Google Scholar]
- House, M.R.; Pyles, M.R.; White, D. Velocity distributions in streambed simulation culverts used for fish passage. J. Am. Water Resour. Assoc. 2005, 41, 209–217. [Google Scholar] [CrossRef]
- Paik, J.; Park, S.D. (Eds.) Numerical Simulation of Flood and Debris Flows through Drainage Culvert. Ital. J. Eng. Geol. Environ. Book 2011, 11, 487–493. [Google Scholar] [CrossRef]
- Feurich, R.; Boubée, J.; Olsen, N. Improvement of fish passage in culverts using CFD. Ecol. Eng. 2012, 47, 1–8. [Google Scholar] [CrossRef]
- Ball, J.; Babister, M.; Nathan, R.; Weeks, W.; Weinmann, E. Australian Rainfall and Runoff: A Guide to Flood Estimation; Commonwealth of Australia (Geoscience Australia): Symonston, Australia, 2016.
- Schall, J.D.; Thompson, P.L.; Zerges, S.M.; Kilgore, R.T.; Morris, J.L. Hydraulic Design of Highway Culverts, 3rd ed.; Hydraulic Design Series; U.S. Dept. of Transportation, Federal Highway Administration: Washington, DC, USA, 2012; Volume 5.
- Deutsches Institut für Normung e.V. Hydraulic structures—Part 1: Crossing Works, Culvert Works and Drain Works; Deutsches Institut für Normung (DIN): Berlin, Germany, 1998. [Google Scholar]
- Straub, L.G. Importance of Inlet Design on Culvert Capacity; University of Minnesota: Minneapolis, MN, USA, 1953. [Google Scholar]
- Day, R.A. Preliminary observations of turbulent flow at culvert inlets. J. Hydraul. Eng. 1997, 123, 116–124. [Google Scholar] [CrossRef]
- Chanson, H. Introducing originality and innovation in engineering teaching: The hydraulic design of culverts. Eur. J. Eng. Educ. 2000, 25, 377–391. [Google Scholar] [CrossRef]
- Jones, J.S.; Kerenyi, K.; Stein, S. Effects of Inlet Geometry on Hydraulic Performance of Box Culverts: Laboratory Report; U.S. Dept. of Transportation, Federal Highway Administration, Turner-Fairbank Highway Research Center: McLean, VA, USA, 2004.
- Hunt, M.; Clark, S.; Tkach, R. Velocity distributions near the inlet of corrugated steel pipe culverts. Can. J. Civ. Eng. 2012, 39, 1243–1251. [Google Scholar] [CrossRef]
- Kolerski, T.; Wielgat, P. Velocity field characteristics at the inlet to a pipe culvert. Arch. Hydroeng. Environ. Mech. 2014, 61, 127–140. [Google Scholar] [CrossRef]
- Guven, A.; Hassan, M.; Sabir, S. Experimental investigation on discharge coefficient for a combined broad crested weir-box culvert structure. J. Hydrol. 2013, 500, 97–103. [Google Scholar] [CrossRef]
- Olsen, A.H.; Tullis, B.P. Laboratory Study of Fish Passage and Discharge Capacity in Slip-Lined, Baffled Culverts. J. Hydraul. Eng. 2013, 139, 424–432. [Google Scholar] [CrossRef]
- Blanc, J.; Wallerstein, N.P.; Wright, G.B.; Arthur, S. Analysis of the performance of debris screens at culverts. Proc. Inst. Civ. Eng. Water Manag. 2014, 167, 219–229. [Google Scholar] [CrossRef]
- McKay, G.R. Design of Minimum Energy Culverts; University of Queensland, Department of Civil Engineering: St Lucia, Australia, 1971. [Google Scholar]
- Arnbjerg-Nielsen, K.; Willems, P.; Olsson, J.; Beecham, S.; Pathirana, A.; Bülow Gregersen, I.; Madsen, H.; Nguyen, V.T.V. Impacts of climate change on rainfall extremes and urban drainage systems: A review. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2013, 68, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Peters, G.P.; Andrew, R.M.; Boden, T.; Canadell, J.G.; Ciais, P.; Le Quéré, C.; Marland, G.; Raupach, M.R.; Wilson, C. The challenge to keep global warming below 2 degree C. Nat. Clim. Chang. 2013, 3, 4–6. [Google Scholar] [CrossRef]
- Wasko, C.; Sharma, A. Global assessment of flood and storm extremes with increased temperatures. Sci. Rep. 2017, 7, 7945. [Google Scholar] [CrossRef] [PubMed]
- Hettiarachchi, S.; Wasko, C.; Sharma, A. Increase in flood risk resulting from climate change in a developed urban watershed—The role of storm temporal patterns. Hydrol. Earth Syst. Sci. 2018, 22, 2041–2056. [Google Scholar] [CrossRef]
- Verstraten, L.; Wasko, C.; Ashford, G.; Sharma, A. Sensitivity of Australian roof drainage structures to design rainfall variability and climatic change. Build. Environ. 2019, 161, 106230. [Google Scholar] [CrossRef]
- Kilgore, R.T.; Bergendahl, B.S.; Hotchkiss, R.H. Culvert Design for Aquatic Organism Passage, 1st ed.; Hydraulic Engineering Circular; U.S. Federal Highway Administration, Central Federal Lands Highway Division: Lakewood, CO, USA, 2010; Volume 26.
- Yazdanfar, Z.; Sharma, A. Urban drainage system planning and design–challenges with climate change and urbanization: A review. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2015, 72, 165–179. [Google Scholar] [CrossRef]
- Zahmatkesh, Z.; Karamouz, M.; Goharian, E.; Burian, S.J. Analysis of the Effects of Climate Change on Urban Storm Water Runoff Using Statistically Downscaled Precipitation Data and a Change Factor Approach. J. Hydrol. Eng. 2015, 20, 05014022. [Google Scholar] [CrossRef]
- Kang, N.; Kim, S.; Kim, Y.; Noh, H.; Hong, S.; Kim, H. Urban Drainage System Improvement for Climate Change Adaptation. Water 2016, 8, 268. [Google Scholar] [CrossRef]
- ANSYS Fluent. Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Boussinesq, J. Théorie Analytique de la Chaleur; Gauthier-Villars: Paris, France, 1921. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Larsson, I.A.S.; Lindmark, E.M.; Lundström, T.S.; Nathan, G.J. Secondary Flow in Semi-Circular Ducts. J. Fluids Eng. 2011, 133, 101206. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Turner, B.N.; Gold, S.A. A review of melt extrusion additive manufacturing processes: II. Materials, dimensional accuracy, and surface roughness. Rapid Prototyp. J. 2015, 21, 250–261. [Google Scholar] [CrossRef]
- Hager, W.H.; Del Giudice, G. Generalized culvert design diagram. J. Irrig. Drain. Eng. 1998, 124, 271–274. [Google Scholar] [CrossRef]
- Novák, P.; Čábelka, J. Models in Hydraulic Engineering: Physical Principles and Design Applications; Monographs and Surveys in Water Resources Engineering; Novák, P., Čábelka, J., Eds.; Pitman: Boston,MA, USA; London, UK, 1981; Volume 4. [Google Scholar]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]


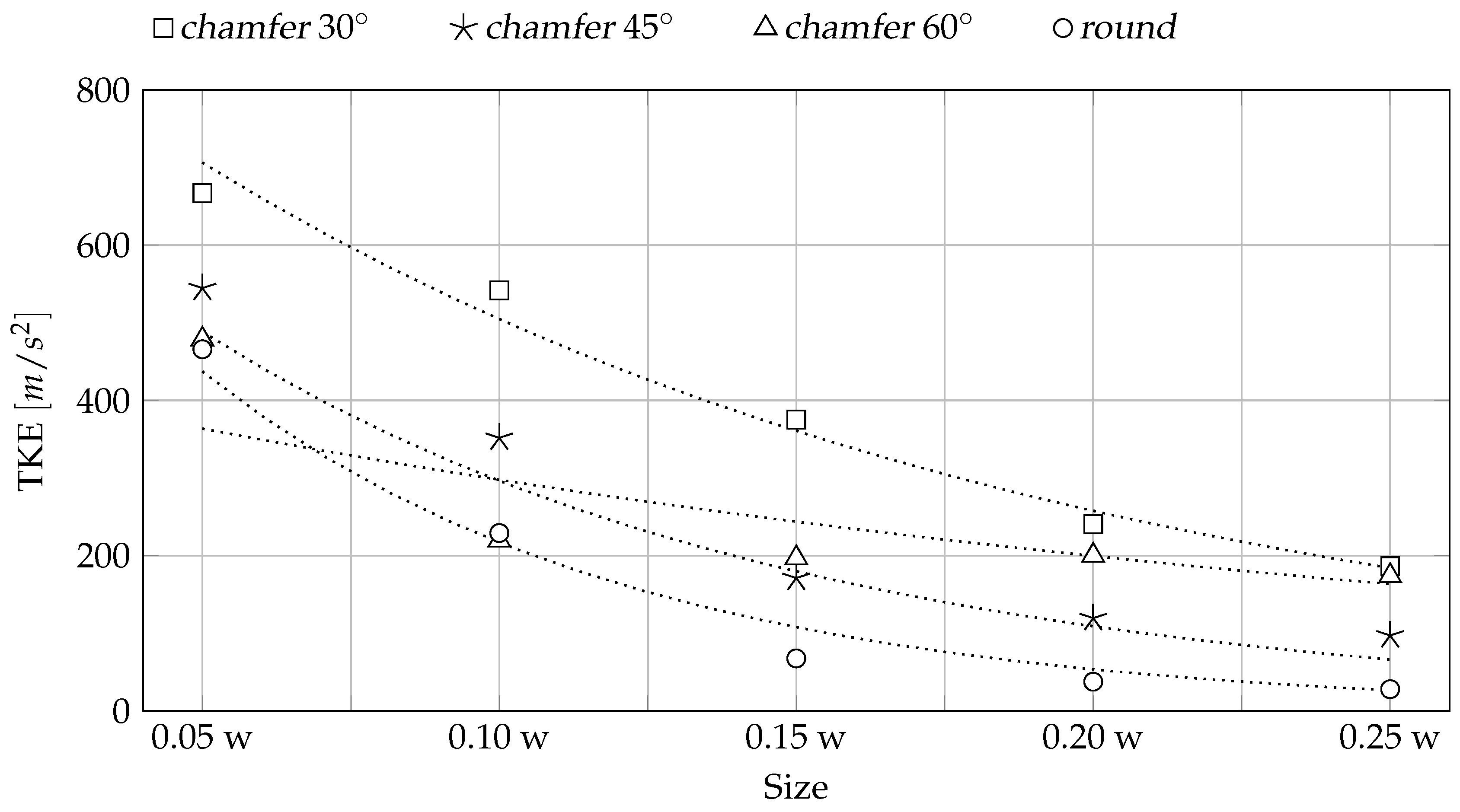
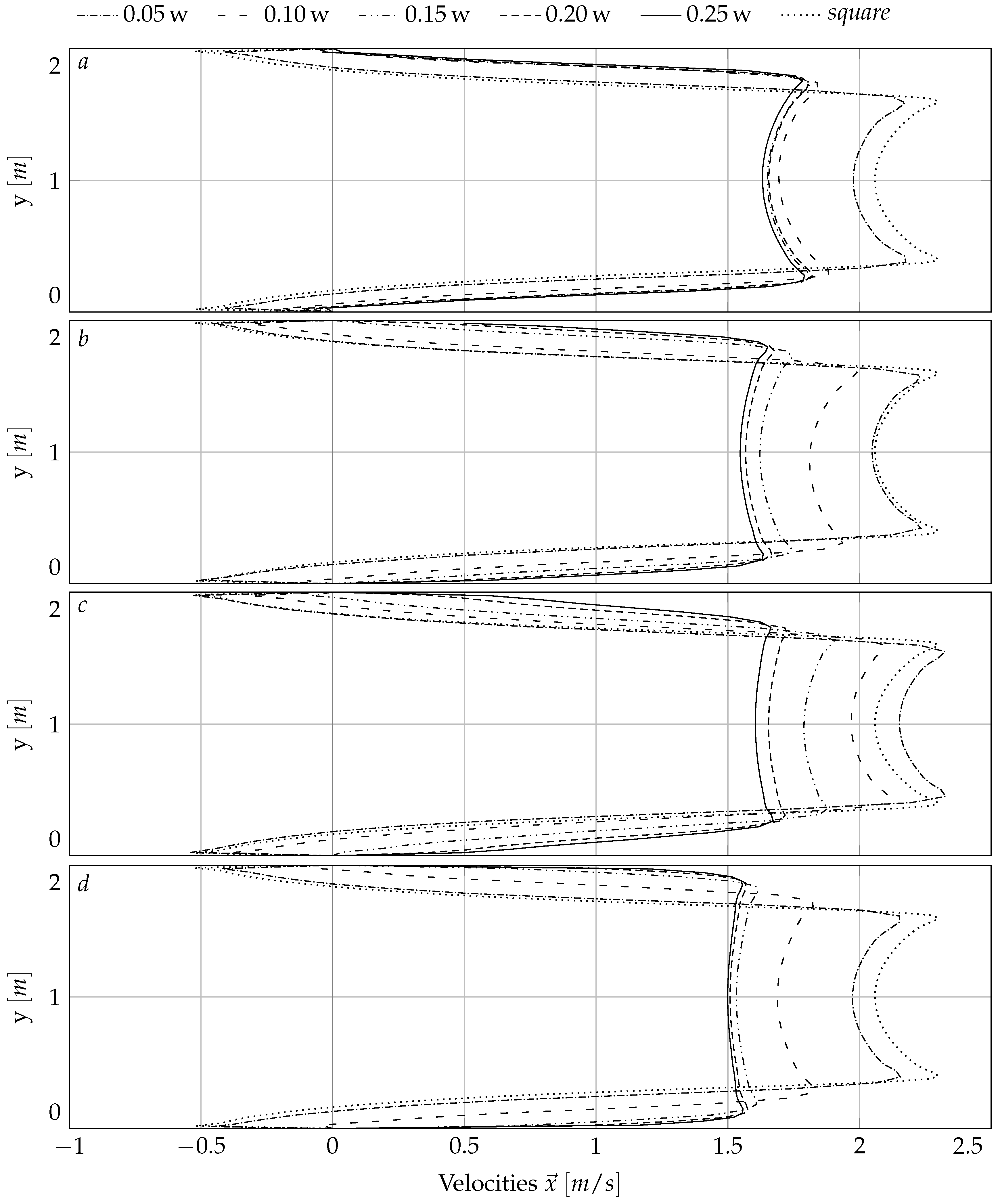
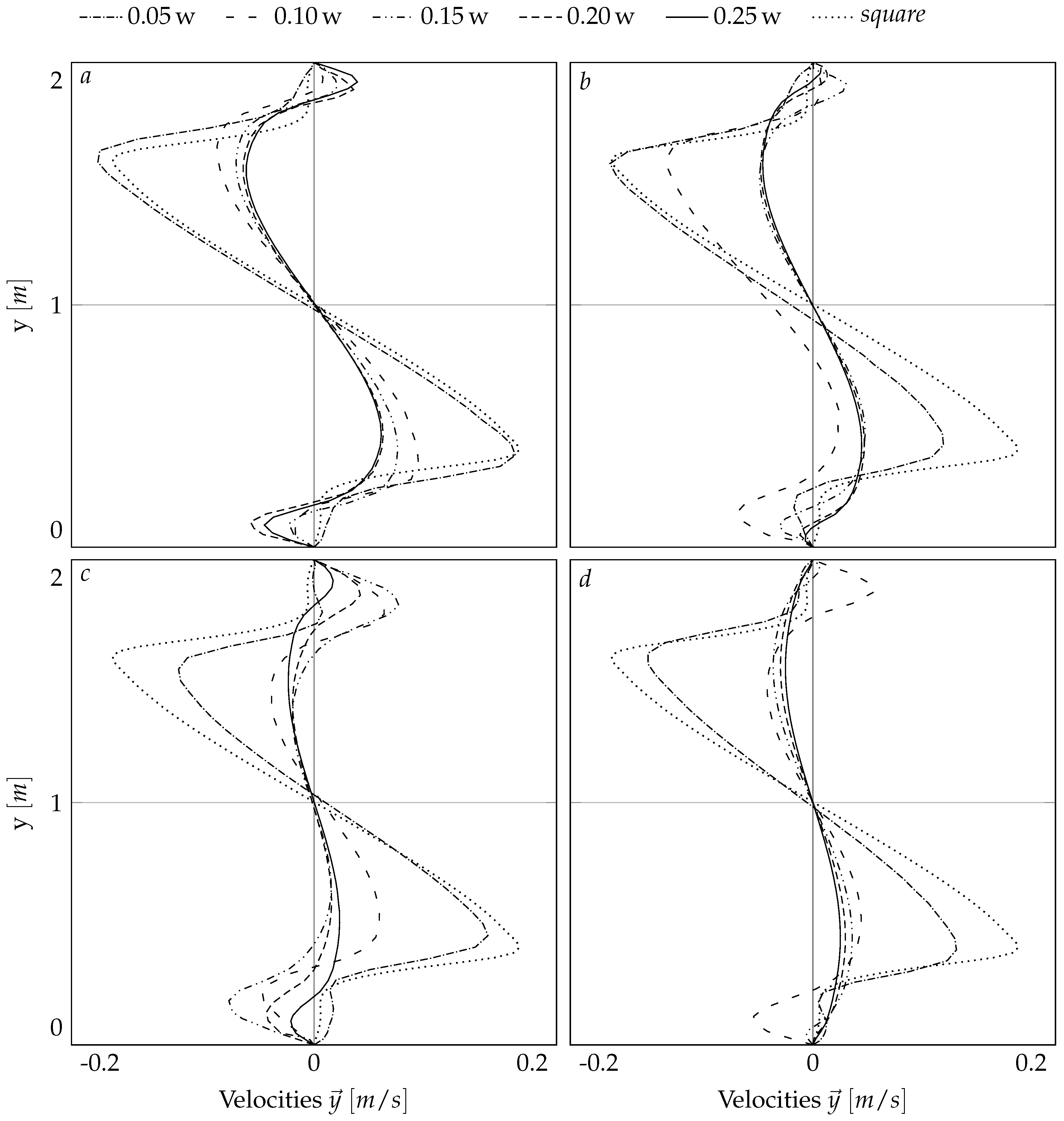
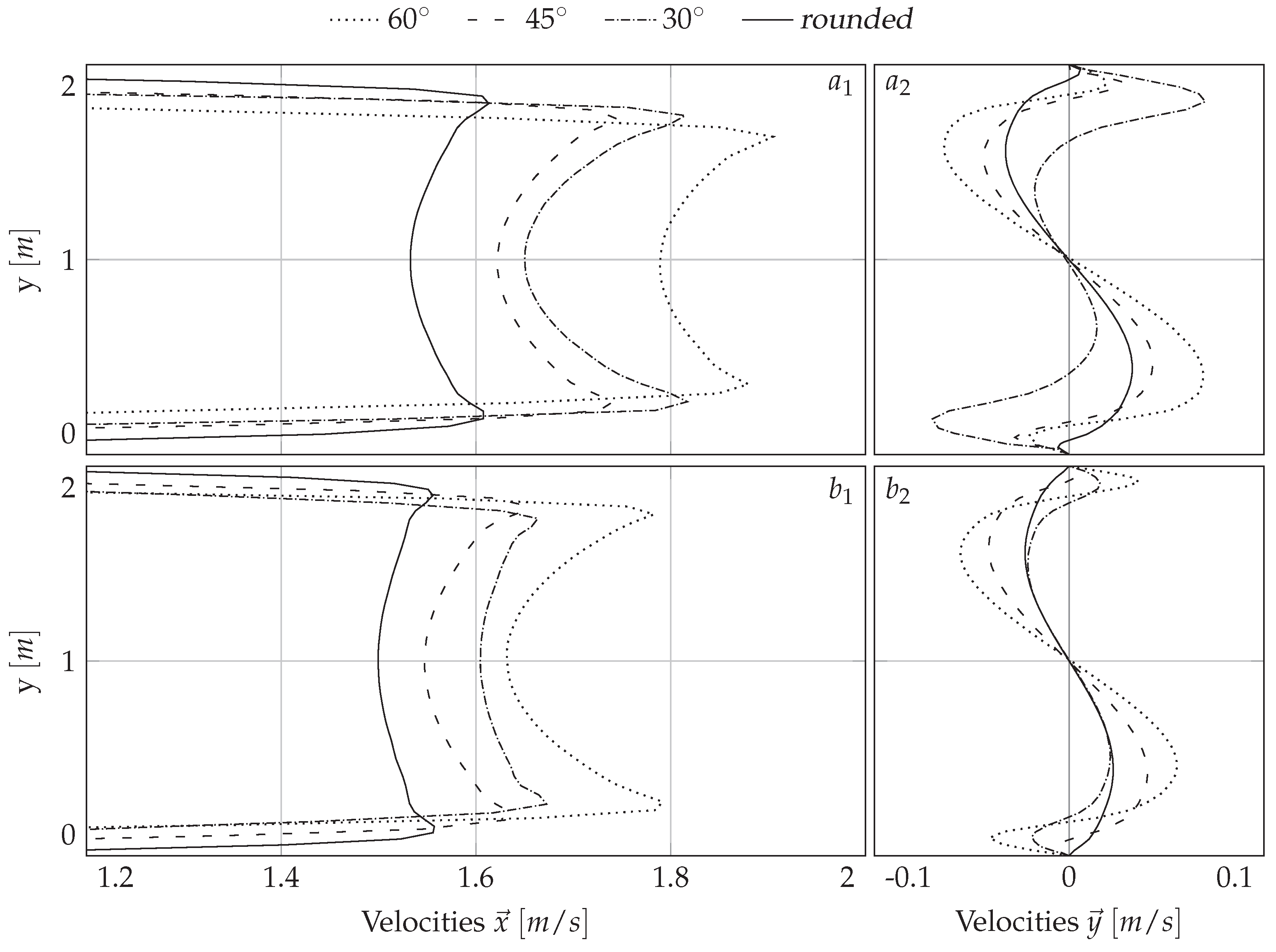

| Inlet Type | Configurations | Abbreviation |
|---|---|---|
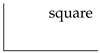 | none | square |
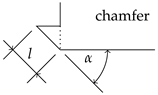 | ||
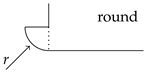 |
| Size | ||||||
|---|---|---|---|---|---|---|
| - | 0.05 w | 0.10 w | 0.15 w | 0.20 w | 0.25 w | |
| square | 0.64 | - | - | - | - | - |
| 30° | - | 0.64 | 0.70 | 0.76 | 0.84 | 0.87 |
| 45° | - | 0.65 | 0.70 | 0.84 | 0.87 | 0.88 |
| 60° | - | 0.67 | 0.81 | 0.82 | 0.82 | 0.84 |
| round | - | 0.68 | 0.81 | 0.89 | 0.91 | 0.92 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaeger, R.; Tondera, K.; Jacobs, C.; Porter, M.; Tindale, N. Numerical and Physical Modeling to Improve Discharge Rates in Open Channel Infrastructures. Water 2019, 11, 1414. https://doi.org/10.3390/w11071414
Jaeger R, Tondera K, Jacobs C, Porter M, Tindale N. Numerical and Physical Modeling to Improve Discharge Rates in Open Channel Infrastructures. Water. 2019; 11(7):1414. https://doi.org/10.3390/w11071414
Chicago/Turabian StyleJaeger, Rick, Katharina Tondera, Carolyn Jacobs, Mark Porter, and Neil Tindale. 2019. "Numerical and Physical Modeling to Improve Discharge Rates in Open Channel Infrastructures" Water 11, no. 7: 1414. https://doi.org/10.3390/w11071414
APA StyleJaeger, R., Tondera, K., Jacobs, C., Porter, M., & Tindale, N. (2019). Numerical and Physical Modeling to Improve Discharge Rates in Open Channel Infrastructures. Water, 11(7), 1414. https://doi.org/10.3390/w11071414




