Height–Area–Storage Functional Models for Evaporation-Loss Inclusion in Reservoir-Planning Analysis
Abstract
1. Introduction
- (i).
- empirically fitting linear and nonlinear H–A–S functions to the observed bathymetric area, volume, and height data for the selected reservoirs, as well as extracting existing functions in the GRanD database;
- (ii).
- assessing the biases or errors associated with the use of various functions for predicting the exposed surface areas of reservoirs at different reservoir storage states;
- (iii).
- carrying out reservoir-planning analyses with and without evaporation consideration, and hence assessing the evaporation effects on capacity estimates for various H–A–S functions; and
- (iv).
- critically examining the results in (ii) and (iii) to identify the most effective model(s) for explicitly accommodating evaporation loss in reservoir-planning analysis and make recommendations.
2. Materials and Methods
2.1. Data Collection
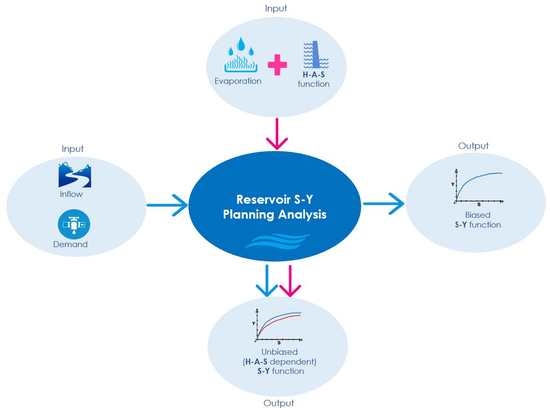
2.2. Reservoir-Planning Techniques for Accommodating Evaporation Loss
2.2.1. MSPA with Area–Storage Function
- (i).
- Determine Kt+1 = max (0.0, Kt + Dt − Qt) for all time periods, t = 1, 2, …, N
- (ii).
- If KN = K0, then go to (iii); else, if this is the first iteration, set K0 = KN and go to (i); else, STOP: the SPA has failed because gross period demand is higher than the average inflow.
- (iii).
- Reservoir active storage capacity, Ka = max(Kt).
- (i).
- Determine reservoir states St using the Ka and Kt obtained in Step 1, i.e.,Note that as a critical period technique, the initial storage state, So = Ka, i.e., the reservoir is initially full.St = Ka − Kt; 0 ≤ t ≤ N
- (ii).
- Using St, determine = corresponding exposed area At from the H–A–S model. The mean exposed surface area in interval [t, t + 1] becomes:Av = 0.5 (At + At+1)
- (iii).
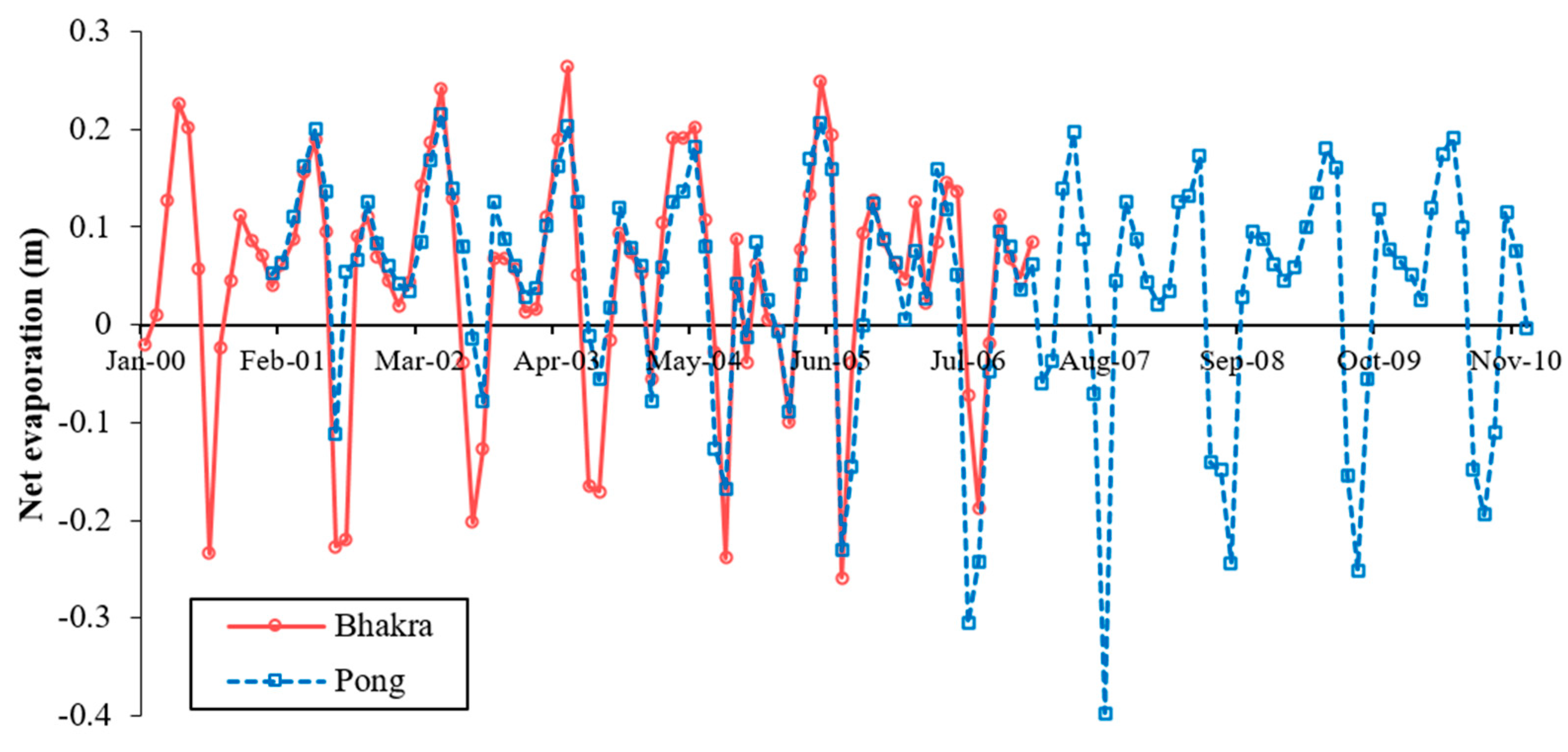
- Determine the net evaporation volume (m3) in the interval, EVt, as:where Et and Pt are the evaporation and precipitation depths (m), respectively, during t.EVt = Av (Et − Pt)
- (iv).
- Rerun Step 1 to now include evaporation. This effectively involves modifying Step 1i to:Evaporation-adjusted capacity Ka* then becomes:Kt+1 = max (0.0, Kt + Dt + EVt − Qt); 0 ≤ t ≤ NKa* = max (Kt + 1).
- (v).
- However, as noted by [14], the difference between Ka and Ka* may not be entirely due to the inclusion of EVt, but also due to a shift in the critical period. To remove this effect, Montaseri and Adeloye [15] recommend the following iterative steps to obtain the correct evaporation-impacted active storage-capacity estimate:
- Using the estimated Ka and Ka*, determine the β = ; if β ≤ 0.0001, then STOP, because Ka* is the exact active storage capacity, otherwise, go to step (b)
- Set Ka = Ka*
- Determine the new storages (St) using Equation (1) for all t = 1, 2, …, N.
- Determine new storage capacity Ka* by including the EVt values [8].
- Go to (a) and check the value of β.
2.2.2. MSPA with Height–Storage Function
- (i).
- Determine St (t = 1, 2, …, N) using Equation (1). Using St, determine corresponding height Ht using the height–storage function.
- (ii).
- Adjust the reservoir level for the effect of net evaporation by algebraically deducting the net evaporation depth:where Ht,adj is the adjusted reservoir level (m); Ht is the unadjusted reservoir level (m).Ht,adj = Ht − (Et − Pt)
- (iii).
- Convert Ht,adj back to adjusted storage St,adj using the height–storage function.
- (iv).
- Determine the volumetric evaporation loss as:EVt = St,adj − St
- (v).
- Rerun Step 1 to now include evaporation by modifying the expression for Kt+1 to:Kt+1 = max (0.0, Kt + Dt + EVt − Qt); 0 ≤ t ≤ N
- (vi).
- Complete the necessary checks as described in Section 2.2.1 (Step 2v) to determine evaporation adjusted capacity Ka*.
2.3. Specification and Parameterization of H–A–S Models
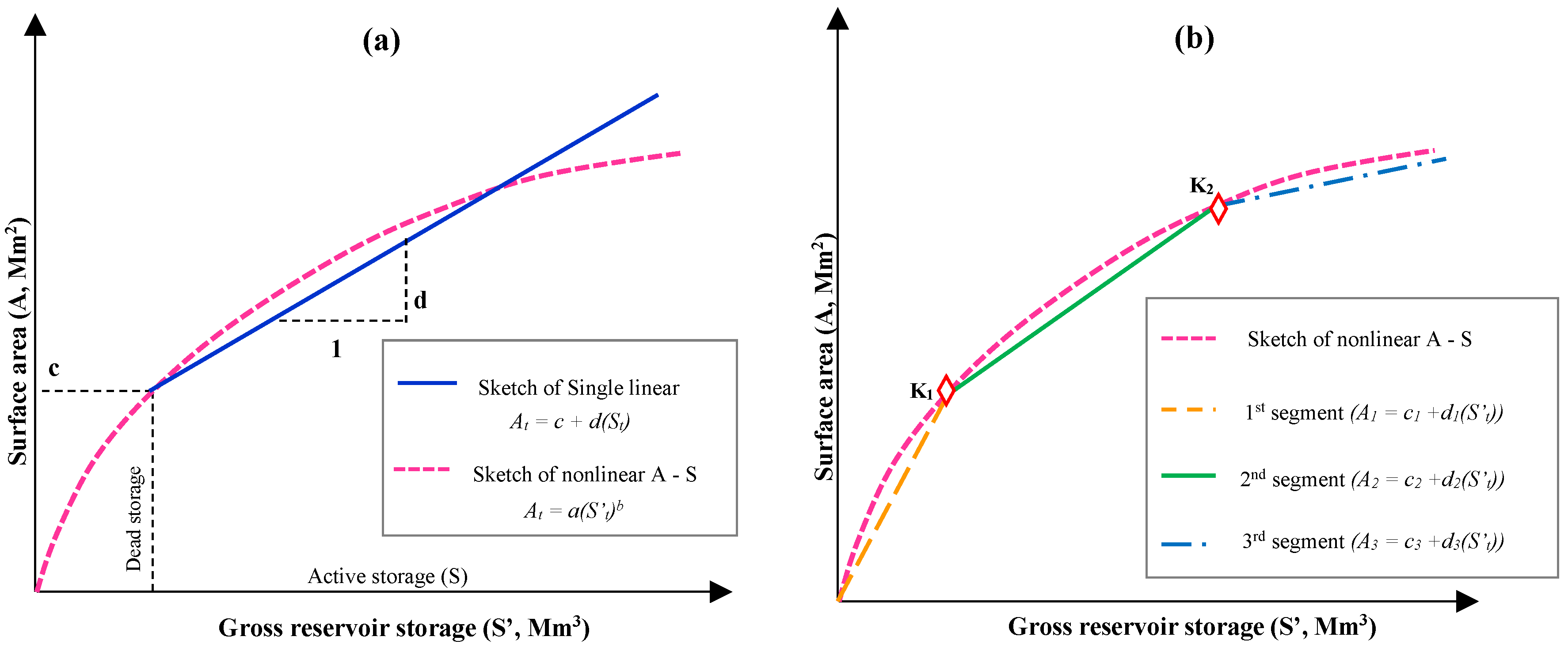
2.3.1. Nonlinear Area–Storage Equation
2.3.2. Single Linear Area–Storage Equation
2.3.3. Multiple (3) Piecewise Linear Area–Storage Equations
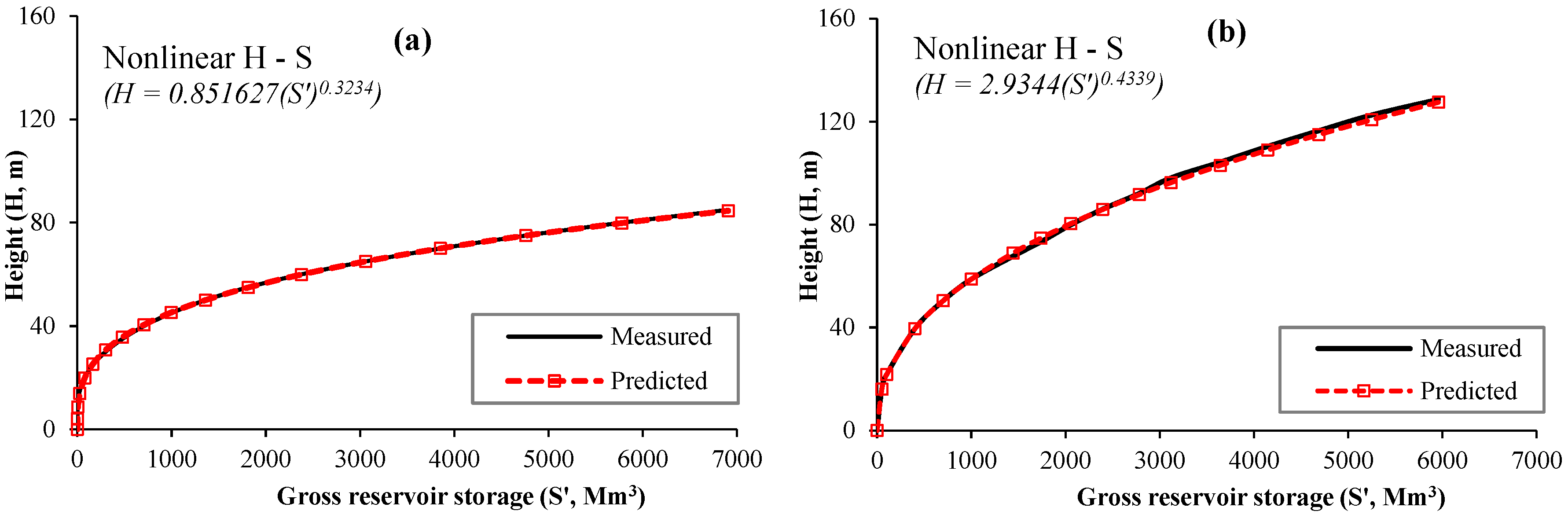
2.3.4. Nonlinear Height–Storage Equation
2.3.5. GRanD Volume–Area Equation
2.4. Performance Assessment of H–A–S Formulations
3. Results and Discussion
3.1. Case Study
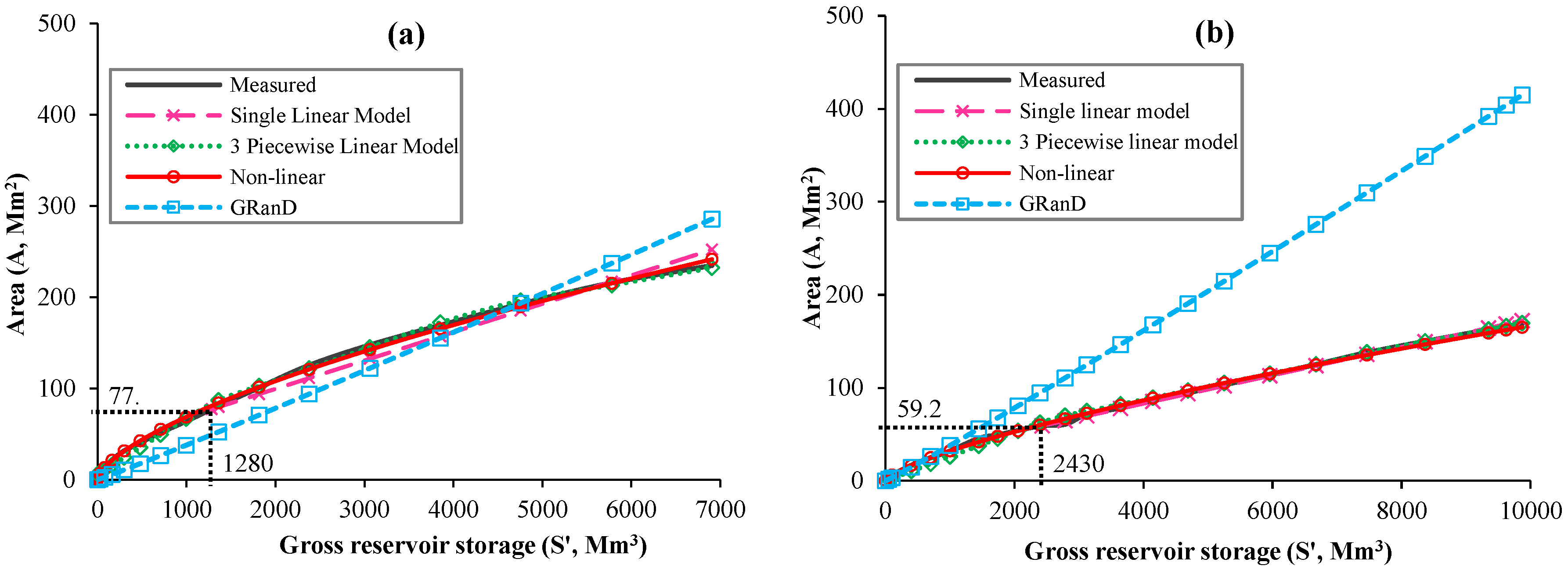
3.2. Height–Area–Storage Curves of the Reservoirs
3.3. Height–Area–Storage Models of the Reservoirs
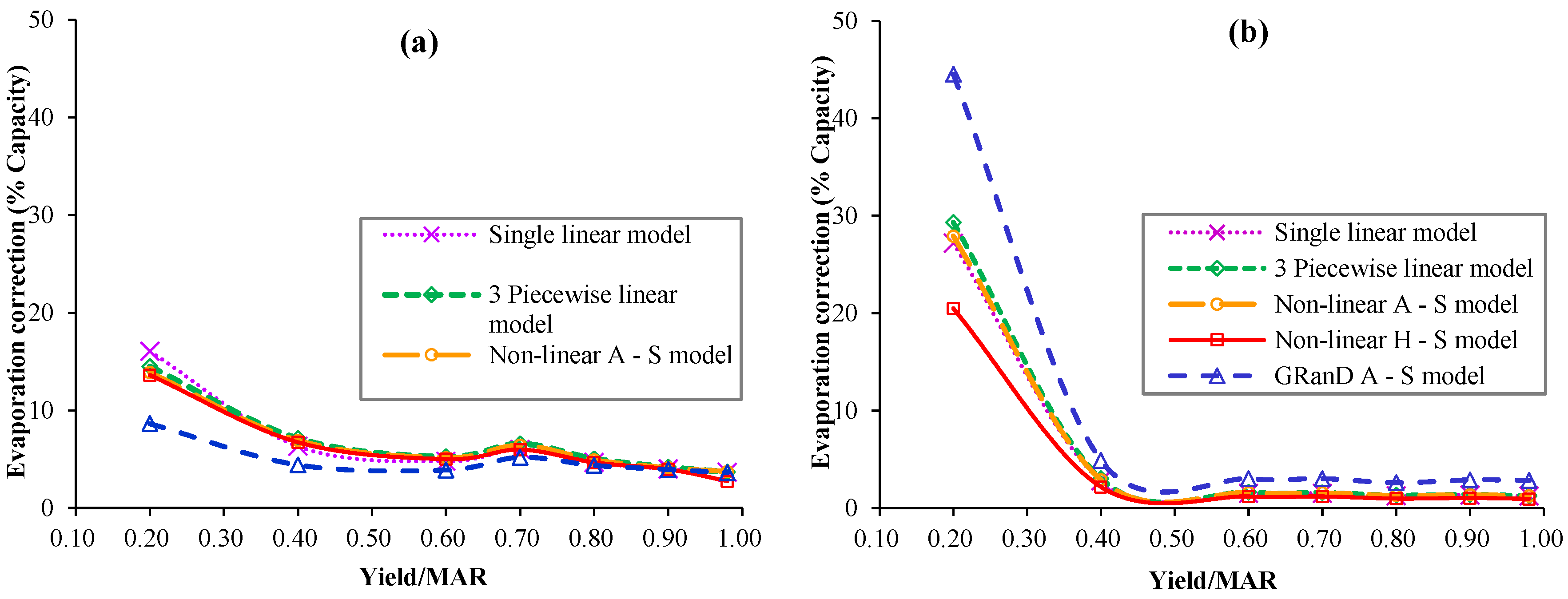
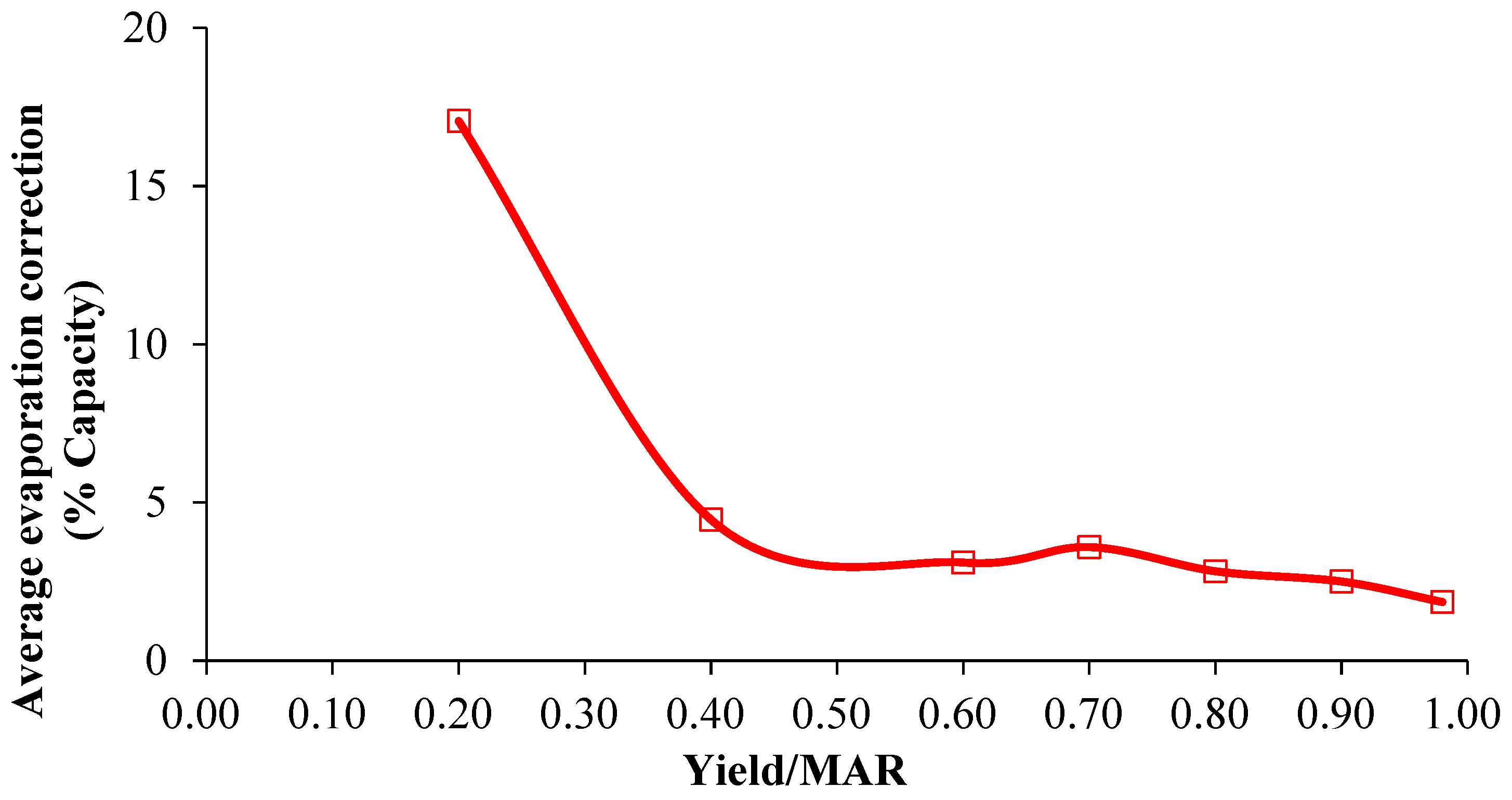
3.4. Assessed Effects of Evaporation Loss on Reservoir Storage Capacity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adeloye, A.J. Hydrological sizing of water supply reservoirs. In Encyclopedia of Lakes and Reservoirs; Springer: Dordrecht, The Netherlands, 2012; pp. 346–356. [Google Scholar]
- Campos, J.N.B.; Lima Neto, I.N.B.; Studart, T.M.C.; Nascimento, L.S.V. Trade-off between reservoir yield and evaporation losses as a function of lake morphology in semi-arid Brazil. Anais da Academia Brasileira de Ciencias 2016, 88, 1113–1125. [Google Scholar] [CrossRef] [PubMed]
- Clifford, N.J. Hydrology: The changing paradigm. Prog. Phys. Geogr. 2002, 26, 290–301. [Google Scholar] [CrossRef]
- Kenabatho, P.K.; Parida, B.P. Evaporation losses as a major factor in determining allowable yield from water supply reservoirs: The case of Botswana’s major reservoirs. WIT Trans. Ecol. Environ. (River Basin Manag. III) 2005, 83, 631–638. [Google Scholar]
- McMahon, T.A.; Pegram, G.G.S.; Vogel, R.M.; Peel, M.C. Revisiting reservoir storage—Yield relationships using a global streamflow database. Adv. Water Resour. 2007, 30, 1858–1872. [Google Scholar] [CrossRef]
- de Araújo, J.C.; Güntner, A.; Bronstert, A. Loss of reservoir volume by sediment deposition and its impact on water availability in semiarid Brazil. Hydrol. Sci. J. 2006, 51, 157–170. [Google Scholar] [CrossRef]
- Montaseri, M.; Adeloye, A.J. A graphical rule for volumetric evaporation loss correction in reservoir capacity-yield-performance planning in Urmia region, Iran. Water Resour. Manag. 2004, 18, 55–74. [Google Scholar] [CrossRef]
- McMahon, T.A.; Adeloye, A.J. Water Resources Yield; Water Resources Publications: Highlands Ranch, CO, USA, 2005; 220p. [Google Scholar]
- Loucks, D.P.; Stedinger, J.R.; Haith, D.A. Water Resources Systems Planning and Analysis; Prentice Hall Inc.: Englewood Cliffs, NJ, USA, 1981; 559p. [Google Scholar]
- Adeloye, A.J.; Montaseri, M.; Garmann, C. Curing the misbehavior of reservoir capacity statistics by controlling shortfall during failures using the modified sequent peak algorithm. Water Resour. Res. 2001, 37, 73–82. [Google Scholar] [CrossRef]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vorosmarty, C.; Fekete, B.; Crouzet, P.; Doll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
- Seiber, J.; Purkey, D. Water Evaluation and Planning (WEAP) User Guide, Stockholm Environment Institute (SEI), 2015, 109p. Available online: www.tellus.org (accessed on 10 December 2018).
- Pretto, P.B.; Chiew, F.H.S.; McMahon, T.A.; Vogel, R.M.; Stedinger, J.R. The (mis)behavior of behavior analysis storage estimates. Water Resour. Res. 1997, 33, 703–709. [Google Scholar] [CrossRef]
- Montaseri, M. Stochastic Investigation of the Planning Characteristics of within-the-Year and over-Year Reservoir System. Ph.D. Thesis, Department of Civil and Offshore Engineering, Heriot-Watt University, Edinburgh, UK, 1999. [Google Scholar]
- Montaseri, M.; Adeloye, A.J. Critical period of reservoir systems for planning purposes. J. Hydrol. 1999, 224, 115–136. [Google Scholar] [CrossRef]
- van Bemmelen, C.W.T.; Mann, M.; de Ridder, M.P.; Rutten, M.M.; van de Giesen, N.C. Determining water reservoir characteristics with global elevation data. Geophys. Res. Lett. 2016, 43, 11278–11286. [Google Scholar] [CrossRef]
- Shukla, S.; Jain, S.K.; Kansal, M.L.; Chandniha, S.K. Assessment of sedimentation in Pong and Bhakra reservoirs in Himachal Pradesh, India, using geospatial technique. Remote Sens. Appl. Soc. Environ. 2017, 8, 148–156. [Google Scholar] [CrossRef]
- BBMB. Bhakra Beas Management Board. Available online: www.210.212.64.190/BBMB (accessed on 15 December 2018).
- Nawaz, N.R.; Adeloye, A.J.; Montaseri, M. The impact of climate change on storage-yield curves of multi-reservoir systems. Nord. Hydrol. 1999, 30, 129–146. [Google Scholar] [CrossRef]
- Liebe, J.; van de Giesen, N.; Andreini, M. Estimation of small reservoir storage capacities in a semi-arid environment: A case study in the Upper East Region of Ghana. Phys. Chem. Earth Parts A/B/C 2005, 30, 448–454. [Google Scholar] [CrossRef]
- Sawunyama, T.; Senzanje, A.; Mhizha, A. Estimation of small reservoir storage capacities in Limpopo River Basin using geographical information systems (GIS) and remotely sensed surface areas: Case of Mzingwane catchment. Phys. Chem. Earth Part A/B/C 2006, 31, 935–943. [Google Scholar] [CrossRef]
- Annor, F.O.; van de Giesen, N.; Liebe, J.; van de Zaag, P.; Tilmant, A.; Odai, S.N. Delineation of small reservoirs using radar imagery in a semi-arid environment: A case study in the upper east region of Ghana. Phys. Chem. Earth 2009, 34, 309–315. [Google Scholar] [CrossRef]
- Meigh, J. The impact of small farm reservoirs on urban water supplies in Botswana. Nat. Resour. Forum 1995, 19, 71–83. [Google Scholar] [CrossRef]
- Rodrigues, L.N.; Sano, E.E.; Steenhuis, T.S.; Passo, D.P. Estimation of small reservoir storage capacities with remote sensing in the Brazilian Savannah region. Water Resour. Manag. 2012, 26, 873–882. [Google Scholar] [CrossRef]
- Kaveh, K.; Hosseinjanzadeh, H.; Hosseini, K. A new equation for calculation of reservoir’s area-capacity curves. KSCE J. Civ. Eng. 2013, 17, 1149–1156. [Google Scholar] [CrossRef]
- Fennessey, N.M. Sensitivity of reservoir-yield estimates to model time step surface-moisture fluxes. J. Water Resour. Plan. Manag. ASCE 1995, 121, 310–317. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Lallemand, F.; McMahon, T.A. Regression models for within-year capacity adjustment in reservoir planning. Hydrol. Sci. J. 2003, 48, 539–552. [Google Scholar] [CrossRef][Green Version]


| Description | Pong Reservoir | Bhakra Reservoir |
|---|---|---|
| Catchment area (km2) | 12,560 | 56,980 |
| Surface area at full capacity (km2) | 240 | 162.48 |
| Gross storage capacity (Mm3) | 8570 | 9621 |
| Active (live) storage capacity (Mm3) | 7290 | 7191 |
| Dead storage capacity (Mm3) | 1280 | 2430 |
| Elevation at top of dam (masl.) | 435.86 | 518.16 |
| Height above river bed (m) | 61 | 167.64 |
| Minimum annual flow (Mm3) | 5211 | 12,346 |
| Maximum annual flow (Mm3) | 9621 | 18,928 |
| Mean annual flow (Mm3) | 7621 | 16,567 |
| CV | 0.20 | 0.15 |
| Models | Pong Reservoir | Bhakra Reservoir | ||||
|---|---|---|---|---|---|---|
| Equation | RMSE | R2 | Equation | RMSE | R2 | |
| Single Linear A–S | A = 77.17 + 0.0311(S) | 15.13 | 0.960 | A = 59.16 + 0.0152(S) | 1.92 | 0.997 |
| 3-Piecewise Linear A–S | A1 = 5.91 + 0.0613(S′) (if S′ < 1280 Mm3) A2 = 40.68 + 0.0341(S′) (if 1280 ≤ S′ < 4365 Mm3) A3 = 116.2 + 0.0168(S′) (if S′ > 4365 Mm3) | 4.18 | 0.970 | A1 = 17.18 + 0.0185(S′) (if S′ < 2430 Mm3) A2 = 20.32 + 0.0172(S′) (if 2430 ≤ S′ < 7276 Mm3) A3 = 32.23 + 0.0155S′ (if S′ > 7276 Mm3) | 3.52 | 0.970 |
| Nonlinear A–S | A = 0.7773538(S′)0.6492 | 3.03 | 0.998 | A = 0.2284(S′)0.7158 | 2.77 | 0.993 |
| Nonlinear H–S | H = 4.851627(S′)0.3234 | 0.54 | 0.999 | H = 2.9344(S′)0.4339 | 1.42 | 0.997 |
| GRanD Nonlinear S–A | S′ = 30.684(A)0.9578 | 22.72 | 0.800 | S′ = 30.684(A)0.9578 | 133.24 | 0.800 |
| Yield (MAR) | Without Evaporation | With Evaporation for Different H–A–S Formulations | ||||
|---|---|---|---|---|---|---|
| Single Linear | Multiple Linear | Nonlinear A–S | Nonlinear H–S | GRanD A–S | ||
| 0.2 | 11.5 | 13.3 | 13.1 | 13.1 | 13 | 12.5 |
| 0.4 | 76.9 | 81.8 | 82.4 | 82.3 | 82.1 | 80.3 |
| 0.6 | 167.6 | 175.6 | 176.4 | 176.3 | 175.9 | 174.1 |
| 0.7 | 225.6 | 239.2 | 240.5 | 240.1 | 239.1 | 237.4 |
| 0.8 | 336.8 | 352.5 | 353.7 | 353.4 | 352.5 | 351.5 |
| 0.9 | 447.9 | 465.9 | 466.6 | 466.4 | 465.6 | 465.6 |
| 0.98 | 510.7 | 529.4 | 529.5 | 529.7 | 524.8 | 529.2 |
| Yield (MAR) | Without Evaporation | With Evaporation for Different H–A–S Formulations | ||||
|---|---|---|---|---|---|---|
| Single Linear | Multiple Linear | Nonlinear A–S | Nonlinear H–S | GRanD A–S | ||
| 0.2 | 2.8 | 3.6 | 3.6 | 3.6 | 3.4 | 4.1 |
| 0.4 | 82.8 | 85.2 | 85.4 | 85.3 | 84.6 | 86.9 |
| 0.6 | 219.5 | 222.8 | 223.1 | 223.0 | 222.1 | 226.1 |
| 0.7 | 309.0 | 313.7 | 313.9 | 313.8 | 312.7 | 318.4 |
| 0.8 | 400.2 | 405.3 | 405.5 | 405.4 | 404.1 | 410.6 |
| 0.9 | 585.5 | 593.5 | 593.7 | 593.6 | 591.6 | 602.5 |
| 0.98 | 758.7 | 768.3 | 768.4 | 768.2 | 766.0 | 780.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeloye, A.J.; Wuni, I.Y.; Dau, Q.V.; Soundharajan, B.-S.; Kasiviswanathan, K.S. Height–Area–Storage Functional Models for Evaporation-Loss Inclusion in Reservoir-Planning Analysis. Water 2019, 11, 1413. https://doi.org/10.3390/w11071413
Adeloye AJ, Wuni IY, Dau QV, Soundharajan B-S, Kasiviswanathan KS. Height–Area–Storage Functional Models for Evaporation-Loss Inclusion in Reservoir-Planning Analysis. Water. 2019; 11(7):1413. https://doi.org/10.3390/w11071413
Chicago/Turabian StyleAdeloye, Adebayo J., Ibrahim Y. Wuni, Quan V. Dau, B.-S. Soundharajan, and K. S. Kasiviswanathan. 2019. "Height–Area–Storage Functional Models for Evaporation-Loss Inclusion in Reservoir-Planning Analysis" Water 11, no. 7: 1413. https://doi.org/10.3390/w11071413
APA StyleAdeloye, A. J., Wuni, I. Y., Dau, Q. V., Soundharajan, B.-S., & Kasiviswanathan, K. S. (2019). Height–Area–Storage Functional Models for Evaporation-Loss Inclusion in Reservoir-Planning Analysis. Water, 11(7), 1413. https://doi.org/10.3390/w11071413