The Analysis of Short-Term Dataset of Water Stable Isotopes Provides Information on Hydrological Processes Occurring in Large Catchments from the Northern Italian Apennines

Abstract

This study discusses a dataset of water stable isotopes from precipitation (4 rain gauges) and surficial water (9 rivers) from the northern Italian Apennines, an area in which clay-rich bedrocks widely outcrop and the runoff response to precipitation events is very rapid. The dataset has been compiled starting from existing data that had previously been published in the literature and consists of monthly values of stable isotopes oxygen-18 (¹⁸O) and deuterium (²H) lasting over the period from January 2003 to December 2006 (precipitation) and from January 2006 to December 2007 (surficial water). For this period, mean residence times estimated by means of a sine-wave fitting technique make evident the significant differences over time spent by water molecules within the 9 catchments. Moreover, isotopic compositions of rivers deviated from those of precipitations revealing the influence of some catchment characteristics in differentiating the isotopic composition in rivers. Further correlations between mean residence times of river water and selected catchment characteristics reveal the role of orography and bedrocks in delaying the water molecules during their flow-paths. In addition, time series and cross–correlation analyses indicate a certain control by the main watershed divide on the isotopic composition of river waters, which is reflected in a progressive isotopic variation with longitude. The study shows that, despite using a short-time dataset (2-years for surficial water) of sparse stable isotopes can provide remarkable indications for depicting hydrological processes in large catchments made up of clay-rich bedrocks.

1. Introduction

Catchments are complex hydrological systems in which the understanding and quantification of the several processes participating in the final runoff is a challenge [1]. This is because the hydrological processes are heterogeneous and their full understanding is not achieved even on small scales (i.e., that of the slope). Thus, extrapolating hydrological processes occurring at the slope scale to a larger scale (i.e., that of catchment) is difficult. Among others, oxygen (¹⁸O and ¹⁶O) and hydrogen isotopes (²H and ¹H) compose the water molecules and have commonly been considered powerful tools for gaining information on the hydrological processes for a long time [2,3]. At the catchment scale, they have been extensively used to understand the runoff mechanisms by collecting isotopic data from the different components participating in the hydrological cycle. The number of components to be monitored depends on the type of catchment. For example, in glacierized catchments, the isotopic data of the snow and glacier melt water, in addition to those of precipitation and runoff, are essential [4,5]. In catchments located at lower altitudes, it is common to collect water isotopes from precipitation, runoff, soil moisture and groundwater [6,7,8].

The above-mentioned studies have mainly involved small-catchments (in which areas are generally less than 100 km²) as the complexity and heterogeneity of hydrological processes are often less there. In larger catchments, the use of water isotopes may be less effective as the number of components with different isotopic compositions generally become higher and their signal unclear. For example, the runoff in large catchments can be fed by aquifers with different isotopic signals while rainfall may not have a unique isotopic value if it takes place at different altitudes (i.e., altitude effect).

Moreover, when considering the annual seasonality of isotope data, isotopic variations in river discharges are generally damped due to the times spent by water molecules travelling along the catchments (i.e., transit times) and to the contribution of groundwater, which has a relatively constant isotopic signal. As a result, the longer the paths are (and/or the larger is the contribution of groundwater to rivers) the more the variation of the isotopes in rivers is damped. In the case of large catchments characterized by long transit times or catchments in which the quota of groundwater in discharge is prevalent, the isotopic variation of isotopes in river water may even be nil [9].

In addition, several processes can take place on a catchment scale modifying the former isotopic signal of precipitation collected in rain gauges. These processes are usually enhanced in large catchments. Among others and without claiming to be exhaustive, evapotranspiration occurring within the soils during specific periods of the year or anthropogenic impacts due to reservoirs, irrigation and water treatment plants are responsible for river water that is typically enriched in heavy isotopes compared to the precipitation. The same effect (i.e., river water enriched in heavy isotopes compared to precipitation) is related to sublimation processes acting on the snowpack accumulating in the uppermost parts of the catchments [10,11].

Due to the problems outlined above, few studies in the literature have used water isotope time-series to depict hydrological processes from large catchments worldwide (see, for instance and without claiming to be exhaustive: [12,13,14,15,16,17,18,19]). Consequently, even fewer studies have compared the temporal and spatial behaviour of water isotopes from rivers at a regional scale. A recent paper by [20] has analysed the temporal and spatial patterns of water isotopes in nine large catchments from Germany and their relationships with isotopic composition in precipitation and some selected catchment characteristics. Firstly, the Authors confirmed that the use of the time series of water isotopes provides information on the hydrological processes in large catchments. Secondly, water isotopes in the river can deviate from the isotopic compositions of precipitations collected in the large catchments because of natural and anthropogenic processes such as evapotranspiration from the soils and river network as well as evaporation from reservoirs. Furthermore, they verified statistical associations between the average isotopic values recorded in catchments and some specific physiographic characteristics.

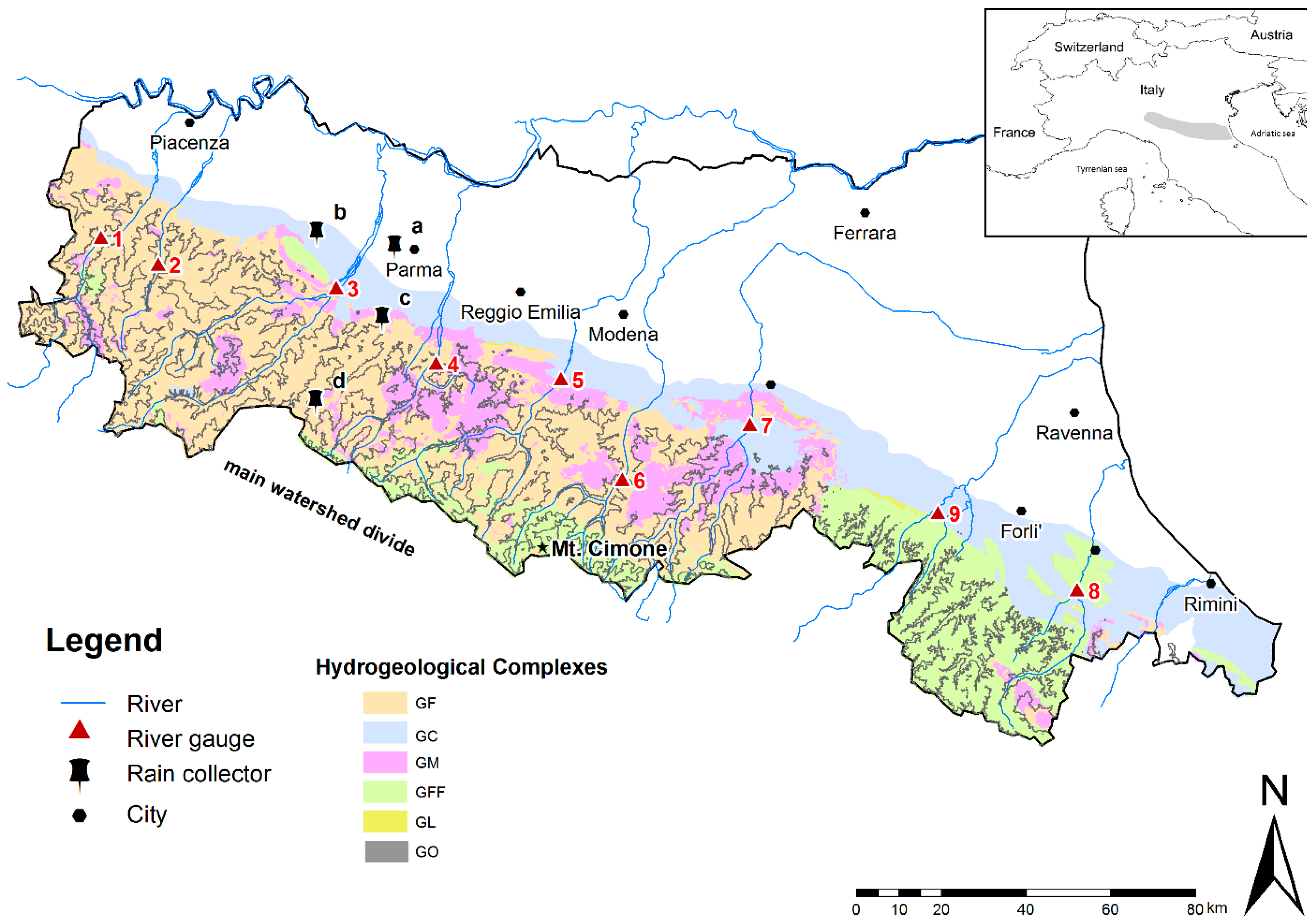
In this study, we have combined several existing datasets concerning both rains and rivers from the northern Italian Apennines, an area in which the runoff response to precipitation events is usually rapid in all the rivers due to the widely outcrop of clay-rich bedrocks. A final dataset was created and includes monthly isotopic data collected in 4 rain gauges (period January 2003–December 2006) and 9 rivers (period January 2006–December 2007). The data are integrated with the corresponding monthly discharges in river gauges where water isotopes were collected.

The purpose of this work is to verify which information can be gained by this short-time (2 years) isotopic dataset consisting of grabbed water samples from large catchments made up of clay-rich bedrocks. Despite the use of short-time (<3 years) and scattered isotopic series in rivers being uncommon, their temporal fluctuations should be enhanced by the poorly permeable bedrocks so that some hydrological information can be preserved. In this the paper, we will provide an overview of the spatial and temporal variability of isotopic composition in precipitations and river waters together with estimates of residence times in catchments. Finally, time series analysis of the isotopes in rivers is tested and possible statistical associations with selected catchment characteristics will be investigated.

2. Study Area

The study area extends over 6261 km² in the northern Italian Apennines and includes 9 catchments between the Trebbia River and the Savio River (Figure 1). Elevation decreases toward NE direction and ranges from the 2165 m a.s.l of Mt. Cimone to approximately 40 m a.s.l. of the Savio River gauge. As reported in [21], the mean annual rainfall distribution over the period 1990–2015 exceeds 2200 mm/y near the main watershed divide and progressively decreases to about 900 mm/y in foothills. The rainfall distribution during the year is characterized by a marked minimum in the summer season and two maxima during autumn (the main one) and spring. At the end of the winter season and in the vicinity of the main watershed divide, the cumulative annual snow cover can reach 2–3 m. Potential evapotranspiration ranges from about 500 mm/y up to 650 mm/y in the lowlands and is mainly active during the summer months. All the 9 rivers included in this study originate from the main watershed divide and flow toward NE. Six rivers (namely, Trebbia, Nure, Taro, Enza, Secchia and Panaro) are tributaries of the Po River while the other 3 (Reno, Lamone and Savio) enter the Adriatic sea after the sampling sites. Catchment areas are between 193 km² (Lamone) and 1300 km² (Secchia), while flow lengths range from 28 km (Enza) to 85.2 km (Secchia). Mean annual discharges over the period 2006–2016 are included between 8.4 m³ s⁻¹ (Savio) and 30.4 m³ s⁻¹ (Secchia).

Recently, [22] grouped all the bedrocks outcropping in the northern Italian Apennines into six main hydrogeological complexes (namely: clay, marl, flysch, foreland flysch, ophiolite, limestone). Among them, the most represented (in terms of areal coverage) are those composed of clay-rich materials (clay, marl and flysch hydrogeological complexes; see Figure 1). These are considered as impermeable or poorly permeable bedrocks leading to a runoff response of rivers that closely follows the rainfall distribution during the year (pluvial discharge regime). Rivers originating from the most elevated parts of the main watershed divide (Secchia, Panaro) are characterized by a nival-pluvial discharges regime as they are influenced by the melting of snow cover accumulated during the winter months in the upper parts of their catchments.

Due to this, marked low-flows take place in the summer-beginning of autumn periods (August, September and October) while floods usually occur in autumn (October and November) and spring (March and April). With reference to intense precipitation events occurring in the wettest periods, the time-lag of peak discharges is usually less than 24 h.

3. Dataset

3.1. Isotopic Data

Stable oxygen and hydrogen isotope data from precipitation located in the study area were collected from an unpublished master’s thesis [23] and from selected published papers [24,25]. The result of these activities is a final dataset consisting of monthly isotopic data from 4 rain gauges (maximum time window: January 2003–December 2006) located at different altitudes along the northern Apennines (Figure 1). Monthly data of the oxygen and hydrogen isotopes from 9 rivers in the study area are derived from [26]. In the case of both precipitation and river waters, isotopic analyses were carried out by using Isotope Ratio Mass Spectrometry (IRMS). The results are reported as a deviation of the sample from the standard (Vienna Standard Mean Oceanic Water: V-SMOW) and presented in the δ-notation as per mil (‰), where δ = [(R_S/R_V-SMOW) − 1] × 1000; R_S represents either the ¹⁸O/¹⁶O or the ²H/¹H ratio of the sample and R_V-SMOW is ¹⁸O/¹⁶O or the ²H/¹H ratio of the V-SMOW. In all the cases, instrument precision (1σ) was in the order of ±0.05‰ for δ¹⁸O and 0.7‰ for δ²H.

Starting from δ¹⁸O and δ²H values, the deuterium-excess (d^E; [27]) was calculated for each sample as:

d^E (‰) = δ²H − 8 δ¹⁸O

Corresponding uncertainty on d^E were assessed as ±0.7‰. All the data are reported in the form of Supplementary material.

3.2. River Discharge and Catchment Data

River discharge data from the 9 gauges in which [26] sampled water for isotopic analyses were provided by [28]. They consist of daily discharge data from 1 January 2006 to 31 December 2007. It is worth nothing that all the 9 catchments are characterized by a low degree of urbanization and no presence of remarkable artificial reservoirs and/or diversions.

Following [20], 7 catchment characteristics (or descriptors) related to catchment area (A), elevation (H), precipitation (P), flow length (F) and specific mean annual runoff (q) were used to identify associations with water isotopes and the estimated residence times. As a further catchment characteristic, the specific river runoff exceeded for 95% of the observation period 2006–2007 was taken into account (q95). The latter is a low flow index that is used worldwide for the regionalization procedure and can be estimated even from a relatively short time series of daily runoffs [29,30].

A summary of the 8 descriptors is given in

Table 1. Catchment descriptors included in the analysis.

Acronym	Variable	Units	Minimum	Mean	Maximum
A	Catchment area	km2	193	696	1303
Hmin	Altitude of stream gauge	m	43	171	421
Hmax	Maximum altitude	m	1158	1784	2165
Hmean	Mean altitude	m	526	754	944
P	Precipitation	mm	924	1090	1304
F	Flow length	km	20.9	55.5	85.2
q	Specific mean annual runoff	L s−1 km−2	2.2	15.0	36.3
q95	Specific runoff exceeded for 95% of the time	L s−1 km−2	0.0	1.0	1.7

and

Table 2. Selected catchment characteristics for the 9 rivers considered in this study.

River (Code)	Catchment Characteristics
	Hmin (m a.s.l.)	Catchment Area (km2)	Hmax (m a.s.l.)	Hmean (m a.s.l.)	q (L s−1 km−2)	q95 (L s−1 km−2)	P (mm)	Flow Length (km)
Trebbia (1)	257	655	1735	938	19.4	1.6	1304	65.5
Nure (2)	421	208	1753	944	15.7	1.3	1094	20.9
Taro (3)	135	1246	1799	712	8.4	1.0	990	71
Enza (4)	231	430	2016	802	22.4	0.7	924	28
Secchia (5)	47	1303	2121	694	36.3	1.0	999	85.2
Panaro (6)	212	584	2165	939	7.4	1.7	1017	40.9
Reno (7)	60	1056	1945	639	10.8	1.1	1063	81.8
Lamone (8)	135	193	1158	593	2.2	0.5	1257	28.5
Savio (9)	43	586	1361	526	9.8	0.0	1167	77.4

. In more detail, average annual precipitation (P) was calculated for the corresponding reference period (2006–2007) for 42 stations. The average values for catchments were estimated by spatial interpolation via ordinary kriging [31]. Area (A), elevation (H_min, H_max, H_mean) and Flow length (F) were derived from a 5 × 5 m gridded digital terrain model that was created by the digitalization and linear interpolation of contour lines represented in the regional topography map at a scale of 1:5000.

4. Methodology

4.1. Comparison between Isotopic Compositions in Precipitations and Surficial Water

Averages were computed for isotopic time series of precipitation and river discharge. In detail, the statistical analyses of isotope ratios (δ) and d^E were carried out by both (1) arithmetic mean M_A and (2) weighted mean M_w as follows:

$$M_A=\frac{{{\displaystyle \sum }}_{i=1}^N{\mathsf{\delta }}_i}{N}$$

(1)

$$M_w=\frac{{{\displaystyle \sum }}_{i=1}^N{\mathsf{\delta }}_i{W}_i}{{{\displaystyle \sum }}_{i=1}^{N}Wi}$$

(2)

where W_i and δ_i are the amount of precipitation (or river discharge) and the measured monthly isotopic compositions in the i-th month of the series, respectively. N is the number of observations.

Furthermore, linear regression models were used to compare the relationship between δ¹⁸O and δ²H in water from precipitation and rivers; the linear relationships are referred to as Meteoric Water Lines (MWLs) and River Water Lines (RWLs). The predictive performances of the regression models were tested by means of Pearson’s correlation coefficient coupled with the t-distribution test.

4.2. Estimation of Mean Residence Times (MRTs) in Rivers

Mean Residence Time (MRT) represents the average time (in months) spent by water molecules within a catchment. Among others, MRTs in catchments can be estimated by comparing the δ¹⁸O time series in precipitation and river waters [9]. The method (sine-wave fitting) exploits the seasonal changes of δ¹⁸O values in precipitations and rivers, which commonly approximate input (precipitation) and output (rivers) sinusoids with different amplitudes. In fact, amplitudes of sinusoids from river waters are usually reduced as compared with those affecting precipitations because of the time spent by the water molecules travelling along their catchments. It is worth noting that the longer the path spent by the water molecules, the more dampened the δ¹⁸O output signal is. Therefore, if we consider the same input signal, smoother output sinusoids indicate catchments with higher MRTs.

From a mathematical point of view, input (precipitation) and output (rivers) sinusoids of the observed δ¹⁸O time series can be calculated following the procedures reported in [32,33,34]. In greater detail, the input time series of δ¹⁸O in precipitation can be approximated with a sinusoid δ¹⁸O_in(i) representing the predicted isotopic composition of precipitation at time i (in months):

$${\mathsf{\delta }}^{18}{O}_{in}\left(i\right)={\mathsf{\delta }}^{18}{O}_{mean}+A_{in}\cos \left(\omega i\right)$$

(3)

in which A_in is the amplitude, ω is the angular frequency (which is equal to 2π/T, where T is the period between two consecutive δ¹⁸O peaks, here sets are equal to 12 months), δ¹⁸O_mean is the estimated mean δ¹⁸O of precipitation over the whole period. The output time series δ¹⁸O_out(i) in river has a smaller amplitude A_out and a phase lag $\Phi$ with respect to the input sinusoid δ¹⁸O_in(i):

$${\mathsf{\delta }}^{18}{O}_{out}\left(i\right)={\mathsf{\delta }}^{18}{O}_{mean}+A_{out}\cos \left(\omega i+ \Phi \right)$$

(4)

If we process both Equations (3) and (4), MRTs (in months) for each river can finally be obtained as:

$$\mathrm{MRT}=\frac{\sqrt{{\left[\frac{A_{in}}{A_{out}}\right]}^2-1}}{\omega }$$

(5)

It should be noted that the method requires the a priori weighting procedure of the former δ¹⁸O time series in precipitation and rivers as their isotopic compositions are linked to the precipitation and discharge patterns [9]. Here, we followed the procedure reported in [35], where the input δ¹⁸O time series (i.e., δ¹⁸O_in(i)) is obtained by weighting the δ¹⁸O_i of monthly precipitation with its volume (P, in mm):

$${\mathsf{\delta }}^{18}{O}_{in}\left(i\right)=\frac{N{P}_i}{{{\displaystyle \sum }}_{i=1}^N{P}_i}\left({\mathsf{\delta }}^{18}{O}_i-{\mathsf{\delta }}^{18}{O}_G\right)+ {\mathsf{\delta }}^{18}{O}_G$$

(6)

where N is the number of months for which isotopes have been collected (in our case from January 2003 to December 2006, i.e., 48), while δ¹⁸O_G is the long-term mean input isotope ratio, which is calculated as:

$${\mathsf{\delta }}^{18}{O}_G=\frac{{{\displaystyle \sum }}_{i=1}^N{P}_i{\mathsf{\delta }}^{18}{O}_i}{{{\displaystyle \sum }}_{i=1}^N{P}_i}$$

(7)

This approach represents an attempt to approximate the real mass precipitation flux contributing to the river discharge. As in the case of the input δ¹⁸O time series, also the output δ¹⁸O_out time series must consider the river discharge pattern. The output δ¹⁸O_out(i) time series for each river was reconstructed by using the above-mentioned Equations (6) and (7), in which Q_i (discharge at the i-month) is used instead of P_i.

Goodness of fits (coefficient of determination R² and p-value) are given for both the input (δ¹⁸O_in) and output (δ¹⁸O_out) functions. Uncertainties of the MRTs are also reported and were calculated with the error propagation method (see [36]). As pointed out by [1], the above-mentioned MRT estimates may be affected by remarkable aggregation bias. The latter is mainly due to a certain degree of heterogeneity within the catchment, which leads relationships between tracer cycle amplitudes to be largely nonlinear. Moreover, [1] also highlighted a problem of non-stationarity as the ratio between the volume of water stored within the catchment and the average water flux is unlikely to be constant in time (i.e., steady-state condition is often not reached). The bias increases with the size of the catchment (i.e., high spatial heterogeneity and long residence times) and the simultaneous presence of sub-catchments with different travel times, which in turn leads MRTs to be largely underestimated. However, [1] confirmed that A_out/A_in ratios are themselves “aggregated with very little bias and also very small random errors.” In order to further check the possible presence of aggregation bias within the 9 catchments, A_out/A_in ratios were compared with the corresponding MRTs. In case the size of the catchments (here we recall that catchments areas vary of 1 order of magnitude being included between 208 km² and 1303 km², see Table 2) do not lead to aggregation bias, A_out/A_in–MRT pairs should line up according to a straight line.

4.3. Reference Isotopic Compositions in Precipitations from the Northern Apennines of Italy

Precipitation waters worldwide show δ¹⁸O and δ²H values that are aligned along a regression line (i.e., the “Global Meteorological Water Line”: GMWL; [37]), which is defined as:

δ²H(‰) = 8.0 δ¹⁸O + 10.0

Although this relation is valid everywhere, more accurate regression lines can be obtained by selecting δ¹⁸O and δ²H values from reduced areas. This is due to the specific isotopic fractionation processes (i.e., vapour pressure and temperature conditions) controlling the precipitation over each area. For instance, by taking into account the precipitation waters alone from the Mediterranean area, [38] obtained the Mediterranean Meteoric Water Line (MMWL):

δ²H(‰) = 8.0 δ¹⁸O + 22.0

in which the intercept is slightly higher than that of the GMWL. On the contrary, air vapour originating from Central Europe area is recognized to provide precipitation with lower intercepts than the above-mentioned ones (see the meteoric water line, here abbreviated CEMWL for convenience, recently obtained by [39] for the Balkan zone: δ²H(‰) = 7.4 δ¹⁸O + 2.7).

This fact allows us to roughly discriminate precipitation waters originating from the Atlantic ocean (d^E close to +10.0) from those of the Mediterranean Sea (mainly the Tyrrhenian sea; higher values of d^E) and Central European areas (lower values of d^E).

Recently, several authors have dealt with the isotopic composition of precipitations from several areas in the northern Apennines of Italy [40,41,42,43,44,45]. They obtained a number of Local Meteoric Water Lines (LMWLs) in which the slopes are close to that of the GMWL, MMWL and CEMWL (between 7.7 and 9.0) while intercepts are characterized by higher variability (from 6.8 to 21.5).

The high variation affecting the “intercept” parameter confirms the contributions of precipitation coming from either northern/central Europe and the Atlantic Ocean and the Tyrrhenian Sea [43]. It should be pointed out that these three main areas of origin of the vapour masses have been further confirmed by means of the back trajectories calculation with different atmospheric tracers [46].

Isotopic gradients (i.e., the variation of δ¹⁸O or δ²H every 100 m of altitude) in the investigated area are not univocal as they vary more significantly than other mountainous areas in Italy. In particular and with reference to δ¹⁸O-altitude most of the δ¹⁸O gradients are between −0.15 to −0.25‰/100 m [43,47] but at a local scale may be much more negative (see, for instance, [44], 2017: −0.45‰/100 m) or even nil. For the northern Italian Apennines, [43] explained this behaviour as a consequence of the location of the rain collector (for which the gradient is obtained) with respect to the prevailing wind direction of the air masses. In fact, mountain reliefs play a “shadow effect” in which the relatively dry air masses on the leeside of mountain ranges have water that is enriched in ¹⁶O with respect to wetter air masses on the windward side [48,49,50]. The higher the range, the more pronounced the isotopic rain shadow, and thus the area located in the vicinity of the main watershed divide may be more affected by this phenomenon. It should be highlighted that leeward and windward sides change depending on the origins of the air masses. In the case of precipitation related to air masses originating from the Tyrrhenian Sea, the sector of the northern Apennines located north eastward of the main watershed divide, that is, our study area, is defined as the leeward side. On the contrary, water vapour from northern and central Europe condenses in the study area that is now considered the windward side.

In addition, [42] reported an anomalous depletion of δ¹⁸O in the foothills of the northern Italian Apennines for the period 2002–2004, which led to mean annual isotopic compositions that were considerably more negative than the normal ones characterizing the lower altitudes. This was due to the marked decrease in the spring and summer precipitation so that the mean annual isotopic values were slightly depleted in ¹⁸O. As a result of the δ¹⁸O—depletion in the lowland areas such as that which occurred in 2002–2004, the isotopic gradients may be nil or even positive. [25] pointed out that the same effect (i.e., change of mean annual δ-values in rain collectors) can be related to changes in the relative proportion of air masses of different origin (Tyrrhenian, Atlantic and Central European origin) that leads the final isotopic composition to be modified.

4.4. Hierarchic Cluster Analysis

The hierarchical cluster analysis was carried out to identify similarities among the isotopic time series from the 9 different catchments. Clustering was done according to unweighted pair-group average (or centroid) method, in which each group consisted of a δ¹⁸O time series from a river. The method was based on a step-by-step procedure in which, by the end, δ¹⁸O time series were grouped into branched clusters (dendrogram) based on their similarities to one another. Among the several δ¹⁸O time series from rivers, the two most similar ones were selected and linked based on the smallest average distance between all δ¹⁸O values. Progressively more dissimilar time series were linked at greater distances; at the end, they all were joined to one single cluster. The cophenetic coefficient was used as a measure of similarity between each pair of clusters; being analysed more than 2 time series, the dendrogram was supported by a cophenetic distance matrix. Further details on this methodcan be found in [51].

4.5. Multivariate Analysis of Variance (Manova)

In order to identify similarities between river sample sites and their isotopic time series, a One-way Multivariate Analysis of Variance (MANOVA) was carried out. This is the multivariate version of the univariate ANOVA testing whether two (or more) groups have the same multivariate mean. The analysis is carried out by pairwise comparisons, in which the within-group covariance matrix pooled over all groups participating in the MANOVA. Tests are significant with p < 0.01. Further details can be found in [51].

5. Results

Table 3. Meteoric water lines (RWLs) along with unweighted (M_A) and weighted average (M_W) compositions of the precipitation at each rain collector.

Rain Gauge (Altitude in m a.s.l.)	Code	Meteoric Water Lines (MWLs)			Unweighted Average (MA)			Weighted Average (MW)
		Slope	Intercept	R2	δ18O	δ2H	dE	δ18O	δ2H	dE
Parma (65)	a	7.6	6.9	0.98	−8.96	−61.1	10.6	−9.48	−64.3	11.6
Lodesana (150)	b	7.8	7.8	0.99	−9.44	−65.5	10.0	−9.68	−67.0	10.4
Langhirano (220)	c	7.8	7.6	0.99	−9.67	−67.5	9.8	−9.93	−69.1	10.3
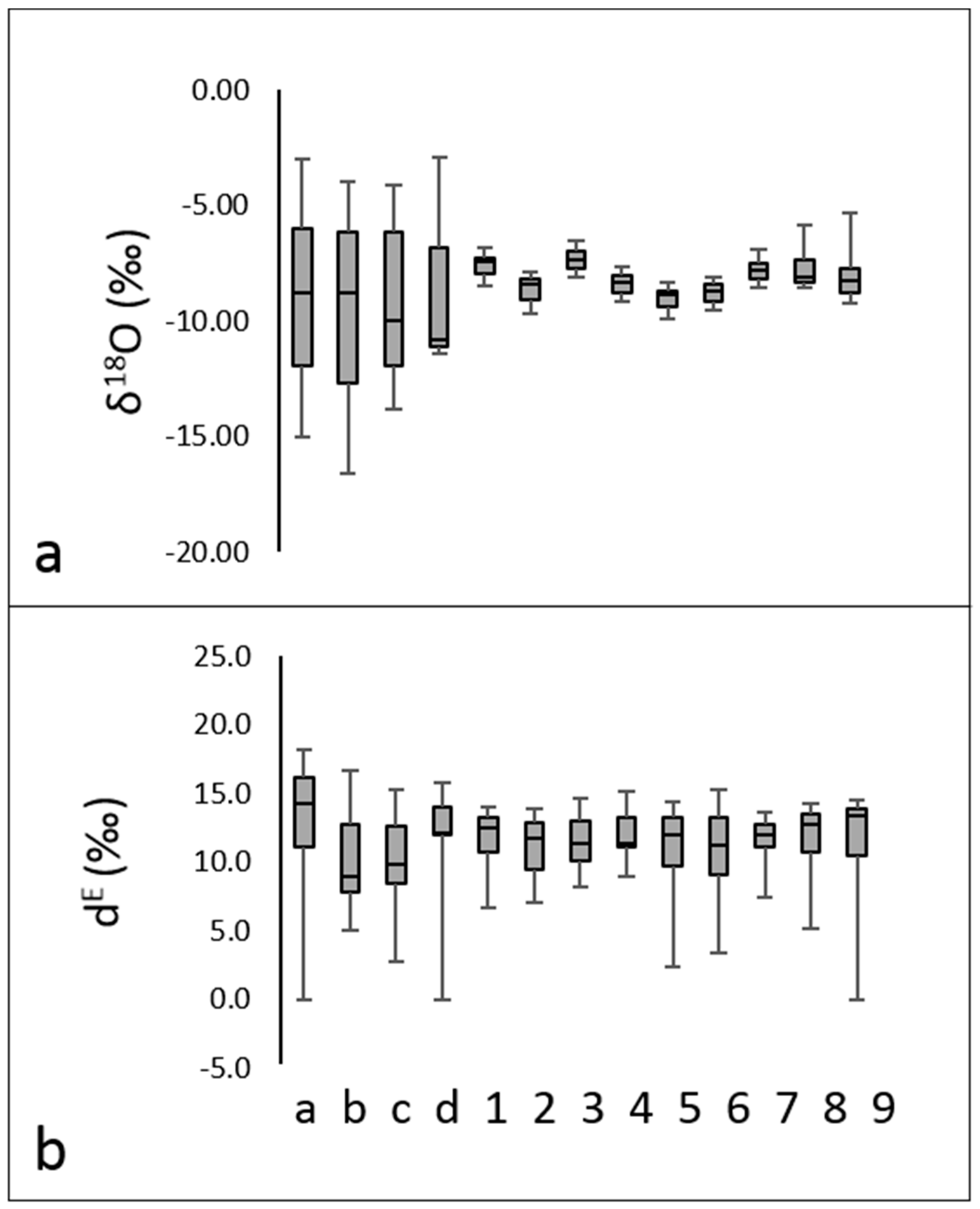
Berceto (800)	d	6.9	−1.9	0.99	−9.13	−63.0	10.1	−9.77	−67.9	10.3

summarizes the mean (M_A) and weighted (Mw) values of δ¹⁸O, δ²H and d^E in water from the rain collector. δ¹⁸O-M_A and δ²H-M_A ranges from −8.96‰ (Parma) to −9.67‰ (Langhirano) and from −61.1‰ (Parma) to −67.5‰ (Langhirano). d^E is between 9.8‰ (Langhirano) and 10.6‰ (Parma). Distributions of δ¹⁸O and d^E values from rain collectors were skewed, with mean values that may differ remarkably from the median (see box plots in Figure 2). Weighted averages (δ¹⁸O-M_W and δ²H-M_W) were slightly negative than the aforementioned unweighted means being between −9.48‰ (Parma) and −9.93‰ (Langhirano) and −64.3‰ (Parma) and −69.1‰ (Langhirano), respectively. In all the rain collectors, d^E-M_W was higher than the corresponding M_A values as they ranged from 10.3‰ (Langhirano, Berceto) to 11.6‰ (Parma). The aforementioned variation between M_A and M_W pair values is due to the fact that precipitation amount as well as its isotopic composition is not uniformly distributed during the year. 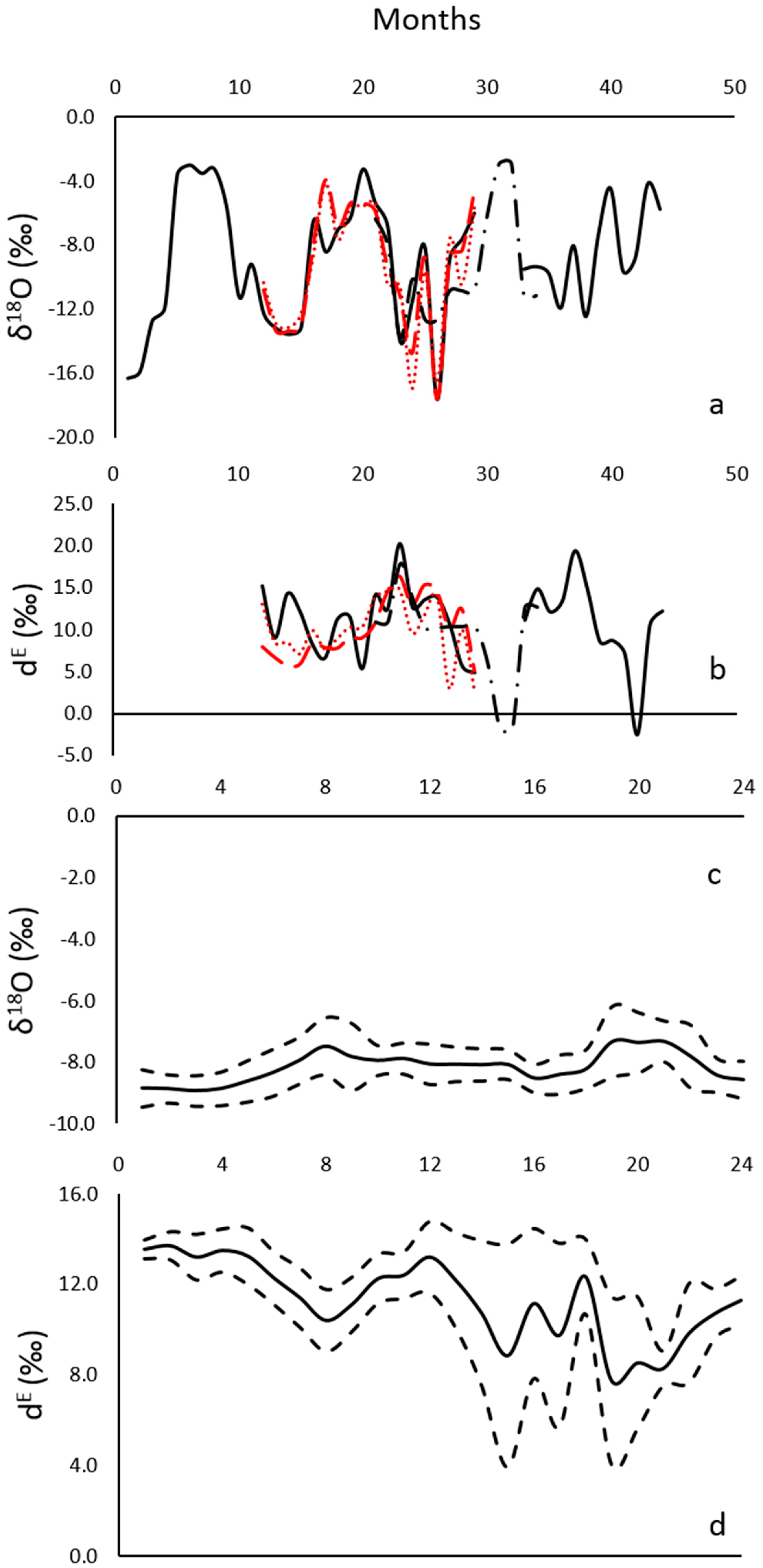In detail, and with reference to the Parma rain collector (here considered as representative of the behaviour of others rain collectors, as clearly visible in Figure 2a), δ¹⁸O values showed seasonal variations with a minimum in winter (February 2005: −17.64‰) and a maximum in summer (July 2003: −3.02‰).

The same behaviour is noticed for δ²H (not shown in Figure 2 being characterized by the same pattern of the δ¹⁸O), which in case of the Parma rain collector showed a minimum of −127.3‰ (February 2005) and maximum of −13.41‰ (July 2003). When δ¹⁸O-M_W and δ²H-M_W were more negative than the corresponding δ¹⁸O-M_A and δ²H-M_A, this meant the specific year was characterized by a larger amount of winter precipitation (i.e., more depleted isotopic values) and/or a lower quantity of summer precipitations. As d^E is obtained from the data of δ¹⁸O and δ²H, its composition in precipitation varies during the year and is usually higher in the period between the end of the autumn and spring seasons (Figure 2b; November 2004: 20.2‰; January2006: 19.3‰) and lower in summer (June 2006: −2.3‰). As a result, a larger amount of autumn-spring precipitations leads to a higher value of d^E.

By considering the river waters (

Table 4. River water lines (RWLs) along with unweighted (M_A) and weighted average (M_W) compositions of the river water.

River (Code)	River Water Lines (RWLs)			Unweighted Average (MA)			Weighted Average (MW)
	Slope	Intercept	R2	δ18O	δ2H	dE	δ18O	δ2H	dE
Trebbia (1)	5.00	−10.8	0.63	−7.55	−48.6	11.8	−7.62	−48.5	12.5
Nure (2)	6.09	−5.3	0.97	−8.57	−57.3	11.2	−8.74	−58.0	11.9
Taro (3)	6.19	−2.0	0.90	−7.46	−48.2	11.5	−7.60	−49.5	11.3
Enza (4)	5.40	−9.9	0.82	−8.41	−55.3	12.0	−8.69	−56.8	12.7
Secchia (5)	4.28	−22.8	0.33	−9.01	−61.4	10.5	−9.09	−61.1	11.6
Panaro (6)	4.80	−17.5	0.36	−8.77	−59.7	10.5	−8.91	−60.9	10.4
Reno (7)	5.63	−6.7	0.80	−7.80	−50.7	11.7	−8.15	−52.5	12.7
Lamone (8)	5.45	−7.8	0.95	−7.72	−49.9	11.9	−8.26	−52.8	13.3
Savio (9)	5.00	−13.73	0.82	−8.10	−54.3	10.6	−8.66	−57.5	11.8

and Figure 2c,d), unweighted means are more positive than the corresponding values from rains. In fact, the δ¹⁸O-M_A are included between –7.46‰ (Taro) and −9.01‰ (Secchia) while δ²H-M_A are between −48.2‰ (Taro) and −61.4‰ (Secchia), respectively. d^E-M_W values are slightly higher than in the rain as they range between 10.5‰ (Secchia, Panaro) and 12.0‰ (Enza). By considering the weighted averages, all δ¹⁸O-M_W values became more negative as they are between −7–60‰(Taro) and −9.09‰(Secchia). δ²H-M_W values were not all more negative than δ²H-M_W and are included between −48.5‰ (Trebbia) and −61.1‰(Secchia). The d^E-M_W values are slightly more positive than the corresponding d^E-M_A being between −10.4‰ (Panaro) and 12.7‰ (Secchia). As in the case of precipitation, the mismatch between unweighted (M_A) and weighted averages (M_W) pair values reflects an isotopic composition that was not uniformly distributed during the year (Figure 2c). In fact, water in rivers was much more enriched in δ¹⁸O at the end of the summer season (June, July, August) when the flow rates were lower.

Samples from rivers showed a strong attenuation of the δ¹⁸O signatures in comparison with precipitation data (Figure 3). In detail, the Lamone and Savio rivers were characterized by a higher dispersion of the δ¹⁸O values than the other rivers. On the contrary, d^E distributions from river samples were poorly attenuated with box limits (i.e., the 25th and 75th percentiles) that are often in range with those from rain water (Figure 3). This was evident for the Secchia, Panaro, Savio and Lamone rivers.

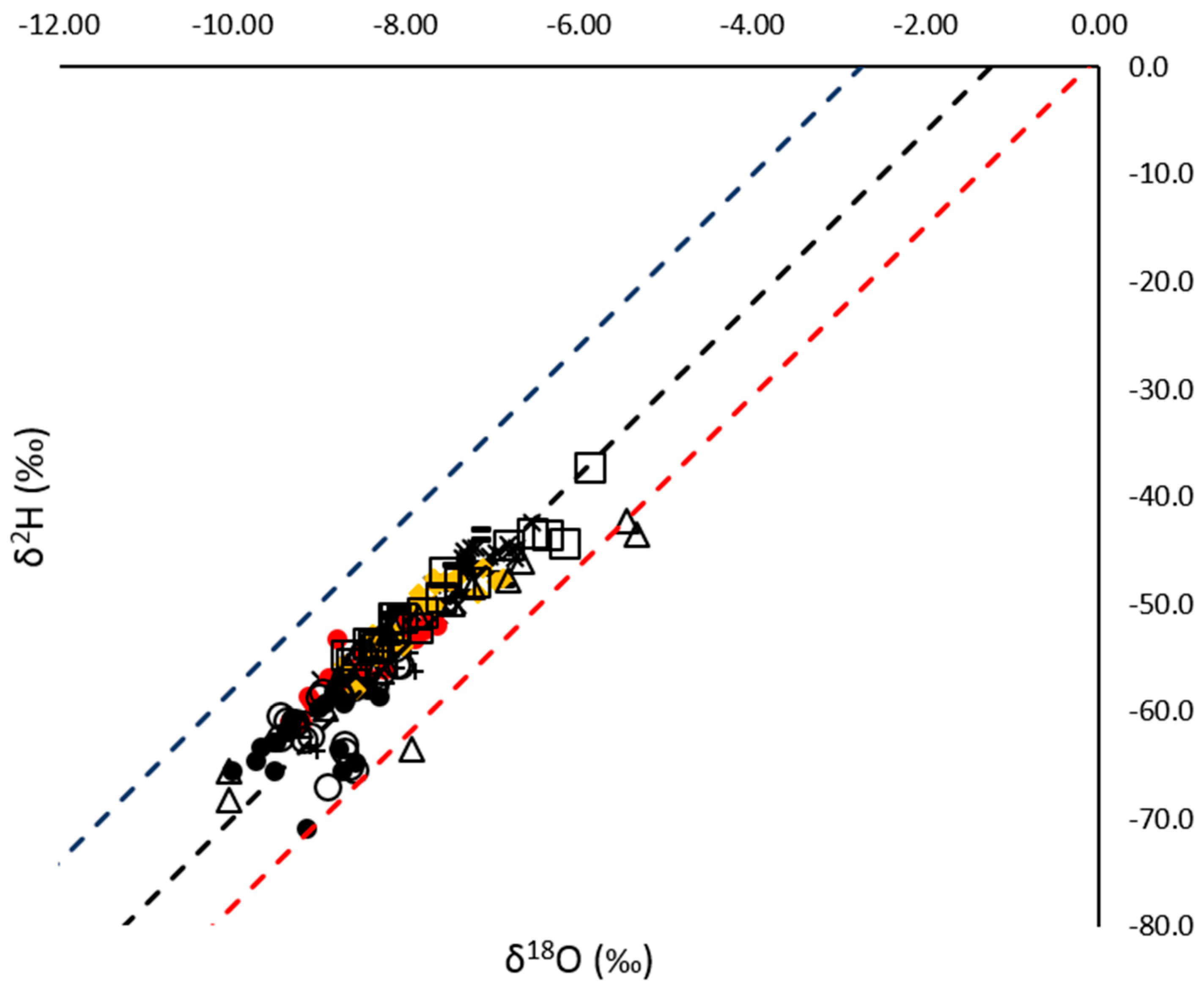
δ¹⁸O and δ²H were correlated, both in the case of precipitation and river water. The δ¹⁸O–δ²H relationships are summarized in Table 3 (Meteoric Water Lines MWLs from rain gauges) and Table 4 (River Water Lines RWLs from rivers), in which slopes, intercepts and coefficients of determinations (R²) are reported separately. Slopes obtained interpolating δ¹⁸O–δ²H pairs from rain collectors (MWLs) ranged between 6.9 (Berceto) and 7.8 (Lodesana, Langhirano). With the exception of the Berceto rain collector (−1.9), all intercepts were positive, being between 6.9 (Parma) and 7.8 (Lodesana). Slopes from RWLs were lower and ranged from 4.3 (Secchia) to 6.2 (Taro). Intercepts were always negative showing values from −2.0 (Taro) and −22.8 (Secchia). In the case of the Secchia and Panaro rivers, R² values (0.33 and 0.36, respectively) indicate weaker correlations that are due to 4 monthly samples from January 2017 to April 2017 lying far below the alignment of the others (not shown).

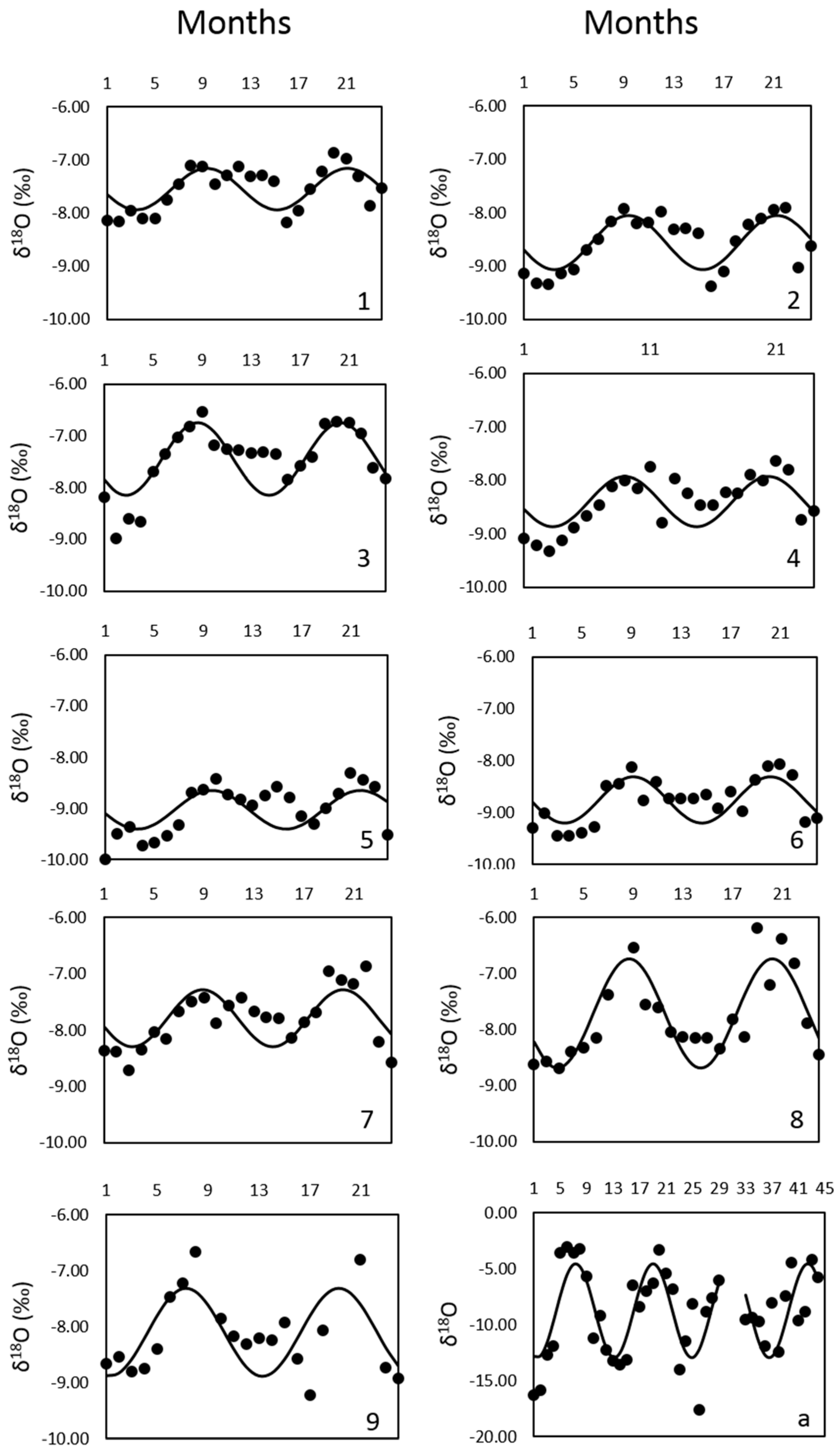
As described in Section 4.2, residence times of the river were estimated starting from a representative input function (Figure 4). A sinusoid was fitted to the δ¹⁸O data of precipitation and the corresponding amplitude (A_in = 4.250) together with the goodness of fits are summarised in

Table 5. Summary of the results for residence times. Estimates are reported (in months) along with uncertainties and sinusoidal fittings parameters.

Sinusoid (Code)	R2	A	p-Value	Residence Time (Months)	Uncertainties (Months)
Precipitation (a)	0.84	4.250	<0.0001	n.a.	n.a.
Trebbia (1)	0.52	0.402	0.0004	21	±9
Nure (2)	0.57	0.512	<0.0001	16	±10
Taro (3)	0.66	0.705	<0.0001	12	±7
Enza (4)	0.51	0.471	0.0005	18	±11
Secchia (5)	0.48	0.397	0.0016	21	±15
Panaro (6)	0.57	0.498	0.0001	17	±9
Reno (7)	0.54	0.505	0.0002	17	±10
Lamone (8)	0.76	0.974	<0.0001	8	±4
Savio (9)	0.30	0.794	0.0392	10	±9

. Fit was statistically robust (p < 0.0001) and the coefficient of determination was in the order of those obtained in other studies (see, for instance: [52,53,54]).

Modelled output sinusoids for rivers are also reported in Table 5. With the exception of the Savio River (p value remarkably higher than 0.0001 and R² = 0.30), the fits were characterized by coefficients of determination (R²) that were higher than 0.48 and always, or close to being, statistically significant (p < 0.0001). Amplitudes of output sinusoids (A_out) differed slightly as they were between 0.397 (Secchia) and 0.974 (Lamone).

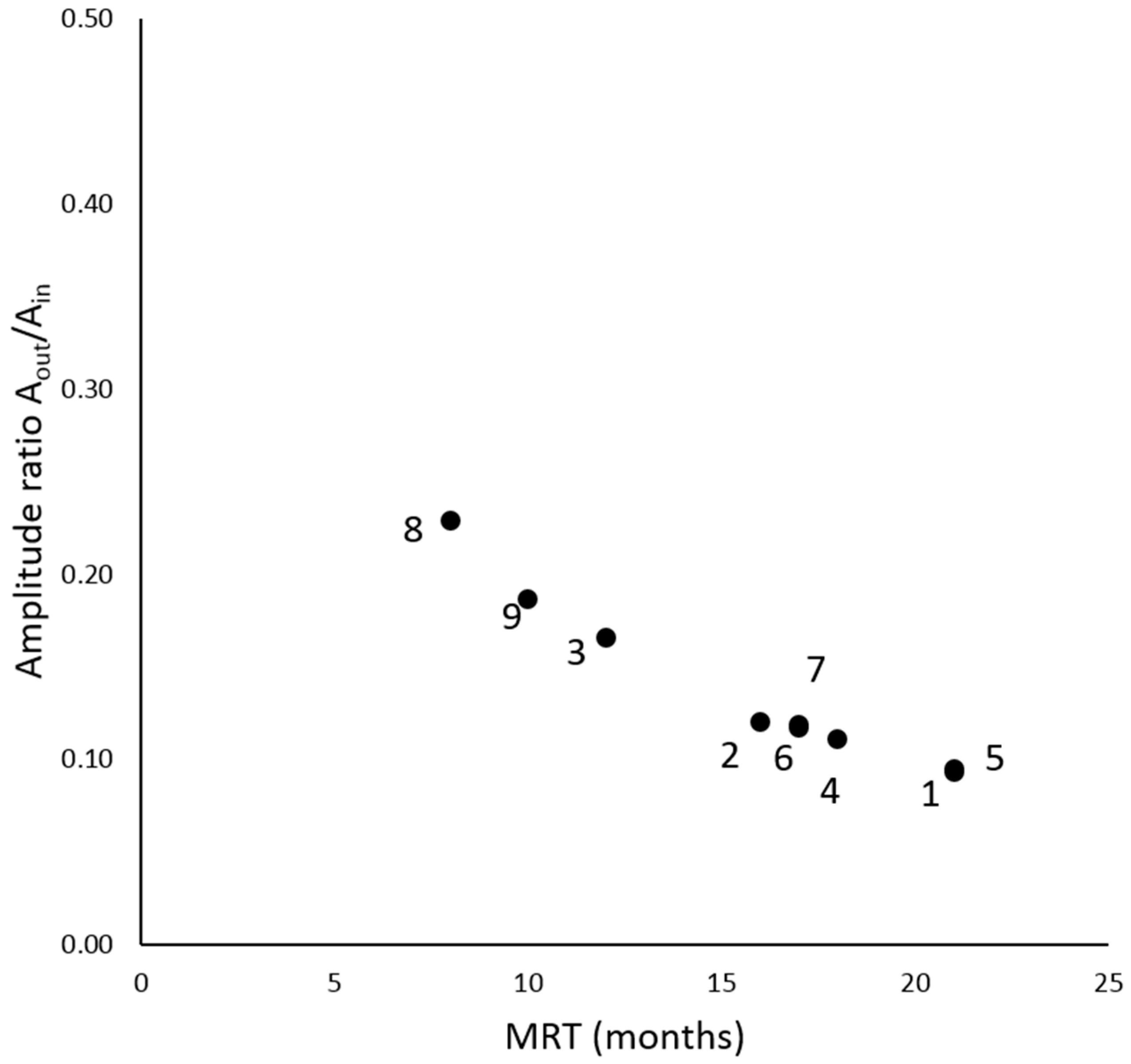
MRTs were estimated with Equation (5) and are also reported in Table 5; they ranged between 8 (Lamone) and 21 (Secchia, Trebbia) months. As shown in Figure 5, the relationship between the A_out/A_in ratios and the MRTs for the 9 catchments deviated little from a linear function, indicating a reduced effect of aggregation bias on the MRT estimates due to a large quota of river waters with fast transit time (lower than 1 year). Thus, the consequent underestimation effects did not significantly affect the final MRT values.

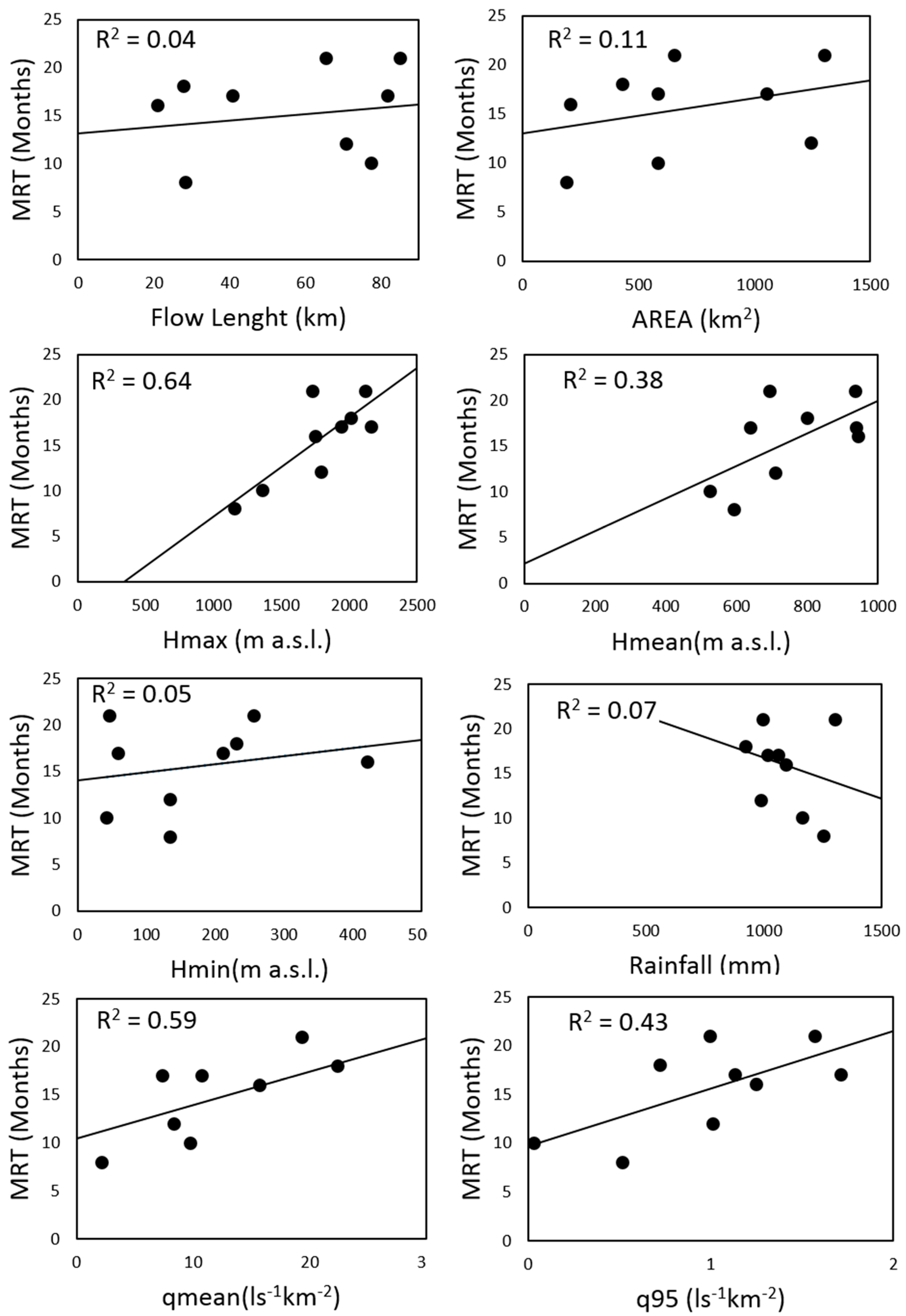
Linear relationships between catchment characteristics and the weighted δ¹⁸O and d^E averages were not significant as p values were always greater than 0.01 (plots are not reported). On the contrary, some catchment characteristics were correlated with the MRTs of rivers (Figure 6). This was the case for the mean annual specific runoff (q; R² = 0.59 and p < 0.01), the maximum altitude (Hmax; R² = 0.63 and p < 0.01) and the specific low flow discharge q95 (R² = 0.44 and p < 0.01).

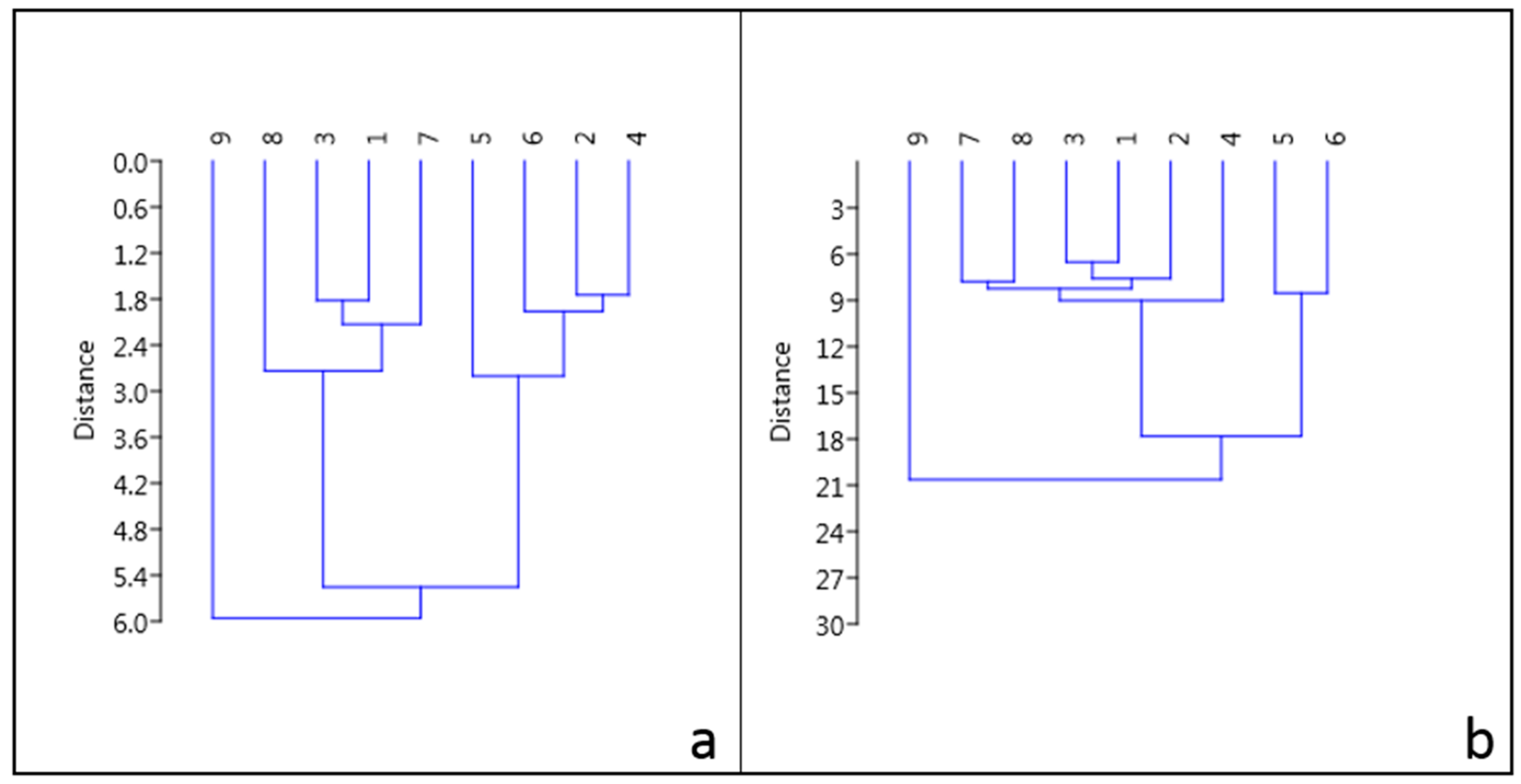
In

Table 6. Correlation matrix reporting δ¹⁸O associations among the time series in rivers. A progressively more intense green colour is associated with a higher correlation coefficient. * not significant at p = 0.01.

	Trebbia	Nure	Taro	Enza	Secchia	Panaro	Reno	Lamone	Savio
Trebbia	-
Nure	0.95	-
Taro	0.77	0.86	-
Enza	0.68	0.78	0.85	-
Secchia	0.87	0.89	0.86	0.84	-
Panaro	0.71	0.79	0.87	0.89	0.93	-
Reno	0.80	0.83	0.85	0.82	0.86	0.87	-
Lamone	0.67	0.71	0.77	0.81	0.75	0.81	0.80	-
Savio	0.45 *	0.30 *	0.40 *	0.30 *	0.38 *	0.33 *	0.40 *	0.43 *	-

, correlation coefficients between pairs of δ¹⁸O time series from the 9 rivers are reported in the form of a correlation matrix (Manova analysis). With the exception of the south-easternmost river of the area (Savio River), the monthly isotopic composition of rivers strongly correlated with each other (R² > 0.67). However, some pairs of rivers were characterized by higher correlation coefficients: this is the case of Trebbia-Nure and Secchia-Panaro rivers, with R² equal to 0.95 and 0.93, respectively. The cluster analysis (Figure 7a) among the δ¹⁸O time series from rivers demonstrated that the Savio river was associated with none of the other rivers while two main groups of catchments were clearly separated: the first one comprises Enza, Nure, Secchia and Panaro while the other group was Trebbia, Taro, Reno and Lamone. Different results were obtained from the analyses of the d^E time series: correlation coefficients were always lower than in case of δ¹⁸O time series and more rivers were not associated with each other (see

Table 7. Correlation matrix reporting d^E associations among the time series in rivers. A progressively more intense green colour is associated with a higher correlation coefficient. * not significant at p = 0.01.

	Trebbia	Nure	Taro	Enza	Secchia	Panaro	Reno	Lamone	Savio
Trebbia	-
Nure	0.74	-
Taro	0.77	0.64	-
Enza	0.59	0.62	0.59	-
Secchia	0.22 *	0.31 *	0.17 *	0.40 *	-
Panaro	0.28 *	0.32 *	0.17 *	0.44 *	0.86	-
Reno	0.68	0.64	0.51	0.35 *	0.01 *	0.05 *	-
Lamone	0.69	0.73	0.69	0.57	0.04 *	0.14 *	0.73	-
Savio	0.58	0.51	0.41*	0.36 *	0.23 *	0.31 *	0.38 *	0.56	-

and Figure 7b). In detail, the d^E time series of Taro, Trebbia and Nure were associated, as well as those of Secchia and Panaro. This was also the case of the d^E time series from Lamone and Reno rivers.

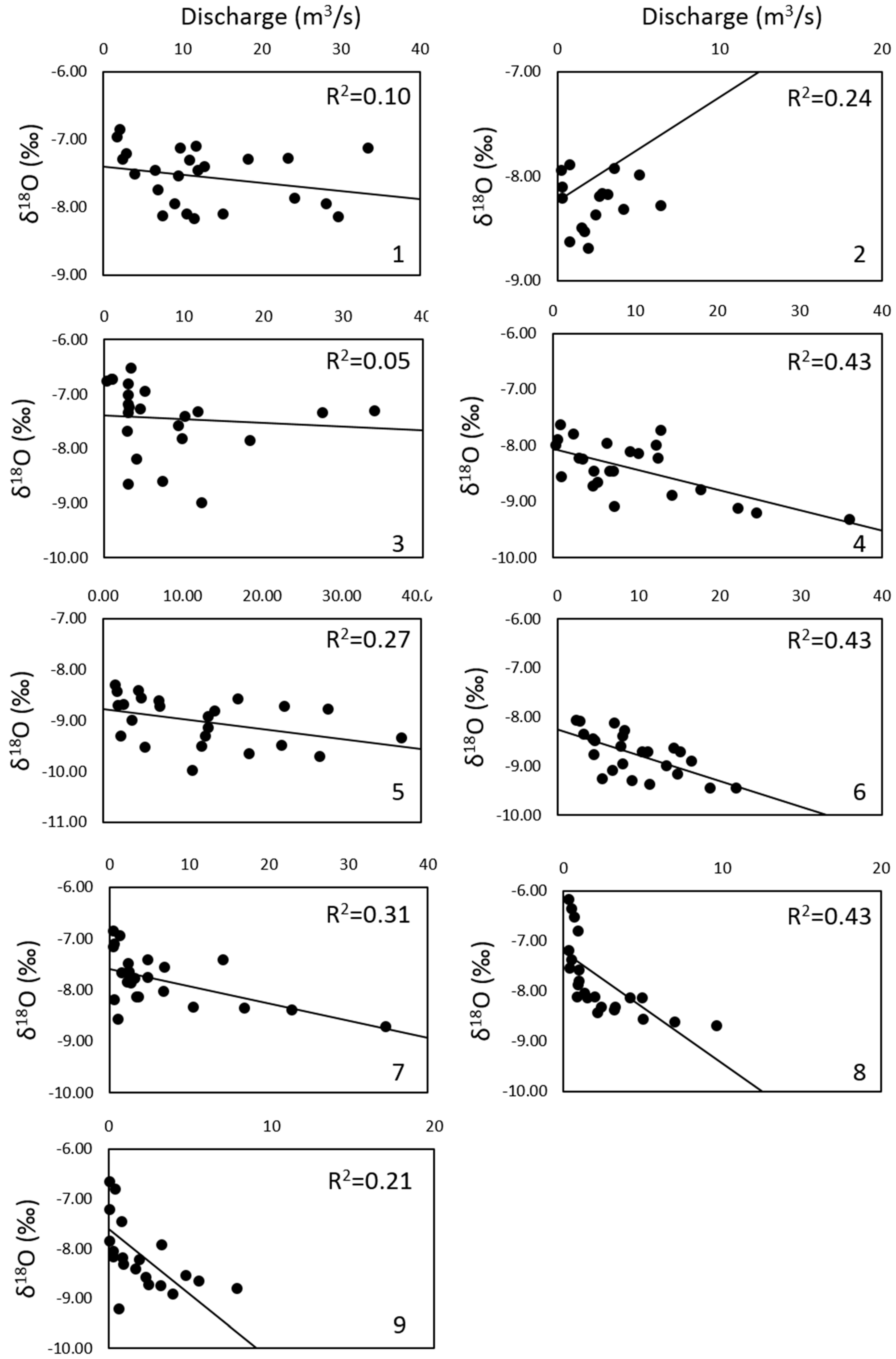
River monthly discharges affected the isotopic composition of river water. In detail, with the exception of the Taro river, values of δ¹⁸O depleted with increasing flow rates (Figure 8). On the contrary, the d^E values in the river water increased with discharge in almost all rivers (Figure 9). In the case of δ¹⁸O-discharge relationships, statistical analyses were significant for 4 rivers (Enza, Panaro, Reno, Lamone). In some cases (namely: Lamone and Savio), the relationship looks exponential rather than linear. d^E -discharge linear regressions were statistically significant for 5 rivers (Trebbia, Nure, Enza, Lamone). It must be specified that, as in the case of δ¹⁸O-discharge relationships, d^E-discharge regressions also appeared to be exponential (Reno, Lamone, Savio).

6. Discussion

6.1. Isotopic Comparison between Precipitation and Rivers and Mean Residence Time of Surface Water

For the considered time period (January 2003–December 2006), δ-values from rain collectors were not characterized by altitude-effect, that is, no depletion of δ¹⁸O (and δ²H) with altitude were noticed. In particular, while the rain collectors located at lower altitudes (Parma, Lodensana and Langhirano) showed the depletion effect (which leads to a gradient of about −0.22‰/100 m), those located at the highest altitude and in the vicinity of the main watershed divide (Berceto; 800 m a.s.l.) were characterized by enriched values of δ¹⁸O. The latter isotopic value should instead characterize lowland areas in normal periods.

As already anticipated in Section 4.3, [43] have confirmed an overall isotopic gradient (of δ¹⁸O) between −0.15 to −0.25‰/100 m that may be affected by changes in space and time. As explained by both [43] and [25], this behaviour depends on (i) local topographical effects (leeward/windward with respect to the origin of the air masses) (ii) modification in the precipitation pattern during the year and (iii) changes in the relative proportion of precipitations by air masses of different origin. In the considered time period (January 2003–December 2006), the most negative δ–values were related to a reduction in the mean annual precipitation that occurred over the lowland areas (from value of 900 mm to about 500 mm). This reduction partially took place during the spring and summer months, that is, when precipitations are usually characterized by enriched values of δ¹⁸O and δ²H. [42] have confirmed this reduction in the precipitations in lowlands areas at the foothills of the northern Apennines for the period 2004–2006. Nonetheless, [25] highlighted that the proportion of air masses of different origin had changed in the considered time period and precipitations in the vicinity of the main watershed divide were mainly controlled by air masses of Tyrrhenian origin that exhausted their condensation there. This fact is supported by the sampling of a low-yield spring located near the main watershed divide in which δ¹⁸O values were in the order of −8.50‰ [25].

In the study area, mean annual values of δ¹⁸O (and δ²H as well) in water samples from rivers were less negative than those from rain collectors (Table 3 and Table 4 and Figure 3). This is true, even taking into account the weighted δ-values with monthly amounts of precipitation (in rain collectors) and flow rates (in rivers).

δ¹⁸O enrichment noticed in rivers may indicate that these waters have been subjected to evaporative and/or evapotranspirative processes that have led to ¹⁶O enrichment. δ¹⁸O–δ²H relationships are reported in Table 3 (Meteoric Water Lines MWLs from rain gauges) and Table 4 (River Water Lines RWLs from rivers) together with slopes, intercepts and coefficients of determinations (R²). Being between 4.3 to 6.2, slopes of the RWLs were always lower than those of the precipitations from the northern Apennines (slopes from 6.9 to 7.8). In addition, in this study all intercepts in RMLs were negatives compared to those of MWLs. These values were in the order of those reported by [25] and [55] for other rivers from the northern Apennines and confirmed that these waters have undergone evaporation.

Some authors highlighted that the lowering in slopes from δ¹⁸O–δ²H relationships in rivers is due to instream evaporation. Such processes (i.e., instream evaporation) inducing slope lowering in δ¹⁸O–δ²H relationships have already been detected in rivers from non-arid environments such as Germany [20], USA [56], India [57] and Australia [58]. Moreover, they were already reported in some rivers from Italy (Arno River: [14]; Reno River: [59]; Po river: [60]).

If so, and as also suggested by [20] and by [57], a statistical association between river flow-lengths (or catchment area) and δ¹⁸O should have been found. In detail, such an association should be represented by an increase in δ¹⁸O values with flow-lengths or with catchments areas because of the progressive instream evaporation along the catchment.

In the study area, no relationships were found between unweighted (or weighted δ¹⁸O values) with flow-lengths (and catchment areas) of rivers. This leads us to suppose that, even if active, instream evaporative/evapotranspirative processes are not mainly responsible for the δ¹⁸O enrichment. Moreover, the comparison of the δ¹⁸O weighted and unweighted values with other catchment characteristics allows us to state that the process of δ¹⁸O enrichment along catchments is not linked to these factors.

Although [24,34,44,45] have recently reported for the area a number of low-yield springs in which water isotopes were not modified by evapotranspiration processes, slopes between 4 and 6 were found in several freshwater springs [61,62,63]. In this case, there is evidence of a pre-infiltrative evaporation/evapotranspiration that acted by modifying the waters before their infiltration towards the aquifer and, subsequently, to the base flow of rivers.

This is in agreement with the increase in d^E detected in river water as the contribution of the base flow from springs in the upper part of the catchments (see [25]). In fact, as in the case of δ-values, there were differences in the weighted d^E obtained from the water of the rain collectors and those of the rivers. In detail and with the exception of the Panaro river, values are always slightly higher in rivers than in rain collectors.

MRTs are between 8 and 21 months indicating hydrological differences among catchments that are not explained by aggregation biases (i.e., underestimation effects in MRT estimates are reduced). In order to identify such differences, linear relationships between selected catchment characteristics (namely: catchment area, altitude of stream gauge, maximum altitude, mean altitude, precipitation, flow length, specific mean annual runoff and specific runoff exceeded for 95% of the time) and the weighted δ¹⁸O and d^E averages were carried out. All linear relationships were not significant as p values were always greater than 0.01. On the contrary, 3 catchment characteristics were positively correlated with the MRTs of rivers (Figure 6). This is the case of the mean annual specific runoff q (R² = 0.59 and p < 0.01), the maximum altitude (Hmax; R² = 0.64 and p < 0.01) and the specific low flow discharge q95 (R² = 0.44 and p < 0.01).

As pointed out by [22], in the northern Italian Apennines, the specific low flow discharge q95 is related to the permeability of the geological formations outcropping in the catchment. The higher the permeability of the geological formations outcropping in the basin, the greater the q95 that represents the quota of groundwater released to the river network through springs. It is evident that an increase in q95 indicates a greater quantity of groundwater that makes up the flow of the watercourse; these waters are characterized by longer paths leading to an increase in the MRT. Therefore, the correlation between q95 and MRTS of water, albeit weak, could be due to the groundwater signal in the flow of rivers. The correlation between MRTs and maximum altitude of the catchments is significantly higher (R² = 0.64); this may be due to a number of concurring causes related to the Hmax descriptor. Firstly, and as already evidenced by [22], the catchment developing from the main watershed divide (i.e., the areas with higher mountain peaks) is characterized by a large number of springs. Secondly, as anticipated in Section 2, the higher areas are characterized by the presence of a snow cover that blocks the water molecules in solid form for a few months until they melt, resulting in an increase of the MRTs of water in the catchment.

6.2. Longitudinal Control on Monthly δ¹⁸O and d^E Time Series from Rivers

While the value of δ¹⁸O is linked to the condensation temperature of the drops in the clouds, d^E is linked to the temperature of evaporation of the moistures composing the air masses. It is evident that δ¹⁸O and d^E time series from rivers may indicate important evidence of similarity in the mechanisms of condensations (orographic precipitations etc.) and in the main source area of the air masses over the catchments. By following [64], we firstly plotted the δ¹⁸O–δ²H values from rivers together with the three main meteoric lines GMWL, MMWL and CEMWL reported in Section 4.3 (Figure 10). All the isotopic pairs were included with MMWL and CEMWL, while most of the samples lay above the GMWL. This means that all water were of Tyrrhenian, Central European and Atlantic origin. With more detail, some samples lay above CEMWL while others in the vicinity of the MMWL indicating that some waters were more probably related to air masses from Central Europe and the Tyrrhenian Sea, respectively. Among the others, samples close to the CEMWL came mainly from the central and easternmost part of the study area (namely: Secchia, Panaro, Lamone, Savio; Figure 10).

With reference to δ¹⁸O time-series, all rivers were clustered to one main group with the only exception of the Savio river (Figure 7a). Two sub-groups made up the main group: the first one included Lamone, Trebbia, Taro and Reno rivers while the second one contained Secchia, Panaro, Nure and Enza rivers. It should be pointed out that some neighbour catchments are more similar than distant ones. For instance, this is the case of Taro-Trebbia, Nure-Enza and Secchia-Panaro. This is also confirmed by looking at correlation values among the different δ¹⁸O time-series (correlation matrix in Table 6), from which it again emerges that all the rivers (with the exception of Savio) are strongly associated.

The same analyses carried out with d^E indicated that all rivers were clustered to one main group with the exception of the Savio river (Figure 7b). Three sub-groups namely Trebbia-Taro-Nure (western sector of the study area), Secchia-Panaro (central sector of the study area) and Reno-Lamone (eastern sector of the study area), were evident and clearly separated. These three sub-groups are evidenced in the correlation matrix (Table 7).

These results lead us to suppose a certain control made by the orography (and thus by the main watershed divide) over the δ¹⁸O and d^E time-series. In fact, and as already reported in Section 3.2, the main watershed divide is oriented NW-SE (Figure 1) and is close to the Tyrrhenian sea in the westernmost portion of the study area. This may allow air masses originating from the Tyrrhenian Sea to reach the upper parts of the catchments (Trebbia, Taro, Nure, Secchia and Panaro) in the study area (leeward site), having already suffered a significant enrichment of ¹⁶O and ¹H in the windward site. Moving eastward, this phenomenon is remarkably reduced as a quota of precipitation from the Tyrrhenian Sea is progressively in favour of air masses from Central Europe. For the considered time-period (2006–2007), the control made by air masses of Tyrrhenian origin over precipitation in the vicinity of the main watershed divide is also evidenced by the isotopic composition of water from the Berceto rain gauge.

Furthermore, we cannot neglect the role of sublimation processes acting on snow cover during the winter and spring seasons. In fact, sublimation occurring during sunny days can modify the former isotopic composition of the superficial snow layers allowing the release of a vapour phase from the solid skeleton to the atmosphere. In this case, the final snow cover does not preserve the isotopic composition of the original snowfall from which it was derived [10,11]. As anticipated in Section 2, Secchia and Panaro rivers (i.e., the central sector of the study area with the highest reliefs) are characterized by nival-pluvial discharges due to the melting of the snow cover in the upper part of the catchments during the spring months. In the δ¹⁸O and d^E time series there are evidences of sublimation in water samples from January 2017 to April 2017 that lead to weaker correlation in the corresponding RMWLs (as already seen in Table 4).

7. Conclusions

This study shows that a short-time series of scattered water isotopes can be useful in order to depict hydrological processes occurring in large catchments composed of clay-rich bedrocks. We believe that this is an important point given both the expensive costs of the more recent in-continuous and in-field sampling/analysis techniques for water isotopes and for the large number of short-time series made of scattered isotopes already available from large and clay-rich catchments worldwide. The analyses of our short-term datasets consisting of monthly values of water stable isotopes from 4 rain collectors (4-years) and 9 large catchments (2-years) have revealed further insights into the hydrological behaviour of large catchments from the northern Italian Apennines. Firstly, the role of the orography has been confirmed (and thus the main watershed divide) in selecting precipitations originating from the Tyrrhenian Sea, which were progressively reduced, moving eastward in favour of those from the Central Europe.

Secondly, MRTs in catchments from northern Italian Apennines are positively correlated with three descriptors, namely maximum altitude as well as mean annual specific runoff and (even if weakly) specific low flow discharge q95. These descriptors recall the effect of the snow cover (maximum altitude) and bedrocks (specific low flow discharge q95) on delaying the water molecules along the catchments. These statistical associations are further confirmed by verifying the almost linear relationship between the amplitudes ratios of isotopic signals from precipitation and catchments with the MRTs estimates, which in turn indicate a low degree of aggregation biases due to the large quota of water with a fast travel time.

Although a short-time isotopic dataset allowed us to obtain a certain amount of information for these catchments, further efforts should focus on investigating the spatial and temporal patterns observed in precipitations and, in particular, the role of the main watershed divide in selecting the air masses that originated elsewhere. This is a crucial point that could allow us to better define the input isotopic signal and, therefore, further improve the calculation of surficial water MRTs. Moreover, a large number of rain collectors (uniformly distributed over the northern Apennines) would allow us to verify the presence of local isotopic anomalies and of any areas where depletion of the isotopic composition with the altitude (altitude-effect) exists. In addition, isotopic data from snow cover accumulated in the central sector of study area (at least in the vicinity of the main watershed divide) should be acquired to reduce uncertainties related to sublimation processes during winter and spring months. Isotopic river monitoring should be implemented with the collection of a longer time series (at least 5 years) to reduce errors in the calculation of the MRTs. In view of the fact that discharge in rivers from the northern Apennines might change suddenly after rainfall (especially during the wet seasons), water sampling for the isotopic analyses should be performed at least hourly during the floods in order to take into account the bulk samples rather than the grab ones.