Risk Evaluation Model of Life Loss Caused by Dam-Break Flood and Its Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Risk Formation Path of Life Loss Caused by Dam-break Flood Based on the Disaster Process
2.2. Evaluation Indicator System of Life Loss Caused by Dam-Break Flood.
2.3. Risk Classification Standard of Life Loss Risk Indicators
2.4. Variable Fuzzy Evaluation Model of Life Loss Risk
2.4.1. Determining the Matrix of the Sample Eigenvalue
2.4.2. Determining the Matrix of the Standard Interval of Indicators
2.4.3. Determining the Matrix of Standard Interval Point Value
2.4.4. Determining the Matrix of Relative Membership Degree of the Indicator xij to Each Level
2.4.5. Determining the Comprehensive Membership Degree of the Indicator
2.4.6. Calculating the Comprehensive Evaluation of Grade Eigenvalue
3. Case Study
4. Result and Discussions
4.1. Model Calculation
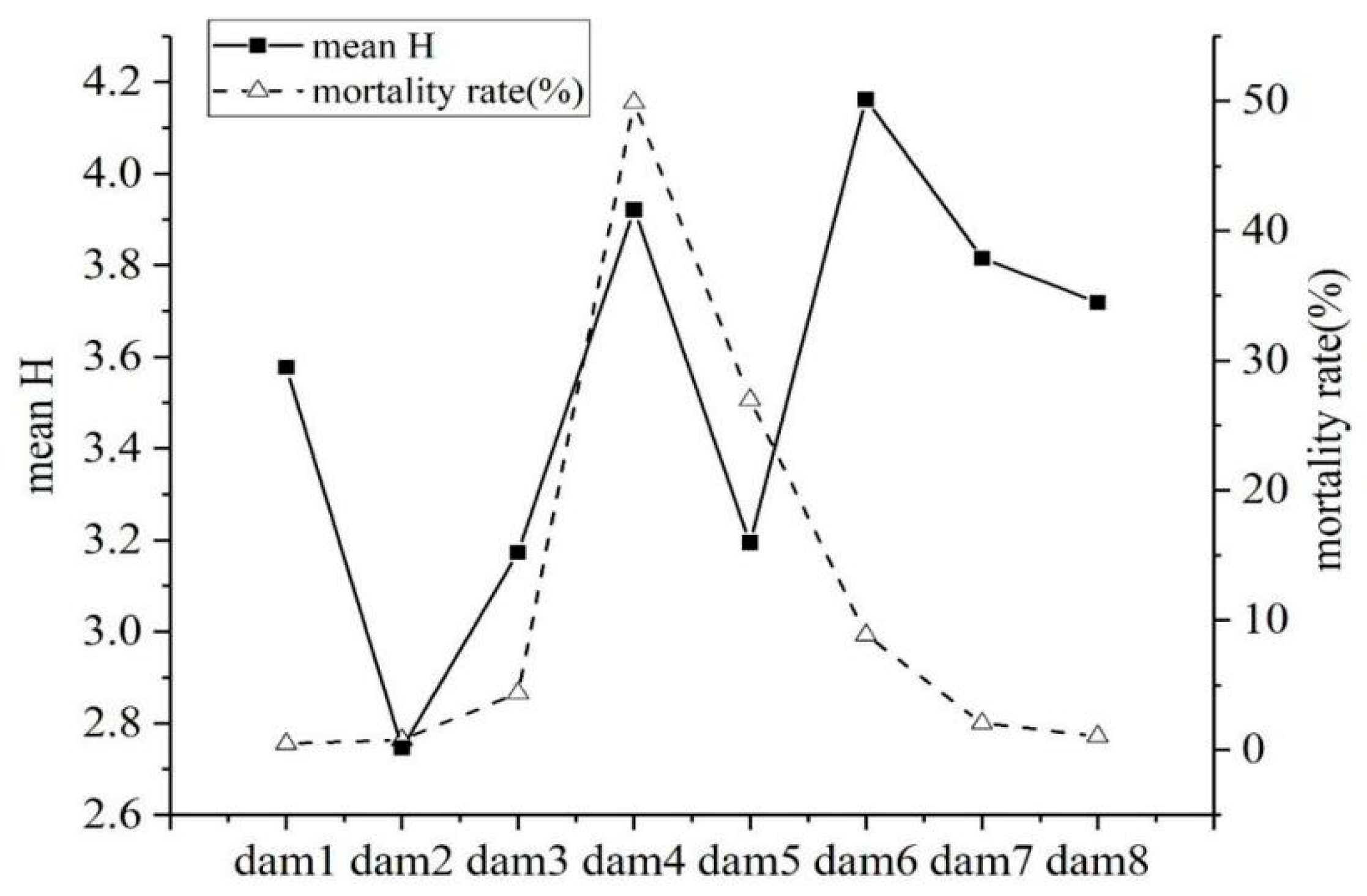
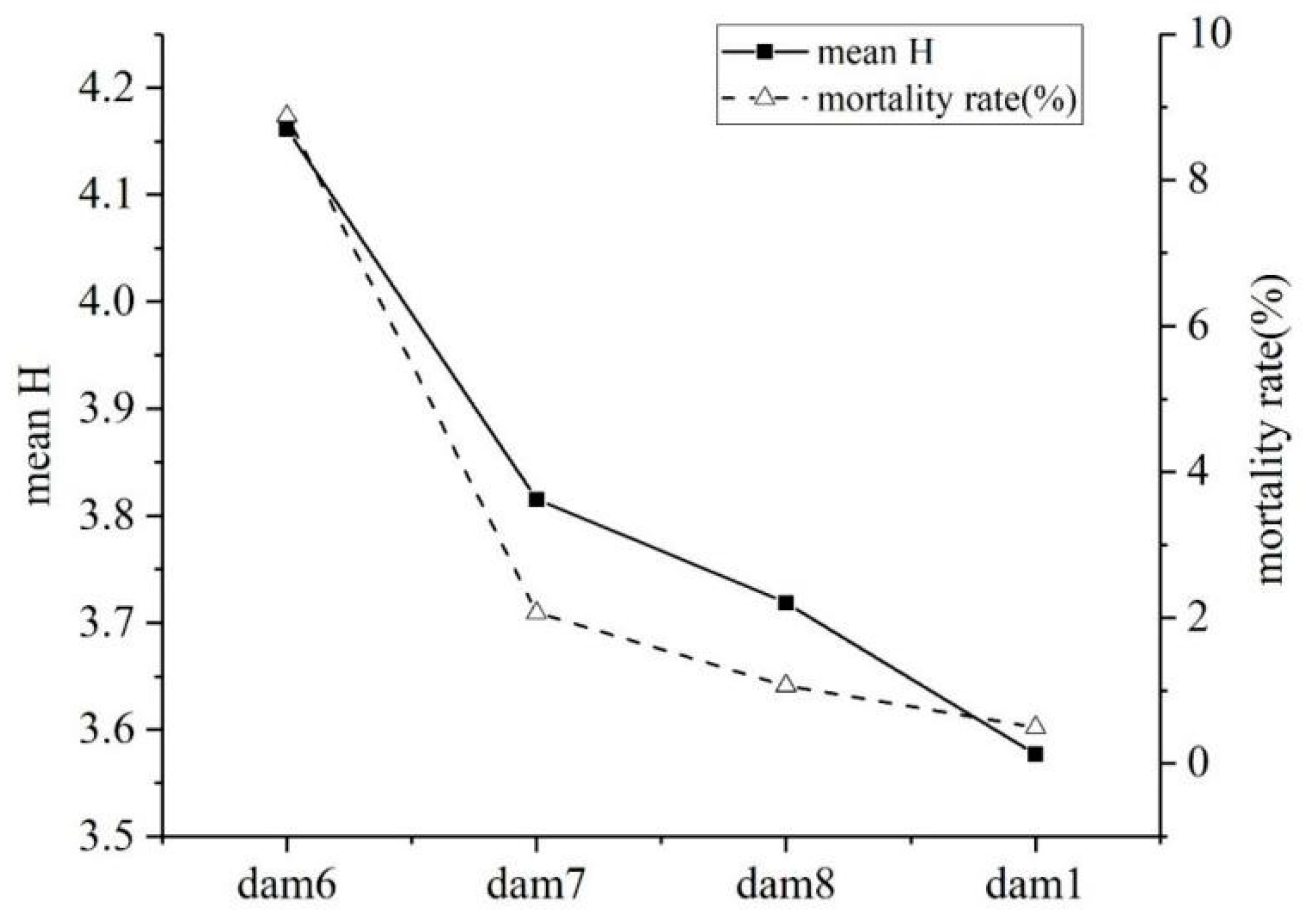
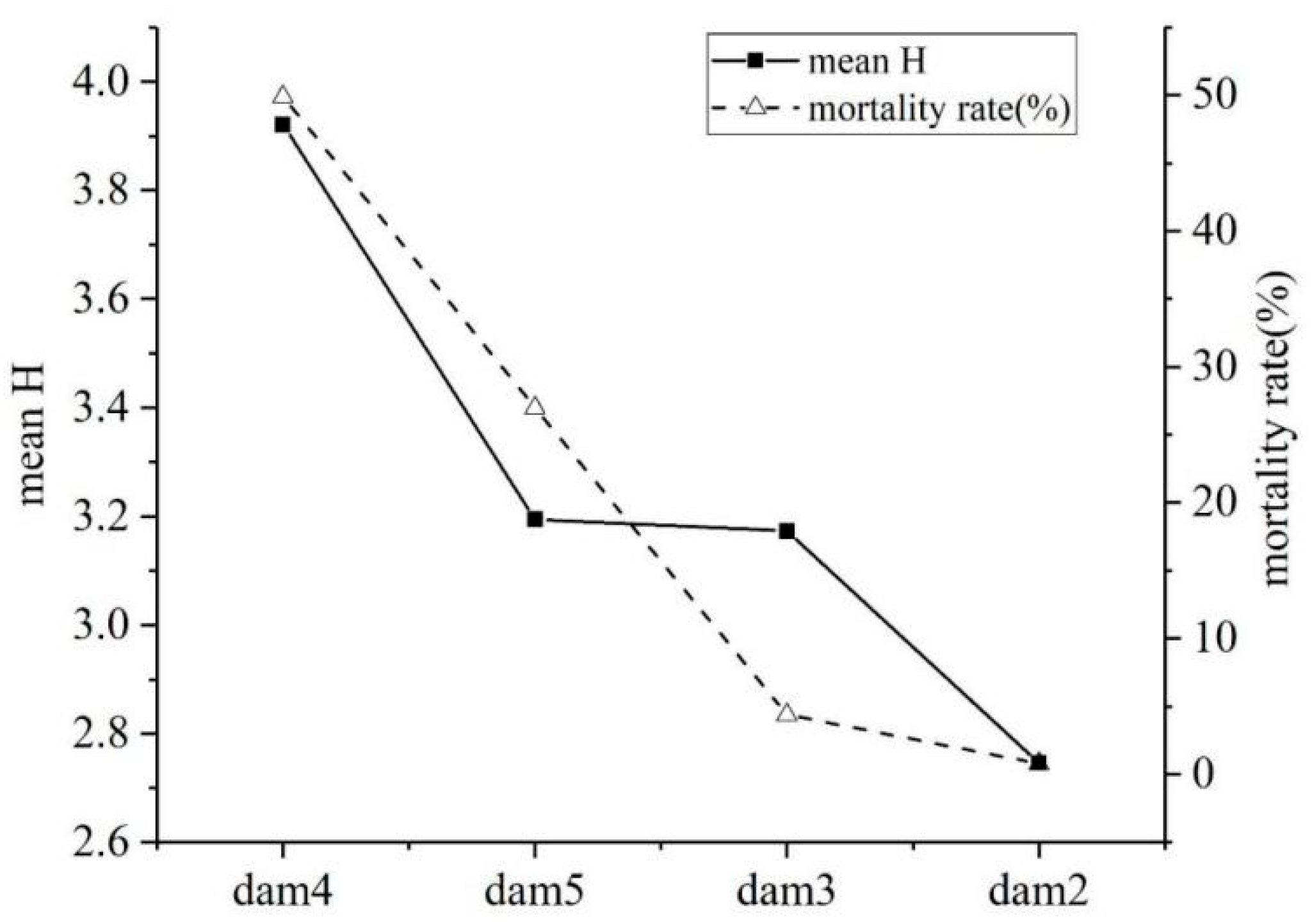
4.2. Results Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ge, W.; Li, Z.; Liang, R.Y.; Li, W.; Cai, Y. Methodology for Establishing Risk Criteria for Dams in Developing Countries, Case Study of China. Water Resour. Manag. 2017, 31, 4063–4074. [Google Scholar] [CrossRef]
- Matalas, N.C.; Jr, C.F.N. Ministry of Water Resources of the People’s Republic of China. First National Water Conservancy Survey Bulletin; China Water Resources and Hydropower Press: Beijing, China, 2013. [Google Scholar]
- Li, L.; Wang, R.; Sheng, J. Risk Assessment and Risk Management of Mycotoxins in Food; China Water Resources and Hydropower Press: Beijing, China, 2006. [Google Scholar]
- Fan, Q.; Tian, Z.; Wang, W. Study on risk assessment and early warning of flood-affected areas when a dam break occurs in a mountain river. Water 2018, 10, 1369. [Google Scholar] [CrossRef]
- Li, Z.; Ge, W.; Wang, J.; Li, W. Strategic consideration of dam safety management and risk management in China. Adv. Water Resour. 2015, 26, 589–595. [Google Scholar] [CrossRef]
- Álvarez, M.; Puertas, J.; Peña, E.; Bermúdez, M. Two-dimensional dam-break flood analysis in data-scarce regions: The case study of Chipembe dam, Mozambique. Water 2017, 9, 432. [Google Scholar] [CrossRef]
- Brown, C.A.; Graham, W.J. Assessing the threat to life from dam failure. J. Am. Water Resour. Assoc. 1988, 24, 1303–1309. [Google Scholar] [CrossRef]
- Reiter, P. Loss of Life Caused by Dam Failure: The RESCDAM LOL Method and Its Application to Kyrkosjarvi Dam in Seinajoki; Final Report of PR Water Consulting Ltd.: Helsinki, Finland, 2001. [Google Scholar]
- Assaf, H.; Hartford, D. A virtual reality approach to public protection and emergency preparedness planning in dam safety analysis. Proceedings of Canadian Dam Association, Victoria, BC, Canada, October 2002. [Google Scholar]
- Aboelata, M.; Bowles, D.S.; McClelland, D.M. A model for estimating dam failure life loss. In Proceedings of the Australian Committee on Large Dams Risk Workshop, Launceston, Tasmania, Australia, October 2003. [Google Scholar]
- Dekay, M.L.; Mcclelland, G.H. Predicting loss of life in cases of dam failure and flash flood. Insur. Math Econ. 1993, 13, 193–205. [Google Scholar] [CrossRef]
- Lee, J.S. Uncertainties in the predicted number of life loss due to the dam breach floods. KSCE J. Civ. Eng. 2003, 7, 81–91. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Godfroy, M.; Sebastian, A.; Kolen, B. Brief communication: Post-event analysis of loss of life due to hurricane Harvey. Nat. Hazards 2018, 18, 1073–1078. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Vrijling, J.K.; Vrouwenvelder, A.C.W.M. Methods for the estimation of loss of life due to floods: a literature review and a proposal for a new method. Nat. Hazards 2008, 46, 353–389. [Google Scholar] [CrossRef]
- Li, L.; Zhou, K. Research Status of Life Loss Estimation Methods Caused by Dam Breakdown. Adv. Water Resour. 2006, 26, 76–80. [Google Scholar]
- Sun, Y.; Zhong, D.; Mingchao, L.I.; Ying, L.I. Theory and Application of Loss of Life Risk Analysis for Dam Break. J. Tianjin Univ., Sci. Technol. 2010, 16, 383–387. [Google Scholar] [CrossRef]
- Peng, M.; Zhang, L.M. Analysis of human risks due to dam-break floods—part 1: A new model based on Bayesian networks. Nat. Hazards 2012, 64, 903–933. [Google Scholar] [CrossRef]
- Peng, M.; Zhang, L.M. Analysis of human risks due to dam break floods—part 2: Application to Tangjiashan landslide dam failure. Nat. Hazards 2012, 64, 1899–1923. [Google Scholar] [CrossRef]
- Wu, M.; Ge, W.; Li, Z.; Wu, Z.; Zhang, H.; Li, J.; Pan, Y. Improved Set Pair Analysis and Its Application to Environmental Impact Evaluation of Dam Break. Water 2019, 11, 82. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Ge, W. Weight analysis of influencing factors of dam break risk consequences. Nat. Hazard Earth Syst. 2018, 18, 3355–3362. [Google Scholar] [CrossRef]
- Gu, S.; Zheng, X.; Ren, L.; Xie, H.; Huang, Y.; Wei, J.; Shao, S. SWE-SPHysics simulation of dam break flows at South-Gate Gorges Reservoir. Water 2017, 9, 387. [Google Scholar] [CrossRef]
- Ragas, A.M.; Huijbregts, M.A.; Henning De Jong, I.; Leuven, R.S. Uncertainty in environmental risk assessment: implications for risk-based management of river basins. Integr. Environ. Asses. 2010, 5, 27–37. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Wang, X.L.; Sun, R.R.; Ao, X.F.; Sun, X.P.; Song, M.R. Study of the comprehensive risk analysis of dam-break flooding based on the numerical simulation of flood routing. Part II: Model application and results. Nat. Hazards 2014, 72, 675–700. [Google Scholar] [CrossRef]
- Latrubesse, E.M.; Arima, E.Y.; Dunne, T.; Park, E.; Baker, V.R.; D’Horta, F.M.; Wight, C.; Wittmann, F.; Zuanon, J.; Baker, P.A. Damming the rivers of the Amazon basin. Nature 2017, 546, 363–369. [Google Scholar] [CrossRef]
- Dutta, D.; Herath, S.; Musiake, K. A mathematical model for flood loss estimation. J. Hydrol. 2003, 277, 24–49. [Google Scholar] [CrossRef]
- Zhou, K. Research on Analysis Method of Life Loss of Dam Failure; Nanjing Hydraulic Research Institute: Nanjing, China, 2006. [Google Scholar]
- Huang, D.; Yu, Z.; Li, Y.; Han, D.; Zhao, L.; Chu, Q. Calculation method and application of loss of life caused by dam break in China. Nat. Hazards 2017, 85, 39–57. [Google Scholar] [CrossRef]
- Chen, S.Y.; Xue, Z.C.; Li, M.; Zhu, X.P. Variable sets method for urban flood vulnerability assessment. Sci. China 2013, 56, 3129–3136. [Google Scholar] [CrossRef]
- Chen, S.Y.; Xue, Z.C.; Min, L.I. Variable Sets principle and method for flood classification. Sci. China Technol. Sci. 2013, 56, 2343–2348. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Ge, W.; Xu, H. Dam Breach Environmental Impact Evaluation Based on Set Pair Analysis-Variable Fuzzy Set Coupling Model. J. Tianjin U. (Sci. Technol.) 2019, 3, 269–276. [Google Scholar]
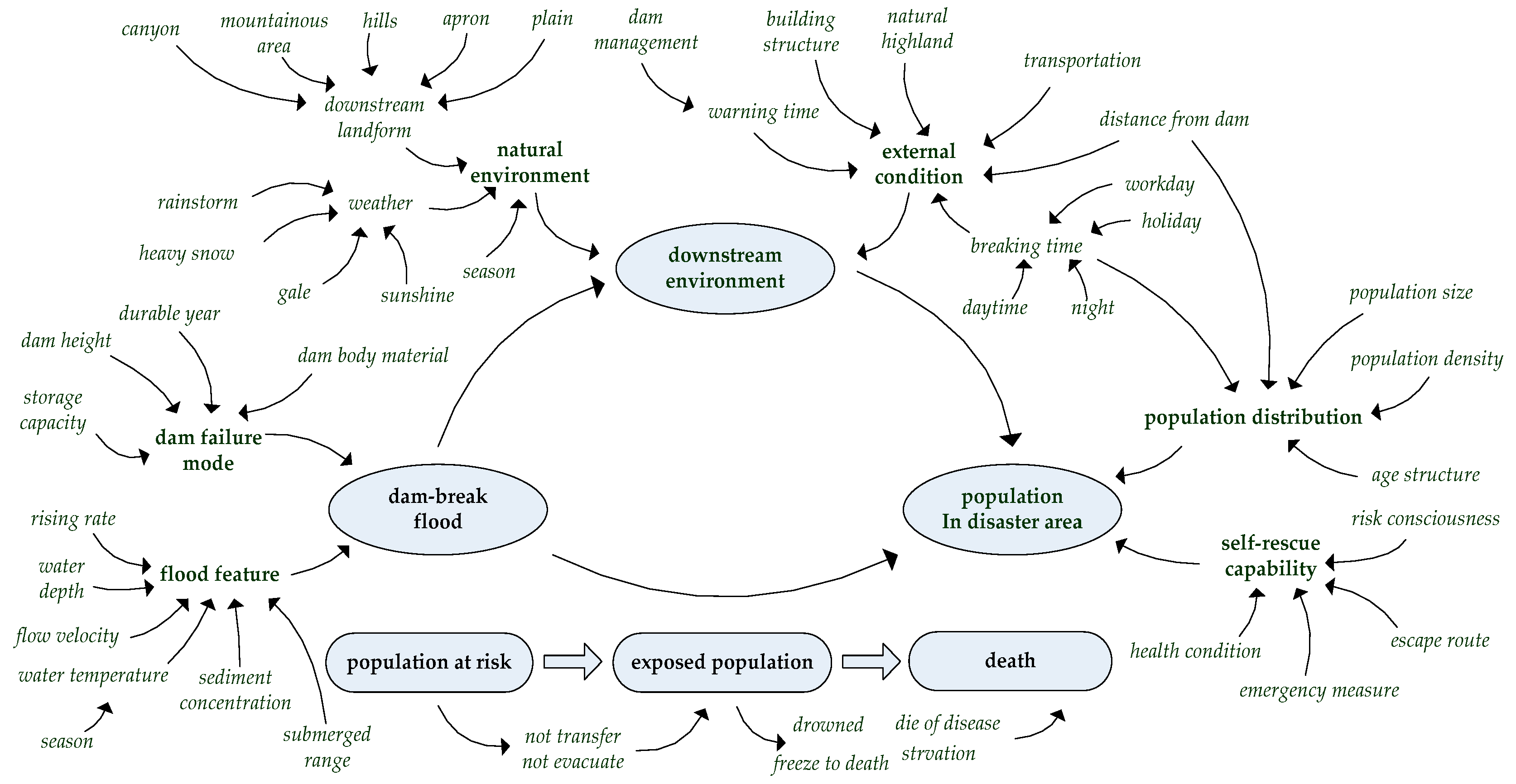
| Categories | Indicators | Indicator Meaning | Selecting Reason |
|---|---|---|---|
| Hazards indicators X1 | X11 | Dam height HD/(m) | Dam height and reservoir capacity often determine the severity of the flood, affecting the downstream submerged range and duration. With increasing flood intensity, the flexibility and stability of human bodies in the water get worse. |
| X12 | Dam capacity CR/(105 m3) | ||
| X13 | Flood intensity SF/(m2/s) | ||
| Exposure indicators X2 | X21 | Distance from dam LD/(km) | The farther away from the dam location, the less the population is affected. The prompt warning will win time for the downstream evacuation, and the breaking time affects the prompt warning capability and the dynamic distribution of the downstream population. |
| X22 | Time of warning TW/(h) | ||
| X23 | Time of breaking TB | ||
| Vulnerability indicators X3 | X31 | Population at risk PR/(person) | The more the population at risk is, the greater the threat of life loss in the region is. The more serious the understanding of the severity of the flood, the higher the probability of escape. Self-rescue capability refers to the escape conditions and methods that may be taken when the dam breaks, expressed as the success rate of the rescue. |
| X32 | Understanding level of flood severity UB | ||
| X33 | Self-rescue capability RC/(%) |
| Categories | Indicators | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| Slight | General | Medium | Serious | Extremely Serious | ||
| Hazards indicator X1 | HD (X11) | 0–10 | 10–30 | 30–70 | 70–100 | >100 |
| CR (X12) | 1–10 | 10–102 | 102–103 | 103–104 | >104 | |
| SF (X13) | 0–0.5 | 0.5–4.6 | 4.6–12.0 | 12.0–15.0 | >15.0 | |
| Exposure indicator X2 | LD (X21) | >50 | 50–20 | 20–10 | 10–5 | 5–0 |
| TW (X22) | >1 | 1–0.75 | 0.75–0.5 | 0.5–0.25 | 0.25–0 | |
| TB (X23) | daytime | weeknight | holiday night | early morning on workday | early morning on holiday | |
| Vulnerability indicator X3 | PR (X31) | 1–102 | 102–103 | 103–104 | 104–105 | >105 |
| UB (X32) | very clear | clear | common | unclear | very unclear | |
| RC (X33) | 100–80 | 80–60 | 60–40 | 40–20 | 20–0 |
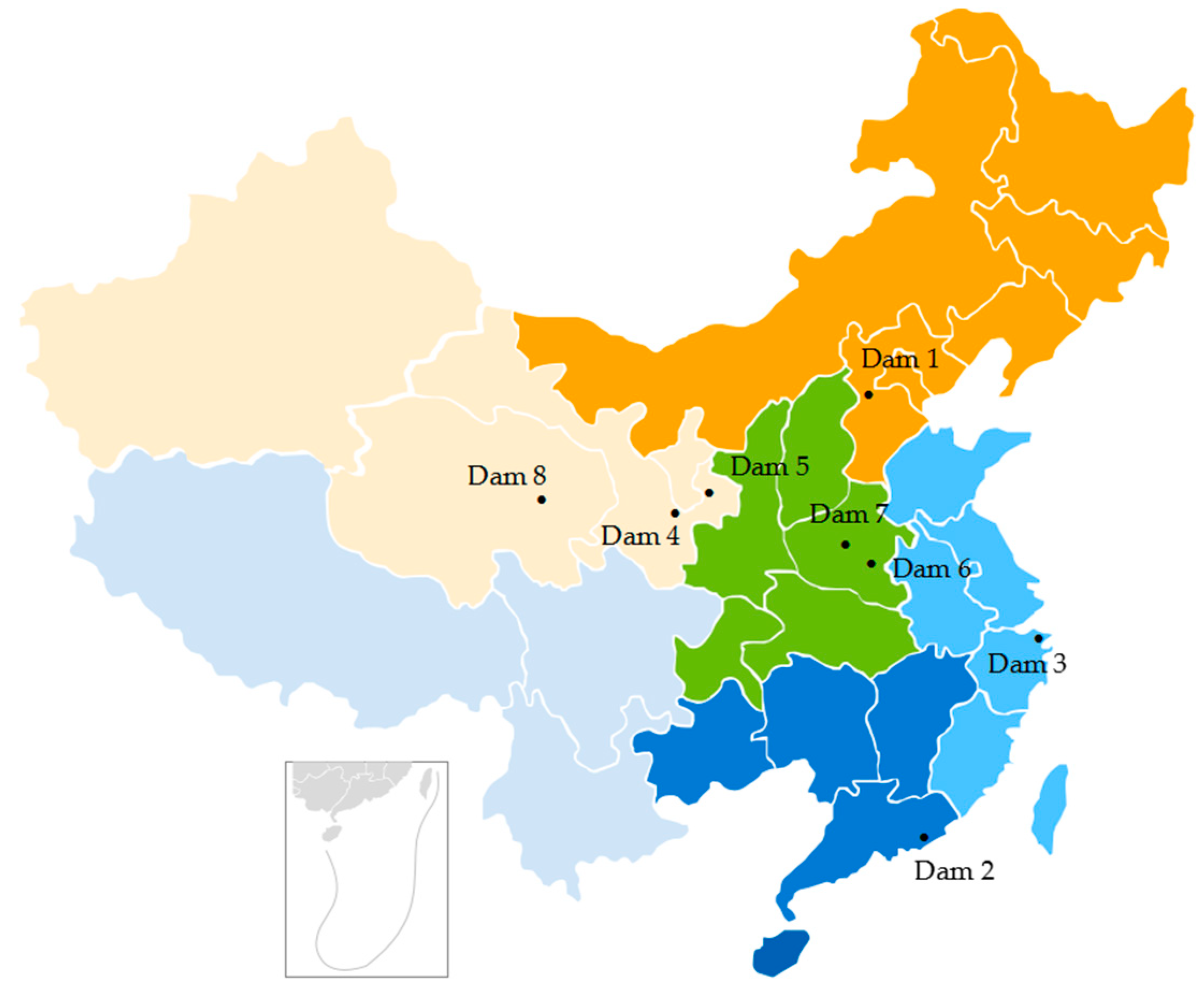
| No. | Dam Break Samples | Province | Date | Dam Type | Dam Height/m | Capacity/105 m3 | Dam Break Time | Population at Risk |
|---|---|---|---|---|---|---|---|---|
| 1 | Liujiatai | Hebei | 1963-08-08 | Clay core dam | 35.9 | 405.4 | 03:55 | 11,929 |
| 2 | Hengjiang | Guangdong | 1970-09-15 | Homogeneous earth dam | 48.4 | 787.9 | 08:00 | 2500 |
| 3 | Dongkoumiao | Zhejiang | 1971-06-02 | Homogeneous earth dam | 21.5 | 25.5 | 05:50 | 3500 |
| 4 | Lijiatsui | Gansu | 1973-04-29 | Homogeneous earth dam | 25.0 | 11.4 | 23:30 | 1034 |
| 5 | Shijiagou | Gansu | 1973-08-25 | Homogeneous earth dam | 28.6 | 8.6 | 05:30 | 300 |
| 6 | Banqiao | Henan | 1975-08-08 | Clay heart wall dam | 24.5 | 4920.0 | 01:00 | 180,000 |
| 7 | Shimantan | Henan | 1975-08-08 | Homogeneous earth dam | 25.0 | 918.0 | 00:00 | 72,422 |
| 8 | Gouhou | Qinghai | 1993-08-27 | Concrete face dam | 71.0 | 33.0 | 22:00 | 30,000 |
| Indicator | X11 | X12 | X13 | X21 | X22 | X23 | X31 | X32 | X33 |
|---|---|---|---|---|---|---|---|---|---|
| Weights | 0.0135 | 0.0225 | 0.2282 | 0.0219 | 0.1722 | 0.0442 | 0.3210 | 0.0424 | 0.1341 |
| No. | Dam Break Samples | Level Eigenvalue H | Loss of Life (people) | Mortality Rate (%) | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | Liujiatai | 3.5850 | 3.6129 | 3.4846 | 3.6250 | 3.5769 | 60 | 0.50 |
| 2 | Hengjiang | 2.8345 | 3.0475 | 2.4262 | 2.6770 | 2.7463 | 20 | 0.80 |
| 3 | Dongkoumiao | 3.2366 | 3.2944 | 3.0324 | 3.1283 | 3.1729 | 154 | 4.40 |
| 4 | Lijiatsui | 3.8492 | 3.5430 | 4.4748 | 3.8165 | 3.9209 | 516 | 49.90 |
| 5 | Shijiagou | 3.3062 | 3.2151 | 3.3087 | 2.9489 | 3.1947 | 81 | 27.00 |
| 6 | Banqiao | 4.0103 | 3.9112 | 4.4435 | 4.2807 | 4.1614 | 15982 | 8.88 |
| 7 | Shimantan | 3.7725 | 3.6617 | 4.0104 | 3.8170 | 3.8154 | 1500 | 2.07 |
| 8 | Gouhou | 3.6652 | 3.6091 | 3.8517 | 3.7486 | 3.7186 | 320 | 1.07 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Li, Z.; Ge, W.; Wu, S. Risk Evaluation Model of Life Loss Caused by Dam-Break Flood and Its Application. Water 2019, 11, 1359. https://doi.org/10.3390/w11071359
Li W, Li Z, Ge W, Wu S. Risk Evaluation Model of Life Loss Caused by Dam-Break Flood and Its Application. Water. 2019; 11(7):1359. https://doi.org/10.3390/w11071359
Chicago/Turabian StyleLi, Wei, Zongkun Li, Wei Ge, and Sai Wu. 2019. "Risk Evaluation Model of Life Loss Caused by Dam-Break Flood and Its Application" Water 11, no. 7: 1359. https://doi.org/10.3390/w11071359
APA StyleLi, W., Li, Z., Ge, W., & Wu, S. (2019). Risk Evaluation Model of Life Loss Caused by Dam-Break Flood and Its Application. Water, 11(7), 1359. https://doi.org/10.3390/w11071359





